2. 天津大学 建筑工程学院,天津 300350
2. School of Civil Engineering, Tianjin University, Tianjin 300350, China
北极冰区主要是北冰洋及其沿岸,其重要的经济和战略价值不可估量。贯穿其中的北极航线可以为我国国际海运降低巨大的成本,未来全球航运、国际贸易和能源供应等形式及规则都可能因北极而改写。冰区航行船舶不同于破冰船,并不具备强大的破冰条件,因此应尽量保持在冰区航道或薄冰覆盖海域,并做好频繁改变航向规避风险的准备,这对船舶的操纵性产生了较高的要求。
国内外专家学者对船舶极地航行进行了大量的研究。李凡[1]基于MMG分离模型思想,建立了船舶三自由度的平面运动数学模型并模拟出了船舶的回转运动;同时基于PMM试验的研究方法,模拟并分析了船舶纯横荡、纯首摇2种船舶操纵运动形式。Tue-Fee K等[2]基于船身两侧所受横向冰载荷不对称等一系列假设,建立了一种半经验模型并推导出冰船接触产生的横向作用力和首摇力矩,提出了船舶横荡和首摇两自由度的操纵性运动方程。秦尧等[3]研究了北极航道影响船舶操纵性的因素,总结了船舶操纵性的表征指标以及提高措施。师超等[4]基于ITTC推荐的操纵性自航模试验不确定度分析导则,采用ISO-GUM方法构建了操纵性自航模试验不确定度分析方法。在海冰性质和冰船作用规律方面,童波等[5]基于Voronoi图,开展了对不规则几何形状的浮冰的参数化建模,开展了浮冰尺度概率分布的优化研究,得出了浮冰阻力平均值随浮冰平均尺度增大呈负指数幂函数减小趋势的结论。Seong-Rak等[6]基于方形浮冰的冰池试验,分析了浮冰尺寸与冰阻力的关系,提出一种快速计算冰密集度的方法。黄焱等[7]进行了不同速度下冰排和柔性直立结构相互作用的冰激振试验,研究了引发冰激振现象的原因。郭春雨等[8]计算出60%、80%和90%碎冰密集度下4个速度点的冰船相互作用力数值。Lindstrom等[9]基于弹性地基弹性板的动力方程,通过数值计算得到了冰船相互作用近似解,构建了模拟船舶极地冰区航行操纵运动体系。南明宇等[10]利用内外动力学耦合原理首次求解出冰船碰撞过程中的恢复系数。随着计算机技术的不断发展,数值模拟仿真成为专家学者探索冰区航行操纵性等问题的又一研究方向。齐江辉等[11]运用欧拉多相流结合离散元多相相互作用模型,进行了船舶碎冰区航行数值模拟。Moon-Chan Kim等[12]以一艘冰区货船模型为例,进行了统一碎冰尺寸下60%、80%和90%三种碎冰密集度、0.1、0.3和0.6 m/s三个速度点的碎冰阻力模拟。国威等[13]针对典型的极地冰区航行船舶,采用了CFD和DEM相结合的数值模拟方法,建立了流体和碎冰间浮力和拖曳力模型,研究了航速和碎冰厚度对船体所受冰载荷的影响规律。这些研究大多数集中在船冰荷载性能方面,对于在浮冰海域船舶的操纵性能研究则相对较少。
1 极地航行船舶回转操纵性理论分析对于浮冰区航行船舶的回转运动,将多点同时作用的冰载荷等效为作用于船舶某一点的集中力和力矩。将固定于船上的随船动坐标系中沿ox轴方向的匀速直线运动设置为初始状态,用Fcx和Fcy分别表示船舶受到的冰载荷力沿ox、oy轴正向的分量,Nc表示由冰载荷集中力对O点的力矩。可得到线性化的偏离匀速直线运动的扰动运动方程:
| $ { \begin{aligned}\left\{ \begin{array}{l} \left({m\text-}{{X}}_{\dot{{u}}}\right)\dot{{u}}\text-{{X}}_{{u}}\text{Δ}{u}\text={{F}}_{{cx}},\\ \left({m\text-}{{Y}}_{\dot{{v}}}\right)\dot{{v}}\text-{{Y}}_{{v}}{v}\text+\left({m}{{x}}_{{G}}\text-{{Y}}_{\dot{{r}}}\right)\dot{{r}}\text+\left({m}{{u}}_{\text{1}}\text-{{Y}}_{{r}}\right){r}\text={{Y}}_{{\delta}}{\delta}\text+{{F}}_{{cy}},\\ \left({m}{{x}}_{{G}}\text-{{N}}_{\dot{{v}}}\right)\dot{{v}}\text-{{N}}_{{v}}{v}\text+\left({{I}}_{{z}}\text-{{N}}_{\dot{{r}}}\right)\dot{{r}}\text+\left({m}{{x}}_{{G}}{{u}}_{\text{1}}\text-{{N}}_{{r}}\right){r}\text={{N}}_{{\delta}}{\delta}\text+{{N}}_{{c}}。\end{array}\right.\end{aligned}} $ | (1) |
式中:
1)转舵阶段。自开始转舵起至舵角达到预定值δc为止。
在第1阶段中,舵的转动产生由舵角引起的侧向力和力矩,在线性简化下,可以用下式描述转舵阶段船舶的运动:
| $ \begin{array}{c}\left\{\begin{array}{c}\left({m}\text-{{Y}}_{\dot{{v}}}\right)\dot{{v}}\text+\left({m}{{x}}_{{G}}\text-{{Y}}_{\dot{{r}}}\right)\dot{{r}}\text={{Y}}_{{\delta}}{\delta},\\ \left({m}{{x}}_{{G}}\text-{{N}}_{\dot{{v}}}\right)\dot{{v}}\text+\left({{I}}_{{z}}\text-{{N}}_{\dot{{r}}}\right)\dot{{r}}\text={{N}}_{{\delta}}{\delta},\end{array}\text{}\left({\delta}\leqslant{{\delta}}_{{c}}\right)\right.。\end{array} $ | (2) |
2)过渡阶段。从转舵阶段结束到船舶开始定常回转运动。
过渡阶段(见图1)中,各变量不断变化,舵角为常数δ=δc。作用于船舶的各种力和力矩使得船首部出现回转,船舶运动轨迹为向心运动。
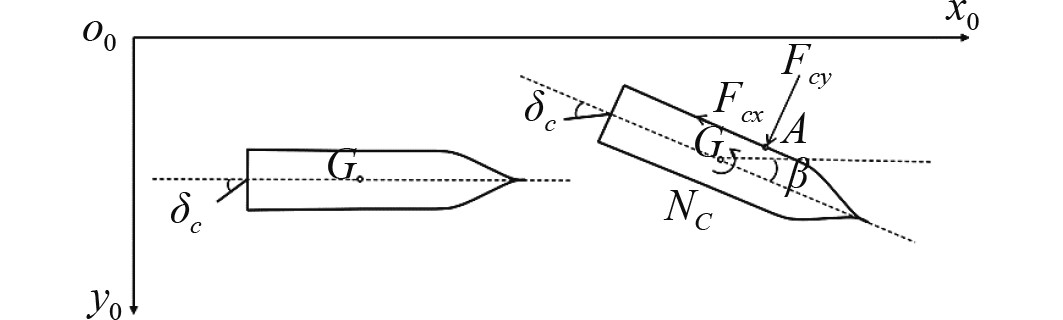
|
图 1 过渡阶段起始状态示意图 Fig. 1 Schematic diagram of the initial state of the transition phase |
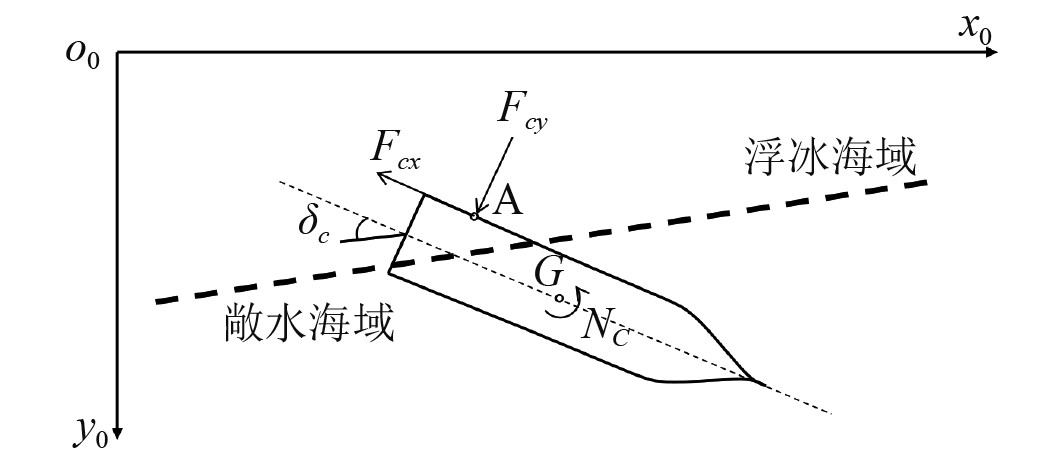
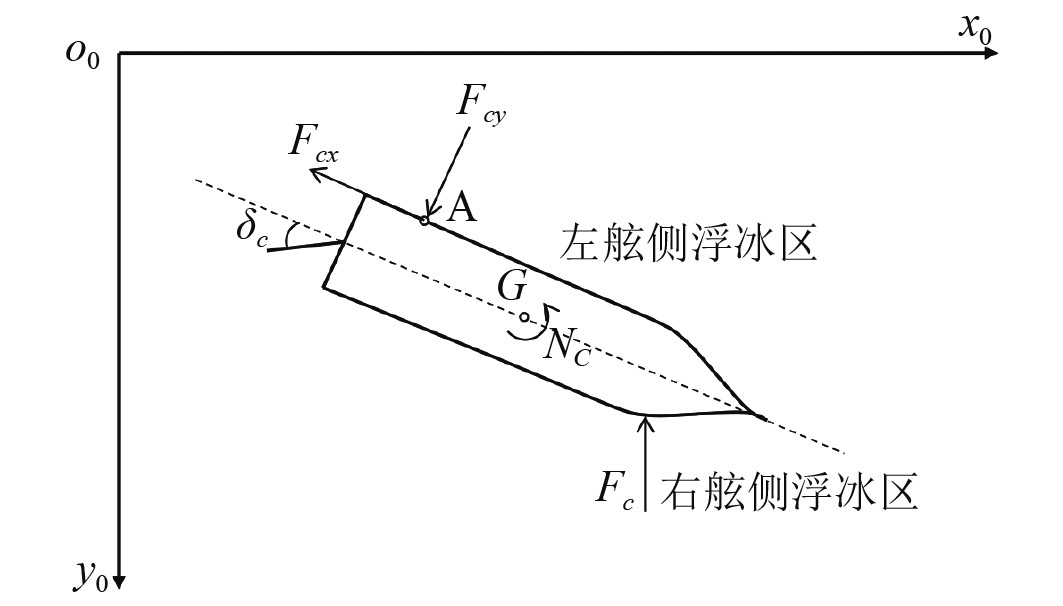
浮冰区冰的分布情况很复杂,船舶回转运动航行过程中与冰的接触形式不尽相同,可简化为3种场景,如图2~图4所示。

|
图 2 场景一−冰船首部接触 Fig. 2 Scenario 1−ice ship bow contact |
|
图 3 场景二−冰船尾部接触 Fig. 3 Scenario 2−ice ship tail contact |
|
图 4 场景三−冰船首尾接触 Fig. 4 Scenario 3−ice ship head and tail contact |
在线性简化下,回转运动方程:
| $ \left(m - Y_{\dot{v}}\right)\dot{v} - Y_vv + \left(mx_G - Y_{\dot{r}}\right)\dot{r} + \left(mu_1 - Y_r\right)r = Y_{\delta}{\delta }_c + F_cy,$ | (3) |
| $\left(mx_G - N_{\dot{v}}\right)\dot{v} - N_v v + \left(I_z - N_{\dot{r}}\right) \dot{r} + \left(mx_G u_1 - N_r\right)r = N_{\delta }{\delta }_c + N_c。$ | (4) |
3)近似稳定回转阶段。经过转舵阶段和过渡阶段之后,作用于冰区加强船舶上的各种力和力矩将达到近似平衡状态。主要是由于浮冰碰撞力的随机性,导致船舶的运动状态为以一定的侧向速度和回转角速度的相对匀速圆周运动。
平均回转直径:
| $ {{D}}_{{c}}=\displaystyle\frac{{2}{{u}}_{{1}}\left[{{N}}_{{v}}\left({m}{{u}}_{{1}}-{{Y}}_{{r}}\right)-{{Y}}_{{v}}\left({m}{{x}}_{{G}}{{u}}_{{1}}-{{N}}_{{r}}\right)\right]}{\left({{N}}_{{v}}{{Y}}_{{\delta}}-{{Y}}_{{v}}{{N}}_{{\delta}}\right){{\delta}}_{{c}}+{{N}}_{{v}}{{F}}_{{cy}}-{{Y}}_{{v}}{{N}}_{{c}}}。$ | (5) |
上述给出了回转不同阶段的船舶运动控制方程。但由于浮冰撞击具有较大的随机性,给出一个稳定的冰荷载有较大难度。因此,上述理论难以给出船舶实时的、准确的运动参数,只能做近似估算。为获得实时准确的船舶运动状态,本文开展了基于离散元方法的船舶回转运动仿真研究。
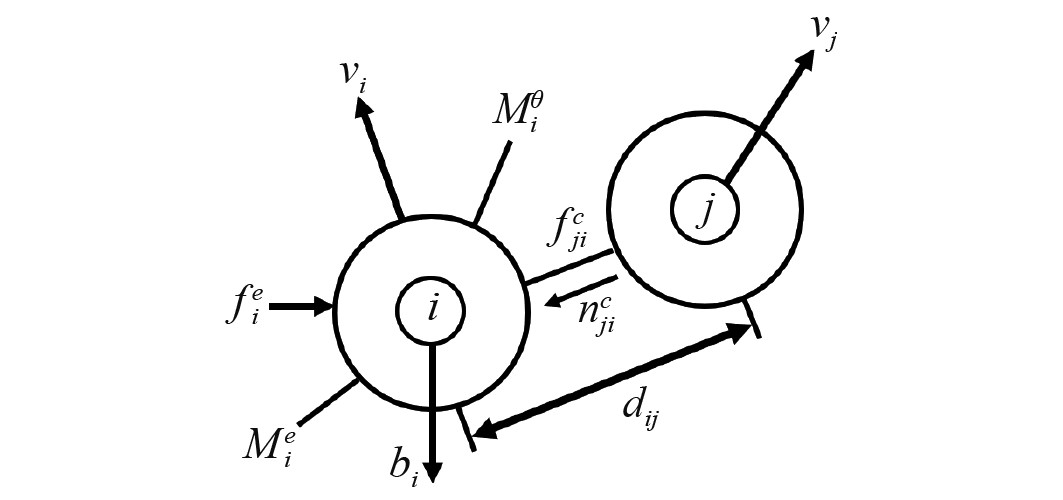
2 仿真计算的理论基础 2.1 离散元方法离散元方法(Discrete Element Method,DEM)的基本原理包括本构关系以及运动方程[14 - 15]。本构关系是指单元之间的接触模型,通过2个单元之间的相对位移求解接触力;运动方程即牛顿第二定律,用于求解单元受到外力而产生的加速度、速度与位移。每个离散相的单元个体自身的运动都必须满足运动方程。以2个球形单元i、j的接触为例,其受力如图5所示。
|
图 5 球形颗粒单元的接触 Fig. 5 Contact of spherical particle elements |
在每一个极短的时间步内,单元的运动均要满足以下运动方程:
| $ {m}_{i}\displaystyle\frac{{{\rm d}\mathit{v}}_{i}}{{\rm d}t}=\sum _{j=1}^{{n}_{c}}{\boldsymbol{F}}_{ji}^{c}+{\boldsymbol{F}}_{i}^{e}+{\boldsymbol{b}}_{i},$ | (6) |
| $ {I}_{i}\frac{{{\rm d}{\omega }}_{i}}{{\rm d}t}=\sum _{j=1}^{{n}_{c}} {\boldsymbol{F}}_{ji}^{cs}{r}_{ij}+{\boldsymbol{M}}_{i}^{\theta }+{\boldsymbol{M}}_{i}^{e}。$ | (7) |
式(6)为单元i在外力作用下应满足的平移运动的线性动量守恒方程。式中:
| $ \begin{array}{c}{\boldsymbol{F}}_{ji}^{c}={\boldsymbol{F}}_{ji}^{cn}+{\boldsymbol{F}}_{ji}^{cs}。\end{array} $ | (8) |
式中:
式(7)为单元i在外力矩的作用下应满足的旋转运动的角动量守恒方程。式中:
单元之间法向与切向接触力通过离散单元的相对位移求解。在单位时间步内,接触力和转动力矩的增量可由以下本构方程得到:
| $ \begin{aligned} &\Delta {F}_{ji}^{cn}=-{k}_{n}\Delta {u}_{ji}^{n}+{c}_{n}\Delta {\dot{u}}_{ji}^{n} ,\\ &\Delta {F}_{ji}^{cs}=-{k}_{s}\Delta {u}_{ji}^{s}+{c}_{s}\Delta {\dot{u}}_{ji}^{s},\\ &\Delta {M}_{i}^{\theta }=-{k}_{\theta }\Delta {\theta }_{i}+{c}_{\theta }\Delta {\dot{\theta }}_{i}。\end{aligned}$ | (9) |
式中:
离散元方法的接触力模型通常是弹簧-阻尼器模型。2个单元之间的接触力在接触点上可分解为法向力和切向力,并分别由一组弹簧-阻尼器模型进行表示,如图6所示。在弹簧-阻尼器模型中,弹簧考虑响应的弹性部分,产生弹性恢复力;阻尼器则考虑碰撞期间的能量耗散,产生粘性阻尼力。本文使用的Hertz-Mindlin接触模型是一种非线性弹簧-阻尼器接触模型[14]。

|
图 6 球形单元接触模型 Fig. 6 Contact model of spherical elements |
本文采用某型号极地航行船舶进行仿真研究,其设计主尺度如表1所示。
|
|
表 1 船舶设计主尺度 Tab.1 Main dimensions of ship design |
本例分别设置了远场域计算网格和近场域计算网格2套自动网格,采用全模重叠网格进行迭代计算,在保证网格加密和求解精度、保障标量场景可观察性的前提下,应尽可能减少迭代计算量。在船舶回转航行仿真中,相对敏感性较高的是船舶的横荡、首摇和横倾3个自由度,为此在图9中除船体表面壁面之外,再补充了中横剖面、中纵剖面、水线面以及螺旋桨截面,更直观的观察上述3个自由度的运动情况。计算中选用了虚拟将桨盘模型给船一个持续的向前的推进力,保证船体模型在自由水面静止的环境条件下拥有自航动力。仿真模拟中还需要构建散碎浮冰模型,在连续体中选择拉格朗日多项离散元模型(DEM),建立拉格朗日冰相,恒密度为916.72 kg/m³的复合固体离散元颗粒,由于实际散碎浮冰形状非常复杂,本文选取不规则棱柱体近似模拟单个浮冰块,颗粒直径采用对数正态分布形式,直径区间在1.2~2.3 m中间,平均值为1.8 m。最后,由于船体模型的航迹的不确定有许,在计算中没有采用一次性全场域覆盖加冰,而采用逐步加冰的方式进行浮冰区域铺设。
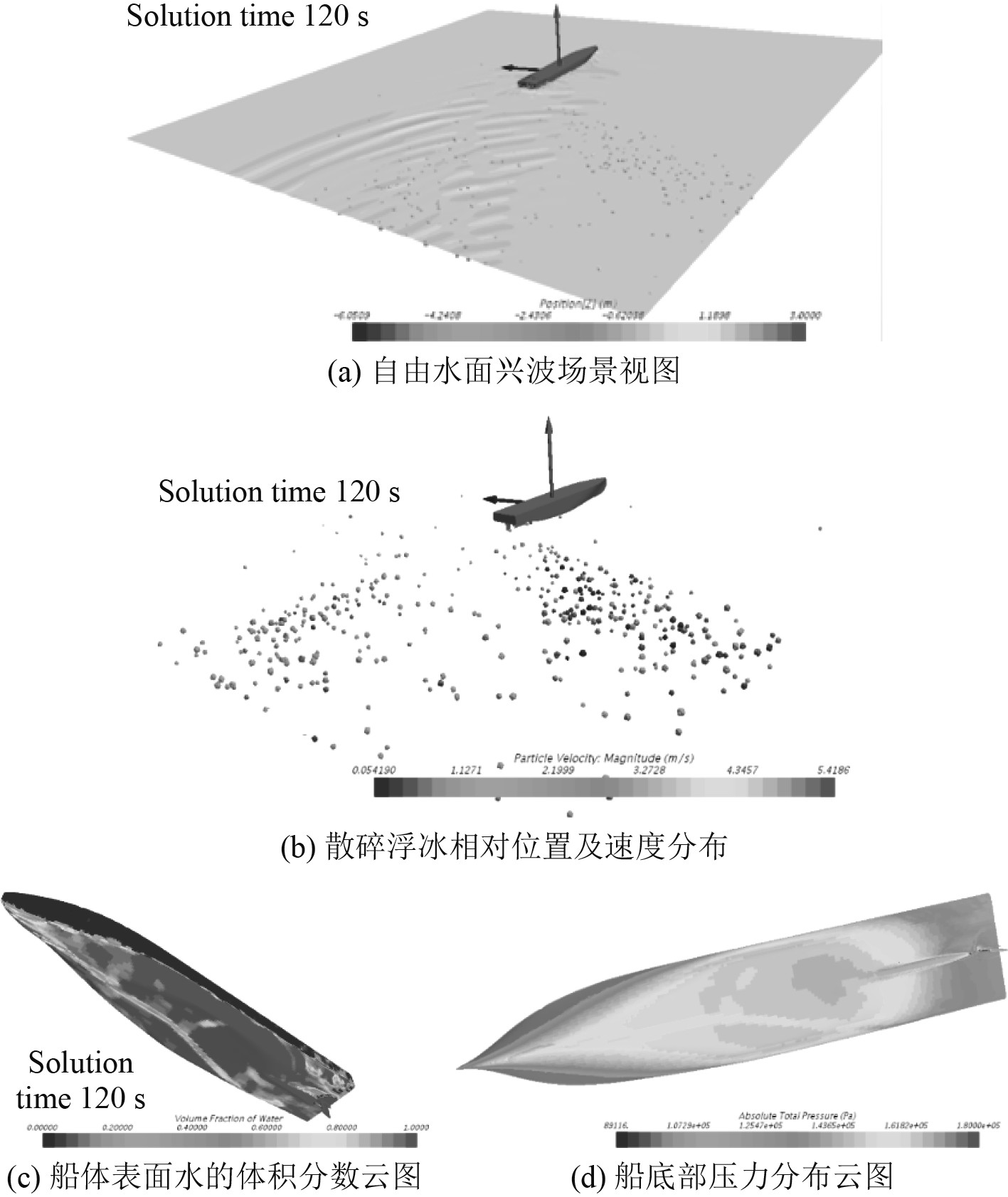
|
图 9 小舵角10°回转操纵下船体在浮冰海域的航行模型 Fig. 9 Navigation model of ship in floating ice sea with a rudder angle of 10 ° |
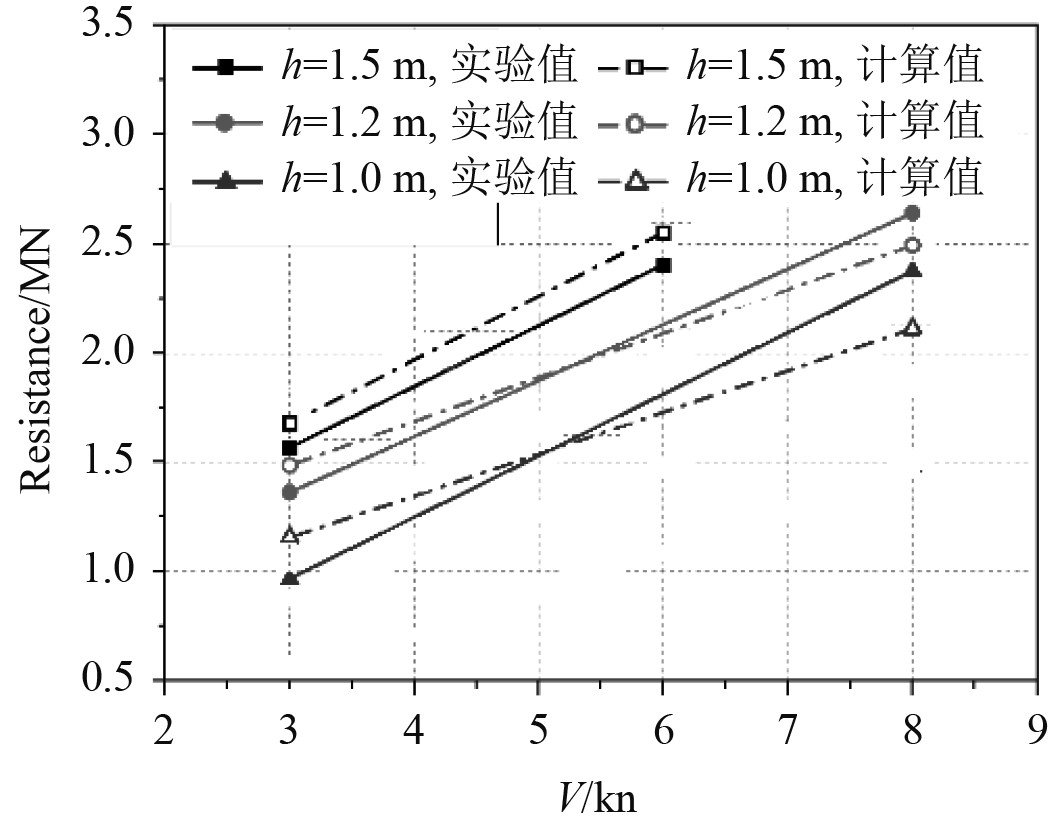
为保证模型的可靠性和计算的准确性。在进行回转航行仿真计算之前,首先对模型在直航状态下对应航速3~8 kn的冰阻力进行了模型实验,将实验结果和直航仿真结果进行了对比。模型试验的几何比尺为1:20(即λ=20),表2为实验的尺度比。实验结果和计算结果对比如图7所示。
|
|
表 2 实验尺度比 Tab.2 Experimental scale ratio |
|
图 7 模型试验及仿真计算对比 Fig. 7 Comparison of model tests and simulation calculations |
在85%~90%的冰覆盖率下,CPP 推进油船在冰厚1.5 m 的浮冰区以6 kn航速航行时的阻力为2.405 MN,在冰厚1.2 m 的浮冰区以8 kn 航速航行时的阻力为2.640 MN,在冰厚1.0 m 的浮冰区以8 kn 航速航行时的阻力为2.376 MN;从实验结果对比课件。本计算中建立的模型及其计算仿真结果和实验结果比较接近,误差率基本在10%以内,由于浮冰区冰荷载具有较大的随机性,因此误差率还较高,但基本可以保证进行回转计算仿真的要求
5 算例结果输出与分析 5.1 仿真模型的场景可视化输出1)直航操纵下船体穿行浮冰海域的接触模型如图8所示。

|
图 8 直航操纵下船体穿行浮冰海域的接触模型 Fig. 8 Contact model of ship passing through floating ice sea area under direct navigation control |
2)小舵角10°回转操纵下船体在浮冰海域的航行模型如图9所示。
3)常规舵角22.5°回转操纵下船体在浮冰海域的航行模型如图10所示。
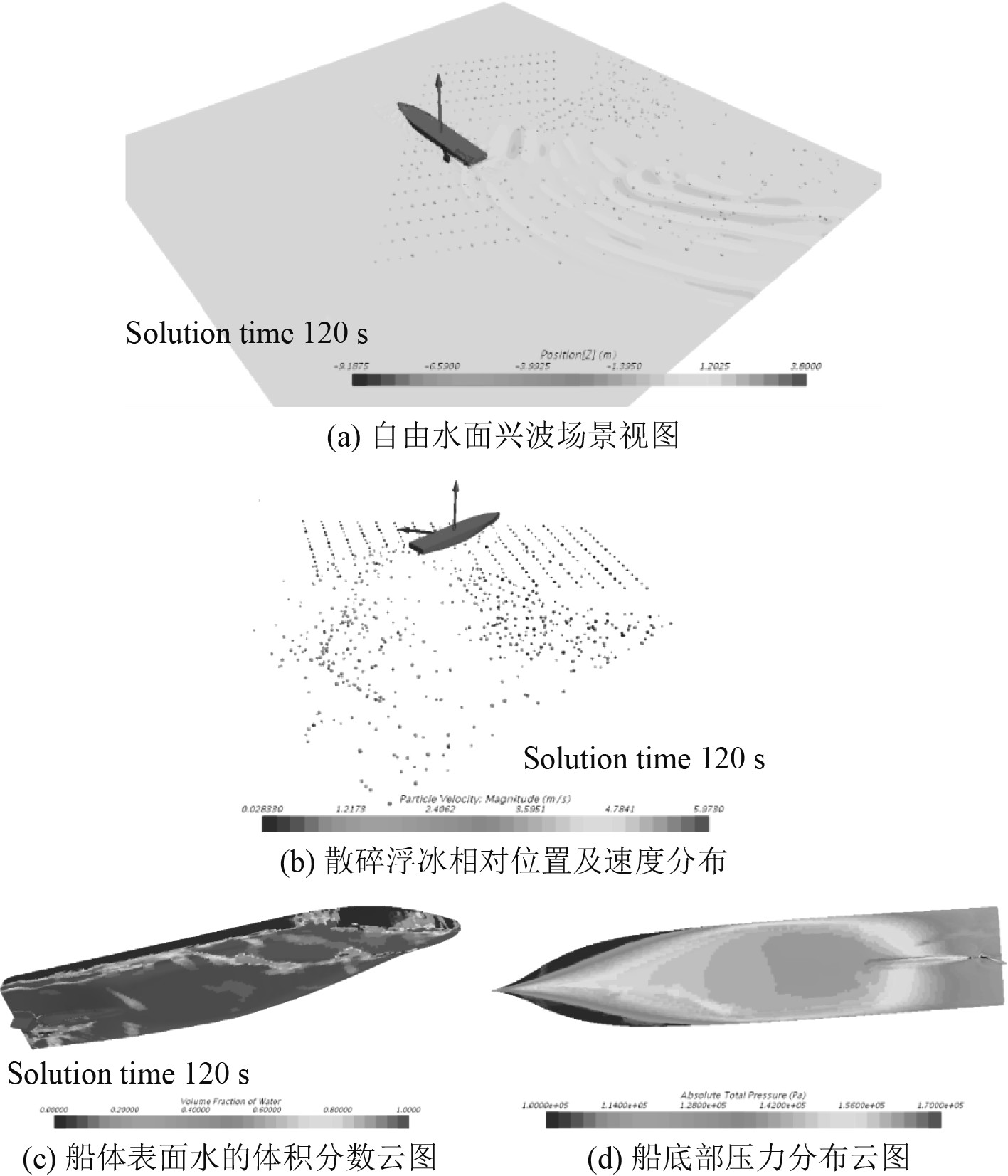
|
图 10 常规舵角22.5°回转操纵下船体在浮冰海域的航行模型 Fig. 10 Navigation model of ship in floating ice sea with a rudder angle of 22.5° |
4)大舵角30°回转操纵下船体在浮冰海域紧急回航模型如图11所示。
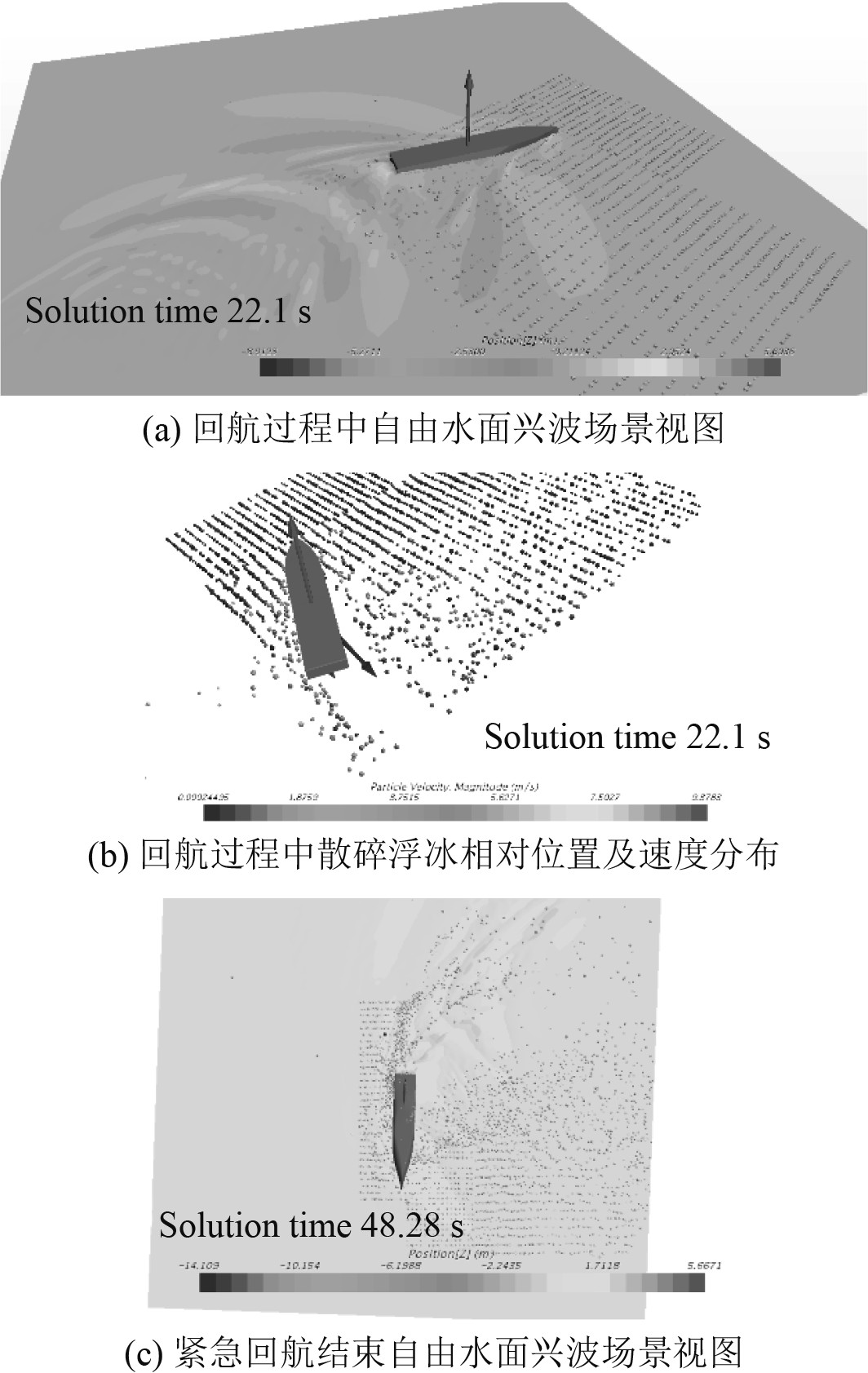
|
图 11 大舵角30°浮冰海域紧急回航模型 Fig. 11 Navigation model of ship in floating ice sea with a rudder angle of 30° |
1)船舶三自由度旋转角度曲线如图12所示。
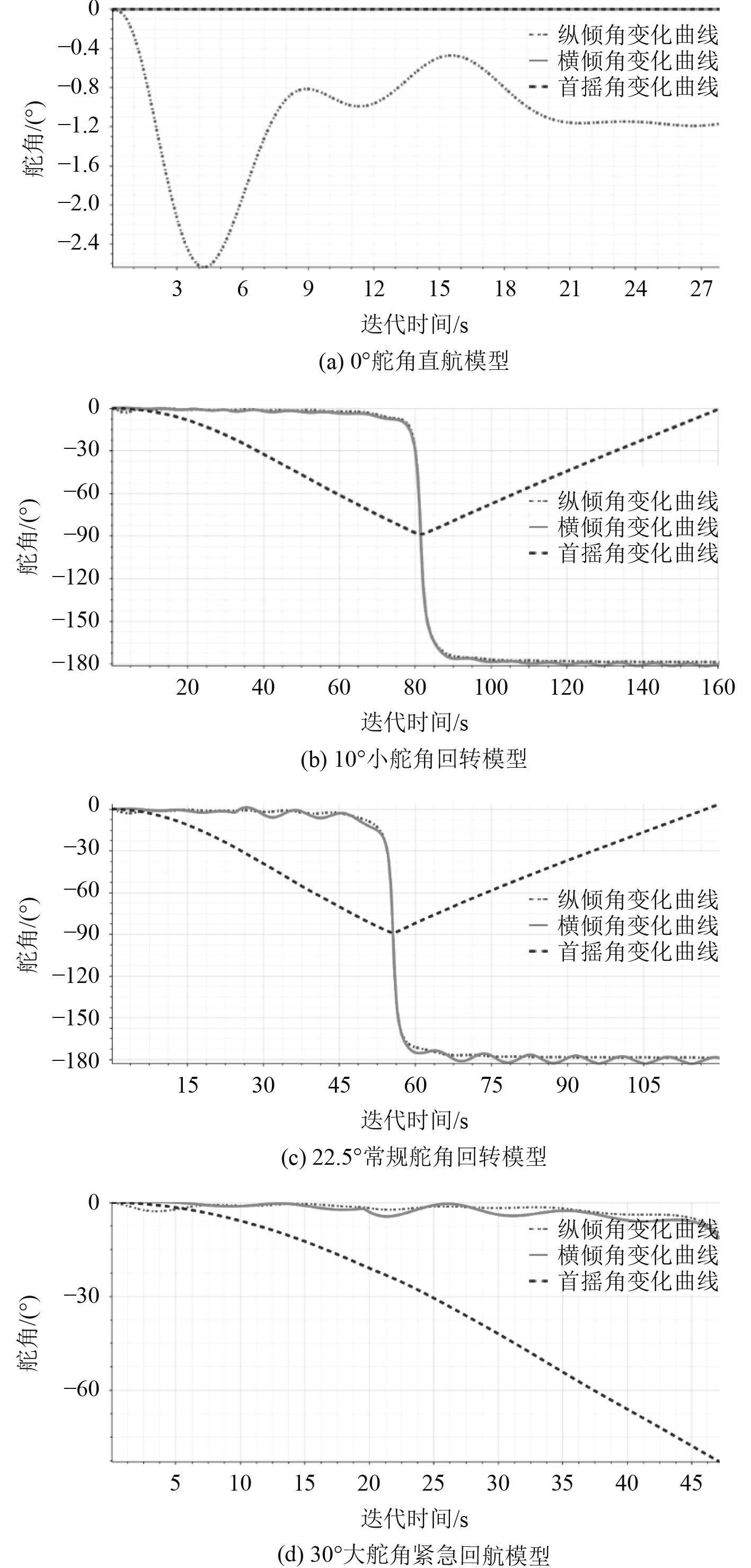
|
图 12 不同舵角下船舶回转三自由度运动曲线 Fig. 12 Three degree of freedom motion curve of ship rotation under different rudder angles |
2)船舶回转航行轨迹绘制如图13所示。
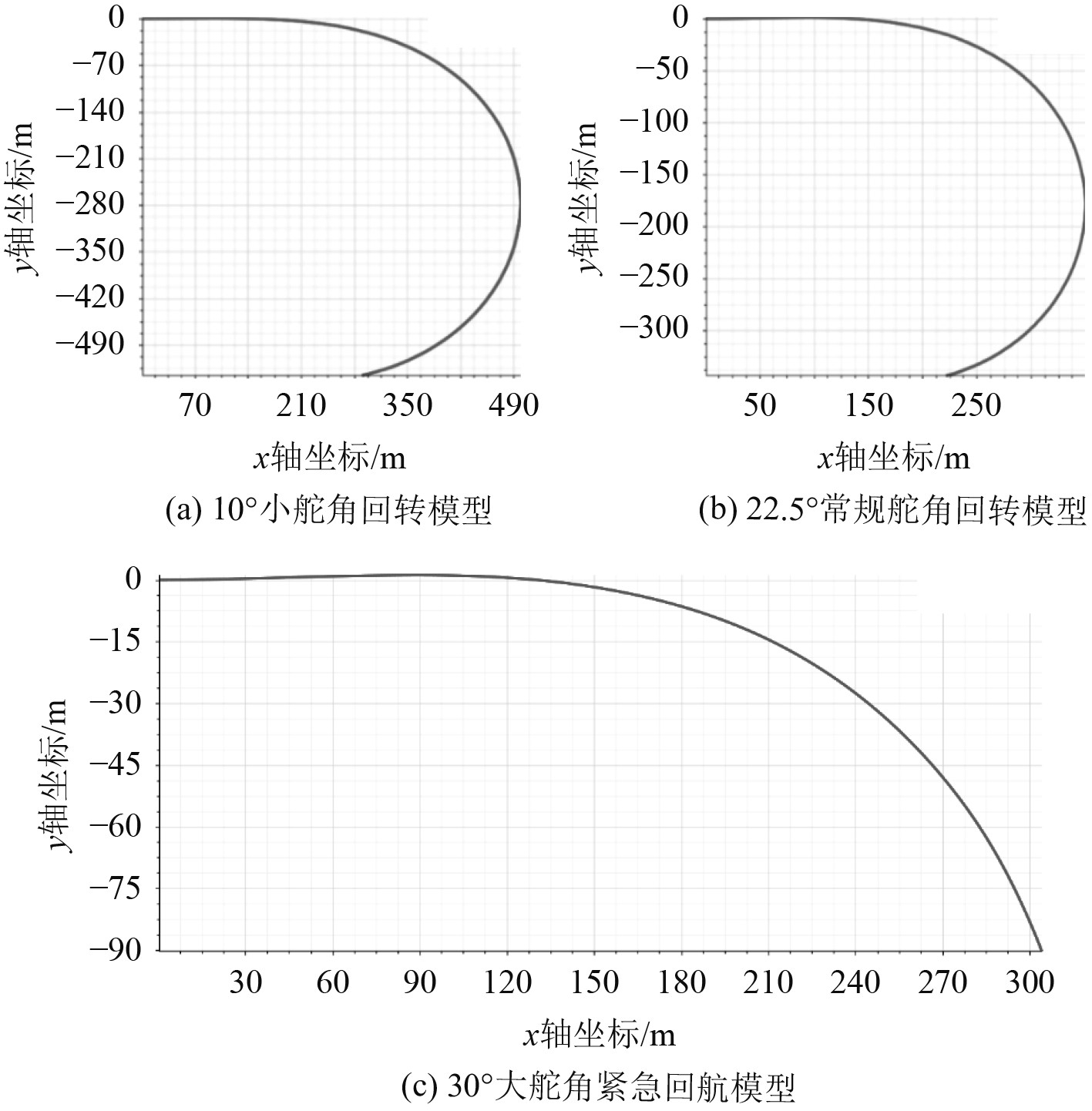
|
图 13 不同舵角下船舶轨迹图 Fig. 13 Ship trajectory under different rudder angles |
与操纵性预报相关的阻力、稳定回转线速度以及角速度数值如表3~表6所示。
|
|
表 3 随船动坐标系下X轴受力大小和方向 Tab.3 Force on the X-axis in the ship coordinate system |
|
|
表 4 随船动坐标系下Y轴受力大小和方向 Tab.4 Force on the Y-axis in the ship coordinate system |
|
|
表 5 随船动坐标系下Z轴受力大小和方向 Tab.5 Force on the Z-axis in the ship coordinate system |
|
|
表 6 随船动坐标系下X轴稳定速度大小和方向 Tab.6 Velocity of the X-axis in the ship coordinate system |
相同舵角的工况下,X轴所受分力都是浮冰海域大于敞水海域,负号代表力的方向与船行进方向相反,故X轴所受分力为船行阻力,数值多出部分应为冰载荷的作用力大小,但阻力中占比主要的仍是海水阻力。Z轴上的分力数值显示的是船身重力与所受海水浮力的差值,受纵倾、横倾以及升沉运动的不断变化,其数值不一定为0,但大小相较于船的重力可忽略。
由于船自身的对称性,故在0°舵角直航操纵的情况下不会产生侧向力,在给定舵角的工况下侧向力即为船体回转运动的向心力;对比中间两组数据,10°浮冰海域稳定回转侧向力小于敞水海域稳定回转,而22.5°浮冰海域稳定回转侧向力则大于敞水海域稳定回转,前者冰船相互作用多发生在船艏右舷一侧,冰载荷在Y轴方向上的分力与水动力方向相反,而后者冰船相互作用更多发生在船中或船尾左舷一侧,此时冰载荷Y轴方向的分力与水动力方向相同。由此也可以推断出,冰船相互作用对操纵性的影响碰撞压力大于摩擦切向力。
根据表7~表10中数据可以得出,回转操纵舵角越大,船舶回转降速越明显;而综合稳定速度数值大小和方向分析,散碎浮冰在船舶整个直航或是回转运动过程中,对随船动坐标系下X轴方向上的速度影响不大;而与船舶之间的法向碰撞压力相互作用,会直接关系到船舶在回转过程中所受到的Y轴侧向力大小,直接的表现为船舶稳定回转时Y轴向的稳定速度大小和方向。
|
|
表 7 随船动坐标系下Y轴稳定速度大小和方向 Tab.7 Velocity of the Y-axis in the ship coordinate system |
|
|
表 8 随船动坐标系下Z轴稳定速度大小和方向 Tab.8 Velocity of the Z-axis in the ship coordinate system |
|
|
表 9 回转稳定角速度大小和方向 Tab.9 stable angular velocity of rotation |
|
|
表 10 回转最大角速度大小和方向 Tab.10 Maximum angular velocity and direction of rotation |
在整个回转运动直至稳定的过程中,角速度的变化趋势始终是先增大,而后逐渐振荡回落,稳定在一个固定值左右范围。不同的舵角情况下,无论是回转稳定角速度还是回转最大角速度,数值上的差别都是较大的;而在相同舵角的情况下,敞水海域航行船舶角速度与浮冰海域航行船舶角速度相比,有一定的大小差异。
6 结 语针对船舶冰区航行操纵性问题,本文分3种冰船相互作用情形对船舶回转操纵性运动方程进行了补充和修正,进而采用CFD-DEM相结合的方法,建立了模拟开敞水域浮冰区的数值冰水池和浮冰的离散元模型,开展了回转运动的仿真计算,得到的结论如下:
1) 适当求解冰荷载作用,通过修正冰荷载的船舶回转操纵性运动方程,可以得到某一瞬时状态下船舶的角速度、稳定回转运动状态下的船舶回转直径和回转周期等参数结果,但由于浮冰区冰河在的随机性,难以给出稳定的求解。
2)船舶在密度较大的浮冰区域进行直航或是回转操纵时,冰船相互作用的影响不可忽略,其中散碎浮冰与船舶之间的切向摩擦相互作用对船舶回转运动状态的影响较小;而与船舶之间的法向碰撞压力相互作用,会直接关系到船舶在回转过程中所受到的Y轴侧向力大小,直接的表现为船舶稳定回转时Y轴向的稳定速度大小有较明显的数值变动。
3) 相同舵角下,无论是敞水海域还是浮冰海域进行回转操纵,升沉高度、纵倾角变化幅度不大,趋势差别微小,船舶的横倾角度变化较大。因此在进行回转操作时,应加以特别的关注。另外由于向心速度、回转角速度以及舵角的变化,会引起船舶航行所受阻力增加,回转降速更加明显。
4)整个回转运动直至稳定的过程中,角速度的变化趋势是先增大,而后逐渐振荡回落,稳定在一个固定值左右范围。不同的舵角情况下,无论是回转稳定角速度还是回转最大角速度,数值上的差别较大,应加以足够的关注。
| [1] |
李凡. 航行于碎冰区船舶冰载荷研究[D]. 大连:大连理工大学, 2019.
|
| [2] |
TUE-FEE K, KEINONEN A J. Full-scale maneuvering tests in level ice of canmar kigoriak and robert lemeur[J]. Marine Technology, 1986, 23(2): 131-138. |
| [3] |
秦尧, 李勇跃, 梁艳楠, 等. 极地船舶操纵性预报研究[J]. 船舶设计通讯, 2017(1): 20-26. QIN Yao, LI Yongyue, LIANG Yannan, et al. Research on prediction of maneuverability of vessels sailing in the polar region[J]. Journal of Ship Design, 2017(1): 20-26. |
| [4] |
师超, 韩阳. 船舶操纵性自航模试验不确定度分析[J]. 中国造船, 2021, 62(1): 89-96. SHI Chao, HAN Yan. Uncertainty assessment of free-running maneuvering model test for surface ships[J]. Shipbuilding of China, 2021, 62(1): 89-96. |
| [5] |
童波, 涂勋程, 谷家扬, 等. 基于参数化设计的浮冰区船舶冰阻力研究[J]. 船舶力学, 2019, 23(7): 755-762. TONG Bo, TU Xuncheng, GU Jiayang, et al. Study on ship ice resistance based on parametric design of brash ice zone[J]. Journal of Ship Mechanics, 2019, 23(7): 755-762. |
| [6] |
SEONG-R C, SEONG-YEOB J, SUNGSU L. Development of effective model test in pack ice conditions of square-type ice model basin[J]. Ocean Engineering, 2013, 67: 35-44. DOI:10.1016/j.oceaneng.2013.04.011 |
| [7] |
YAN H, SHi Q, AN S. Model test study of the interaction between ice and a compliant vertical narrow structure[J]. Cold Regions Science & Technology, 2007, 49(2): 151-160. |
| [8] |
郭春雨, 李夏炎, 王帅, 等. 冰区航行船舶碎冰阻力预报数值模拟方法[J]. 哈尔滨工程大学学报, 2016, 37(2): 145-150+156. GUO Chunyu, LI Xiayan, WANG Shuai, et al. A numerical simulation method for resistance prediction of ship in pack ice[J]. Journal of Harbin Engineering University, 2016, 37(2): 145-150+156. |
| [9] |
LIU J. Mathematical modeling ice-hull interaction for real time simulations of ship maneuvering in level ice[J]. 2009.
|
| [10] |
南明宇, 胡嘉骏, 汪雪良. 基于内外动力学耦合原理的船冰碰撞载荷特性研究[J]. 船舶力学, 2020, 24(9): 1167-1174. NAN Mingyu, HU Jiajun, WANG Xueliang. Research on characteristics of ship-ice collision load based on coupling internal and external dynamics[J]. Journal of Ship Mechanic, 2020, 24(9): 1167-1174. |
| [11] |
齐江辉, 郭翔, 陈强, 等. 碎冰区航行船舶阻力预报数值模拟研究[J]. 兵器装备工程学报, 2019, 40(11): 207-212. QI Jianghui, GUO Xiang, CHEN Qiang, et al. A Numerical Simulation Research for Resistance Prediction of Ship in Crushed Ice Area[J]. Journal of Ordnance Equipment Engineering, 2019, 40(11): 207-212. |
| [12] |
KIM M C, LEE S K, LEE W J, et al. Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions[J]. International Journal of Naval Architecture & Ocean Engineering, 2013, 5(1): 116-131. |
| [13] |
国威, 赵桥生, 王习建, 等. 碎冰条件下冰区船冰水动力数值模拟研究[J]. 船舶力学, 2020, 24(4): 456-464. Guo Wei, ZHAO Qiaosheng, WANG Xijian, et al. The numerical simulation research on ice and water combined force acting on ice-going ship in pack ice[J]. Journal of Ship Mechanic, 2020, 24(4): 456-464. |
| [14] |
李紫麟. 船舶在碎冰区航行的离散元模型及冰荷载分析[D]. 大连: 大连理工大学, 2013.
|
| [15] |
金强. 基于CFD-DEM极地浮/碎冰船舶冰阻力数值预报[D]. 大连: 大连海事大学, 2020.
|
 2024, Vol. 46
2024, Vol. 46
