2. 中国人民解放军91001部队,北京 100000
2. No. 91001 Unit of PLA, Beijing 100000, China
利用声呐信号解算目标运动要素一直是水声领域的难题。国内外关于被动声呐纯方位目标运动分析算法已有成熟的理论研究和广泛的实际应用,基于目标方位频率信息的目标运动分析算法也有较成熟的理论分析和实验验证。国外方面,Passerieux[1]和CHAN[2]提出利用方位、频率信息进行目标运动分析,指出由于频率与方位相关,导致估计结果有偏,并提出利用辅助变量消除偏差;Johannesson[3]给出一种用卡尔曼滤波方法进行基于方位-频率信息的目标运动分析的算法;Rosenqvist[4]提出一种方位、频率分别估计的两步走伪线性算法,利用方位信息估计目标航向和相对速度,然后利用频率信息估计目标速度和距离,仿真表明该算法结果接近克拉美罗下限;Jauffret[5]分析了方位-频率算法以及多阵观测条件下目标运动的可观测性。国内方面,胡青[6]提出了基于伪线性方程和极大似然估计的目标运动分析算法,并进行了水下实验,估计误差小于30%。李龙[7]提出了一种频率搜索优化算法。占荣辉[8]分析了方位-频率目标运动分析的可解条件,指出当目标相对于观测平台方位变化率或距离变化率为0时,目标运动要素不可解。刘健[9]提出一种基于扩展卡尔曼滤波的目标运动要素解算方法。程善政[10]提出一种基于滤波的改进纯方位要素解算方法。
总体而言,现在大部分方位-频率目标运动分析算法是基于目标辐射的线谱噪声,很少有关于脉冲信号方位-频率的算法研究。事实上,主动声呐脉冲信号具有声源级高、频带窄、信噪比高的特点,利用这些特点,可较精确地测量声呐脉冲信号的方位和频率信息从而解算目标运动要素。基于此,本文提出一种利用主动声呐脉冲的多普勒目标运动要素解算方法,与基于纯方位信息的目标运动分析算法相比,该算法对本平台机动方面没有特殊要求,且与基于目标辐射噪声线谱频率-方位的目标运动分析算法相比,可以最大限度提前发现目标。
1 基于脉冲方位的多普勒解要素算法原理 1.1 基于方位-频率的目标运动分析算法如图1所示,设目标航向为Hm,航速为Vm,本平台进行匀速直线运动,航向Hw,航速Vw,首次收到目标主动声呐脉冲时的距离为D1、方位F1。目标以间隔Ts为周期发射中心频率为f0的窄带脉冲信号。受多普勒因素影响,平台接收到的脉冲信号中心频率为:

|
图 1 目标运动分析态势示意图 Fig. 1 Schematic diagram of target motion analysis situation |
| $ {f_i} = {f_0}\frac{{1 + \dfrac{{{V_w}}}{C}\cos \left( {{H_w} - {F_i}} \right)}}{{1 + \dfrac{{{V_m}}}{C}\cos \left( {{H_m} - {F_i}} \right)}},i = 1,2,3 \cdots 。$ | (1) |
对上式变形可得:
| $ {f_0}\left( {1 + \frac{{{V_w}\cos \left( {{H_w} - {F_i}} \right)}}{C}} \right) - {f_i}\frac{{\cos {F_i}}}{C}{V_{mx}} - {f_i}\frac{{\sin {F_i}}}{C}{V_{my}} = {f_i}。$ | (2) |
式中:Vmx=Vm cosHm,Vmy=Vm sinHm,分别为目标在X方向和Y方向的速度分量。测得3个不同时刻的脉冲方位F1、F2、F3和频率f1、f2 、f3,即可解得Vmx、Vmy以及f0,从而得到目标的绝对速度Vm。同时,根据纯方位解要素算法原理可知,当本平台未做机动时,可以解算目标航向Hm和相对速度Vm/D1 ,结合目标绝对速度Vm,即可得到目标的全部运动要素。
事实上,利用多普勒估算目标速度的算法与位置态势无关,因而在解算过程中并不需要本平台做特殊机动。在实际中,一方面,应当利用多个脉冲信号进行最小二乘估计,当目标连续长时间使用主动脉冲时,应当综合利用极大似然估计和最优搜索等算法,得到收敛解。另一方面,当目标主动声呐脉冲方位和频率变化率较小时,本平台可进行适当机动,以便算法尽快收敛。
1.2 脉冲时间定位与频率测量 1.2.1 脉冲信号的时间定位脉冲信号的探测定位采用过门限检测的方法。利用平方检波器获取信号的包络,在信号包络的上升沿,当包络超过门限时,认为信号抵达;在信号包络的下降沿,当包络低于门限时,认为信号结束。
在脉冲检测定位过程中,有2个问题需要特别关注,一是门限值的选取,门限值选取过高会导致脉冲的漏检,选取过低会导致虚警概率增加,为频率测量引入额外的误差;一般而言脉冲信号的能量超过背景噪声10 dB以上,可以选择以信号在一个脉冲间隔周期内的平均能量作为噪声功率的估计,以7 dB作为脉冲起始和结束的门限。二是脉冲的筛选,由于多途效应引起的脉冲波形畸变,在同一个脉冲内部,过门限检测方法可能会检测到多个脉冲分段,在短脉冲中这种现象尤其明显。一般来说,在浅海区域,直达信号与多途信号及混响相比,脉冲能量大,持续时间长,波形稳定,抵达时间较早。应根据这些特点,对同一个脉冲持续时间内检测到的多个脉冲分段进行筛选,选择抵达时间早、能量大、包络稳定的一个分段作为脉冲抵达时间和波形的估计。
1.2.2 脉冲信号的频率测量在获得脉冲的起始与结束时刻后,需要利用这一时间段内的信号作为输入,进行频率估计。本文所采用的高精度频率估计算法是一种基于信号
对于LFM信号:
| $ x\left( t \right) = \cos \left( {{\upsilon _0}t + {s_0}{t^2}} \right) 。$ | (3) |
| $ {x_\beta }\left( t \right) = \cos \left( {{\upsilon _0}\left( {1 + \beta } \right)t + {s_0}{{\left( {1 + \beta } \right)}^2}{t^2}} \right)。$ | (4) |
式中:
LFM信号
| $ \upsilon = ks + b 。$ | (5) |
利用FFT对多普勒频移后的LFM信号进行Chirplet变换并计算其
对出现峰值点的
| $ \upsilon = k's + b' 。$ | (6) |
另一方面,LFM信号
| $ \upsilon = {\upsilon _0}\left( {1 + \beta } \right) \text{,} s = {s_0}{\left( {1 + \beta } \right)^2} 。$ | (7) |
联立式(6)~式(8)求解,即等效为对多普勒前后LFM信号频率—切变分布的能量峰拟合得到峰脊直线和抛物线在
该方法在信噪比10 dB左右估计精度可以达到甚至超过无偏估计的克拉美罗下限,与music算法相比精度相当,但是该算法基于FFT,可以快速实现,能够兼顾计算的精度和速度。此外,该算法基于以线性调频信号为核函数的Chirplet变换,不但可以估计单频信号的频率,也可以进行调频信号的参数估计,从而估计调频信号多普勒频移,具有较宽的应用范围。
1.2.3 非线性回归算法基于主动脉冲的目标运动分析方法与基于连续线谱的方法相比,频率测量的计算量较大,而目标运动要素结算的计算量相对较小。并考虑到功能拓展与升级,采用非线性回归的方法。将每一个脉冲的时刻、方位、频率以及本平台相应时刻的速度和位置组成的多维向量,看做样本空间中的一个点,根据频率和方位与本平台航速、位置以及目标初距和航速的函数关系,进行非线性拟合,从而获得目标运动要素的估计值。
以本平台初始位置为坐标原点,正东为X轴,正北为Y轴,建立坐标系,设目标初始位置为(Dx,Dy),目标速度为(Vmx,Vmy),主动脉冲的中心频率为fc,在时刻t,本平台位置为(Px,Py ),速度为(Vwx,Vwy),测得目标方位为F,脉冲频率为f,考虑到样本i=1,2,···n以及误差
| $ {f_i} = {f_0} \times \left[ {1 + \frac{{\left( {{V _{wxi}} - {V _{mxi}}} \right)\sin {F_i} + \left( {{V _{wyi}} - {V _{myi}}} \right)\cos {F_i}}}{C}} \right] + {\varepsilon _{{f_i}}} 。$ | (8) |
Fi可表示为:
| $ {F_i} = \arctan \left( {\frac{{{D_x} + {V_{mx}}{t_i} - {P_{xi}}}}{{{D_y} + {V_{my}}{t_i} - {P_{yi}}}}} \right) + {\varepsilon _{{F_i}}}。$ | (9) |
基于高斯牛顿迭代法,利用频率信息可以估计出Vmx,Vmy,再利用方位信息可以估计出Dx,Dy,从而实现目标运动要素的结算。
值得注意的是,当本平台未做机动时,本算法由多元非线性拟合退化为一元非线性拟合,当本平台进行机动时,也可以直接利用纯方位信息进行回归分析,解算目标运动要素。
2 脉冲时间定位与测频实测数据结果分析海上试验海域水深为8.9 m,声速剖面为微弱负梯度,声速从海面至海底由1 510.5 m/s减小至1 509.5 m/s,海况4级。试验初始收发船距离约1.63 n mile,收发船均为匀速直线运动,发射2组信号,第1组信号210 s内共50个脉冲,第2组480 s内36个脉冲。
图2为第1组实测脉冲信号的时间和频率估计,识别定位为48个,识别率为96%。经频率估计并剔除频率偏差较大的脉冲后,还有42个,总体识别率为84%,频率有十几赫兹的变化,剔除随时间变化的影响后,标准差为2.78 Hz。
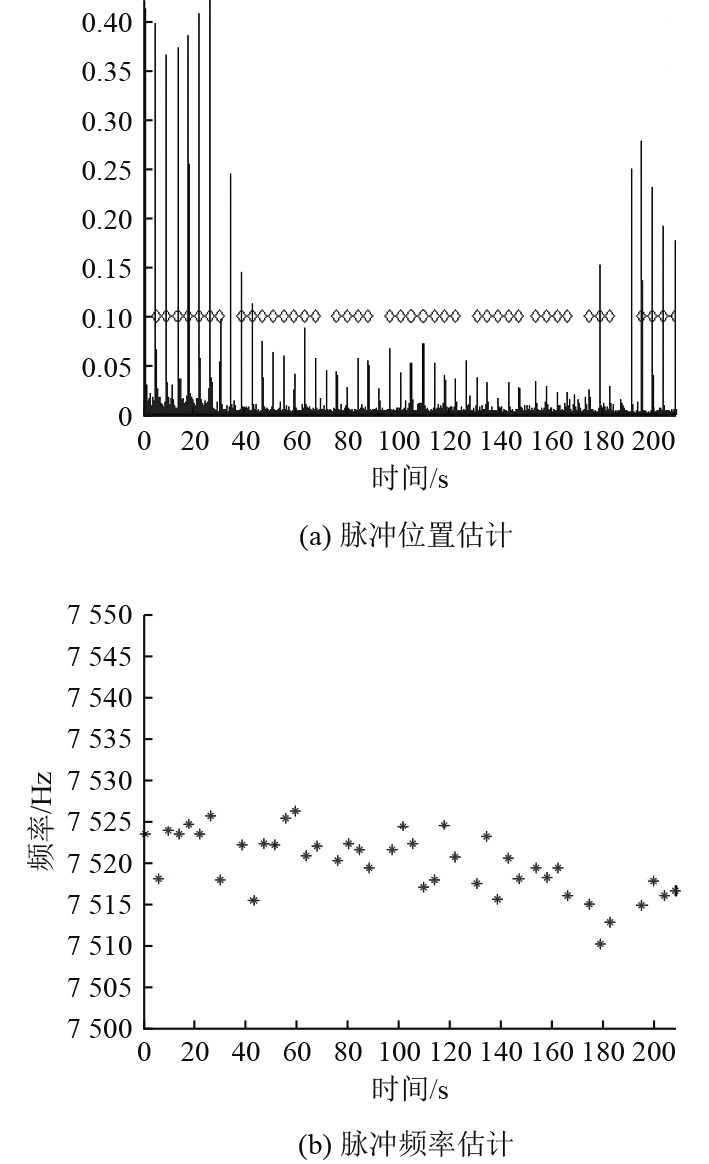
|
图 2 第1组脉冲时间位置及频率估计 Fig. 2 Time position and frequency estimation of the first set of pulses |
图3中信号的频率保持在5 204 Hz左右,频率标准差为0.5 Hz,480 s内36个脉冲共识别34个,识别率率为94.4%。总体而言,这样的频率估计精度可以满足目标运动分析的要求。

|
图 3 第2组脉冲时间位置及频率估计 Fig. 3 Time position and frequency estimation of the second set of pulses |
仿真初始态势为:目标航向95°,航速20 kn,初始距离100链,初始方位285°,主动脉冲中心频率7 500 Hz,间隔10 s。
假定平台采用方位航向,航速4 kn,主动脉冲方位均方误差为0.5°,频率均方误差为3 Hz。首先估计来袭脉冲的时间位置及频率,结合非线性回归方法迭代计算目标距离,跟踪效果如图4所示,图中曲线为目标实时解算距离,横向上限两侧虚线分别为5%和10%误差界限,随着时间推移,样本数增加,逐次迭代,在800 s后基本可以稳定距离跟踪。
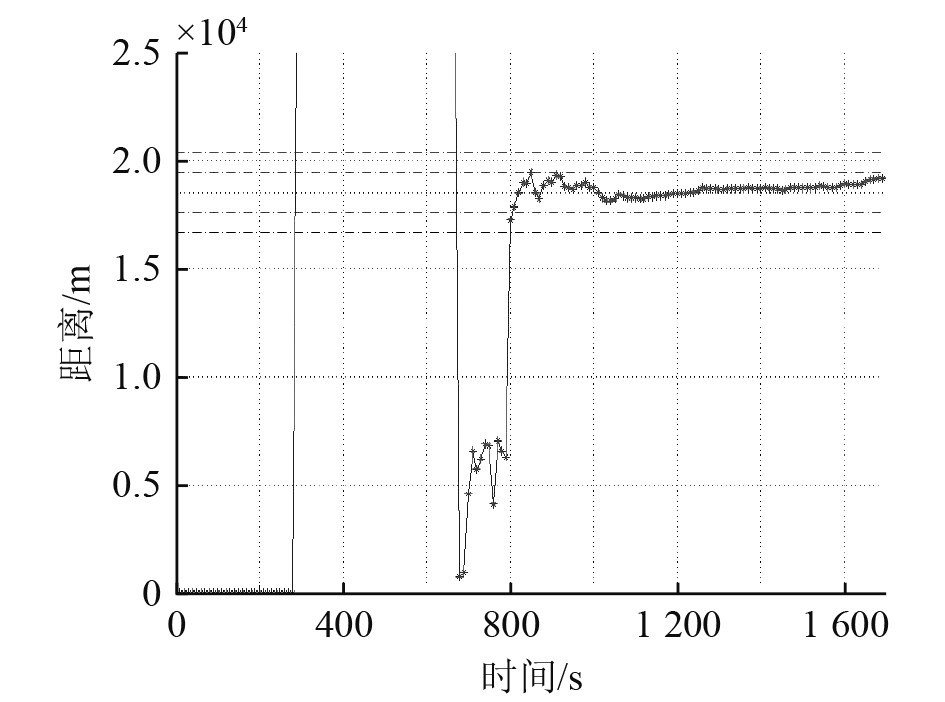
|
图 4 方位航向时的距离估计 Fig. 4 Distance estimation using the azimuth course |
同样初始态势下,平台采取机动措施,采用离开航向200°,跟踪效果如图5所示,可知,新算法最早在400s可以获得概略位置,在600 s左右,解算距离稳定收敛,可实现目标的距离跟踪。
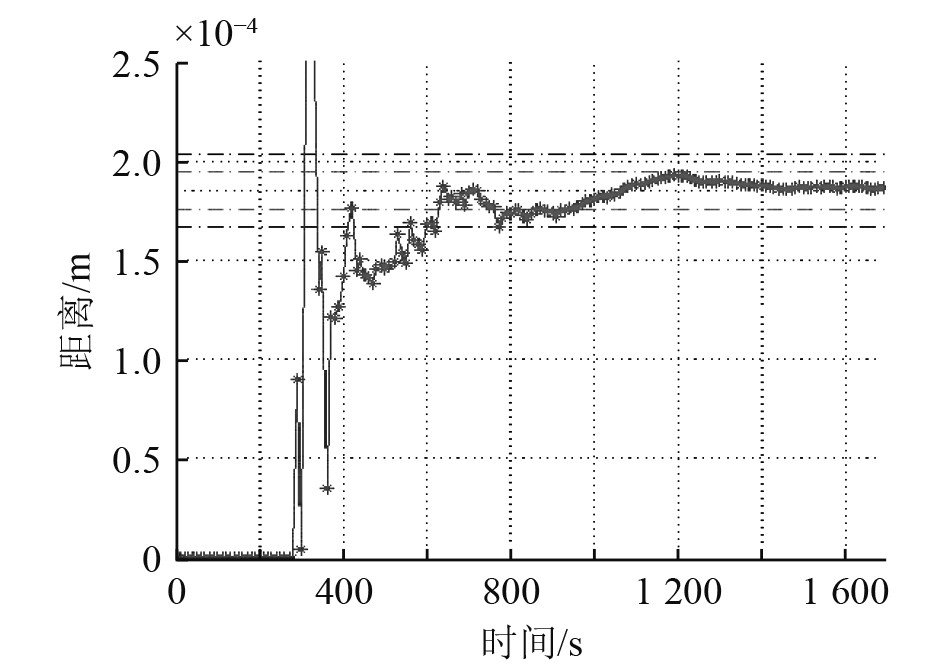
|
图 5 离开航向时的距离估计 Fig. 5 Distance estimation using the departure course |
同样初始态势下,为使速度解算尽快收敛,考虑平台采用连续变向机动措施。本平台航速不变前提下,航向由方位航向逆时针转动,转动角速度为0.1°/s,利用新算法获取的跟踪效果如图6所示,可知在500 s左右,实现目标的距离稳定跟踪。
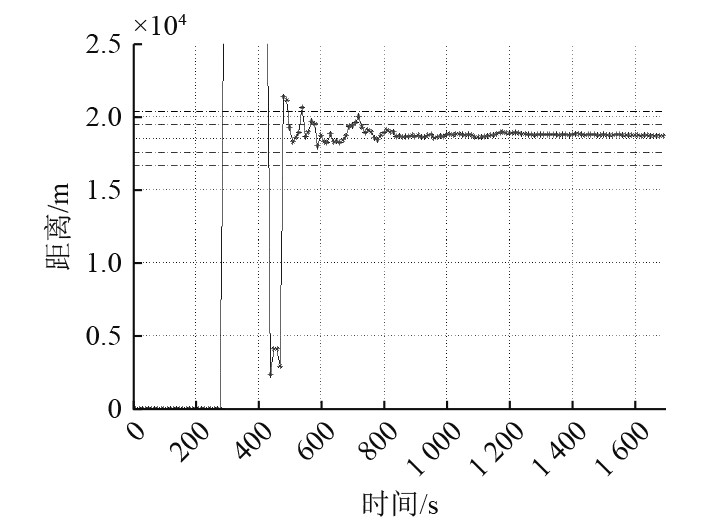
|
图 6 本平台机动时的距离估计 Fig. 6 Distance estimation during platform maneuvering |
图7为本平台机动条件下,方位-频率算法与纯方位算法的结果对比,平台0~5 min采用方位航向,5~10 min采用离开航向,10~15min恢复原航向。从仿真结果来看,本文提出的基于脉冲方位-频率的解要素算法比纯方位算法收敛时间更早,效果更好。

|
图 7 方位-频率算法与纯方位算法的结果对比 Fig. 7 Comparison of Results between Azimuth Frequency Algorithm and TMA |
通过仿真实验结果可看出:
1)当本平台采用适当的机动措施可使结果快速收敛,但即使不机动,最终在结果也可以收敛;
2)当本平台机动时,同样条件下方位-频率算法与纯方位算法相比,收敛时间更快。
4 结 语利用主动声呐脉冲信号声源级高,频带窄,信噪比高的特点,提出一种基于主动声呐脉冲方位的多普勒解要素新算法。试验数据分析及仿真分析结果表明,相比于传统的纯方位解要素算法,新算法对接收平台的机动要求宽容,且相同条件下,新算法对目标运动要素解算收敛时间更快。
当然,算法也存在一定不足,一是在主动脉冲测量的过程中,由于脉冲自身频率漂移和其他因素的影响,个别脉冲的频率估计值与其前后脉冲的估值差别很大,需要设置一定的频率标准差上限,对于频率异常的数据进行剔除,以减小频率误差对结算结果的影响。二是实际目标在发射主动脉冲过程中,其航向、航速是随时可能发生改变的,有可能在解算结果收敛以前,目标已经变速变向,解算过程会无法收敛。针对这种情况,不防假设目标在解算过程中进行了一次变速或变向,速度在较短时间内从(Vmx1,Vmy1)变至(Vmx2,Vmy2),那么在1.2.3节给出的回归方程中,可以考虑用某种具有简单参数的关于时间的S型函数(例如反正切函数),连接(Vmx1,Vmy1)以及(Vmx2,Vmy2),替代单一的(Vmx,Vmy),从而实现对目标的连续跟踪和要素结算。在这种情况下,系统的可观测性、S型函数的参数维数等问题都需要进一步研究解决。
| [1] |
PASSERIEUX J M, PILLON D, BLANC-BENON, et al. Target motion analysis with bearings and frequencies measurements via instrumental variable estimator[J]. Proc Int. Conf. Acoustics Speech and Signal Processing, 1989, 2(4): 2645-2648. |
| [2] |
CHAN Y T, RUDNICKI S W. Bearings –only and Doppler-bearing tracking using instrumental variables[J]. IEEE trans. , aerospace, electronic system, 1992, 1(28): 1077-1083. |
| [3] |
JOHANNESSON P, HOLST J, ROSENQVIST A, et al. On kalman filtering in Doppler-bearing tracking[C]// Procession Conference. Undersea Denfence Technology. London, 1994: 433-440.
|
| [4] |
ROSENQVIST A. Passive Doppler-bearing tracking using a pseudo-linear estimator[J]. IEEE Journal of Oceanic Engineering, 1995, 1(20): 114-118. |
| [5] |
JAUFFRET C, PILLON D. Observability in passive target motion analysis[J]. IEEE transations on , Aerospace, Electronic System, 1996, 32(4): 1290-1300. DOI:10.1109/7.543850 |
| [6] |
胡青, 宫先仪. 方位/频率目标运动分析实验研究[J]. 声学学报, 2005, 30(2): 120-124. DOI:10.3321/j.issn:0371-0025.2005.02.005 |
| [7] |
李龙, 鞠阳, 燕雪峰. 一种多普勒频移优化搜索的目标运动分析算法[J]. 计算机技术与发展, 2015, 25(7): 45-48. |
| [8] |
占荣辉, 王玲, 万建伟. 基于方位角和多普勒的机动目标无源定位跟踪可观测条件[J]. 国防科技大学学报, 2007, 29(1): 54-58. DOI:10.3969/j.issn.1001-2486.2007.01.012 |
| [9] |
刘健, 刘忠, 玄兆林. 基于方位频率测量的水下被动目标运动分析算法[J]. 舰船科学技术, 2006, 28(3): 66-69. LIU Jian, LIU Zhong, XUAN Zhaolin. The research of underwater passive TMA algorithm with bearings and frequencies measurements[J]. Ship Science and Technology, 2006, 28(3): 66-69. |
| [10] |
程善政, 陈双, 何心怡. 一种目标运动要素纯方位解算方法. 舰船科学技术, 2020, 42(12): 129-132. CHENG Shanzheng, CHEN Shuang, HE Xinyi A pure azimuth solution method for target motion element. Ship Science and Technology, 2020, 42(12): 129-132. |
| [11] |
YANG G, XING B, et al. High precision Doppler estimation method for LFM signals based on chirplet transform [C]//2022 IEEE 5th Advanced Information Management Communicates Electronic and Automation Control Conference. ChongQing, 2022: 1089-1092.
|
 2024, Vol. 46
2024, Vol. 46
