2. 深海技术科学太湖实验室,江苏 无锡 214082;
3. 深海载人装备全国重点实验室,江苏 无锡 214082
2. Tai Hu Laboratory of Deep-sea Technological Science, Wuxi 214082, China;
3. State Key Laboratory of Deep-sea Manned Vehicles, Wuxi 214082, China
环肋圆柱壳结构是深海潜器典型的耐压结构形式之一,在开展环肋圆柱壳结构设计过程中,其典型位置的强度问题是重要的研究内容之一,通常需要开展缩比模型静水外压试验来获得结构的应力情况。整个试验涉及到模型加工、形状检测、材料检验、试验开展、数据处理等多个环节,对试验结果产生影响的因素较多,为保证试验结果的准确性,需要对模型强度试验进行不确定度分析。
目前,不确定度研究在工程接和学术界引起人们越来越多的重视,为此,ISO发布了《测量不确定度表示指南》[1](GUM)用于指导测量不确定度的评定与表示方法,我国以此为基础也发布了《测量不确定度评定与表示》作为测量不确定度评定与表示的技术法规依据。在船舶力学研究领域,ITTC(国际船模拖曳水池会议)针对CFD数值模拟和水动力模型试验均给出了不确定度研究的推荐规程和评估方法,并要求其成员单位在进行模型试验时,需要提供相应的测量不确定度分析结果用于交流比较。张立等[2]针对船模拖曳水池的阻力试验开展了不确定分析研究,计算了船模几何形状、仪器设备、水温等对总阻力的影响。马向能等[3]将ITTC会议公布的测量不确定度分析方法和《测量不确定度表示指南》(GUM)给出的不确定度分析方法应用于旋臂水池操作性模型试验中,并分析比较了2种方法的差异性。沈泓萃等[4]基于正交试验设计、方差分析方法以及统计推断理论,提出了一套针对CFD的不确定度分析理论。吴乘胜等[5]基于该理论,针对水面船标模DTMB5415数值水池试验开展了不确定度分析的验证和确认,给出了对数值试验结果有重要影响的试验因素和交互作用以及各类不确定度分量的大小。司海龙等[6]基于不确定度扩展定律,对某超大型集装箱船的波浪载荷模型试验进行不确定度分析,研究表明标定系数、转动惯量对船中垂向弯矩影响较大。汪雪良等[7 − 8]对大型LNG船和双体船波浪载荷试验的不确定度开展研究,分析了测试系统和弯矩标定对试验不确定度的影响。
在水下耐压结构强度试验不确定研究方面目前我国开展的研究还相对较少,对试验过程中存在的误差源及其影响程度认识不足,因此有必要对水下耐压结构强度试验的不确定度问题开展细致的研究工作。本文以一个小尺度环肋圆柱壳精车模型为研究对象,通过对其强度试验的试验流程进行分析研究,提取可能对试验结果产生影响的误差源,并基于《测量不确定度表示指南》(GUM)中给出的测量不确定度评定方法分析各个误差源的不确定度,进而得到模型典型位置应力试验结果在一定置信水平下的扩展不确定度。
1 不确定度分析原理对于某一试验测量模型,其输出量
| $ {y}={f}({x}_{1},{x}_{2},{x}_{3},\dots ,{x}_{n})。$ | (1) |
试验的测量结果受到随机误差和系统误差的影响往往具有一定的分散性,为表征试验结果的分散性,测量结果的不确定度u采用标准偏差来表示。由于试验结果不确定度由多个分量组成,按照不确定度分量的评定方法可以分为两类:一类是用一系列测量数据的统计分析方法进行估算,即A类不确定度;另一类是借助一切可利用的有关信息和经验进行假定概率分布估算,即B类不确定度。
1.1 A类不确定度评定方法A类不确定度评定是指对被测量采取
| $ {s}\left({x}_{i}\right)=\sqrt{\frac{\displaystyle\sum _{i}^{n}{({x}_{i}-\bar{x})}^{2}}{n-1}}。$ | (2) |
进而得到A类不确定度的计算公式为:
| $ {u}_{A}=\frac{s\left({x}_{i}\right)}{\sqrt{n}}。$ | (3) |
B类不确定度的评定需根据有关信息和经验,判断被测量的可能值区间为[
| $ {u}_{B}=\frac{\alpha }{k} 。$ | (4) |
其中:
此外,若测量仪器说明书、校准证书、手册等给出了扩展不确定度U和倍数k时,则标准不确定度uB=U/k。以“级”使用的仪器,当测量仪器检定证书上给出准确度级别时,可按检定系统或检定规程所规定的该级别最大允许误差进行评定。
1.3 合成不确定度根据测量模型的各输入量的标准不确定度即可获得模型输出量的标准不确定度,即各标准不确定度分量合成的标准不确定度。合成标准不确定度用符号
| $ {u}_{c}= \sqrt{{\sum _{i=1}^{n}{\left[\frac{\partial f}{\partial {x}_{i}}\right]}^{2}u}^{2} \left({x}_{i}\right) + 2\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}\frac{\partial f}{\partial {x}_{i}}\frac{\partial f}{\partial {x}_{j}}{\rho }_{ij}u\left({x}_{i}\right)u\left({x}_{j}\right)} 。$ | (5) |
式中:
当各输入量彼此独立时,则相关系数
| $ {u}_{c}=\sqrt{{\sum _{i=1}^{n}{\left[\frac{\partial f}{\partial {x}_{i}}\right]}^{2}u}^{2}\left({x}_{i}\right)}。$ | (6) |
合成标准不确定度与包含因子
为确定包含因子
| $ {\nu }_{i}\approx \frac{1}{2}\frac{{u}^{2}\left({x}_{i}\right)}{{\sigma }^{2}\left[{u}\left({x}_{i}\right)\right]}\approx \frac{1}{2}{\left[\frac{\mathrm{\Delta }\left[u\right({x}_{i}\left)\right]}{u\left({x}_{i}\right)}\right]}^{-2}。$ | (7) |
合成标准不确定度
| $ {\nu }_{\mathrm{eff}}=\frac{{u}_{c}^{4}\left(y\right)}{\displaystyle\sum _{i=1}^{n}\frac{{u}_{i}^{4}\left(y\right)}{{\nu }_{i}}} 。$ | (8) |
得到
在对环肋圆柱壳强度试验开展不确定度研究前,首先需要对试验的流程进行分析,明确试验过程中的误差源[10]。环肋圆柱壳强度试验流程极为复杂,可能对试验结果造成影响的因素繁多:在模型加工阶段,模型的总长度、直径、壳板厚度、肋骨及壳板初挠度、肋骨间距、肋骨波纹度等尺度往往存在一定偏差,模型加工所用材料的力学性能如杨氏模量、屈服强度、抗拉强度、断后延伸率以及截面收缩率等参数也有所不同,这些都对最终的试验结果产生影响;在试验准备阶段,需要开展测点定位、应变片粘贴、测点密封、电阻测量等工作,测点定位的精度、应变片的密封效果、电阻测量的准确性等都会导致测量数据的不同;在应变测量阶段,环境温度、压力、运行的其他设备等都会对应变值产生一定程度的影响,另外,应变测量所用的应变仪、压力表等仪器本身也有其不确定度,从而造成测量值的偏差。
综上所述,在模型整个强度试验过程中可能存在的不确定度因素较多,无法全部顾及,而且有些因素的灵敏系数、因素间的相关系数等也无法直接确定,为较为精确的掌握环肋圆柱壳强度试验的不确定度情况,本文选择影响较大且无法避免的影响因素进行分析,探索性的建立一套适用于水下耐压环肋圆柱壳强度试验的不确定度分析方法。
3 环肋圆柱壳强度试验不确定度分析方法通过对环肋圆柱壳强度试验流程进行综合分析,可以确定误差源主要包括:
1)模型板厚偏差。模型加工过程中,由于加工工艺的限制,模型的实际板厚与理论厚度之间往往存在一定的偏差,对模型的应力分布产生一定的影响。
2)模型初挠度偏差。在模型加工的过程中,模型的壳板及肋骨会存在径向初挠度偏差,对模型的应力和承载能力产生一定的影响。
3)材料性能偏差。环肋圆柱壳通常采用高强度钢作为其建造材料,加工所用的不同钢板的实际材料性能尤其是杨氏模量通常存在一定差异,所加工的模型的力学性能也将有所不同。
4)压力表。模型静水外压试验过程中,通常利用压力表来监测压力筒中的实时压力,当压力表显示压力达到规定的测试压力时,即开始对模型的应力应变数据进行测量,压力表的测量误差将对试验结果产生影响。
5)数据测量。在模型的数据测量阶段,受到试验设备、测试系统、外部环境等的影响,每次测量数据均存在一定偏差。
误差源性质的不同,所采用的不确定度分析方法也有所不同。其中,模型的板厚、初挠度、杨氏模量、数据测量等因素的不确定度分析可采用A类评定方法;压力表等仪器设备因素可以采用B类评定标准。
对于环肋圆柱壳强度试验的试验结果,有:
| $ \mathrm{\sigma }={f}(t,E,r,p,\mu )。$ | (9) |
式中:
假设各个因素对试验结果的影响相互独立,根据式(6),试验结果的合成不确定度可表示为:
| $ {u}_{1}\left(\sigma \right)=\sqrt{\frac{\displaystyle\sum _{i}^{n}{({\mu }_{i}-\bar{\mu })}^{2}}{n(n-1)}} 。$ | (10) |
| $ { {u}_{2}\left(\sigma \right) = \sqrt{\dfrac{\partial f}{\partial t}u\left(t\right) + \dfrac{\partial f}{\partial E}u\left(E\right) + \dfrac{\partial f}{\partial r}u\left(r\right) + \dfrac{\partial f}{\partial w}u\left(w\right) + \dfrac{\partial f}{\partial p}u\left(p\right)}。} $ | (11) |
在对应力数据测量因素的不确定度开展重复性试验时,需要注意在每次应力数据测量开始前均需重新对系统进行初始平衡,以便计入初始平衡的随机变化导致的不确定分量。对于壳板厚度t、弹性模量E、模型几何初挠度
本次试验对象采用图1所示的小尺度环肋圆柱壳精车模型。模型总长666 mm,试验段长度为432 mm,圆柱壳内径571 mm,试验段壳板厚度3 mm,共分为12个肋位,肋骨间距54 mm,肋骨采用矩形剖面形式,高度为30 mm,厚度为4.8 mm。为避免端部弯曲应力对试验段结构的影响,在模型两端设置过渡段,采用大肋骨和厚板组合加强,同时将过渡段肋间缩减为45 mm,以避免模型在过渡段发生失稳破坏。

|
图 1 小尺度环肋圆柱壳精车模型 Fig. 1 Fine-turning model of small-scale ring-ribbed cylindrical shell |
环肋圆柱壳强度试验中,模型跨中壳板中面周向应力
环肋圆柱壳模型试验段壳板的名义厚度为3 mm,在模型实际加工过程中,壳板厚度会产生一定程度的偏差,该模型整体采用精车加工的方式,根据加工控制能力和以往的加工经验,壳板的厚度偏差通常≯±0.1 mm。采用测厚仪分别测量各个肋位不同母线跨中壳板的厚度,并将偏差结果记录于表1,按照式(3)即可计算出板厚的标准不确定度。
|
|
表 1 模型板厚误差 Tab.1 Model plate thickness deviation |
采用数值模拟的方法,分别计算板厚偏差在−0.1、−0.08、−0.06、−0.04、−0.02、0.0、0.02、0.04、0.06、0.08、0.1 mm情况下模型的应力结果,并将计算结果记录见表2和表3。
|
|
表 2 不同板厚偏差下模型的跨中壳板中面周向应力 Tab.2 Circumferential stress at the mid-plane of the mid-span shell of the model under different plate thickness deviations |
|
|
表 3 不同板厚偏差下模型的跨端壳板内表面纵向应力 Tab.3 Longitudinal stress on the inner surface of the end-span shell of the model under different plate thickness deviations |
对表2数据进行分析,拟合出板厚偏差与跨中壳板中面周向应力之间的关系曲线,如图2(a)所示。可以发现,跨中壳板中面周向应力与板厚偏差呈线性变化,拟合公式为:
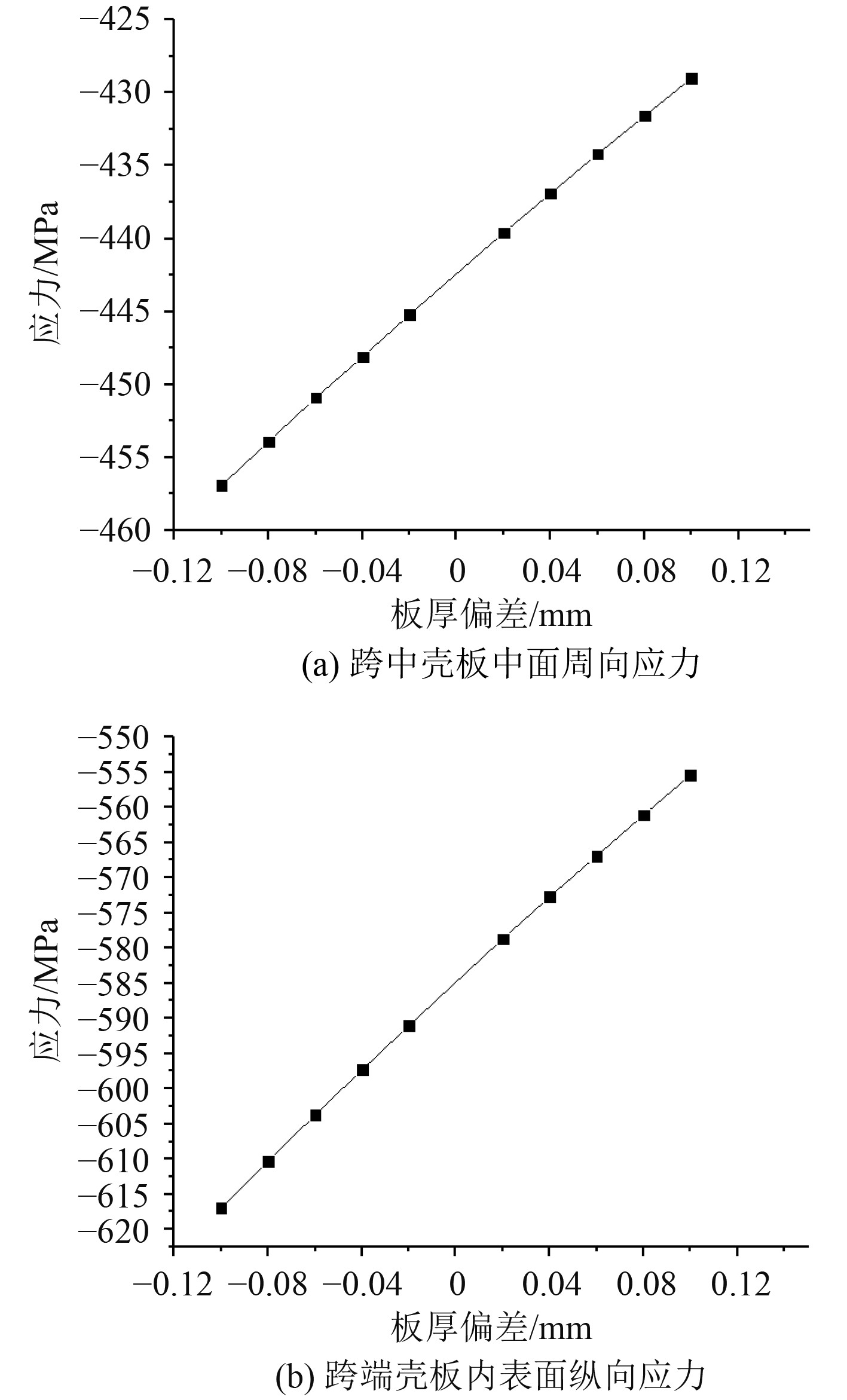
|
图 2 不同板厚偏差下的模型应力 Fig. 2 Model stresses under different plate thickness deviations |
| $ {\sigma }_{2}^{0} =139.45t-442.63。$ | (12) |
故板厚偏差对跨中壳板中面周向应力的灵敏系数为139.45。
对表3数据进行分析,拟合出板厚偏差与跨端壳板内表面纵向应力之间的关系曲线,如图2(b)所示。可以发现,跨端壳板内表面纵向应力与板厚偏差呈线性变化,随着板厚的增加,纵向应力变小。两者的拟合公式为:
| $ {\sigma }_{1} =307.36t-585.4。$ | (13) |
故板厚偏差对跨端壳板内表面纵向应力的灵敏系数为307.36。
4.2 材料属性该环肋圆柱壳模型采用高强度钢锻件建造而成。建造前,需要在锻件的两端切割试件,并进行拉伸试验,获得材料的弹性模量、泊松比、屈服强度等性能参数。由于每块锻件的性能有所差异,因此建造的模型力学性能也有所差别。为验证材料性能对试验结果的影响,选择材料性能中对应力试验结果影响较大的杨氏模量作为研究对象,对模型加工过程中实测的杨氏模量数据进行整理,记录见表4,并按照式(3)即可计算出杨氏模量的标准不确定度。
|
|
表 4 材料杨氏模量 Tab.4 Material Young′s modulus |
为研究材料杨氏模量对模型结构强度的灵敏系数,利用数值模拟方法,分别计算不同杨氏模量下模型的跨中壳板中面周向应力和跨端壳板内表面纵向应力,计算结果见表5。对计算结果进行拟合分别得到应力与杨氏模量的关系曲线,如图3所示。根据拟合结果可以发现,模型跨中壳板中面周向应力和跨端壳板内表面纵向应力与杨氏模量呈线性关系,且随着杨氏模量的增大,所测应力逐渐减小;跨中壳板中面周向应力和跨端壳板内表面纵向应力关于杨氏模量的灵敏系数分别为
|
|
表 5 不同杨氏模量对应的模型应力 Tab.5 Model stress corresponding to different Young′s modulus |
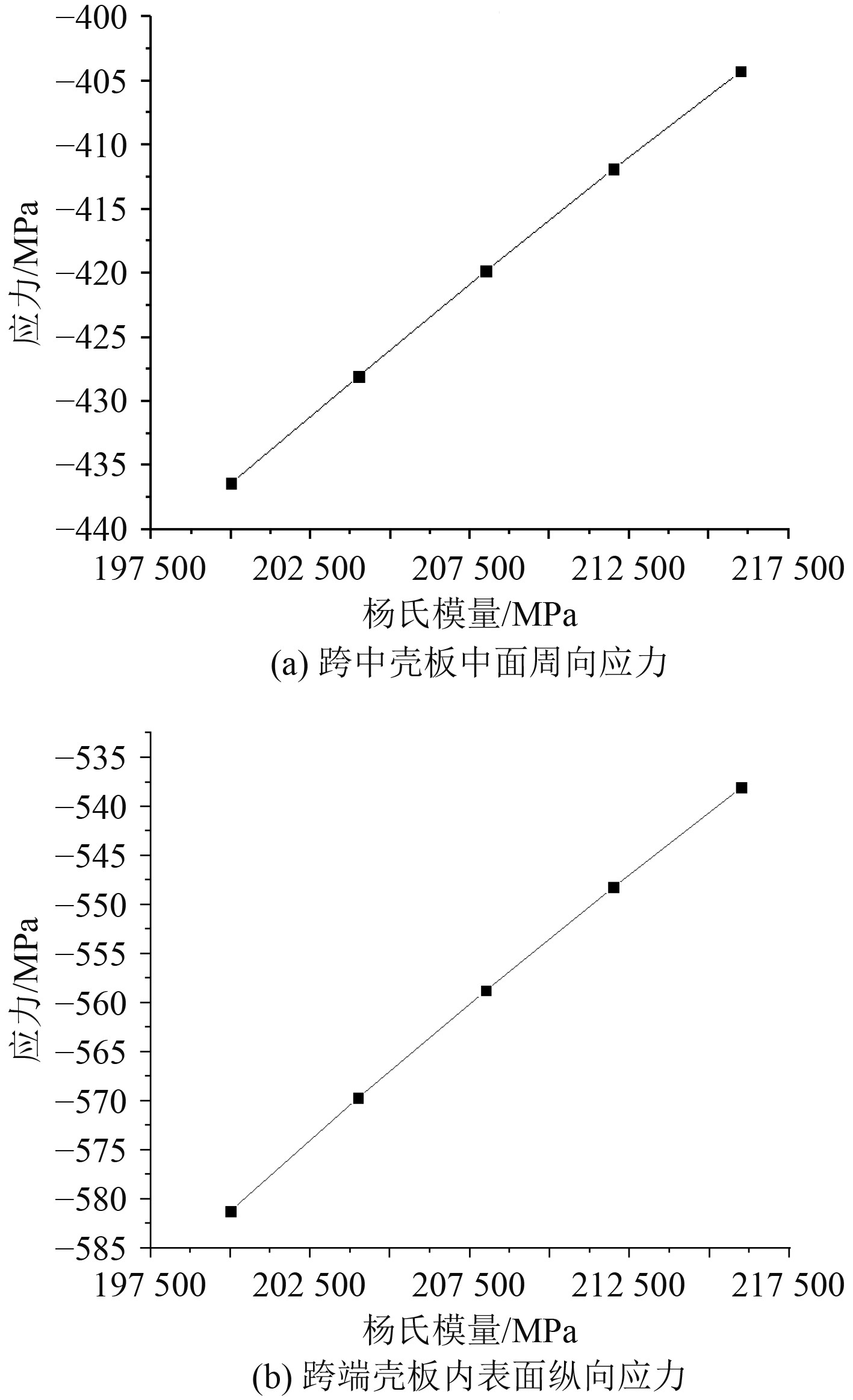
|
图 3 不同杨氏模量对应的模型应力 Fig. 3 Model stress corresponding to different Young′s modulus |
| $ {\mathrm{\sigma }}_{2}^{0} =0.00201E-837.89 ,$ | (14) |
| $ {\sigma }_{1} =0.0027E-1119.95。$ | (15) |
模型试验前需要对模型壳板及肋骨的初挠度进行测量,初挠度偏差会对模型的应力产生影响。根据模型加工技术要求的规定,模型壳板初挠度和肋骨初挠度的偏差应控制在≯0.1 mm。为验证初挠度偏差对模型力学性能的影响,借助激光跟踪仪测量圆柱壳模型肋骨及跨中壳板的初挠度,测量结果记录见表6。根据式(3)即可计算出模型初挠度的标准不确定度为
|
|
表 6 模型初挠度 Tab.6 Model shell initial deflection |
为获得模型初挠度对结构强度的影响,在满足模型加工技术要求的前提下,采用数值模拟的方法,选择模型的一阶屈服模态作为模型的初挠度形式,调整模型的最大初挠度值,分别计算不同初挠度所对应的模型跨中壳板中面周向应力和跨端壳板内表面纵向应力,计算结果记录见表7。对计算结果进行拟合得到初挠度偏差与壳板中面周向应力及跨端壳板内表面纵向应力的关系曲线,如图4所示。从拟合结果可以发现,模型的最大初挠度偏差与模型的周向应力和纵向应力呈线性关系,随着初挠度偏差的增大,模型典型位置的周向应力和纵向应力也随之增大,但在加工技术要求的控制范围内,应力的变化幅值不大,对结构的安全性影响相对较小。根据拟合公式可知跨中壳板中面周向应力和跨端壳板内表面纵向应力关于初挠度偏差的灵敏系数分别为−103和−37.75。
|
|
表 7 不同初挠度下模型的应力 Tab.7 The stress of the model under different initial deflection |

|
图 4 不同初挠度偏差对应的模型应力 Fig. 4 Model stresses corresponding to different initial deflection deviations |
| $ {\sigma }_{2}^{0} =-103r-436.2 ,$ | (16) |
| $ {\sigma }_{1} =-37.75r-580.92。$ | (17) |
在开展模型强度试验过程中需要用压力表监测压力筒内的压力,试验所用的压力表为数字压力表,型号为MD-S280,测量精度为0.4级,量程为0~10 MPa,假设压力表的测量结果为均匀分布,则压力表的标准不确定度为0.4%×10/
根据结构的弹性理论可知,当结构处在弹性阶段时,其应力与压力呈线性关系。根据数值模拟计算结果,可以得到压力表关于周向应力和纵向应力的灵敏系数分别为−66.12和−88.07。
4.5 数据测量在模型试验过程中,为了确保试验结果的准确性,需要开展多次重复性试验,在每次试验前,需要重新初始平衡,以避免环境对试验数据的影响。表8为重复性试验中测量的模型跨中壳板中面周向应力和跨段壳板内表面纵向应力数据,根据式(3)即可计算出重复性试验的标准不确定度。
|
|
表 8 应力测量 Tab.8 Stress measurement |
表9和表10分别为模型应力关于各个误差源的灵敏系数、自由度、标准不确定度以及
|
|
表 9 跨中壳板中面周向应力不确定度汇总 Tab.9 Summary of uncertainty of circumferential stress at midplane of midspan shell |
|
|
表 10 跨端壳板内表面纵向应力不确定度汇总 Tab.10 Summary of uncertainty of longitudinal stress on the inner surface of end shell |
根据上文对环肋圆柱壳强度试验各影响因素的标准不确定度和灵敏系数的分析,利用式(6)即可得到模型跨中壳板中面周向应力的合成不确定度
根据《测量不确定度表示指南》(GUM)中给出的测量不确定度评定方法,本文对水下耐压环肋圆柱壳强度试验进行了不确定度分析,提取了试验过程中影响较大的误差源,分析了各个分量的不确定度,给出了环肋圆柱壳跨中壳板中面周向应力和跨端壳板内表面纵向应力在95%置信水平下的置信区间,并得出如下结论:
1)对于小尺度环肋圆柱壳精车模型的壳板应力,应力数据测量和加工所用材料性能的偏差引起的不确定度相对较大,板厚和初挠度引起的不确定度较小;
2)压力表对试验结果的不确定度会产生一定的影响,因此,选择合适量程的压力表对提升试验结果精度有积极意义;
3)与焊接模型相比,精车模型可以很好地降低因加工误差对试验结果带来的影响,试验数据可用于相关计算方法的验证。
| [1] |
Guide to the Expression of Uncertainty in Measurement(GUM)[S]. ISO, 3st edition, 2008.
|
| [2] |
张立, 陈建挺, 陈伟民, 等. 标准船模的阻力单航次试验不确定度分析[J]. 华中科技大学学报, 2020, 48(4): 85-90.. ZHANG Li, CHEN Jianting, CHEN Weimin, et al. Uncertainty analysis of calibration ship model single-run resistance tests[J]. Journal of Huazhong University of Science and Technology, 2020, 48(4): 85-90.. |
| [3] |
马向能, 孙张群, 冯骏. 测量不确定度分析在操纵性试验中的应用[J]. 船舶力学, 2004, 8(5): 52-61. MA Xiangneng, SUN Zhangqun, FENG Jun. Uncertainty analysis in captive model test[J]. Journal of Ship Mechanics, 2004, 8(5): 52-61. DOI:10.3969/j.issn.1007-7294.2004.05.007 |
| [4] |
沈泓翠, 姚震球, 吴宝山, 等. 船舶CFD模拟不确定度分析与评估新方法研究[J]. 船舶力学, 2010, 14(10): 1071−1083. SHEN Hongcui, YAO Zhenqiu, WU Baoshan, et al. A new method on uncertainty analysis and assessment in ship CFD[J]. Journal of Ship Mechanics, 2010, 14(10): 1071−1083. |
| [5] |
吴乘胜, 邱耿耀, 魏泽, 等. 船模阻力数值水池试验不确定度评估[J]. 船舶力学, 2015, 19(10): 1197-1208. WU Chengsheng, QIU Gengyao, WEI Ze, et al. Uncertainty analysis on numerical computation of ship model resistance.[J]. Journal of Ship Mechanics, 2015, 19(10): 1197-1208. DOI:10.3969/j.issn.1007-7294.2015.10.004 |
| [6] |
司海龙, 顾学康, 胡嘉骏, 等. 船模波浪载荷试验不确定度分析方法研究[J]. 船舶力学, 2022, 26(2): 202-214. SI Hailong, GU Xuekang, HU Jiajun, et al. Uncertainty analysis of ship model wave-induced load experiment[J]. Journal of Ship Mechanics, 2022, 26(2): 202-214. DOI:10.3969/j.issn.1007-7294.2022.02.005 |
| [7] |
汪雪良, 顾学康, 胡嘉骏, 等. 大型LNG船波激振动模型试验研究[J]. 中国造船, 2012, 53(4): 1-12. WANG Xueliang, GU Xuekang, HU Jiajun, et al. Experimental investigation of springing responses of a large LNG carrier[J]. Shipbuilding of China, 2012, 53(4): 1-12. DOI:10.3969/j.issn.1000-4882.2012.04.003 |
| [8] |
汪雪良, 顾学康, 胡嘉骏, 等. 双体船波浪载荷测试技术研究[J]. 舰船科学技术, 2010, 32(1): 28-37. WANG Xueliang, GU Xuekang, HU Jiajun, et al. Study on the testing technology of wave-induced loads of catamarans[J]. Ship Science and Technology, 2010, 32(1): 28-37. DOI:10.3404/j.issn.1672-7649.2010.01.003 |
| [9] |
郑红. 测量不确定度的自由度计算[J]. 计量与测试技术, 2014, 41(12): 44-48. ZHENG Hong. Calcutation of degrees of freedom of uncertainty in measurement[J]. Metrology and Testing Technology, 2014, 41(12): 44-48. |
| [10] |
徐秉汉, 朱邦俊, 等. 潜艇结构强度理论与试验方法[M]. 北京: 国防工业出版社, 2007.
|
 2024, Vol. 46
2024, Vol. 46
