随着水下空间成为国际竞争的新焦点,UUV等水下航行器在海洋开发利用和海洋国土防卫等领域逐步发挥着重要作用[1]。探测系统和通信系统是UUV普遍配备的电子设备,也是现有水下信息系统不可或缺的组成部分。然而,当前探测及通讯系统相互独立,彼此之间缺乏统一规划设计,占据了大量的平台空间,容易恶化平台附近的水声条件,对平台整体的机动性、隐蔽性以及安全性造成了较大的影响[2]。为了解决以上问题,研究人员提出了水下探测通信一体化系统工作体制。其中,基于共享信号的探测通信一体化通过复用探测及通信系统的信道、基阵等资源,发射一种共享信号同时实现目标探测和水声通信的功能[3]。
探测通信一体化理论最先在雷达领域提出并得到广泛关注,技术发展较快。20世纪80年代,美国海军实验室首次共用雷达和通信系统硬件,验证了探测通信一体化理论的应用可行性。2016年,美国空军实验室提出了PSK-LFM探测通信一体化波形,并分析了相位变化与雷达探测性能间的关系[4]。2017年,Bulnt等[5]提出了一种基于连续相位调制方法(Continuous Phase Modulation, CPM)调制LFM信号的一体化波形。张林让等[6]通过循环编码阵列的方法在LFM-CPM一体化波形中引入了时间步进量,实现了发射波束的空域覆盖。杨卜镔等[7]则深入研究了多普勒效应对一体化技术的影响,针对LFM-MSK信号模型,提出了相关的频率偏移估计算法。此外,基于OFDM信号的探测通信一体化信号形式也得到了广泛的研究,相比LFM等探测波形,有望实现更高的通信速率,但探测性能无法保障[8]。然而直到目前为止,探测通信一体化技术在声纳,特别是在UUV等水下机动平台的研究较少,尚无突出进展。
在针对上述问题需求,本文提出了一种基于Costas-DPSK编码的水下探测通信一体化波形设计方法,采用Costas序列对单频信号进行跳频编码,并将通信信息序列调制到频率编码子脉冲相位上,同时实现了目标探测和水声通信功能。文中分别给出了一体化波形模型及相关信号处理方案,并通过仿真实验分析证明,该信号同时具备与LFM信号类似的目标探测能力以及DPSK调制的通信能力,是一种可行的水下探测通信一体化信号形式。
1 信号模型 1.1 Costas频率编码Costas序列是一种特殊的置换矩阵,与序列本身向任何方向的平移拷贝之间的重合元素数量不大于1。与递增序列相比,Costas序列的特殊结构使得其自相关矩阵副瓣相对均匀的分布在整个矩阵中。因此,若以Costas序列对信号进行频率编码,信号可以实现高而尖锐的模糊度函数主瓣,即近似“图钉状”[9]。
Costas频率编码信号利用N阶Costas序列对单频信号进行频率编码调制,其复数表达式如下:
| $ s(t) = \sqrt {\frac{1}{{{T_b}}}} \sum\limits_{n = 0}^{N - 1} {{u_n}(t - n{T_b})},$ | (1) |
| $ \qquad u(t)={e}^{j2{\text{π}} {f}_{0}t} \cdot {e}^{j2{\text{π}} {f}_{n}t},0\leqslant t\leqslant {T}_{b}。$ | (2) |
式中:
图1为一个22阶的Costas频率编码信号的模糊度函数结果,信号参数如下:子信号脉冲宽度为4 ms,起始频率为20 kHz,调频间隔为250 Hz,子信号初始相位均为0。根据图中结果可知,Costas频率编码信号的模糊度函数主瓣高而尖锐,旁瓣低且平坦,具备较高的时延和频移分辨力。本文以Costas频率编码信号作为水声通信信息调制的载波,可以提升探测通信一体化信号的自相关性能,有利于实现目标检测。

|
图 1 Costas信号模糊度函数 Fig. 1 Ambiguity function of Costas signal |
上述一体化信号已使用Costas序列进行频率编码,因此,常规的通信信息调制方法中可使用幅度调制或相位调制,其中幅度调制对信号包络影响较大且抗干扰能力较差。鉴于此,本文中使用DPSK调制方法,通过载波相位变化表示通信信息,具有一定的抗干扰能力,且能够有效的对抗相位调制中“反向工作”问题[10]。
在Costas频率编码的基础上对子信号的相位进行信息调制得到Costas-DPSK信号的复数形式如下:
| $ s(t) = \sqrt {\frac{1}{{{T_b}}}} \sum\limits_{n = 0}^{N - 1} {{u_n}(t - n{T_b})\exp \left(j\frac{m}{M}{\text π} \right)}。$ | (3) |
式中:M为相位调制阶数;
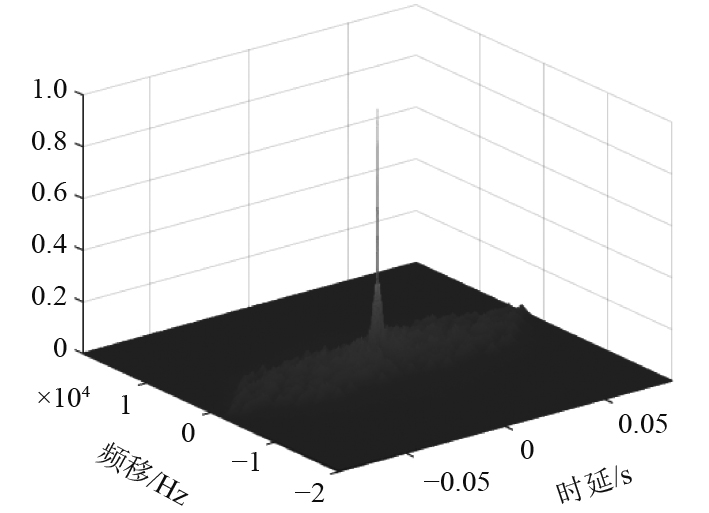
通常情况下,信号的相位改变会导致其模糊度函数状态产生一定的变化。为衡量通信信息序列DPSK调制对Costas编码信号自相关能力的影响,采用随机序列对信号进行DPSK调制,其余信号参数与图1中保持一致,则此时的Costas-DPSK信号模糊度函数如图2所示。
|
图 2 Costas-DPSK信号模糊度函数 Fig. 2 Ambiguity function of Costas-DPSK signal |
可知,经过DPSK调制的Costas频率编码信号模糊度函数未发生明显变化,仍旧近似于“图钉状”,具备良好的时延和频移分辨力。
1.3 探通一体化信号由于UUV等水下航行器运动时的多普勒效应导致水声信号受到严重的压缩或展宽,因此,一体化信号的结构设计中应添加部分导引信号,用以实现对于通信信号的捕获和同步,继而实现对接收端信号的精确补偿,抵消水下航行器平台运动产生的不良影响。
本文设计的探测通信一体化信号结构如图3所示,利用Costas-DPSK信号实现探测及通信,HFM+CW信号进行导引。其中,可根据任务需求采用同阶的不同Costas序列增加探测通信帧长度,提高单次发射信号携带的通信信息。导引帧中的HFM信号[11]用于对接收端信号的检测、捕获;CW信号具备较高的频移分辨力,可完成接收信号多普勒频移,从而达成对接收信号的多普勒补偿。

|
图 3 一体化信号结构 Fig. 3 The structure of the integrated signal |
探通一体化信号采用周期式脉冲发射,在基阵接收端可使用匹配滤波对目标反射信号进行处理,完成目标探测。本文中主要对通信信息解调方案进行分析。
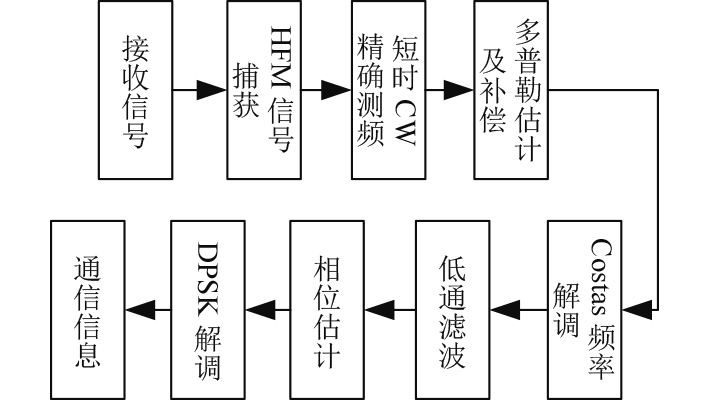
通信信息处理流程如图4所示。信息解调的基础是将通信信号从接收信号中完成提取出来。首先,利用HFM信号匹配滤波捕获通信信号位置,其次采用精确测频算法确定CW信号的中心频率,从而实现通信多普勒因子估计及补偿,之后根据约定的Costas序列依次对子脉冲进行频率解调,经过低通滤波器之后,对各子脉冲相位进行估计,最后通过DPSK解调器获得通信信息序列。
|
图 4 通信信息处理流程框图 Fig. 4 The diagram of communication information processing |
在上述方案中,多普勒估计后续流程与常规DPSK解调无明显区别。因此,通信信号捕获及多普勒因子估计精度在很大程度上决定了通信性能水平。文中采用具备良好自相关性能和宽多普勒容限的HFM信号保证信号捕获能力,而多普勒因子估计问题则使用Rife[12]等短时序列精确测频方法解决。
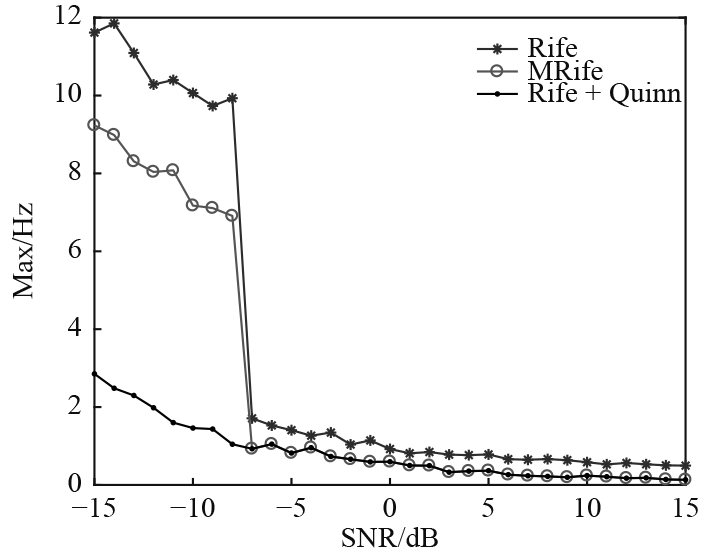
对于脉冲宽度为40 ms,中心频率为17.5 kHz,采样频率为100 kHz的单频信号,采用Rife等算法进行频率估计,在
|
图 5 频率估计精度曲线 Fig. 5 The accuracy curve of frequency estimation |
可知,随着SNR的提升,单频信号的频率估计最大误差逐渐降低。当SNR提升至−7 dB以上时,3种算法的最大估计误差降低至2 Hz以内,当SNR提升至0 dB以上时,最大估计误差降低至1 Hz以内。根据
本文主要通过对波形模糊度图、零多普勒切片曲线、零时延切片曲线以及自相关性能等指标对探测性能进行分析,其中自相关指标包括主瓣宽度和峰值旁瓣比。
主瓣宽度定义为零多普勒切片曲线主瓣−3 dB的时间宽度,单位为s。峰值旁瓣比定义如式(4)所示,为零多普勒切片曲线的最大旁瓣峰值与主瓣峰值的比值,单位为dB。
| $ PSLR = 20\lg \frac{{\left| {{P_s}} \right|}}{{\left| {{P_m}} \right|}}。$ | (4) |
对于波形的通信性能,本文从通信误码率进行分析,定义如下:
| $ {P}_{b}=\frac{错误比特数}{总比特数}。$ | (5) |
仿真参数设置如下:子脉冲信号宽度为4 ms,起始调制频率为20 kHz,频率编码序列为22阶Costas序列[4, 1, 9, 3, 19, 7, 16, 15, 10, 8, 21, 17, 20, 12, 18, 2, 14, 5, 6, 11, 13],跳频间隔为250 Hz,DPSK调制序列为随机序列。此时,信号的模糊度函数如图2所示,近似“图钉型”。
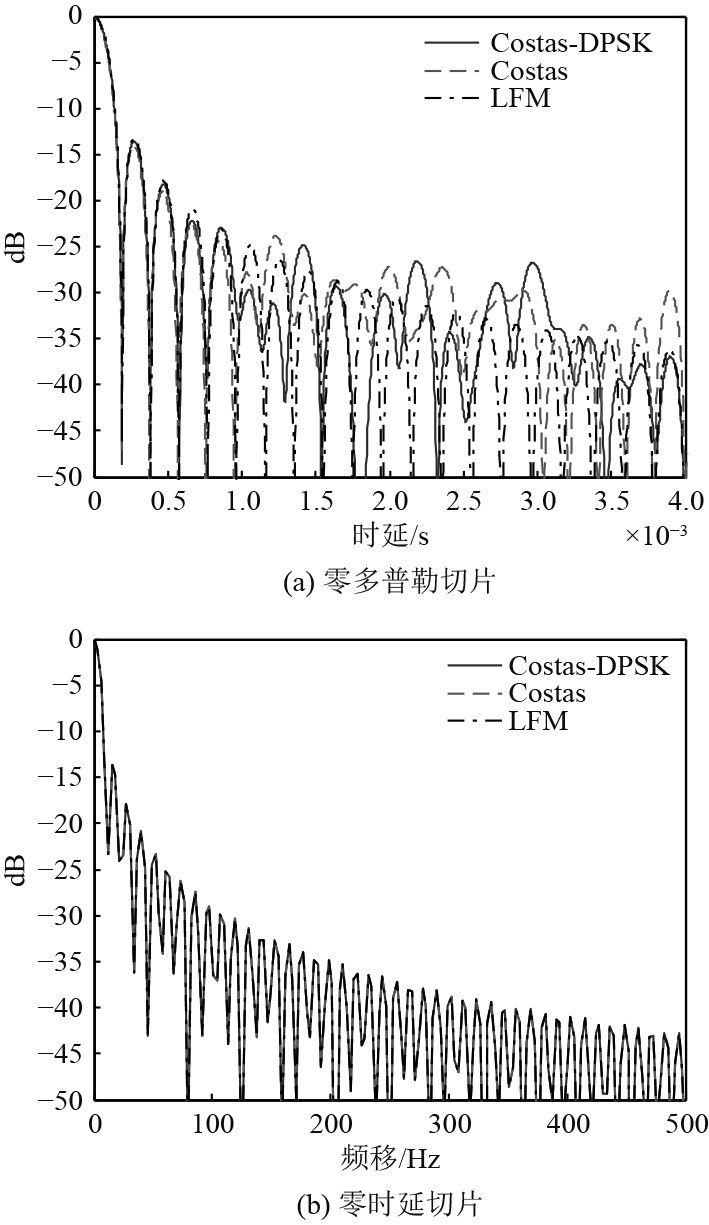
图6为LFM、Costas以及Costas-DPSK信号的模糊函数零多普勒切片曲线和零时延切片曲线。表1为3种信号的自相关能力对比结果。其中,Costas参数与Costas-DPSK参数保持一致,子脉冲初始相位均为0,LFM信号与其余两者保持相同的脉宽和带宽。
|
图 6 一体化信号模糊度函数切片图 Fig. 6 The slices of ambiguity function of the integrated signal |
|
|
表 1 自相关能力对比 Tab.1 The comparison of autocorrelation performance |
根据图6及表1结果可知,3种信号的模糊函数零时延切片曲线重合,即Costas-DPSK信号与同等条件下的Costas信号、LFM信号具备相同的频移分辨能力。在零多普勒切片曲线上,Costas-DPSK信号与其余2种信号的主瓣及最大旁瓣基本重合,Costas-DPSK信号主瓣宽度约为0.15 ms,峰值旁瓣比约−13.77 dB,略优于LFM信号以及Costas信号。LFM信号零多普勒切片旁瓣峰值随时延增大不断降低,Costas-DPSK信号的旁瓣峰值则最终保持在−30 dB左右,在大时延条件下旁瓣峰值高于LFM信号。总体而言,Costas-DPSK信号与同等脉宽、带宽条件下的LFM信号具备相近的探测性能。
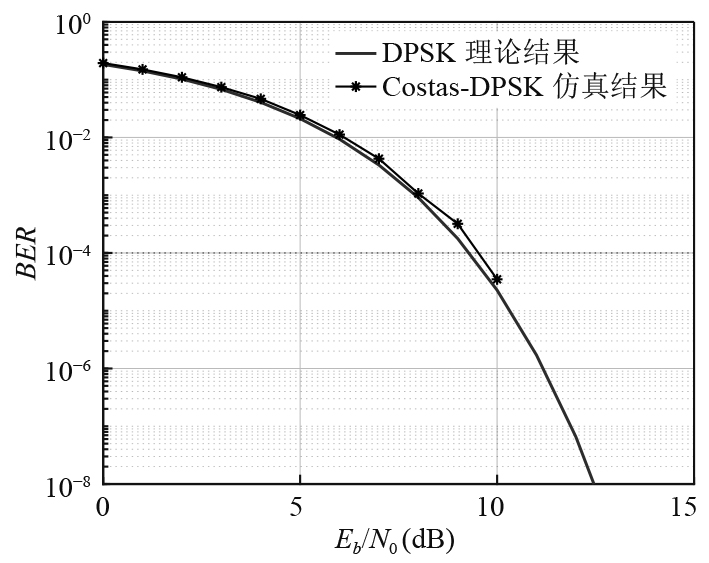
3.3 通信能力仿真分析在第3.2节中参数设置下,本文通过计算机仿真给出了Costas-DPSK信号的误码率-信噪比曲线。由图7可知,Costas-DPSK信号的误码率结果与DPSK信号的理论误码率基本保持一致,当比特信噪比在10 dB以上时,误码率可达到10−4以下。考虑到探测通信一体化系统采用探测基阵发射信号,发射源级远高于普通水声通信换能器源级,且水声通信为单程传播链路,信号传播损失低于同等距离下目标探测产生的传播损失,在理论上可以达到较高的接收端信噪比,实现较低的通信误码率。
|
图 7 误码率曲线 Fig. 7 The curves of bit error rate |
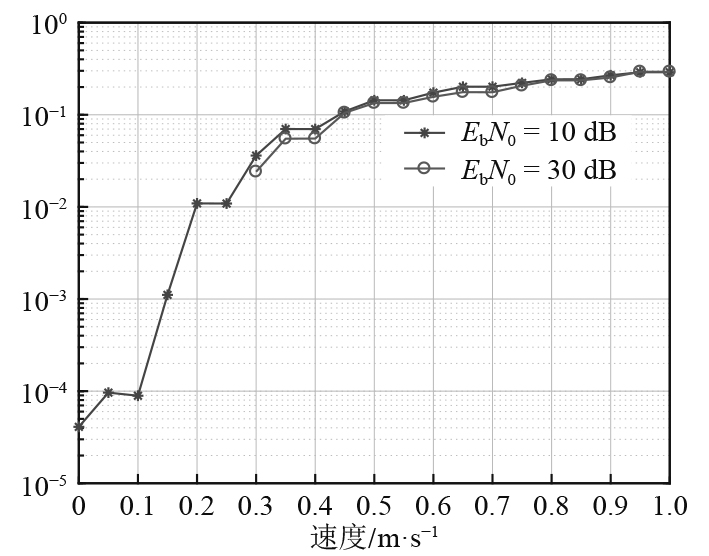
同时,由于UUV等水下航行体与通信目标之间处于多普勒运动状态,比特信噪比为10、30 dB条件下多普勒运动速度对误码率的影响仿真结果如图8所示。可知,在10 dB的比特信噪比条件下,当多普勒运动速度不超过0.1 m/s时,误码率保持在10−4左右,随着多普勒运动速度增加,误码率增大到10−1量级。在30 dB的比特信噪比条件下,在多普勒运动速度低于0.3 m/s时,受限于仿真次数,无误码情况发生,多普勒运动速度超过0.3m/s,误码率增大到10−1量级。由第2节结论可知,在比特信噪比10 dB(约接收端信噪比−10 dB)的条件下,经过短时序列精确测频后的最大多普勒频移估计误差约2 Hz,速度估计误差不超过0.17 m/s,即误码率上限约为10−3。
|
图 8 多普勒运动下误码率曲线 Fig. 8 The curves of bit error rate with doppler |
针对UUV等水下航行器探测通信一体化需求,本文提出了一种基于Costas-DPSK编码的探测通信一体化信号形式,在此基础上给出了导引信号设计及相关信息处理方法。经过仿真实验表明,该信号具备“图钉型”模糊度函数,与同等条件下LFM信号具备近似的频移、时延分辨能力,自相关峰值旁瓣低于−13 dB;在通信方面,该信号误码率与DPSK理论结果接近,且HFM+CW形式的导引信号结构保证了良好的多普勒估计和补偿能力,是一种可行的水下航行器探测通信一体化信号形式。
| [1] |
钟宏伟. 国外无人水下航行器装备与技术现状及展望[J]. 水下无人系统学报, 2017, 25(4): 215−225. ZHONG Hongwei. Development of large displacement unmanned undersea vehicle in foreign countries: a review[J]. Journal of Unmanned Undersea Systems, 2017, 25(4): 215−225 |
| [2] |
卢俊, 张群飞, 史文涛. 水下探测通信一体化关键技术分析[J]. 水下无人系统学报, 2018, 26(5): 470-479. LU Jun, ZHANG Qun-fei, SHI Wen-tao. Analysis on the key technology of integrated underwater detection and communication[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 470-479. |
| [3] |
梁兴东, 李强, 王杰, 等. 雷达通信一体化技术研究综述[J]. 信号处理, 2020, 36(10): 1615-1627. LIANG Xingdong, LI Qiang, WANG Jie, et al. Joint wireless communication and radar sensing: review and future prospects[J]. Journal of Signal Processing, 2020, 36(10): 1615-1627. |
| [4] |
NOWAK M, WICKS M, Zhang Z, et al. Co-designed radar-communication using linear frequency modulation waveform[J]. IEEE Aerospace and Electronic Systems Magazine, 2016, 31(10): 28−35.
|
| [5] |
SAHIN C, JAKABOSKY J, Mccormick P. M, et al. A novel approach for embedding communication symbols into physical radar waveforms[C]//IEEE Raclar Conference, 2017.
|
| [6] |
ZHANG Qiuyue, ZHOU Yu, ZHANG Linrang , et al. Application of LFM-CPM signal into a DFRC system based on circulating code array[J]. Elsevier Bv, 2020, 101: 102712. |
| [7] |
杨卜镔. MSK-LFM雷达通信一体化中多普勒频移估计研究[D]. 西安: 西安电子科技大学, 2021.
|
| [8] |
王冠, 康勇, 王金宇, 等. OFDM-CPM-LFM雷达通信一体化信号研究[J/OL]. 微电子学与计算机, 2023(08): 80−86[2023-10-16].
|
| [9] |
黄琼丹, 李勇, 卢光跃. 脉间Costas跳频脉内多载波混沌相位编码雷达信号设计与分析[J]. 电子与信息学报, 2015, 37(6): 1483-1489. HUANG Qiongdan, LI Yong, LU Guangyue. Design and analysis of inter-pulse costas frequency hopping and intra-pulse multi-carrier chaotic phase coded radar signal[J]. Journal of Electronics & Information Technology, 2015, 37(6): 1483-1489. |
| [10] |
张奕中, 岳玲, 吕林夏, 等. 基于MC-FH/DPSK水声通信信道编码研究[J]. 舰船科学技术, 2023, 45(7): 144-148. ZHANG yi-zhong, YUE ling, LV lin-xia, et al. Research on channel coding of underwater acoustic communication based on MC-FH/DPSK[J]. Ship Science and Technology, 2023, 45(7): 144-148. |
| [11] |
陈永兴, 王中, 樊书宏, 等. 基于双曲调频信号的水声通信帧同步方法[J]. 舰船科学技术, 2023, 45(3): 111-116. CHEN Yongxing, WANG Zhong, FAN Shuhong, et al. A frame synchronization method of underwater acoustic communication based on hyperbolic frequency modulated signal[J]. Ship Science and Technology, 2023, 45(3): 111-116. |
| [12] |
詹启东, 涂亚庆. 基于Rife法的线性调频连续波雷达测距算法及实现[J]. 兵工学报, 2014, 35(5): 748-752. ZHAN Qidong, TU Yaqing. Analysis and Implementation of Rife-based Ranging Algorithm for Linear Frequency Modulated Continuous Wave Radar[J]. ACTA ARMAMENTARII, 2014, 35(5): 748-752. |
 2024, Vol. 46
2024, Vol. 46
