2. 中国船舶集团有限公司第七一三研究所,河南 郑州 450015
2. The 713 Research Institute of CSSC, Zhengzhou 450015, China
电动缸是一种将电机与丝杠一体化设计的电动执行元件,其工作原理通过部件之间的运动,将电机的旋转运动转化为丝杆螺母的直线往复运动[1]。电动缸的功能与气压缸和液压缸类似,能够在实现直线运动的同时提供推拉作用力,但与后者相比,电动缸省去了气、液系统的管路结构,大多采用电气化和模块化设计,具备结构简单紧凑、传动效率高、响应速度快、定位精度高和无污染、易保养等优势[2-3]。因此,电动缸作为全新的机电一体化产品,在航空航天、海洋船舶、工业机械等诸多领域得到了广泛应用。
为实现深海环境下某有限空间内的作业能力,需要设计一台紧凑型电动缸来牵引负载进行往复运动。如图1所示,电动缸的轴向截面为扇形,整体通过两侧的支耳固定在圆柱体上,其动力由直流伺服电机提供,通过齿轮传动机构传递到滚珠丝杆。特殊的工作背景对电动缸运行的灵敏性、可靠性、稳定性等性能提出了较高要求。在此需求下,电动缸的齿轮传动机构设计就成了关键部分。因此本文根据技术要求,对电动缸的齿轮传动机构进行设计研究,并以动力学仿真软件ADAMS为平台,对齿轮传动机构的虚拟样机模型进行仿真与分析。

|
图 1 深海电动缸示意图 Fig. 1 Schematic diagram of deep-sea electric cylinder |
深海电动缸的传动过程如图2所示,电机作为电动缸的动力源,高速正向或反向驱动输入轴做旋转运动,而后经齿轮传动机构进行降速,最终通过滚珠丝杆副将旋转运动转化为输出轴的直线往复运动。电动缸的输入端所用电机为直流无刷电机,额定功率为100 W;额定转速为600 r/min;输出端的滚珠丝杆的规格为14 mm×4 mm;推/拉负载为
|
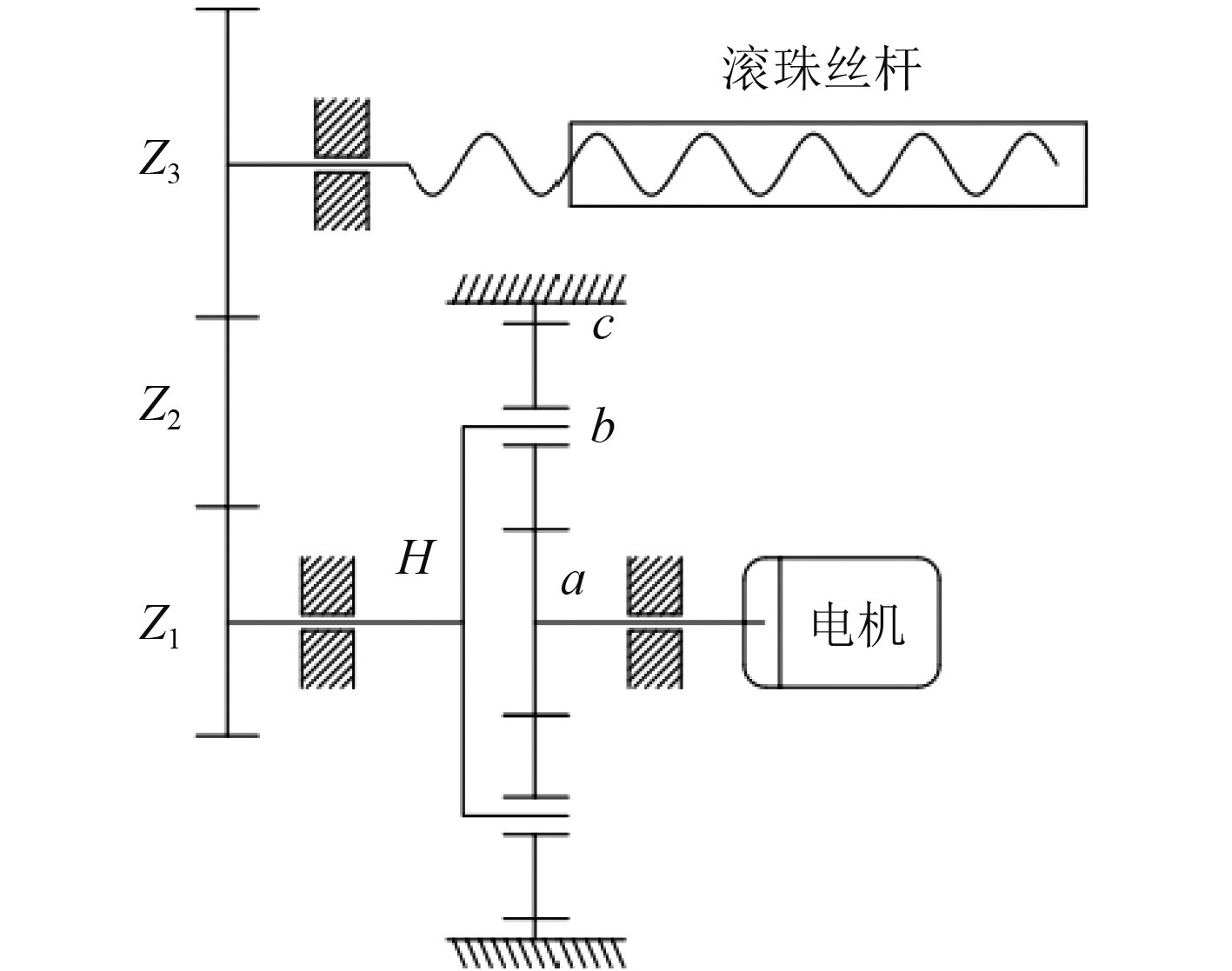
图 2 深海电动缸传动机构简图 Fig. 2 Structure diagram of deep-sea electric cylinder transmission mechanism |
根据负载特点、工作形式以及电机驱动指标分析,该传动系统的设计难点是输出载荷大、可用空间小、传动比大。由于该型深海电动缸的空间体积和重量限制,因此齿轮传动机构选用定轴轮系和行星轮系组合而成的混合轮系。混合轮系中,定轴轮系的主要作用是配合行星轮系完成传动比的分配及旋转轴线的过渡,而行星轮系的主要贡献是在有限的空间体积内提供较大的传动比[4]。常用的行星轮系根据传动机构中齿轮的啮合方式可分为NGW、NN、NW、NGWN和ZUWGW等类型。其中的字母含义是W代表外啮合;N代表内啮合;G代表内外啮合公用行星齿轮;ZU代表锥齿轮。相比于其他类型,NGW型行星齿轮传动具有体积小、重量轻、结构紧凑、传动比范围广、传递效率高等一系列的优点,因此混合传动方案中行星轮系选择NGW型行星齿轮[5-6]。在传动流程中,电机产生动力,由输入轴传递到行星轮系的太阳轮a,经均载装置保持3个行星轮b载荷均匀分布和功率均匀分流,行星架H主轴降速旋转,然后由定轴齿轮Z1、Z2和Z3传动至滚珠丝杆输出。
1.2 参数计算深海电动缸的齿轮传动机构中齿轮的基本参数有:齿数z、压力角α、模数m、顶隙系数c*和齿顶高系数h*。考虑到电动缸的维修性及齿轮零件的可替代性,齿轮均选用渐开线标准直齿圆柱齿轮,其压力角α=20°;顶隙系数c*=0.25;齿顶高系数h*=1。而各齿轮的齿数分配则以满足总传动比作为前提[7]。
行星轮系作为传动系统中复杂且关键的部件,如果各轮齿数匹配不当,可能导致轮系运动干涉或者无法装配等情况。在设计齿数时应满足传动比条件、装配条件、同心条件以及邻接条件[8]。传动比条件即各轮齿数与传动比的关系,在该传动机构中,输入为太阳轮,输出为行星架,则单级传动比为:
传动机构中定轴轮系的3个齿轮的轴线平行且位于同一平面,在齿数设计中仅需要满足传动比条件和装配条件。齿轮Z1嵌套在行星轮系的输出端,与行星架H同步旋转,齿轮Z2与齿轮Z1、Z3分别啮合,不参与传动比的分配,仅用于调整齿轮间距。齿轮Z3嵌套在滚珠丝杆的输入端,与滚珠丝杆同步旋转。由此可以得出,定轴轮系需满足的传动比条件关系式为:
深海电动缸齿轮传动机构的主要作用是改变转速和传递扭矩,因此所有齿轮都需要满足由负载产生的强度条件。当得到齿轮传动系统的总传动比及齿数关系式后,进行齿数的确认,并结合其他参数校核其能否满足强度条件。经计算,得到齿轮传动机构的齿数,如表1所示。
|
|
表 1 齿轮传动机构的齿数 Tab.1 Number of teeth in gear gear transmission mechanism |
基于传动机构的结构参数建立三维物理模型,借助于虚拟样机技术,进行传动机构的运动仿真模拟。ADAMS作为一种虚拟样机专业分析软件,经常用于机械结构的静力学、运动学和动力学分析中,以输出位移、速度、加速度和作用力等曲线,具有良好的可视化效果和后处理功能,且与常用的三维建模软件有专业接口[9]。基于以上因素,选用ADAMS软件作为电动缸传动机构进行运动仿真的环境。
根据表1提供的电动缸齿轮传动机构的参数,使用三维建模软件SolidWorks 分别建立行星轮、太阳轮、内齿圈、定轴齿轮和滚珠丝杆等零件的物理模型,并完成齿轮对的虚拟装配。将装配好的模型另存为Parasolid格式,而后导入到ADAMS软件。为提高计算效率,去除齿轮模型的圆角特征。导入后的虚拟样机模型如图3所示,为方便观察齿轮传动内部结构,显示界面隐藏了内齿圈。手动赋予各实体的材料参数后,ADAMS将自动生成各实体所对应的质量和转动惯量等信息。

|
图 3 齿轮传动机构虚拟样机模型 Fig. 3 Physical model of gear transmission mechanism |
根据传动机构的运动规律,对虚拟样机模型施加约束和载荷[10]分别为:1)在行星轮系中,内齿圈由于始终处于静止状态,因此与大地之间视为固定旋转副;2)行星架、太阳轮、定轴齿轮与大地之间施加旋转副;3)行星轮与行星架之间添加旋转副;4)由于行星架与定轴齿轮Z1,定轴齿轮Z3与滚珠丝杆均保持同步旋转,因此视为2个固定旋转副;5)太阳轮上施加来自电机的驱动转速;6)定轴齿轮Z3上施加来自输出端的负载转矩。
2.3 接触的定义齿轮传动机构在啮合过程中由于相互碰撞产生接触力,其由2部分组成,即齿轮相互切入产生的弹性力和相对速度产生的阻尼力。在ADAMS中采用冲击函数法(impact)计算齿轮对之间的接触力。接触力的定义形式如下式。
| $ F = \left\{ \begin{gathered} {\text{max}} \left[ {{\text{0,}}K{{\left( {{x_{\text{0}}}, x} \right)}^e} - {\text{STEP}}\left( {x, {x_0} - d, C, {x_{\text{0}}}, 0} \right)\dot x} \right], x < {x_{\text{0}}} ,\\ {\text{0,}}x \geqslant {x_{\text{0}}}。\\ \end{gathered} \right. $ | (1) |
式中:F为接触力;K为接触刚度;x0为接触参考距离;x为碰撞齿轮的实际距离;e为刚性力系数;STEP为阶跃函数;d为齿轮的切入深度;C为阻尼系数。
根据Hertz碰撞理论[11],将齿轮碰撞产生的冲击力看作2个变曲率圆柱体的碰撞情景,则接触刚度K取决于齿轮形状和材料,如下式:
| $ K = \frac{4}{3}{R^{0.5}}{E^{\text{*}}} 。$ | (2) |
式中:R为综合曲率半径;E*为综合弹性模量。
综合曲率半径R的计算式如下式:
| $ \frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}。$ | (3) |
式中:R1、R2为接触点的当量半径,可由接触齿轮的分度圆半径替代。
综合弹性模量如下式:
| $ \frac{1}{{{E^{\text{*}}}}} = \frac{{\left( {1{{ - }}\mu _1^2} \right)}}{{{E_1}}} + \frac{{\left( {1{{ - }}\mu _2^2} \right)}}{{{E_2}}} 。$ | (4) |
式中:E1、E2为接触齿轮的弹性模量;μ1、μ2为接触齿轮的泊松比。
该传动机构需要添加接触力的齿轮:太阳轮与行星轮、星轮与内齿圈、定轴齿轮Z1与Z2、Z2与Z3。已知齿轮材料的弹性模量为2.06×109 Pa,泊松比为0.27,将齿轮的形状和材料参数代入,可计算出以上齿轮对应的接触刚度K分别为8.38×107、1.07×108、1.07×108、1.11×107 N·m,齿轮切入深度d=0.1 mm,刚性力指数e=1.5,阻尼系数C=0.01 K。
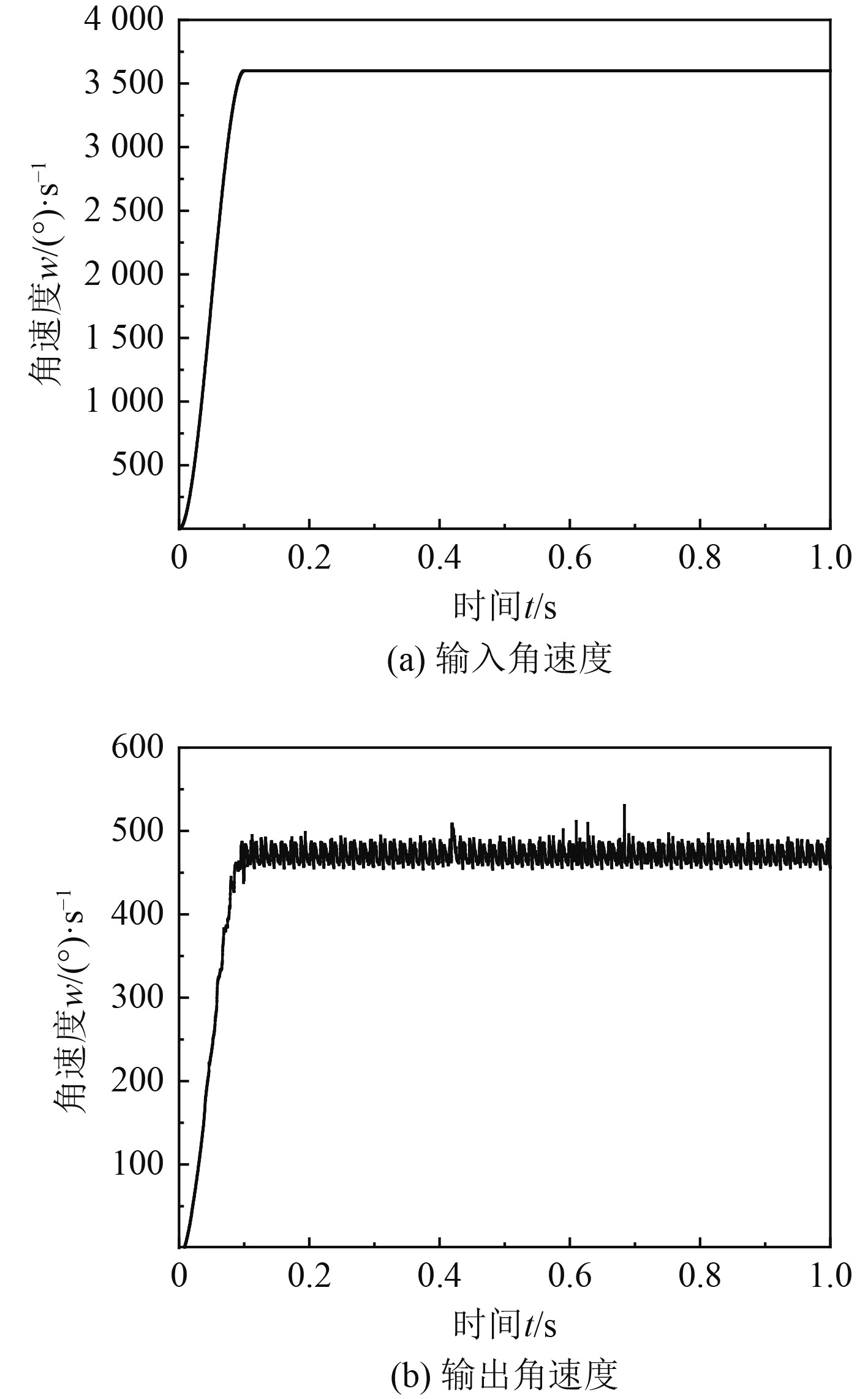
3 仿真分析 3.1 运动学仿真基于虚拟样机模型,在传动机构的输入轴即太阳轮上施加驱动转速,转速值为600 r/min。在输出轴即滚珠丝杆上施加负载扭矩,扭矩值为3.01 N·m。为避免驱动或负载的突变导致解算过程收敛困难和仿真结果的失真,使用Step过渡函数使太阳轮的驱动转速平缓加载,输入和输出过程曲线如图4所示。在Solve求解器中设置仿真时间为1 s,计算步数为
|
图 4 传动机构输入/输出运动曲线 Fig. 4 Input/output motion curve of transmission mechanism |
由输出轴的角速度过程曲线可知,在虚拟样机模型启动阶段,输出轴角速度由0快速爬升。运行0.1 s后,输出轴角速度在平均值附近上下小幅波动,并呈现出一定的周期性特征,这是由齿轮啮入和啮出过程中产生的周期性刚度冲击造成的。由仿真计算出的输出轴角速度平均值为474.5°/s;与理论值472.4°/s对比误差为0.44%;仿真传动比为7.59;与理论传动比7.62对比误差为0.4%。由图5可知,行星轮质心在x、y方向上呈现固定相位差的正弦波位移曲线,即行星轮严格按照运动规律绕太阳轮公转。由此可见,仿真结果与理论相吻合,证明了虚拟样机模型的合理性和可靠性。

|
图 5 行星轮质心位移曲线 Fig. 5 Displacement curve of planetary gear center of mass |
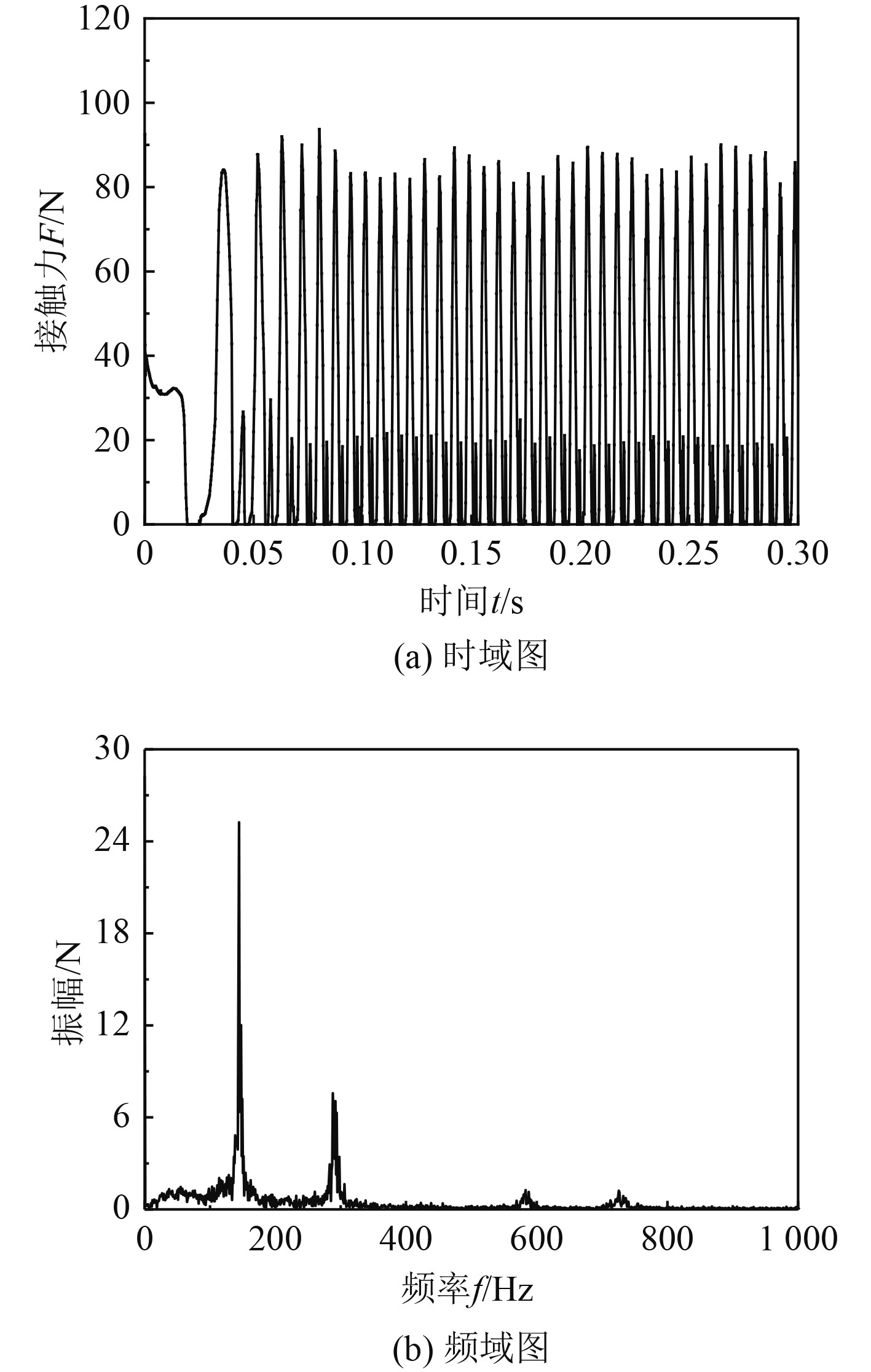
深海电动缸的传动机构动力学模型中各齿轮接触力的动态变化反映了动力的传递情况,对接触力进行仿真分析,图6~图9为各级齿轮接触力的时域和频域曲线。
|
图 6 太阳轮-行星轮啮合接触力 Fig. 6 Contact force between solar and planetary gears |
|
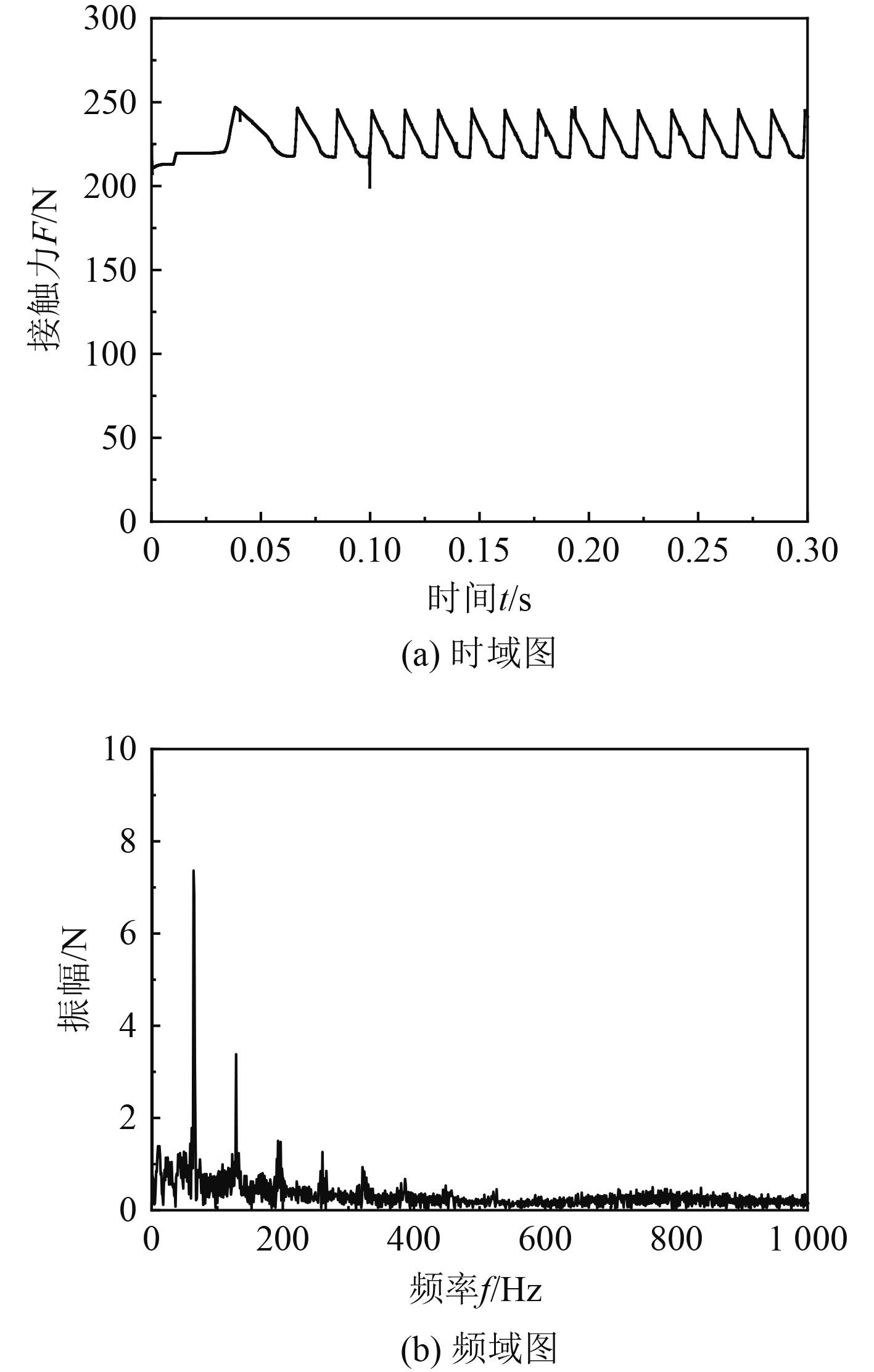
图 9 定轴齿轮Z2-Z3接触力 Fig. 9 Contact force of fixed shaft gear Z2-Z3 |
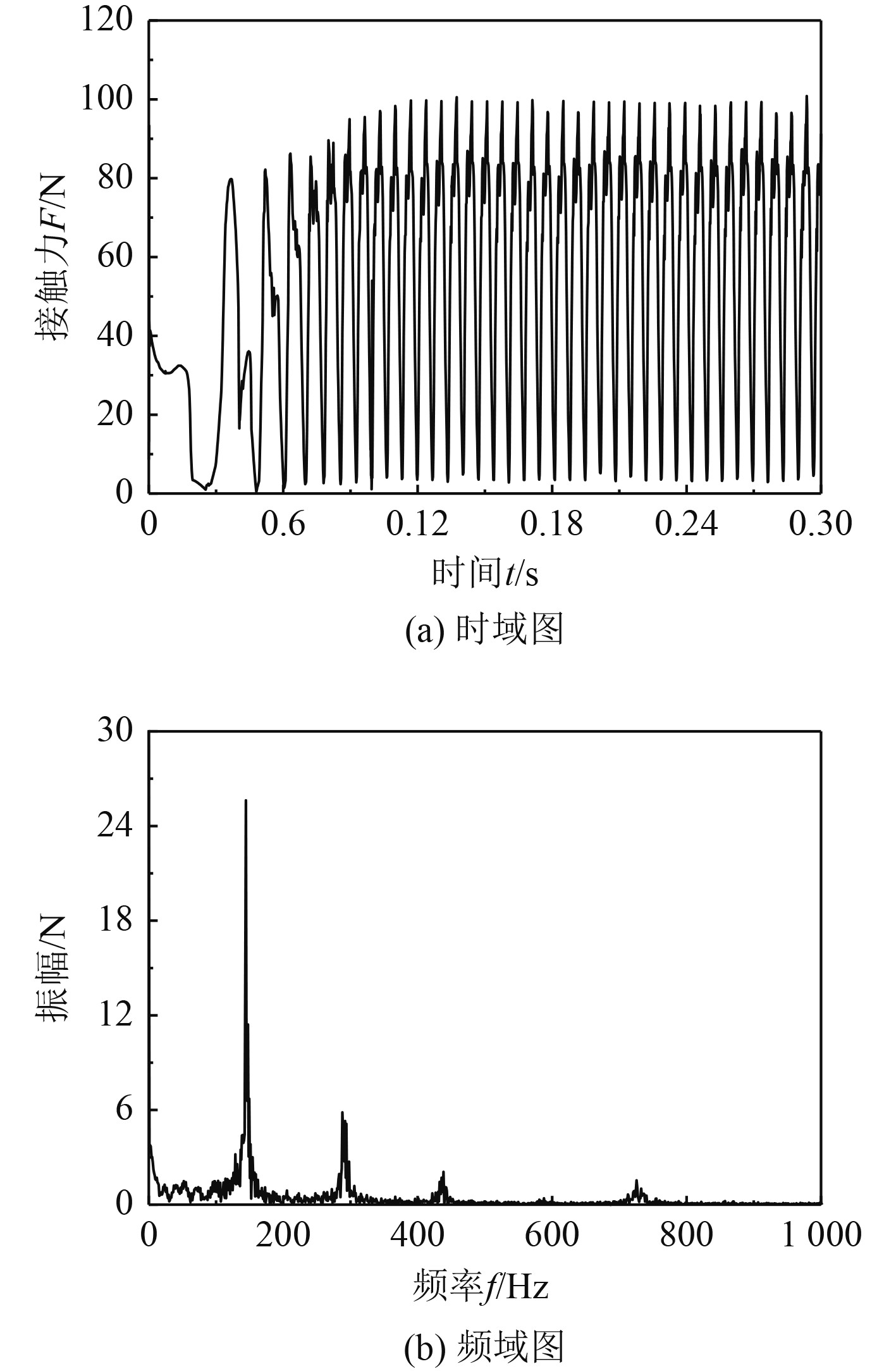
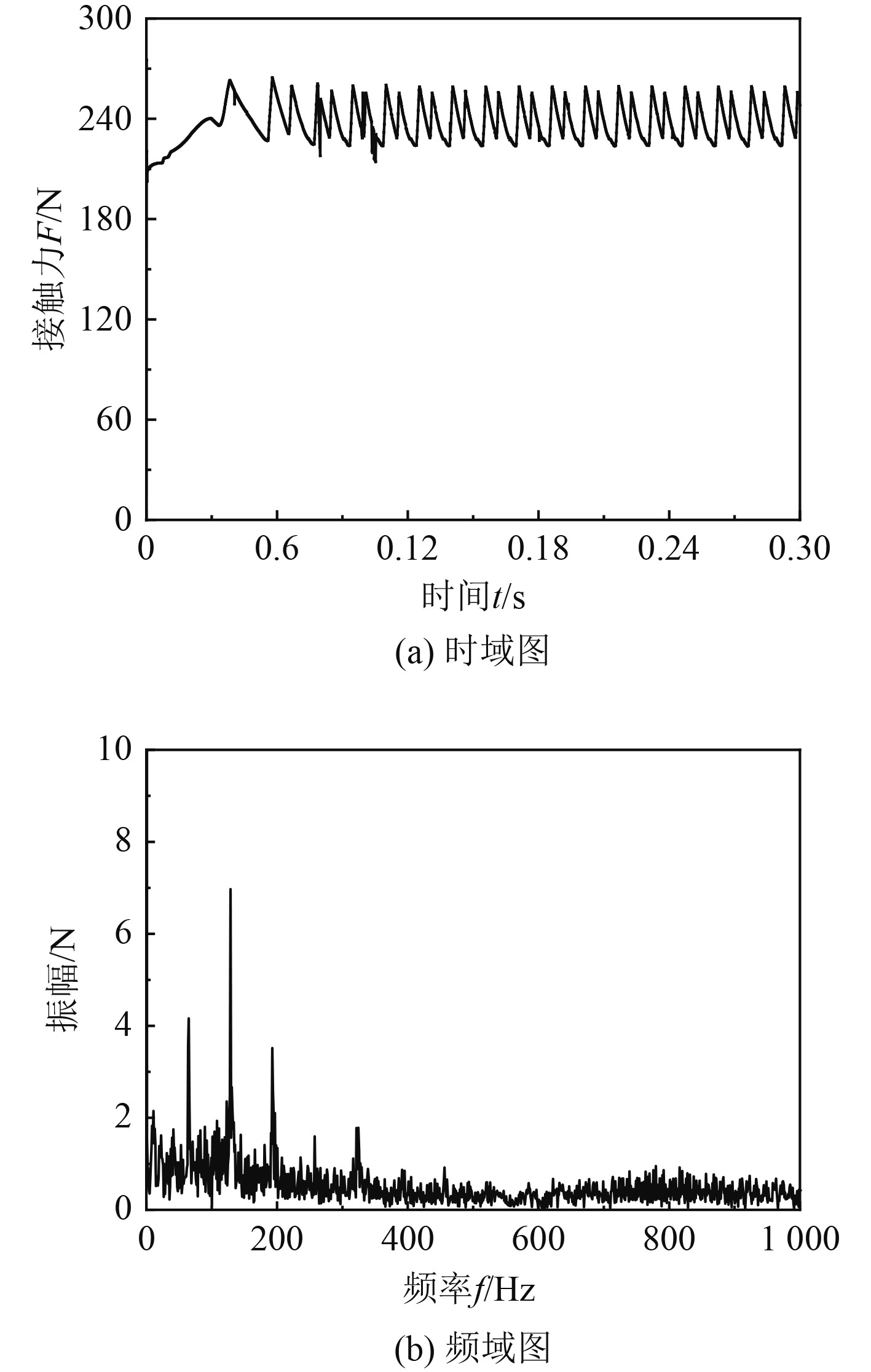
由图6太阳轮-行星轮啮合接触力的时域曲线分析得知,在0~0.1 s系统加速阶段,接触力从0急剧增加,呈现无规则的剧烈波动,但随时间波动周期逐渐收窄。在0.1 s之后,系统进入稳定阶段,接触力在平均值附近处于周期性的上下波动状态,但波动幅度较大,约为平均值28 N的2~3倍。太阳轮-行星轮啮合接触力极大值为86.7 N,极小值为0。由频域曲线分析得知,接触力表现出明显的周期性特征,行星轮-内齿圈啮合接触力的最大峰值对应的主频率为147.16 Hz,与理论计算出的齿轮啮合基频147.02 Hz相比误差仅为0.1%。随后峰值对应的频率为293.69 Hz,约为主频率的2倍,即为谐波频率,其为齿轮接触力响应频率为啮合基频的整数倍。图7中,行星轮-内齿圈啮合接触力的极大值为97.8 N;极小值为5.5 N;平均值56 N是太阳轮-行星轮啮合接触力的2倍。但频率特征基本一致。图8和图9中定轴轮系的接触力时域变化规律与行星轮系相似,经过加速冲击阶段后进入稳定波动状态,在频域曲线上比较明显的峰值对应频率是啮合基频65.62 Hz的整数倍。
|
图 7 太阳轮-内齿圈啮合接触力 Fig. 7 Contact force between the sun gear and the inner gear |
|
图 8 定轴齿轮Z1-Z2接触力 Fig. 8 Contact force of fixed shaft gear Z1-Z2 |
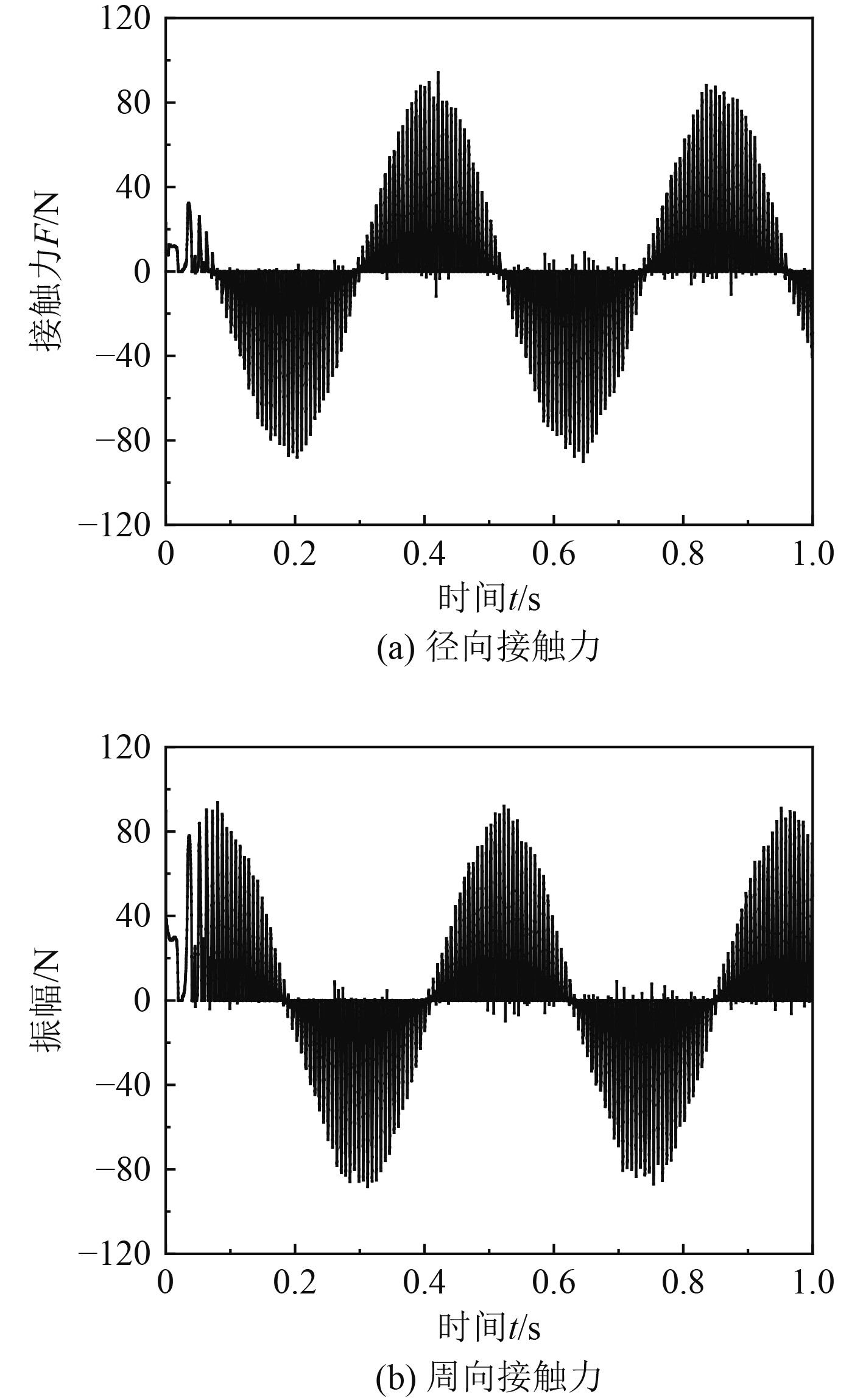
为了更直观地观察太阳轮和行星轮的啮合力的变化规律,提取太阳轮与行星轮在啮合过程中的径向力和切向力,其随时间的变化曲线如图10所示。如图,径向力和切向力围绕0值上下波动,最大幅值约为90 N,呈现出明显的调制现象。二者在波动幅度上基本一致,但在相位上存在约90°的差值。
|
图 10 太阳轮与行星轮在2个方向上的接触力 Fig. 10 Contact force between solar and planetary gears in two directions |
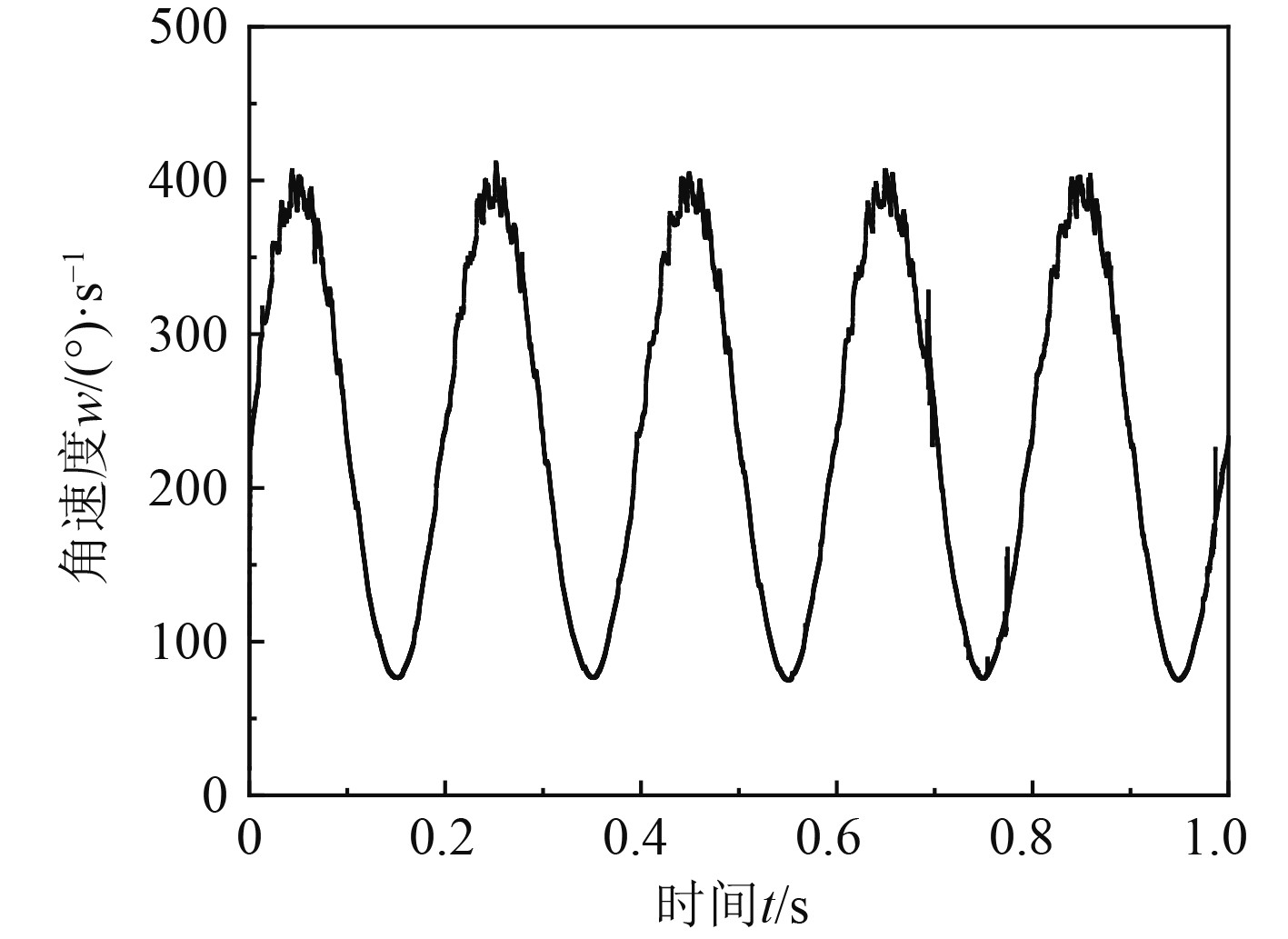
考虑到深海电动缸在实际运行过程中可能会遇到电机转速改变、末端交变载荷等非额定工况的情景,因此在齿轮传动机构的输入端施加200~400 r/min按照正弦规律波动的驱动转速,在末端齿轮施加2~4 N·m按照正弦规律波动的负载转矩,分别对应ADAMS中模拟样机模型的驱动函数
|
图 11 动态转速下输出角速度 Fig. 11 Output angular velocity at dynamic speed |
|
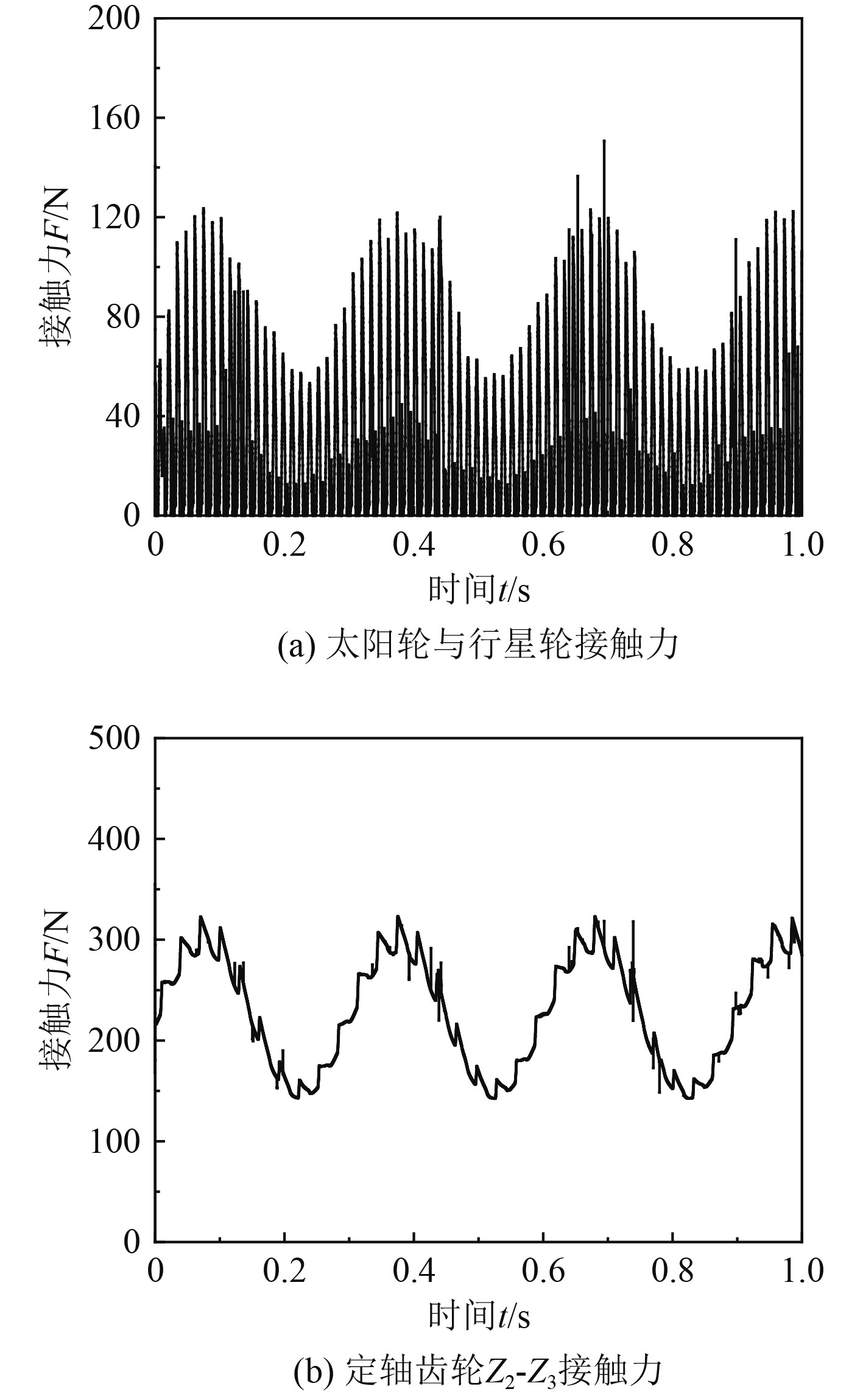
图 12 动态负载下的齿轮接触力 Fig. 12 Gear contact force under dynamic load |
可以看出,输出角速度呈现规律的正弦波形,波动周期与驱动转速的变化周期相同,均为0.2 s。行星齿轮和定轴齿轮在面对动态负载时,接触力表现出相同的波动特性,波动周期与动态负载一致。负载转矩对齿轮接触力的动态响应影响类似于调制作用,可以看做是静态转矩和波动转矩的共同叠加作用[12]。
4 结 语1) 根据深海电动缸的工作环境和性能要求对齿轮传动机构进行结构设计,设计了星轮轮系和定轴轮系组成的混合轮系传动方案,确定了行星轮系和定轴轮系的传动比及各齿轮的齿数、模数、压力角等结构参数。
2) 以动力学分析软件ADAMS为平台,建立齿轮传动机构的虚拟样机模型,基于赫兹碰撞理论定义齿轮准确的接触参数,其运动学仿真结果验证了理论设计及虚拟样机模型的正确性。
3) 针对虚拟样机模型进行动力学仿真,计算了各齿轮的接触力,接触力在齿轮加速阶段剧烈波动,在速度稳定后呈现周期性变化规律。行星轮的内外啮合接触力频幅曲线相似且存在基频整数倍的谐波频率,径向力和切向力幅值基本一致且存在90°的相位差。
4) 在动态激励下,齿轮传动机构输出角速度取决于驱动函数,齿轮接触力受到静态转矩和动态转矩的叠加作用。仿真分析结果将为深海电动缸的齿轮传动机构的强度校核及优化设计等,提供重要数值参考。
| [1] |
潘平. 适用于深海的电动缸设计[J]. 舰船科学技术, 2021, 43(13): 109-113. PAN Ping. Design of electric cylinder suitable for deep-sea[J]. Ship Science and Technology, 2021, 43(13): 109-113. |
| [2] |
陈超, 赵升吨, 崔敏超, 等. 电动缸的研究现状与发展趋势[J]. 机械传动, 2015, 39(3): 181-186. |
| [3] |
骆立强. 船舶电动执行机构应用与发展[J]. 船舶工程, 2007(5): 40-43. DOI:10.3969/j.issn.1000-6982.2007.05.002 |
| [4] |
冯立艳. 机械原理[M]. 北京: 机械工业出版社, 2012.
|
| [5] |
张旭东, 杨林杰, 曹延军, 等. 行星齿轮传动系统发展及关键技术研究进展[J]. 化工机械, 2021, 48(6): 803-809. DOI:10.3969/j.issn.0254-6094.2021.06.003 |
| [6] |
吴鲁纪, 耿福震. 高速齿轮传动技术与装置综述[J]. 机械传动, 2019, 43(11): 172-175. |
| [7] |
闻邦椿. 机械设计手册(第6版)[M]. 北京: 机械工业出版社, 2017.
|
| [8] |
伍琼仙. NGW型行星齿轮减速机构设计自动化系统研究[D]. 成都: 西南交通大学, 2012.
|
| [9] |
闫伟. 船舶动力传动系统振动特性的ADAMS仿真研究[J]. 舰船科学技术, 2017, 39(22): 82-84. YAN Wei. ADAMS simulation study on vibration characteristics of ship power transmission system[J]. Ship Science and Technology, 2017, 39(22): 82-84. |
| [10] |
占文锋, 杜群贵, 任少云, 等. 渐开线行星齿轮啮合力的动态仿真[J]. 机械设计与制造, 2007(8): 71−73.
|
| [11] |
李金玉, 勾志践, 李媛. 基于ADAMS的齿轮啮合过程中齿轮力的动态仿真[J]. 机械, 2005(3): 15-17. DOI:10.3969/j.issn.1006-0316.2005.03.006 |
| [12] |
黄中华, 张晓建, 周玉军. 渐开线齿轮啮合碰撞力仿真[J]. 中南大学学报(自然科学版), 2011, 42(2): 379-383. |
 2024, Vol. 46
2024, Vol. 46
