2. 中国舰船设计研究中心,湖北 武汉 430070
2. China Shipbuilding Reseasrch and Design Center, Wuhan 430070, China
大型舰船推进轴系的振动响应直接关系到舰船的隐身性能,在设计和安装过程中对舰船主推进轴系开展隔振性能研究具有重要意义[1 - 2]。当今相关研究主要集中在潜艇动力装置和主要的辅助设备,对大型水面舰船主推进装置,特别是大功率的电力推进装置的主电机进行隔振处理的还比较少见,但随着舰船声隐身技术的发展,新一代大型水面舰船隐身性能已成为行业关注的热点和焦点。对于大型舰船电力推进轴系在螺旋桨激励下的振动响应,付建等[3]对螺旋桨激励的研究表明,螺旋桨垂向激励主要由叶频次和倍叶频次激励引起,因此拟对螺旋桨叶频次和倍叶频次激励的振动响应进行隔振方案设计和传递特性研究。
舰船推进系统的隔振方案设计目前有单层隔振装置、双层隔振装置、浮筏隔振装置等。张华良等[4]研究了隔振系统中隔振器的刚度、阻尼和基座等参数,胡泽超[5]等研究了气囊隔振器的布置,证明了隔振器刚度、阻尼、隔振器的数量和隔振器的布置对隔振系统的隔振性能都有一定程度的影响。其中,单层隔振装置由于在高频区间的隔振效果不佳目前主要用于隔振要求不高或者有严格对中要求的推进轴系[6],对此,Chen等[7]提出一种夹芯板式弹性结构的单层隔振方法,查长松等[8]研究了带泡沫铝冲击吸能器的单层隔振系统,陈谦等[9 - 10]研究了单层隔振系统中限位器的应用设计。对于所研究的大型低速双电机推进轴系,其有严格对中要求且电机转速较低,因此仍采用单层隔振设计,主要关注隔振器的选择与布置方案对传递特性和隔振效果的影响。
根据该大型低速双电机推进轴系的实际构成,考虑轴承的阻尼作用建立该推进轴系有限元混合模型,对隔振器选型与布置进行方案设计,通过Ansys Workbench有限元分析软件对各方案隔振性能和传递特性进行模态和谐响应计算与分析。验证方案可行性并比较隔振效果,提出优化方案,为该型船舶提供设计参考,为后续其他大型水面舰船电力推进装置的声隐身性能分析提供理论支撑。
1 隔振方案设计 1.1 装置构成该推进装置主要由螺旋桨、螺旋桨轴、后尾轴架轴承、前尾轴架轴承、液压联轴器、尾管轴、尾轴管轴承、中间轴、中间轴承、推力轴及推力轴承、高弹性联轴器、主推进电机(双电机)组成,如图1所示。

|
图 1 推进装置构成图 Fig. 1 Propulsion assembly diagram |
其中,螺旋桨为五叶桨,集中载荷为142 kN;各轴承参数如表1所示。2台串联推进电机机组总重量为180 t,额定转速为200 r/min,螺旋桨激励的轴频频率为3.33 Hz,叶频频率为16.66 Hz,倍叶频频率为33.33 Hz,电机机组安装基座尺寸为
|
|
表 1 轴承参数 Tab.1 Bearing parameters |
隔振器选型与布置一般需要考虑设备尺寸、设备质量、隔振能力等因素。目前大型舰船主推进装置主要采用橡胶隔振器,橡胶隔振器的刚度参数是固定不可调节的,其在承受载荷时呈现较强的非线性,通过施加载荷并测量其形变量的方法计算出其静刚度系数。
为满足实际工程的要求和隔振器的选型原则[11 - 12],该电机安装基座可安装的隔振器数量不超过32个;隔振器布置应与机组主惯性轴对称;隔振器应采用额定载荷比实际载荷大10%左右,阻尼比在0.04~0.2之间,固有频率避开激励力频率且同型号的隔振器。选择CM系列隔振器组成隔振系统,其具体参数如表2所示。
|
|
表 2 隔振器参数 Tab.2 Vibration isolator parameters |
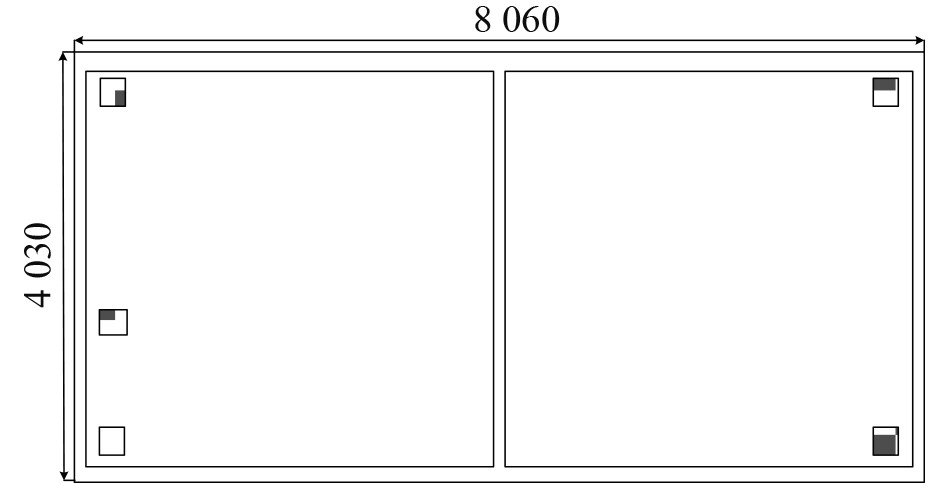
为确定隔振系统的总静刚度,分别采用28个CM-60型、CM-90型或CM-150型隔振器组成方案1、方案2和方案3,3个方案的总静刚度依次增大,分别为154、210、308 kN/mm,布置方式如图2所示,图中斜线区域为选定的安装位置。
|
图 2 隔振器布置方案 Fig. 2 Vibration isolator layout scheme |
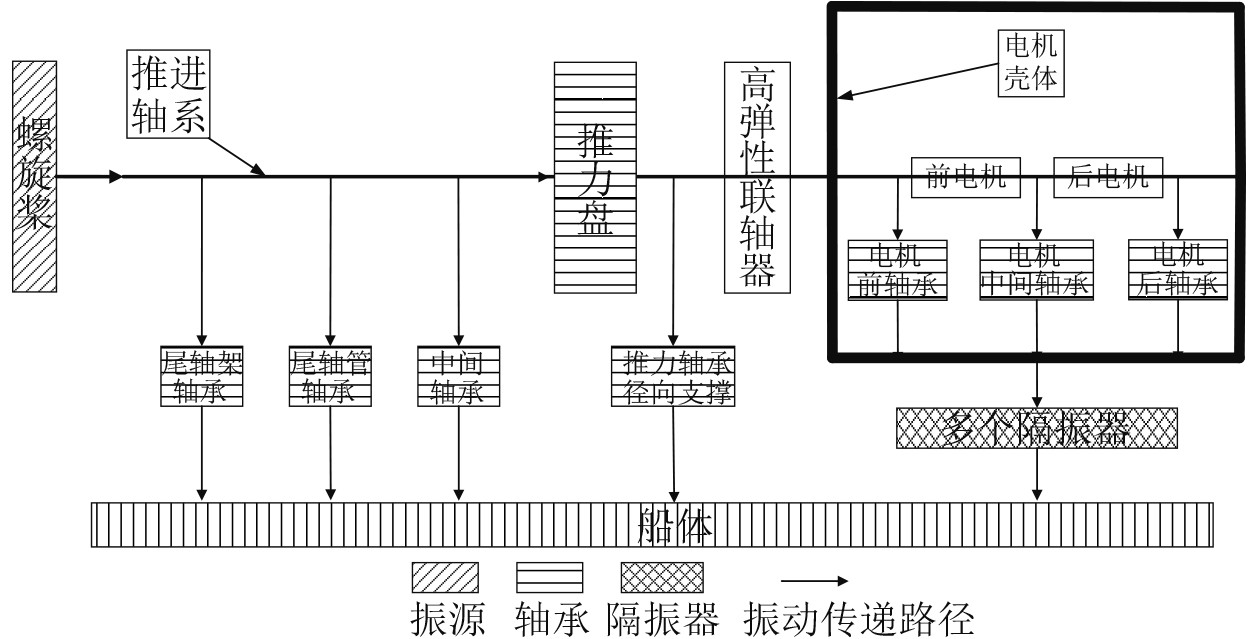
主要关注的振源为该推进装置的螺旋桨激励,隔振系统振动能量传递路径如图3所示。其中尾轴架轴承、尾轴管轴承、中间轴承、推力轴承通过基座与船体刚性连接,电机轴承与电机壳体刚性连接,电机壳体通过隔振器与安装基座连接,安装基座通过螺栓与船体连接。螺旋桨产生的激励力经过轴段、轴承和高弹性联轴器衰减后传递至电机转子,通过电机轴承传递给电机壳体,再通过隔振系统传递给安装基座。该隔振装置可以看作单层隔振系统,其传递的振动力以1/ω2的趋势衰减,其中ω为频率,从而可以有效降低传递至船体的振动能量。
|
图 3 双电机隔振系统振动传递路径示意图 Fig. 3 Vibration transmission path diagram of dual motor floating raft isolation system |
对于螺旋桨和各轴段,基于舰船推进校中理论将螺旋桨简化为作用在重心位置的集中质量点,并施加集中载荷。由于不需要提取螺旋桨轴、尾管轴、中间轴的截面响应,因此参照该轴系螺旋桨到推力轴法兰处的当量参数表将各轴段简化为梁模型。利用bearing单元模拟各尾轴架轴承、尾轴管轴承和中间轴承的径向支撑刚度和径向阻尼,各轴承参数如表1所示。
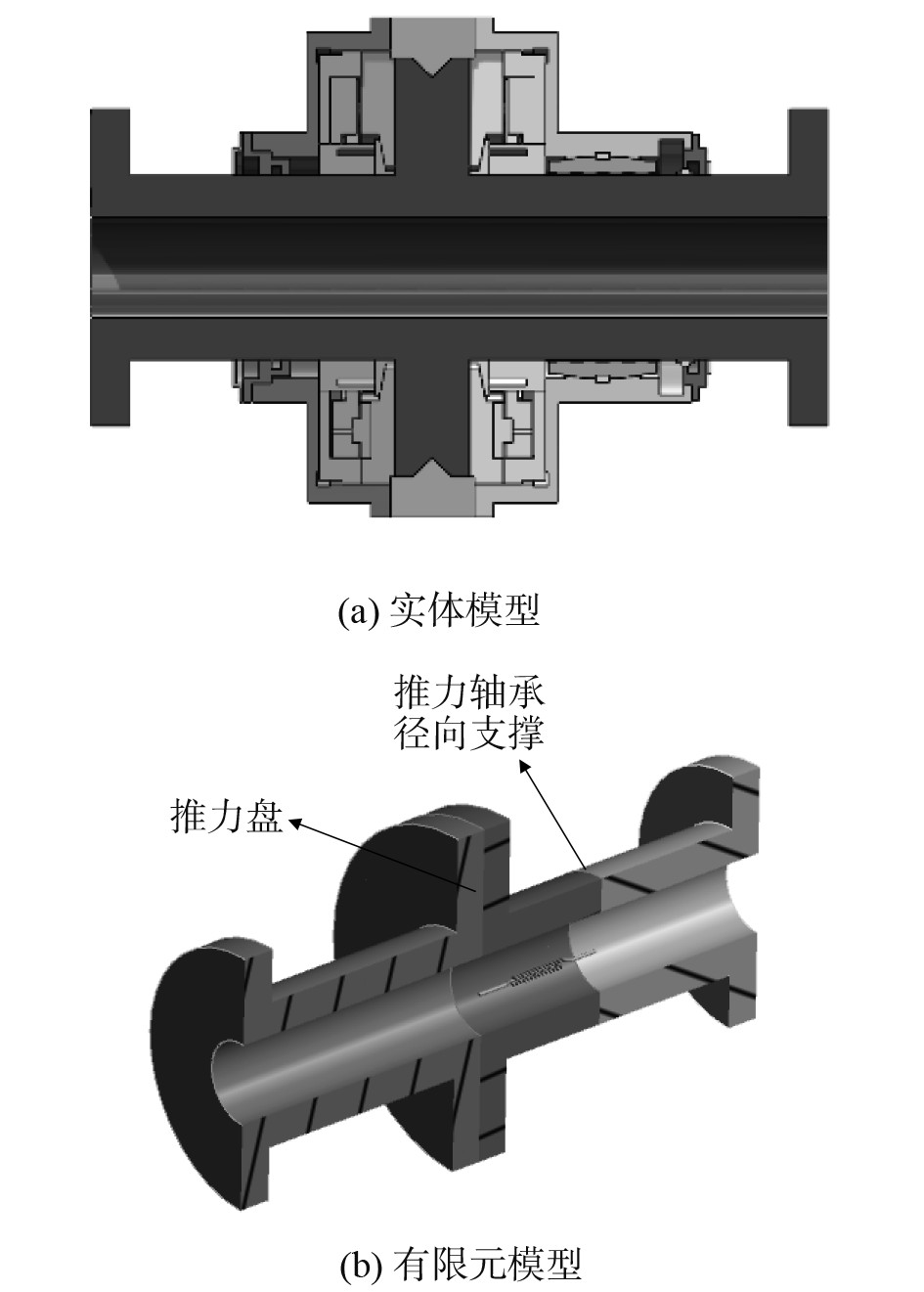
对于推力轴承及推力轴,推力轴承外壳及推力块等结构组件在振动传递过程中的作用可以用边界条件代替,推力轴和推力盘则可采用等效实体模型,在推力盘处添加纵向的spring单元模拟推力盘推力刚度,在推力轴承径向支撑处添加bearing单元模拟其径向刚度和径向阻尼,推力轴承参数如表1所示,推力轴承及推力轴剖面图如图4所示。
|
图 4 推力轴承及推力轴剖面图 Fig. 4 Thrust bearing and thrust shaft profile |
由于推力轴与其他轴段分别采用实体单元和梁单元,两者自由度不同,为了使振动响应正确传递,两者连接处采用固定连接副连接,并开启可变形。
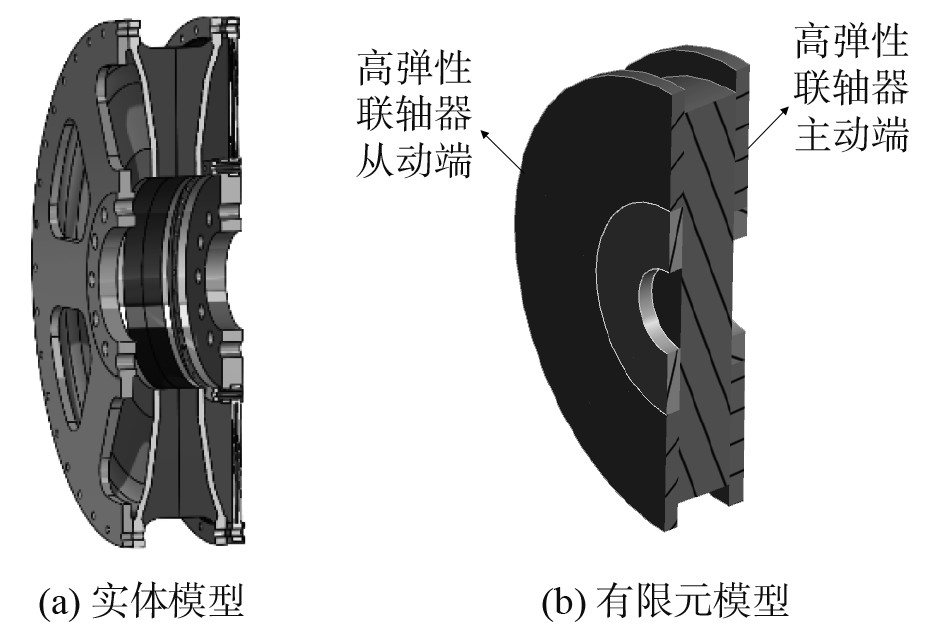
对于高弹性联轴器,作为弹性元件其结构对振动传递过程的影响很大。该轴系采用的单排多膜片式高弹性联轴器结构相当复杂,其实体模型剖面图如图5(a)所示,如果直接使用完全实体模型进行计算会对网格划分和计算速度带来不利的影响。因此将膜片按照厚度组成一个整体,不考虑其他多余部分,将其简化为从动端法兰、从动端膜片、橡胶组件、主动端膜片和主动端法兰5个部分,建立高弹性联轴器的当量等效模型。通过改变不同部分的材料性质使得当量等效模型与完全实体模型有相同的质量和刚度,其有限元模型剖面图如图5(b)所示。
|
图 5 高弹性联轴器剖面图 Fig. 5 High elastic coupling profile |
对于电机机组与隔振器,参照该轴系的电机实物,建立电机轴、电机转子、转子线圈、电机壳体的等效实体模型,如图6所示,使模型的质量和刚度与实物保持一致。使用bushing单元连接电机轴和电机壳体,连接方法选择“远程连接”,模拟电机轴承的径向支撑刚度和径向阻尼,电机轴承参数如表1所示。

|
图 6 电机有限元模型剖面图 Fig. 6 Profile of motor finite element analysis model |
安装基座建立实体模型,在安装基座螺栓处添加固定支撑模拟螺栓对底座的固定效果。在geometry中使用“点载荷”的方法,在电机壳体底部和安装基座顶部创建对应的隔振器安装位置。使用bushing单元分别连接电机壳体与基座对应安装位置,输入表2中对应型号隔振器的刚度、阻尼参数,连接类型选择“body-body”,连接方法选择“直接连接”,模拟隔振器在横向和垂向上的刚度和阻尼。使用bushing单元的好处是可以同时设定x、y、z 方向的刚度与阻尼值。
建立隔振系统有限元分析混合模型,如图7所示,该模型考虑了尾轴架轴承、尾轴管轴承、中间轴承、推力轴承径向支撑和电机轴承的径向阻尼以及高弹性联轴器和隔振器对传递特性的影响。根据宋金明等[13]的研究可知在100 Hz以上的中高频区间不考虑质量影响的简化模型会因为驻波效应的影响与实际值产生较大偏差,但主要关注的螺旋桨激励频率处于0~50 Hz的低频区间,因此该模型可以较好的满足该轴系隔振系统的振动分析。

|
图 7 推进轴系有限元分析模型 Fig. 7 Finite element analysis model of propulsion shafting |
为具体分析整个隔振系统的模态特征,利用Ansys软件中的模态分析模块,使用第2节中建立的有限元分析混合模型,模态分析阶数设置为30,开启阻尼,求解器类型选择完全阻尼,计算出隔振系统的前30阶模态的频率和振型。由于振动响应主要是前两阶优势模态决定的,因此提取出3种方案垂向的前两阶优势模态频率与振型图,如表3和图8所示。
|
|
表 3 隔振系统的前两阶优势模态频率和振型 Tab.3 The first two dominant mode frequencies and modes of vibration isolation system |
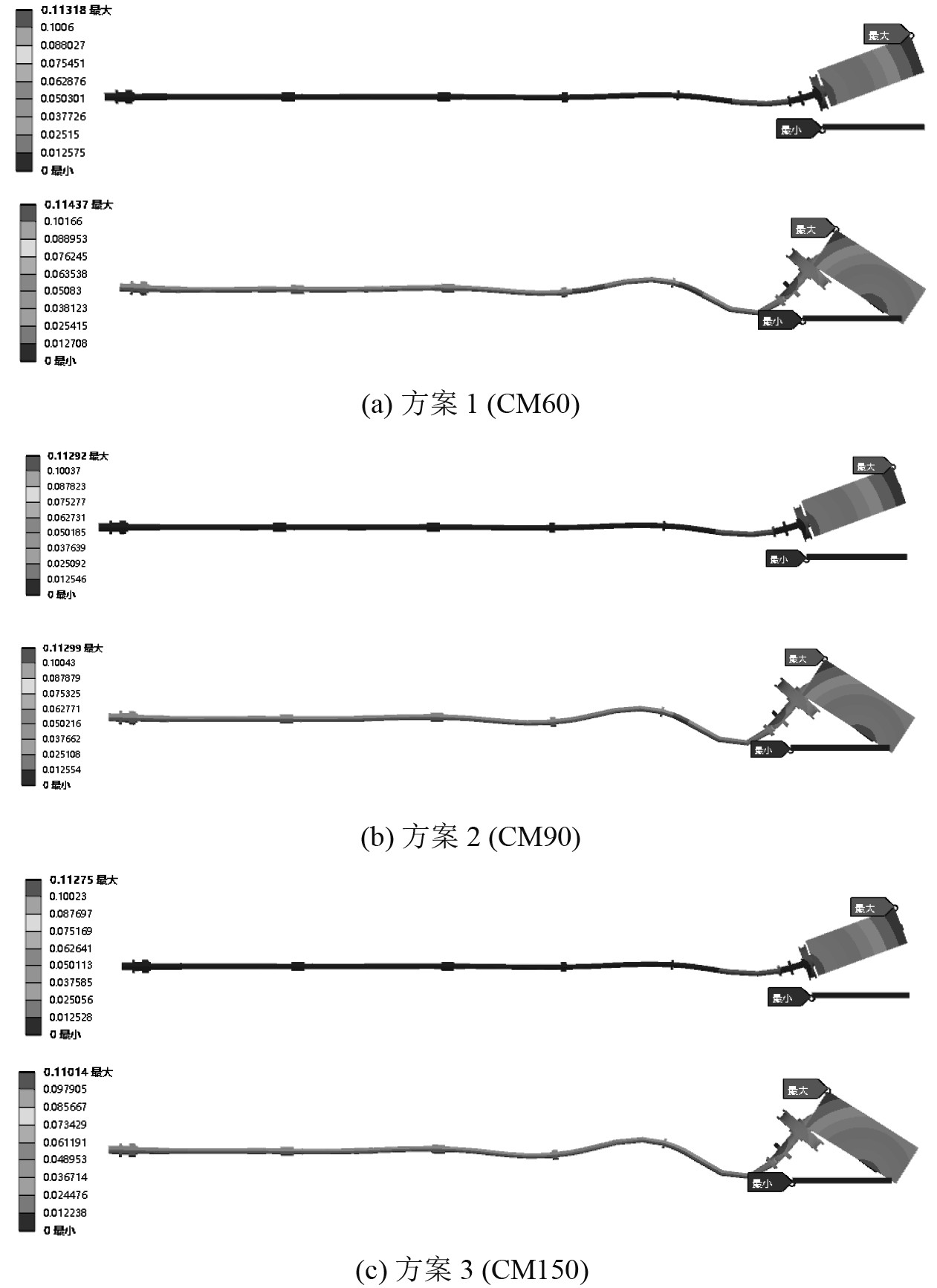
|
图 8 3种方案前两阶优势模态振型图 Fig. 8 Figure of the first two dominant modes of the three schemes |
对于关注的垂向振动来说,3个方案的前两阶优势频率随隔振器整体静刚度变大而变大,符合已知规律。3个方案的前两阶优势振型完全相同,说明在隔振器布置方案相同的情况下,改变隔振系统的总静刚度不会改变其优势振型。
3个方案前两阶优势频率与螺旋桨激励频率并不重叠,因此在轴系稳定运行时不会发生共振,3个方案都具有实际可行性。3个方案的优势模态变形量最大处均在电机机组轴向前后两端,在隔振方案设计时应重点关注这2个区域。
3.2 隔振性能评价方法振级落差被广泛应用于实际设计过程中,其优点在于计算方便且生成的频率-振级落差曲线可以直观地显示出不同频段下的隔振效果。根据所取响应的不同,振级落差一般被分为位移振级落差、速度振级落差和加速度振级落差,采用加速度振级落差作为该轴系传递特性分析中评价隔振效果的指标。
对于弹性安装系统,其加速度振级落差LD的定义为[6]被测量的2个点之间用dB为单位来表示的加速度响应的差值,记为LD,其计算表达式为:
| $ {L_D} = 20\lg \frac{{{{{a_1}/ {a_0}} }}}{{a_2}/ {a_0}} = 20\lg \frac{{{a_1}}}{a_0} - 20\lg \frac{{{a_2}}}{{{a_0}}} = {L_{{a_1}}} - {L_{{a_2}}}。$ | (1) |
式中:
以式(1)计算方法为基础,使用叶频次和倍叶频次加速度响应的叠加作为总加速度响应。同时,为了减小误差,以上下测量点的平均值作为加速度的测量结果,则平均振级落差
| $ {\tilde{L}_D} = 10\lg \left(\frac{1}{n}\sum\limits_{i = 1}^n {\frac{{{a_i}}}{{{a_0}}}}\right ) - 10\lg \left(\frac{1}{n}\sum\limits_{j = 1}^n {\frac{{{a_j}}}{{{a_0}}}} \right) ={\tilde {L}_{{a_i}}} - {\tilde {L}_{{a_j}}} 。$ | (2) |
式中:n为测点数量;
螺旋桨激励力产生的原因是螺旋桨在不断旋转的过程中通过了不均匀的尾部伴流场,因而各桨叶产生的推力和旋转阻力合力不通过轴线且不为零。由此传递给船体3个脉动分力和3个脉动力矩,它们的大小均与推力大小相关。对于垂直于桨轴的垂向力引起的叶频次和倍叶频次激励,根据陈志坚[14]的研究结合该轴系的实际情况,该轴系的垂向螺旋桨叶频次激励力为推力的5%,倍叶频次激励力为推力的3%。该轴系的螺旋桨推力为
为具体分析3个方案的隔振性能区别,采用Ansys软件谐响应分析模块,使用3中的有限元模型,分别在螺旋桨集中载荷点处施加0~50 Hz的
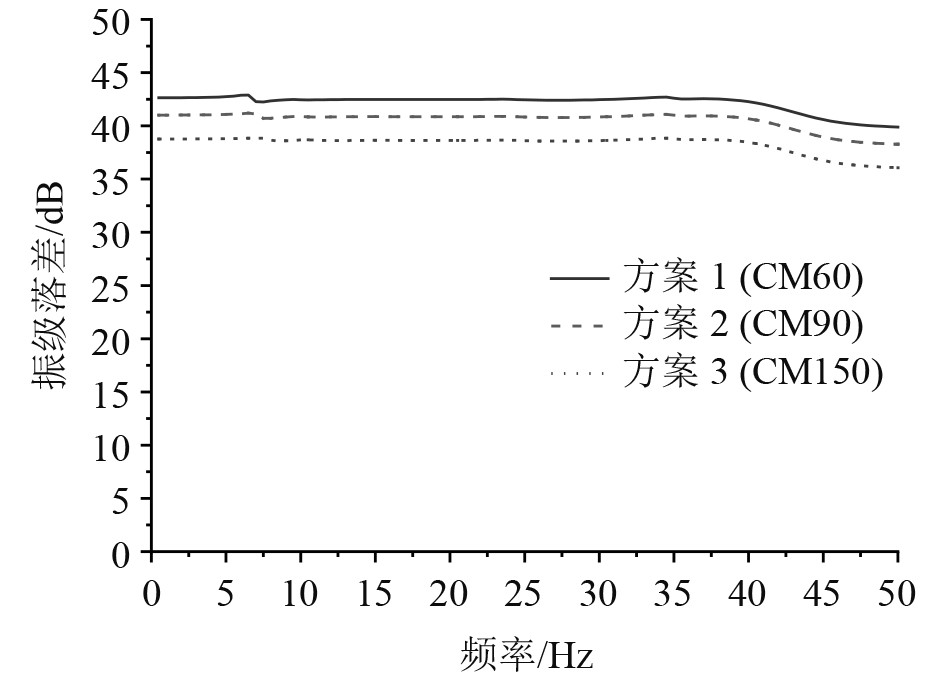
|
图 9 3种方案隔振器上下机脚处的振级落差曲线图 Fig. 9 Three schemes vibration level drop curves at the upper and lower feet of the isolator |
3种方案在0~50 Hz的低频区间内有相似的振级落差曲线,方案1平均振级落差为42.1 dB,方案2平均振级落差为40.5 dB,方案3平均振级落差为38.3 dB,振级落差大小随总静刚度减小而增大。激励力频率比隔振系统的固有频率大
由3.4节可知,采用方案1的总静刚度154 kN/mm能取得更好的隔振效果。为分析在相同总静刚度下,隔振器数量对隔振效果的影响,分别采用20个CM-90型和13个CM-150型隔振器组成方案4和方案5与方案1进行对比,两方案总静刚度与方案1相同,方案布置如图10所示。
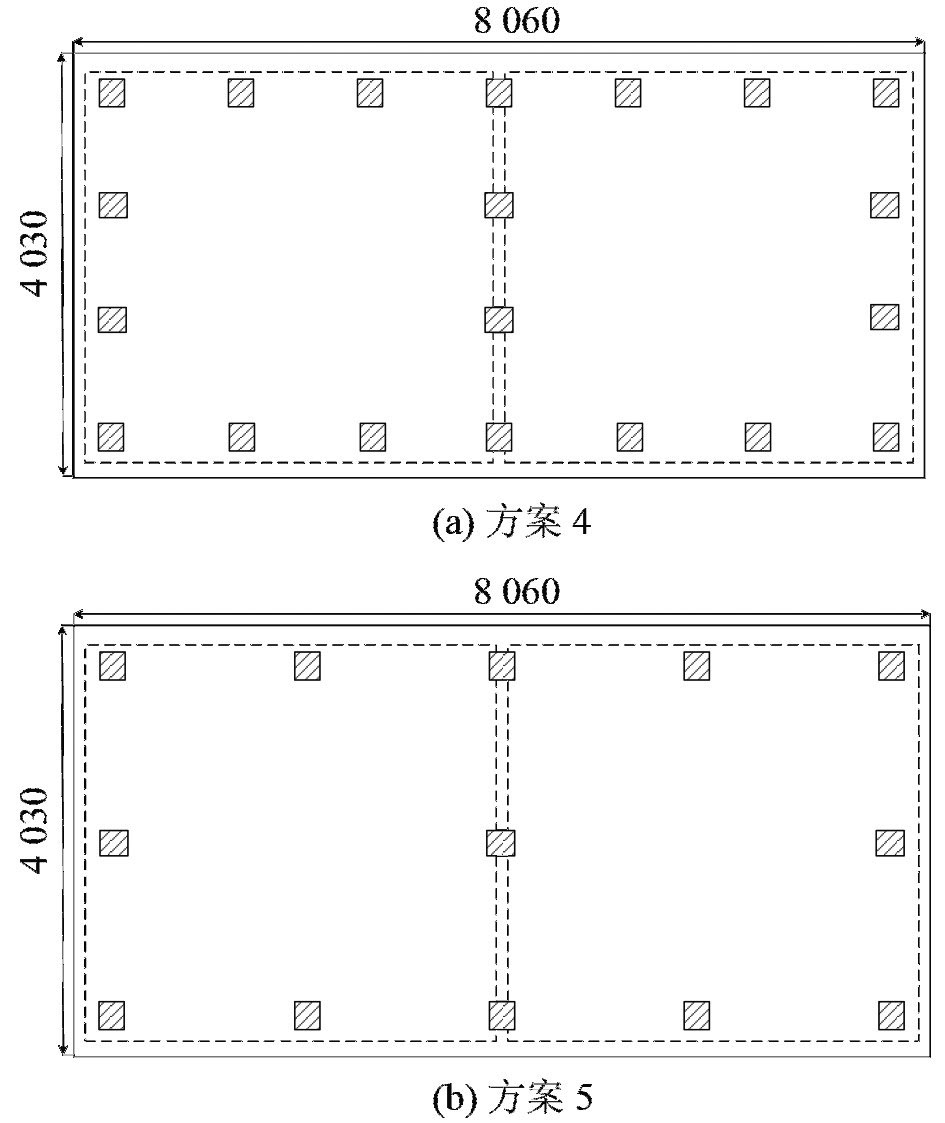
|
图 10 两方案隔振器布置方案 Fig. 10 Two schemes vibration isolator layout scheme |
方案1、方案4和方案5的优势模态频率与振型如表4所示,平均振级落差曲线如图11所示。方案4和5的优势模态频率和优势模态振型同方案1几乎完全相同。方案1的平均振级落差为42.1 dB,方案4的平均振级落差为41.8 dB,方案5的平均振级落差为41.9 dB,三者差值在0.3 dB以内。因此在隔振系统总静刚度相同的情况下,使用单个刚度更大的隔振器来改变隔振器的数量不会对系统的优势模态和隔振落差产生影响。综合安装使用成本和检修便利性,采用13个CM-150型隔振器的方案5是更好的选择。
|
|
表 4 隔振系统的前两阶优势模态频率和振型 Tab.4 The first two dominant mode frequencies and modes of vibration isolation system |
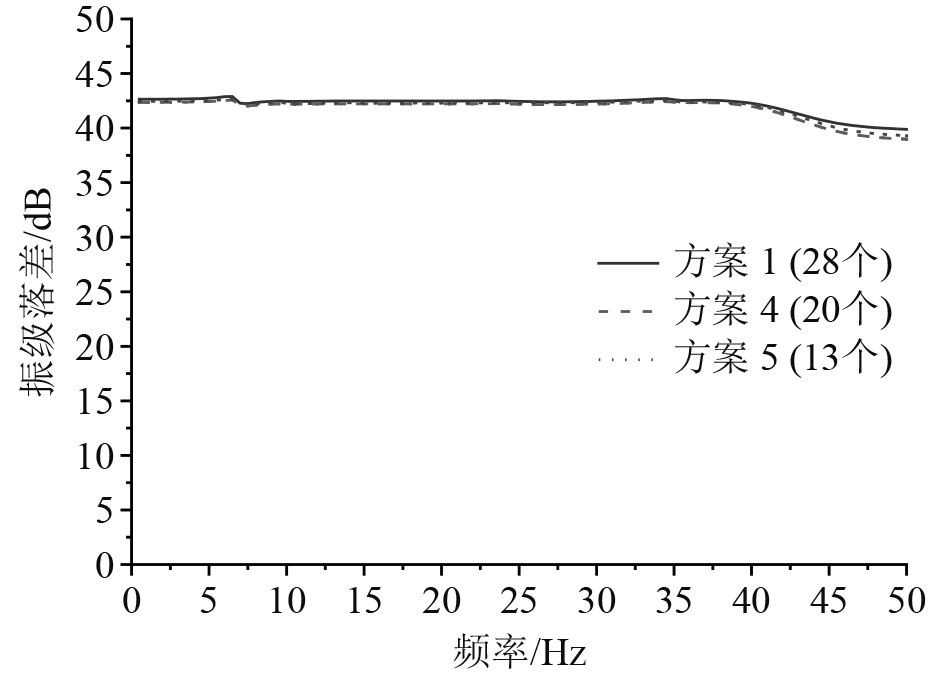
|
图 11 3种方案隔振器上下机脚处的振级落差曲线图 Fig. 11 Three schemes vibration level drop curves at the upper and lower feet of the isolator |
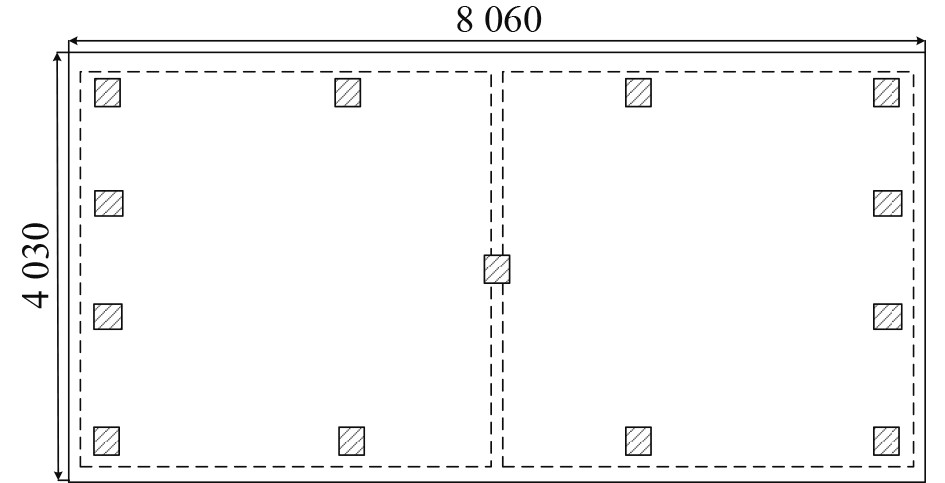
根据3.1节和4.1节中对优势模态振型的分析得出,该装置优势模态振动变形主要集中在机组轴向前后两端,为解决该问题,尝试在方案5的基础上把隔振器更多的布置在变形最大的两边上组成方案6,布置方案如图12所示。
|
图 12 方案6隔振器布置方案 Fig. 12 Scheme 6 layout of vibration isolators |
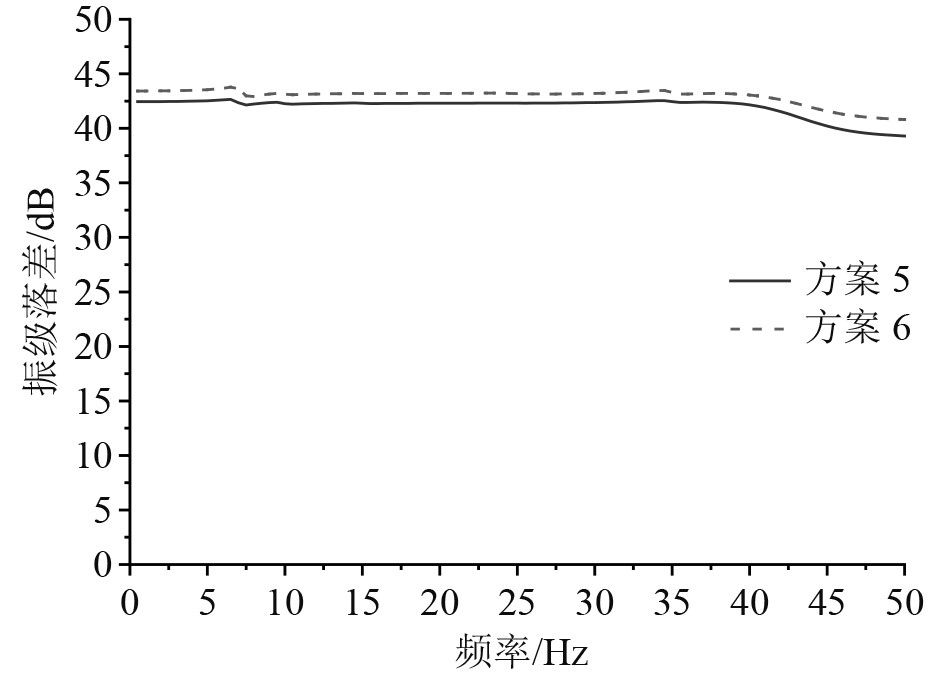
方案5和方案6的优势模态频率与振型如表5所示,平均振级落差曲线如图13所示。两者在优势模态上的区别不大,方案5的平均振级落差为41.9 dB,方案6的平均振级落差为42.9 dB,两者相差1 dB,因此在系统总静刚度不变,隔振器数量不变的情况下,方案6比方案5有更好的隔振效果。
|
|
表 5 隔振系统的前两阶优势模态频率和振型 Tab.5 The first two dominant mode frequencies and modes of vibration isolation system |
|
图 13 2种方案隔振器上下机脚处的振级落差曲线图 Fig. 13 Two schemes vibration level drop curves at the upper and lower feet of the isolator |
针对某大型低速双电机串联推进轴系在螺旋桨叶频次和倍叶频次激励下的振动响应和隔振设计问题,提出了6种隔振方案,并利用Ansys软件对其进行模态和隔振性能分析,得出结论:
1)6种方案在工作转速内均不会发生共振,具有实际可行性,且在0~50 Hz的低频区间有40 dB左右的振级落差,说明对大型电力推进轴系在螺旋桨激励下的振动有较好的抑制作用;
2)激励力频率比隔振系统的固有频率大
3)在系统总静刚度相同的情况下,采用单个静刚度更大,隔振器数量更少的方案,几乎不会对系统优势模态和隔振性能产生影响,方案5在性能、成本和维修性之间做出了更好的平衡;
4)该推进轴系的前两阶优势模态的变形集中在轴向前后两端处,方案6采用的增加该位置处的隔振器数量的方法可以一定程度上解决该问题,使振级落差有1 dB左右的提升,可作为该轴系隔振方案的参考设计。
| [1] |
何琳, 徐伟. 舰船隔振装置技术及其进展[J]. 声学学报, 2013, 38(2): 128-136. HE Lin, XU Wei. Ship vibration isolation device technology and its progress[J]. Journal of Acoustics, 2013, 38(2): 128-136. |
| [2] |
RUAN D Y, LIANG X, HUA X Y, et al. Isolating low-frequency vibration from power systems on a ship using spiral phononic crystals[J]. Ocean Engineering, 2021, 225: 108804(1−10).
|
| [3] |
付建, 王永生, 丁科, 等. 螺旋桨激振力作用下船体振动及水下辐射噪声研究[J]. 船舶力学, 2015, 19(4): 470-476. FU Jian, WANG Yongsheng, DING Ke, et al. Research on hull vibration and underwater radiation noise under propeller excitation Force[J]. Ship Mechanics, 2015, 19(4): 470-476. |
| [4] |
张华良, 傅志方. 浮筏隔振系统各主要参数对系统隔振性能的影响[J]. 振动与冲击, 2000, 19(2): 5−8. ZhANG Hualiang, FU Zhifang. Influence of main parameters on the vibration isolation performance of floating raft vibration isolation system[J]. Vibration and Shock, 2000, 19(2): 5−8. |
| [5] |
胡泽超, 何琳, 李彦. 隔振器分布对浮筏隔振系统隔振性能的影响[J]. 舰船科学技术, 2016, 38(21): 48-52. HU Zechao, HE Lin, LI Yan. Effect of vibration isolator distribution on vibration isolation performance of floating raft vibration isolation system[J]. Ship Science and Technology, 2016, 38(21): 48-52. |
| [6] |
朱石坚, 何琳. 船舶机械振动控制[M]. 国防工业出版社, 2006.
|
| [7] |
CHEN D, ZI H, LI Y, et al. Low frequency ship vibration isolation using the band gap concept of sandwich plate-type elastic metastructures[J]. Ocean Engineering, 2021, 235: 109460. DOI:10.1016/j.oceaneng.2021.109460 |
| [8] |
查长松, 黄炼. 带泡沫铝冲击吸能器的单层隔振系统隔冲效果评估[J]. 舰船科学技术, 2010, 32(9): 35-38. CHA Changsong, HUANG Lian. Evaluation of impact isolation effect of single-layer vibration isolation system with aluminum foam impact absorber[J]. Ship Science and Technology, 2010, 32(9): 35-38. |
| [9] |
陈谦, 肖邵予, 张冠军. 带分段限位刚度的双向限位单层隔振系统冲击动力学理论模型研究[J/OL]. 中国舰船研究: 1−8. [2023-10-19]. https: //doi. org/10.19693/j. issn. 1673-3185.03292. CHEN Qian, XIAO Shaoyu, ZHANG Guanjun. Theoretical modeling of impact dynamics of bi-directionally limited single-layer vibration isolation system with segmental limiting stiffness[J/OL]. Chinese Ship Research: 1−8. [2023-10-19]. https://doi.org/10.19693/j.issn.1673-3185.03292. |
| [10] |
韩阳, 谌勇, 陈锋. 单层隔振系统中塑性限位器应用设计[J]. 噪声与振动控制, 2016, 36(3): 184-189. HAN Yang, CHEN Yong, CHEN Feng. Design of plasticity limiter application in single-layer vibration isolation system[J]. Noise and Vibration Control, 2016, 36(3): 184-189. |
| [11] |
宋玉超, 于洪亮. 隔振器最佳选择方案[J]. 大连海事大学学报, 2007(1): 87-89. SONG Yuchao, YU Hongliang. Optimal selection scheme of vibration isolator[J]. Journal of Dalian Maritime University, 2007(1): 87-89. |
| [12] |
赵禹. 柴油发电机组隔振设计及优化分析[D]. 大连: 大连理工大学, 2014.
|
| [13] |
宋金明, 张乔斌, 尹成彬, 等. 隔振器参数及高频驻波效应对浮筏隔振性能的影响[J]. 船电技术, 2012, 32(12): 4-7. SONG Jinminng, ZHANG Qiaobin, YIN Chengbin, et al. Influence of vibration isolator parameters and high frequency standing wave effect on vibration isolation performance of floating raft[J]. Marine Electric Technology, 2012, 32(12): 4-7. |
| [14] |
陈志坚. 舰艇振动学[M]. 北京: 国防工业出版社, 2010.
|
 2024, Vol. 46
2024, Vol. 46
