2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 上海交通大学 海洋装备研究院,上海 200240;
4. 中国船舶集团 有限公司上海船舶研究设计院,上海 201203
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. Institute of Marine Equipment, Shanghai Jiao Tong University, Shanghai 200240, China;
4. Shanghai Merchant Ship Design and Research Institute, CSSC, Shanghai 201203, China
随着全球气候变暖,极地冰层的融化为人类提供了更长时间内深入北极的机会。由于北极航线窗口期的扩大以及该区域丰富的自然资源和科考价值,世界各国纷纷加强对冰区运输船的研发,并致力于提升冰区船舶的航行性能[1]。
预报冰区船舶碎冰阻力的方法通常有理论分析经验公式法、模型试验法以及数值计算法。早期研究冰载荷的学者通常采用理论分析和经验公式的方法。芬兰-瑞典冰级规范(FSICR)[2]提供的新建船舶在破冰船开辟的碎冰航道中航行所受冰阻力计算经验公式是现在国际上认定的使用较为广泛的公式。经验公式法简单直接,能够快速得到阻力预报结果,但是该方法使用范围较窄,只适用于固定船型,针对新船设计存在较多不足。模型试验法是预报船舶阻力最有效的方法,该方法精确度高但是耗时长、成本高,而且对设备有较高的要求。1964年,Corlett等[3]首次采用石蜡作为非冻结模型冰,进行了模型试验,试验对象为在波罗的海航行的小型破冰船。国内,黄焱等[4]利用冰水池进行了运输船模型的船舶阻力试验,重点探讨了船模的航速以及冰覆盖率对冰阻力的影响。郭春雨等[5]学者则通过模型试验的方式对某极地集装箱船的阻力进行了预报,并与国外试验结果进行了对比,验证结果良好。
近年来,随着科技的不断革新,利用数值模拟方法来预测船舶阻力的研究逐渐取得了显著进展。从20世纪末开始,离散元方法在船舶与海洋工程领域的引入,尤其是与计算流体力学相结合的数值计算方法,在船舶阻力研究中得到了广泛应用。Hansen等[6]于1999年首次应用了二维离散元方法对船舶碎冰阻力进行研究;Vroegrijk[7]基于离散元法采用商用软件STAR-CCM+预报了船舶碎冰阻力,碎冰模型形状为圆球形;国威等[8]学者基于计算流体力学和离散元方法相耦合的计算方法对船舶碎冰航行性能进行了研究;骆婉珍[9]针对某冰区加强型散货船,基于离散元方法进行了船-冰的单项耦合和双向耦合,预报了船舶受航速与密集度影响下的碎冰阻力。在采用CFD-DEM方法预测船舶碎冰阻力的研究中,数值碎冰模型的形状多种多样。张远双[10]、齐江辉[11]和Jianing Zhang[12]等将数值碎冰模型形状定义为金字塔形和不规则多面体形,碎冰航道由这2种碎冰模型均匀分布共同组成;王超等[13]将碎冰模型定义为水分子和正方形冰排的形状,低密集度碎冰航道采用水分子形状数值碎冰模型,高密集度碎冰航道同时采用2种碎冰模型并通过改变这2种碎冰模型在航道中所占比例调节碎冰航道的密集度;Hansen和Loset[6]、Karulin[14]、李紫麟[15]、郭麒[16]和国威[8]等定义数值碎冰模型形状为三维圆盘形;金强[17]采用正方形和三角形混合的数值碎冰模型填充碎冰航道并预报了船体碎冰阻力;何宾峰[18]定义碎冰模型形状为长方体;Wang Chao等[19]、Xiangjie Tang等[20]选用正方形为数值碎冰模型的形状。然而,在众多形状中,并没有确切的定论表明哪一种形状能更好地预测船舶碎冰阻力,因此对数值碎冰模型形状的研究变得尤为关键。
本文以某极地环保多用途运输船为对象,选取7种不同形状片状数值碎冰模型建立了船舶-碎冰CFD-DEM耦合数值计算模型,通过将数值模拟中的碎冰阻力预测结果与HSVA冰冰池试验结果进行对比,研究了不同形状数值碎冰模型对船舶碎冰阻力预报的影响。
1 理论基础 1.1 CFD-DEM耦合中流体相控制方程本文采用了计算流体力学的方法来实现对流体相的控制。在对自由液面的处理中选择VOF(Volume of Fluid)方法,并采用
连续性方程:
| $ \frac{{\partial {\rho _f}{\alpha _f}}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}{\alpha _f}{\mu _f}} \right) = 0,$ | (1) |
动量守恒方程:
| $ {\displaystyle\frac{{\partial \left( {{\rho _f}{\alpha _f}{\mu _f}} \right)}}{{\partial t}} + \nabla \cdot \left( {{\rho _f}{\alpha _f}{\mu _f} \cdot {\mu _f}} \right) = - {\alpha _f}\nabla p - \nabla \cdot \left( {{\alpha _f}{\tau _f}} \right) + {\rho _f}{\alpha _f}g - F。} $ | (2) |
式中:
| ${\alpha _f} = 1 - {\alpha _p},{\alpha _p} =\displaystyle \mathop \sum \limits_{i = 1}^{{n_p}} {V_{{p_i}}}/\Delta V 。$ | (3) |
式中:
离散相采用离散元的方法进行控制,将研究对象离散化为相互独立的个体单元,其核心算法基于牛顿第二定律[22]。
在本文的计算过程中,将计算涉及到的碎冰模型离散为由多个DEM基本球形颗粒组成的复合模型。每个模型在任意时刻都遵循牛顿第二定律,在力和力矩的作用下,其运动方程分别为:
| $ {m_i}\frac{{{\mathrm{d}}{v_i}}}{{{\mathrm{d}}t}} = \mathop \sum \limits_j \left( {{F_{cn,ij}} + {F_{cs,ij}} + {F_{dn,ij}}} \right) + {m_i}g,$ | (4) |
| $ {I_i}\frac{{{\mathrm{d}}{\omega _i}}}{{{\mathrm{d}}t}} = \mathop \sum \limits_j \left( {{R_i} \cdot {F_{cs,ij}}} \right)。$ | (5) |
式中:
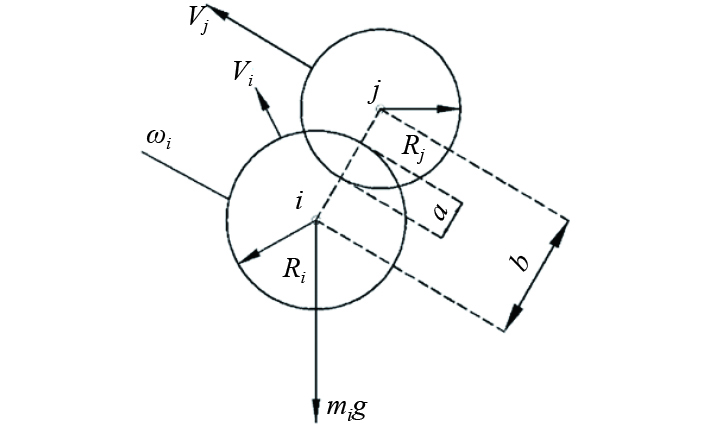
假定模型单元为不可破碎的无变形刚形体,通过判断单元与单元之间的重叠量来判断单元之间的接触与碰撞,如图(1)所示。图1中的
|
图 1 离散模型单元间碰撞是的假定重叠量 Fig. 1 The assumed overlap in collision between units |
|
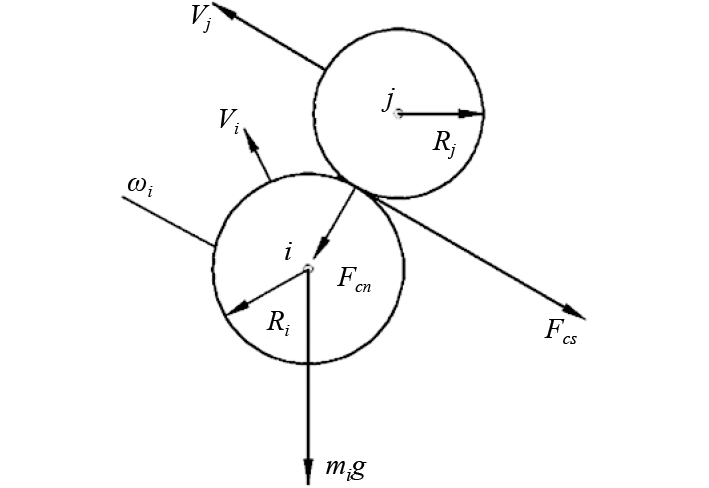
图 2 离散模型单元之间力和力矩的关系示意图 Fig. 2 The relationship between forces and moments between units |
本文所采用的是Hertz-Mindlin无滑移接触模型,其力学关系可表示为:
| $ {F_{contact}} = {F_n} + {F_t}。$ | (6) |
式中:
法向力分量可以写成:
| $ \begin{array}[b]{c} {F}_{n}=-{K}_{n}{d}_{n}-{N}_{n}{v}_{n},\\ {K}_{n}=\displaystyle \frac{4}{3}{E}_{eq}\sqrt{{d}_{n}{R}_{eq}},\\ {N}_{n}=\sqrt{5{K}_{n}{M}_{eq}}{N}_{n damp}。\end{array} $ | (7) |
切向力分量可以写成:
| $ \begin{array}[b]{c} {F}_{t}=\displaystyle\frac{\left|{K}_{n}{d}_{n}\right|{C}_{fs}{d}_{t}} {\left|{d}_{t}\right|},\\ {K}_{t}=8{G}_{eq}\sqrt{{d}_{n}{R}_{eq}},\\ {N}_{t}=\sqrt{5{K}_{t}{M}_{eq}}{N}_{t\text{ }damp}。\end{array} $ | (8) |
式中:
当颗粒与壁面相互接触时,公式保持不变,可以假设壁面半径
本文模型试验和数值计算所使用的模型为某极地环保多用途运输船,实船在碎冰航道航行速度为5 kn,实船和模型试验的缩尺比为29.508,船模材料为木质。
运输船主要参数如表1所示,模型试验水池为汉堡冰水池[23]。
|
|
表 1 运输船主要参数 Tab.1 Main parameters of transport vessel |
根据北极航道冰况,实船在碎冰航道航行的冰厚的大约为1.47 m,通过换算可以得到模型试验碎冰厚度保持在50 mm左右。表2为汉堡冰水池试验报告提供的船舶在IA冰级条件下,高水位线(UIWL)吃水工况的试验相关参数与船模阻力试验结果。表3船模以0.4735 m/s的航速进行敞水航行阻力试验的结果[24]。
|
|
表 2 IA冰级、UIWL吃水工况下船模碎冰航道阻力试验相关参数与结果 Tab.2 Relevant parameters and results of model test in brash ice channel under IA and UIWL draft conditions |
|
|
表 3 船模敞水阻力试验相关参数与结果 Tab.3 Relevant parameters and results of model test in open water |
本文数值碎冰模型根据模型试验图像采用复合颗粒的方式进行建模。在船舶进行非冻结模型冰阻力试验时,片状碎冰的典型形状包括正方形、正五边形、圆形、不规则多边形、椭圆形、梯形和正六边形。这7种碎冰模型形状与实际模型试验中的碎冰图像相对应,如图3(a)所示。本文基于这7种碎冰模型形状采用复合颗粒模型建立数值片状碎冰模型如图3(b)和图3(c)所示。参照模型试验相关参数[23],7种片状碎冰模型高度为50 mm,片状圆形碎冰模型半径为50 mm,片状正方形模型边长为0.1 m,其余形状碎冰模型表面积均保持与圆形和正方形相似。根据实尺度冰属性与模型缩尺比[25],数值碎冰模型弹性模量为293.33 MPa[26],泊松比

|
图 3 汉堡冰池试验碎冰数值片状碎冰模型 Fig. 3 Brash ice models in HSVA tests and numerical flaky brash ice models |
本文CFD-DEM碎冰航道完全根据《芬兰-瑞典冰级规范》[2]以及汉堡冰池试验的要求设定,数值碎冰航道的长度为50 m,宽度为船宽的2倍。图4(a)和图4(c)为数值模拟的碎冰航道,图4(b)为模型试验碎冰航道,数值碎冰航道参照模型试验的标准和规格。片状碎冰模型从零部件喷射器均匀喷射进入流体,碎冰模型的密集度与模型试验保持一致。平整冰区域厚度与试验厚度保持一致,船模在碎冰航道航行的试验过程中不会与层冰发生接触和碰撞,因此将平整冰看作刚性体以简化数值计算。

|
图 4 模型试验与数值碎冰航道 Fig. 4 Brash ice channel of the model test and numerical simulation |
本文研究对象为某极地环保多功能运输船,数值船模与冰池试验船模保持一致,缩尺比为29.508,数值船模垂线间长为7.547 m,型宽为1.093 m,高水位线为0.451 m,船模航速
图5为船模在碎冰航道中航行数值模拟的计算区域和边界条件,船舶碎冰航行数值模型满足对称条件,因此在船模的中纵剖面处设置对称面取一半进行计算分析。参照模型试验相关数据[23],计算域范围在流向上长度为54 m,垂直方向上长度为18.8 m,横向上长度为6 m。

|
图 5 船舶在碎冰航道航行数值模拟的计算域和边界条件 Fig. 5 Computational domains and Boundary conditions for numerical simulation of ship navigation in the brash ice channel |
本文采用包含棱柱型边界层网格的切割体网格模型对极地环保多用途运输船的CFD-DEM计算区域进行网格划分,并在船身周围划分边界层网格。在船舶的自由表面和首尾区域进行网格加密,并以不同策略对边界层网格进行了划分。计算域范围内的网格划分如图6所示,总网格数量为93万。

|
图 6 数值计算网格 Fig. 6 Computational mesh |
合理的网格密度在某种程度上决定了数值计算的准确度和计算效率。根据ITTC网格无关性分析[27],本文选用满足一定细化率要求的粗、中、细3套网格,以船模航速为0.474 m/s,片状圆形数值碎冰模型为例,在相同计算条件下进行网格无关性分析,结果如表4所示,其中总阻力试验值由HSVA冰池试验报告得到,误差一栏的计算公式为
|
|
表 4 网格无关性分析 Tab.4 Grid independence analysis |
从上述计算结果可以看出,随着网格数量的增加,计算所需运行时间迅速增加,总阻力误差逐渐减小又增大。当采用基础尺寸为0.1125 m,计算网格数约93.07万时,数值计算误差最小,计算运行时长适中。因此,为确保数值计算的准确性并节约计算成本,本文后续计算将统一采用中等网格参数进行网格划分。
4.2 碎冰运动分析当船舶穿越碎航道时,模型冰与船体会发生接触和碰撞。由于船首型线曲度和船首兴波的影响,模型冰与船体接触后沿着船体曲面切线方向发生相对运动,这被称为碎冰的翻转现象[28]。随着船舶持续航行,能够明显观察到船首上的碎冰堆积和碎冰沿着船舶舷侧向后滑移的现象。图7通过水下仰视视角展示了模型试验与不同形状的片状数值碎冰模型在船艏堆积和偏移的现象;图8通过水下侧视视角呈现了不同形状片状数值碎冰模型沿着舷侧滑移的情况。

|
图 7 不同形状碎冰在船艏的数值模拟与模型试验现象 Fig. 7 Numerical and experimental phenomena for different shapes of brash ice on the bow |

|
图 8 不同形状碎冰在舷侧的数值模拟与模型试验现象 Fig. 8 Numerical and experimental phenomena for different shapes of brash ice on the side |
从这2种典型现象的对比图中可以看出,所有形状的数值碎冰模型均能模拟出相应试验现象。在船首处,片状圆形冰、正五边形冰和正六边形冰与船体发生碰撞后的翻转现象更为明显;片状正方形冰、圆形冰、正五边形冰、正六边形冰和梯形冰能更好的模拟船舶驶入碎冰航道后碎冰遭到挤压并向航道两侧扩散的现象;在舷侧,片状正方形冰、梯形冰和不规则多边形冰具有更为尖锐的轮廓,相比于片状圆形、正五边形、正六边形等轮廓光滑的碎冰,它们在模拟舷侧碎冰滑移现象时与模型试验碎冰粒子更为接近。
以圆形片状数值碎冰航道为例,图9通过水下仰视视角展现了船舶在碎冰航道航行模型试验与数值模拟的全过程。从图中可以很明显的观察到船首碎冰的堆积和舷侧碎冰的滑移现象,在船舶在航行阶段的末期,沿着舷侧滑移的碎冰会继续向后滑移并在船尾处形成堆积并随着船舶驶过留下一条略窄于船宽的开阔航道,之后船尾的碎冰就会随着船舶尾流的流动逐渐向碎冰航道的中间聚拢,使开阔航道就会变得更加狭窄。因此,本文建立的基于CFD-DEM的极地船舶碎冰航行数值模型能较好的模拟碎冰堆积、翻转、偏移和滑动等现象,与模型试验现象匹配较好。

|
图 9 船舶在碎冰航道航行全过程的模型试验和数值模拟现象对比 Fig. 9 Comparison of experimental and numerical phenomena on the whole process of ship navigation in the brash ice channel |
船舶在碎冰航道航行的总阻力包括敞水阻力和碎冰阻力,总阻力可以表示为:
| $ {R_T} = {R_{ch}} + {R_{OW}}。$ | (9) |
式中:
图10为数值碎冰模型为片状圆形时船舶碎冰阻力曲线图,实线代表碎冰阻力瞬时值,虚线代表碎冰阻力平均值。从阻力曲线图中可以观察到,船舶所受碎冰阻力逐渐上升,直到第20 s时趋于稳定。这是因为在船舶航行阶段的初期,船体接触到的碎冰较少,因此碎冰阻力较小,随着船舶完全驶入碎冰航道,碎冰受到周围的层冰和船体的作用导致碎冰与船体的接触和碰撞增加,从而使碎冰阻力增大,当整个船体穿越碎冰航道后,碎冰与船体的接触何碰撞都将趋于稳定,即碎冰阻力达到一个平稳状态。

|
图 10 片状圆形数值碎冰航道中船舶受到的阻力 Fig. 10 The resistance of ship in the flaky circle numerical brash ice channel |
本文分别计算了船模以

|
图 11 多边形数值碎冰航道中船舶所受碎冰阻力 Fig. 11 Resistance of ships in flaky polygonal numerical brash ice channel |
船舶碎冰阻力试验结果由汉堡冰池试验报告获得。将船舶在7种不同形状数值片状碎冰模型中的总阻力均值与模型试验数据相对比,如表5所示,其中误差一栏的计算公式为
|
|
表 5 碎冰阻力数值计算与模型试验对比 Tab.5 Comparison of numerical calculation and model test of brash ice resistance |
可知,数值模拟中选用片状圆形数值碎冰模型计算误差最小,比模型试验值高2.04%,其次为正六边形,计算结果比模型试验高2.5%;选用片状椭圆形数值碎冰模型计算误差最大,比模型试验高29.69%。因此在以阻力预报为目的进行船舶碎冰航道航行数值计算时推荐使用片状圆形数值碎冰模型。
5 结 语本文以某极地环保多用途运输船为研究对象,建立了圆形、正六边形、正五边形、椭圆形、梯形和不规则多边形7种不同形状数值片状碎冰模型和CFD-DEM耦合数值计算模型。将船舶碎冰阻力数值预报结果与模型试验结果相对比,研究发现数值碎冰模型形状对船舶碎冰阻力预报的准确性具有显著影响,因此对数值碎冰模型形状的研究在冰区船舶碎冰阻力预报中至关重要。本文主要结论如下:
1)数值模拟中,本文建立的基于CFD-DEM计算方法的极地船舶碎冰航行数值模型可以模拟碎冰堆积、翻转、偏移和滑动等现象,与模型试验现象匹配较好。
2)本文研究了不同数值片状碎冰模型形状对船舶碎冰阻力预报的影响。数值模拟与试验现象对比发现7种形状碎冰模型均能模拟船舶在碎冰航道航行过程中船体与碎冰的碰撞现象。碎冰阻力数值计算结果与模型试验对比发现采用片状圆形数值碎冰模型预报船舶碎冰阻力更准确,其计算结果比模型试验值大2.04%,因此在以阻力预报为目的的CFD-DEM数值模拟中,采用片状圆形数值碎冰模型计算更优。
本文针对数值片状碎冰模型形状对船舶碎冰阻力预报进行了研究,但没有计算船速、碎冰密集度、碎冰厚度等其他因素对碎冰阻力预报的影响,也没有考虑到风和波浪的作用,后续在研究碎冰阻力预报时将考虑更多影响因素。
| [1] |
KARAMPERIDIS S, VALANTASIS-KANELLOS N. Northern Sea route as an emerging option for global transport networks: a policy perspective [J]. WMU Journal of Maritime Affairs, 2022.
|
| [2] |
Finnish Maritime Administration. Finnish and Swedish Ice Class Rules[S]. 2017.
|
| [3] |
CORLETT E C B, SNAITH G R. Some aspects of icebreaker design[J]. Trans. RINA, 1964, 106(4): 389-413. |
| [4] |
黄焱, 李伟, 王迎晖, 等. 大型运输船极地浮冰区航行阻力的模型试验[J]. 中国造船, 2016, 57(3): 26-35. DOI:10.3969/j.issn.1000-4882.2016.03.004 |
| [5] |
郭春雨, 李夏炎, 王帅, 等. 冰区航行船舶碎冰阻力预报数值模拟方法[J]. 哈尔滨工程大学学报, 2016, 37(2): 145-156. |
| [6] |
HANSEN E H, LOSET S. Modelling floating offshore units moored in broken ice: model description[J]. Cold Regions Science and Technology, 1999, 29(2): 97-106. DOI:10.1016/S0165-232X(99)00023-3 |
| [7] |
VROEGRIJK E. Validation of CFD+ DEM against measured data[C]// American Society of Mechanical Engineers. ASME 2015 34th International Conference on Offshore Mechanics and Arctic Engineering. Canada, Newfoundland: ASME, 2015: 1−7.
|
| [8] |
国威, 赵桥生, 王习建, 等. 碎冰条件下冰区船冰水动力数值模拟研究[J]. 船舶力学, 2020, 24(4): 456-464. GUO Wei, ZHAO Qiaosheng, WANG Xijian, et al. The numerical simulation research on ice and water combined force acting on ice-going ship in pack ice[J]. Journal of Ship Mechanics, 2020, 24(4): 456-464. DOI:10.3969/j.issn.1007-7294.2020.04.005 |
| [9] |
骆婉珍, 姜大鹏, 吴铁成, 等. 冰区加强型散货船碎冰航道航行阻力数值计算研究[J]. 中国造船, 2020, 61(1): 41-49. DOI:10.3969/j.issn.1000-4882.2020.01.004 |
| [10] |
张远双, 齐江辉, 郑亚雄, 等. 冰区加强型集装箱船碎冰航道航行阻力数值模拟[J]. 舰船科学技术, 2020, 42(21): 49-54. ZHANG Yuanshuang, QI Jianghui, ZHEN Yaxiong, et al. A numerical simulation research for resistance of ice-strengthening container ship in crushed ice channel[J]. Ship Science and Technology, 2020, 42(21): 49-54. DOI:10.3404/j.issn.1672-7649.2020.11.010 |
| [11] |
齐江辉, 郭翔, 陈强, 等. 碎冰区航行船舶阻力预报数值模拟研究[J]. 兵器装备工程学报, 2019, 40(11): 207-212. DOI:10.11809/bqzbgcxb2019.11.041 |
| [12] |
ZHANG J, ZHANG Y, SHANG Y, et al. CFD-DEM based full-scale ship-ice interaction research under FSICR ice condition in restricted brash ice channel[J]. Cold Regions Science and Technology, 2022, 194.
|
| [13] |
王超, 封振, 李兴, 等. 航行于碎冰区船舶冰阻力与冰响应探析[J]. 中国舰船研究, 2018, 13(1): 73-78. WANG Chao, FENG Zhen, LI Xing, et al. Analysis on ice resistance and ice response of ships sailing in brash ice[J]. Chinese Journal of Ship Research, 2018, 13(1): 73-78. DOI:10.3969/j.issn.1673-3185.2018.01.011 |
| [14] |
KARULIN EB K M. Numerical and physical simulations of moored tanker behaviour[J]. Ship and Offshore Structures, 2011, 6(3): 179-184. DOI:10.1080/17445302.2010.544087 |
| [15] |
李紫麟, 刘煜, 孙珊珊, 等. 船舶在碎冰区航行的离散元模型及冰载荷分析[J]. 力学学报, 2013, 45(6): 868−877.
|
| [16] |
郭麒. 基于扩展圆盘离散元方法的海冰问题模拟与分析[D]. 大连: 大连理工大学, 2022.
|
| [17] |
金强, 张佳宁, 葛媛, 等. 基于离散元方法的极地浮碎冰区船舶冰阻力[J]. 船舶工程, 2020, 42(1): 35-41. JING Qiang, ZHANG Jianing, GE Yuan, et al. Ship ice resistance in polar brash/broken ice area based on discrete element method[J]. Ship Engineering, 2020, 42(1): 35-41. |
| [18] |
何宾峰, 詹成胜, 赵桥生, 等. 浮冰区船舶冰阻力数值计算研究[J]. 武汉理工大学学报(交通科学与工程版), 2022, 46(1): 71-75. |
| [19] |
WANG C, HU X, TIAN T, et al. Numerical simulation of ice loads on a ship in broken ice fields using an elastic ice model[J]. International Journal of Naval Architecture and Ocean Engineering, 2020, 12: 414-427. DOI:10.1016/j.ijnaoe.2020.03.001 |
| [20] |
TANG X, ZOU M, ZOU Z, et al. A parametric study on the ice resistance of a ship sailing in pack ice based on CFD-DEM method[J]. Ocean Engineering, 2022, 265.
|
| [21] |
STEPHEN B. Pope turbulent flows[M]. United Kingdom: Cambridge University Press, 2010.
|
| [22] |
孙其诚, 王光谦. 颗粒物质力学导论[M]. 北京: 科学出版社, 2009.
|
| [23] |
Brash ice tests for 68k MPV with ice class 1A: HSVA Report[R]. 2022.
|
| [24] |
Calm water model tests for a 68000DWT pulp carrier: SDARI Report[R]. 2022.
|
| [25] |
TIMCO G W. Ice forces on structures: physical modelling techniques[C]//Second IAHR State-of-the-Art Report on Ice Forces on Structures, Proceedings of the IAHR Symposium on Ice. Germany, Hamburg, 1984 (2): 34.
|
| [26] |
TIMCO G W, WEEKS W F. A review of the engineering properties of sea ice[J]. Cold Regions Science and Technology, 2010, 60(2): 107-129. DOI:10.1016/j.coldregions.2009.10.003 |
| [27] |
Uncertainty analysis in CFD, Examples for resistance and flow, ITTC Recommended Procedures, 1999.
|
| [28] |
陈昭炀. 船舶在人造浮冰中的阻力试验研究[D]. 大连: 大连理工大学, 2020.
|
 2024, Vol. 46
2024, Vol. 46
