2. 湖北工业大学 现代制造质量工程湖北省重点实验室,湖北 武汉 430068;
3. 武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;
4. 中国海警局直属某局,海南 三亚 572000
2. Key Laboratory of Modern Manufacturing Quality Engineering in Hubei Province, Hubei University of Technology, Wuhan 430068, China;
3. School of Marine and Energy Power Engineering, Wuhan University of Technology, Wuhan 430063, China;
4. A Direct Branch of China Coast Guard, Sanya 572000, China
三维数控弯板机可用于高效冷弯成形船体双曲度外板,该设备具有高度可调的上、下两组模具,上模具的压头数量比下模具少,上、下模具的压头交错规则排列且尺寸相同[1]。但双曲度板材的几何形状、板厚尺寸、材料性能和成形载荷等重要因素的变化均会导致板材回弹量出现难以预测的问题[2],并降低板材加工成形精度。为了满足三维数控弯板机加工成形质量,有效控制回弹对板材成形精度的影响,需要对板材成形回弹预测问题进行研究。
双曲度板材冲压成形的回弹预测是一个难以用理论模型求解的非线性多参数耦合问题[3],但随着计算机技术的发展,利用高性能计算机进行有限元仿真可以较为快速地获取板材成形回弹预测结果。本文针对板厚尺寸和成形载荷对板材成形回弹的影响,基于有限元数值模拟的结果,构建双曲度板材成形回弹数据集,采用长短时记忆网络模型对双曲度板的成形回弹量进行预测,并利用改进后的麻雀搜索算法优化网络模型的相关参数,降低人工设置参数带来的误差,提高网络模型对回弹量预测的精度。
1 改进SSA-LSTM模型 1.1 麻雀搜索算法麻雀搜索算法(Sparrow Search Algorithm,SSA)是模仿麻雀寻找食物的行为的优化算法[4]。麻雀种群包含发现者和追随者,通过种群中的发现者寻找食物的位置,追随者跟随表现最优的发现者移动位置,直到种群搜索到全局最优解。其中,靠近天敌的麻雀需要移动到安全区域获得食物。
发现者更新位置的式[5]如下:
| $ {X}_{i,j}^{u+1}=\left\{\begin{array}{l}{X}_{i,j}^{u}\cdot {\rm{exp}}\left(\displaystyle\frac{-i}{{r}_{1}\cdot M}\right)\text{,}R < S\text{,}\\ {X}_{i,j}^{u}+Q\cdot {\boldsymbol L}\text{,}R \geqslant S。\end{array}\right. $ | (1) |
式中:
追随者更新位置[6]如下式:
| $ {X}_{i,j}^{u+1}=\left\{\begin{array}{l}{X}_{p}^{u+1}+\left|{X}_{i,j}^{u}-{X}_{p}^{u+1}\right|\cdot {A}^+\cdot {\boldsymbol{L}}\text{,}i \leqslant \displaystyle\frac{n}{2}\text{,}\\ Q\cdot exp\left(\displaystyle\frac{{X}_{\rm{worst}}^{u}-{X}_{i,j}^{u}}{{i}^{2}}\right)\text{,}i > \displaystyle\frac{n}{2}。\end{array}\right. $ | (2) |
式中:
靠近天敌的个体更新位置的计算式为:
| $ {X}_{i,j}^{u+1}=\left\{\begin{array}{l}{X}_{\rm{best}}^{u}+\beta \cdot \left|{X}_{i,j}^{u}-{X}_{\rm{best}}^{u}\right|\text{,}{f}_{i} > {f}_{g}\text{,}\\ {X}_{i,j}^{u}+K\cdot \left(\displaystyle\frac{\left|{X}_{i,j}^{u}-{X}_{\rm{worst}}^{u}\right|}{\left({f}_{i}-{f}_{w}\right)+\varepsilon }\right)\text{,}{f}_{i}={f}_{g}。\end{array}\right. $ | (3) |
式中:
1)Circle混沌映射初始化策略
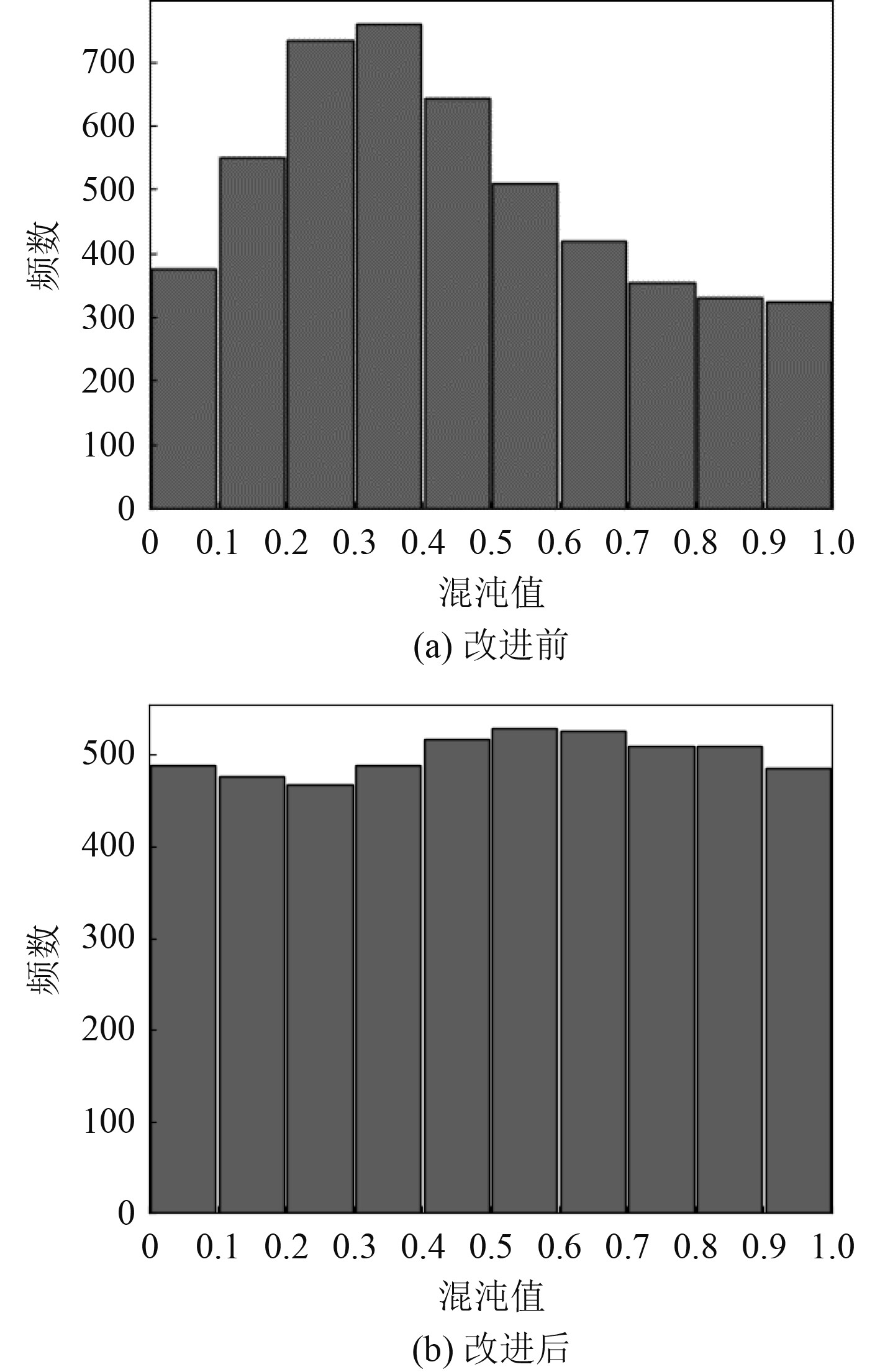
由于麻雀搜索算法在初始阶段都随机生成种群,易导致种群位置分布不均,影响算法寻优结果[7]。引入混沌映射初始化种群,可减少种群群聚现象,扩大空间位置范围。本文采用Circle混沌映射获得混沌序列初始化种群[8],如图1(a)所示,Circle混沌映射混沌值主要分布在[0.1,0.6]之间,为保证初始化种群的多样性,对Circle混沌映射表达式进行改进,改进后的表达式为:
|
图 1 Circle混沌映射频率分布直方图 Fig. 1 Distribution histogram of Circle chaotic map frequency |
| $ {c}_{i+1}=mod\left({3c}_{i}+0.44-\left(\frac{0.6}{3{\text{π}} }\right)\mathrm{sin}\left(3{\text{π}} \times {c}_{i}\right)\text{,}1\right) 。$ | (4) |
式中:
由图1(b)可以看出,与改进前Circle混沌映射混沌值相比,改进后的混沌值在(0,1)之间均匀性更好,故Circle映射可扩大算法搜索范围。
2)反向学习策略
发现者更新位置的过程中,麻雀个体的搜索范围会不断减小,逐步向最优个体靠近,这会导致算法快速陷入局部最优。发现者可以通过反向学习策略获得当前位置的反向解,生成新的个体位置,防止算法在极值区域内迭代,增加种群的多样性。反向学习策略如下式[9]:
| $ {x'}_{j}={L}_{j}+{\mathrm{\phi }(U}_{j}-{x}_{j})。$ | (5) |
式中:
3)高斯与柯西变异扰动
模仿生物的变异特征,在优化算法中融入变异个体。本文采用高斯与柯西结合的策略对麻雀个体进行扰动[10],有助于SSA算法跳出局部最优解,在全局范围内寻优,如下式:
| $ {x'}_{i,j}={x}_{i,j}\left[1+{\mu }_{1}\mathrm{C}\left(0,1\right)+{\mu }_{2}\mathrm{G}\left(0,1\right)\right],$ | (6) |
| $ {\mu }_{1}=\left(1-\frac{t}{M}\right){e}^{-\frac{t}{M}} , {\mu }_{2}=1-{\mu }_{1},$ | (7) |
| $ {f}\left(z\text{;}0,1\right)=\frac{1}{\sqrt{2{\text{π}} }}{\rm{exp}}\left(-\frac{{z}^{2}}{2}\right) ,$ | (8) |
| $ {f}\left(x\text{;}0,1\right)=\frac{1}{{\text{π}} \left(1+{x}^{2}\right)}。$ | (9) |
式中:
Circle映射序列扰动公式如下:
| $ {x}_{i,j}^{\rm{new}}={L}_{i,j}+{c}_{i+1}\left({{U}_{i,j}-L}_{i,j}\right),$ | (10) |
| $ {x'}_{i,j}=\frac{1}{2}\left({x}_{i,j}+{x}_{i,j}^{\rm{new}}\right)。$ | (11) |
式中:
长短时记忆网络(Long Short-term Memory,LSTM)是一种循环神经网络(Recurrent Neural Network,RNN) 的特例模型,可以实现多个时间步的数据学习[11]。但LSTM神经网络内部结构复杂,存在网络参数量大、计算复杂、训练效率低等缺点。针对LSTM神经网络的不足之处,提出改进SSA-LSTM模型,减小人工调节参数对神经网络模型运行结果的影响,扩大数据搜索范围,提高预测结果精度。本文利用改进的SSA算法对LSTM模型的学习率、迭代次数、隐藏层的神经元个数进行优化。该模型构建的具体步骤如下:
步骤1 划分训练集与测试集,并归一化处理。
步骤2 确定LSTM神经网络结构。
步骤3 确定麻雀搜索算法的迭代次数、种群数量、发现者比例、寻优参数的上下限值,利用Circle混沌映射初始化模型的寻优参数值。
步骤4 取LSTM模型的测试集均方损失误差函数用作优化算法中的适应度函数,获得适应度值并排序,划分种群的发现者和跟随者。
步骤5 根据式(1)更新发现者位置,再利用反向学习公式(5)更新位置,对比反向学习前后的适应度值,择优保留个体位置。根据式(2)更新跟随者位置,再利用式(3)更新遇见天敌个体的位置。
步骤6 算法在一次迭代完成后,计算种群的平均适应度值,对适应度值小于平均值的个体进行高斯与柯西扰动,再利用式(4)的Circle混沌映射序列对适应度值大于平均值的个体进行扰动,最终根据贪婪策略,择优保留扰动前后的个体位置信息。直到满足停止移动的条件−测试集均方损失误差函数值最小,麻雀停止更新位置,输出优化好的LSTM模型参数。
步骤7 带入上述优化好的参数,重新训练LSTM模型,得到最终改进的SSA-LSTM模型预测值。
2 双曲度板成形回弹仿真如图2所示,本文基于船舶三维数控弯板机上/下模具单个压头分别与下/上模具的4个压头相对应的结构特点,利用ABAQUS有限元软件进行4个压头支撑板材情况下的单压头冲压仿真。其中,上压头的尺寸为40 mm×40 mm,选取板厚尺寸为3、5、7、9、11、13 mm的160 mm×160 mm的Q235方形钢板,在不同成形载荷下进行冲压成形回弹模拟。模型的上下模具网格划分成相同大小,尺寸为2.5 mm,单元类型设为三维四边形单元(R3D4),板材单元类型选择8节点六面体单元(C3D8R)。模具与板材之间的接触关系采用通用接触方式,摩擦系数设为0.15。模型的上模具压头约束住x、z方向上的平动和y方向上的转动,下模具压头采用自由旋转的方式。本实验采用显式求解方式来完成仿真,设置2个分析步,第1个分析步模拟施加载荷的过程,第2个分析步模拟板材回弹过程。

|
图 2 压头排列示意图 Fig. 2 Schematic diagram of the head arrangement |
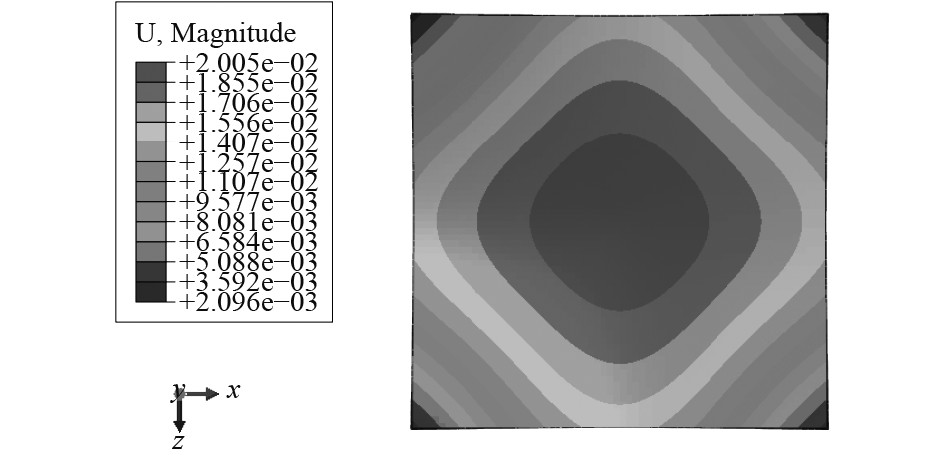
板厚3 mm的板材,在施加
|
图 3 加载完成后的板厚方向位移图 Fig. 3 Displacement diagram of plate thickness direction after loading |
|
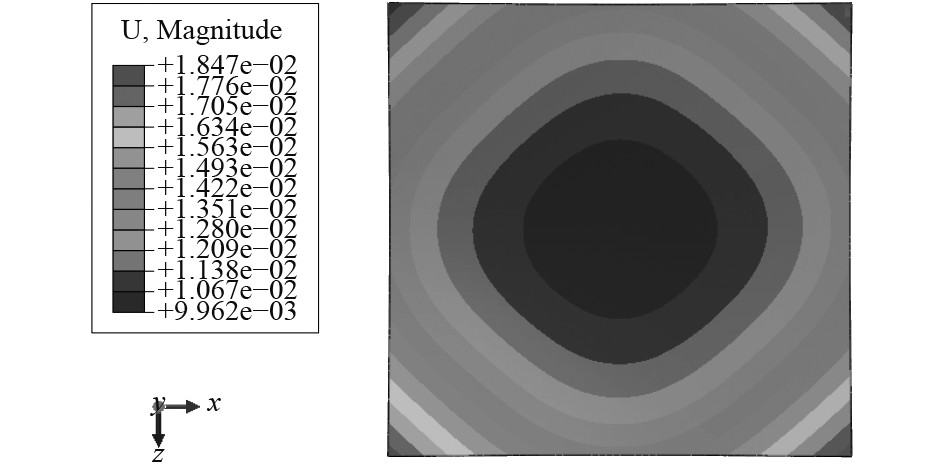
图 4 卸载回弹后的板厚方向位移图 Fig. 4 Displacement diagram of plate thickness direction after spring back |
本文选取有限元数值模拟的结果构建数据集,输入到模型的时序样本数据由有限元仿真加载过程和回弹过程的增量步组成,输入的特征变量为成形载荷、板厚尺寸、板厚方向上的位移值,输出样本数据由回弹的最后一个增量步位移值构成。最终选取的数据共450组,其中360组作为训练集,剩余的90组数据作为测试集。
本文将改进SSA-LSTM模型中,麻雀种群数量设为10;发现者比例设为0.2;最大迭代次数为15。学习率、迭代次数、隐藏层的神经元个数为寻优参数,上限分别为0.01、180、10,下限为0.001、80、1。为了验证实验结果的可靠性,其他对比模型的迭代次数都为150;学习率为0.001;输入特征为5;输出特征为1。
3.2 评价指标为有效评价模型的稳定性和预测精度,引入均方误差值(Mean Square Error,MSE)、最大绝对误差值、最小绝对误差值、平均绝对误差值(Mean Absolute Error,MAE),最大与最小绝对误差值可表明模型预测偏差的极限,MAE能够反映回弹位移真实值与模型获得预测值的整体偏差,MSE可以表明不同预测模型的整体预测精度。MAE、MSE值越小,真实值与预测值的偏差越小,模型预测越精确。
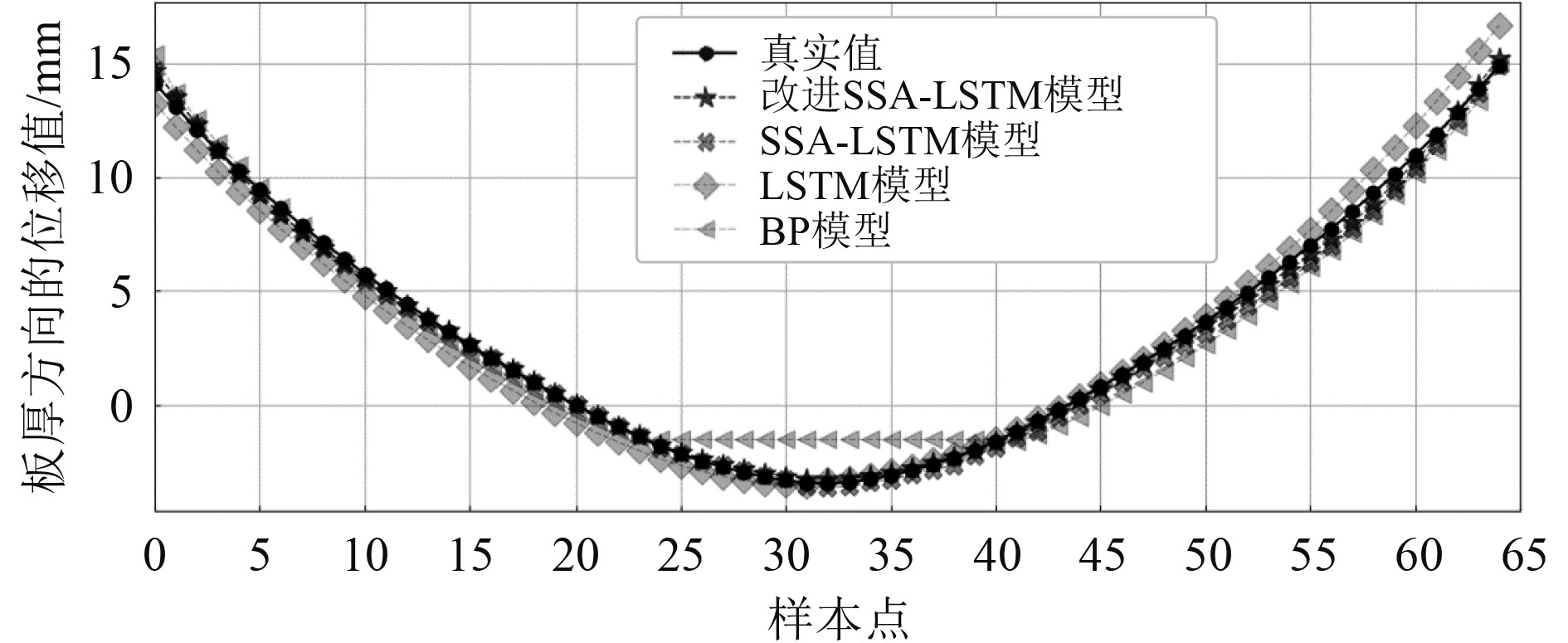
3.3 预测结果对比分析为了更好地体现改进SSA-LSTM模型方法回弹预测的精确性,采用BP神经网络模型和未经优化的LSTM模型、未改进的SSA-LSTM模型进行对比实验,将不同的神经网络模型在相同的数据集上进行训练,并完成回弹预测。图5是板材在板厚尺寸为13 mm且成形载荷为
|
图 5 模型预测值与真实值对比 Fig. 5 Comparison of predicted values and true values of models |
可以看出,BP神经网络模型与未经优化的LSTM模型预测结果偏离真实值的程度较为明显,改进SSA-LSTM模型对比其他3个模型的预测值更加贴近于真实值,与真实值的拟合度更高。改进SSA-LSTM模型预测的结果值能够根据真实值的分布情况及时、准确地做出合理调整,使预测结果数据在整体分布上尽可能符合真实数据。
表1对比了3种模型回弹预测的评价指标,改进SSA-LSTM模型在最大与最小绝对误差值上比其他模型有明显降低,说明该模型可降低预测结果与真实值的极限偏差值,且改进SSA-LSTM模型相较于其他3种模型的MAE、MSE值最小,MAE和MSE分别达到了0.142、0.041。根据预测值与真实值对比结果曲线和评价指标对比结果可以发现,经过改进的麻雀搜索算法优化后的LSTM预测模型的整体预测效果最好,证明改进SSA-LSTM模型能够有效提高双曲度板材回弹预测的预测精度,在船体双曲度外板回弹预测方面具有一定优越性。
|
|
表 1 回弹预测评价指标对比 Tab.1 Comparison of evaluation indexes of spring back prediction |
本文总结了船舶三维数控弯板机冲压双曲度板材的工艺流程,提出可将板材成形回弹过程离散为,若干个单个压头冲压4个压头支撑板材的成形回弹过程,并进行了有限元仿真实验,构建了基于板厚尺寸和成形载荷的板材成形回弹数据集,提出基于改进SSA算法优化LSTM模型的双曲度板回弹预测方法。与传统的BP神经网络模型、LSTM模型和SSA-LSTM模型相比,改进SSA-LSTM模型预测方法具有拟合程度高、自适应强等优点,具有一定通用性,在工程的实际应用中具有较高价值。
| [1] |
华剑锋, 胡勇, 王呈方, 等. 复杂曲面船体外板非对压多压头成形技术[J]. 船舶工程, 2011, 33(2): 63-66. HUA Jianfeng, HU Yong, WANG Chengfang, et al. No-pair dins forming technology for complex curved surface of ship hull plate[J]. Ship Engineering, 2011, 33(2): 63-66. DOI:10.3969/j.issn.1000-6982.2011.02.015 |
| [2] |
赵涵, 胡勇, 蔡一杰, 等. 典型双曲度板材冲压成形回弹差异分析[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(3): 486-490. ZHAO Han, HU Yong, CAI Yijie, et al. Springback difference analysis of typical doubly curved metal plate forming[J]. Journal of Wuhan University of Technology ( Transportation Science & Engineering), 2020, 44(3): 486-490. |
| [3] |
苏绍娟, 胡勇, 王呈方. 基于SVM的船体外板冷弯回弹预测模型研究[J]. 舰船科学技术, 2015, 37(5): 104-108. SU Shaojuan, HU Yong, WANG Chengfang. Research on prediction model of hull plate bending springback based on SVM[J]. Ship Science and Technology, 2015, 37(5): 104-108. DOI:10.3404/j.issn.1672-7649.2015.05.022 |
| [4] |
XUE J, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22−34.
|
| [5] |
张伟康, 刘升, 任春慧. 混合策略改进的麻雀搜索算法[J]. 计算机工程与应用, 2021, 57(24): 74-82. ZHANG Weikang, LIU Sheng, REN Chunhui. Mixed strategy improved sparrow search algorithm[J]. Computer Engineering and Applications, 2021, 57(24): 74-82. DOI:10.3778/j.issn.1002-8331.2101-0161 |
| [6] |
吕鑫, 慕晓冬, 张钧, 等. 混沌麻雀搜索优化算法[J]. 北京航空航天大学学报, 2021, 47(8): 1712-1720. LU Xin, MU Xiaodong, ZHANG Jun, et al. Chaos sparrow search optimization algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1712-1720. |
| [7] |
李雅丽, 王淑琴, 陈倩茹, 等. 若干新型群智能优化算法的对比研究[J]. 计算机工程与应用, 2020, 56(22): 1-12. LI Yali, WANG Shunqin, CHEN Qianru, et al. Comparative study of several new swarm intelligence optimization algorithms[J]. Computer Engineering and Applications, 2020, 56(22): 1-12. DOI:10.3778/j.issn.1002-8331.2006-0291 |
| [8] |
胡啸, 薛霖, 景洁, 等. 基于改进SSA-GA-BP神经网络的热连轧轧制力预测[J]. 塑性工程学报, 2023, 30(8): 122-129. HU Xiao, XUE Lin, JING Jie, et al. Rolling force prediction of hot continuous rolling based on improved SSA-GA-BP neural network[J]. Journal of Plasticity Engineering, 2023, 30(8): 122-129. DOI:10.3969/j.issn.1007-2012.2023.08.014 |
| [9] |
陈刚, 林东, 陈飞, 等. 基于Logistic回归麻雀算法的图像分割[J]. 北京航空航天大学学报, 2023, 49(3): 636-646. CHEN Gang, LIN Dong, CHEN Fei, et al. Image segmentation based on Logistic regression sparrow algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(3): 636-646. |
| [10] |
毛清华, 张强. 融合柯西变异和反向学习的改进麻雀算法[J]. 计算机科学与探索, 2021, 15(6): 1155-1164. MAO Qinghua, ZHANG Qiang. Improved sparrow algorithm combining cauchy mutation and opposition-based learning[J]. Journal of Frontiers of Computer Science and Technology, 2021, 15(6): 1155-1164. DOI:10.3778/j.issn.1673-9418.2010032 |
| [11] |
李艳波, 尹镨, 陈俊硕, 等. 结合改进残差网络和Bi-LSTM的短期电力负荷预测[J]. 哈尔滨工业大学学报, 2023, 55(8): 79-86. LI Yanbo, YIN Pu, CHEN Junshuo, et al. Combining residual network and Bi-LSTM for short term power load forecasting[J]. Journal of Harbin Institute of Technology, 2023, 55(8): 79-86. DOI:10.11918/202208110 |
 2024, Vol. 46
2024, Vol. 46
