2. 上海交通大学 三亚崖州湾深海科技研究院,海南 三亚 572000
2. Sanya Yazhou Bay Institute of Deepsea Science and Technology, Shanghai Jiao Tong University Sayan, 572000, China
随着全球人口和世界经济的不断增长,全球范围内的资源矛盾和环境恶化问题日益尖锐。世界各国逐渐开始对蕴含丰富能源与矿物资源的海洋大规模开发利用,深水作业船随之成为海洋油气深水勘探开发的重要工具,因此对船舶动力定位技术的要求也越来越高。船舶动力定位技术是一种可使船舶仅利用自身推进器的相互配合抵御风、浪、流等外界扰动的影响,继而准确跟踪给定轨迹或以一定姿态保持在水面目标位置的技术,具有机动性强、定位精度高、定位成本低等优点[1]。近年来在学者们的努力下,许多先进的控制算法在DP船或无人水面舰艇(Unmanned Surface Vessel, USV)的轨迹跟踪控制领域得到应用,例如非线性反步控制方法[2]、动态面控制方法[3]、滑模控制[4]、鲁棒控制[5]、自适应控制[6]、神经网络控制[7]等。
在实际海洋环境中,外部环境扰动是常见且无法忽略的。针对这一问题,最流行的处理方法之一是扰动观测器(Disturbance Observer, DO)模型 [8]。Du等[9]将DO与动态面控制方法相结合,增强了USV的跟踪控制效果。Abdelaal等[10]在研究欠驱动USV的状态跟踪问题时,也采用NDO估计环境扰动,并将其反馈到预测模型中以加强控制器的鲁棒性。在此基础上,为了进一步提高系统的鲁棒性,本文采用一种具有固定时间稳定性的连续FTDO用于扰动估计。
除了未知环境扰动,DP船航行中对于状态(位置和速度)约束的需求也在迅速增长,忽视这些约束可能会使DP船的跟踪性能受到影响,甚至使其处于危险之中,故研究具有状态约束的DP船轨迹跟踪控制方法很有必要[11]。BLF方法是近年来大多数处理DP船状态约束问题时的有效解。Yin等[12]在研究扰动不确定和状态约束下水面舰船跟踪问题时,使用BLF方法实现了全状态约束。但传统BLF方法具有微分运算量较大、收敛区域小、构造复杂等缺点。Zheng等[13]通过集成一种新的tan型BLF方法来实现船舶位置误差约束。Wang等[14]在研究无人机编队控制问题时,通过时变tan型BLF方法保证了视线(LOS)范围和角度跟踪误差的约束。因此,本文采用tan型BLF方法来处理误差约束问题。
此外,由于DP船的执行器实际上能提供的控制力和力矩有限,所以受限的执行器功能,即执行器饱和,也是DP船运动控制律设计中需要考虑的重要因素。Yang等[15]将扰动估计结合到非线性模型预测控制(Nonlinear Model Predictive Control, NMPC)的后退优化问题求解,从而保证了输入约束。Zheng等[16]采用光滑双曲正切函数逼近解决饱和问题,并引入努斯鲍姆函数补偿饱和近似并确保系统稳定性。近年来,带辅助变量的抗饱和补偿器成为大量相关研究中使用的解决方法。Zheng等[17]开发了由平滑切换函数控制的辅助系统,有效应对了系统输入饱和。Park[18]为了解决USV的欠驱动和输入饱和困难,开发了辅助变量,并引入接近角来执行多种路径任务。Chen等[19]引入辅助设计系统,并将其与自适应技术相结合,在减少执行器饱和影响方面取得了很好的效果。本文将利用辅助系统来近似输入饱和,并通过自适应估计技术补偿饱和差,从而解决DP船轨迹跟踪控制中的执行器饱和问题。
基于上述分析,本文提出一种新的DP船在环境扰动、状态约束和执行器饱和下的自适应轨迹跟踪控制方法。首先,设计一种基于积分滑模(Integral Sliding Mode, ISM)控制和固定时间稳定性的连续FTDO来估计环境扰动。接着采用带辅助变量的抗饱和补偿器以应对执行器饱和,并通过对称tan型BLF将系统状态约束在给定界限内。最后通过自适应技术估计包括扰动不确定、输入饱和差和RBFNN近似误差在内的未知项界限。
1 DP船数学模型定义函数
|
|
表 1 符号意义 Tab.1 Symbols and meanings |
一般来说,水面DP船只需要考虑水平面三自由度运动。如Sorensen[20]所述,DP船的运动学模型和动力学模型如下:
| $ \dot \eta = {\boldsymbol R}(\psi )\nu ,$ | (1) |
| $ {\boldsymbol M}\dot \nu + {\boldsymbol C}(\nu )\nu + {\boldsymbol D}(\nu )\nu = \tau + {\tau _{env}} 。$ | (2) |
式中:
| $ {\boldsymbol R}\left( \psi \right) = \left( {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&1 \\ {\sin \psi }&{\cos \psi }&1 \\ 1&1&1 \end{array}} \right),$ | (3) |
| $ \dot {\boldsymbol R}(\psi ) = {\boldsymbol R}(\psi ){\boldsymbol S}(r),$ | (4) |
| $ {\boldsymbol S}(r) = \left( {\begin{array}{*{20}{c}} 0&{ - r}&0 \\ r&0&0 \\ 0&0&0 \end{array}} \right)。$ | (5) |
| $ {\boldsymbol M} = \left( {\begin{array}{*{20}{c}} {{m_{11}}}&0&0 \\ 0&{{m_{22}}}&{{m_{23}}} \\ 0&{{m_{32}}}&{{m_{33}}} \end{array}} \right),$ | (6) |
| $ {\boldsymbol C}\left( v \right) = \left( {\begin{array}{*{20}{c}} 0&0&{ - {m_{22}}v - {m_{23}}r} \\ 0&0&{{m_{11}}u} \\ {{m_{22}}v + {m_{23}}r}&{ - {m_{11}}u}&0 \end{array}} \right) ,$ | (7) |
| $ {\boldsymbol D} = \left( {\begin{array}{*{20}{c}} {{d_{11}}}&0&0 \\ 0&{{d_{22}}}&{{d_{23}}} \\ 0&{{d_{32}}}&{{d_{33}}} \end{array}} \right) 。$ | (8) |
| $ {\boldsymbol M}\dot \nu + {\boldsymbol C}(\nu )\nu + {\boldsymbol D}\nu = {\tau _c} + \Delta \tau + {\tau _{env}}。$ | (9) |
式中:
假设1
备注1 由于海洋环境不断变化,并且具有的能量有限,作用在DP船上的扰动可以被视为未知时变且有界的信号。因此,假设1合理。
1.2 控制分配控制力一般由推进器系统动力学决定,通过控制器算出指令控制矢量。本文根据Johansen等[21]给出的一种典型序列二次规划法得到实际控制律
| $ \tau (t) = {\boldsymbol A}(\alpha (t)){\boldsymbol u}(t) 。$ | (10) |
式中:
| $ {A_i}\left( {{\alpha _i}(t)} \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\alpha _i}(t)} \\ {\sin {\alpha _i}(t)} \\ {{l_{xi}}\sin {\alpha _i}(t) - {l_{yi}}\cos {\alpha _i}(t)} \end{array}} \right],{\text{ }}i = 1,2, \ldots ,n。$ | (11) |
式中:(lxi, lyi)为第i个执行器的位置。根据Xu等[22]所述,每一步指令控制向量τc的推力分配都能转化为时间迭代序列二次规划问题:
| $ \begin{gathered} \min J({{\Delta }}\alpha ,{\boldsymbol u},{\boldsymbol s}) = {\left( {{{\boldsymbol u}_0} + {{\Delta }}{\boldsymbol u}} \right)^{\rm T}}{\boldsymbol W}\left( {{{\boldsymbol u}_0} + {{\Delta }}{\boldsymbol u}} \right) + {s^{\rm T}}{\boldsymbol Q}s +\\ {{\Delta }}{\alpha ^{\rm T}}{\mathbf{\Omega}}{{\Delta }}\alpha + \frac{{\mathrm{d}}}{{{\mathrm{d}}\alpha }}{\left( {\frac{\rho }{{\varepsilon + \det \left( {{\boldsymbol A}(\alpha ){{\boldsymbol A}^{\rm T}}(\alpha )} \right)}}} \right)_{\alpha = {\alpha _0}}}{{\Delta }}\alpha,\\ \end{gathered} $ | (12) |
| $ {\mathrm{s.t.s}}+{\boldsymbol A}\left({\alpha }_{0}\right)\text{Δ}{\boldsymbol u}+{\frac{\partial }{\partial \alpha }({\boldsymbol A}(\alpha ){\boldsymbol u})| }_{\begin{array}{c}\alpha ={\alpha }_{0}\\ u={u}_{0}\end{array}} \text{Δ}\alpha ={\tau }_{c}-{\boldsymbol A}\left({\alpha }_{0}\right){\boldsymbol u}_{0}。$ | (13) |
| $ {{\Delta {\mathrm{min}}(}}{\boldsymbol u}) \leqslant {{\Delta }}{\boldsymbol u} \leqslant {{\Delta {\mathrm{max}}(}}{\boldsymbol u}),{\text{min(}}{\boldsymbol u}) - {{\boldsymbol u}_0} \leqslant {{\Delta }}{\boldsymbol u} \leqslant {\text{max(}}{\boldsymbol u}) - {{\boldsymbol u}_0}, $ | (14) |
| $ {{\Delta {\mathrm{min}}(}}\alpha ) \leqslant {{\Delta }}\alpha \leqslant {{\Delta {\mathrm{max}}(}}\alpha ),{{ {\mathrm{min}}(}}\alpha ) - {\alpha _0} \leqslant {{\Delta }}\alpha \leqslant {{{\mathrm{max}}(}}\alpha ) - {\alpha _0}。$ | (15) |
式中:W、Q和Ω均为权重矩阵;u0和α0分别为最后样本中执行器力和方位角;∆u、∆α分别为现样本与前样本间力和方位角变化;s为松弛变量。[min(u), max(u)],[min(α), max(α)]是执行器的输入约束。ρ> 0为标量权重,ρ> 0;ε> 0为任意小的数,ε> 0。
2 自适应跟踪控制设计 2.1 扰动观测器设计为了减轻由环境扰动引起的跟踪误差,需要对其进行测量或估计。传统扰动观测器只能实现渐近稳定性,这可能会带来收敛时间过长的问题。本节将设计一种基于ISM算法的连续固定时间扰动观测器来对扰动进行估计。
FTDO的设计如下:
| $ \left\{ {\begin{array}{*{20}{l}} {\boldsymbol M}\dot {\hat v} = - {\boldsymbol C}(v)v - {\boldsymbol D}v + {\tau _c} + \Delta \tau + {{\hat \tau }_{env}} ,\\ {{\boldsymbol e}_0} = {{\boldsymbol v}} - \hat {\boldsymbol v} ,\\ {{\dot {\boldsymbol e}}_I} = {{\boldsymbol q}_1}\dot {e}_0^{[{\chi _1}]} + {{\boldsymbol q}_2}\dot {e}_0^{[{\chi _2}]} ,\\ {\boldsymbol s} = {\boldsymbol M}{{\dot {e}}_0} + {\boldsymbol p}{{\boldsymbol e}_I} ,\\ {\hat \tau }_{env} = \displaystyle \int {\boldsymbol p}{{\dot {e}}_I}(\tau ) + {{\boldsymbol g}_1}{{\boldsymbol s}^{[{\chi _1}]}}(\tau ) + {{\boldsymbol g}_2}{\boldsymbol s}^{[{\chi _2}]}(\tau ) +\\ \quad\quad\;\; {\boldsymbol g}_3{\mathrm{sgn}}({\boldsymbol s}(\tau )){\mathrm{d}}\tau ,\\ {{\boldsymbol e}_0}(0) = {\boldsymbol v}(0) - \hat {\boldsymbol v}(0),{\text{ }}{\boldsymbol p}{{\boldsymbol e}_I}(0) = - {\boldsymbol M}{{\dot e}_0}(0) 。\end{array}} \right. $ | (16) |
式中:
如果FTDO按系统(9)下式(16)设计,可通过选择设计参数
| $ {t_f} \leqslant \frac{2}{{{F_1}(1 - {\chi _1})}} + \frac{2}{{{F_2}({\chi _2} - 1)}} + {t_2}。$ | (17) |
式中:
稳定性证明 选Lyapunov函数如下:
| $ V = \frac{1}{2}{s^{\mathrm{T}}}s,$ | (18) |
对
| $ \begin{aligned} \dot V = &{s^{\mathrm{T}}}{{\dot \tau }_{env}} - {s^{\mathrm{T}}}{g_1}{s^{[{\chi _1}]}} - {s^{\mathrm{T}}}{g_2}{s^{[{\chi _2}]}} - {s^{\mathrm{T}}}{g_3}{\mathrm{sign}}(s) \leqslant\\ & - {2^{\frac{{{\chi _1} + 1}}{2}}}{\lambda _{\min }}({g_1}){(\frac{1}{2}{s^{\mathrm{T}}}s)^{\frac{{{\chi _1} + 1}}{2}}} - \\ & {3^{\frac{{1 - {\chi _2}}}{2}}}{2^{\frac{{{\chi _2} + 1}}{2}}}{\lambda _{\min }}({g_2}){(\frac{1}{2}{s^{\mathrm{T}}}s)^{\frac{{{\chi _2} + 1}}{2}}} =\\ & - {F_1}{V_1}^{\frac{{{\chi _1} + 1}}{2}} - {F_2}{V_1}^{\frac{{{\chi _2} + 1}}{2}}。\end{aligned} $ | (19) |
参照Zheng [23],式(16)给出的积分滑模变量
| $ {t_1} \leqslant \frac{2}{{{F_1}(1 - {\chi _1})}} + \frac{2}{{{F_2}({\chi _2} - 1)}} 。$ | (20) |
参照Zuo [24],
| $ {t_2} \leqslant \frac{1}{{{\lambda _{\min }}({{\boldsymbol q}_1}|{{\boldsymbol M}^{ - 1}}{\boldsymbol p}{|^{{\chi _1}}})(1 - {\chi _1})}} + \frac{1}{{{\lambda _{\min }}({{\boldsymbol q}_2}|{{\boldsymbol M}^{ - 1}}{\boldsymbol p}{|^{{\chi _2}}})(1 - {\chi _2})}}。$ | (21) |
此外,
| $\begin{split} {t_f} \leqslant &\frac{2}{{{F_1}(1 - {\chi _1})}} + \frac{2}{{{F_2}({\chi _2} - 1)}} + \frac{1}{{{\lambda _{\min }}({{\boldsymbol q}_1}|{{\boldsymbol M}^{ - 1}}{\boldsymbol p}{|^{{\chi _1}}})(1 - {\chi _1})}} +\\ &\frac{1}{{{\lambda _{\min }}({{\boldsymbol q}_2}|{{\boldsymbol M}^{ - 1}}{\boldsymbol p}{|^{{\chi _2}}})(1 - {\chi _2})}}。\\[-1pt]\end{split} $ | (22) |
证明完毕。
2.2 运动控制器设计针对DP船,构造一种基于抗饱和补偿技术、tan型BLF和RBFNN的自适应状态约束轨迹跟踪控制器,该控制器结合了FTDO来跟踪所需的轨迹。设计过程包含以下步骤:
步骤1 构建带辅助变量的抗饱和补偿器来处理输入饱和,设计为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot \xi }_1} = - {{\boldsymbol K}_1}{\xi _1} + {\boldsymbol R}(\psi ){\xi _2}},\\ {{{\dot \xi }_2} = - {{\boldsymbol K}_2}{\xi _2} + {{\boldsymbol M}^{ - 1}}\Delta \tau }。\end{array}} \right. $ | (23) |
式中:
步骤2 定义轨迹跟踪误差向量
| $ {e_1} = {[{e_{11}},{e_{12}},{e_{13}}]^{\rm T}} = {{\boldsymbol R}^{\rm T}}(\psi )(\eta - {\eta _d} - {\xi _1}),$ | (24) |
| $ e_2^* = {[{e_{21}},{e_{22}},{e_{23}}]^{\rm T}} = v - \alpha - {\xi _2} ,$ | (25) |
式中:
| $ {{\text π} _d}{\dot \beta _d} = - \alpha - {\beta _d},{\text{ }}\alpha (0) = {\beta _d}(0)。$ | (26) |
滤波器误差为
| $ {\dot Y_{\text{e}}} = {\dot \beta _d} - \dot \alpha = - \frac{1}{{{{\text π} _d}}}{Y_e} - \dot \alpha。$ | (27) |
所以,重新定义速度误差面向量
| $ {e_2} = {[{e_{21}},{e_{22}},{e_{23}}]^{\rm T}} = v - {\beta _d} - {\xi _2}。$ | (28) |
步骤3 对式(24)求导可得
| $ {\dot e_1} = {{\boldsymbol R}^{\rm T}}(r){e_1} + v - {v_d} + {{\boldsymbol R}^{\rm T}}(\psi ){{\boldsymbol K}_1}{\xi _1} - {\xi _2}。$ | (29) |
选择tan型BLF
| $ {V_{{e_{1i}}}} = \frac{{k_{1i}^2(t)}}{\text π }\tan \left( {{A_i}} \right),{\text{ }}{e_{1i}}(0) \lt {k_{1i}}(0),{\text{ }}i = 1,2,3 。$ | (30) |
式中:
求式(30)的导数,可得
| $ {\dot V_{{e_{1i}}}} = \frac{{2{k_{1i}}{{\dot k}_{1i}}}}{{\text π} }\tan \left( {{A_i}} \right) + {e_{1i}}{\sec ^2}\left( {{A_i}} \right)\left( {{{\dot e}_{1i}} - \frac{{{{\dot k}_{1i}}}}{{{k_{1i}}}}{e_{1i}}} \right) 。$ | (31) |
提出运动控制律为
| $ \alpha = - {{\boldsymbol R}^{\rm T}}(r){e_1} + {v_d} - {{\boldsymbol R}^{\rm T}}(\psi ){{\boldsymbol K}_1}{\xi _1} - {{\boldsymbol Z}_1} - {\boldsymbol H}{{\boldsymbol Z}_2} 。$ | (32) |
式中:
步骤4 对式(28)求导可得
| $ {\dot e_2} = {{\boldsymbol M}^{ - 1}}(f(v) + {\tau _c} + {\tau _{env}}) + {{\boldsymbol K}_2}{\xi _2} 。$ | (33) |
式中:
| $ f(v) = {W^{*{\mathrm{T}}}}{\varphi ^*}(X) + {\varepsilon ^*} 。$ | (34) |
式中:
然后,选择一个新的tan型BLF
| $ {V_{{e_{2i}}}} = \frac{{k_{2i}^2(t)}}{{\text π} }\tan \left( {{B_i}} \right),{\text{ }}{e_{2i}}(0) \lt {k_{2i}}(0),{\text{ }}i = 1,2,3 。$ | (35) |
式中:
求式(35)的导数,可得
| $\begin{split} {\dot V_{{e_{2i}}}} =& \frac{{2{k_{2i}}{{\dot k}_{2i}}}}{{\text π} }\tan \left( {{B_i}} \right) + {e_{2i}}{\sec ^2}\left( {{B_i}} \right)\\ &\left [ {({M^{ - 1}}(f(v) + {\tau _c} + {\tau _{env}}) + {K_2}{\xi _2}) - \frac{{{{\dot k}_{2i}}}}{{{k_{2i}}}}{e_{2i}}} \right] 。\end{split}$ | (36) |
定义
| $ \varphi = {[{\varphi ^*}(\boldsymbol X),{\text{ }}{{\boldsymbol K}_2}{\xi _2} - \zeta ]^{\mathrm{T}}},$ | (37) |
式中:
| $ \begin{split} &{\zeta _i} =\displaystyle\frac{{{{\dot k}_{2i}}{e_{2i}}}}{{{k_{2i}}}} - \displaystyle\frac{{2{k_{2i}}{{\dot k}_{2i}}\tan ({B_i})}}{{{\text π} {e_{2i}}{{\sec }^2}({B_i})}} - \displaystyle\frac{{{\gamma _{2i}}k_{2i}^2\tan ({B_i})}}{{{\text π} {e_{2i}}{{\sec }^2}({B_i})}} -\\& \displaystyle\frac{{{e_{1i}}{{\sec }^2}({A_i}){e_{2i}}}}{{{e_{2i}}{{\sec }^2}({B_i})}} - \displaystyle\frac{{e_{1i}^2{{\sec }^4}({A_i})}}{{{e_{2i}}{{\sec }^2}({B_i})}} {{\text{ }} - {e_{2i}}{{\sec }^2}({B_i}), {\text{ }}i = 1,2,3} 。\end{split} $ | (38) |
式中:
最后,给出控制律
| $ {\tau _c} = - {\hat {\boldsymbol W}^{\rm T}}\varphi - {\hat \tau _{env}} 。$ | (39) |
式中:
| $ \dot \hat {\boldsymbol W} = \lambda \varphi \Lambda - \lambda \rho \hat {\boldsymbol W} 。$ | (40) |
式中:
考虑候选BLF如下
| $ V = {V_1} + {V_2} + \frac{1}{2}{\boldsymbol Y}_e^{\rm T}{{\boldsymbol Y}_e} + \frac{1}{{2\lambda }}Tr({M^{ - 1}}{\tilde {\boldsymbol W}^{\rm T}}\tilde {\boldsymbol W}) ,$ | (41) |
| $ {V_i} = \sum\limits_{j = 1}^3 {{V_{{e_{ij}}}} + \frac{1}{2}} \xi _i^T{\xi _i},{\text{ }}i = 1,2 。$ | (42) |
对式(42)求导并将式(23)、式(31)和式(36)代入,可得
| $ \begin{split} {{\dot V}_1} =& \sum\limits_{i = 1}^3 {\left[ {{e_{1i}}{{\sec }^2}({A_i}){e_{2i}}} \right]} + \sum\limits_{i = 1}^3 {\left[ {{e_{1i}}{{\sec }^2}({A_i}){Y_{ei}}} \right]} -\\& \sum\limits_{i = 1}^3 {\left[ {\frac{{{\gamma _{1i}}k_{1i}^2(t)}}{{\text π} }\tan ({A_i})} \right]} - \xi _1^{\mathrm{T}}{K_1}{\xi _1} + \xi _1^{\mathrm{T}}R(\psi ){\xi _2} \end{split}。$ | (43) |
其中
| $ \begin{split} {{\dot V}_2} =& \sum\limits_{i = 1}^3 {\left\{ {\frac{{2{k_{2i}}{{\dot k}_{2i}}}}{{\text π} }\tan ({B_i}) + {e_{2i}}{{\sec }^2}({B_i})\left[ {{{({M^{ - 1}}(f(v) + {\tau _c} + {\tau _{env}}) + {K_2}{\xi _2})}_i} - \frac{{{{\dot k}_{2i}}}}{{{k_{2i}}}}{e_{2i}}} \right]} \right\}} - \xi _2^{\mathrm{T}}{K_2}{\xi _2} + \xi _2^{\mathrm{T}}{M^{ - 1}}\Delta \tau = \\ & \sum\limits_{i = 1}^3 {\left[ {{e_{2i}}{{\sec }^2}({B_i}){{\left( {{M^{ - 1}}( - {{\tilde W}^{\mathrm{T}}}\varphi + {\varepsilon ^*})} \right)}_i} - \frac{{{\gamma _{2i}}k_{2i}^2\tan ({B_i})}}{{\text π} } - {e_{1i}}{{\sec }^2}({A_i}){e_{2i}}} \right]} - \sum\limits_{i = 1}^3 {\left[ {\frac{{e_{1i}^2{{\sec }^4}({A_i})}}{2}} \right]} - \\ & \sum\limits_{i = 1}^3 {\left[ {\frac{{e_{2i}^2{{\sec }^4}({B_i})}}{2}} \right]} + \sum\limits_{i = 1}^3 {\left[ {{e_{2i}}{{\sec }^2}({B_i}){{({M^{ - 1}}{{\tilde \tau }_{env}})}_i}} \right]} - \xi _2^{\mathrm{T}}{K_2}{\xi _2} + \xi _2^{\mathrm{T}}{M^{ - 1}}\Delta \tau 。\end{split} $ | (44) |
综合式(27)、式(40)和Young's不等式,对式(41)求导,可得
| $ \begin{split} & \dot V = {{\dot V}_1} + {{\dot V}_2} + Y_e^{\mathrm{T}}{{\dot Y}_e} + \frac{1}{\lambda }Tr({M^{ - 1}}{{\tilde W}^{\mathrm{T}}}\dot \hat W) \leqslant -\\ & \sum\limits_{i = 1}^3 {\left[ {\frac{{{\gamma _{1i}}k_{1i}^2(t)}}{\text{π}}\tan ({A_i})} \right]} + \sum\limits_{i = 1}^3 {\left[ {{e_{1i}}{{\sec }^2}({A_i}){Y_{ei}}} \right]} - \\ & \xi _1^{\mathrm{T}}{K_1}{\xi _1} + \xi _1^{\mathrm{T}}R(\psi ){\xi _2} - \sum\limits_{i = 1}^3 {\left[ {\frac{{{\gamma _{2i}}k_{2i}^2(t)}}{{\text π} }\tan ({B_i})} \right]} +\\ & \sum\limits_{i = 1}^3 {\left[ {{e_{2i}}{{\sec }^2}({B_i}){\varepsilon ^*}} \right]} - \sum\limits_{i = 1}^3 {\left[ {\frac{{e_{1i}^2{{\sec }^4}({A_i})}}{2}} \right]} - \\ & \sum\limits_{i = 1}^3 {\left[ {e_{2i}^2{{\sec }^4}({B_i})} \right]} + \sum\limits_{i = 1}^3 {\left[ {{e_{2i}}{{\sec }^2}({B_i}){{({M^{ - 1}}{{\tilde \tau }_{env}})}_i}} \right]} - \xi _2^{\mathrm{T}}{K_2}{\xi _2} +\\ & \xi _2^{\mathrm{T}}{M^{ - 1}}\Delta \tau - \rho Tr({M^{ - 1}}{{\tilde W}^{\mathrm{T}}}\hat W) - Y_e^{\mathrm{T}}{\text π} _d^{ - 1}{Y_e} - {Y_e}\dot \alpha。\\[-1pt] \end{split} $ | (45) |
根据Young's不等式,有下式成立
| $ \begin{split} & \dot V \leqslant - \sum\limits_{i = 1}^3 {\left[ {\frac{{{\gamma _{1i}}k_{1i}^2(t)}}{\text{π} }\tan ({A_i})} \right]} - \xi _1^{\mathrm{T}}{{\bar K}_1}{\xi _1} - \\ &\sum\limits_{i = 1}^3 {\left[ {\frac{{{\gamma _{2i}}k_{2i}^2(t)}}{\text{π}}\tan ({B_i})} \right]} - \xi _2^{\mathrm{T}}{{\bar K}_2}{\xi _2} - Y_e^{\mathrm{T}}\text{π} _d^{ - 1}{Y_e} + \\ & \frac{1}{2}Y_e^{\mathrm{T}}{Y_e} - \frac{\rho }{2}Tr({M^{ - 1}}{{\tilde W}^{\mathrm{T}}}\tilde W) + \frac{1}{{2{\lambda _{\min }}(M)}}{\left\| {\Delta \tau } \right\|^2} + \\ & \frac{\sigma }{2} + \frac{\varsigma }{{2||M|{|^2}}} + \frac{\rho }{2}Tr({W^{\mathrm{T}}}W) \leqslant - \mu V + \delta 。\end{split} $ | (46) |
式中:
| $\begin{split} \mu =& \min [\mathop {\min }\limits_{i = 1,2,3} {\gamma _{1i}},\mathop {\min }\limits_{i = 1,2,3} {\gamma _{2i}},{\lambda _{\min }}2{\bar K_1},{\lambda _{\min }}2{\bar K_2},\\ &{\lambda _{\min }}(2\text{π} _d^{ - 1} - {I_{3 \times 3}}),\lambda \rho ] \text{,} \end{split} $ |
| $ \delta = \frac{1}{{2{\lambda _{\min }}(M)}}{\left\| {\Delta \tau } \right\|^2} + \frac{\sigma }{2} + \frac{\varsigma }{{2||M|{|^2}}} + \frac{\rho }{2}Tr({W^{\mathrm{T}}}W)\text{。} $ |
因此可得V是半全局一致有界的。根据式(41)、式(42),可知
求解式(46),可得
| $ V \leqslant \left(V(0) - \frac{\delta }{\mu }\right)\exp ( - \mu t) + \frac{\delta }{\mu } \leqslant V(0) + \frac{\delta }{\mu } 。$ | (47) |
根据式(42)和式(47),可得
| $ |{e_{ij}}| \leqslant \sqrt {\frac{{2k_{ij}^2}}{{\text π} }\arctan \left[ {\frac{{\text π} }{{k_{ij}^2}}\left( {V(0) + \frac{\delta }{\mu }} \right)} \right]} \lt {k_{ij}},{{ i = 1,2}}。$ | (48) |
综上所述,该闭环系统的状态变量能够实现半全局渐近收敛。在受到未知环境扰动和执行器饱和影响的情况下,状态约束轨迹的跟踪误差在固定时间内可取得良好的收敛结果。
3 仿真结果和分析 3.1 模型参数和环境条件本次DP船模拟中采用的模型与Kayacan等[25]采用的模型一致,船舶动力学模型(9)的主要参数如表2所示。船舶模型配置有4个方位角推进器,No.1~No.4螺旋桨分别位于坐标(0.4,0.2)、(−0.4,0.2)、(−0.4,−0.2)、(0.4,−0.2),船重心位于(0,0)。每个方位角推进器都受到推力输入饱和的限制,例如
|
|
表 2 仿真参数设置 Tab.2 Parameter setting of simulation |
为了简化研究,本次模拟中没有考虑波浪频率扰动引起的船舶振荡运动。参照Fossen[26],随体坐标系中的时变环境扰动设置如下:
| $ {\tau _{env}} = {R^{\mathrm{T}}}(\psi )\omega ,$ | (49) |
| $ \dot \omega = - T_{env}^{ - 1}\omega + \Psi \bar \omega 。$ | (50) |
式中:
船舶的期望轨迹设置为ηd=(xd,yd,ψd)T,其中xd =
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{11}}(t) = 2\exp ( - 0.03t) + 0.1} ,\\ {{k_{12}}(t) = 20\exp ( - 0.03t) + 0.1} ,\\ {{k_{13}}(t) = 20\exp ( - 0.03t) + 0.1} ,\end{array}} \right. $ | (51) |
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{21}}(t) = 2\exp ( - 0.03t) + 0.1} ,\\ {{k_{22}}(t) = 20\exp ( - 0.03t) + 0.1} ,\\ {{k_{23}}(t) = 20\exp ( - 0.03t) + 0.1} 。\end{array}} \right. $ | (52) |
控制器的可调节参数选择H1 =diag(γ11,γ12,γ13) = diag(0.5,0.5,0.1),H2 = diag(γ21,γ22,γ23) =diag(100,100,100),K1 = diag(20,20,20),K2 = diag(20,20,20),πd = diag(0.2,0.2,0.1),α = 0.8,β = 1.5;观测器参数选择p = diag(10,10,10),q1 = q2 = diag(2,2,1),g1 = g2 = diag(2,2,1),g3 = diag(10,10,10),
推力分配算法加权矩阵设置为W = diag(1,1,1,1),Q = diag(10,10,10,10)和Ω = diag(1×1012,1×1012,1×1012,1×1012)。
经过一系列仿真分析后,最终为RBFNN选择11个节点来有效逼近未知项,令激活函数向量
结果包括:1)船舶受到的外部扰动
图1为FTDO观测结果与实际值的比较,可以看出,两者基本一致,本文提出的FTDO可以有效且快速地提供外部环境载荷的估计,证明本文使用的观测器可以满足精度要求。
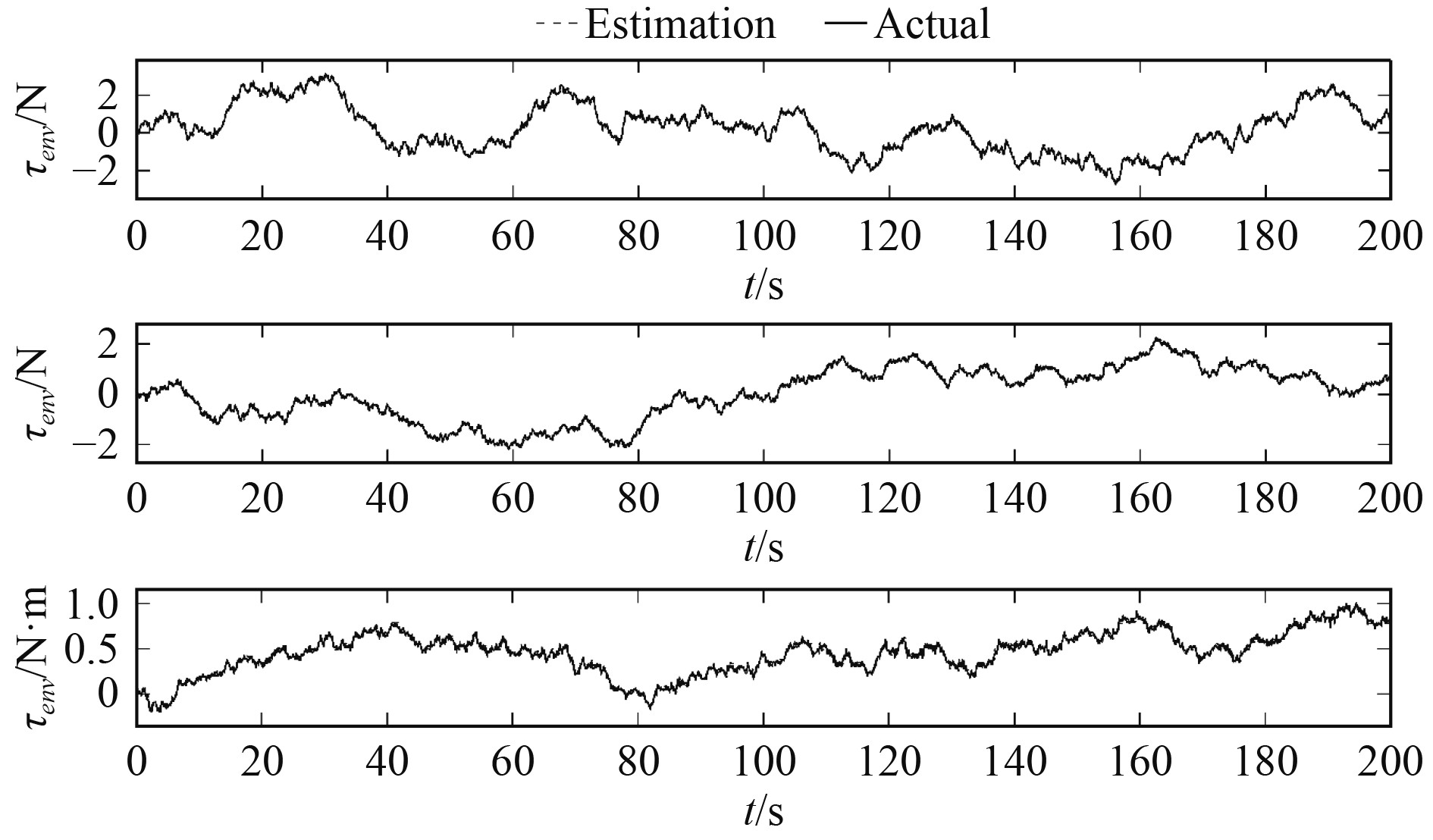
|
图 1
环境扰动 |
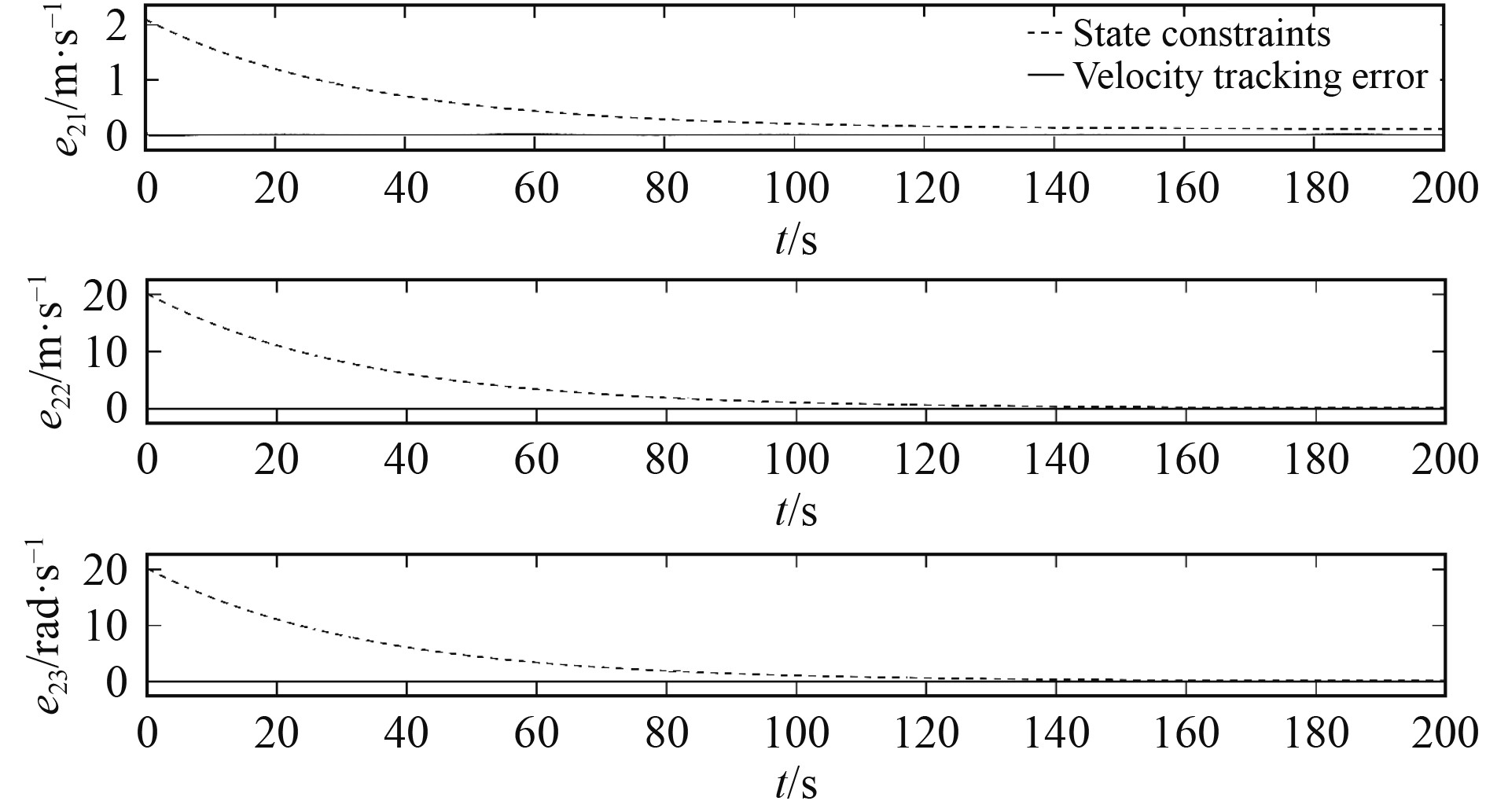
由图2和图3可知,x可以以较高精度追踪xd,对应的位置轨迹跟踪误差s1在初始偏差后快速向0逼近,并在之后始终保持在给定的约束边界内;由图4和图5可知,尽管最初调整幅度较大,但在经过短短数秒后v便可以很好地追踪vd,对应的速度轨迹跟踪误差s2也都满足状态约束条件。显然,本文所设计的控制律能够使船舶航行状态稳定调节到期望轨迹上,并保证所有位置和速度轨迹跟踪误差被限制在约束范围内。
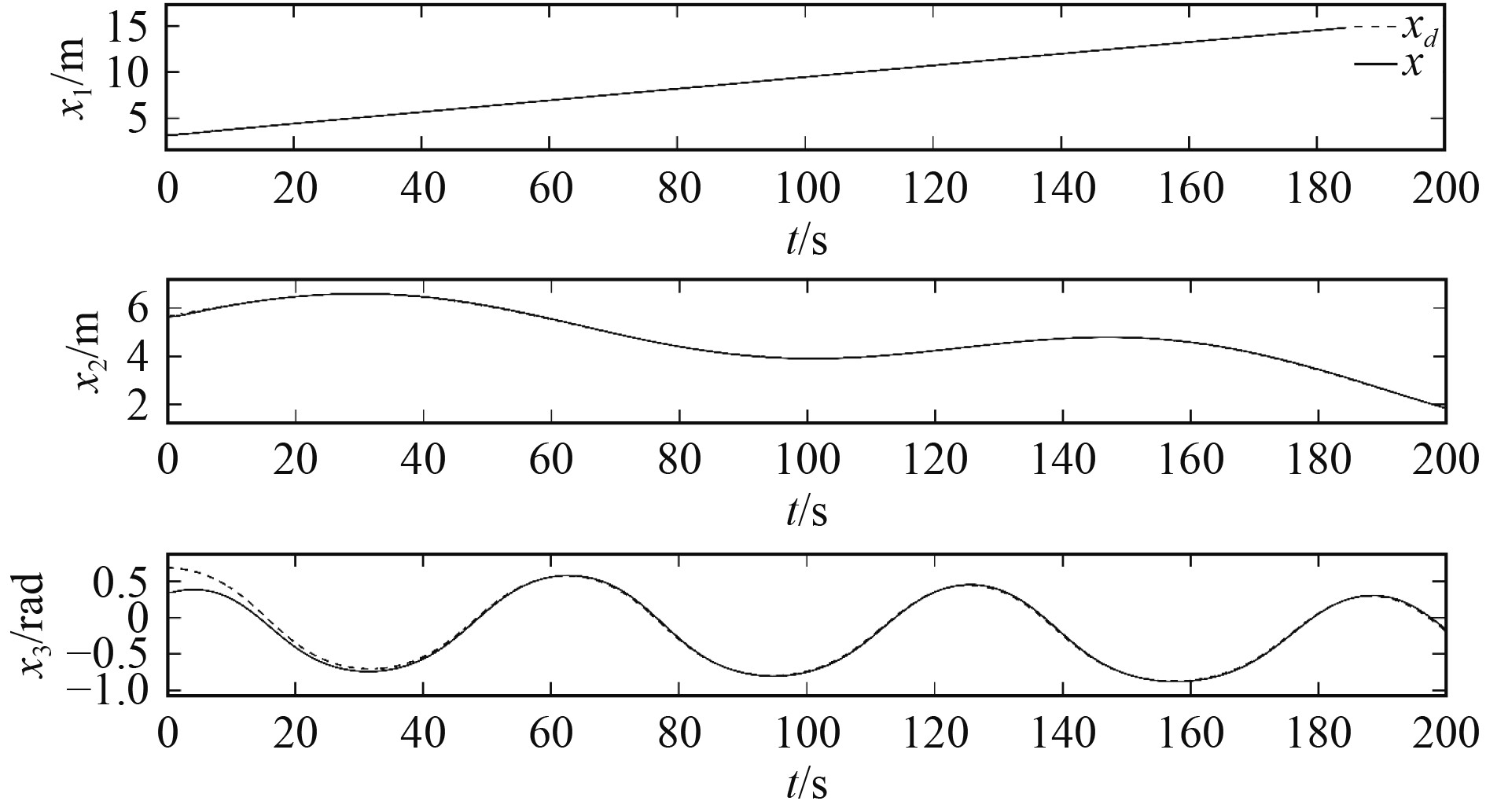
|
图 2 DP船位置x与期望位置xd比较 Fig. 2 Comparison of the position x with desired position xd |
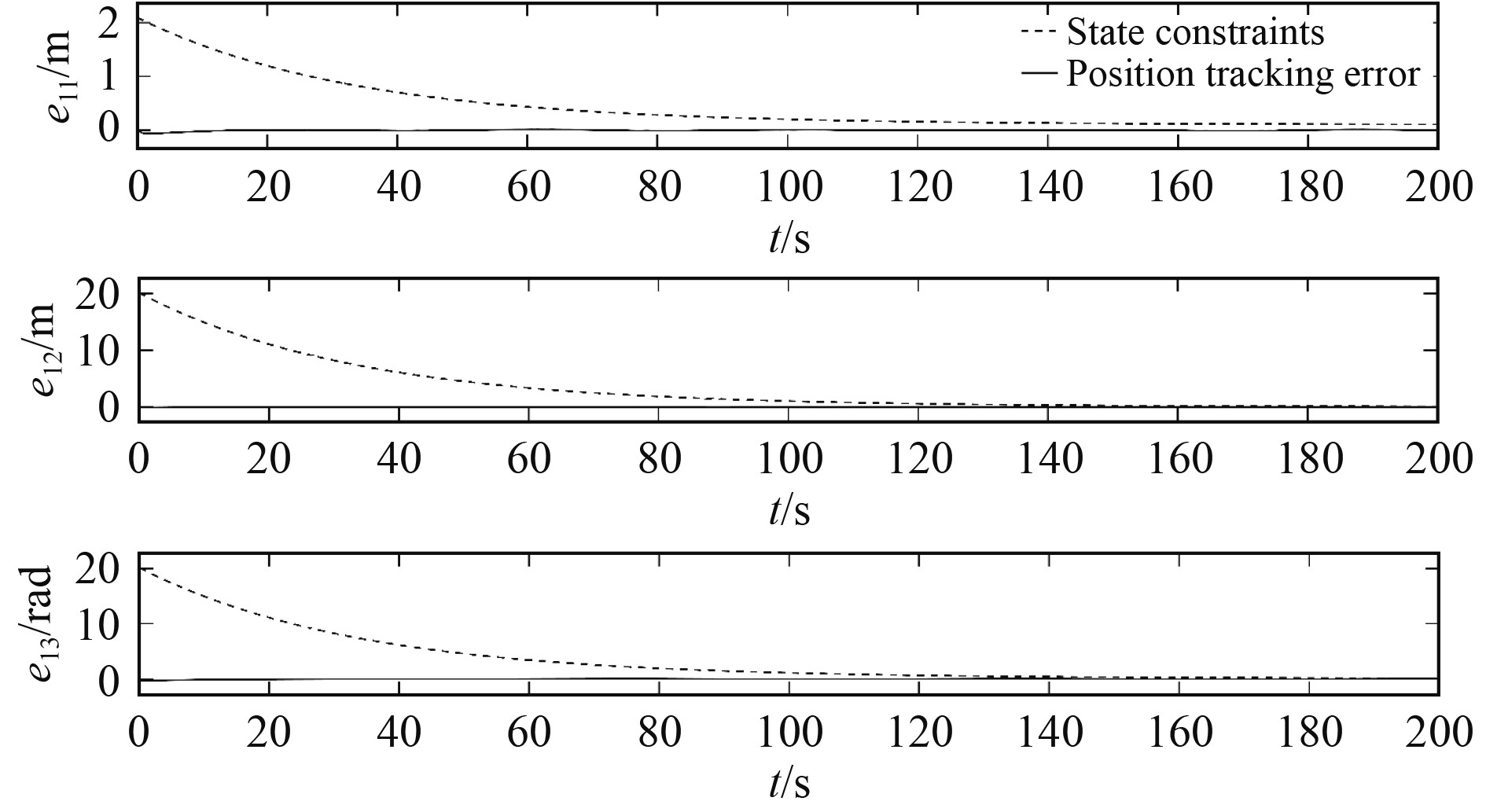
|
图 3 DP船的位置轨迹跟踪误差e1 Fig. 3 Position trajectory tracking error e1 |
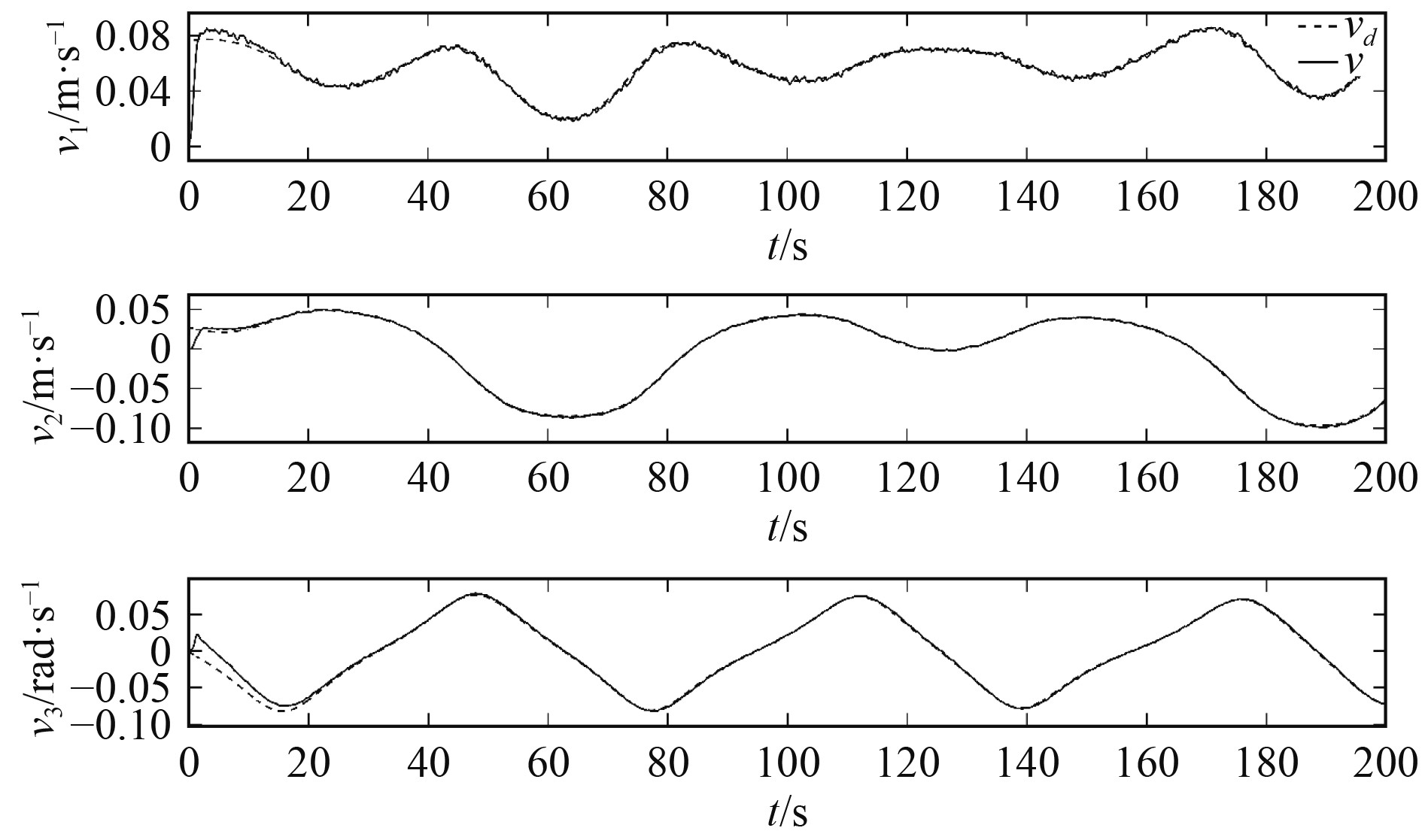
|
图 4 DP船速度v与期望速度vd比较 Fig. 4 Comparison of the velocity v with desired velocity vd |
|
图 5 DP船的速度轨迹跟踪误差e2 Fig. 5 Velocity trajectory tracking error e2 |
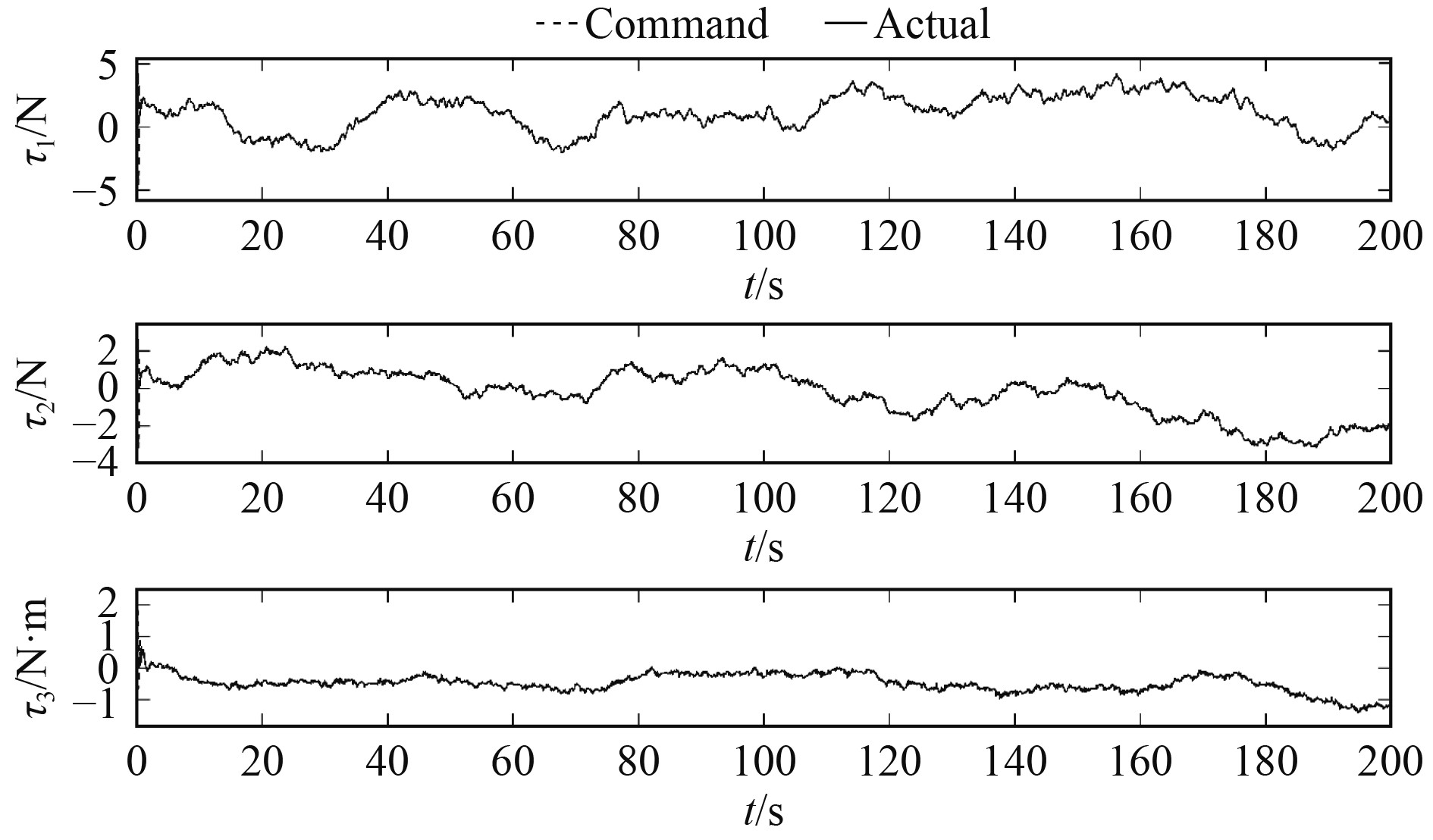
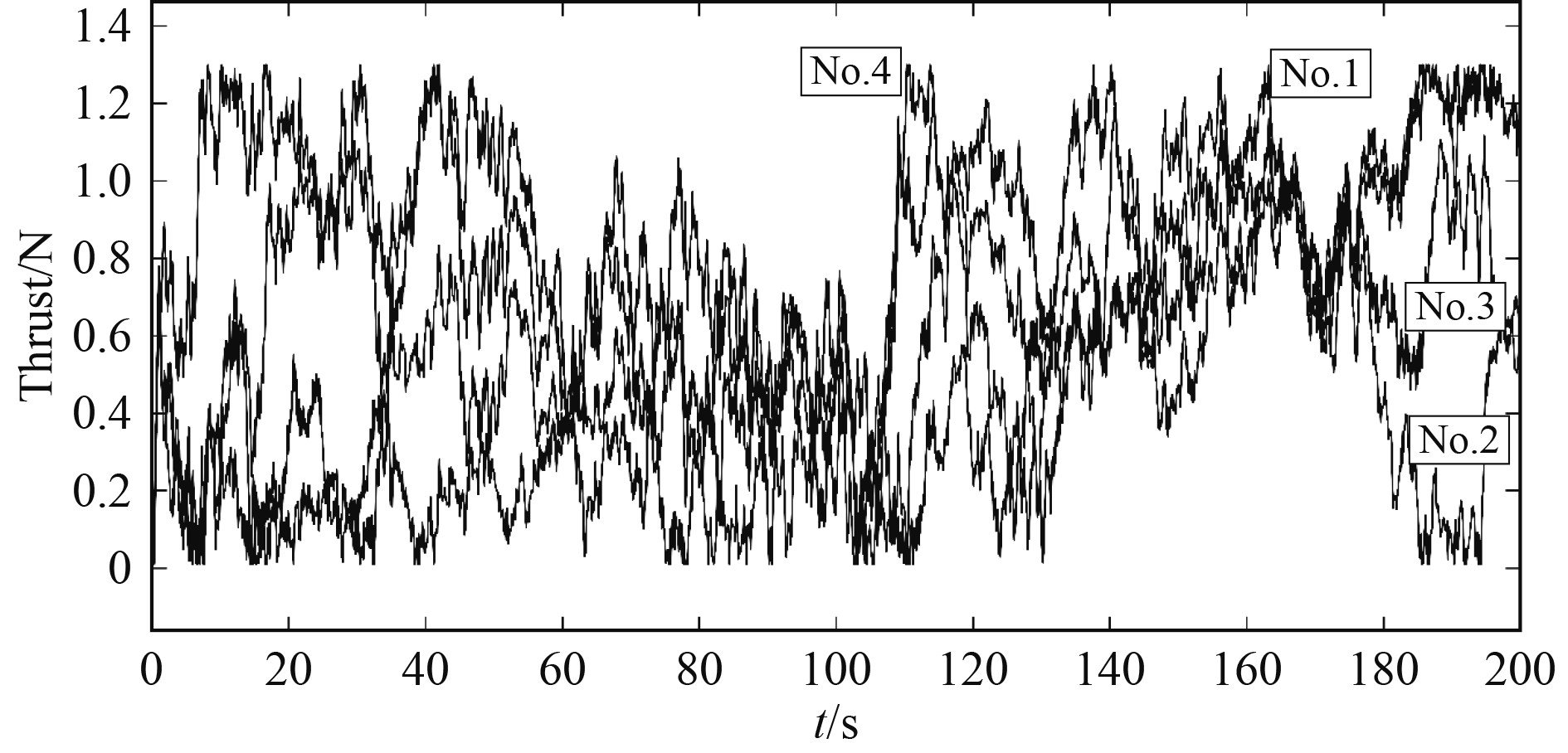
图6为DP船的指令控制输入和实际控制输入之比,尤其在初始时刻,与指令控制输入相比,实际控制输入及其变化趋势是有界且稳定的;图7为DP船No.1-No.4推进器输出推力,可以发现,各推进器的输出都在推力饱和的限制范围内。它证明该控制方案在执行器饱和情况下有效。因此,本文所提出的自适应轨迹跟踪控制方法可以有效提高DP船在复杂海洋环境中的控制能力。
|
图 6 DP船的指令控制力和实际控制力 Fig. 6 Command control and actual control |
|
图 7 No.1-No.4推进器推力 Fig. 7 No.1-No.4 Thruster |
总之,与现有的一些算法[27 − 29]相比,本文的研究同时考虑了环境扰动、状态约束和输入饱和来解决DP船的轨迹跟踪问题。数值仿真结果表明,实际轨迹可以实现对期望轨迹的精确跟踪,不违反全状态约束,并且可以始终将实际输入限制在输入饱和幅度内。
4 结 语本文对扰动不确定、状态约束和执行器饱和影响下的动力定位船轨迹跟踪策略进行了研究。首先,采用基于积分滑模控制和固定时间稳定性的连续FTDO来估计环境扰动,之后引入抗饱和补偿器用于消除输入饱和差,并进一步将反步法、tan型BLF和RBFNN相结合设计了一种自适应状态约束轨迹跟踪控制器。
在所提出的控制方案下,动力定位船的实际轨迹可以很好地逼近期望轨迹,并保证动力定位闭环控制系统的所有信号是一致有界的。本文最后对上述动力定位控制律进行了仿真实验,结果验证了算法的有效性。
| [1] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, 2011.
|
| [2] |
WITKOWSKA A, MIERZCHALSKI R. Adaptive dynamic control allocation for dynamic positioning of marine vessel based on backstepping method and sequential quadratic programming[J]. Ocean Engineering, 2018, 163, 570–582.
|
| [3] |
LU Y, ZHANG G, SUN Z, et al. Adaptive cooperative formation control of autonomous surface vessels with uncertain dynamics and external disturbances[J]. Ocean Engineering, 2018, 167: 36-44. DOI:10.1016/j.oceaneng.2018.08.020 |
| [4] |
LIANG K, LIN X G, CHEN Y, et al. Adaptive sliding mode output feedback control for dynamic positioning ships with input saturation[J]. Ocean Engineering, 2020, 206: 107245. DOI:10.1016/j.oceaneng.2020.107245 |
| [5] |
LIU Yeye, LIN Xiaogong, LIANG Kun. Robust tracking control for dynamic positioning ships subject to dynamic safety constraints[J]. Ocean Engineering, 15 (2), 1–8.
|
| [6] |
CHU Z, XIANG X, ZHU D, et al. Adaptive trajectory tracking control for remotely operated vehicles considering thruster dynamics and saturation constraints[J]. ISA Trans, 2020, 100, 28–37.
|
| [7] |
HE W, YIN Z, SUN C Y. Adaptive neural network control of a marine vessel with constraints using the asymmetric barrier Lyapunov function[C]// IEEE Trans. Cybern, 2017, 47 (7), 1641–1651.
|
| [8] |
HU Q, JIANG B, ZHANG Y. Observer-based output feedback attitude stabilization for spacecraft with finite-time convergence[C]// IEEE Transactions on Control Systems Technology PP, 2017, 1–9.
|
| [9] |
DU J, HU X, SUN Y. Robust dynamic positioning of ships with disturbances under input saturation[J]. Automatica, 2016, 73, 207–214.
|
| [10] |
ABDELAAL M, FRÄNZLE M, HAHN A. Nonlinear model predictive control for tra-jectory tracking and collision avoidance of underactuated vessels with disturbances[J]. Ocean Engineering, 2018, 160, 168–180.
|
| [11] |
DU J, HU X, LIU H, et al. Adaptive robust output feedback control for a marine dynamic positioning system based on a high-gain observer[C]// IEEE Trans. Neural Netw. Learn. Syst, 2015, 26 (11): 2775–2786.
|
| [12] |
YIN Z, HE W, YANG C. G. Tracking control of a marine surface vessel with full-state constraints[J]. Int. J. Syst. Sci, 2017, 48(3): 535–546
|
| [13] |
ZHENG Z. W, SUN L, XIE L. H. Error-constrained LOS path following of a surface vessel with actuator saturation and faults[C]// IEEE Trans. Syst. Man Cybern. -Syst, 2017, 48(10), 1794–1805 .
|
| [14] |
WANG D, GE S S, FU M, et al. Bioinspired neurodynamics based formation control for unmanned surface vehicles with line-of-sight range and angle constraints[J]. Neurocomputing, 2021, 425, 127–134.
|
| [15] |
YANG H, DENG F, HE Y, et al. Robust nonlinear model predictive control for reference tracking of dynamic positioning ships based on nonlinear disturbance observer[J]. Ocean Engineering, 2020, 215, 107885.
|
| [16] |
ZHENG Z, HUANG Y, XIE L, et al. Adaptive trajectory tracking control of a fully actuated surface vessel with asymmetrically constrained input and output[C]// IEEE Trans. Control Syst. Technol, 2017, 26 (5), 1851–1859.
|
| [17] |
ZHENG Z. W, FEROSKHAN M. Path following of a surface vessel with prescribed performance in the presence of input saturation and external disturbances, IEEE-ASME Trans[J]. Mechatron, 2017, 22 (6), 2564–2575 .
|
| [18] |
PARK B S. A simple output-feedback control for trajectory tracking of underactuated surface vessels[J]. Ocean Engineering, 2017, 143, 133–139.
|
| [19] |
CHEN M, GE S S, REN B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints[J]. Automatica, 2011, 47 (3), 452−465.
|
| [20] |
SØRENSEN A. A survey of dynamic positioning control systems[J]. Annual Reviews in Control, 2011, 35, 123–136.
|
| [21] |
JOHANSEN T A, FOSSEN T I. Control allocationa survey[J]. Automatica, 2013, 49, 1087–1103.
|
| [22] |
XU S, WANG X, YANG J, et al. A fuzzy rule-based pid controller for dynamic positioning of vessels in variable environmental disturbances[J]. Journal of Marine Science and Technology, 2020, 914–924.
|
| [23] |
ZHENG Z, FEROSKHAN M, SUN L. Adaptive fixed-time trajectory tracking control of a stratospheric airship[J]. ISA Transactions, 2018, 76, 134–144.
|
| [24] |
ZUO Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks[J]. Automatica, 2015, 54, 305–309.
|
| [25] |
KAYACAN E, PARK S, RATTI C, et al. Learning-based Nonlinear Model Predictive Control of Reconfigurable Autonomous Robotic Boats: Roboats[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2019: 8230−8237.
|
| [26] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. John Wiley & Sons, 2011.306−306
|
| [27] |
赵向涛, 阎妍, 于双和, 等. 基于屏障函数的船舶自适应控制[J]. 江苏大学学报(自然科版), 2021, 42(06): 715-720. |
| [28] |
HE W, YIN Z, SUN C. Adaptive neural network control of a marine vessel with constraints using the asymmetric barrier Lyapunov function. IEEE Trans[J]. Cybern, 2016, 47 (7), 1641–1651.
|
| [29] |
WU G, MENG X. Nonlinear disturbance observer based robust backstepping control for a flexible air-breathing hypersonic vehicle[J]. Aerospace Science and Technology, 2016, 54, 174–182.
|
 2024, Vol. 46
2024, Vol. 46
