2. 青岛智能导航与控制研究所,山东 青岛 266071
2. Qingdao Intelligent Navigation and Control Research Institute, Qingdao 266071, China
无人水下航行器(Unmanned Underwater Vehicle, UUV)以其全面的水下作业能力,已然成为海洋探测、科学研究、生态保护以及国防等多个领域中最广泛应用的水下设备之一[1]。水下导航和定位技术作为UUV能正常运行的基础,重要性日益凸显。然而,由于水下环境中无线电信号传播受限,传统的全球导航卫星系统(Global Navigation Satellite System,GNSS)无法直接应用于水下导航,使得水下导航定位面临着独特的挑战[2]。
航位推算(Dead Reckoning,DR)方法和长基线(Long Baseline,LBL)水下定位方法被广泛采用。DR因其积分形式的计算方法,长时间运行会导致误差累积[3],可用LBL进行校正;传统长基线水下定位方法对测距数据的数量有较高的要求,但实际应用中常因海洋环境和各种噪声影响,无法接收到所需要数量信号,影响解算[4]。曹方方等[5]提出基于单信标的组合导航方法,虽然每次解算只需一个测距数据与航速、航向信息组合,但因系统可观性受限,需适当的机动航行路径,且定位结果收敛较慢。另一方面,现有的水声定位算法在应用时假设声速已知,但实际中声速难以实时测量,信号传播路径的声速分布更难以精确测量,这会对距离解算造成误差,最终影响定位精度[6 - 10]。
根据实际实验的情况,本文提出一种自适应多信标DR/LBL紧组合导航方法。基于扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法,在每个测量周期中,使用时延作为观测量,根据接收到的随机数量的时延信息,自适应构建观测方程,计算雅克比矩阵,对预测结果进行修正。此方法适应性强,更符合实际情况,定位效率更高。实验表明,本方法在各个测量周期中信标应答信号接收不稳定时,能够准确、快速的对UUV推算位置进行校正,实现快速收敛,具有较强的实用性。
1 DR/LBL组合导航运动模型考虑到水声定位作用范围较小(十几公里范围内),可认为其处于水平直角坐标系,其位置用直角坐标
考虑UUV深度已知,建立其二维运动方程,以其位置和声速作为状态,系统状态和外部输入分别为:
| $ X = \left[ \begin{gathered} x \\ y \\ C \\ \end{gathered} \right],$ | (1) |
| $ u = \left[ \begin{gathered} v \\ \varphi \\ \end{gathered} \right]。$ | (2) |
式中:
建立运动学方程:
| $ \dot X = \left[ \begin{gathered} (v + {\omega _v}) \cdot \cos (\varphi + {\omega _\varphi }) \\ (v + {\omega _v}) \cdot \sin (\varphi + {\omega _\varphi }) \\ {\mu _C} \\ \end{gathered} \right]。$ | (3) |
系统测量输出为:
| $ {{Z}} = \left[ {\begin{array}{*{20}{c}} {\Delta {\tau _1}} \\ \vdots \\ {\Delta {\tau _i}} \end{array}} \right]。$ | (4) |
式中:
| $ \Delta {\tau _{\text{i}}} = \frac{{2\sqrt {{{(x - {x_{bi}})}^2} + {{(y - {y_{bi}})}^2}{\text{ + }}{{(h - {h_{bi}})}^2}} }}{C}。$ | (5) |
式中:
将式(3)离散化,得离散系统方程:
| $ {\left\{ \begin{array}{c}\\ \begin{array}{l}{X}_{k\text+1}=\left[ \begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array} \right]{X}_{k}+\left[ \begin{array}{c}\Delta T{\text{(v}}_{k}+{\omega }_{{\text{v}}_{k}})\cdot \mathrm{cos}({\phi }_{k}+{\omega }_{{\phi }_{k}})\\ \Delta T{\text{(v}}_{k}+{\omega }_{{\text{v}}_{k}})\cdot \mathrm{sin}({\phi }_{k}+{\omega }_{{\phi }_{k}})\\ 0\end{array} \right]+\left[ \begin{array}{c}0\\ 0\\ {\mu }_{{C}_{k}}\end{array} \right],\\ {Z}_{k}=h({X}_{k})+{V}_{k}\text=\left[ \begin{array}{c}\displaystyle\frac{2\sqrt{{({x}_{k}-{x}_{b1})}^{2}+{({y}_{k}-{y}_{b1})}^{2}\text+{(h-{h}_{b1})}^{2}}}{{C}_{k}}\\ \vdots \\ \displaystyle\frac{2\sqrt{{({x}_{k}-{x}_{bi})}^{2}+{({y}_{k}-{y}_{bi})}^{2}\text+{(h-{h}_{bi})}^{2}}}{{C}_{k}}\end{array} \right]\text+{V}_{{k}},\end{array}\end{array}\right.} $ | (6) |
式中:
如图1所示,UUV通过航速、航向信息对位置进行推算;当其接近信标时,航行器发送问答信号,并接受信标的回信,通过测量在此期间信号的传播时延
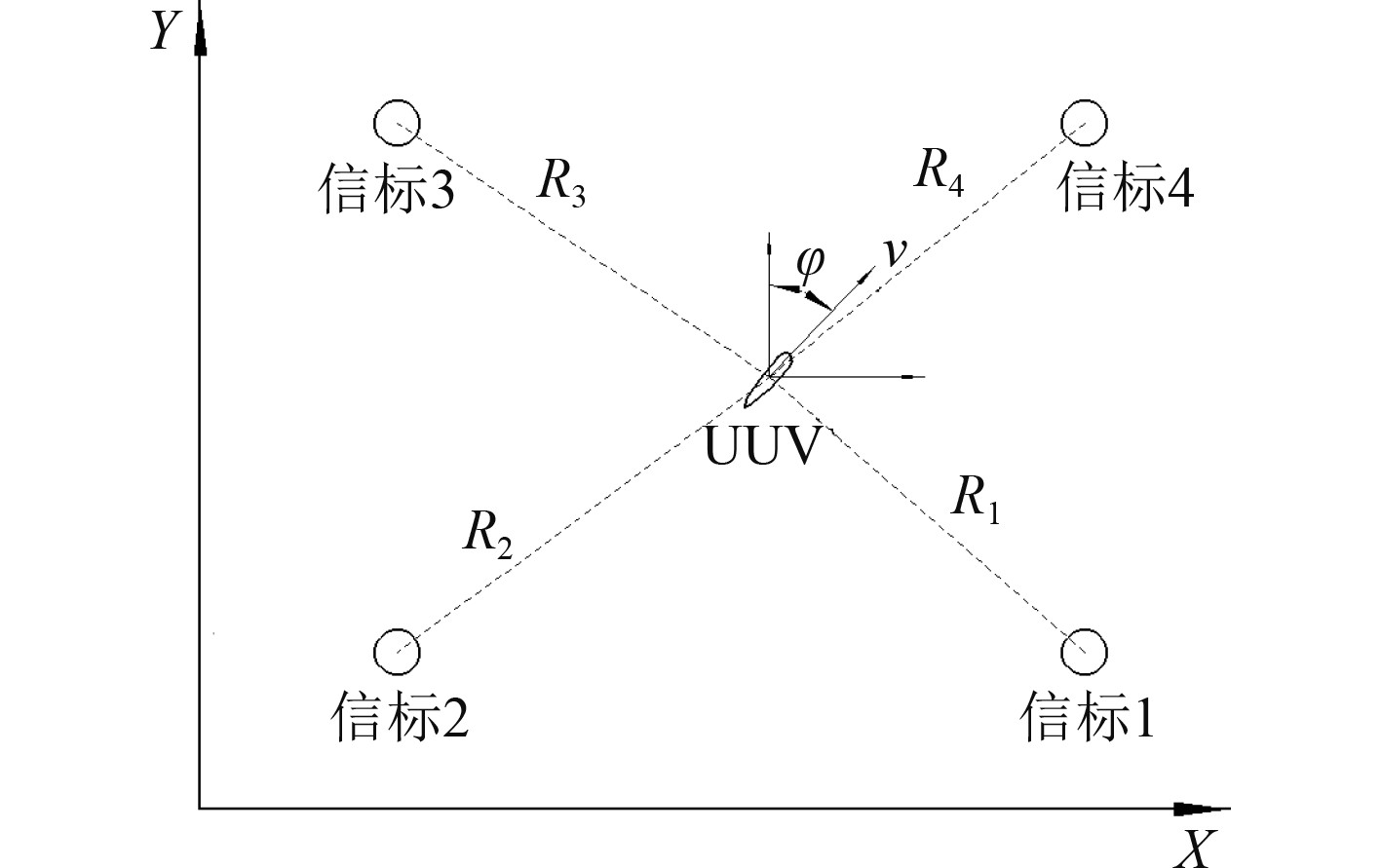
|
图 1 自适应多信标DR/LBL紧组合导航示意图 Fig. 1 Adaptive multi-beacon DR/LBL tight integration navigation schematic |
| $ {R}_{i}=\frac{\Delta {\tau }_{i}\cdot C}{2}。$ | (7) |
现有LBL中,需要至少收到3个信标的距离信息,才能进行定位运算,对推算结果进行校正。在实际应用中,受海洋环境、UUV相对位置和航向等影响,在每一次测量过程中,UUV很难接收到全部3个或4个应答信号,此时便无法采用LBL计算位置,无法对推算进行标校。基于单信标的组合导航方法,虽然每次解算只需一个测距数据与航速和航向信息组合,但因环境噪声影响的随机性大,常常会出现在一次测量周期中,收到了测距信号,但不是算法指定的信标的测距信号,此时也无法进行解算,造成了数据的浪费。
2 自适应信标数量DR/LBL紧组合导航滤波方法本文提出一种自适应多信标DR/LBL紧组合导航方法,其流程如图2所示。
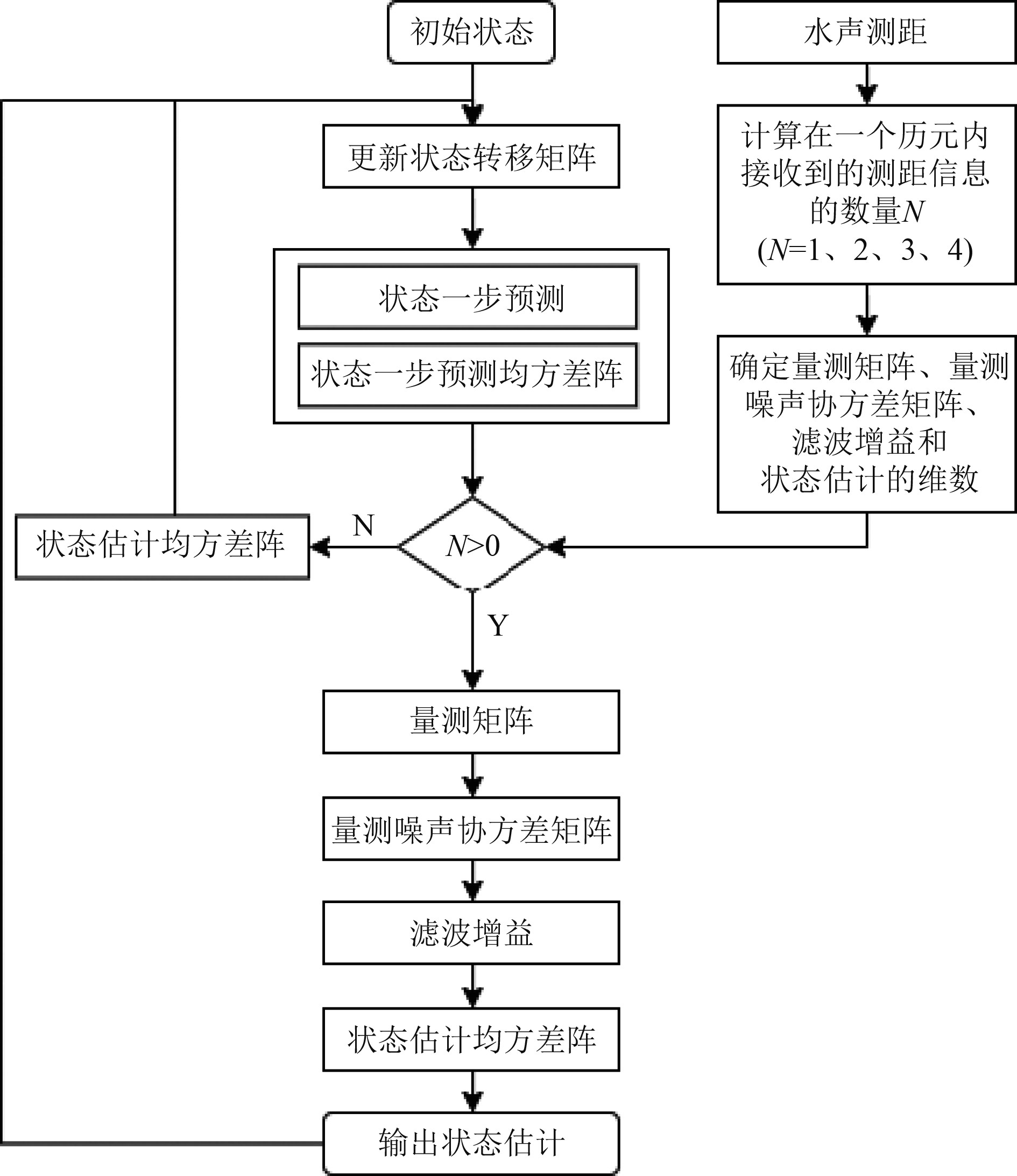
|
图 2 自适应多信标DR/LBL紧组合导航滤波方法流程图 Fig. 2 Adaptive multi-beacon DR/LBL tight integration navigation filtering method flowchart |
式(6)构成一个非线性的组合导航模型,利用扩展卡尔曼滤波方法进行计算。
状态一步预测:
| $ {\widehat{X}}_{k+1,k}=f\text{(}{\widehat{X}}_{k},{u}_{k}\text{,0)}=A{\widehat{X}}_{k}+\left[\begin{array}{cc}\Delta T& 0\\ 0& \Delta T\\ 0& 0\end{array}\right]\left[\begin{array}{c}{\text{v}}_{k}\cdot \mathrm{cos}{\varphi }_{k}\\ {\text{v}}_{k}\cdot \mathrm{sin}{\varphi }_{k}\end{array}\right]。$ | (8) |
式中:
状态方程关于
| $ {F}_{\omega k}=\frac{\partial f}{\partial {w}_{k}}=\left[\begin{array}{ccc}\mathrm{cos}{\phi }_{k}\cdot \Delta {T}& -{\nu }_{k}\cdot \mathrm{sin}{\phi }_{k}\cdot \Delta {T}& 0\\ \mathrm{sin}{\phi }_{k}\cdot \Delta {T}& {\nu }_{k}\cdot \mathrm{cos}{\phi }_{k}\cdot \Delta {T}& 0\\ 0& 0& 1\end{array}\right] 。$ | (9) |
式中:
状态一步预测均方误差阵:
| $ {P_{k + 1,k}} = A{P_k}{A^{\mathrm{T}}} + {F_{wk}}{Q_k}{F_{wk}}^{\mathrm{T}} 。$ | (10) |
式中:
量测矩阵:
| $\begin{aligned} {H_{k + 1}} = &{\left. {\frac{{\partial h({{\hat X}_{k + 1}})}}{{\partial {X_{k{\text{ + }}1}}}}} \right|_{{{\hat X}_{k + 1}} = {{\hat X}_{k + 1,k}}}} = \\ & \left[ {\begin{array}{*{20}{c}} \displaystyle{\frac{{2({{\hat x}_{k + 1,k}} - {x_{b1}})}}{{{{\hat C}_{k + 1,k}}{R_1}}}}& \displaystyle{\frac{{2({{\hat y}_{k + 1,k}} - {y_{b1}})}}{{{{\hat C}_{k + 1,k}}{R_1}}}}& \displaystyle{ - \frac{{2{R_1}}}{{{{\hat C}^2}_{k + 1,k}}}} \\ {}& \vdots &{} \\ \displaystyle{\frac{{2({{\hat x}_{k + 1,k}} - {x_{b{\text{i}}}})}}{{{{\hat C}_{k + 1,k}}{R_i}}}}& \displaystyle{\frac{{2({{\hat y}_{k + 1,k}} - {y_{bi}})}}{{{{\hat C}_{k + 1,k}}{R_i}}}}& \displaystyle{ - \frac{{2{R_i}}}{{{{\hat C}^2}_{k + 1,k}}}} \end{array}} \right]。\end{aligned}$ | (11) |
式中:
滤波增益:
| $ {K_{k + 1}} = P{ _{k + 1,k}}{H^{\text{T}}}_{k + 1}{({H_{k + 1}}P{ _{k + 1}}{H^{\text{T}}}_{k + 1} + {S_{k + 1}})^{ - 1}}。$ | (12) |
式中:
系统量测矩阵和系统量测协方差矩阵的维度根据收到的测距信号的数量而相应改变。例如,当仅接收到“信标2”、“信标3”的应答时,量测矩阵为:
| $ {H_{k + 1}} = \left[ {\begin{array}{*{20}{c}} \displaystyle{\frac{{2({{\hat x}_{k + 1,k}} - {x_{b2}})}}{{{{\hat C}_{k + 1,k}}{R_2}}}}& \displaystyle{\frac{{2({{\hat y}_{k + 1,k}}- {y_{b2}})}}{{{{\hat C}_{k + 1,k}}{R_2}}}}& \displaystyle{ - \frac{{2{R_2}}}{{{{\hat C}^2}_{k + 1,k}}}} \\ \displaystyle{\frac{{2({{\hat x}_{k + 1,k}} - {x_{b3}})}}{{{{\hat C}_{k + 1,k}}{R_3}}}}& \displaystyle{\frac{{2({{\hat y}_{k + 1,k}} - {y_{b3}})}}{{{{\hat C}_{k + 1,k}}{R_3}}}}& \displaystyle{ - \frac{{2{R_3}}}{{{{\hat C}^2}_{k + 1,k}}}} \end{array}} \right] 。$ | (13) |
式中:
| $ \begin{gathered} {R_2} = \sqrt {{{({{\hat x}_{k + 1,k}} - {x_{b2}})}^2} + {{({{\hat y}_{k + 1,k}} - {y_{b2}})}^2}{\text{ + }}{{(h - {h_{b2}})}^2}},\\ {R_3} = \sqrt {{{({{\hat x}_{k + 1,k}} - {x_{b3}})}^2} + {{({{\hat y}_{k + 1,k}} - {y_{b3}})}^2}{\text{ + }}{{(h - {h_{b3}})}^2}}。\\ \end{gathered} $ | (14) |
系统量测噪声协方差矩阵为:
| $ {S_k} = \left[ {\begin{array}{*{20}{c}} {{\sigma _{\Delta {\tau _2}}}^2}&0 \\ 0&{{\sigma _{\Delta \tau 3}}^2} \end{array}} \right]。$ | (15) |
状态估计:
| $ {\hat X_{k + 1}} = {\hat X_{k + 1,k}} + {K_{k + 1}}\left[ {{Z_{k + 1}} - h({{\hat X}_{k + 1,k}})} \right]。$ | (16) |
根据每个信标的位置,提前将其在量测矩阵(11)中所对应的公式提前写好,实际应用中,根据当前测量周期实际数据接收情况,自适应的组成对应的量测矩阵参与滤波。
3 实验验证为了验证本文提出的自适应多信标DR/LBL紧组合导航方法在实际应用中的效果,在青岛近海进行验证实验。采用实验船搭载卫星接收机和水声问答机模拟航行器的真实行驶过程。
首先,将4个信标投入海中,构成边长为1 km左右的矩形长基线阵,位置标定后,得到长基线阵4个信标的准确位置如表1所示。
|
|
表 1 信标位置 Tab.1 Beacon locations |
实验船携带实验设备在长基线阵中移动,水声问答机持续向各个信标发送问答信号并接收回令,记录信号传播时间;卫星接收机不断解算实验船的位置信息,利用卫星定位信息做位置差分,再根据多普勒计程仪和罗经的数据特性分别加入方差为0.2(m/s)2和0.6°2的高斯噪声,来模拟航向和航速数据用于后续解算。
通过声速剖面仪测得海水平均声速为

|
图 3 真实航行轨迹 Fig. 3 Actual navigation trajectory |
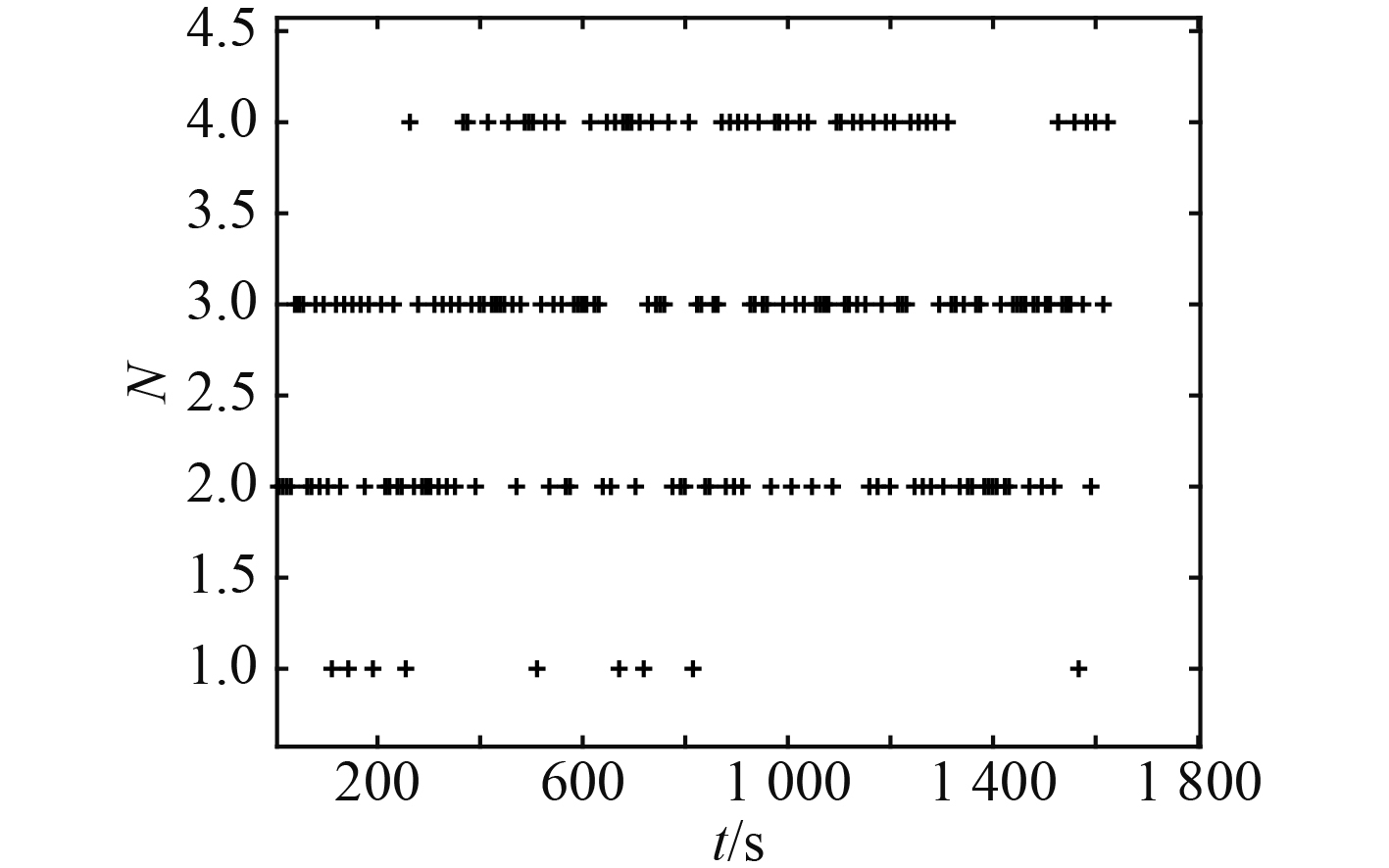
|
图 4 每个测量周期接收到测距信号的数量 Fig. 4 Number of range signals received in each measurement cycle |
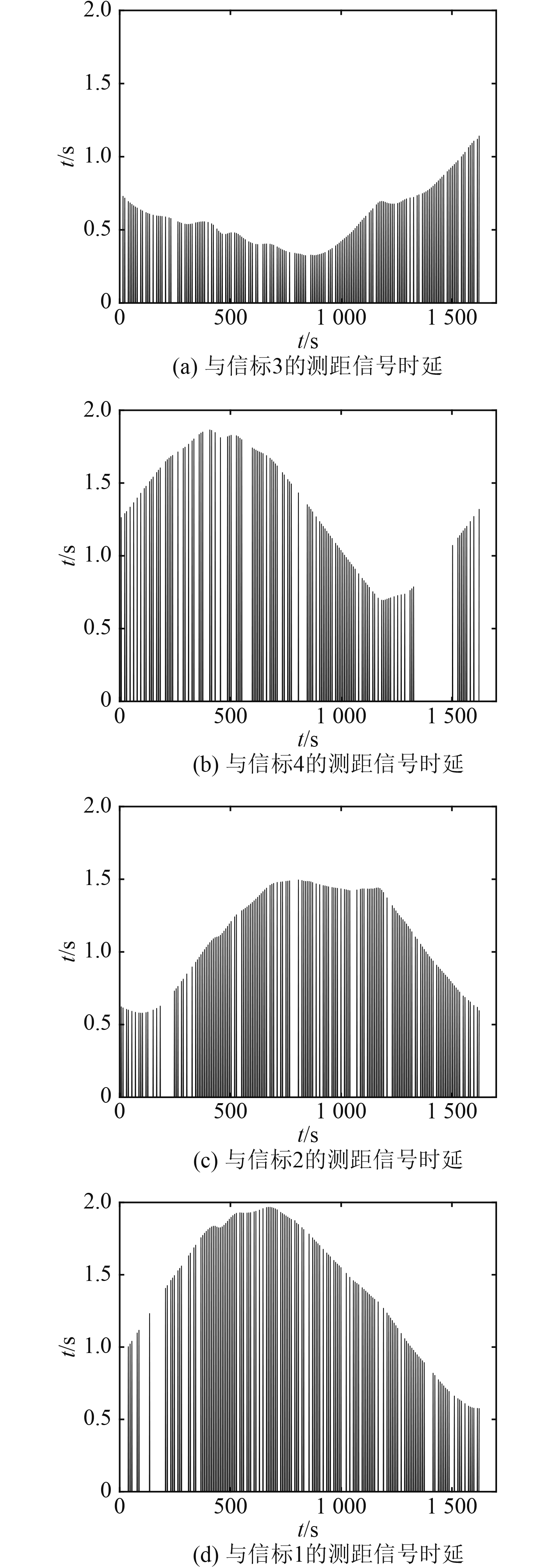
|
图 5 与各个信标的测距信号时延 Fig. 5 Time delay of range signals from each beacon |
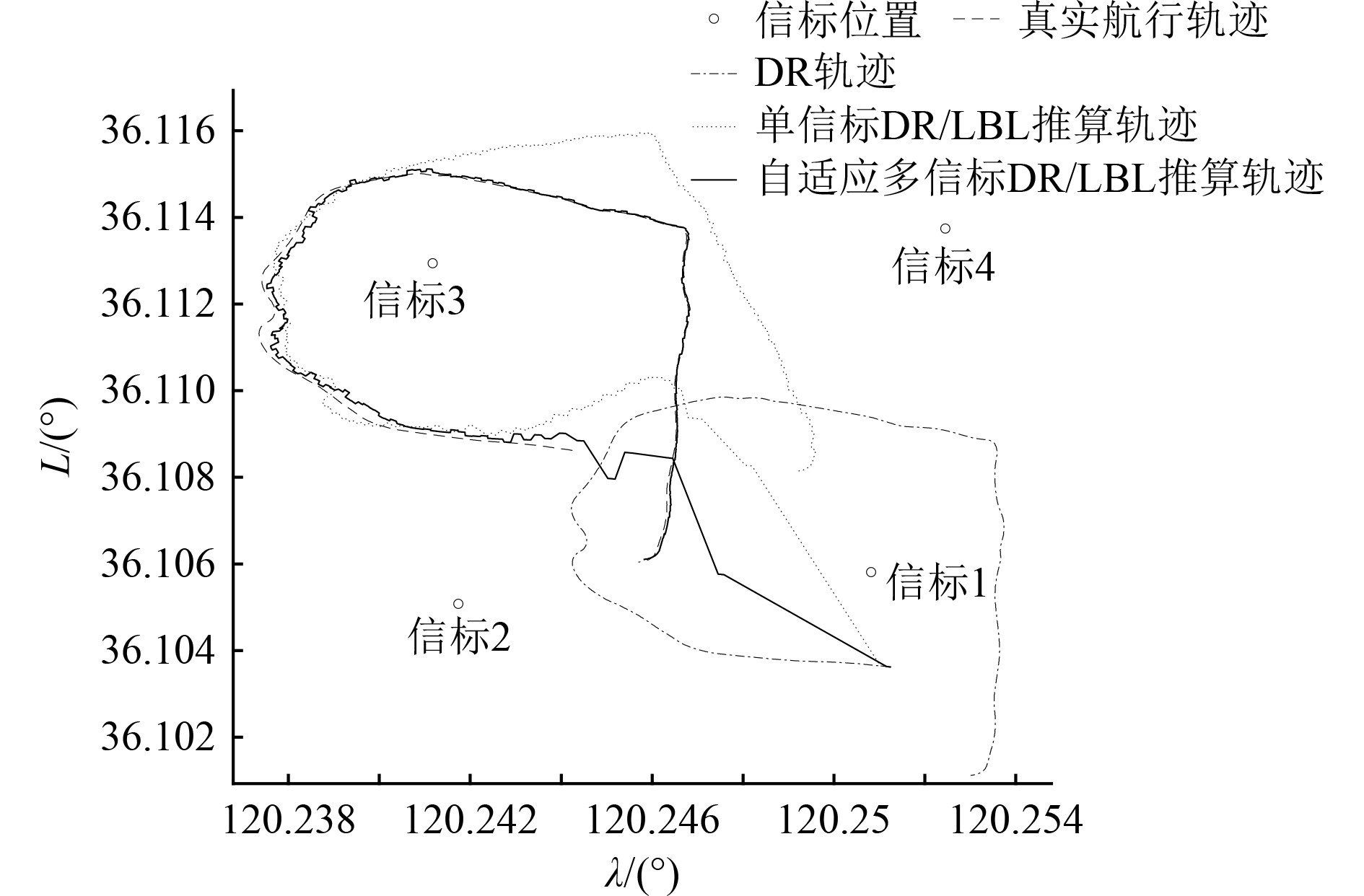
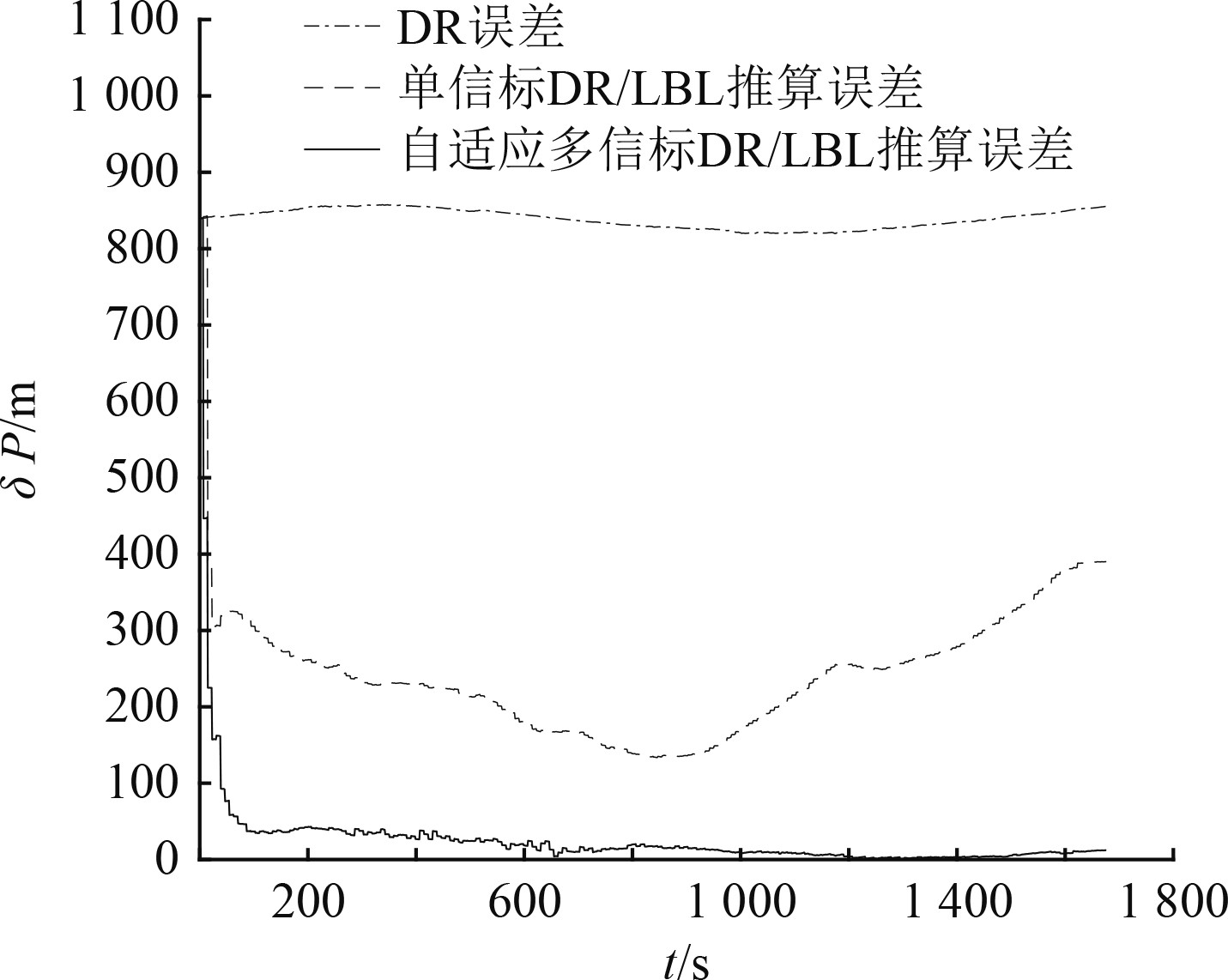
根据实测数据,人为加入了840 m的初始位置偏差,以模拟水下航行器长时间航行造成的位置累积误差。分别采用DR、基于单信标的DR/LBL紧组合导航方法(固定接收信标3的测距信号)和自适应多信标DR/LBL紧组合导航方法进行解算,解算结果如图6所示,定位误差对比如图7所示,可知,航位推算的解算误差虽在实验期间没有明显增大,但其无法对自身累积误差进行修正,所以只适合在位置校正后的短时间内使用;基于单信标的DR/LBL紧组合导航方法的定位结果,虽然能在初始阶段缓慢收敛,但因系统可观性受限,解算误差没有收敛到可用的精度范围内;而自适应多信标DR/LBL紧组合导航方法,因数据的利用率高,系统可观性好,定位结果能很快的收敛并维持在较高的精度内。
|
图 6 位置解算结果 Fig. 6 Position calculation results |
|
图 7 定位误差对比 Fig. 7 Positioning error comparison |
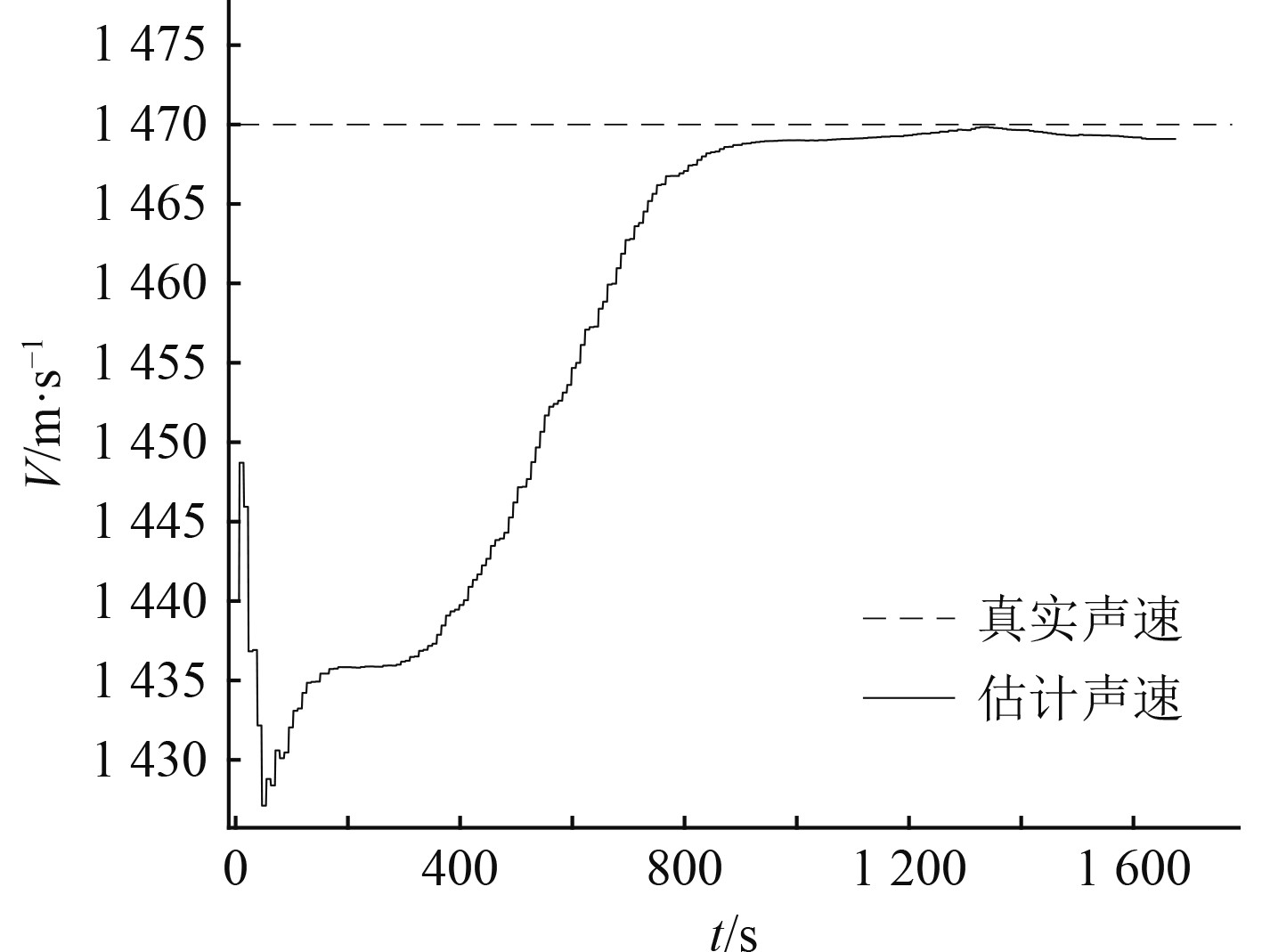
平均声速估计结果如图8所示,经过一段时间后也收敛到了真实值附近,为位置解算提供了良好的支撑。
|
图 8 平均声速估计结果 Fig. 8 Estimated average sound velocity |
本文所述的导航算法,能在水下航行器利用长基线进行位置校正时,自适应的处理因受海洋环境等因素影响而造成的在不测量周期中信标测距信号各种接收情况,相较于基于单信标的DR/LBL紧组合导航算法,数据利用率高、解算收敛更快,解算结果也更稳定,并且可以实时估计海水的平均声速,以应对海水声速在一定区域内测量困难的问题。
本文假设通过将测得的时延数据乘以等效平均声速,可以得出信标与水下航行器之间斜距的2倍。然而,这个假设建立在UUV在测距信号发送到接收的整个过程中位置保持不变的前提之上,这与实际情况并不一致。在实际的信号收发过程中,UUV的位置并不始终保持不变,导致测量数据存在一定的误差。因此,我们需要进一步深入研究这一问题,以更准确地理解和解决由于UUV位置变化引起的数据误差。
| [1] |
高清泽. 一种水下航行器运动自导航及轨迹跟踪方法[J]. 舰船科学技术. 2019, 41(4): 94−99.
|
| [2] |
黄玉龙, 张勇刚, 赵玉新. 自主水下航行器导航方法综述[J]. 水下无人系统学报. 2019, 27(3): 232−253.
|
| [3] |
潘爽, 施建礼, 聂永芳, 等. 自主水下航行器同时定位与制图技术研究[J]. 舰船科学技术. 2018, 40(6): 124−127.
|
| [4] |
于燕婷, 许江宁, 林恩凡, 等. 单信标水声定位技术研究现状及应用展望[J]. 导航定位学报. 2022, 10(2): 13−20.
|
| [5] |
曹方方, 刘卫东, 李娟丽. 基于EKF的UUV单信标水声导航定位方法研究[J]. 计算机测量与控制. 2011, 19(9): 2234−2236.
|
| [6] |
BATISTA P, SILVESTRE C, OLIVEIRA P. Single beacon navigation: Observability analysis and filter design[C] //IEEE, 2010.
|
| [7] |
S. E W, L. L W, R. M E. Advances in decentralized single-beacon acoustic navigation for underwater vehicles: Theory and simulation[C]// 2010.
|
| [8] |
王燕, 张新宇, 孙思博, 等. 水下单信标导航算法研究及置信区间分析[J]. 哈尔滨工程大学学报. 2022, 43(1): 119−129.
|
| [9] |
邝英才, 吕志平, 李林阳, 等. GNSS-A水下定位的动态非线性Gauss-Helmert模型及其抗差总体卡尔曼滤波算法[J]. 测绘学报, 2023, 52(4): 559-570. DOI:10.11947/j.AGCS.2023.20210467 |
| [10] |
孙伟, 段顺利, 丁伟, 等. GPS单点测速方法的比较分析[J]. 导航定位学报. 2017, 5(1): 81−85.
|
| [11] |
辛明真, 阳凡林, 薛树强, 等. 顾及波束入射角的常梯度声线跟踪水下定位算法[J]. 测绘学报. 2020, 49(12): 1535−1542.
|
 2024, Vol. 46
2024, Vol. 46

