随着水声技术的发展,潜艇等水下目标的辐射噪声也得到了大幅度的降低,与此同时,随着材料技术的日新月异,潜艇的隐身技术也有一定程度的突破。这导致了被动声呐对这一类目标的探测距离减小,而主动低频的主动声呐的作用尤为突出[1]。
常见的主动声呐为单基地模式,在该平台上同时拥有发射基阵和接收基阵,这种模式数据处理简单,但易被潜艇发现并规避。多基地模式可以采用多个声源发射基阵和不同位置的多个接收基阵组成[2],其接收基阵具有多样化,可以使用声呐浮标、吊放声呐、舰载声呐、岸基声呐等[3],在不同的使用场景下因其探测覆盖率高、潜艇不易规避等优点,在航空声呐反潜中应用广泛。
常规的多基地探测例如声呐浮标探测,一般首先使用多枚被动声呐浮标布阵[4],既可以对潜艇出现概率较大的海域进行大面积搜素,也可以在较短时间内封锁潜艇可能经过的路径[5]。在确定潜艇可能存在的概略区域后,可以使用主动声呐浮标与被动声呐浮标组合投放布阵,确定潜艇的深度、精确s方位等[6-7],从而规划下一步动作。除此之外常见的还有吊放声呐与声呐浮标结合探测[8],在利用声呐浮标按照预定的阵型布阵探测并已知潜艇或目标可能出现的概率区域后,可利用反潜机群飞至指定海域,按照各自的探测区域,悬停下放吊放声呐进行主动探测,确定潜艇的精确位置。
目前,水下声学探测技术呈现出无人化与智能化的发展趋势,水下无人平台搭载水声探测载荷被广泛使用[9]。水下无人平台是由多台水下无人探潜设备通过一定方式实现信息传递的系统。在需要进行大深度探潜、长距离搜潜等作战任务时,通过配置不同需求的水下无人平台可以开展相应的侦察、搜潜、干扰等任务。水下无人平台因其无人化的特点,决定其不受到海、陆、空等环境限制,满足非接触、非对称等要求,能够开展长时间、高危险、超极限的作战任务[10]。目前较为广泛使用的典型水下无人平台包括侦察型、反水雷型、有效载荷投送型等多种应用各类作战使用场景的水下无人平台[11]。
相比于常规的无动力多基地平台,无人运动平台具有损耗小、成本低的特点,即使在探测过程中个别节点受到损坏,也可以进行阵型或位置的调整,不影响探测性能。除此之外,探测效率高、容错能力强,无人运动平台比常规无动力平台具有更大优势。水下无人运动平台可以通过设计运动轨迹[12],覆盖面积较大的实时探测区域,并可以灵活配置运动平台、实时动态监测等,在执行搜潜任务中具有突出优势[13]。目前国内对水下多无人平台的关注日渐突出,但对其联合探测效能分析方法研究较少。
1 水下无人平台多基地探测模型 1.1 多基地声呐探测模型对某多基地声呐探测模型进行仿真,假设发射基阵

|
图 1 多基地示意图 Fig. 1 Multi-site diagram |
如用多基地声呐探测目标的等效距离
| $ R = \sqrt {{R_{{t}}}{R_{{r}}}}。$ | (1) |
与单基地声呐探测相比,多基地声呐探测可以提供更长的探测距离、增加检测概率、使潜艇的战术情况更加复杂化、多个接收基地同时检测可以提高分类、跟踪等性能、提高了被动声呐浮标在战术上的应用场景和途径。
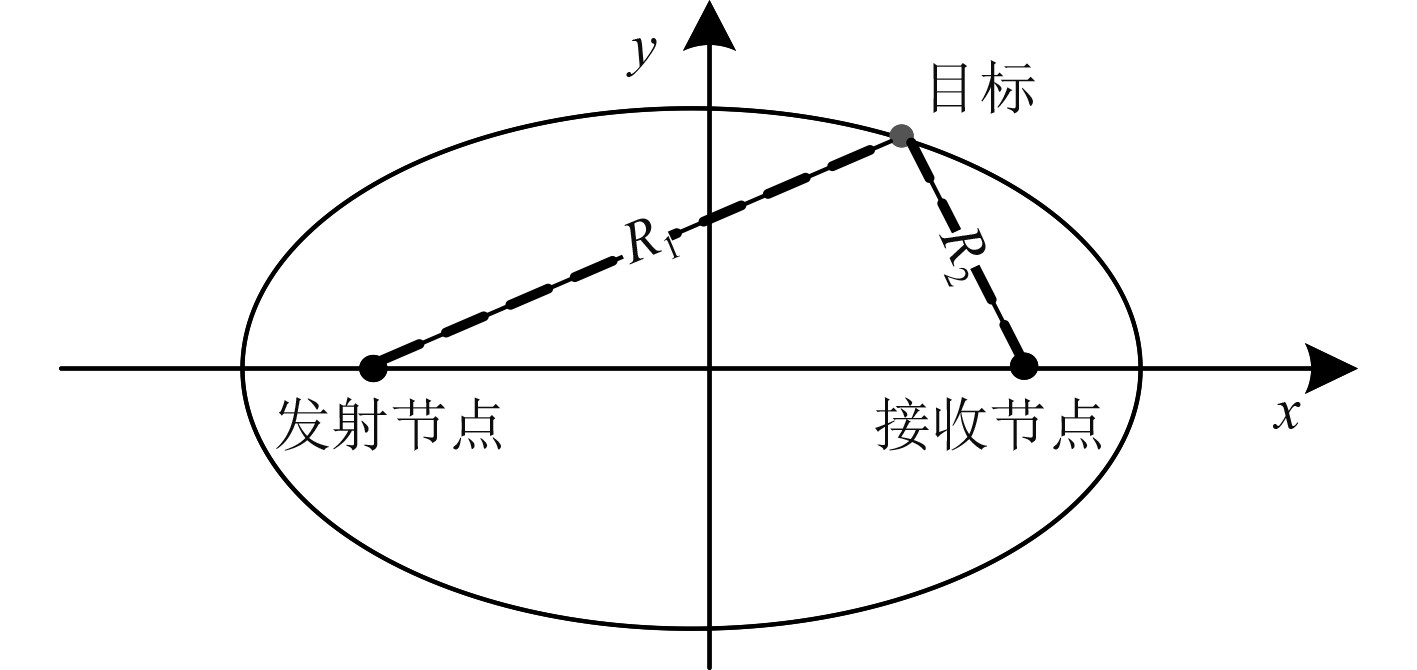
基于卡西尼椭圆定义多基地模型,如图2所示。多基地的笛卡尔方程定义为:
|
图 2 多基地三角形示意图 Fig. 2 Multi-site triangle diagram |
| $ \left[ {{{\left( {x - a} \right)}^2} + {y^2}} \right]\left[ {{{\left( {x + a} \right)}^2} + {y^2}} \right] = {b^2} 。$ | (2) |
其中:
由于卡西尼椭圆相对于横、纵坐标轴对称,因此该条件下的多基地探测面积可表示为:
| $ S = \left\{ \begin{gathered} {4\displaystyle\int_0^{\sqrt {{a^2} + {b^2}} } \qquad{{f_C}\left( x \right){\rm d}x} ,a/b \leqslant 1} ,\\ {4\displaystyle\int_{\sqrt {{a^2} - {b^2}} }^{\sqrt {{a^2} + {b^2}} } \qquad{{f_C}\left( x \right){\rm d}x} ,a/b > 1。} \end{gathered} \right. $ | (3) |
式中:
水下无人航行器(UUV)具有机动性强、活动范围大、作业效率高等特点[14],在国外的水下无人航行器定义为无人、自带能源、可以自主行驶、自主编程控制的一种航潜器。常规的水下无人航行器可分类为不能自主航行、需要遥控操控的遥控水下航行器(ROV)、具备自主导航功能的自主水下航行器(UUV)[14]以及许多适应不同工作环境和任务需求的多种类型的水下航行器。若采用多个水下无人航行器以某种编队方式、某种阵型预设、某种运动路径规划组成水下无人集群平台,不仅可以进行集群探测,提高探测覆盖率,也具有可扩展性高、容错率高的特点。
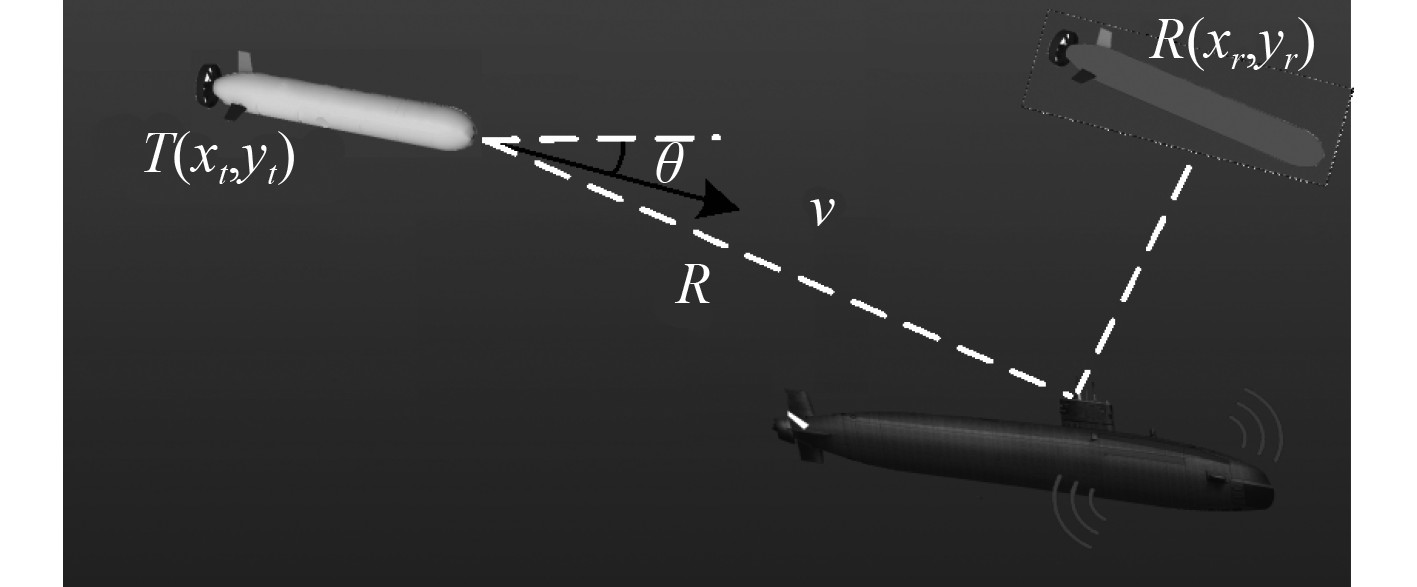
假设水下无人平台中的每个航行器均携带一个发射基阵
|
图 3 无人平台多基地探测示意图 Fig. 3 Unmanned platform multi-base detection diagram |
| $ S = \left\{ \begin{gathered} {4m\displaystyle\int_0^{\sqrt {{a^2} + {b^2}} } {{f_C}\left( x \right){\rm d}x} + 2avt \cdot \sin \left( \theta \right),a/b \leqslant 1} ,\\ {4m\displaystyle\int_{\sqrt {{a^2} - {b^2}} }^{\sqrt {{a^2} + {b^2}} } {{f_C}\left( x \right){\rm d}x + 2avt \cdot \sin \left( \theta \right)} ,a/b > 1。} \end{gathered} \right.$ | (4) |
其中,
假设声基阵的作用距离为
| $ {P_d} = \frac{1}{{1 + {{10}^{{{\left( {{R \mathord{\left/ {\vphantom {R {{R_0} - 1}}} \right. } {{R_0} - 1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{R \mathord{\left/ {\vphantom {R {{R_0} - 1}}} \right. } {{R_0} - 1}}} \right)} b}} \right. } b}}}}} 。$ | (5) |
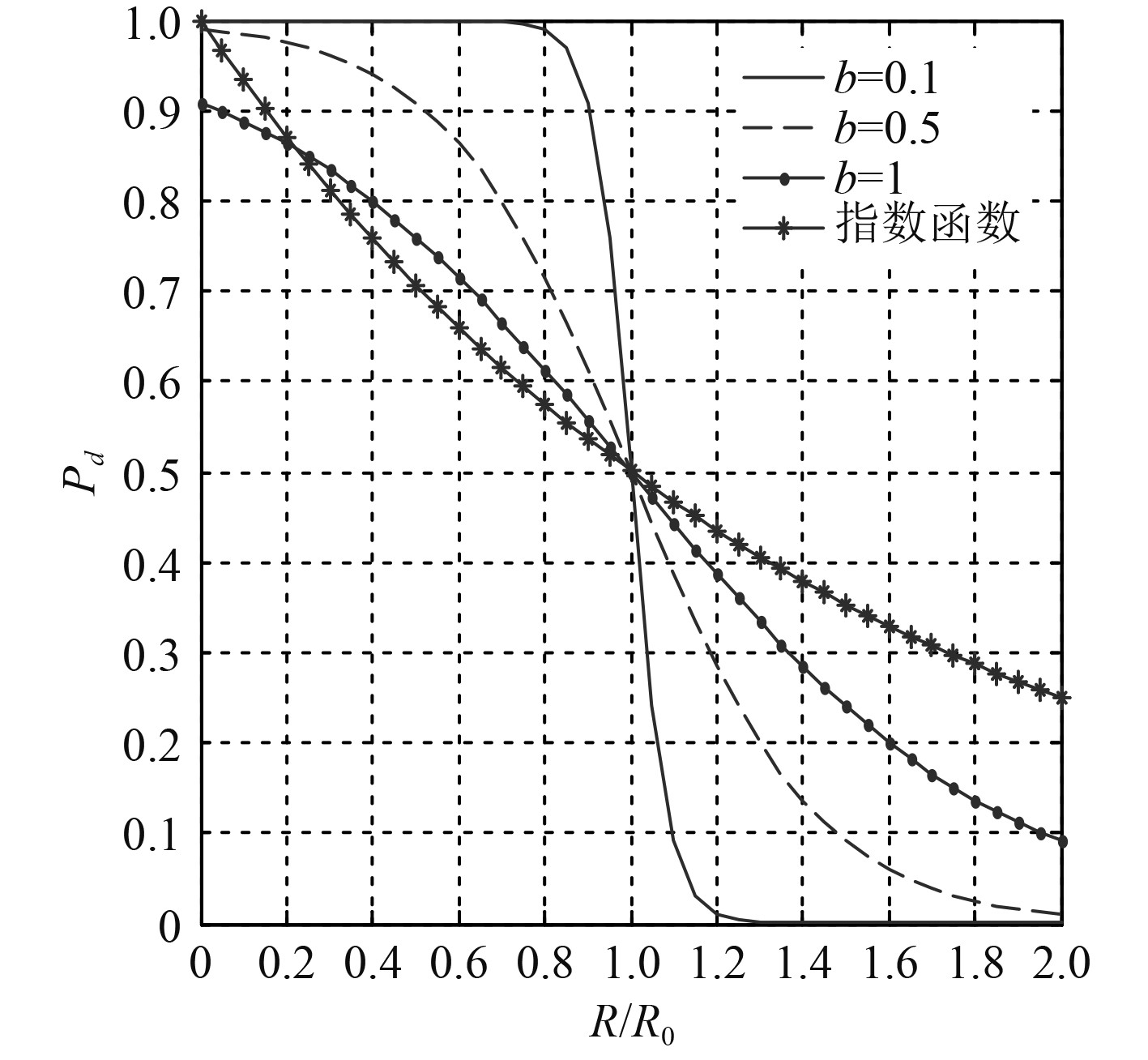
式中:b为距离-探测概率函数的扩散系数。费米函数在不同扩散系数下的距离-探测概率函数和指数函数的对比如图4所示。当扩散系数在0~1区间内,声基阵的作用距离
|
图 4 距离-探测概率函数曲线 Fig. 4 Range-probe probability function curve |
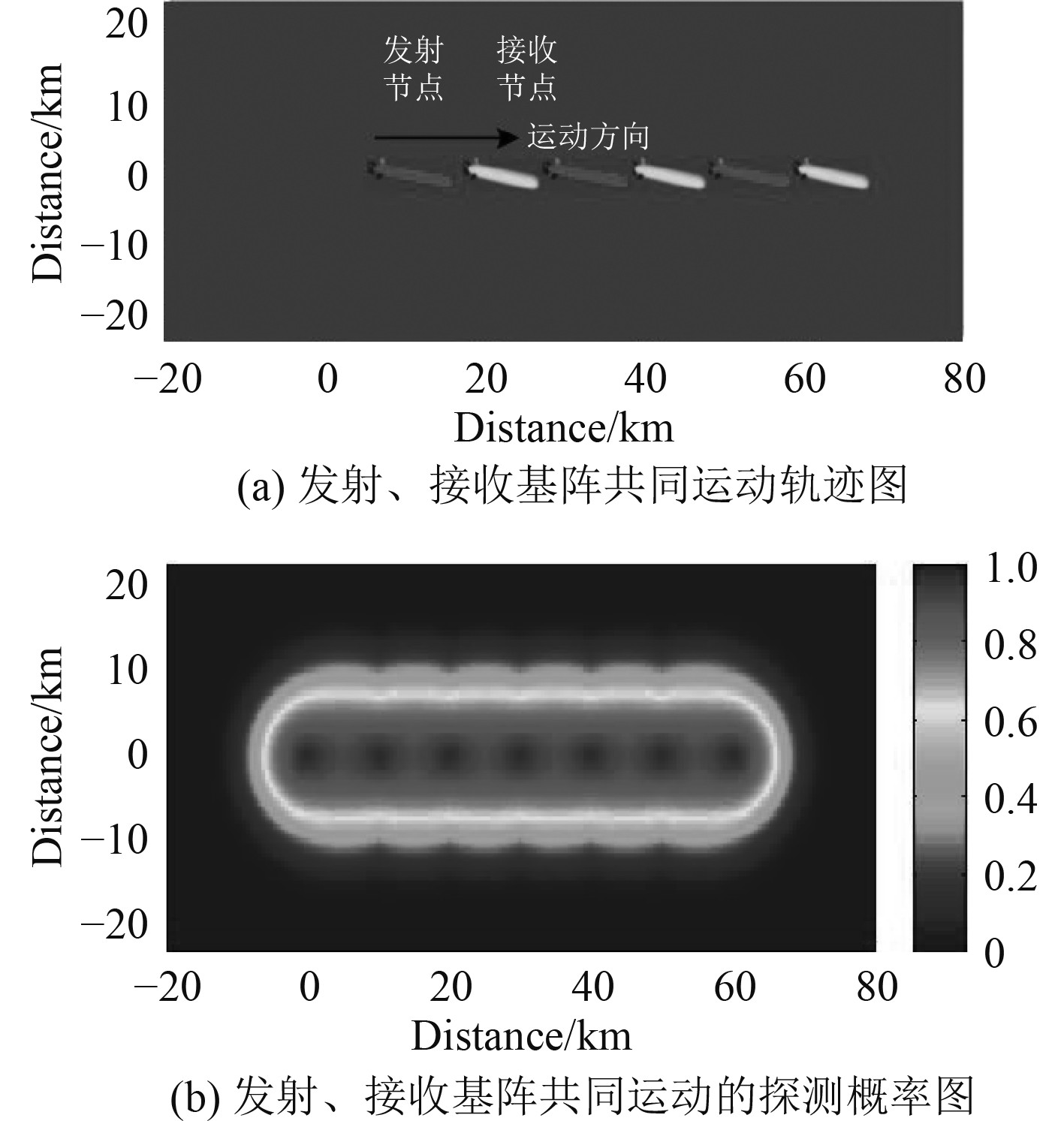
根据水下无人平台的运动轨迹不同,分别考虑仅水下无人平台发射基阵运动、仅接收基阵运动、发射基阵和接收基阵同时运动的3种情况下的探测概率[16]。以双基地为例,假设发射基阵(★标记)处于原点位置不动,接收基阵沿其水平方向由原点位置反向运动至50 km处的运动轨迹如图5(a)所示,探测概率三维图如图5(b)所示。假设接收基阵位置不动,发射基阵沿其水平方向由原点位置反向运动至50 km处的运动轨迹如图6(a)所示,探测概率三维图如图6(b)所示。假设发射基阵与接收基阵间距不变,两者同时沿其水平方向由原点位置同向运动至50 km处的运动轨迹图如图7(a)所示,探测概率三维图如图7(b)所示。

|
图 5 接收基阵运动轨迹及探测概率图 Fig. 5 Motion trajectory diagram and detection probability graph of receiving array motion |

|
图 6 发射基阵运动轨迹及探测概率图 Fig. 6 Motion trajectory diagram and detection probability graph of firing array motion |
|
图 7 发射、接收基阵共同运动轨迹及探测概率图 Fig. 7 Motion trajectory diagram and detection probability graph of transmitting and receiving array joint motion |
从仿真结果可以发现,无论发射基阵或接收基阵任何一方相对彼此进行反向运动时,因发射基阵与接收基阵之间间距增大,探测概率随之降低;而当发射基阵与接收基阵相对共同运动时,可在一定程度上减缓基阵间距增大的速度或可基本保持基阵间距不变,因此水下无人平台多基地声呐探测范围也随之扩大,探测效能增加。
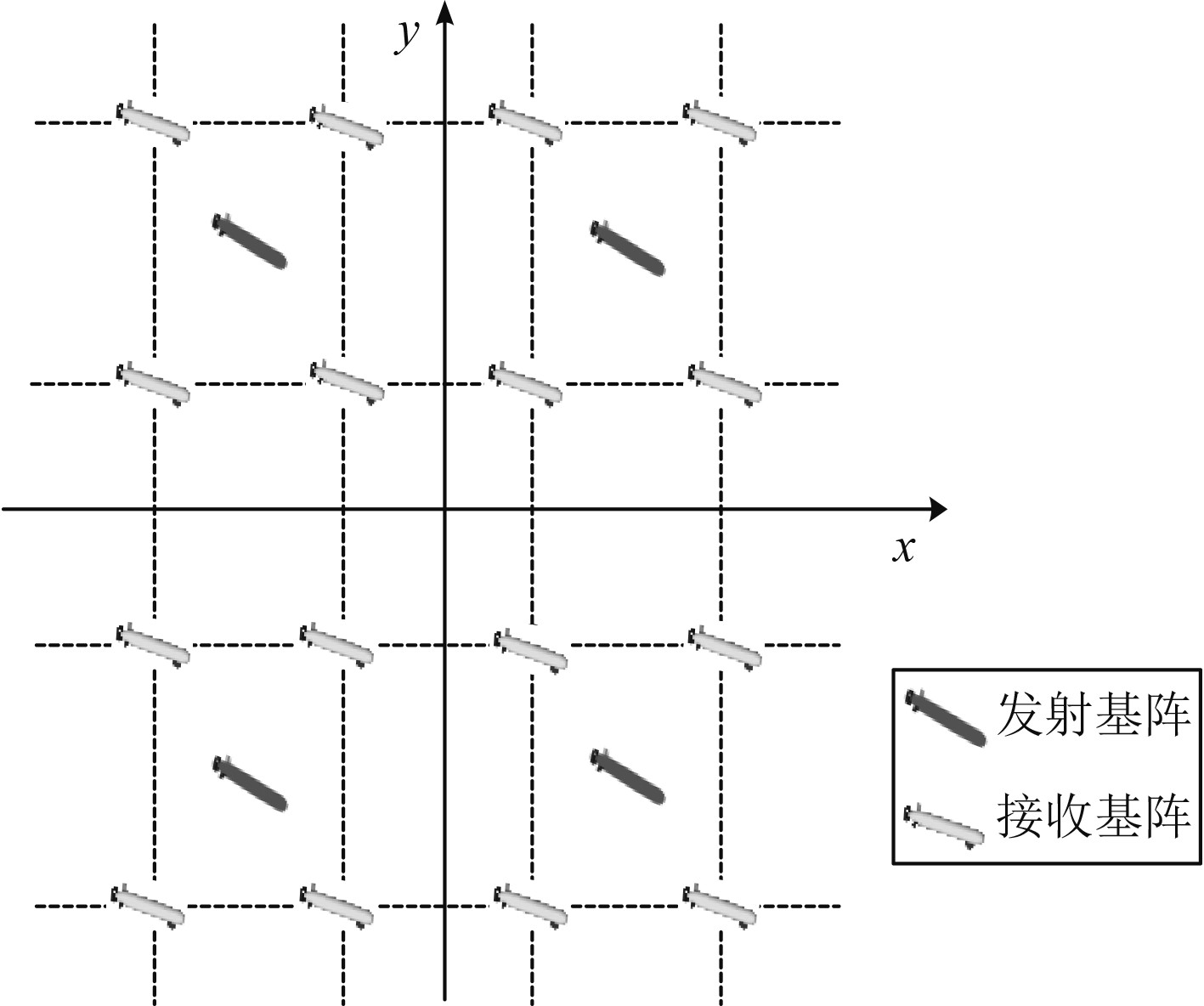
2.2 水下无人平台多基地声呐阵探测效能分析对4行×4列的20元矩形水下无人平台声呐阵进行效能分析,该20元基阵可视为4个4元接收基阵包围1个发射基阵的阵型组合叠加,如图8所示。若第m个发射基地和第n个接收基地构成的多基地探测概率为
|
图 8 水下无人多基地平台阵型图 Fig. 8 Underwater unmanned multi-base platform formation diagram |
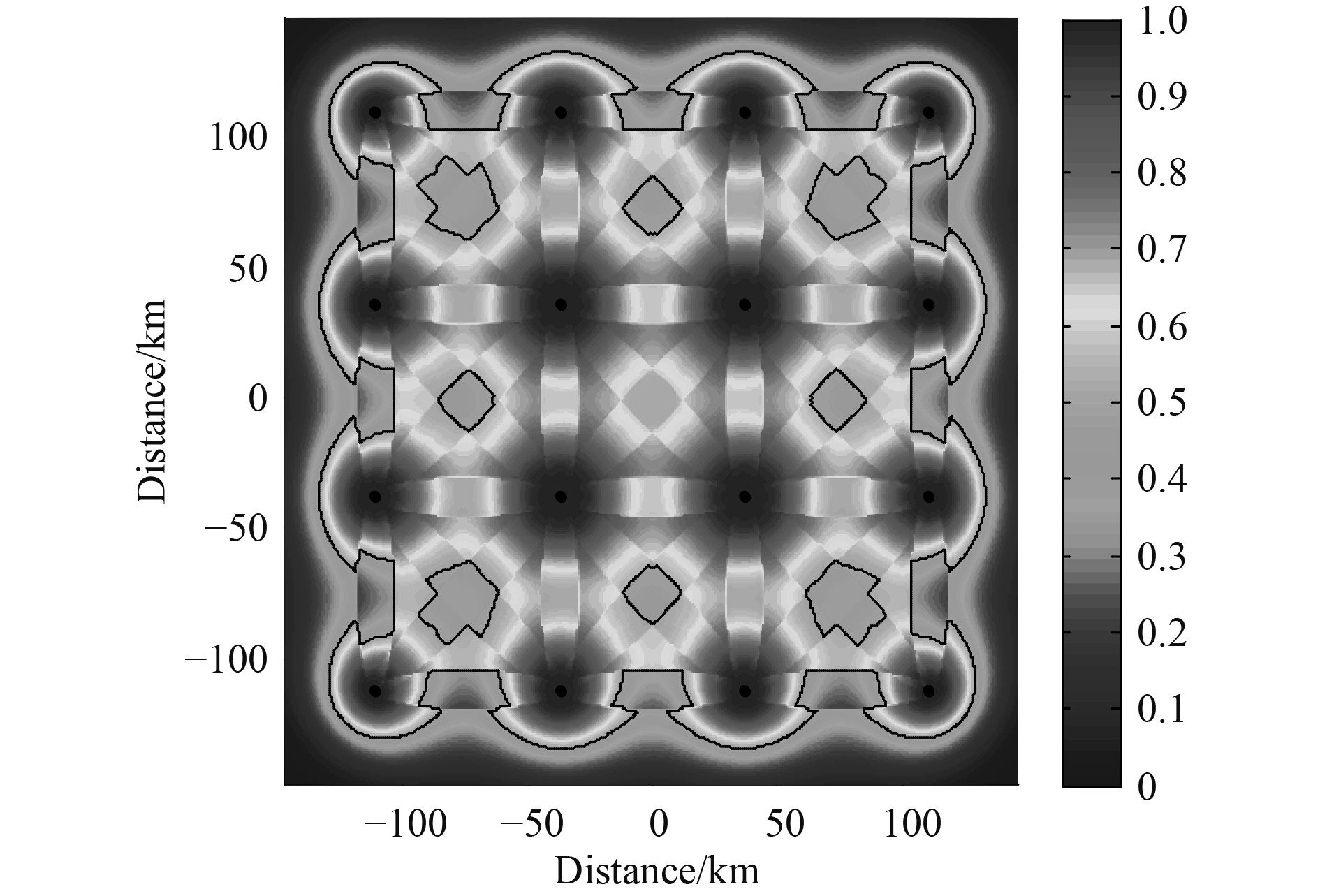
|
图 9 多基地探测概率分布三维图 Fig. 9 Three-dimensional probability distribution of multi-base detection |
| $ P = 1 - \prod\limits_{m = 1}^4 {\prod\limits_{n = 1}^{12} {(1 - {P_{mn}})} } 。$ | (6) |
对水下无人平台多基地声呐探测不同运动轨迹下的探测效能进行分析,分别分析比较发射基阵和接收基阵匀速朝同一方向运动、向外均匀散射线形运动、分组匀速向两侧相反方向运动的运动轨迹下探测效能,并与固定式多基地平台进行对比,如图10~图12所示。得到3种运动轨迹下水下无人平台的多基地声呐探测概率如图13所示。

|
图 10 水下无人平台运动轨迹图1 Fig. 10 Motion trajectory diagram of underwater unmanned platform I |
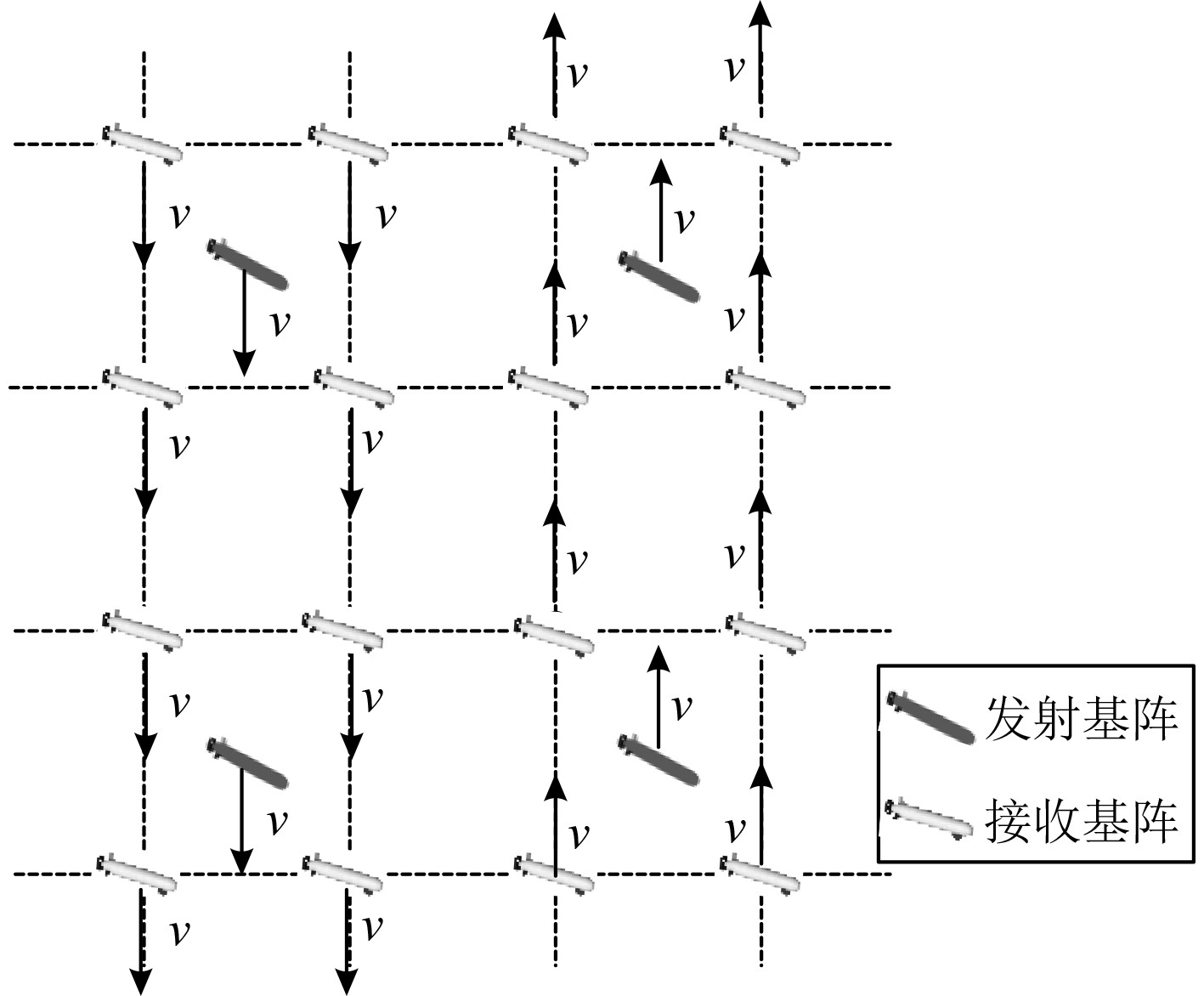
|
图 12 水下无人平台运动轨迹图三 Fig. 12 Motion trajectory diagram of underwater unmanned platform III |
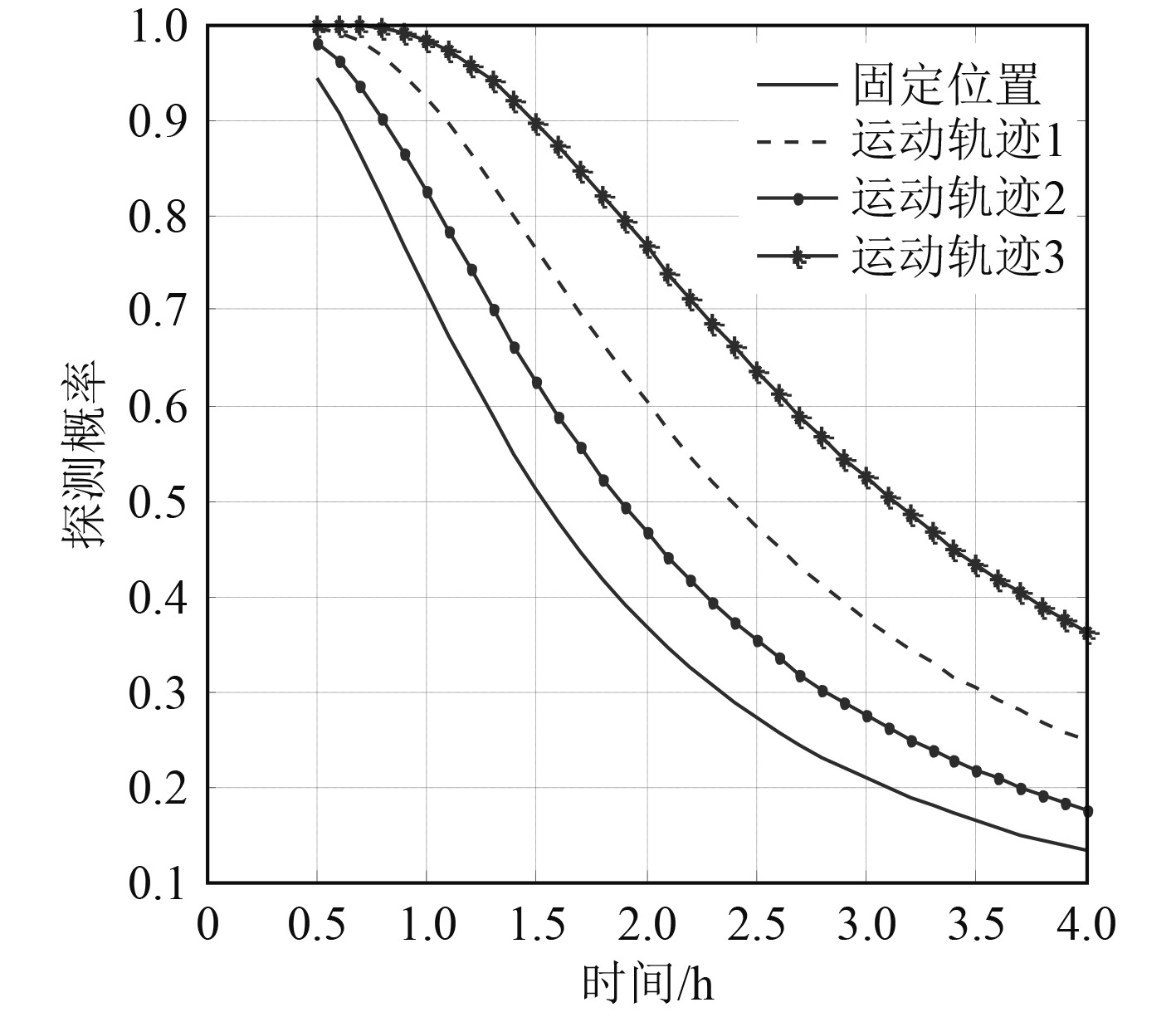
|
图 13 探测概率曲线 Fig. 13 Detection probability curve |
可知,随着水下无人平台多基地探测时间的增加,因潜艇逃逸可能性增大,探测概率也随之迅速的下降;水下无人平台多基地保持当前固定式位置不动时探测概率最低,当水下无人平台多基地匀速朝同一方向运动时(见图10),探测概率可提高20%左右,当水下无人平台多基地向外均匀散射线形运动时(见图11),因其运动散射范围较扩散,发射接收基阵间距逐渐增大,探测概率仅提高不足10%,当水下无人平台分2组匀速向两侧相反方向运动(见图12)的运动轨迹的探测概率最高,可提高约35%左右。

|
图 11 水下无人平台运动轨迹图2 Fig. 11 Motion trajectory diagram of underwater unmanned platform II |
本文建立了水下无人平台对多基地声呐探测效能模型,提出了适用于水下无人运动平台的多基地水声探测效能方法,并对水下无人平台在不同运动方式和运动轨迹下的探测效能进行了仿真分析,结果表明:
1)相比于常规的无动力式多基地声呐探测,水下无人运动平台多基地声呐探测概率更高;
2)对于水下无人平台多基地声呐,当发射基阵与接收基阵共同运动情况下,可减缓基阵间距增大的速度或可基本保持基阵间距不变,在该条件下的声呐探测概率比发射基阵或接收基阵单独运动高;
3)水下无人平台多基地声呐基阵的运动轨迹会影响其探测概率,在本文的仿真条件下,当水下无人平台分2组匀速向两侧相反方向运动的运动轨迹探测覆盖面积更大、探测概率更高。
本文研究结果可为水下无人探测平台的轨迹规划提供理论支撑。但在实际应用中应综合考虑单个声基阵的作用距离、声基阵间距、布置声基阵的时间、并根据水下目标的逃逸变化方法适时调整。
| [1] |
陈芳香, 卢术平, 丁烽. 基于跟踪起始准则的多基地声呐阵位优化算法[J]. 声学技术, 2021, 40(6): 864-873. DOI:10.3969/j.issn.1000-3630.2021.6.sxjs202106019 |
| [2] |
田坦. 声呐技术[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010: 67−121.
|
| [3] |
邹吉武. 多基地声呐关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
| [4] |
孙溢新, 李伟, 张佳琪, 等. 多基地水下探测目标接收技术[J]. 舰船科学科技, 2022, 44(16): 130-133. |
| [5] |
杜向辉, 王永恒, 刘亭. 航空声呐浮标多基地探测阵型性能分析[J]. 舰船电子工程, 2022, 42(12) 140−146.
|
| [6] |
屈也频. 反潜巡逻飞机搜潜辅助决策系统建模与仿真研究[D]. 长沙: 国防科学技术大学, 2009.
|
| [7] |
吴天舒, 苏军, 连梓旭. 基于TODA信息的多基地声呐系统定位算法[J]. 舰船科学技术, 2023, 45(5): 112−117.
|
| [8] |
李天宇. 基于水下无人平台的目标深度估计技术研究[D]. 北京:中国科学院大学,2020.
|
| [9] |
鞠建波, 李沛宗, 周烨, 等. 基于反潜直升机平台的吊放声呐与浮标多基地模式应召搜潜概率仿真研究[J]. 航空兵器, 2020, 27(4): 74−79.
|
| [10] |
郝宇, 邱龙皓, 邹男, 等. 无人平台自主探测声呐的发展现状和展望[J]. 哈尔滨工程大学学报, 2021, 42(9): 1347−1354.
|
| [11] |
尚燕丽. 海军发展无人作战平台的需求、现状与展望[J]. 国防技术基础, 2009(1): 40-43+54. |
| [12] |
徐晓强, 宋佳平, 郭东田. 水下无人作战平台现状及技术发展[J]. 中国科技纵横, 2020(4): 241-242. |
| [13] |
赵晨, 白剑, 周颖, 等. 一种基于目标定位的水下无人平台自主航迹规划方法[P]. CN115655273A, 2024-07-25.
|
| [14] |
陈玮, 吴泽伟, 吴晓锋.水下无人平台协同探测行动过程[J]. 四川兵工学报, 2009, 30(6): 36−40, 43
|
| [15] |
冯景祥, 姚尧, 潘峰, 等. 国外水下无人装备研究现状及发展趋势[J]. 舰船科学技术, 2021, 43(23): 1−8.
|
| [16] |
陈立纲. 声呐浮标多基地探测综合效能分析方法研究[J]. 声学与电子工程, 2022(2): 7-9+32. |
 2024, Vol. 46
2024, Vol. 46
