船舶电场信号是船舶在海洋环境中呈现的重要非声物理场信号,主要来源于船舶异种金属电化学反应和船体阴极保护产生的腐蚀和防腐电流。船舶电场信号具有时域通过特性明显、低频线谱特征丰富的特点,可被水下检测装置所感知,是水下探测识别的重要信息源。目前国外已经研制了海底阵、浮标、潜标等多种形式的探测装置,用于船舶电场的探测识别。水下电场特征模拟是船舶电场特性研究和应用的重要手段,通过建立船舶电场模型可以实现典型海洋环境下船舶电场空间分布仿真计算和特征信号生成,可为电场检测阵型设定、检测算法优化与验证、检验效能评价提供信息支撑。
水下电场模拟方法一般分为数值模拟和物理模拟。数值模拟是基于电磁场基本方程,通过边界元、有限元和等效源的方法建立电场方程,通过数值解计算电场分布。物理模拟则是利用船舶电场实物缩比模型或电模拟源,在实验室水池或水槽中模拟电场分布,通过传感器实现电场分布的测试。卢新城等[1]利用时谐电流元,推导出了轴频电场的数学建模方法,利用测量数据拟合出海船所产生的轴频电场分布。余定峰等[2]利用时谐偶极子模型在深海环境下的交变电场信号,对船舶轴频电场进行了仿真模拟。岳瑞永等[3]基于时谐电偶极子模型,通过数值仿真对舰船轴频电场的衰减规律进行了研究。熊露等[4]对水平直流电偶极子在三层介质下的电磁场分布进行了求解,并发现在极低频频段内可用水平直流电偶极子模型来替代水平时谐电偶极子。潘龙等[5]利用有限元方法对轴频电场进行建模,提高了其计算精度。目前国内对船舶电场的建模仍以数值建模为主,本文利用LabVIEW和Fortran语言以及配套硬件,实现了对船舶电场模型的半实物模拟。
半实物模拟是电场模拟的一种新的方法,利用数值模型产生电场数字信号,通过数模转换将数字信号转换为物理电压信号,该信号可直接输入到后端检测装置,也可驱动相关激励装置产生实际电场信号。该方法实现基于数学模型驱动的电场物理模拟,具有效费比高、模型加载灵活、研发周期短、模拟精度高的特点,在检测系统验证、算法优化等方面具有广泛应用前景。
本文将数学建模与虚拟仪器技术相结合,以LabVIEW为开发平台,以水平电偶极子模型为电场等效源模型,通过动态链接库调用方式实现模型加载和数字信号生成,通过驱动高精度D/A转换卡实现电场模拟电压信号生成,并将电压实测信号与模型信号进行了对比,验证了方法的有效性和准确性,为后期船舶电场信号高精度模拟提供了方法。
1 船舶电场产生机理与数学建模船舶在海水中浸泡腐蚀会产生腐蚀电流。同时,为了保护船舶壳体不被海水腐蚀,一般采用外加电流阴极保护的方法(ICCP)或者牺牲阳极阴极保护的方法(PCP)。无论采取何种方式对壳体进行保护,腐蚀电流和保护电流都会从船体经过海水流向螺旋桨,然后通过船内的各种线路从螺旋桨返回到船壳,形成船舶静电场。而在螺旋桨转动过程中,由于主轴与船体之间接触不恒定,接触电阻发生周期变化,令腐蚀和防腐蚀电流被调制,产生轴频电场[6]。船舶的轴频电场频率特征明显,可被探测距离长,且螺旋桨转动,轴频电场无法避免,使其已经成为船舶目标识别与定位的重要特征之一。
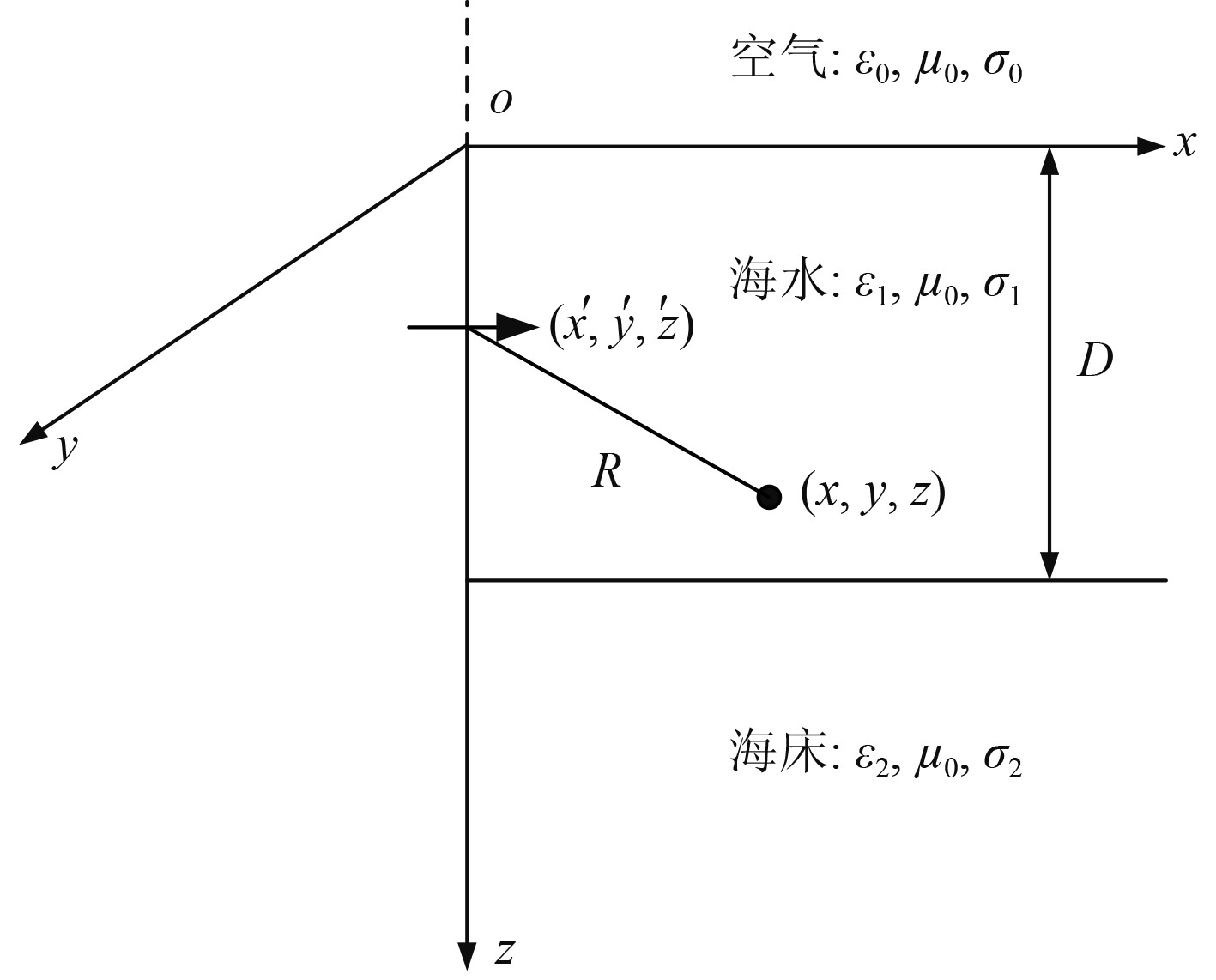
船舶的轴频电场一般基于水平时谐电偶极子来建模。文献[7~8]对海水中水平时谐偶极子产生的电场进行了理论求解与数值计算。假定海洋环境为空气—海水—海床三层、线性、均匀、各向同性的媒质模型。设
|
图 1 空气—海水—海床三层模型示意图 Fig. 1 Air-seawater-seabed three-layer model |
结合相应边界条件,通过求解电场微分方程,可以得到在空气—海水—海床3层模型下,电偶极子在海水中产生的水下电场的数学表达式为:
| $ \begin{split} {E_x} =& - i\omega \left\{ {\left. {M\frac{{{e^{ - i{k_1}R}}}}{R} + \int_0^\infty {({f_{1x}}{e^{ - {u_1}z}} + } {g_{1x}}{e^{{u_1}z}}){J_0}(\lambda r){\rm d}\lambda } \right\}} \right. + \frac{M}{{{\mu _0}{\sigma _1}}}\left\{ \frac{{3{{(x - {x^{'}})}^2}}}{{{R^5}}} + \frac{{3i{k_1}{{(x - {x^{'}})}^2}}}{{{R^4}}} - \frac{{1 + k_1^2{{(x - {x^{'}})}^2}}}{{{R^3}}} - \frac{{i{k_1}}}{{{R^2}}}\right\} {e^{ - i{k_1}R}} + \\ &\frac{1}{{{\mu _0}{\sigma _1}}}\left\{ {(\frac{{2{{(x - {x^{'}})}^2}}}{{{r^3}}} - \frac{1}{r})\int_0^\infty {({f_{1x}}{e^{ - {u_1}z}} + {g_{1x}}{e^{{u_1}z}}){J_1}} (\lambda r)\lambda {\rm d}\lambda } \right. - \left. {\frac{{(x - {x^{'}})}}{{{r^2}}}\int_0^\infty {({f_{1x}}{e^{ - {u_1}z}} + {g_{1x}}{e^{{u_1}z}}} ){\lambda ^2}{J_0}(\lambda r){\rm d}\lambda } \right\} + \\ &\frac{1}{{{\mu _0}{\sigma _1}}}\left\{ {(\frac{1}{r} - \frac{{2{{(x - {x^{'}})}^2}}}{{{r^3}}})\int_0^\infty {\left( { - {f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}}} \right){J_1}\left( {\lambda r} \right){u_1}{\rm d}\lambda } } \right. + \left. {\frac{{{{(x - x')}^2}}}{{{r^2}}}\int_0^\infty {\left( { - {f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}}} \right){J_0}\left( {\lambda r} \right)\lambda {u_1}{\rm d}\lambda } } \right\} 。\end{split} $ | (1) |
| $ \begin{split} {E_y} =& \frac{1}{{{\mu _0}{\sigma _1}}}\left[ {\frac{{2{{(x - {x^{'}})}^2}(y - {y^{'}})}}{{{r^3}}}\int_0^\infty {({f_{1x}}{e^{ - {\mu _1}z}} + {g_{1x}}{e^{{\mu _1}z}}){J_1}} (\lambda r)\lambda {\rm{d}}\lambda } \right. - \left. {\frac{{(x - {x^{'}})(y - {y^{'}})}}{{{r^3}}}\int_0^\infty {({f_{1x}}{e^{ - {u_1}z}} + {g_{1x}}{e^{{u_1}z}}){\lambda ^2}{J_0}} (\lambda r)\lambda {\rm{d}}\lambda } \right] + \\ &\frac{1}{{{\mu _0}{\sigma _1}}}\left\{ {\frac{{ - 2(x - {x^{'}})(y - {y^{'}})}}{{{r^3}}}\int_0^\infty {( - {f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}}){u_1}{J_1}} (\lambda r){\rm{d}}\lambda } \right. + \left. {\frac{{(x - {x^{'}})(y - {y^{'}})}}{{{r^2}}}\int_0^\infty {( - {f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}}){u_1}\lambda {J_0}} (\lambda r){\rm{d}}\lambda } \right\} + \\ & \frac{M}{{{\mu _0}{\sigma _1}}}\left\{ {\frac{{3(x - {x^{'}})(y - {y^{'}})}}{{{R^5}}} + \frac{{3i{k_1}(x - {x^{'}})(y - {y^{'}})}}{{{R^4}}} - \frac{{k_1^2(x - {x^{'}})(y - {y^{'}})}}{{{R^3}}}} \right\}{e^{ - i{k_1}R}} 。\end{split} $ | (2) |
| $ \begin{split} {E_z} =& - i\omega \frac{{(x - {x^{'}})}}{r}\int_0^\infty {\left( {{f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}}} \right){J_1}} (\lambda r){\rm{d}}\lambda + \frac{1}{{{\mu _0}{\sigma _1}}}\left\{ { - \frac{{(x -{x^{'}})}}{r}\int_0^\infty {( - {f_{1x}}{e^{ - {u_1}z}} + {g_{1x}}{e^{{u_1}z}}){u_1}\lambda {J_1}} (\lambda r){\rm{d}}\lambda } \right. + \\ & \left. {\frac{{(x - {x^{'}})}}{r}\int_0^\infty {({f_{1z}}{e^{ - {u_1}z}} + {g_{1z}}{e^{{u_1}z}})u_1^2{J_1}} (\lambda r){\rm{d}}\lambda } \right\} + \left. {\frac{M}{{{\mu _0}{\sigma _1}}}[\frac{{3(x - {x^{'}})(z - {z^{'}})}}{{{R^5}}} + \frac{{3i{k_1}(x - {x^{'}})(z - {z^{'}})}}{{{R^4}}} - \frac{{k_1^2(x - {x^{'}})(z - {z^{'}})}}{{{R^3}}}} \right]{e^{ - i{k_1}R}} 。\end{split} $ | (3) |
根据式(1)~式(3)可以建立起以电偶极子为等效源的船舶轴频电场理论模型。当
LabVIEW是一种图形化的编程语言,同标准的实验室仪器相比,LabVIEW要更加灵活且便于理解,搭配上计算机和嵌入式硬件共同组成一个可以完全配置的虚拟仪器(VI)。李斌等[9]利用VC和LabVIEW开发了模拟应答式水声定位系统测阵。郭燕子等[10]用虚拟仪器技术开发了长基线水声导航定位系统目标模拟器。利用虚拟仪器技术搭建半实物模型的方法已有研究,基于软件的控制方式使其能够根据需要来构造不同环境条件下的各类船舶的电场信号,而成本远低于利用实物模型进行测量的传统方法,并缩短了开发周期。
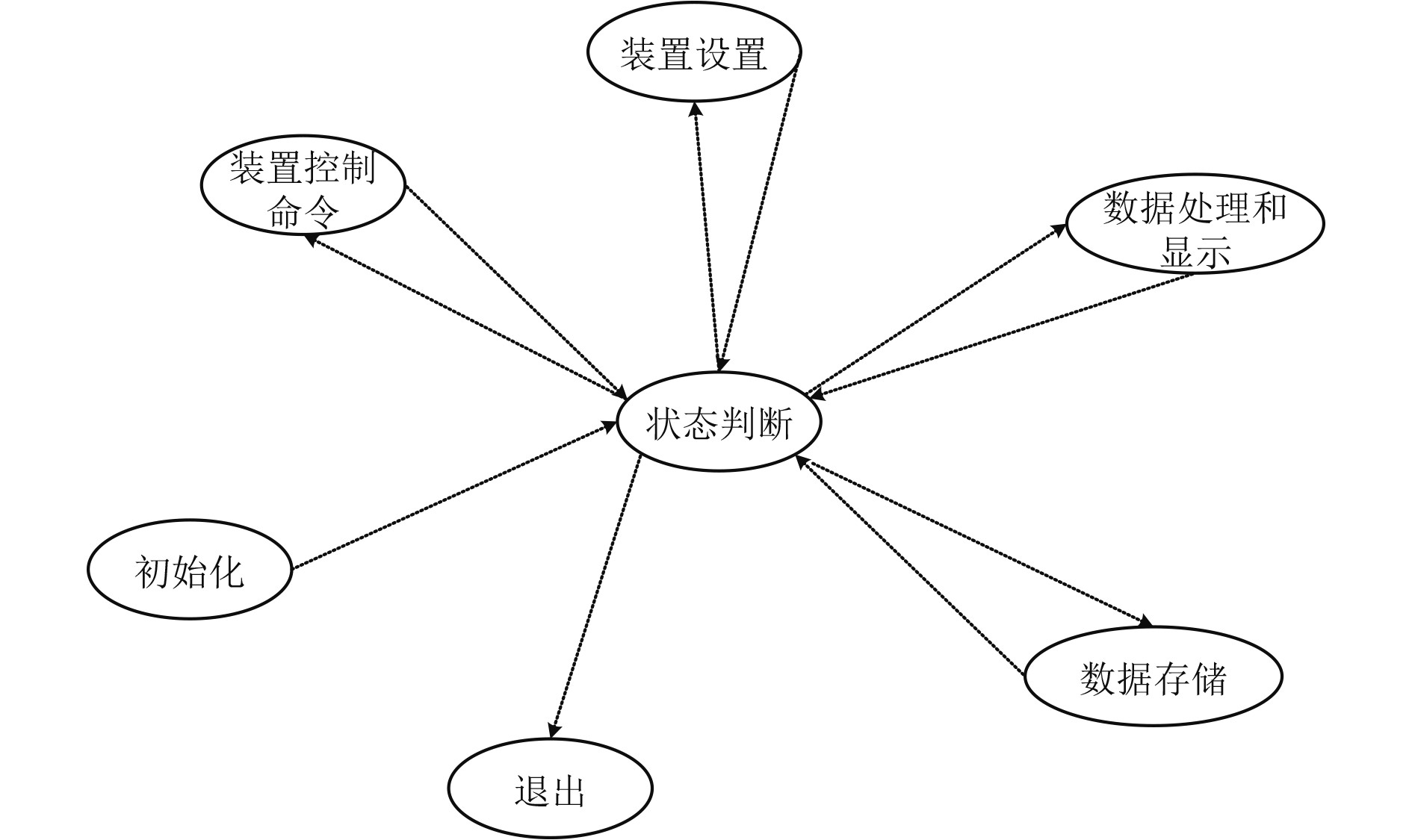
2.1 电场模拟装置的软件设计电场模拟装置测量与控制软件整体采用C/S架构,基于模块化编程思想和状态机结构,利用NI、LabVIEW和Fortran语言进行设计与开发。软件功能设计包括装置参数设置、装置控制、数据处理和显示、数据存储等功能。软件通过驱动可编程D/A转换卡实现将数学模型生成的电压数字信号转换为模拟信号输出;通过属性节点调用动态链接库(DLL)的方式实现LabVIEW和Fortran的混合编程和电场数学模型调用。动态链接库提供了一种方法,使得LabVIEW可以调用其他语言所编写的函数,扩展了其可应用范围,并提高了软件单元的复用度和开发效率。软件可以根据理论数学模型公式计算得到在某一空间区域的海水介质中,任意位置的点电流源或电偶极子产生的电场,进而得到观测点位置处三分量方向的电场信号函数。软件结构设计示意如图2所示。
|
图 2 电场模拟装置软件结构设计示意图 Fig. 2 Software structure of the electric field simulation device |
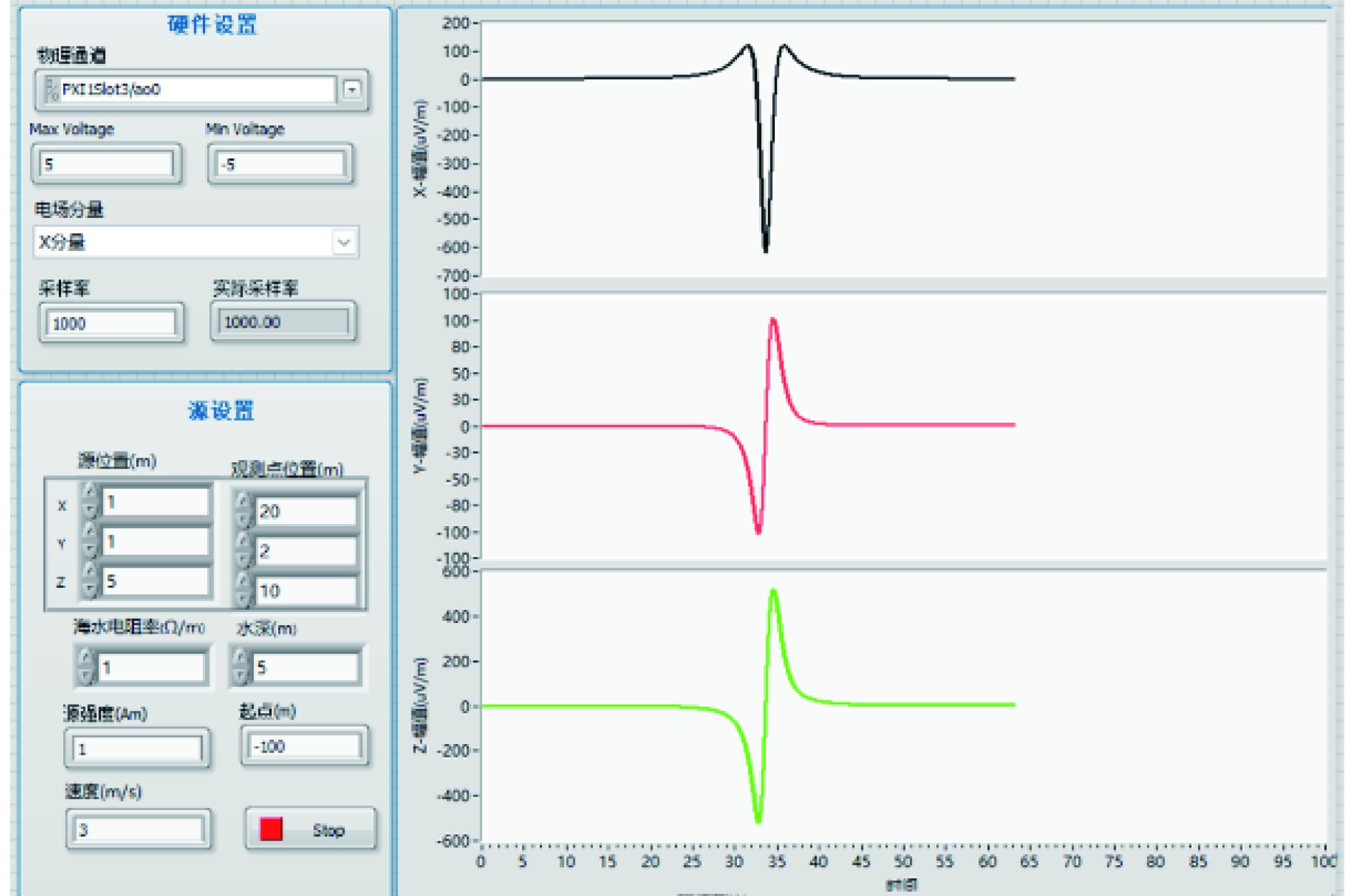
电场仿真模拟软件面板如图3所示,电场仿真软件主要包括3个部分,左侧上部分为硬件参数设置单元,主要用于D/A通道的选择、电场模拟分量的选择以及采样点数等。左侧下部分为电场数学仿真模型参数设置,主要包括模拟源位置设置、观测点位置设置、电导率设置、源速度设置、源强度设置以及放大量设置等。右侧图形部分为仿真的电场三分量时域曲线图,横坐标为时间,纵坐标为电场长度,用于显示仿真的电场三分量。电场建模计算模块用于目标静电场信号的仿真计算,利用LabVIEW内的调用库函数节点,对已经制作完成的等效源模型动态链接库文件进行直接调用,可根据输入的源强度、海洋环境等参数信息实现典型航速、潜深、环境下的静电场和轴频电场仿真计算。将生成的仿真数据通过DAQmx写入VI中,通过D/A卡输出模拟信号。
|
图 3 电场模拟装置软件面板 Fig. 3 Software panel for electric field simulator |
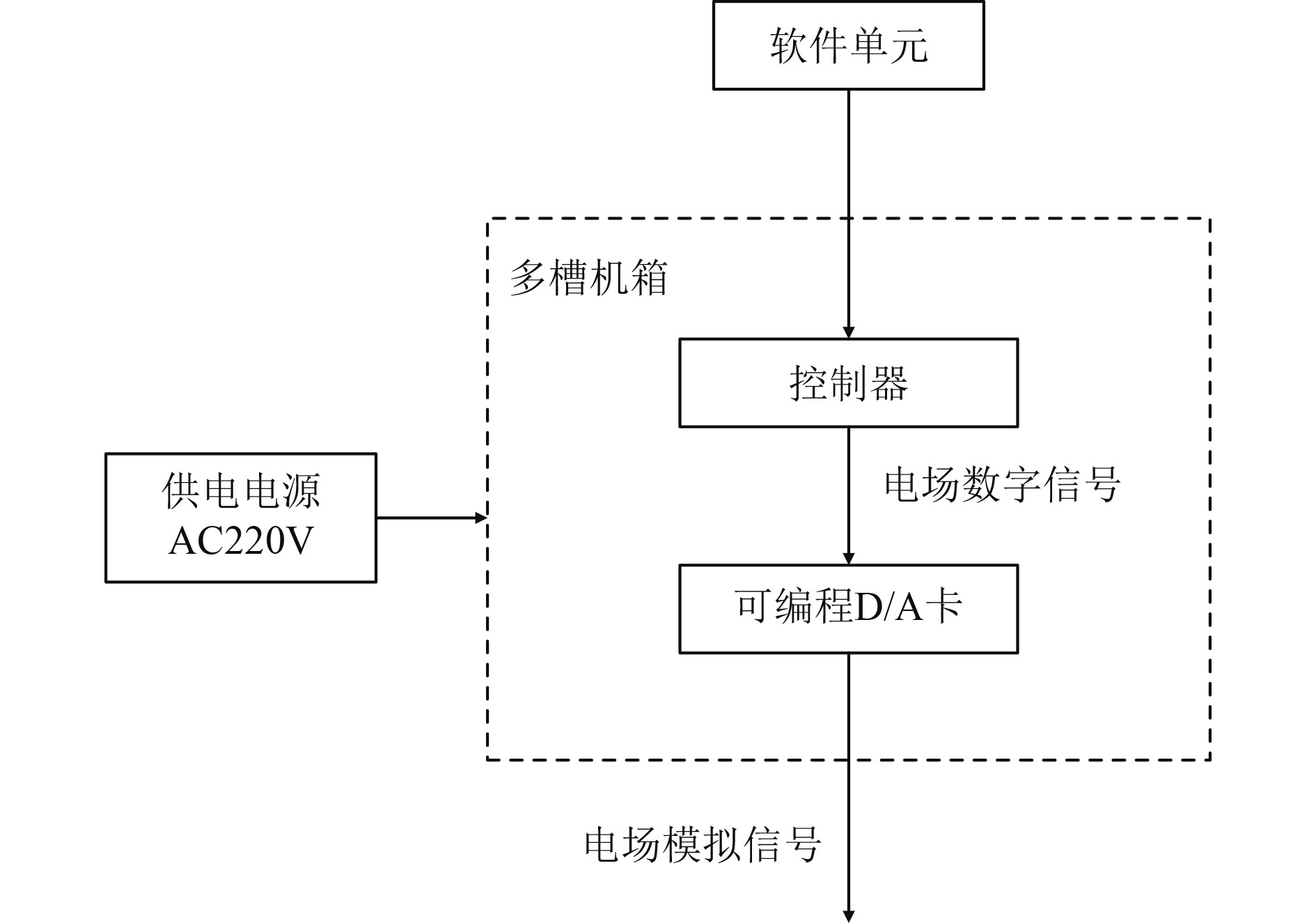
船舶电场仿真模拟装置所需的硬件包括控制计算机、可编程D/A转换卡、供电电源等。其组成结构如图4所示。
|
图 4 电场仿真模拟装置组成结构图 Fig. 4 Electric field simulation device composition structure diagram |
选用NI公司的4461D/A卡,D/A卡具有2个数模转换通道,遵循PXI总线接口,与控制计算机通过PXI总线进行数据交互,可以通过软件控制模拟电压信号输出,物理接口为BNC连接器、SMB母头。
同时,选用带有PXI插槽的控制计算机作为仿真软件运行的平台。控制计算机具有8个PXI插槽,最多可以扩展4-7块D/A转换卡,控制计算机与D/A卡通过PXI总线进行数据交互。
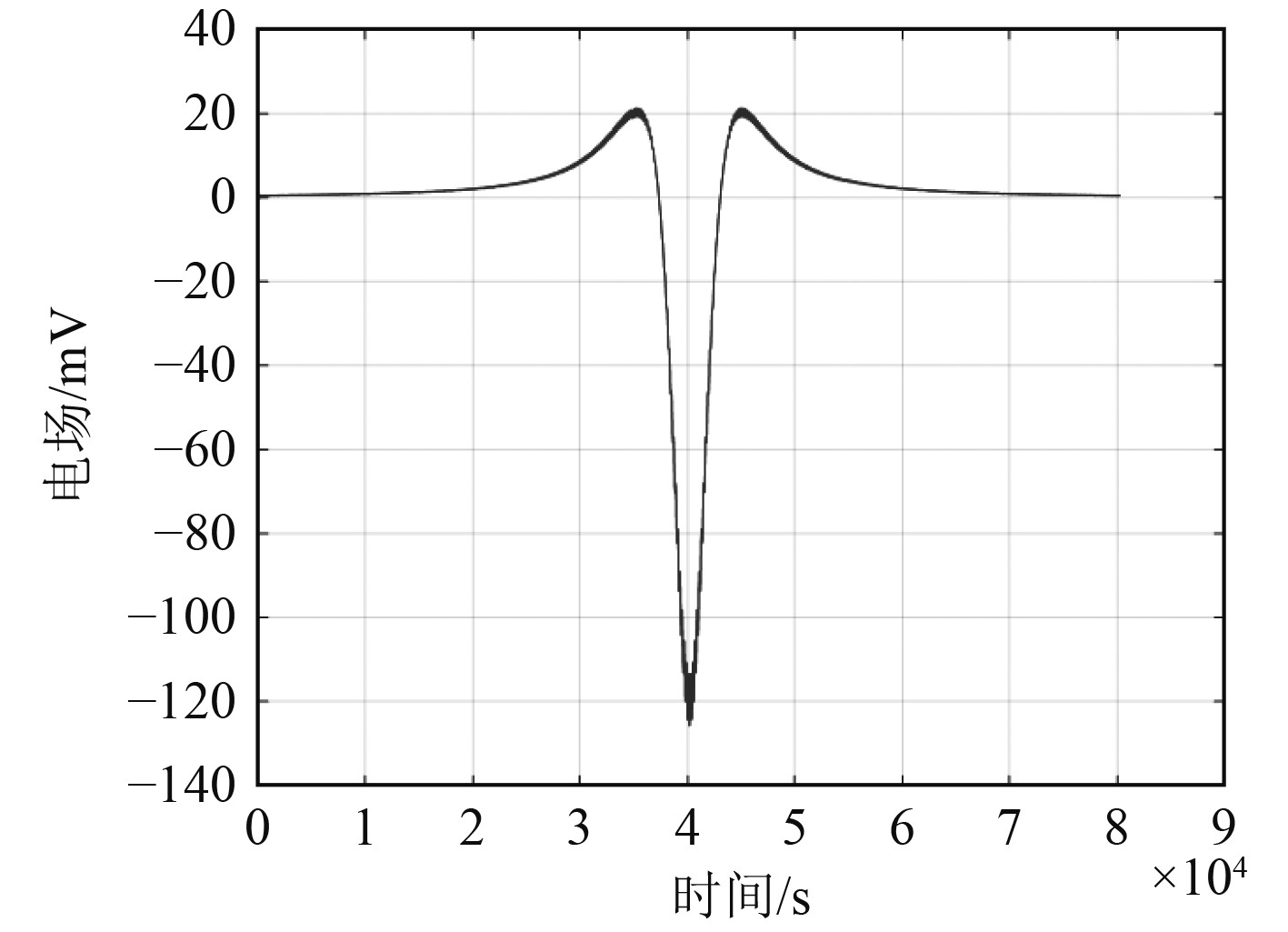
3 模拟实验及效果验证船舶电场模拟装置调试完成后,对模拟装置进行了实际测试。使用计算机控制4461D/A卡输出电场模拟信号,然后由多通道数据采集器进行信号采集,以此来验证电场模拟装置的可行性与一致性。图5为当采样率设置为1 kHz时,模拟静电场和5 Hz轴频电场信号叠加,并以
|
图 5 软件模拟输出的电场信号 Fig. 5 Electric field signals generated by software |
|
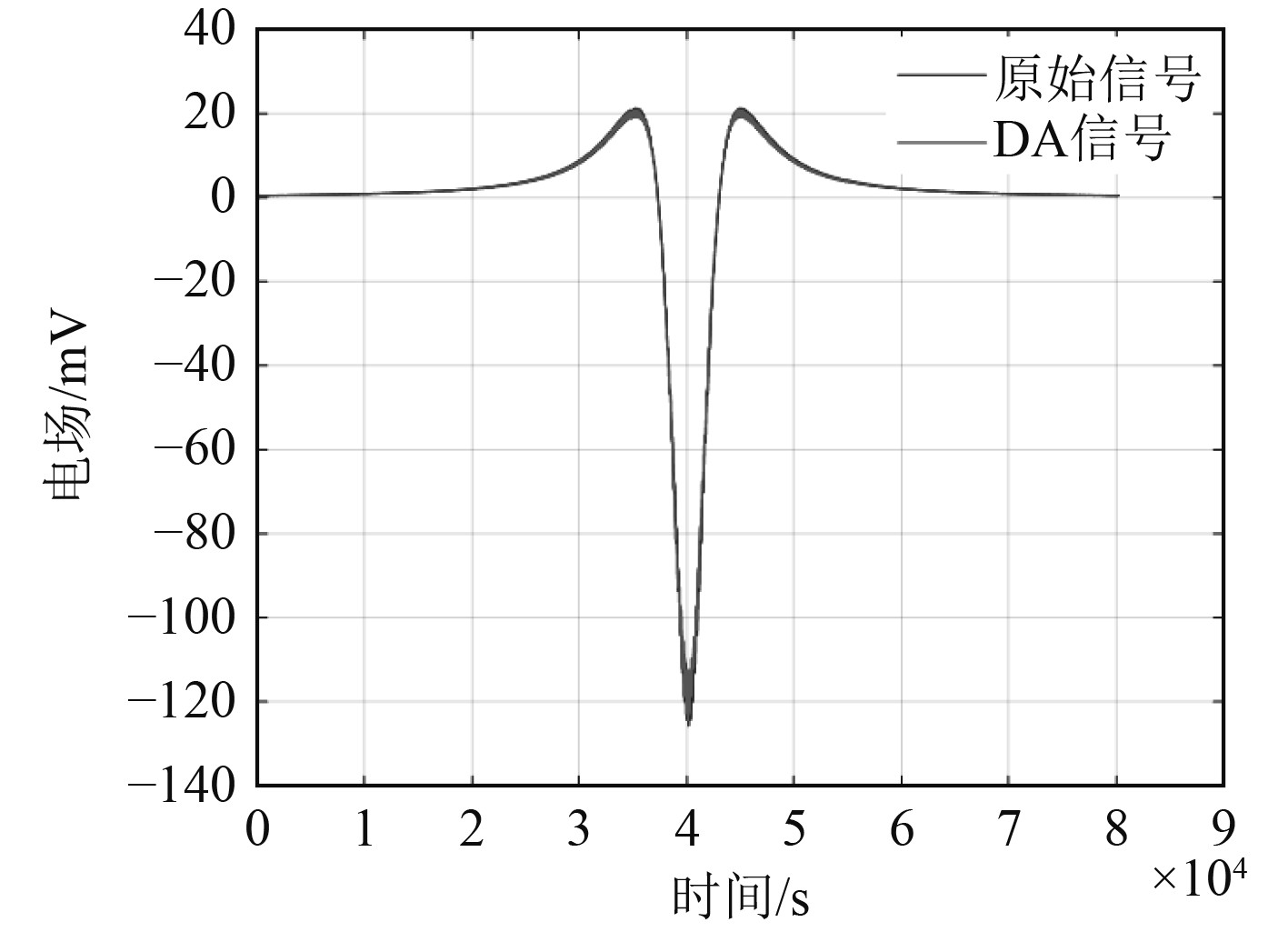
图 6 D/A输出电场时域信号与原始信号对比 Fig. 6 Comparison of electric field time-domain signal output by D/A signal and original signal |
|
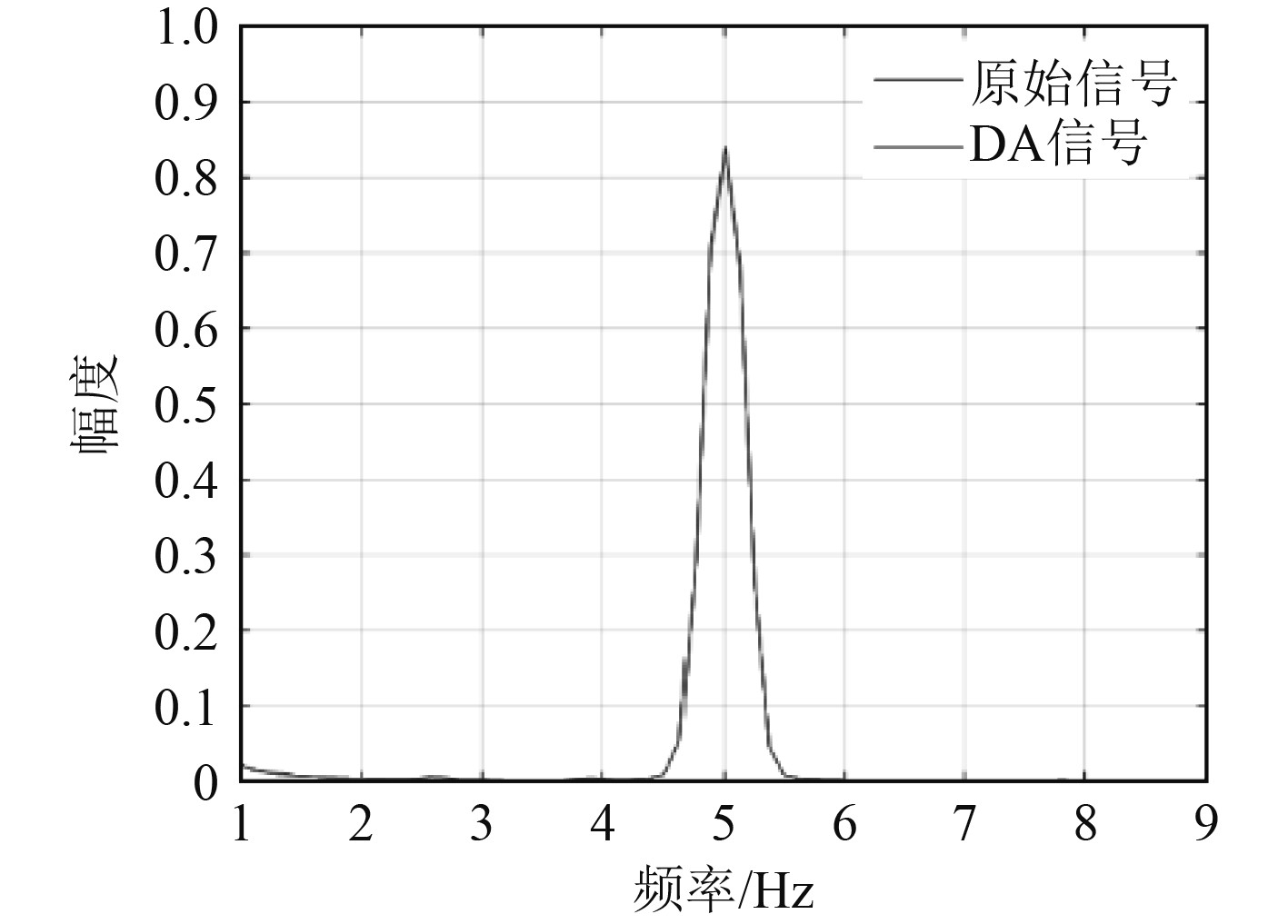
图 7 D/A输出电场频谱信号与原始信号对比 Fig. 7 Comparison of electric field spectrum signal output by D/A and original signal |
|
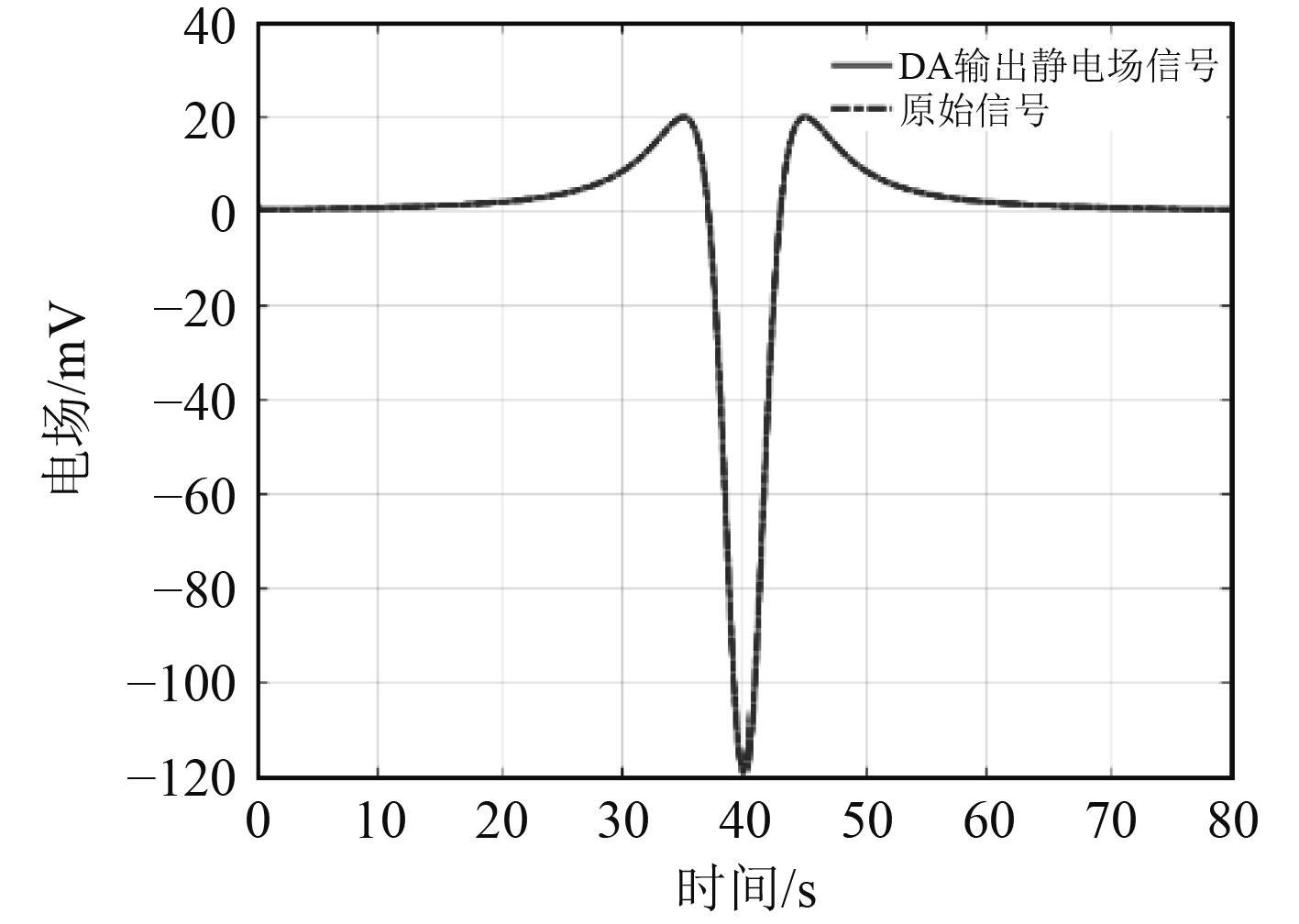
图 8 D/A输出静电场信号与原始信号对比 Fig. 8 Comparison of electrostatic field signal output by D/A and original signal |
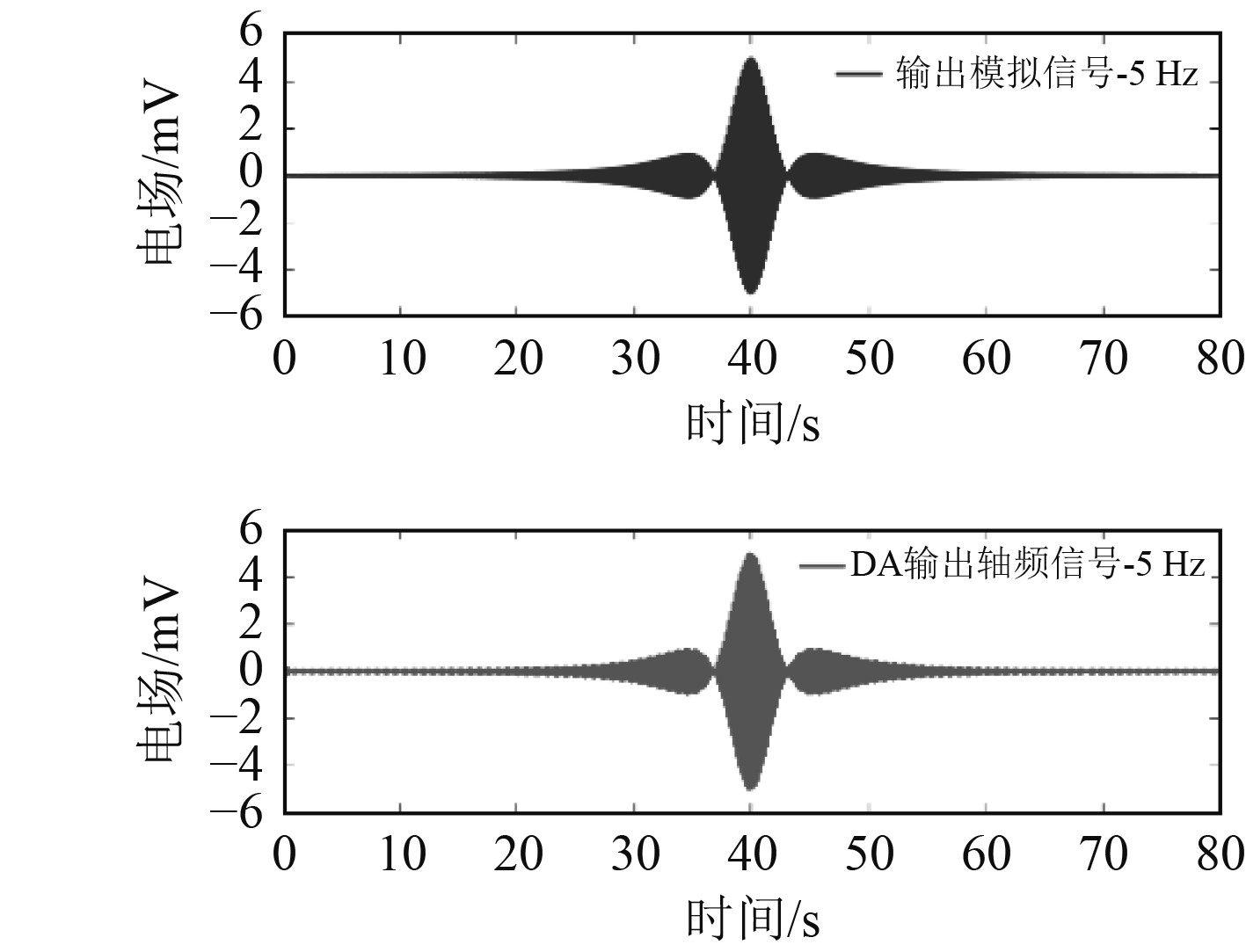
|
图 9 D/A输出轴频电场信号与原始信号对比 Fig. 9 Comparison of axial frequency electric field signal output by D/A and original signal |
本文介绍了一种水中船舶静电场和轴频电场模拟系统的设计以及实现。使用LabVIEW和Fortran语言开发出船舶电场等效源模型,并通过动态链接库实现模型生成,通过D/A卡实现信号输出。由实验结果证明,船舶电场模拟仿真装置在实验室内成功仿真模拟出电场信号,可以保障船舶电场的半实物测试,验证了系统的可行性和良好精度。下一步的研究方向是利用该系统进行复杂模型载入和宽频信号的模拟生成,使得仿真模拟的准确度更高,可行性更加广泛。
| [1] |
卢新城, 王婷, 陈新刚, 等. 海船轴频电场建模方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2012, 36(1): 168-170. LU Xincheng, WANG Ting, CHEN Xingang, et al. Research on the modeling method of a sea going vessel’s shaft-rate electric fields[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2012, 36(1): 168-170. |
| [2] |
余定峰, 耿攀, 杨勇, 等. 基于时谐偶极子模型的船舶轴频电场特性分析[J]. 船电技术, 2014, 34(10): 11-14. YU Dingfeng, GENG Pan, YANG Yong, et al. Analysis on shaft-rate electric field of a shipbased on time harmonic dipole[J]. Marine Electric & Electronic Engineering, 2014, 34(10): 11-14. DOI:10.13632/j.meee.2014.10.003 |
| [3] |
岳瑞永, 田作喜, 吕俊军, 等. 基于时谐电偶极子模型的舰船轴频电场衰减规律研究[J]. 舰船科学技术, 2009, 31(10): 21-25. YUE Ruiyong, TIAN Zuoxi, LV Junjun, et al. Study on attenuation law of the vessel’s shaft rate electric field based on the time-harmonic electric dipole model[J]. Ship Science and Technology, 2009, 31(10): 21-25. |
| [4] |
熊露, 姜润翔, 龚沈光. 浅海中船舶轴频电场建模方法[J]. 国防科技大学学报, 2014, 36(1): 98-103. XIONG Lu, JIANG Run-xiang, GONG Shen-guang. Ship modeling method of shaft-ELFE in shallow sea[J]. Journal of National University of Defense Technology, 2014, 36(1): 98-103. |
| [5] |
潘龙, 胡佳飞, 谢瑞芳, 等. 基于有限元的船舶轴频电场模拟源模型仿真[J]. 船舶科学技术, 2016, 38(3): 102-106. PAN Long, HU Jiafei, XIE Ruifang, et al. Simulation of marine shaft-rate frequency electric field of simulationsource model based on finite element method[J]. Ship Science and Technology, 2016, 38(3): 102-106. |
| [6] |
林春生, 龚沈光. 船舶物理场[M]. 北京: 兵器工业出版社, 2007.
|
| [7] |
卢新城, 龚沈光, 周骏, 等. 海水中极低频水平电偶极子电磁场的解析解[J]. 电波科学学报, 2004(3): 290-295. LU Xincheng, GONG Shenguang, ZHOU Jun, et al. Analytical expressions of the electromagnetic fields producedby a ELF time-harmonic HED embedded in the sea[J]. Chinese Journal of Radio Science, 2004(3): 290-295. DOI:10.13443/j.cjors.2004.03.008 |
| [8] |
毛伟, 林春生. 两层介质中运动水平时谐偶极子产生的电磁场[J]. 兵工学报, 2009, 30(5): 555-560. MAO Wei, LIN Chunsheng. The EM fields produced by amoving horizontally-directed time-harmonic dipole intwo-layer media[J]. Acta Armamentarii, 2009, 30(5): 555-560. |
| [9] |
李斌, 赵珩. 基于LabVIEW的应答式水声定位系统目标模拟器[J]. 船舶电子工程, 2012, 32(10): 90-91+112. LI Bin, ZHAO Heng. Target simulator of response type underwater acoustic positioning system based on LabVIEW[J]. Ship Electronic Engineering, 2012, 32(10): 90-91+112. |
| [10] |
郭燕子, 李国良, 刘明波. 基于虚拟仪器技术的长基线系统目标模拟器[J]. 船舶电子工程, 2018, 38(6): 66-69. GUO Yanzi, LI Guoliang, LIU Mingbo. Long baseline system target simulator based on virtualinstrument technology[J]. Ship Electronic Engineering, 2018, 38(6): 66-69. |
 2024, Vol. 46
2024, Vol. 46

