当前,应用于AUV上常见的导航定位装备主要包括惯性导航系统(INS)、多普勒计程仪(DVL)以及水声定位系统[1]。其中INS基于惯性原理工作,不受外界环境影响,能够自主解算出载体的姿态、速度、位置参数,但在水下长时间导航过程中,误差不断累积,单独使用效果不佳,一般用组合导航方法对其进行校正[2]。DVL能够测量AUV对底、对流速度,可修正INS速度信息,但其对位置精度提升具有局限性,无法实现精准定位[3]。水声定位系统一般分为超短基线(USBL)、短基线(SBL)、长基线(LBL),通过测量应答器与声基阵之间的水声信号传播时间或相位差来求解载体位置信息[4-5],其中LBL作用范围广、定位精度高,通过LBL对INS进行校正,可以获得高精度水下导航定位信息。
在AUV采用INS/LBL组合导航系统进行水下导航定位的过程中,受到水下复杂环境影响,仍难以保证定位精度。一方面是由于水声信号传播过程收到干扰而导致系统组合导航模型不够精准;另一方面是传统组合导航采用卡尔曼滤波方法进行数据融合,而常规卡尔曼滤波需要建立精确的系统先验模型,且无法抑制非高斯噪声,这在实际工程应用中难以实现[6]。在水下复杂背景下的组合导航方法上,高胜峰[7]采用序贯滤波方法引入组合导航模型,在长基线信号部分缺失的情况下保证定位精度;董萍等[8]提出一种基于相对信息观测量的INS/USBL非线性组合导航方法,能够解决非线性系统中噪声统计特性未知的问题;杨建[9]提出用滚动时域估计算法解决水声通信延时、丢包问题。
针对水下实际应用中,水声信号传播误差及复杂噪声干扰导致的定位精度受限、定位鲁棒性差的问题,本文设计了一种基于最大熵卡尔曼滤波的水下INS-LBL组合导航方法,通过引入时延误差建立系统状态方程及量测方程,同时采用最大熵卡尔曼滤波进行数据融合,最后通过仿真验证算法有效性。
1 INS/LBL组合导航系统模型 1.1 系统原理LBL定位系统一般由固定在海底的声基阵与安装在AUV上的换能器组成,海底声基阵由数量不小于3个的应答器组成,其距离可达100~
本文设计的水下导航定位系统,利用INS与LBL对同一状态的输出作为量测值,通过最大熵卡尔曼滤波对2个系统的导航信息进行数据融合。传统INS-LBL组合导航系统一般直接用LBL水声定位获得的位置坐标对INS导航信息进行修正。但在实际任务中,由于水声信号在传输过程中产生时延,导致AUV在运动过程中接收声学信号时出现位置偏移,即实际量测的应答器与AUV的距离并非真实距离,因此引入伪距来建立组合导航模型。
1.2 组合导航模型组合导航系统状态方程由分系统INS、LBL两部分组成。对于INS系统,选取姿态角误差
| $ {\dot X_{SINS}} = {F_{SINS}}{X_{SINS}} + {w_{SINS}},$ | (1) |
对于LBL系统,已知海底应答器F1、F2、F3、F4位置坐标为
| $ {\rho_{_{Fi}}} = c \cdot {t_{Fi}} 。$ | (2) |
由于海底应答器与AUV存在系统时间的钟差,而钟差是影响伪距的重要因素,因此选取钟差等效距离
建立LBL的状态方程:
| $ {\dot X_{LBL}} = {F_{LBL}}{X_{LBL}} + {w_{LBL}} = \delta {t_u} + {w_{tu}}。$ | (3) |
INS-LBL系统的状态方程为:
| $ \left[ {\begin{array}{*{20}{c}} {{{\dot X}_{SINS}}} \\ {{{\dot X}_{LBL}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{F_{SINS}}}&0 \\ 0&{{F_{LBL}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{X_{SINS}}} \\ {{X_{LBL}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{w_{SINS}}} \\ {{w_{LBL}}} \end{array}} \right]。$ | (4) |
在此基础上,建立系统量测方程。AUV在水下由INS实时提供位置坐标
| $ \begin{gathered} \rho _{SINS}^{Fi} = \sqrt {{{(x - {x_{Fi}})}^2} + {{(y - {y_{Fi}})}^2} + {{(z - {z_{Fi}})}^2}} \\ (i = 1,2,3,4)。\\ \end{gathered} $ | (5) |
但由于水声时延存在,AUV接收到应答器信号的位置并不一致,因此式(5)需将AUV的位移
| $ \rho _{SINS}^{Fi} = \sqrt {{{(x - \vartriangle x - {x_{Fi}})}^2} + {{(y - \vartriangle y - {y_{Fi}})}^2} + {{(z - \vartriangle z - {z_{Fi}})}^2}}。$ | (6) |
其在AUV坐标真值
| $ \begin{aligned}[b] \rho _{SINS}^{Fi} = &{r_i} + \frac{{{x_t} - \vartriangle x - {x_{Fi}}}}{{{r_i}}}\delta {x_t} + \\ &\frac{{{y_t} - \vartriangle y - {y_{Fi}}}}{{{r_i}}}\delta {y_t} + \frac{{{z_t} - \vartriangle z - {z_{Fi}}}}{{{r_i}}}\delta {z_t} \end{aligned}。$ | (7) |
式中:
| $ {\rho '_{Fi}} = {r_i} - \delta {t_u} - {v_i}。$ | (8) |
式中:
INS-LBL系统的量测量构建为:
| $ \begin{gathered} \left[ {\begin{array}{*{20}{c}} \displaystyle {\frac{{{x_t} - \vartriangle x - {x_{F1}}}}{{{r_1}}}}&\displaystyle{\frac{{{y_t} - \vartriangle y - {y_{F1}}}}{{{r_1}}}}&\displaystyle{\frac{{{z_t} - \vartriangle z - {z_{F1}}}}{{{r_1}}}}&1 \\ \displaystyle{\frac{{{x_t} - \vartriangle x - {x_{F2}}}}{{{r_2}}}}&\displaystyle{\frac{{{y_t} - \vartriangle y - {y_{F2}}}}{{{r_2}}}}&\displaystyle{\frac{{{z_t} - \vartriangle z - {z_{F2}}}}{{{r_2}}}}&1 \\ \displaystyle{\frac{{{x_t} - \vartriangle x - {x_{F3}}}}{{{r_3}}}}&\displaystyle{\frac{{{y_t} - \vartriangle y - {y_{F3}}}}{{{r_3}}}}&\displaystyle{\frac{{{z_t} - \vartriangle z - {z_{F3}}}}{{{r_3}}}}&1 \\ \displaystyle{\frac{{{x_t} - \vartriangle x - {x_{F4}}}}{{{r_4}}}}&\displaystyle{\frac{{{y_t} - \vartriangle y - {y_{F4}}}}{{{r_4}}}}&\displaystyle{\frac{{{z_t} - \vartriangle z - {z_{F4}}}}{{{r_4}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\delta x} \\ {\delta y} \\ {\delta z} \\ {\delta {t_u}} \end{array}} \right] \\ \end{gathered}。$ | (9) |
式中,
| $ Z = H\left[ {\begin{array}{*{20}{c}} {{X_{SINS}}} \\ {{X_{LBL}}} \end{array}} \right] + v 。$ | (10) |
本文利用最大熵卡尔曼滤波算法,针对非高斯噪声背景下的组合导航系统建立滤波模型。
其算法流程如下:
步骤1 设置滤波器状态量初始估计
步骤2 对状态量及噪声协方差阵进行更新:
| $ \begin{aligned}[b] &{{\hat X}_{k/k - 1}} = {F_{k,k - 1}}{{\hat X}_{k - 1}} ,\\ &{\boldsymbol{P}_{k/k - 1}} = {F_{k,k - 1}}{P_{k - 1}}F_{_{k,k - 1}}^{\text{T}} + {Q_{k - 1}}。\end{aligned} $ | (11) |
同时,对系统噪声协方差阵
| $ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{P}_{k/k - 1}}}{} \\ {}& {{\boldsymbol{R}_k}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {B_{k/k - 1}^p{{(B_{k/k - 1}^p)}^{{\mathrm{T}}} }}{} \\ {}& {B_k^r{{(B_k^r)}^{{\mathrm{T}}} }} \end{array}} \right] = {B_k}{B_k}^{\text{T}} 。$ | (12) |
步骤3 根据时间更新结果,计算
| $ \begin{split} & {D_k} = {B_k}^{ - 1}\left[ {\begin{array}{*{20}{c}} {{{\hat X}_{k/k - 1}}} \\ {{Z_k}} \end{array}} \right],{W_k} = {B_k}^{ - 1}\left[ {\begin{array}{*{20}{c}} I \\ {{H_k}} \end{array}} \right],\\ & {e_k} = {D_k} - {W_k}{X_k} ,\\ & {P_{k/k - 1}} = B_{k/k - 1}^p{[{\rm diag}({G_\sigma }({e_{1,k}}), \cdots ,{G_\sigma }({e_{n,k}}))]^{ - 1}}{(B_{k/k - 1}^p)^{\text{T}}},\\ & {R_k} = B_k^r{[{\rm diag}({G_\sigma }({e_{n + 1,k}}), \cdots ,{G_\sigma }({e_{n + m,k}}))]^{ - 1}}{(B_k^r)^{\text{T}}},\\ & {K_k} = {P_{k/k - 1}}H_k^{\text{T}}{({H_k}{P_{k/k - 1}}H_k^{\text{T}} + {R_k})^{ - 1}},\\ & {{\hat X}_k} = {{\hat X}_{k/k - 1}} + {K_k}({Z_k} - {H_k}{{\hat X}_{k/k - 1}})。\\[-1pt] \end{split} $ | (13) |
式中:n=16为16维状态量;m=4为4维量测量。
步骤4 若当前步骤估计
| $ {P_k} = (I - {K_k}{H_k}){P_{k/k - 1}}。$ | (14) |
否则返回步骤3重复迭代。
可以看出,当系统受到噪声干扰时,通过引入残差
LBL系统布设在海底的应答器坐标为
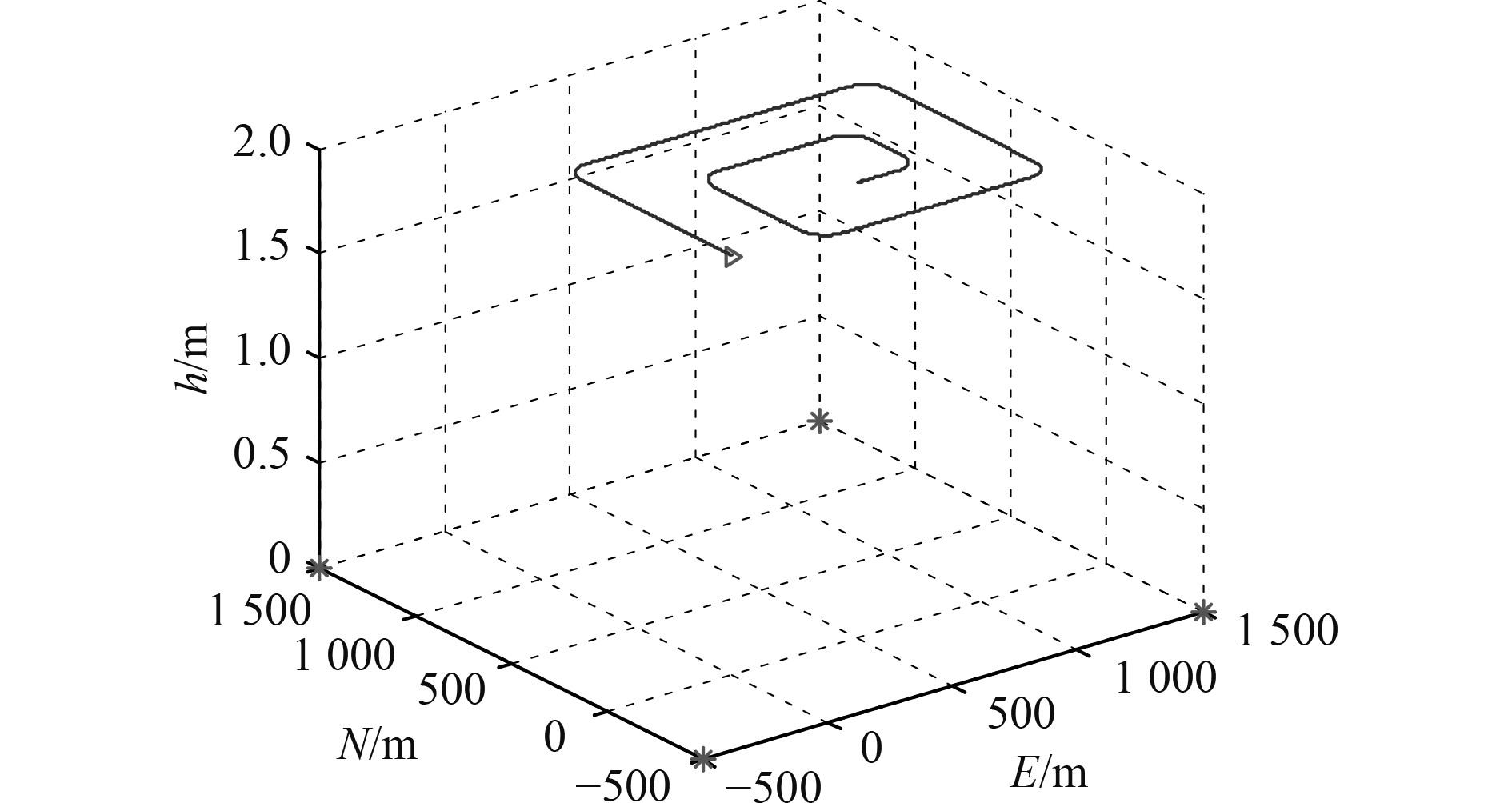
|
图 1 AUV三维轨迹图 Fig. 1 AUV three-dimensional trajectory |

|
图 2 AUV二维轨迹图 Fig. 2 AUV two-dimensional trajectory |
为验证算法有效性,模拟水下噪声干扰情况,在LBL系统给出的三维位置量测量中加入混合高斯噪声,表示为:
| $ v{\text ~}90\text% N(0,R) + 10\text% N(0,4R)。$ | (15) |
图3~图6分别为同一仿真条件下使用常规卡尔曼与使用最大熵卡尔曼滤波的北向、东向速度误差对比与北向、东向位置误差对比,可以看出,基于最大熵卡尔曼滤波的速度、位置误差曲线波动幅度较小,使用卡尔曼滤波的北向位置最大误差达到21.54 m,东向位置最大误差达到25.27 m,而使用最大熵卡尔曼滤波的北向位置最大误差达到7.19 m,东向位置最大误差达到6.67 m。从表1可更直观看出,基于最大熵卡尔曼滤波的INS-LBL组合导航系统输出的速度、位置误差更低,在非高斯噪声干扰下,其定位精度明显提升,鲁棒性更强。
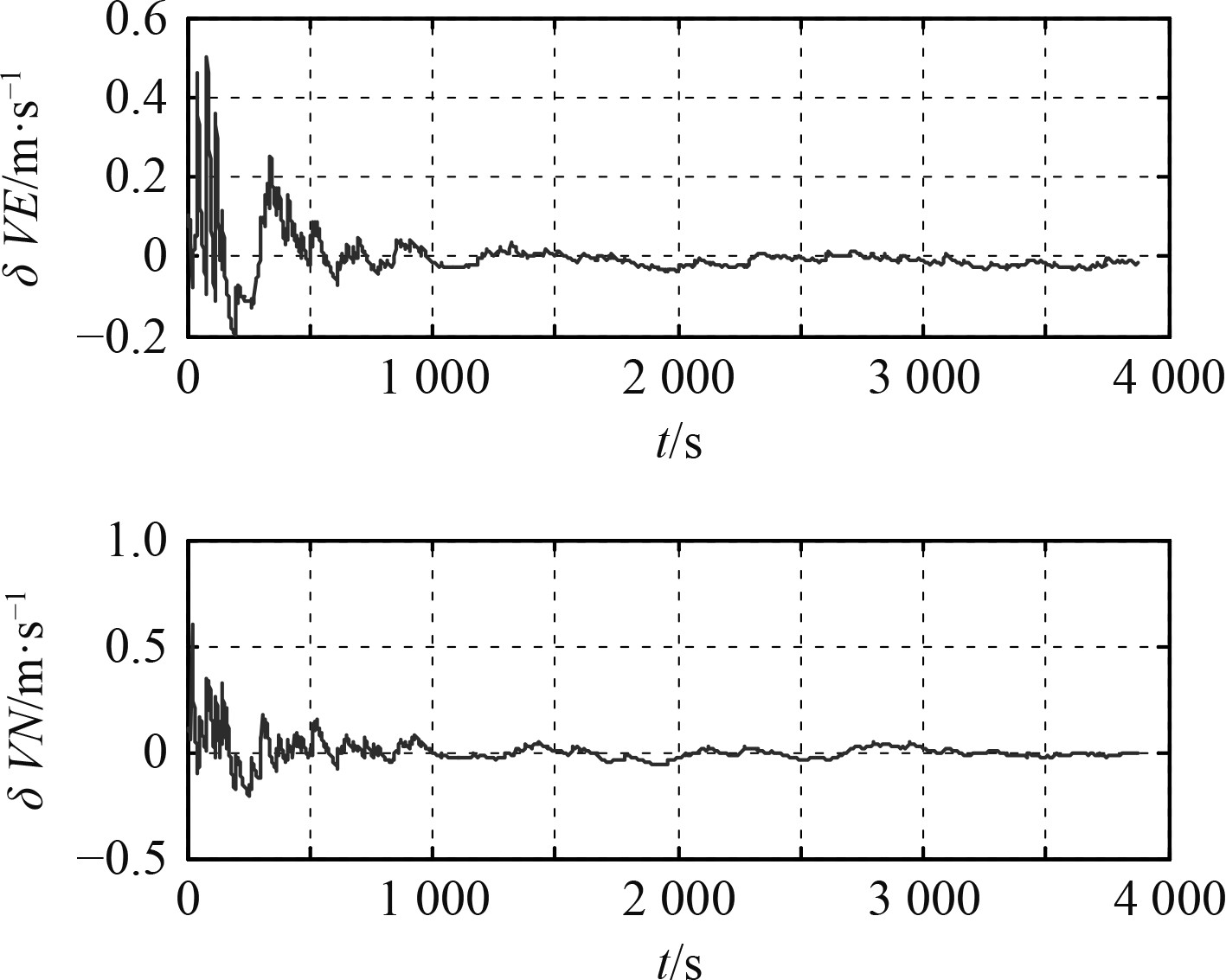
|
图 3 卡尔曼滤波速度误差图 Fig. 3 Kalman filter velocity error diagram |
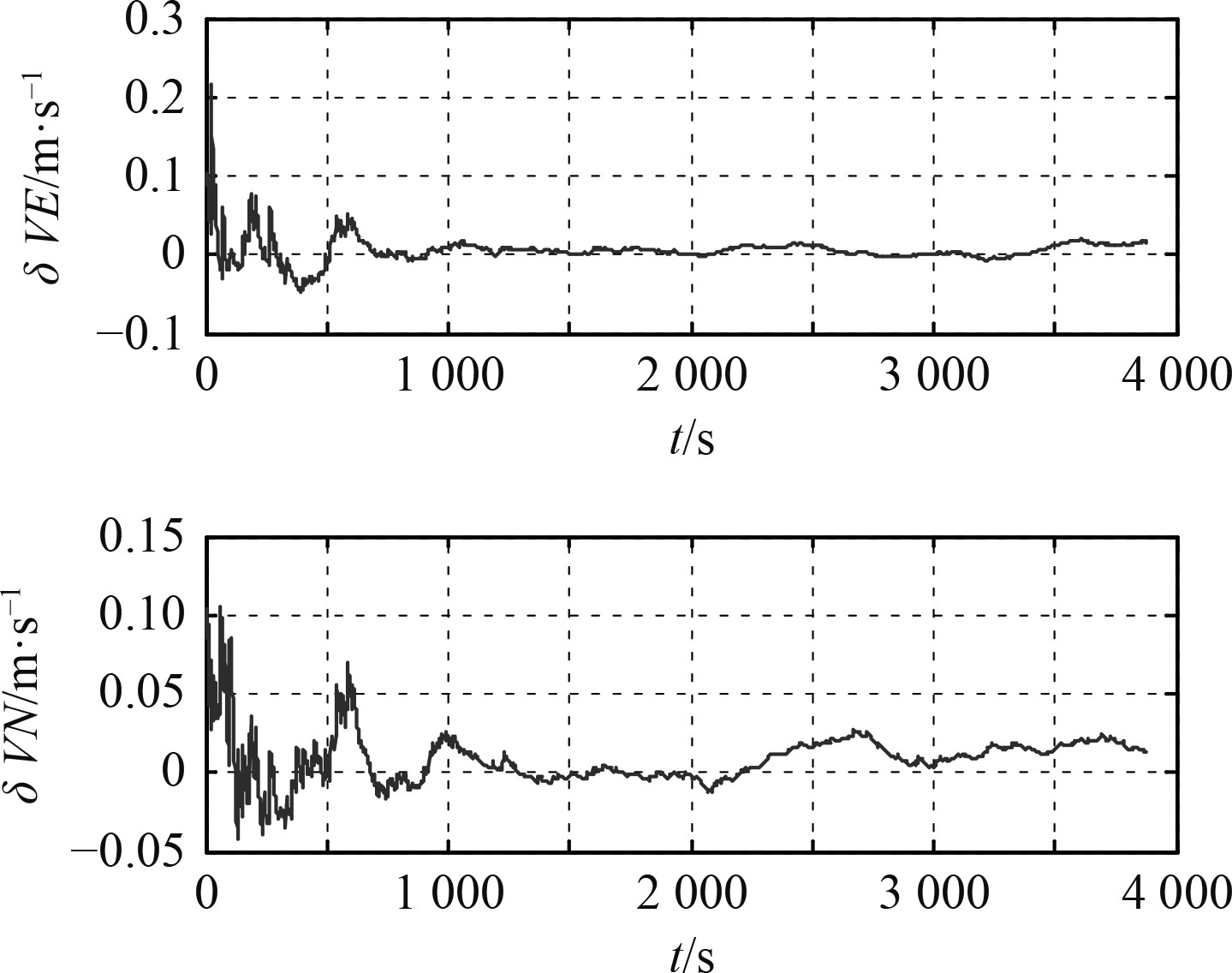
|
图 4 最大熵滤波速度误差图 Fig. 4 Maximum correntropy Kalman filter velocity error diagram |

|
图 5 卡尔曼滤波位置误差图 Fig. 5 Kalman filter position error diagram |
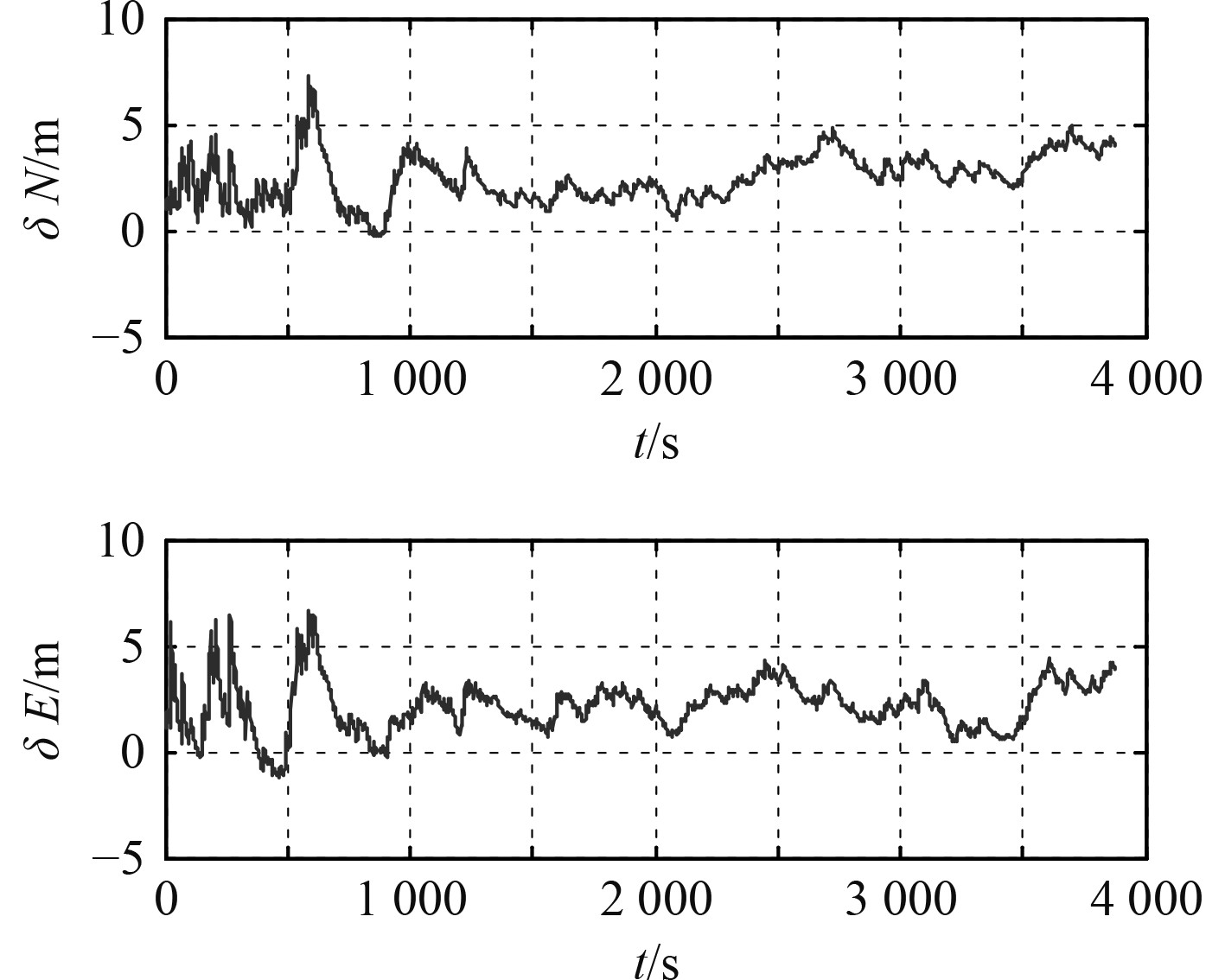
|
图 6 最大熵滤波位置误差图 Fig. 6 Maximum correntropy Kalman filter position error diagram |
|
|
表 1 仿真速度、位置误差均值对比 Tab.1 Comparison of mean velocity and position errors |
本文提出一种非高斯噪声背景的水下INS-LBL组合导航方法,考虑到水声通信时延较大,引入伪距建立组合导航系统的状态方程及量测方程,在此基础上,通过以最大熵为准则的卡尔曼滤波对系统进行数据融合,解决了水下非高斯噪声干扰下,传统方法定位精度下降的问题。仿真结果表明,在受到水下复杂噪声干扰的情况下,本文设计的非高斯噪声背景的水下INS-LBL组合导航方法具有更高的定位精度,能够抑制噪声干扰,满足AUV水下高精度自主定位需求。
| [1] |
黄玉龙, 张勇刚, 赵玉新. 自主水下航行器导航方法综述[J]. 鱼雷技术, 2019, 27(3): 232-253. |
| [2] |
尹伟伟, 郭士荦, YIN, 等. 非卫星水下导航定位技术综述[J]. 舰船电子工程, 2017, 37(3): 8-11. |
| [3] |
赵俊波, 葛锡云, 冯雪磊, 等. 水下SINS/DVL组合导航技术综述[J]. 水下无人系统学报, 2018, 26(1): 2-9. |
| [4] |
张红梅, 赵建虎, 杨鲲, 等. 水下导航定技术[M]. 武汉: 武汉大学出版社, 2010.
|
| [5] |
MORGADO M , BATISTA P , OLIVEIRA P , et al. Position USBL/DVL sensor-based navigation filter in the presence of unknown ocean currents[J]. Automatica, 2011, 47(12): 2604−2614.
|
| [6] |
KANG K , MAROULAS V , SCHIZAS I D . Drift homotopy particle filter for non-Gaussian multi-target tracking[C]//17th International Conference on Information Fusion (FUSION). IEEE, 2014.
|
| [7] |
高胜峰, 陈建华, 朱海. SINS/LBL组合导航序贯滤波方法[J]. 仪器仪表学报, 2017, 38(5): 1071-1078. |
| [8] |
董萍, 程建华, 刘利强, 等. 基于相对信息观测量的INS/USBL非线性组合导航方法 J]. 系统工程与电子技术, 2019, 41(2): 402−408. |
| [9] |
杨建. 滚动时域估计及其在多UUV 协同定位中的应用[D]. 哈尔滨:哈尔滨工程大学, 2015.
|
 2024, Vol. 46
2024, Vol. 46
