0 引　言

由于5G技术的持续发展，无线通信装置总量正以指数形式攀升。基于此情况，无线频谱资源在世界范围内的业内需求量不断提高。为了使有限的频谱资源得到充分利用，通信系统在未来将会与其它电子装置在同一波段共存^[1]，而雷达波段则是公认的最好选择。

雷达技术最早可以追溯到二战时期，随着技术的不断发展和社会需求的增加，雷达系统在军事、民用和科研领域均得到了广泛应用，如军事目标探测、航空导航、地图测绘、大气科学研究等方向。雷达系统应用10 GHz频段以下各波段的特点和优势，包括L频段（1～2 GHz）、S频段（2～4 GHz）和C频段（4～8 GHz）等，以适应不同的军事和民用的应用需求。但在将来，这些波段将会有更多的技术容纳于其中，例如：5 G无线网络和Wi-Fi技术。在较高的波段，5 G毫米波通信波段与机载毫米波雷达的工作频率非常相近。无线技术不断发展，对雷达波段的干扰会越来越严重。

位于毫米波波段的雷达系统与通信系统具有相似的射频前端硬件模块组成、同频段信道传输特性以及高速数据传输和处理等技术。在民用领域，在5 G的发展过程中，有相当数量的新5 G应用，如智能交通系统、智能家居、智能安防等方面。在军事领域，雷达感知、数据通信等无线电通信技术在很长一段时间内都表现出相互割裂的状况，造成了大量的频谱和硬件资源浪费，导致作战平台的性能下降。为了有效地利用频谱资源，满足各种不同的民用和军事应用场合，实现雷达和通信的频谱共享已成为未来的一个重要研究领域。

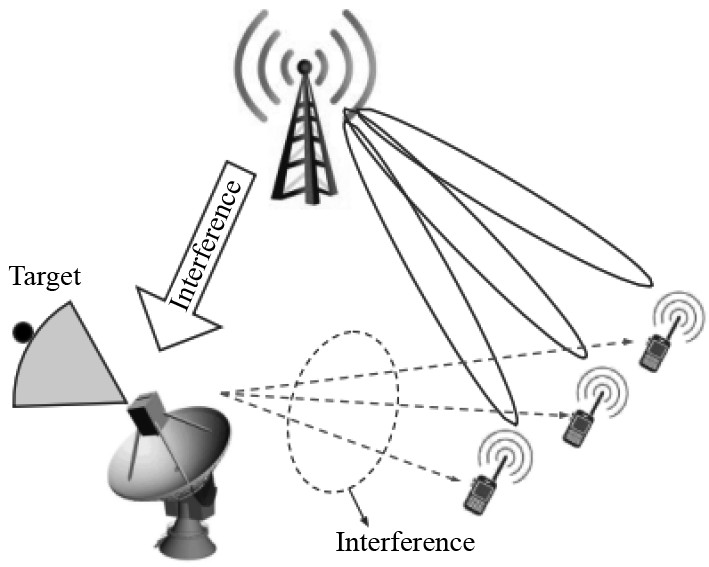
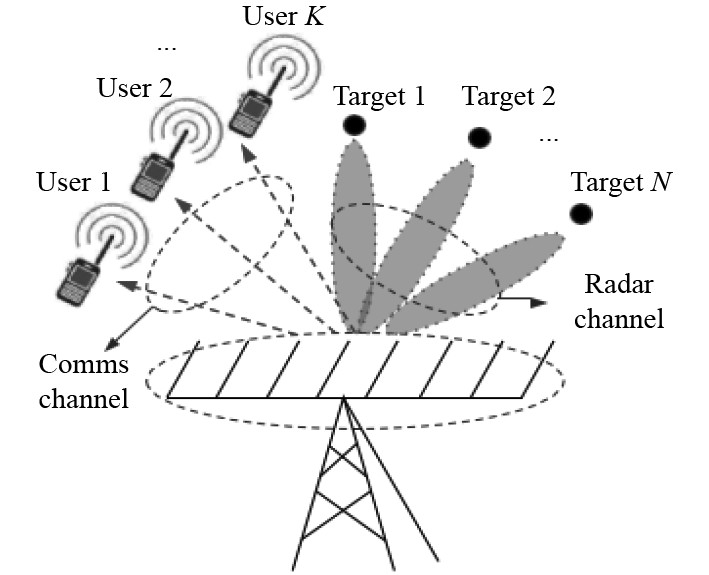
总体而言，雷达与通信的频谱共享技术包含2条研究路径：雷达与通信频谱共存（RCC）^[2-3]与雷达通信一体化（DFRC）^[4]，如图1和图2所示。

其中，RCC技术主要关注如何保证雷达和通信系统之间的互不干扰性。该技术考虑到雷达系统和通信系统所用的频谱重叠特性，目标是解决雷达对通信信号的干扰问题，以及通信系统对雷达信号的干扰问题。因此，雷达系统与通信系统之间需定期进行一定的信息交流，以达到相互协作的目的。这其中包含了雷达的发射脉冲波形和天线波束图样，扩频和数字调制的通信技术和通信帧格式，还有2个系统间的通道质量状态等信息。这些信息的交换有助于双方更好地理解彼此的工作方式和频谱使用情况，从而有效地避免干扰的发生。应用于实际系统时，此信息交流过程的实现较为复杂。

而DFRC技术是针对雷达和通信系统具有相通的硬件架构的基础上，设计雷达通信一体化信号处理方案，达到二者功能同步进行的目的。DFRC技术不必进行额外的数据信息交换，而是直接利用共享硬件平台既可完成频谱的共享。DFRC技术的重点内容为，如何在不影响2个系统中任意一方性能的前提下，能够实现对另一方系统性能的提升。目前，频谱融合技术的发展方向为：一是在雷达信号中调制通信信号，此方向在传统雷达的目标探测和识别等优势领域应用较多，对雷达设备的优化可以降低对通信系统的依赖；二是将雷达信号加入通信信号里进行调制。

通信雷达的频谱共享是一个具有潜力的新兴研究方向，该方法既能实现对频谱资源的高效利用，又能为设计可受益于雷达和通信合作的新型系统提供新思路^[5]。机会频谱共享技术^[6]是一种直接实现将通信和雷达频谱共存的方法，它为通信系统的顺利通信，设计了一种简单方式，即在雷达不占据空域和频谱的情况的情况下进行传输。然而，它并不能同时满足2个系统的需求。鉴于此，该工作提出了零空间投影（NSP）的概念^[7]，这一概念在多输入多输出雷达系统与通信系统的不同频谱共存场景中被广泛采用。在这样的方案中，雷达波束形成器被设计成将信号投射到雷达与终端用户设备间干扰信道的零空间上，这样可以确保雷达对通信的干扰链接为0。然而，这会导致雷达的性能损失，因为波束成形对于目标检测和估计不再是最佳的。雷达和通信性能之间的权衡是本文探讨的重点之一。

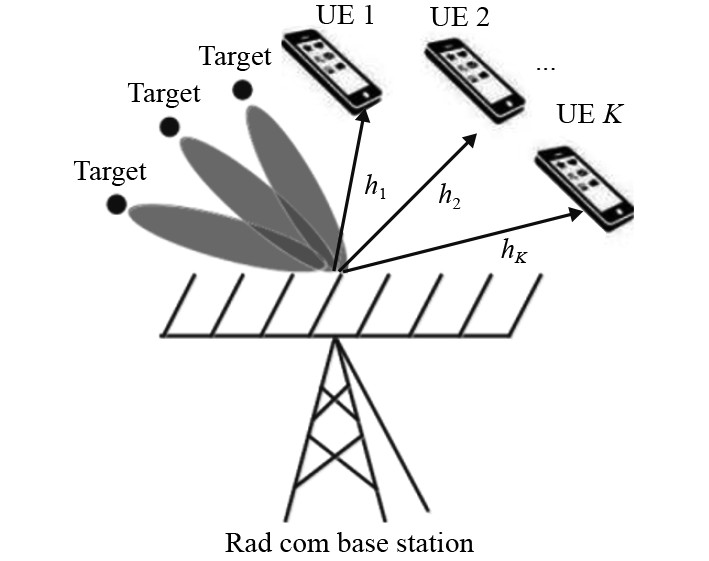
本文通过设计一个双功能MIMO雷达通信感知一体化系统，同时将雷达探测波形发送到目标，并将通信符号发送到下行链路用户。如图3所示，联合系统配备有 N 个天线的均匀线性阵列，在同时检测雷达目标的同时为 K 个单天线用户提供服务。

为便于讨论，本文仅考虑单个目标检测的情况。

窄带干扰的定义为：对于其信号带宽远小于发射信号带宽的干扰信号，以及其信号的绝对带宽较小的干扰信号称为窄带干扰。

在海战场中，敌军发送一同频窄带干扰信号，该干扰和原信号叠加在一起无法区分开，从而达到干扰通信的目的。本文就如何消除窄带干扰进行讨论。

1 集成系统设计 1.1 通信模型

当侧重通信功能的时候，可以通过范数表示最小化多用户干扰（Multi User Interference, MUI）能量来提升用户SINR，进而提升通信性能。

下行用户的接收符号矩阵可表示为：

$ \boldsymbol{Y}=\boldsymbol{H}\boldsymbol{X}+\boldsymbol{W}+{\boldsymbol{I}}_{\boldsymbol{N}\boldsymbol{B}} 。$

(1)

式中：$ \boldsymbol{H}={[{{h}}_{1}+{{h}}_{2}+{{h}}_{3}...+{{h}}_{{k}}]}^{\mathrm{T}}\in {\complement }^{{K}\times {N}} $是信道矩阵；$ {K} $为单天线用户数量，X为天线的均匀线性阵列的数量；$ \boldsymbol{X}={[{{x}}_{1}+{{x}}_{2}+{{x}}_{3}...+{{x}}_{{k}}]}^{\mathrm{T}}\in {\complement }^{N\times {L}} $是传输信号矩阵；L为帧的长度；$ \boldsymbol{W}={[{{w}}_{1}+{{w}}_{2}+{{w}}_{3}...+{{w}}_{{k}}]}^{\mathrm{T}}\in {\complement }^{{N}\times {L}} $是噪声信号矩阵，服从正态分布；其方差$ {\sigma }^{2}={N}_{0}B $，为功率谱密度与带宽的乘积；$ {\boldsymbol{I}}_{\boldsymbol{N}\boldsymbol{B}} $为窄带干扰：

$ {I}_{NB}\left(n\right)=\sum _{l=1}^{L}{A}_{l}{e}^{j(2{\text π} {f}_{l}n+{\varphi }_{l})}。$

(2)

式中：L为假设的单频干扰信号分量的总个数；$ {A}_{l} $为第$ l $个分量的幅值；$ {f}_{l} $为其频率；$ {\phi }_{l} $为其初始相角。

由此可推导出其功率谱为：

$ {S}=2 {{\text π}}\sum _{ {i}=1}^{ {M}}{ {A}}_{ {i}} {\sigma }( {w}-2 {{\text π}}{ {f}}_{ {i}}) 。$

(3)

假设下行传输信道H为平坦型瑞利衰落信道，信号频率响应在一个通信帧或一个雷达脉冲信号周期内呈现平坦分布。给出下行通信用户用于计算的星座符号矩阵为$ \boldsymbol{S}\in {\complement }^{{K}\times {L}} $，则用户接收信号Y可表示为：

$ {Y}=\boldsymbol{S}+(\boldsymbol{H}\mathrm{X}-\boldsymbol{S})+\boldsymbol{W} 。$

(4)

式中：HX-S这一项代表MUI信号。

假设所有用户的符号矩阵S各项均位于相同星座。总MUI能量可测量为：

$ {{P}}_{\mathrm{M}\mathrm{U}\mathrm{I}}=\left|\right|\boldsymbol{H}\boldsymbol{X}-\boldsymbol{S}|{|}_{F}^{2} 。$

(5)

则所有用户可实现的总速率可表示为：

$ {R}=\sum _{{i}=1}^{{K}}\mathrm{l}\mathrm{o}{\mathrm{g}}_{2}(1+{{\gamma }}_{{i}})。$

(6)

式中：$ {{\gamma }}_{{i}} $为第i个用户每帧的SINR，为：

$ { {\gamma }}_{ {i}}=\frac{ {E}\left(\right|{ {s}}_{ {i}, {j}}{|}^{2})}{ {E}\left(\right|{ {h}}_{ {i}}^{\rm{T}}{ {x}}_{ {j}}-{ {s}}_{ {i}, {j}}{|}^{2})+{ {N}}_{0}} 。$

(7)

式中：$ {E}\left(\right|{ {h}}_{ {i}}^{\rm{T}}{ {x}}_{ {j}}-{ {s}}_{ {i}, {j}}{|}^{2}) $为MUI信号能量，总速率与$ {\mathrm{\gamma }}_{\mathrm{i}} $呈正相关，MUI信号能量与$ {\mathrm{\gamma }}_{\mathrm{i}} $呈负相关，控制MUI的减少可以使总速率更高。

1.2 雷达模型

X为双函数波形矩阵^[8]，它具有以下空间协方差矩阵：

$ {\boldsymbol R}_{\boldsymbol x}=\frac{1}{\boldsymbol L}{\boldsymbol X}{\boldsymbol X}^{{\bf{H}}}。$

(8)

假定L≥N，则$ {\boldsymbol R}_{\boldsymbol x} $正定，可得发射波束图为：

$ {P}_{d}\left(\theta \right)={a}^{\bf H}\left(\theta \right){\boldsymbol R}_{\boldsymbol x}a\left(\theta \right) 。$

(9)

式中：θ为检测角度；$ {a}\left(\mathrm{\theta }\right) = [ 1,{{e}}^{{j}2{{\text π}}\Delta \mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\theta }\right)},..., {{e}}^{{j}2{{\text π}}({N}-1)\Delta \mathrm{s}\mathrm{i}\mathrm{n}\left(\mathrm{\theta }\right)} ] $为发射天线阵列的导向矢量；Δ为用波长归一化的相邻天线之间的间距。

1.3 全向波束图案设计

对于全向波束图，传输波形矩阵X必须为正交矩阵，即相应的协方差矩阵必须是恒矩阵。为了最大限度地减少MUI能量，将优化问题表述为：

$ {\mathrm{min}}\left|\right|{\boldsymbol{HX}}-{\boldsymbol S}|{|}_{F}^{2}，$

(10)

$ \mathrm{s}.\mathrm{t}. \frac{1}{L}\boldsymbol{X}{\boldsymbol{X}}^{\bf{H}}=\frac{{{P}}_{{T}}}{\boldsymbol{N}}{\boldsymbol{I}}_{\boldsymbol{N}}。$

(11)

式中：$ {{P}}_{{T}} $为总发射功率；$ {\boldsymbol{I}}_{\boldsymbol{N}} $为N × N单位矩阵。由于等式约束，该优化问题是非凸的，这表明X是Stiefel流形上的一个点。该优化问题可以归类为所谓的正交Procrustes问题（OPP），它具有基于奇异值分解（SVD）的简单封闭形式的全局解，并给出为：

$ \boldsymbol{X}=\sqrt{\frac{{L}{{P}}_{{T}}}{\boldsymbol{N}}}\boldsymbol{U}{\boldsymbol{I}}_{\boldsymbol{N}\times \boldsymbol{L}}{\boldsymbol{V}}^{\bf{H}} 。$

(12)

式中：$ {\boldsymbol{H}}^{H}{\boldsymbol{S}}\mathrm{为}\boldsymbol{U}\sum {\boldsymbol{V}}^{H}={\boldsymbol{H}}^{H}{\boldsymbol{S}} $的SVD；$ \boldsymbol{U}\in {\complement }^{\boldsymbol{N}\times \boldsymbol{N}} $和$ \boldsymbol{U}\in {\complement }^{\boldsymbol{L}\times \boldsymbol{L}} $为酉矩阵，$ {\boldsymbol{I}}_{\boldsymbol{N}\times \boldsymbol{L}} $为由N×N恒等矩阵和N×(L−N)零矩阵组成的N×L矩形矩阵。

全向波束模式设计包括2个矩阵乘法和1个SVD，这总共需要$ \boldsymbol{{\rm O}}(\boldsymbol{N}{K}\boldsymbol{L}+\boldsymbol{N}{\boldsymbol{L}}^{2}) $复杂的浮点操作(flop)，其中一个复杂的flop被定义为一个复杂的加法或乘法。

2 窄带干扰波形设计 2.1 总功率约束

将全向波束图得到的最优解表示为$ {X}_{0} $。则与总功率约束的权衡问题可以表示为：

$ {\mathrm{min}}\rho \left|\right|{\boldsymbol{HX}}-{\boldsymbol S}|{|}_{ F}^{2}+(1-\rho \left)\right||{\boldsymbol X}-{\boldsymbol X}_{0}|{|}_{F}^{2} ，$

(13)

$ \mathrm{s}.\mathrm{t}.\frac{1}{{L}}\left|\right|{X}|{|}_{F}^{2}={{P}}_{{T}}。$

(14)

式中：0≤ρ≤1是一个加权因子，它决定了双功能系统中雷达和通信性能的权值。对总功率进行约束，则权衡设计实际上是一种帕累托最优问题。通过求解式(13)与式(14)中的加权问题，得到的解达到帕累托最优点。F范数定义为矩阵A各项元素绝对值平方的总和开根，可表示为：

$ \left|\right|A|{|}_{F}^{2}=\sqrt{\sum _{i=1}^{m}\sum _{j=1}^{n}|{{a}_{i,j}|}^{2}} 。$

(15)

权衡问题可以表示为：

$ {\mathrm{min}}\left\|\left[ \sqrt{\rho }{\boldsymbol H}^{\text T} , \sqrt{1 - \rho }{\boldsymbol I}_{\boldsymbol N} \right]^{\text T}{\boldsymbol X} - \left[ \sqrt{\rho }{\boldsymbol S}^{\text T} , \sqrt{1 - \rho }{\boldsymbol X}_{o}^{\text T} \right]^{\text T}\right\|_{F}^{2} 。$

(16)

设$ {\boldsymbol A} = [\sqrt{\rho }{\boldsymbol H}^{\rm T} ，\sqrt{1-\rho }{\boldsymbol I}_{\boldsymbol N}{]}^{\rm T} \in {\complement }^{(K+{\boldsymbol N})\times \boldsymbol{N}} $，$ B=[\sqrt{\rho }{S}^{\rm T}，\sqrt{1-\rho }{X}_{o}^{\rm T}{]}^{\rm T} \in {\complement }^{(K+N)\times {L}} $，则上式可以简化为：

$ {\mathrm{min}}\left|\right|{\boldsymbol{AX}}-{\boldsymbol B}|{|}_{F}^{2} ，$

(17)

$ \mathrm{s}.\mathrm{t}.\frac{1}{{L}}\left|\right|{\boldsymbol X}|{|}_{F}^{2}={{P}}_{{T}} 。$

(18)

该优化问题可以认为是一个二次约束二次规划（QCQP）问题，并且是非凸的，通常可以通过SDP松弛来精确求解。以下通过设计一个低复杂度算法，来对上述问题进行最优化求解。

$\begin{aligned}[b] \left|\right|{\boldsymbol{AX}}-{\boldsymbol{B}}|{|}_{F}^{2}=& tr(\left({{\boldsymbol{AX}}-{\boldsymbol{B}})}^{\bf{H}}\right({\boldsymbol{AX}}-{\boldsymbol{B}}\left)\right)= \\ &tr\left({\boldsymbol{X}}^{\bf{H}}{\boldsymbol{A}}^{\bf{H}}{\boldsymbol{AX}}\right)-tr\left({\boldsymbol{X}}^{\bf{H}}{\boldsymbol{A}}^{\bf{H}}{\boldsymbol{B}}\right)-\\ &tr\left({\boldsymbol{B}}^{\bf{H}}{\boldsymbol{AX}}\right)+ tr\left({\boldsymbol{B}}^{\bf{H}}{\boldsymbol{B}}\right) 。\end{aligned}$

(19)

设$ {{\boldsymbol{Q}}={\boldsymbol{A}}}^{\bf{H}}{\boldsymbol{A}} $，$ {G={\boldsymbol{A}}}^{\bf{H}}{\boldsymbol{B}} $，因为$ tr\left({{\boldsymbol{B}}}^{\boldsymbol{H}}{\boldsymbol{B}}\right) $已知，$ tr\left({\boldsymbol X}^{\boldsymbol{H}} {{\boldsymbol{A}}}^{\boldsymbol{H}} B\right) $与$ tr\left({{\boldsymbol{B}}}^{\boldsymbol{H}} {\boldsymbol{A}} {\boldsymbol X}\right) $虚部相抵消，上式可以简化为：

$ \left|\right|{\boldsymbol{A}}{\boldsymbol{X}}-{\boldsymbol{B}}|{|}_{F}^{2}=tr({{\boldsymbol{X}}}^{{\boldsymbol{H}}}{\boldsymbol{QX}})-2Re\left(tr\left({\boldsymbol X}^{\boldsymbol H}G\right)\right)。$

(20)

Q为厄米特矩阵，上述问题可以看做信赖域子问题（TRS），该算法并没有先行确定搜索方向，而是由某种准则来确定位移，如果位移后目标函数值能够得到有效降低，那么就扩大信赖域，并通过这样的迭代过程使目标收敛。该问题为强对偶性，其对偶间隙为0。将上述问题使用拉格朗日乘子表示为

$ \mathcal{L}( {\boldsymbol X},\text{λ} ) = tr\left( {\boldsymbol X}^{\bf H} {\boldsymbol{Q}} {\boldsymbol X} \right) - 2Re\left(tr\right({\boldsymbol X}^{{\mathrm{H}}} G\left)\right) + \text{λ} \left( \right|\left|{\boldsymbol X}\right|{|}_{F}^{2} - L{{P}}_{{T}} )。$

(21)

式中：λ为与等式约束相关联的对偶变量。设$ {X}_{opt} $和$ {\lambda }_{opt} $为对偶间隙为0的原解最优点和对偶最优点，给出上述TRS的最优条件为：

$ \nabla {{L}}({\boldsymbol{X}}_{opt},{\text{λ}}_{opt})=2({\boldsymbol Q}+{\text{λ} }_{opt}{\boldsymbol I}_{\boldsymbol N}){\boldsymbol{X}}_{opt}-2G=0 ，$

(22)

$ \left|\right|{\boldsymbol X}_{opt}|{|}_{F}^{2}=L{{P}}_{{T}} ，$

(23)

$ \boldsymbol{Q}+{\text{λ}}_{opt}{\boldsymbol I}_{\boldsymbol N}\geqslant 0 。$

(24)

式中：2个限制条件分别保证了原始和对偶可行性。由此可以从得出：

$ {\boldsymbol X}_{opt}=({\boldsymbol Q}+{\lambda }_{opt}{\boldsymbol I}_{\boldsymbol N}{)}^+G。$

(25)

$ (·{)}^{+} $为摩尔彭若斯广义逆，代入上述公式，得：

$\begin{aligned}[b] \left|\right|{\boldsymbol X}_{opt}|{|}_{F}^{2}=&|\left|\right({\boldsymbol Q}+{{\text λ} }_{opt}{\boldsymbol I}_{\boldsymbol N}{)}^+G|{|}_{F}^{2} = \\ &\left|\right|{\boldsymbol V}({\text λ} +{{\text λ} }_{opt}{\boldsymbol I}_{\boldsymbol N}{)}^{-1}{\boldsymbol V}^{\boldsymbol H}G|{|}_{F}^{2}=L{{P}}_{{T}} ，\end{aligned}$

(26)

$ {{\text λ} }_{opt}\geqslant -{{\text λ} }_{{\mathrm{min}}} 。$

(27)

式中：$ {\boldsymbol Q}=\boldsymbol{V\Lambda {V}^{{\mathrm{H}}}} $为将$ {\boldsymbol Q} $矩阵按照特征值分解，$ \boldsymbol V $为包含特征向量的正交阵；Λ为包含特征值的对角阵；$ {{\text λ} }_{{\mathrm{min}}} $为$ {\boldsymbol Q} $的最小特征值。

上式可转化为：

$ \left|\right|{\boldsymbol{V}}({\text λ} +{{\text λ} }_{opt}{I}_{\boldsymbol N}{)}^{-1}{{\boldsymbol{V}}}^{\bf H}G|{|}_{F}^{2}=\sum _{i=1}^{\boldsymbol N}\sum _{j=1}^{L}\frac{\left(\right[{{{\boldsymbol{V}}}^{{\mathrm{H}}}G]}_{i,j}{)}^{2}}{({\text λ} +{{{\text λ} }_{i})}^{2}}。$

(28)

式中：$ {{\text λ} }_{i} $为Q的第i个特征值。可以看出，上式在区间 $ \mathrm{{\text λ} }\geqslant -{\mathrm{{\text λ} }}_{\mathrm{m}\mathrm{i}\mathrm{n}} $上严格递减且凸出，通过简单的线搜索方法获得$ {\lambda }_{opt} $，之后求解最优解。

该算法的复杂度主要是由以下3个步骤决定：矩阵乘法分解、伪逆分解和特征值分解分解所决定，其复杂度可以表示为：$ \mathcal{O}({\boldsymbol{N}}^{2}\mathrm{L}+\boldsymbol{N}\boldsymbol{K}{L}+{\boldsymbol{N}}^{3}+{\boldsymbol{N}}^{2}\boldsymbol{K}) $。

2.2 每根天线功率约束

与限制总功率类似，每个天线功率约束的权衡问题可以表示为：

$ {\mathrm{min}}\rho \left|\right|{\boldsymbol{HX}}-{\boldsymbol S}|{|}_{F}^{2}+(1-\rho \left)\right||{\boldsymbol X}-{\boldsymbol X}_{0}|{|}_{F}^{2}，$

(29)

$ \mathrm{s}.\mathrm{t}.\frac{1}{{L}}{\mathrm{diag}}\left({\boldsymbol X}{\boldsymbol X}^{ \bf H}\right)=\frac{{{P}}_{{T}}}{\boldsymbol{N}}\boldsymbol{I}。$

(30)

式中：$ {\mathrm{diag}}(·) $为矩阵对角线组成的向量；I为全1的N×1维向量。同样，借用A，B矩阵的定义，上式可以写成：

$ {\mathrm{min}}\left|\right|{\boldsymbol{AX}}-{\boldsymbol B}|{|}_{F}^{2} ，$

(31)

$ \mathrm{s}.\mathrm{t}.\frac{1}{{L}}{\mathrm{diag}}\left({\boldsymbol X}{\boldsymbol X}^{\bf H}\right)=\frac{{{P}}_{{T}}}{\boldsymbol{N}}\boldsymbol{I}。$

(32)

求解过程中与上文不同之处在于，由于每根天线电源约束，SDR不再是紧的，在这种情况下，必须使用高斯随机化来获得一个近似的秩为1的解。通过黎曼共轭梯度算法，可以在更低的复杂度下找到一个接近最优解。该算法原理是先把约束条件转变成流形（此时流形是一个可行域），此时需要优化的变量就转化成流形中的一个点，目标函数就变成是在流形可行域中一个求最优值的优化函数。目标即为找到一个可行域中函数取得最优值时，自变量的取值。寻找最优值时利用了梯度原理，通过下降梯度找到最小点。

将上述问题的可行域表示为M，给定一个点X∈M，X处的一个切向量被定义为与M上任何平滑曲线在X处相切的向量。所有这些向量都表示切向空间$ {T}_{X}M $，这是一个欧几里得空间。切线空间可以表示成：

$ {T}_{X}M=\{Z\in {C}^{N\times L}|Re\left(\right({X}^{\bf H}Z{)}_{ii})=0,{\forall }_{i}\} 。$

(33)

式中：$ \left(\right(·{\left)\right)}_{ii} $为矩阵的第i个对角线元素，将目标函数表示为$ F\left(X\right)\left|\right|AX-B|{|}_{F}^{2} $，则：

$ \nabla {F}\left({\boldsymbol X}\right)=2{\boldsymbol A}^{\bf H}({\boldsymbol {AX}}-{\boldsymbol B})。$

(34)

$ \nabla {F}\left(X\right) $称为欧几里得梯度，采用黎曼梯度计算下降方向，其定义为在相关切线空间$ {T}_{X}M $上的正交投影，并给出为

$ \mathrm{grad}{F} \left( \boldsymbol{X}\right) = {\mathcal{P}}_{\boldsymbol{X}}\nabla {F}\left({\boldsymbol X}\right) = \nabla {F}\left({\boldsymbol X}\right) - {\boldsymbol X}^{\bf{H}} {\mathrm{ddiag}}\left( Re\left(\nabla {F}({\boldsymbol X})^{{\bf{H}}}{\boldsymbol X} \right) \right) 。$

(35)

式中：$ {\mathrm{ddiag}}(·) $将矩阵的所有非对角元素设置为0。通过收缩映射，它将$ {T}_{X}M $上的点映射到M上。这由式(36)给出：

$ {\mathcal{R}}_{{\boldsymbol X}}\left({\boldsymbol X}\right) = \sqrt{\frac{{L}{{P}}_{{T}}}{\boldsymbol{N}}}\mathrm{d}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(\right(\boldsymbol{H} + \boldsymbol{Z}\left)\right({\boldsymbol{H} + \boldsymbol{Z})}^{\bf{H}}{)}^{ - \frac{1}{2}}(\boldsymbol{H} + \boldsymbol{Z}) 。$

(36)

式中：$ {\boldsymbol Z} \in {T}_{X}M $。将切空间的内积定义为：

$ < \boldsymbol{X},{\boldsymbol Z} > =\mathrm{R}\mathrm{e}\left(\mathrm{t}\mathrm{r}\right({\boldsymbol X}^{{\mathrm{H}}}{\boldsymbol Z}\left)\right)。$

(37)

该算法单次迭代的复杂度主要来自于梯度的计算，即$ \mathcal{O}({ {N}}^{2} {L}+ {N} {K} {L}) $，考虑迭代次数$ {N}_{i} $，总复杂度为$ \mathcal{O}({N}_{i}{ {N}}^{2} {L}+{N}_{i} {N} {K} {L}) $。

3 窄带干扰抑制算法

窄带干扰在频谱图上的分布情况为小范围内密集分布，频域上的波形呈现为较为尖锐的凸起形态。因此，为了便于研究，可把窄带干扰信号拆分成许多单频干扰信号分量，其计算公式如下：

$ {I}_{\boldsymbol{NB}}\left(n\right)=\sum _{l=1}^{L}{A}_{l}{e}^{j(2{\text π} {f}_{l}n+{\varphi }_{l})}。$

(38)

式中：L为假设的单频干扰信号分量的总个数；$ {A}_{l} $为第$ l $个分量的幅值；$ {f}_{l} $为其频率；$ {\varphi }_{l} $为其初始相角。

由此可推导出其功率谱为：

$ {S}=2{{\text π} }\sum _{ {i}=1}^{ {M}}{ {A}}_{ {i}} {\sigma }( {w}-2{{\text π} }{ {f}}_{ {i}}) 。$

(39)

有用信号和窄带干扰信号在功率谱分布上存在显著差异。通常，有用信号在频带内呈现平坦分布，而窄带干扰在频带内表现为小范围密集分布，因此导致了一个大幅度脉冲信号的形成。在此基础上，提出了变换域干扰抑制原理，即对窄带干扰信号进行适当的变换，将其映射成类似于冲激函数的形式。由于有用信号的频谱与干扰信号相比，其频谱具有更高的稳定性，幅值变化也更小，可以利用阈值算法对干扰进行检测，并降低其幅度，以减少或近似消除干扰产生的影响。这一变换需要具有唯一性并且没有歧义性，从而使得信号在经过这一变换后，可以被还原为在时域空间内的信号。干扰抑制技术所利用的有用信号与干扰信号的频率特性、信号幅度和调制方式等差异性越大，通常得到的抗干扰效果越好。变换域干扰抑制基本原理图，如图4所示。

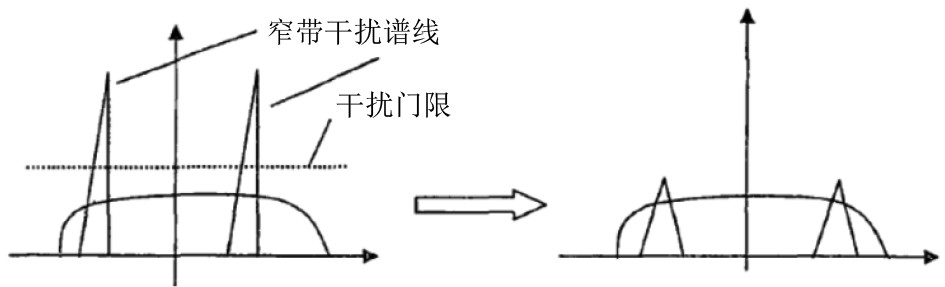
FFT变换干扰抑制算法利用了不同于扩频信号，窄带干扰信号在频谱图上表现为小范围内密集分布这一特性，因此，更便于识别其频域上较为尖锐的凸起波形。由此，针对受到干扰的混合信号，利用FFT变换（见图5）进行处理，将其从时域转换到频域，这样干扰所在的频谱位置就变得清晰可见。在此基础上，通过预先设定适当的阈值，将各谱线的幅值逐个进行对比，幅值高于阈值的频谱线就对应着干扰信号，将这些信号分量做衰减处理，可达到抗窄带干扰的目的。最后，对去除干扰分量后的信号，利用IFFT变换从频域转换回时域后，再完成解扩解调处理。

在FFT变换干扰抑制算法中，干扰门限的选取是一个关键因素，它的合理设置对于算法实现的成败至关重要。如果设定值太大，虽可以保留更多有用信号，但同时也使得干扰信号随之保留下来；如果设定太小，虽然实现切除了较多干扰信号的频谱，但相应的又会造成有效信号较多的缺失。

3.1 门限算法

设计一个门限算法，由于信号在混合一系列服从高斯分布的白噪声后进行扩频处理，能够使其在一定大小的频段内保持相对平坦，因此有用信号在受到干扰后，只有其中混合有窄带干扰这部分的频域波形，会产生相应改变。这就是门限法确定阈值时利用的关键点。门限算法实现过程为：首先将信号进行快速傅里叶变换，将得到的频域信号$ {X}\left( {n}\right) $进行对数放大，即通过$ 10{\rm{lg}} {X}\left( {n}\right) $运算，之后求出幅度均值E和标准差$ {\sigma } $，就能设计干扰门限Th为：

$ {T} {h}= {E}+ {M} {\sigma }。$

(40)

式中：M为权重因子，不同的信道环境下产生不同的均值与标准差，门限Th则会随之改变。

3.2 中值滤波算法

中值滤波的主要思路是计算得到某个数据点的最佳输出值，对该数据点附近的一组数据进行排序，取其中值代替该点处的原输出值作为输出。当利用傅里叶变换到频域的信号再进行扩频处理后，阀值算法往往会设定长度为L=2k+1的窗口在其频谱图上进行滑动，对包含在该窗口中的各个频点的幅值进行比较，然后取其中中间值作为该频点的输出，中值滤波器运算公式如下：

$ {y}_{i}={\mathrm{median}}\left({x}_{i}\right|j=i-k,...,i+k) 。$

(41)

式中：$ {x}_{i} $为原信号输入频点的幅值；$ {y}_{i} $为中值滤波后信号输出频点的幅值。

中值滤波算法可以实现信号的平滑传递，对于窄带干扰信号具有一定的抑制效果，然而，由于其计算量较大，且当信号含有少量或无干扰时，仍进行取中值输出，这将造成波形出现失真的情况，因此为了克服该方法存在的缺陷，提出了能自动设定干扰判定门限的改进条件中值滤波算法，其计算公式为：

$ {y}=\left\{\begin{aligned} &{x}_{i},m > \displaystyle\frac{x_i}{y_i}，\\ &{y}_{i},{\mathrm{otherwise}}。\end{aligned}\right. $

(42)

式中：m为预估参数；$ {y}_{i} $为滑动窗口的中值；$ {x}_{i} $为输入滤波器的信号。若$ \displaystyle\frac{x_i}{y_i} $没有超过m，则对$ {x}_{i} $进行保留，否则视为窄带干扰，用中值$ {y}_{i} $替代$ {x}_{i} $。

该算法优势在于减少了计算量同时也最大程度使信号不失真。

4 仿真实验

在本节中，通过仿真展示波形设计以及权衡设计与功率限制模式对通信及雷达性能的影响。首先定义部分参数数值，令$ {P}_{T}=1 $，信道矩阵H服从标准复高斯分布。在所有的模拟中，设置天线数量N=16，并使用了一个相邻天线之间具有半波长间距的ULA。选用单位功率的QPSK字母表为星座图，即矩阵S中的每个条目功率为1。在不失去一般性的情况下，定义了信噪比$ \mathrm{S}\mathrm{N}\mathrm{R}={P}_{T}/{N}_{0} $，并使用“Omni”来表示全方向和定向的波束模式设计。此外，我们将具有严格等式约束的波形优化和权衡设计表示为“Strict”和“Tradeoff”，并分别对总功率约束优化使用“Total”和“perAnt”。通信帧/雷达脉冲的长度设置为L=30。

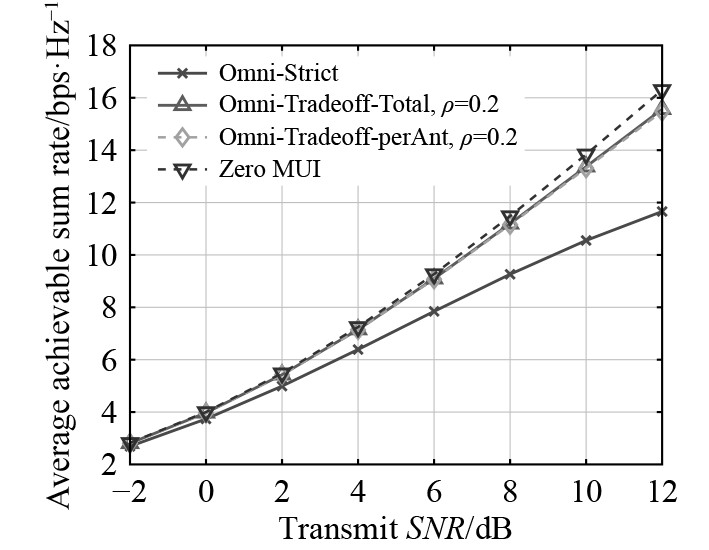
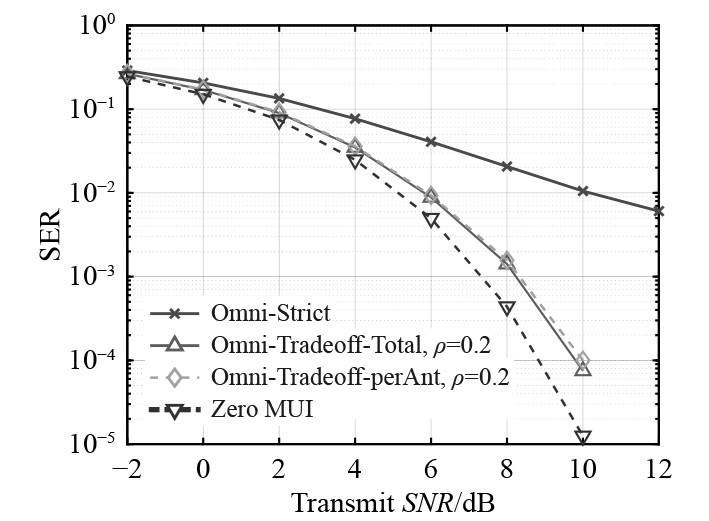
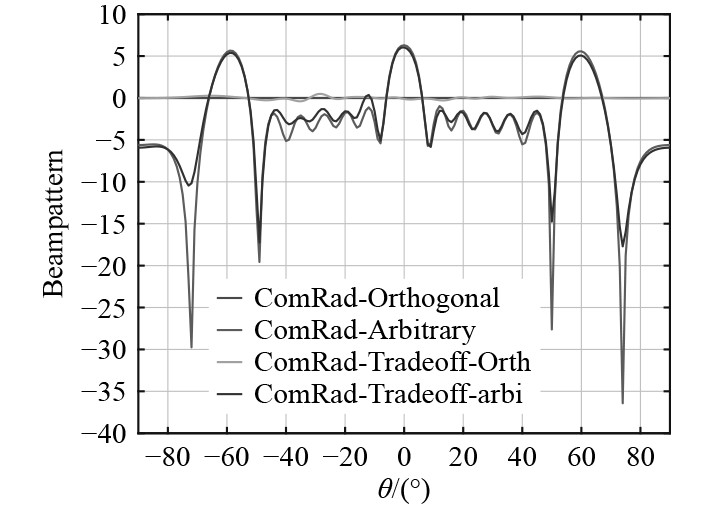
图6和图7为通过不同方法获得的通信性能，分别表示通信的总速率和误码率，图8为相关的雷达波束图。通过在通信侧引入一个小的加权因子ρ=0.2，权衡设计的总速率和SER性能显著提高，同时相应的雷达波束图只经历轻微的性能损失。通过进一步研究每个天线的功率约束设计，从图中可知雷达或通信中对应的性能损失与总功率约束对应的性能损失基本相同，这表明所提出的RCG算法可有效地计算出接近最优的解决方案。

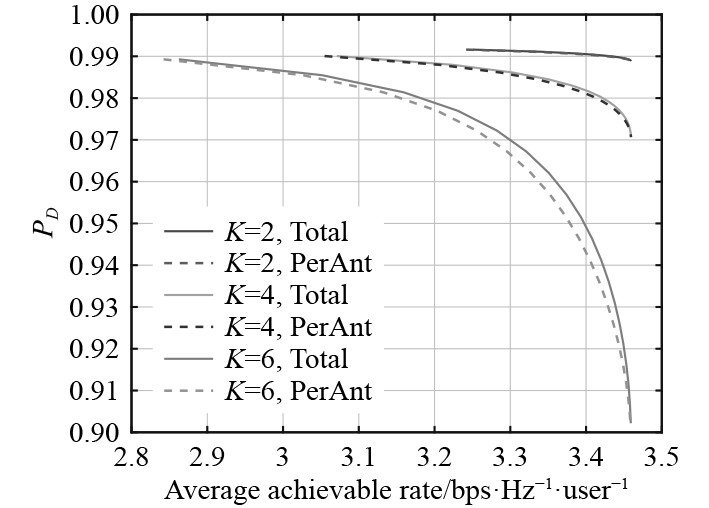
图9为通信和雷达性能之间的权衡。$ {P}_{D} $为雷达检测概率，设定接收SNR为−6 dB，雷达的误报概率为$ {P}{A}={10}^{-7} $。可知，通信系统的传输速率和雷达系统的检测性能二者之间存在相互制约。将雷达检测概率保持不变，若用户总数下降，通信系统的传输速率会随之增加。同时将总功率限制替换为每个天线的限制，相关的性能只会略微下降。

5 结　语

本文首先讨论了通信与感知一体化系统的设计，并引入了衡量通信性能和雷达性能的权衡系数。在引入窄带干扰之后。仿真结果表明了窄带干扰的影响和消除窄带干扰必要性。设计一种自适应阈值算法，并对输出信号进行滤波。仿真实验的结果可以验证该算法具有有效性。通过对经典门限算法的比较，说明了改进算法的优越性。