0 引　言

宽带共形阵在不改变设备外形的前提下实现阵元布局的优化配置，有效提高阵增益，在声呐、雷达和通信等领域的阵列信号处理中得到越来越广泛应用。针对采用节拍延迟线（Tapped Delay Line，TDL）结构和复数加权的宽带共形阵，本文提出的自适应频率不变波束形成器（Frequency Invariant Beamformer，FIB）对宽带入射信号在不同频率上具有基本一致的幅度和相位响应，有效降低宽带波束形成器输出端期望信号的失真^[1]，并且可以实现对非期望信号方向上干扰信号的高效抑制。

Liu等^[2]将最小方差无偏响应 （Minimum Variance Distortionless Response，MVDR）波束形成器转化为对应的标准二阶锥规划（Second Order Cone Programming，SOCP）描述，Strun等^[3]提出的内点方法（Interior-point Method）对该SOCP描述进行有效求解，实现适用于均匀线列阵的旁瓣约束波束形成器设计。Chen等^[4]提出适用于任意结构宽带线列阵的自适应波束形成器设计方法，但该方法仅适用于线列阵波束设计。Duan等^[5]提出将空间响应偏差SRV（Spatial Response Variation）约束应用于宽带阵列FIB设计，但适用范围限定于采用实数加权系数的阵列，导致其性能和应用范围受到一定限制。Chen等^[6]提出的宽带波束形成器设计方法对文献[5]方法进行改进，应用范围扩展到复数加权阵列，但该方法仅适用于宽带线列阵的非自适应FIB设计，无法高效抑制宽带干扰信号。Lucas^[7]根据最小平方最优变换准则构建宽带波束形成器设计，但无法保持宽带波束图在不同频率上的恒定特性。丛雯珊等^[8]提出基于粒子群算法的宽带阵列波束综合设计，但适用范围限制为大阵元间距的宽带平面阵。王华奎^[9]提出基于二阶锥规划的宽带平面阵近场波束优化方法，但该方法无法用于对宽带平面阵远场波束设计。陈鹏等^[10]提出根据在参考频率上预测信号方向无偏响应约束、在参考频率上旁瓣区域旁瓣级约束以及平均空间响应偏差幅度约束这3个条件下最小化波束形成器输出功率的准则进行自适应FIB设计，但该方法适用范围为宽带平面阵，并且由于约束条件较多导致优化计算的复杂度增加。

针对采用节拍延迟线（Tapped Delay Line，TDL）结构和复数加权系数的宽带共形阵，本文提出基于SRV约束的自适应FIB设计。该自适应FIB在参考频率上保持预测信号方向无偏响应以及旁瓣级恒定这2个限制条件下，根据对波束形成器输出功率值与平均空间响应偏差值这2项的加权和进行最小化处理的准则进行设计。本文方法将自适应FIB设计应用扩展到宽带共形阵波束优化，并且通过对约束条件和目标函数的合理调整，降低优化计算复杂度。通过数学变换将这种FIB设计问题转化为标准SOCP形式后，可以采用内点方法对其进行有效求解。仿真结果验证了本文方法对于宽带共形阵自适应FIB设计的有效性。

为简化描述，本文后续采用的部分符号定义为：$*$为共轭，T为转置，H为Hermitian转置，$\otimes$为向量Kronecker积，$c$为信号在介质中传播速度，$o$为原点位置，F&S为滤波和采样操作，${T_s}$为宽带共形阵各阵元接收信号的采样周期，${Re} \{ .\}$和${Im} \{ .\}$分别为取实部和取虚部操作。

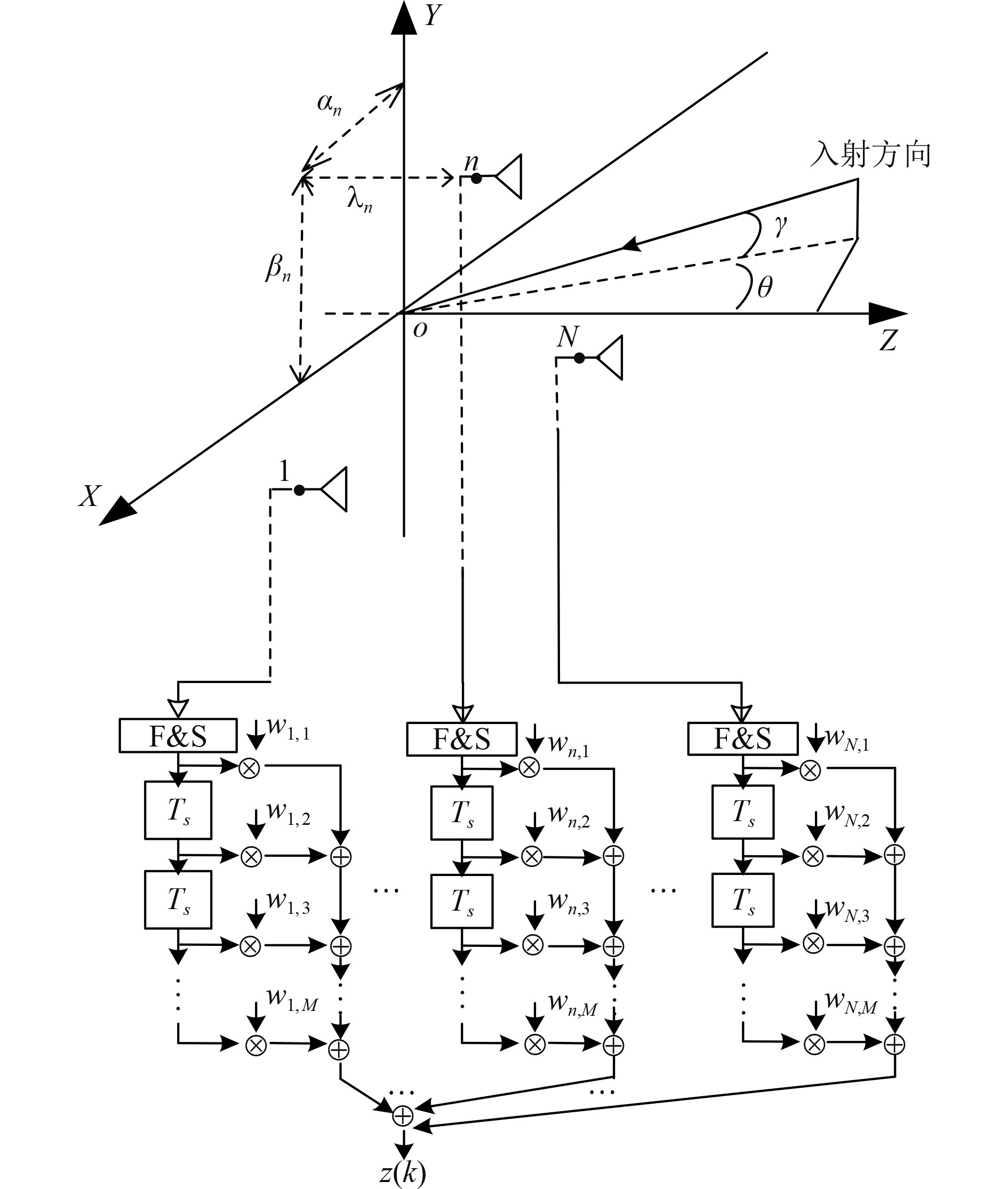
1 背景介绍

对于采用$M$维复数加权节拍延迟线结构的$N$元宽带共形阵，其典型架构组成如图1所示。其中，宽带共形阵的第$n$个阵元位置向量定义为$\boldsymbol{r}_n=[\alpha_n,\beta_n,\lambda_n]^{\mathrm{T}}, 1\leqslant n\leqslant N$；宽带共形阵波束形成器的输出信号定义为$z(k)$；符号$\theta$($- {\text π} /2 \leqslant \theta \leqslant {\text π} /2$)和$\gamma$ ($- {\text π} /2 \leqslant \gamma \leqslant {\text π} /2$)分别为宽带信号入射到共形阵上的水平向方位角和垂直向高低角。定义相对于采样频率${f_s}$的宽带共形阵归一化工作频带为$[{f_L},{f_U}]$、归一化工作带宽$B = {f_U} - {f_L}$以及归一化参考频率${f_r} = ({f_L} + {f_U})/2$。定义宽带共形阵第$n$个阵元上接收信号时间序列${x_n}(t)$的表达式如下：

${x_n}(t) = \sum\limits_{i = 0}^I {{s_i}(t + {\tau _n}({\theta _i},{\gamma _i}){T_s})} + {v_n}(t),n = 1,...,N 。$

(1)

式中：${s_0}(t)$为在方向$({\theta _0},{\gamma _0})$上入射的宽带期望信号；${s_i}(t),i = 1,2,...,I$为在方向$({\theta _i},{\gamma _i})$上入射的宽带干扰信号；${v_n}(t)$为宽带共形阵第$n$个阵元上的加性高斯白噪声；${\tau _n}({\theta _i},{\gamma _i}), i = 0,1,2,...,I$为第$n$个阵元接收到的$({\theta _i},{\gamma _i})$方向上入射宽带信号相对于原点的归一化时延（注：以采样周期${T_s}$为基准），其计算表达式如下：

${\tau _n}({\theta _i},{\gamma _i}) = [({\alpha _n}\cos {\gamma _i}\sin {\theta _i} + {\beta _n}\sin {\gamma _i} + {\lambda _n}\cos {\gamma _i}\cos {\theta _i})/c]/{T_s}。$

(2)

为简化后续计算表达式，定义如下整数变量$g$和$h$，并定义如下${\zeta _g}(\theta ,\gamma )$、${\zeta _h}(\theta ,\gamma )$、${\xi _{g, h}}(\theta ,\gamma )$等3个延时量函数表达式：

$g = ({i_1} - 1)N + {k_1}, {i_1} = 1,2 ,...,M, {k_1} = 1,2 ,...,N，$

(3)

$h = ({i_2} - 1)N + {k_2}, {i_2} = 1,2 ,...,M, {k_2} = 1,2 ,...,N，$

(4)

${\zeta _g}(\theta ,\gamma ) = {\tau _{{k_1}}}(\theta ,\gamma ) - ({i_1} - 1),{i_1} = 1,2 ,...,M, {k_1} = 1,2 ,...,N，$

(5)

${\zeta _h}(\theta ,\gamma ) = {\tau _{{k_{ 2}}}}(\theta ,\gamma ) - ({i_2} - 1), {i_2} = 1,2 ,...,M, {k_2} = 1,2 ,...,N ，$

(6)

${\xi _{g, h}}(\theta ,\gamma ) = {\zeta _g}(\theta ,\gamma ) - {\zeta _h}(\theta ,\gamma )，$

(7)

本文中入射信号${s_i}(t),i = 0,1,2,...,I$和阵元噪声${v}_{n}(t)，n=1,\mathrm{...},N$为零均值的独立高斯白噪声变量，对应的频域公式分别为${S_i}(f) = \sigma _i^2/B,f \in [{f_L},{f_U}]$和${V_n}(f) = \sigma _v^2/B, f \in [{f_L},{f_U}]$。定义$f$为相对于采样频率${f_s}$的归一化工作频率，$\sigma _i^2$和$\sigma _v^2$分别为入射信号${s_i}(t)$和阵元噪声${v_n}(t)$在频带内的总功率。定义宽带共形阵第$n$个阵元的第$m$个节拍上接收信号离散采样序列为：

$\begin{aligned}[b] {x_{n, m}}(k) &= {x_n}(t - (m - 1){T_s}){|_{ t = k{T_s}}},n = 1,...,N;\\ m &= 1,...,M;k = 1,...,K 。\end{aligned}$

(8)

式中，$K$为当前阵列处理选取的总快拍次数。定义$NM \times 1$维节拍堆积向量${\boldsymbol{x}}(k)$、对应$NM \times 1$维复数加权向量${\boldsymbol{w}}$以及对应$NM \times 1$维阵列节拍流形向量${\boldsymbol{a}}(f,\theta ,\gamma )$分别为：

$\begin{aligned}[b] {\boldsymbol{x}}(k) = &[{x_{1, 1}}(k),{x_{2, 1}}(k),...,{x_{N, 1}}(k),{x_{1, 2}}(k),{x_{2, 2}}(k),...,\\ &{x_{N, 2}}(k),...,{x_{1, M}}(k),{x_{2, M}}(k),...,{x_{N, M}}(k)]^{\mathrm{T}}，\end{aligned}$

(9)

$\begin{aligned}[b] {\boldsymbol{w}} = &[{w_{1, 1}}, {w_{2, 1}},..., {w_{N, 1}}, {w_{1, 2}}, {w_{2, 2}}, ..., {w_{N, 2}},..., \\ &{w_{1, M}}, {w_{2, M}},..., {w_{N, M}}]^{\mathrm{T}}，\end{aligned}$

(10)

${\boldsymbol{a}}(f,\theta ,\gamma ) = {{\boldsymbol{a}}_M}(f) \otimes {{\boldsymbol{a}}_N}(f,\theta ,\gamma )。$

(11)

其中，$M \times 1$维节拍向量${{\boldsymbol{a}}_M}(f)$和$N \times 1$维阵列流形向量${{\boldsymbol{a}}_N}(f,\theta ,\gamma )$的定义如下：

${{\boldsymbol{a}}_M}(f) = {[1, {e^{ - j2{\text π} f}},...,{e^{ - j2{\text π} f(M - 1)}}]^{\mathrm{T}}}，$

(12)

${{\boldsymbol{a}}_N}(f,\theta ,\gamma ) = {[{e^{j2{\text π} f{\tau _{ 1}}(\theta ,\gamma )}},{e^{j2{\text π} f{\tau _{ 2}}(\theta ,\gamma )}},...,{e^{j2{\text π} f{\tau _{ N}}(\theta ,\gamma )}}]^{\mathrm{T}}}。$

(13)

根据上述表达式，可以获得宽带共形阵的波束图函数$b(f,\theta ,\gamma )$、波束输出信号$z(k)$以及波束输出功率${P_z}$的计算表达式分别如下：

$b(f,\theta ,\gamma ) = {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{a}}(f,\theta ,\gamma ) = {{\boldsymbol{a}}^{\mathrm{T}}}(f,\theta ,\gamma ){\boldsymbol{w}}，$

(14)

$z(k) = \sum\limits_{n = 1}^N {\sum\limits_{m = 1}^M {{w_{n, m}}{x_{n, m}}(k)} } = {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{x}}(k)，$

(15)

${P_z} = E[z(k){z^H}(k)] = E[{{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{x}}(k){{\boldsymbol{x}}^H}(k){{\boldsymbol{w}}^*}] = {{\boldsymbol{w}}^{\mathrm{T}}}{{\boldsymbol{R}}_x}{{\boldsymbol{w}}^*}。$

(16)

对应节拍堆积向量${\boldsymbol{x}}(k)$的$NM \times NM$维空间协方差矩阵${{\boldsymbol{R}}_x}$计算式为：

$\boldsymbol{R}_x=E[\boldsymbol{x}(k)\boldsymbol{x}^{\mathrm{H}}(k)]=\sum\limits_{i=0}^I\boldsymbol{R}_i+\boldsymbol{R}_v，$

(17)

其中，$NM \times NM$维矩阵${{\boldsymbol{R}}_i}$为对应入射宽带信号${s_i}(t)$的空间协方差矩阵，定义如下：

$\boldsymbol{R}_i=\int_{f_L}^{f_U}S_i(f)\boldsymbol{a}(f,\theta_i,\gamma_i)\boldsymbol{a}^{\mathrm{H}}(f,\theta_i,\gamma_i)\mathrm{d}f。$

(18)

结合表达式(3)～式(7)的定义，对$NM \times NM$维矩阵${{\boldsymbol{R}}_i}$第$(g,h)$个元素的计算表达式如下：

${[{{\boldsymbol{R}}_i}]_{g, h}} = \sigma _i^2{e^{j2{\text π} {f_r}{\xi _{g, h}}({\theta _i},{\gamma _i})}}{{\mathrm{sin}c}} ({\xi _{g, h}}({\theta _i},{\gamma _i})B)。$

(19)

其中，$\mathrm{sin}c(t)=\sin({\text π} t)/({\text π} t)$。由于不同阵元接收信号的噪声成分${v_n}(t)$之间非相关，结合表达式(3)～式(7)的定义，对$NM \times NM$维噪声协方差矩阵${{\boldsymbol{R}}_v}$的第$(g,h)$个元素计算如下：

${[{{\boldsymbol{R}}_v}]_{g, h}} = \left\{ {\begin{array}{*{20}{l}} {\sigma _v^2{e^{-j2{\text π} {f_r}({i_1} - {i_2})}}{\mathrm{sin}c} (-({i_1} - {i_2})B),{k_1} = {k_2}} ，\\ {0,{k_1} \ne {k_2} } 。\end{array}} \right.$

(20)

对于宽带共形阵单个阵元输入信号${x_n}(t)$的信干噪比${{{{SINR}}} _{{\mathrm{input}}}}$，其计算表达式如下：

${{{{SINR}}} _\mathrm{input}} = \frac{{\sigma _0^2}}{{\displaystyle\sum\limits_{i = 1}^I {\sigma _i^2 + \sigma _v^2} }}。$

(21)

对于宽带共形阵波束输出信号$z(k)$的信干噪比${{{{SINR}}} _\mathrm{output}}$，其计算表达式如下：

${{{{SINR}}} _\mathrm{output}} = \frac{{{{\boldsymbol{w}}^{\mathrm{T}}}{{\boldsymbol{R}}_0}{{\boldsymbol{w}}^*}}}{{{{\boldsymbol{w}}^{\mathrm{T}}}\left(\displaystyle\sum\limits_{i = 1}^I {{{\boldsymbol{R}}_i} + } {{\boldsymbol{R}}_v}\right){{\boldsymbol{w}}^*}}}。$

(22)

以上对输入信号及输出信号信干噪比的计算用于对波束形成器的性能进行评估。在自适应波束设计中，宽带共形阵空间协方差矩阵${{\boldsymbol{R}}_x}$需要通过对宽带共形阵接收数据进行如下计算进行估计：

$\widehat {{\boldsymbol{R}}_x} = \frac{1}{K}\sum\limits_{k = 1}^K {\boldsymbol{x}}(k){\boldsymbol{x}}^{\rm{H}}(k)。$

(23)

2 基于SRV约束的波束设计 2.1 基于SRV约束的波束图偏差限制

空间响应偏差函数$SRV(\theta ,\gamma )$定义为波束图$b(f,\theta ,\gamma )$与波束图$b({f_r},\theta ,\gamma )$偏差量绝对值的平方在工作频带上的积分，其计算如下：

$\begin{aligned}[b] SRV(\theta ,\gamma ) =& \frac{1}{B}\int_{{f_L}}^{{f_U}} {|b(f,\theta ,\gamma ) - b({f_r},\theta ,\gamma ){|^2}{\mathrm{d}}f} = \\ & \frac{1}{B}\int_{{f_L}}^{{f_U}} {|{{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{a}}(f,\theta ,\gamma ) - {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{a}}({f_r},\theta ,\gamma ){|^2}{\mathrm{d}}f} = \\ & {{\boldsymbol{w}}^{\mathrm{T}}}\frac{1}{B}\int_{{f_L}}^{{f_U}} {|{\boldsymbol{a}}(f,\theta ,\gamma ) - {\boldsymbol{a}}({f_r},\theta ,\gamma ){|^2}{\mathrm{d}}f} {{\boldsymbol{w}}^*} = \\ & {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{J}}(\theta ,\gamma ){{\boldsymbol{w}}^*}。\end{aligned}$

(24)

其中，$NM \times NM$维矩阵${\boldsymbol{J}}(\theta ,\gamma )$为Hermitian矩阵。结合表达式(3)～式(7)的定义，矩阵${\boldsymbol{J}}(\theta ,\gamma )$第$(g,h)$个元素的计算如下：

$\begin{aligned}[b] {[{\boldsymbol{J}}(\theta ,\gamma )]_{g, h}} &= {[{{\boldsymbol{J}}_1}(\theta ,\gamma )]_{g,h}} - {[{{\boldsymbol{J}}_2}(\theta ,\gamma )]_{g,h}} - \\ {[{{\boldsymbol{J}}_3}(\theta ,\gamma )]_{g,h}} &+ {[{{\boldsymbol{J}}_4}(\theta ,\gamma )]_{g,h}}。\end{aligned}$

(25)

其中，${i_1} = 1,2 ,...,M$,${k_1} = 1,2 ,...,N$，${i_2} = 1,2 ,...,M$，${k_2} = 1,2 ,...,N$。结合表达式(3) ~ 式(7)的定义，式中矩阵${{\boldsymbol{J}}_1}(\theta ,\gamma )$、${{\boldsymbol{J}}_2}(\theta ,\gamma )$、${{\boldsymbol{J}}_3}(\theta ,\gamma )$及${{\boldsymbol{J}}_4}(\theta ,\gamma )$第$(g,h)$个元素的计算如下：

${[{{\boldsymbol{J}}_1}(\theta ,\gamma )]_{g,h}} = \frac{1}{B}\int_{{f_L}}^{{f_U}} {{e^{j2{\text π} f{\xi _{g, h}}(\theta ,\gamma )}}{\mathrm{d}}f}，$

(26)

${[{{\boldsymbol{J}}_2}(\theta ,\gamma )]_{g, h}} = \frac{{{e^{ - j2{\text π} {f_r}{\zeta _{ h}}(\theta , \gamma )}}}}{B}\int_{{f_L}}^{{f_U}} {{e^{j2{\text π} f{\zeta _g}(\theta , \gamma )}}{\mathrm{d}}f}，$

(27)

${[{{\boldsymbol{J}}_3}(\theta ,\gamma )]_{g, h}} = \frac{{{e^{j2{\text π} {f_r}{\zeta _g}(\theta ,\gamma )}}}}{B}\int_{{f_L}}^{{f_U}} {{e^{ - j2{\text π} f{\zeta _h}(\theta ,\gamma )}}{\mathrm{d}}f }，$

(28)

${[{{\boldsymbol{J}}_4}(\theta ,\gamma )]_{g, h}} = {e^{j2{\text π} {f_r}{\xi _{g, h}}(\theta ,\gamma )}} 。$

(29)

使用SRV约束可以有效抑制宽带共形阵在不同工作频率上波束图与参考频率上波束图之间的偏差幅度。为满足自适应FIB在不同工作频率上波束图函数$b(f,\theta ,\gamma )$保持基本一致的要求，对宽带共形阵空间响应偏差函数在$({\phi _{ d}},{\varphi _d}), d = 1,2, ...,D$这$D$个空间方向上进行约束限制，并定义平均空间响应偏差量$\overline {SRV}$，其计算表达式为：

$\overline {SRV} = (1/D)\sum\nolimits_{ d = 1}^D {SRV({\phi _d},{\varphi _d})} = {{\boldsymbol{w}}^{\mathrm{T}}}\overline {\boldsymbol{J}} {{\boldsymbol{w}}^*}，$

(30)

其中，$NM \times NM$维矩阵$\overline {\boldsymbol{J}}$的计算如下：

$\overline {\boldsymbol{J}} = (1/D) \sum\nolimits_{d = 1}^D {{\boldsymbol{J}}({\phi _d},{\varphi _d})}。$

(31)

2.2 二阶锥规划形式的定义

凸锥优化（Convex Conic Optimization）问题的标准表达式如下：

$\mathop {\max }\limits_{\boldsymbol{y}} {{\boldsymbol{b}}^{\mathrm{T}}}{\mathbf{y}} subject to {\mathbf{c}} - {{\boldsymbol{A}}^{\mathrm{T}}}{\boldsymbol{y}} \in \kappa，$

(32)

式中：${\boldsymbol{y}}$为包含设计变量（在本文中即为宽带共形阵加权系数）的向量；${\boldsymbol{A}}$为实系数矩阵；${\boldsymbol{b}}$和${\boldsymbol{c}}$为实系数向量；$\kappa$为由基本锥（elementary cones）乘积构成的对称锥。基本锥由二阶锥SOC（Second Order Cone）和零锥（Zero Cone）构成。定义$(r + 1)$维二阶锥SOC（注：对应不等式限制）的表达式如下：

${{{\mathrm{SOC}}} ^{r + 1}}=\left\{\left[ {\begin{array}{*{20}{c}} \mu \\ {\bf{\text{μ} }} \end{array}} \right] \in \Re \times {{\boldsymbol{G}}^r}|\mu \geqslant ||{\text{μ} }|| \right\}。$

(33)

其中，$\mu$为实数集$\Re$中的一个非负标量，$\mu$为$r \times 1$维复向量集${{\boldsymbol{G}}^r}$中的一个向量。定义零锥（注：对应等式限制）的表达式如下：

$\{ 0\} = \{ \mu \in {\boldsymbol{G}}|\mu = 0\}，$

(34)

其中，$\mu$为复数集${\boldsymbol{G}}$中的一个标量。

2.3 宽带共形阵的自适应FIB设计

本文提出的宽带共形阵自适应FIB属于数据相关的波束形成器，优化计算的复数加权系数向量${\boldsymbol{w}}$与阵列数据的协方差矩阵存在关联。在参考频率上保持预测信号方向无偏响应以及旁瓣级恒定这2个限制条件下，根据对波束形成器输出功率值与平均空间响应偏差值这2项的加权和进行最小化处理的准则进行设计。上述宽带波束形成器设计问题可以描述为：

$\begin{aligned}[b] &\underset{w}{\mathrm{min}}\delta subjectto\\ &\boldsymbol{w}^{{\mathrm{T}}}\boldsymbol a({f}_{0},{\vartheta }_{0},{\psi }_{0})=\\ &1,|\boldsymbol{w}^{{\mathrm{T}}}\boldsymbol a({f}_{0},{\vartheta }_{p},{\psi }_{q})|\leqslant \varsigma ,\boldsymbol{w}^{{\mathrm{T}}}（{\widehat{\boldsymbol R}}_{x}+\epsilon \overline{\boldsymbol J}）\boldsymbol{w}^{*}\leqslant \delta \\ &{\vartheta }_{p}\in [-{90}^{\circ},{\vartheta }_{0}-{\varOmega}/2]\cup [{\vartheta }_{0}+{\varOmega}/2,{90}^{\circ}],\\ &{\psi }_{q}\in [-{90}^{\circ},{\psi }_{0}-{\varOmega}/2]\cup [{\psi }_{0}+{\varOmega} /2,{90}^{\circ}],\\ &p=1,2, ... ,P;q=1,2, ... ,Q。\end{aligned}$

(35)

式中：(${\vartheta _0},{\psi _0}$)为预测信号方向，修正主瓣宽度${\varOmega}$定义为波束图主瓣幅度下降到旁瓣级时的角度范围，$\varsigma$为旁瓣级幅度约束值，方向采样点(${\vartheta _p},{\psi _q}$)隶属于旁瓣区域，$\varepsilon$为加权系数，$\delta$为需要最小化的非负标量。为了应用二阶锥规划方法进行优化计算，首先需要将表达式(35)转化为线性形式。定义$NM \times NM$维Hermitian矩阵${\boldsymbol{R}} = {\widehat {\boldsymbol{R}}_x} + \varepsilon \overline {\boldsymbol{J}}$，其特征分解具有如下形式：

$\boldsymbol{R}=\boldsymbol{U\Lambda U}_{ }^{\mathrm{H}}。$

(36)

其中，$NM \times NM$维矩阵${\boldsymbol{U}}$为矩阵${\boldsymbol{R}}$的特征向量矩阵，$NM \times NM$维矩阵$\varLambda$为矩阵${\boldsymbol{R}}$的特征值矩阵。由于矩阵$\varLambda$为实数矩阵，可以推导获得如下表达式：

$\begin{aligned}[b] {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{R}}{{\boldsymbol{w}}^*} = & {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{U \varLambda U}}_{}^{\mathrm{H}}{{\boldsymbol{w}}^*} = {{\boldsymbol{w}}^{\mathrm{T}}}{\boldsymbol{U}}{({\boldsymbol{ \varLambda }}_{}^{0.5})^{\mathrm{H}}}{\boldsymbol{ \varLambda }}_{}^{0.5}{\boldsymbol{U}}_{}^{\mathrm{H}}{{\boldsymbol{w}}^*} =\\ & {({\boldsymbol{ \varLambda }}_{}^{0.5}{\boldsymbol{U}}_{}^{\mathrm{H}}{{\boldsymbol{w}}^*})^{\mathrm{H}}}({\boldsymbol{ \varLambda }}_{}^{0.5}{\boldsymbol{U}}_{}^{\mathrm{H}}{{\boldsymbol{w}}^*}) = ||{\boldsymbol{L}}_{}^{\mathrm{H}}{{\boldsymbol{w}}^*}|{|^2} 。\end{aligned}$

(37)

其中，$NM \times NM$维矩阵${\boldsymbol{L}}$的定义如下：

${\boldsymbol{L}} = {\boldsymbol{U}}{({\boldsymbol{ \varLambda}}_{}^{0.5})^{\mathrm{H}}} = {\boldsymbol{U \varLambda}}_{}^{0.5}。$

(38)

为了应用二阶锥规划方法进行优化问题求解，表达式(35)还需要被进一步转化为实数形式。为此引入3个$2NM \times 1$维实数向量和1个$2NM \times 2NM$维实数矩阵$\widetilde {\boldsymbol{L}}$：

${{\boldsymbol{a}}_{ 1}}(f,\theta ,\gamma ) = {[{{\mathrm{Re}}} {\{ {\boldsymbol{a}} (f,\theta ,\gamma )\} ^{\mathrm{T}}}, - {{\mathrm{Im}}} {\{ {\boldsymbol{a}} (f,\theta ,\gamma )\} ^{\mathrm{T}}}]^{\mathrm{T}}}，$

(39)

${{\boldsymbol{a}}_{ 2}}(f,\theta ,\gamma ) = {[{{\mathrm{Im}}} {\{ {\boldsymbol{a}} (f,\theta ,\gamma )\} ^{\mathrm{T}}},{{\mathrm{Re}}} {\{ {\boldsymbol{a}} (f,\theta ,\gamma )\} ^{\mathrm{T}}}]^{\mathrm{T}}}，$

(40)

${{\boldsymbol{y}}_2} = {[{{\mathrm{Re}}} {\{ {\boldsymbol{w}}\} ^{\mathrm{T}}},{{\mathrm{Im}}} {\{ {\boldsymbol{w}}\} ^{\mathrm{T}}}]^{\mathrm{T}}}，$

(41)

$\widetilde {\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{{\mathrm{Re}}} \{ {\boldsymbol{L}}_{}^H\} }&{{{\mathrm{Im}}} \{ {\boldsymbol{L}}_{}^H\} } \\ {{{\mathrm{Im}}} \{ {\boldsymbol{L}}_{}^H\} }&{ - {{\mathrm{Re}}} \{ {\boldsymbol{L}}_{}^H\} } \end{array}} \right]。$

(42)

定义2个$(2N M + 1) \times 1$维实数向量如下：

${\boldsymbol{b}} = {[ - 1,0,0,...,0]^{\mathrm{T}}}，$

(43)

${\boldsymbol{y}} = {[{y_1},{\boldsymbol{y}}_2^{\mathrm{T}}]^{\mathrm{T}}}，$

(44)

其中${y_1} = \delta$，则有如下表达式：

${{\boldsymbol{b}}^{\mathrm{T}}}{\boldsymbol{y}} = - {y_1} = - \delta。$

(45)

对表达式(35)中的非负标量$\delta$最小化等价于最大化${{\boldsymbol{b}}^{\mathrm{T}}}{\boldsymbol{y}}$。根据上述表达式可以得到下面表达式：

$\begin{split}||{\boldsymbol{L}}^{\mathrm{H}}{\boldsymbol{w}^*}|| =& ||{{\mathrm{Re}}} ({\boldsymbol{L}}^{\mathrm{H}}{\boldsymbol{w}^*}) + j{{\mathrm{Im}}} ({{\boldsymbol{L}}^{\mathrm{H}}}{\boldsymbol{w}^*})|| =\\ &\left\| {\begin{array}{*{20}{c}} {{\mathrm{Re}}} ({\boldsymbol{L}}^{\mathrm{H}}{\boldsymbol{w}^*}) \\ {{\mathrm{Im}}} ({\boldsymbol{L}}^{\mathrm{H}}{\boldsymbol{w}^*}) \end{array}} \right\| = \left\| {\widetilde {{\boldsymbol{L}}}} {{\boldsymbol{y}}_2} \right\| ，\end{split}$

(46)

$\boldsymbol{a}^{\mathrm{T}}(f,\theta,\gamma)=\boldsymbol{a}_1^{\mathrm{T}}(f,\theta,\gamma)\boldsymbol{y}_2+j\boldsymbol{a}_2^{\mathrm{T}}(f,\theta,\gamma)\boldsymbol{y}_2。$

(47)

利用上述表达式，可以将描述波束形成器的表达式(35)转化为如下具有4个约束条件的标准二阶锥规划形式：

$\begin{gathered} \mathop {\max }\limits_{\boldsymbol{y}} {{\boldsymbol{b}}^{\mathrm{T}}}{\boldsymbol{y}} subject to \\ 1)\, {\boldsymbol{a}}_{ 1}^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0}){{\boldsymbol{y}}_2} = 1, {\boldsymbol{a}}_{ 2}^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0}){{\boldsymbol{y}}_2} = 0; \\ 2)\, |{\boldsymbol{a}}_1^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q}){{\boldsymbol{y}}_2} + j {\boldsymbol{a}}_2^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q}){{\boldsymbol{y}}_2}| \leqslant \varsigma ; \\ 3)\, ||\widetilde {\boldsymbol{L}}{{\boldsymbol{y}}_2}|| \leqslant {y_1}; \\ {\vartheta _p} \in [ - {90^{\circ}},{\vartheta _0} - \varOmega /2] \cup [{\vartheta _0} + \varOmega /2 ,{90^{\circ}}],p = 1,2 , ...,P ，\\ {\psi _q} \in [ - {90^{\circ}},{\psi _0} - \varOmega /2] \cup [{\psi _0} + \varOmega /2 ,{90^{\circ}}],q = 1,2,...,Q 。\\ \end{gathered}$

(48)

根据表达式(48)中的第1个条件，可以构建如下所示的一个二维零锥限制条件：

$\begin{aligned}[b] &\left( {\begin{array}{*{20}{c}} {1 - {\boldsymbol{a}}_1^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0})} \\ {0 - ( - {\boldsymbol{a}}_2^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0}))} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right) - \\ &\left( {\begin{array}{*{20}{c}} 0&{{\boldsymbol{a}}_1^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0})} \\ 0&{ - {\boldsymbol{a}}_2^{\mathrm{T}}({f_r},{\vartheta _0},{\psi _0})} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{{\boldsymbol{y}}_2}} \end{array}} \right) = {{\boldsymbol{c}}_1} - {\boldsymbol{A}}_1^{\mathrm{T}}{\boldsymbol{y}} \in {\{ 0\} ^2}。\end{aligned}$

(49)

其中，$2 \times 1$维向量${{\boldsymbol{c}}_1}$和$2 \times (2NM + 1)$维矩阵${\boldsymbol{A}}_1^{\mathrm{T}}$均在上面的表达式(49)中定义。根据表达式(48)中的第2个条件，可以构建如下$PQ$个三维SOC限制条件：

$\begin{split} & \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{\boldsymbol{a}}_{ 1}^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q}){{\boldsymbol{y}}_2}} \\ {{\boldsymbol{a}}_{ 2}^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q}){{\boldsymbol{y}}_2}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right) - \left[ {\begin{array}{*{20}{c}} { - 1}&{{{\boldsymbol{0}}^{\mathrm{T}}}} \\ 0&{ - {\boldsymbol{a}}_{ 1}^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q})} \\ 0&{ - {\boldsymbol{a}}_{ 2}^{\mathrm{T}}({f_r},{\vartheta _p},{\psi _q})} \end{array}} \right]\\& \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {{{\boldsymbol{y}}_2}} \end{array}} \right) = {{\boldsymbol{c}}_{(p - 1)Q + q + 1}} - {\boldsymbol{A}}_{(p - 1)Q + q + 1}^{\mathrm{T}}{\boldsymbol{y}} \in {{\mathrm{SOC}}^{ 3}}, \\& {\vartheta _p} \in [ - {90^{\circ}},{\vartheta _0} - \varOmega /2] \cup [{\vartheta _0} + \varOmega /2 ,{90^{\circ}}], \\& {\psi _q} \in [ - {90^{\circ}},{\psi _0} - \varOmega /2] \cup [{\psi _0} + \varOmega /2 ,{90^{\circ}}], \\& p = 1,2 , ...,P ; q = 1,2,...,Q。\\[-1pt] \end{split}$

(50)

其中，$3 \times 1$维向量$\boldsymbol{c}_{(p-1)Q+q+1}$和$3 \times (2N M + 1)$维矩阵${\boldsymbol{A}}_{(p - 1)Q + q + 1}^{\mathrm{T}}$均在上面的表达式(50)中定义，${{\mathbf{0}}^{\mathrm{T}}}$为$1 \times 2N M$的零值向量。根据表达式(48)中的第3个条件，可以构建如下的一个$(2NM + 1)$维SOC限制条件：

$\begin{aligned}[b] \left( {\begin{array}{*{20}{c}} {{y_1}} \\ {\widetilde {\boldsymbol{L}}{{\boldsymbol{y}}_2}} \end{array}} \right) = &\left( {\begin{array}{*{20}{c}} 0 \\ {\boldsymbol{0}} \end{array}} \right) - \left( {\begin{array}{*{20}{c}} { - 1}&{{{\boldsymbol{0}}^{\mathrm{T}}}} \\ {\boldsymbol{0}}&{ - \widetilde {\boldsymbol{L}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{y_{ 1}}} \\ {{{\boldsymbol{y}}_2}} \end{array}} \right) = \\ &{{\boldsymbol{c}}_{PQ + 2}} - {\boldsymbol{A}}_{PQ + 2}^{\mathrm{T}}{\boldsymbol{y}} \in {{{\mathrm{SOC}}} ^{ 2N M + 1}} 。\end{aligned}$

(51)

其中，$(2NM + 1) \times 1$维向量${{\boldsymbol{c}}_{PQ + 2}}$和$(2NM + 1) \times (2NM + 1)$维矩阵${\boldsymbol{A}}_{PQ + 2}^{\mathrm{T}}$均在上面的表达式(51)中定义。现在可以构建表达式(32)中的向量${\boldsymbol{c}}$和矩阵${{\boldsymbol{A}}^{\mathrm{T}}}$，其表达式为：

${\boldsymbol{c}} = [{{\boldsymbol{c}}_1},{{\boldsymbol{c}}_2},...,{{\boldsymbol{c}}_{PQ + 1}},{{\boldsymbol{c}}_{PQ + 2}}]，$

(52)

${{\boldsymbol{A}}^{\mathrm{T}}} = [{\boldsymbol{A}}_{ 1}^{\mathrm{T}},{\boldsymbol{A}}_{ 2}^{\mathrm{T}},...,{\boldsymbol{A}}_{PQ + 1}^{\mathrm{T}},{\boldsymbol{A}}_{PQ + 2}^{\mathrm{T}}]。$

(53)

表达式(48)的二阶锥规划设计条件转化为表达式(32)的标准SOCP形式，可以采用内点方法进行求解。其中，对称锥$\kappa$组成为：

$\kappa = {\{ 0\} ^2} \times \underbrace {{{\mathrm{SOC}}^{ 3}} \times \cdot \cdot \cdot \times {{\mathrm{SOC}}^{ 3}}}_{PQ} \times {{\mathrm{SOC}}^{ 2 N M + 1}} \times {{{\mathrm{SOC}}} ^{ 2 N M + 1}} 。$

(54)

现在就可以采用内点方法对宽带共形阵自适应模式FIB设计的标准SOCP问题进行求解。

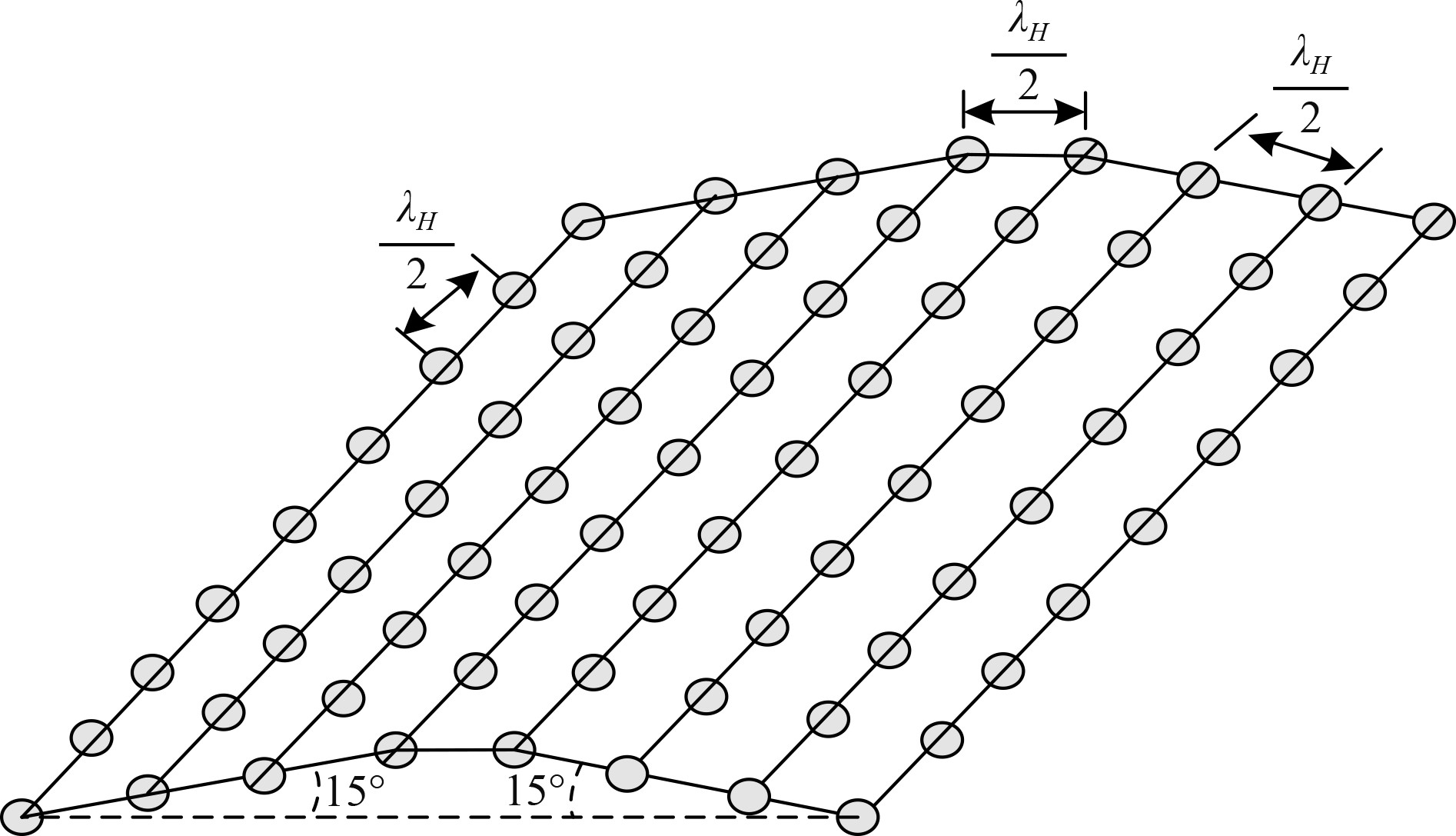
3 仿真验证

本文宽带共形阵优化波束设计方法适用于任意结构的宽带共形阵。本仿真中的宽带共形阵由2个$9 \times 4$平面阵组合而成，具体构成如图2所示。选取阵元间距选取为最高工作频率${f_H}$对应波长${\lambda _H}$的一半，选取节拍数$M = 7$，用于协方差矩阵计算的数据快拍数$K = 6\ 000$，归一化工作频带选取为$[0.2,0.4]$，修正主瓣宽度$\varOmega$选取为35°。表达式(31)中的空间方向$({\phi _{ d}},{\varphi _d})$分别在$[ - {90^{\circ}},{90^{\circ}}]$范围内以3°间隔进行选取，表达式(50)中的水平向方位角${\vartheta _p}$和垂直向高低角${\psi _q}$在$\varOmega \geqslant \sqrt {{{({\vartheta _p} - {\vartheta _0})}^2} + {{({\psi _q} - {\psi _0})}^2}} \geqslant \varOmega /2$靠近主瓣的旁瓣范围内以2度间隔进行选取，在其余旁瓣范围内以5°间隔进行选取。设置期望信号的实际入射方位为$({\theta _0},{\gamma _0}) = ( - {2^{\circ}},{2^{\circ}})$，选取期望信号的预测入射方位为$({\vartheta _0},{\psi _0}) = ({0^{\circ}},{0^{\circ}})$。设置阵元接收数据中的信噪比SNR为$0\ {\mathrm{dB}}$，2个干扰信号的入射方位分别为$({\theta _1},{\gamma _1}) = (30^{\circ},60^{\circ})$和$({\theta _2},{\gamma _2}) = ( - 30^{\circ}, - 60^{\circ})$，阵元接收数据中单个干扰信号的干噪比INR均为$60\ {\mathrm{dB}}$。根据表达式(21)计算，单个阵元接收数据中的信干噪比$SINR\mathrm{_{input}}\approx-66\ \mathrm{dB}$。

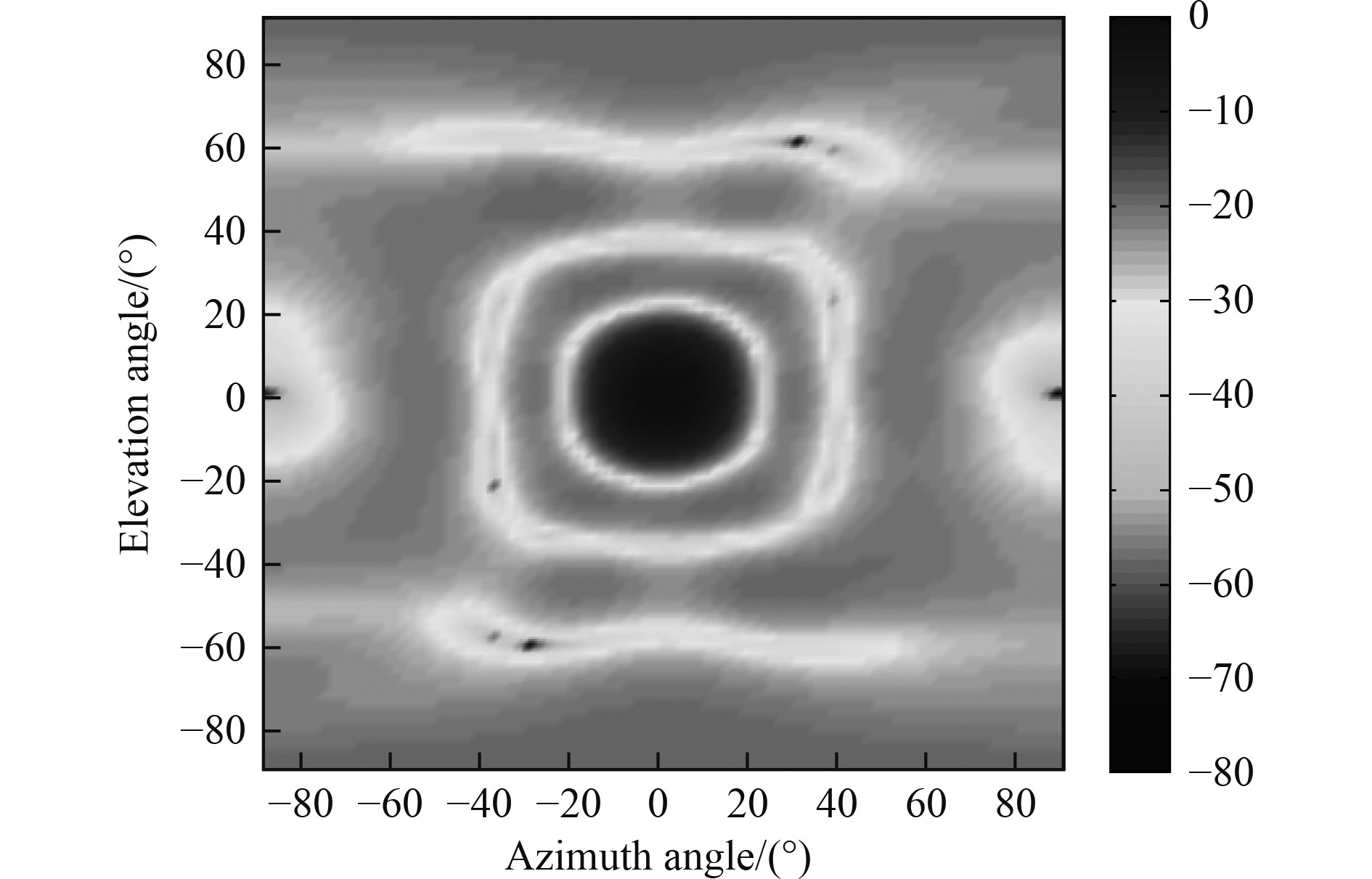
对于表达式(35)选取旁瓣级幅度约束值$\varsigma = 0.1$，设置加权系数$\varepsilon = 10$。采用内点方法计算宽带共形阵自适应FIB的复数加权向量${\boldsymbol{w}}$，根据表达式(22)计算FIB输出信号的信干噪比$SINR\mathrm{_{output}}\approx5.3\ \mathrm{dB}$，可见自适应FIB对空间干扰信号具备较强的抑制能力。自适应FIB波束图在工作频率${f_L}$、${f_r}$和${f_U}$上的结果分别如图3～图5所示，$(30\text{°},60\text{°})$和$( - 30\text{°}, - 60\text{°})$这2个入射方向上的干扰信号被有效抑制。

4 结　语

本文针对具有TDL结构和复数加权系数的宽带共形阵，提出基于SRV约束的自适应FIB设计，在参考频率上保持预测信号方向无偏响应以及旁瓣级恒定这2个限制条件下，根据对波束形成器输出功率值与平均空间响应偏差值这2项的加权和进行最小化处理的准则进行设计。通过将这种 FIB 设计问题转换为标准 SOCP 形式后，可以采用内点方法进行有效求解。相对现有自适应FIB优化设计方法，本文方法通过对约束条件和目标函数的合理调整，有效降低优化计算复杂度。仿真实例验证了该宽带共形阵FIB设计方法的有效性。