2. 中国海洋大学 信息科学与工程学部,山东 青岛 266100
2. School of Information Science and Engineering, Ocean University of China, Qingdao 266100 China
自主式水下航行器(Autonomous Underwater Vehicle,AUV)能够在各种复杂的环境下独立的完成任务[1],在海洋环境探测、海上作战等场合都发挥着重要作用。海洋环境的复杂性以及任务的多样性,使得AUV的控制技术面临更高要求,一方面需要其内部各系统传感器实时精准反馈数据,另一方面需要在海洋中应对各种流、浪以及涌的扰动。由于AUV执行任务时需要长时间维持在水下某一深度,因此如何对AUV进行高精度稳定的深度控制也成为重点问题。
目前在AUV工程应用中,PID控制仍是主要的控制方法之一[2],传统PID控制并没有主动抵抗海浪海流干扰的能力,在复杂多变的海洋环境中往往难以满足需求,因此各学者不断对控制算法进行改进。例如,LIN等[3]针对AUV的深度保持和姿态稳定控制的问题,建立了一种新型的无模型自适应模糊控制器,可以在未知水动力系数和时变外力情况下保持深度和姿态稳定,但是在AUV动态时的深度稳定能力未加验证。LIU等[4]提出一种层次抗扰深度跟踪控制方案,采用自适应前视距离的制导方法,并且对传统自抗扰控制引入了一种改进的速度饱和跟踪微分器,将深度控制问题转化为俯仰控制问题,使控制参数易于调整,克服了系统复杂性的问题。饶志荣等[5]针对欠驱动AUV的内外扰动问题设计了一种滑模控制器,在此基础上引入非线性扰动观测器用来观测外部干扰,所设计控制器可以较好的降低抖振,实现深度控制。杜度[6]针对PID参数调整复杂且耗时的问题,提出一种基于径向基函数神经网络的参数自整定PID控制方法应用于AUV的深度控制,能够快速地使AUV达到期望深度,但是未考虑舵片、推进器等执行机构带来的迟滞问题。
上述研究往往需要获得精确的数学模型,但是AUV具有较强的非线性和耦合性,获得精确的数学模型较为困难,而且各型号之间的AUV模型也不相同,通用性较差。无模型自适应控制(Model Free Adaptive Control,MFAC)是由侯忠生于1994年提出,通过引入伪梯度向量,利用被控对象的输入输出数据来在线估计动态线性化,克服了模型不确定的问题,所以本文采用基于数据驱动的无模型控制方法,仅利用系统的输入输出数据来对其进行控制[7 − 8]。自抗扰控制(Active Disturbance Rejection Control,ADRC)方法自从韩京清提出之后在机器人、电厂领域广为应用,解决了PID控制方法不能克服干扰的问题,但传统的ADRC控制参数整定较多,高志强提出了线性自抗扰控制(Linear Active Disturbance Rejection Control,LADRC),使得参数大大简化,提高了实际应用的便捷性[9 − 11]。
本文针对AUV在实际海洋环境中深度抗干扰能力较差的问题[12],提出一种基于自抗扰的无模型自适应深度控制方法(ADR-MFAC)。首先,通过无模型自适应控制方法(Model-Free Adaptive Control,MFAC)在线辨识AUV输入输出之间的非线性关系[13],设定深度和纵摇角为综合输出,尽量减小深度输出误差,保证AUV的运动平稳性;其次,为了进一步提高深度控制的抗干扰能力,结合自抗扰控制,设计基于自抗扰的无模型自适应控制器来进行深度控制,对其所受的内外扰动进行实时观测与补偿,使AUV在海洋执行任务时能够具备一定的抗海流干扰能力,最后,通过与传统PID控制、LADRC控制算法进行对比,利用Matlab仿真与海试试验证明其控制性能。
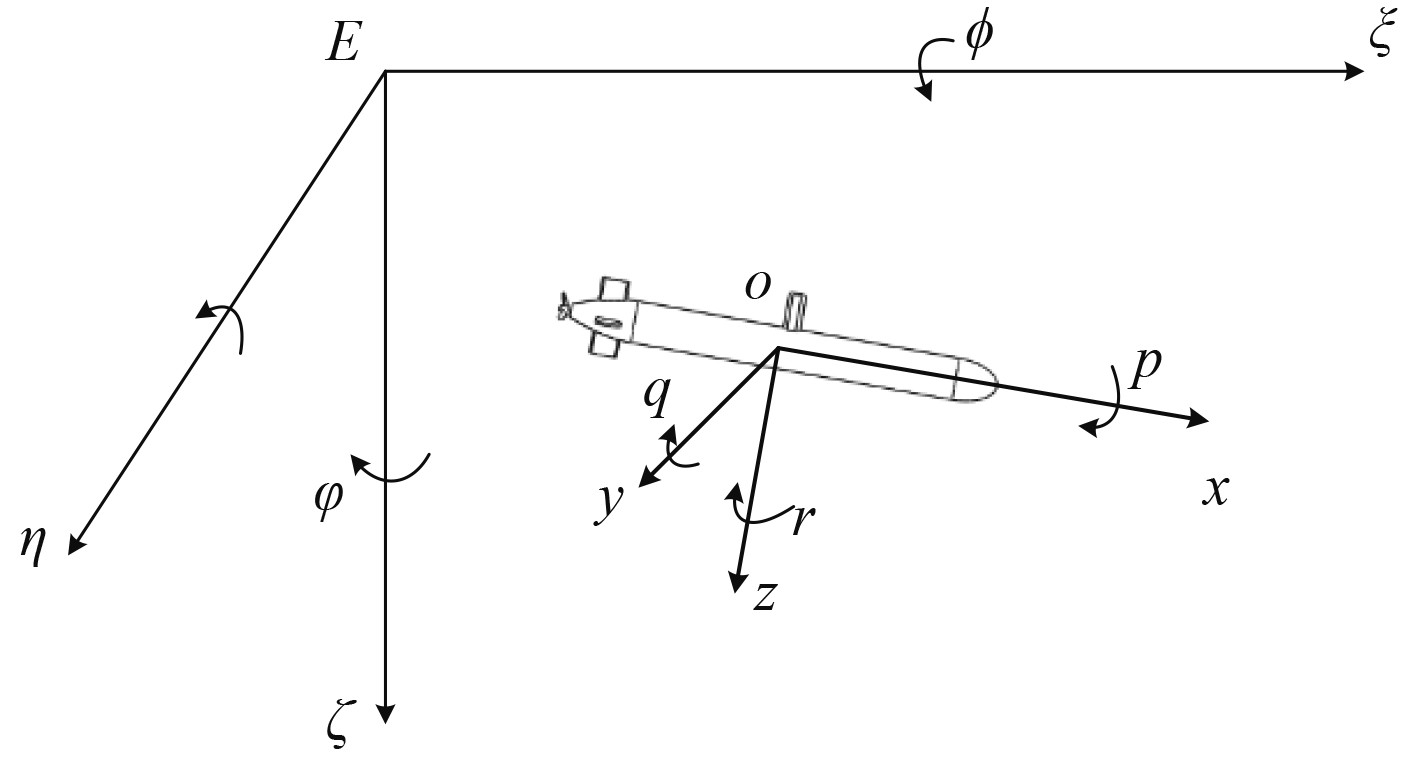
1 模型建立 1.1 AUV动力学方程为了更好地描述AUV的六自由度运动,建立2种坐标系[14],即大地坐标系
|
图 1 AUV坐标系 Fig. 1 AUV coordinate system |
设AUV运动坐标系下所受力和力矩矢量为
|
|
表 1 AUV自由度与参数符号 Tab.1 AUV degrees of freedom and parameter symbols |
本文采用机理法对其进行建模,假设AUV为刚体,在无旋海流中做非定常运动时,基于流体力学理论,其动力学方程为:
| $ {\boldsymbol{M}}\dot v + {\boldsymbol{C(v)}}v + {\boldsymbol{D(v)}}v + {\boldsymbol{g(\eta )}} = {\boldsymbol{\tau }}。$ | (1) |
式中:
AUV在空间进行运动时,地球自身的运动对其可以忽略,只需要考虑AUV在定系下的运动位置和方向,在运动时需要一个坐标转换矩阵来将其线速度角速度等按照一定顺序转换到定系上,欧拉角法较为直观,应用较为广泛,AUV运动学方程为:
| $ \dot \lambda {\text{ = }}{\boldsymbol{J(\lambda )}}v 。$ | (2) |
其中,
| $ {\boldsymbol{J(\lambda )}} = \left[ \begin{gathered} {{\boldsymbol{J}}_{\boldsymbol{1}}}{\boldsymbol{(}}{{\boldsymbol{\lambda }}_{\boldsymbol{a}}}{\boldsymbol{) }}{\text{ }}{0_{3 \times 3}} \\ {\text{ }}{0_{3 \times 3}}{\text{ }}{\boldsymbol{ }}{{\boldsymbol{J}}_{\boldsymbol{2}}}{\boldsymbol{(}}{{\boldsymbol{\lambda }}_{\boldsymbol{a}}}{\boldsymbol{)}} \\ \end{gathered} \right]。$ | (3) |
根据欧拉转动原理,定义由运动坐标系到大地坐标系下的转换矩阵
| $ {{\boldsymbol{J}}_{\boldsymbol{1}}}{\mathbf{(}}{{\boldsymbol{\lambda }}_{\boldsymbol{a}}}{\mathbf{)}} = \left[ \begin{array}{*{20}{c}} \cos \phi \cos \theta &\cos \phi \sin \theta \sin \varphi - \sin \phi \cos \varphi &\cos \phi \sin \theta \cos \varphi + \sin \phi \sin \varphi \\ \sin \phi \cos \theta &\sin \phi \sin \theta \sin \varphi + \cos \phi \cos \varphi &\sin \phi \sin \theta \cos \varphi - \cos \phi \sin \varphi \\ {\text{ }} - \sin \theta &\cos \theta \sin \varphi &\cos \theta \cos \varphi \\ \end{array} \right] 。$ | (4) |
定义由大地坐标系到运动坐标系下的转换矩阵
| $ {{\boldsymbol{J}}_{\boldsymbol{2}}}{\boldsymbol{(}}{{\boldsymbol{\lambda }}_{\boldsymbol{a}}}{\boldsymbol{)}} = \left[ \begin{array}{*{20}{c}} 1&\sin \varphi \tan \theta &\cos \varphi \tan \theta \\ 0&\cos \varphi & - \sin \varphi \\ 0&\sin \varphi /\cos \theta &\cos \varphi /\cos \theta \\ \end{array} \right] 。$ | (5) |
AUV大多搭载X舵或十字舵结构,本文研究的AUV配备十字舵。舵机通过控制水平舵与垂直舵达到期望的角度,从而控制AUV深度与航向,采用电动舵机,规定方向舵右舵为正,舵的数学模型为:
| $ {\delta }_{pra}=\left\{\begin{array}{*{20}{c}} {\delta }_{p\_\mathrm{max}}, {\dot{\delta }}_{r}t > {\delta }_{p\_\mathrm{max}},\\ {\dot{\delta }}_{r}t, {\dot{\delta }}_{r}t < \left|{\delta }_{{r}_{\mathrm{max}}}\right|,\\ \;-{\delta }_{p\_\mathrm{max}}, \;\;{\dot{\delta }}_{r}t < -{\delta }_{p\_\mathrm{max}}。\end{array}\right. $ | (6) |
| $ {\stackrel{·}{\delta }}_{r}=\frac{{\delta }_{p\_\mathrm{max}}}{{T}_{r}} 。$ | (7) |
式中:
可知,对AUV输入期望舵角、主推进器转速,经过动力学方程得到其空间受力,之后经过运动学方程得到其线速度与角速度输出,最后通过坐标变换得到其运动位姿,系统模型如图2所示。

|
图 2 AUV系统模型 Fig. 2 AUV system model |
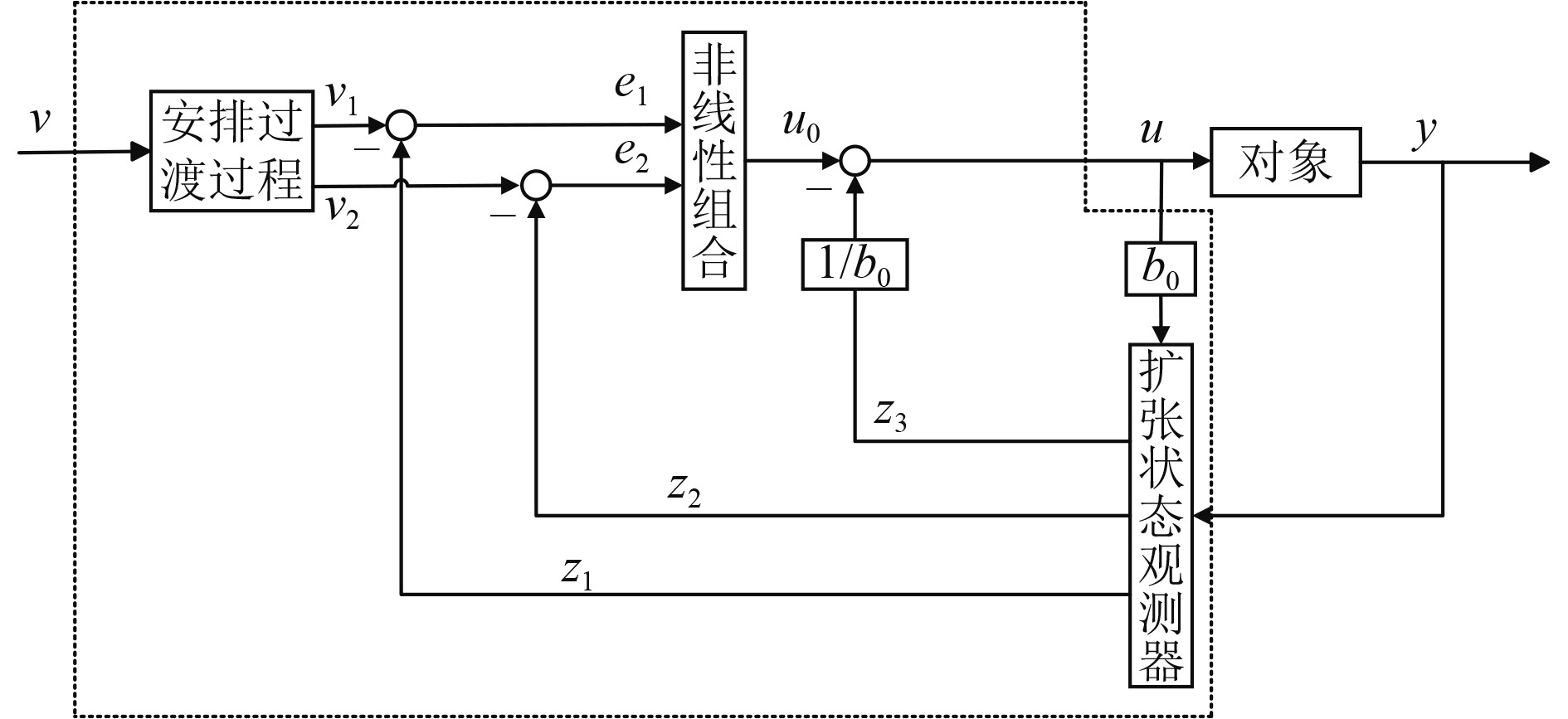
传统自抗扰控制器由跟踪微分器(Tracking Differentiator,TD)、扩张状态观测器(Extended State Observer,ESO)、状态误差反馈律(Nonlinear State Error Feedback,NLSEF)组成,TD用于合理安排过渡过程,ESO观测系统所受扰动,NLSEF形成控制律。本文在保留自抗扰控制器的结构上,采用了线性扩张状态观测器(Linear Expansion State Observer,LESO),并对其采取了无模型自适应控制律进行反馈并补偿扰动[15]。有助于提高系统的稳定性、精确性和鲁棒性,以满足不断变化的工程需求。传统自抗扰控制器框图如图3所示。
|
图 3 自抗扰控制器框图 Fig. 3 Block diagram of the ADRC |
跟踪微分器在系统输入信号突变时,要想使其快速恢复稳态,必然会有较大的超调量,可以合理安排过渡过程,使输入较为平稳的变化,解决快速性和超调性的矛盾,使得整个控制系统易于调整,采用二阶离散表达式如下:
| $ \left\{ \begin{split} &fh = {\rm fhan}({v_1}(k) - v(k),{v_2}(k),r,h) ,\\ & {v_1}(k + {\text{1}}) = {v_1}(k) + h{v_2}(k), \\ & {v_2}(k + {\text{1}}) = {v_2}(k) + h{\text{ }}fh 。\end{split} \right. $ | (8) |
式中:
状态观测器是ADRC的核心部分,对系统所受的扰动进行实时预估并补偿,不基于系统的扰动模型,仅依赖输入输出信息即可,鲁棒性较好。传统的ADRC是非线性状态观测器,但是其需要整定的参数过多,并且在实际中调参较为复杂[16],本文采用线性状态观测器(LESO),参数只有2个,易于调整。
| $ \ddot y = p(y,\dot y,d,t) + bu 。$ | (9) |
式中:
| $ \left\{ \begin{gathered} {{\dot x}_{\text{1}}} = {x_{\text{2}}} , \\ {{\dot x}_{\text{2}}} = {x_{\text{3}}} + {b_{\text{0}}}u, \\ {{\dot x}_{\text{3}}} = \dot p , \\ y = {{\dot x}_{\text{1}}}。\\ \end{gathered} \right. $ | (10) |
式中,
| $ \left\{ \begin{gathered} {{\dot {\hat x}}_{\text{1}}} = {\beta _{\text{1}}}(y - {{\hat x}_{\text{1}}}) + {{\hat x}_{\text{2}}} , \\ {{\dot {\hat x}}_{\text{2}}} = {\beta _{\text{2}}}(y - {{\hat x}_{\text{1}}}) + {{\hat x}_{\text{3}}} + {b_{\text{0}}}u , \\ {{\dot {\hat x}}_{\text{3}}} = {\beta _{\text{3}}}(y - {{\hat x}_{\text{1}}}) 。\\ \end{gathered} \right. $ | (11) |
式中:
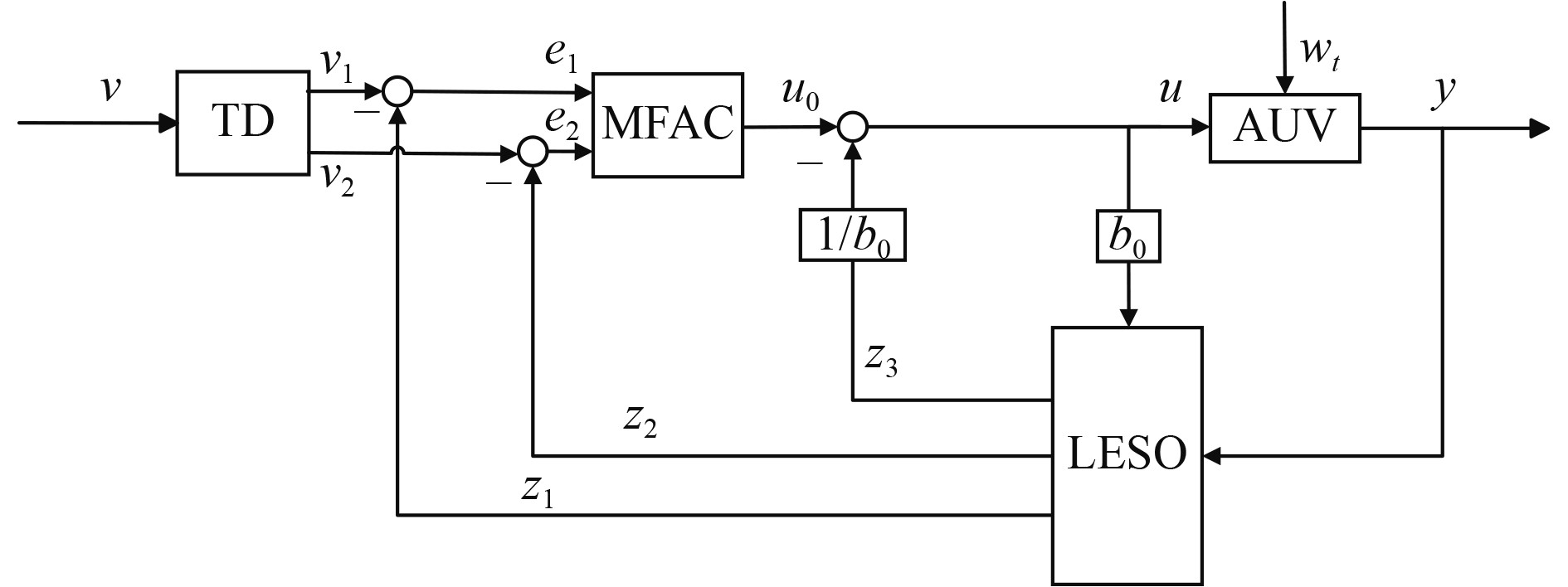
将无模型自适应控制律引入自抗扰控制,MFAC的输入是经过TD的输出,将线性状态观测器的扰动加入到MFAC的控制变量中[18]。系统结构框图如图4所示。
|
图 4 ADR-MFAC框图 Fig. 4 ADR-MFAC block diagram |
有扰动的非线性系统可表示为:
| $ y(k + {\text{1}}) = f(y(k),...,y(k - {i_y}),u(k),...,u(k - {i_u})) + f(k) 。$ | (12) |
系统的动态线性化方程为:
| $ y(k + {\text{1}}) = y(k) + \chi (k)\varDelta u(k)。$ | (13) |
基于PDDL的动态线性化模型如下:
| $ y(k + {\text{1}}) = y(k) + \chi (k)\frac{{\rho \hat \chi (k)}}{{\lambda + {{\left| {\hat \chi (k)} \right|}^2}}}(y*(k + {\text{1}}) - y(k)) + \varDelta f(k)。$ | (14) |
其中
| $ u(k) = u(k - {\text{1}}) - \frac{{\rho \hat \chi (k)}}{{\lambda + {{\left| {\hat \chi (k)} \right|}^2}}}(y*(k + {\text{1}}) - y(k) - \varDelta f(k)) 。$ | (15) |
将TD跟踪输出信号加入到控制变量中,舵角控制律为:
| $ u(k) = u(k - {\text{1}}) - \frac{{\rho \hat \chi (k)}}{{\lambda + {{\left| {\hat \chi (k)} \right|}^2}}}(y*(k + {\text{1}}) - y(k) - \varDelta {f(k)})。$ | (16) |
式中:
为了验证本文所设计的ADR-MFAC方法,本文基于Matlab对AUV深度控制进行仿真,并将ADR-MFAC控制与PID控制和线性自抗扰控制进行了对比。本文基于中国海洋大学研发的旗鱼260型设计了仿真模型:质量m=100 kg,长度L=2.5 m,惯性张量
仿真实验中,设定航速为2 kn,初始深度0 m,仿真时间设置为60 s,步长0.01 s。PID控制参数为:
|
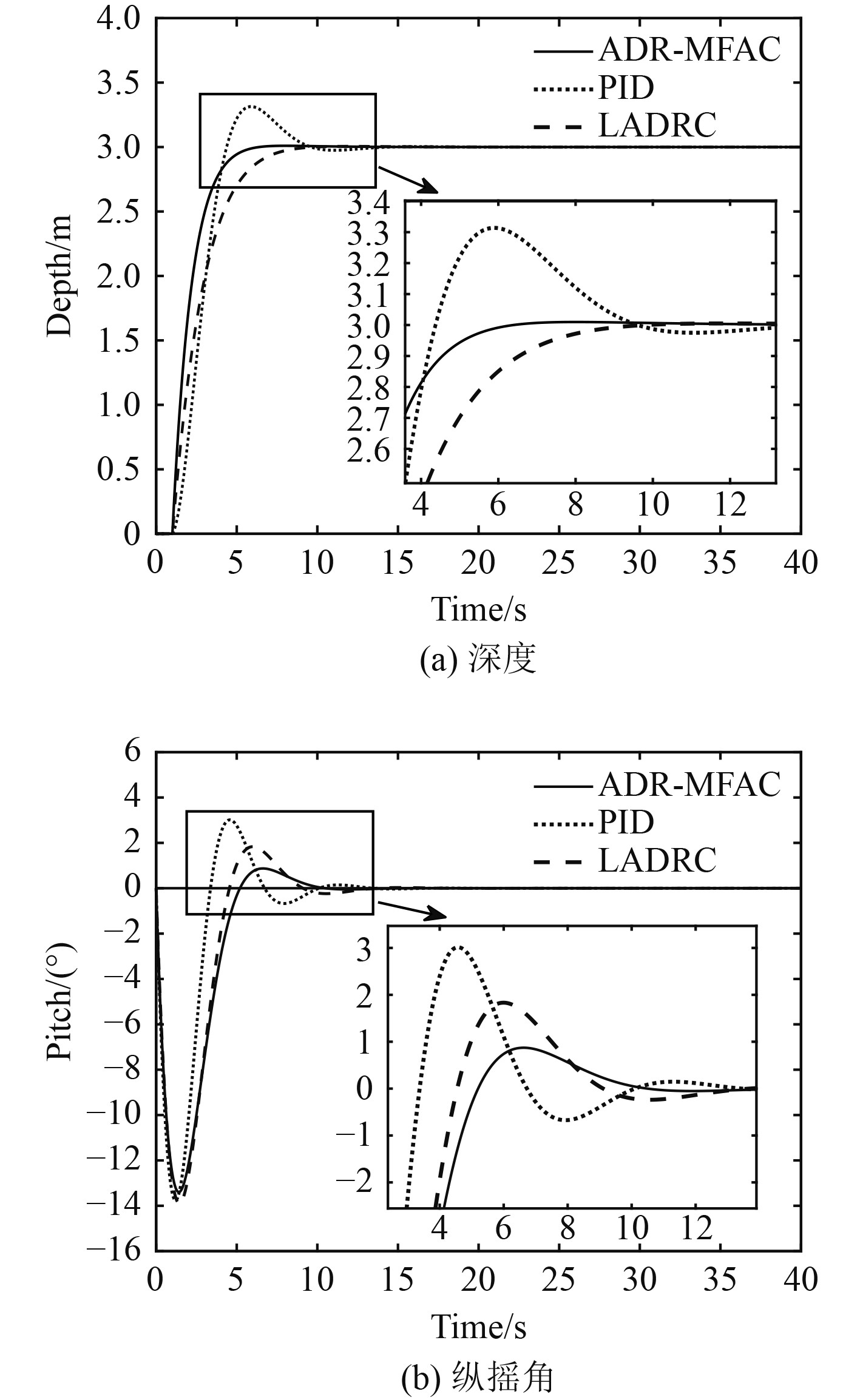
图 5 无干扰下深度与纵摇仿真曲线 Fig. 5 Depth and pitch simulation curves without interference |
由图5(a)可知,在无外加干扰条件下,3种控制方法均能到达期望深度,但是PID控制超调量最大,达到了0.3 m,LADRC和ADR-MFAC控制超调量较小,几乎没有震荡,但是PID和LADRC控制器调整时间较长,需要10 s以上能达到3 m,ADR-MFAC控制器在8.8 s即可调整到期望深度。纵摇角反映了AUV在水下航行时纵向的平稳程度,纵摇角在稳定时越小说明其在水下运动时无较大的波动,对AUV的安全与机动性较为重要。从图5(b)可知,初始下潜时AUV会在2 s内达到大约14°的纵摇角来完成快速下潜,到达期望深度后快速回到0°附近,但是PID与LADRC控制的纵摇角在到达3 m后会有5°和2°的超调,ADR-MFAC控制超调只有1°。因此,ADR-MFAC控制器在无干扰时可以较快的达到期望深度,并保证纵向运动平稳,深度航行比PID、LADRC控制较为稳定。具体控制参数如表2所示。
|
|
表 2 无干扰下控制器性能指标 Tab.2 Controller performance indicators without interference |
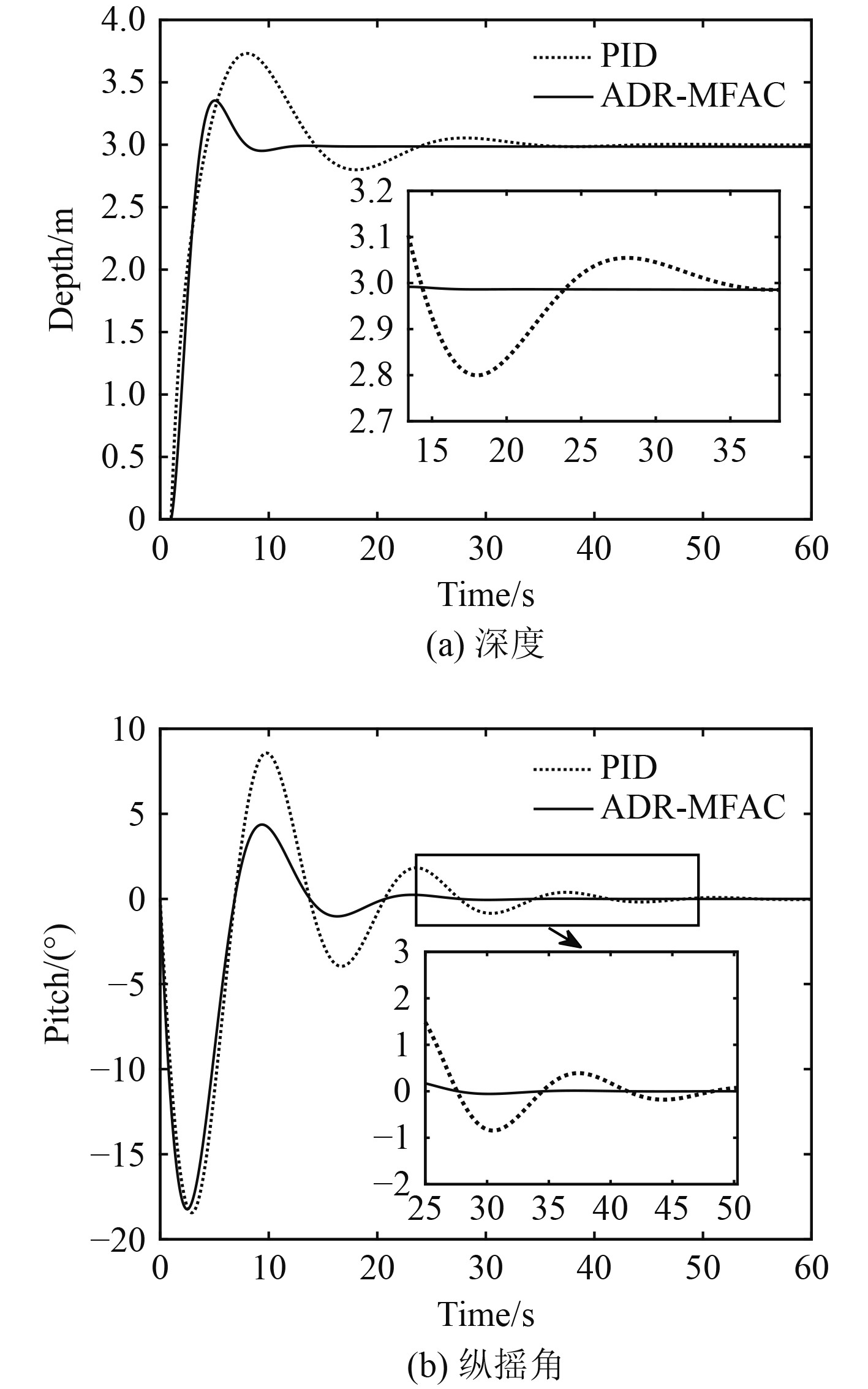
为了验证ADR-MFAC控制器的抗扰动能力,模拟海上真实的工况环境,引入海流干扰
|
图 6 有干扰下深度与纵摇曲线 Fig. 6 Depth and pitch curves under interference |
可知,在施加海流干扰后,PID控制下的深度会出现比较长时间的震荡,震荡幅度在−0.2~0.05 m,超调量达到了0.73 m,ADR-MFAC控制器超调量较小,为0.35 m,几乎没有震荡;PID控制需要30s左右才能进入稳态,而ADR-MFAC控制器在10 s左右就能稳定在3 m深度,这一点从图6(b)也可以看出,PID控制下的纵摇角震荡频率与幅度较大,说明PID控制对于有海流干扰时稳定性较差。ADR-MFAC控制下的纵摇角更小,且其深度控制性能指标优于PID控制。具体控制参数如表3所示。
|
|
表 3 有干扰下控制器性能指标 Tab.3 Controller performance indicators under interference |
综合来看,无外加干扰时,3种控制方法均能到达指定深度,相比于PID控制、LADRC控制,ADR-MFAC方法在保证快速性的同时可以较稳定的实现深度控制;有外界干扰时虽然会产生小幅超调,但是也能较快恢复到稳定状态,鲁棒性较强。本文设计的ADR-MFAC深度控制器充分发挥了自抗扰以及无模型自适应控制的优势,改善了系统模型不确定性的影响,提高了系统的响应速度,并且具有一定的抗扰动性。
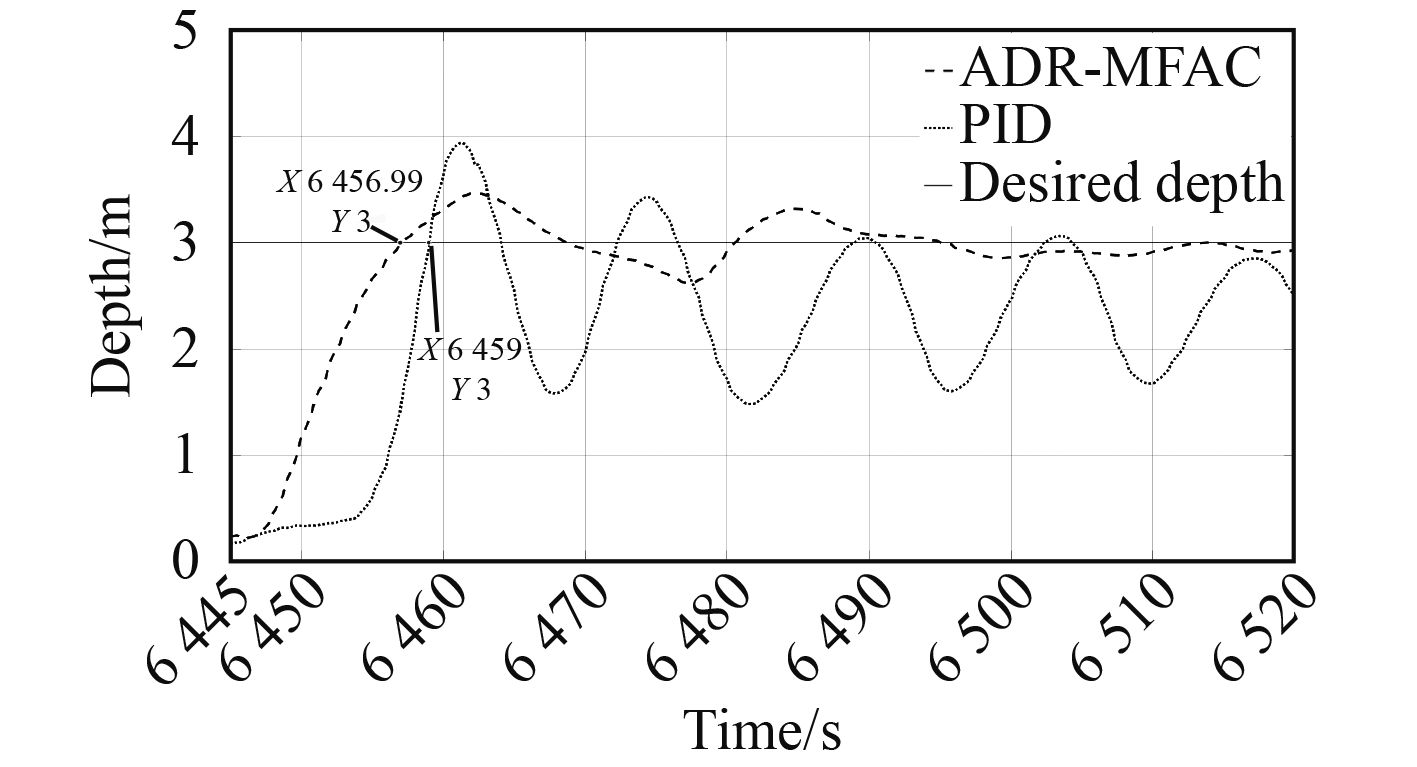
4 海试验证本文采用中国海洋大学UVL实验室自研的旗鱼260型AUV进行海试,搭载尾部主推进器、十字舵设计,最大航速4 kn,海试区域选择青岛团岛湾,海况1级,与PID定深控制器进行对比,验证ADR-MFAC的控制性能。得到定深曲线如图7所示。
|
图 7 3 m定深测试曲线 Fig. 7 3 m depth test curve |
AUV航速设定为2 kn,选择1条直线进行定深试验,在水面航行平稳后对其发送定深指令,期望深度为3 m,AUV收到指令后在
|
|
表 4 海试定深性能指标 Tab.4 Performance indicators of sea trial depth |
相比于PID控制器,ADR-MFAC控制器深度调节时间减小了21.4%,稳态误差缩小70%,均方根值减小了17.8%,超调减小了51%。因此,所设计的ADR-MFAC控制器提高了AUV控制系统的快速性与稳定性,在实际应用中可行。
5 结 语针对AUV深度控制易受扰动的问题,本文设计了一种基于无模型自抗扰(ADR-MFAC)的定深控制器,在自抗扰控制中引入无模型自适应控制律(MFAC),并且利用线性状态观测器(LESO)对扰动进行观测补偿,仿真结果表明,在无干扰情况下,此方法比LADRC控制、PID控制调节时间更短,响应速度较快;在有海流干扰时,ADR-MFAC方法虽然会产生小幅度超调,但是也能较快地稳定到期望深度,具有较高的控制精度。此外,经过海上试验验证了此方法相比于PID控制,可以缩短系统调节时间与稳态误差,均方值更小,具有一定的抗干扰能力。未来将继续研究自抗扰控制的参数整定问题,并拓展到三维路径跟踪中。
| [1] |
侯海平, 付春龙, 赵楠, 等. 智能自主式水下航行器技术发展研究[J]. 舰船科学技术, 2022, 44(1): 86-90. |
| [2] |
陈增强, 宋莞平, 孙明玮, 等. 自主式水下航行器自抗扰控制[J]. 哈尔滨工程大学学报, 2021, 42(11): 1625-1631. |
| [3] |
LIN Y H, YU C M, WU I C, et al. The depth-keeing performance of autonomous underwater vehicle advancing in waves integrating the diving control system with the adaptive fuzzy controller[J]. Ocean Engineering, 2023, 268: 113609. DOI:10.1016/j.oceaneng.2022.113609 |
| [4] |
LIU F, LAN T, WANG S. A collaborative control method for multi-UAVs based on ADRC control[C]//2020 39th Chinese Control Conference (CCC), IEEE, 2020: 7014−7019.
|
| [5] |
饶志荣, 董绍江, 王军, 等. 基于干扰观测器的AUV深度自适应终端滑模控制[J]. 北京化工大学学报(自然科学版), 2021, 48(1): 103-110. |
| [6] |
杜度. 基于RBF神经网络参数自整定的AUV深度控制[J]. 水下无人系统学报, 2019, 27(3): 284-289. |
| [7] |
侯忠生, 许建新. 数据驱动控制理论及方法的回顾和展望[J]. 自动化学报, 2009, 35(6): 650-667. DOI:10.3724/SP.J.1004.2009.00650 |
| [8] |
张茂帅, 侯忠生. 带有迭代学习外环的快速路入口匝道无模型自适应预测控制[J]. 控制理论与应用, 2023, 40(5): 781-791. |
| [9] |
ZHANG F, HOU, J, NING D, et al. Depth control of an oil bladder type deep-sea AUV based on fuzzy adaptive linear active disturbance rejection control[J]. Machines, 2022, 10, 163.
|
| [10] |
SUN Y, CHAI P, ZHANG G, et al. Sliding mode motion control for AUV with dual-observer considering thruster uncertainty[J]. Journal of Marine Science and Engineering, 2022, 10, 349.
|
| [11] |
LIU C, XIANG X, YANG L, et al. A hierarchical disturbance rejection depth tracking control of underactuated AUV with experimental verification[J]. Ocean Engineering, 2022, 264: 112458. DOI:10.1016/j.oceaneng.2022.112458 |
| [12] |
ZHANG Y, DENG H, LI Y. Depth control of AUV using sliding mode active disturbance rejection control[C]//2018 3rd International Conference on Advanced Robotics and Mechatronics (ICARM). IEEE, 2018: 300−305.
|
| [13] |
LI X, REN C, MA S, et al. Compensated model-free adaptive tracking control scheme for autonomous underwater vehicles via extended state observer[J]. Ocean Engineering, 2020, 217: 107976. DOI:10.1016/j.oceaneng.2020.107976 |
| [14] |
ZHANG Z, LIU B, WANG L. Autonomous underwater vehicle depth control based on an improved active disturbance rejection controller[J]. International Journal of Advanced Robotic Systems, 2019, 16(6): 1729881419891536.
|
| [15] |
楼鉴路, 李文魁, 周铸, 等. 基于线性自抗扰控制的AUV深度控制研究[J]. 舰船科学技术, 2023, 45(6): 96-101. |
| [16] |
LIU K, WANG H, XU X, et al. Development and trials of a novel deep-sea multi-joint autonomous underwater vehicle[J]. Ocean Engineering, 2022, 265: 112558. DOI:10.1016/j.oceaneng.2022.112558 |
| [17] |
XU J, HUANG F, WU D, et al. A general motion control framework for an autonomous underwater vehicle through deep reinforcement learning and disturbance observers[J]. Journal of the Franklin Institute, 2023, 360(8): 5728-5758. DOI:10.1016/j.jfranklin.2023.03.056 |
| [18] |
WU C, DAI Y, SHAN L, et al. Attitude angle compensated model-free adaptive trajectory tracking control for autonomous underwater vehicle[C]//2021 International Conference on Intelligent Technology and Embedded Systems (ICITES). IEEE, 2021: 1−7.
|
 2024, Vol. 46
2024, Vol. 46
