2. 河南省水下智能装备重点实验室,河南 郑州 450015;
3. 中国舰船研究院,北京 100192
2. Henan Key Laboratory of Underwater Intelligent Equipment, Zhengzhou 450015, China;
3. China Ship Research and Development Academy, Beijing 100192, China
水下航行器作为探测海洋的重要工具,已经被广泛应用于资源勘探、地形测绘、军事侦察、时敏打击等领域。路径规划作为水下航行器任务规划系统的核心模块,直接体现了水下航行器的智能化程度。常见的路径规划算法有基于图搜索算法的规划方法、基于虚拟力的规划方法以及基于群智能算法的规划方法。基于图搜索算法的规划方法以A*算法[1]、RRT算法[2]为代表,此类方法面临着栅格化环境建模而带来的不平滑路径以及随规划精度迅速增加的计算代价等问题;基于虚拟力的规划方法以人工势场法[3]为代表,此类方法缺乏对全局信息的把握,往往难以规划出全局最优的结果,并会在某些特殊位置出现合力为零而停止前进的情况;群智能算法是一类模拟生物种群行为或自然现象的算法,具有易于实现、适应性强、计算资源可控、求解效果优秀等优点,已被科研人员越来越广泛地应用于各类智能体的路径规划[4]。黄鹤等[5]针对复杂环境下蝠鲼觅食算法全局搜索能力不足、易陷入局部最优等问题,提出了一种改进蝠鲼觅食的优化算法,用于水下航行器的三维路径规划。刘兴盛等[6]针对蚁群算法计算耗时大、求解效果不佳等问题,提出了一种改进蚁群算法,用于水下机器人的路径规划。徐炜翔等[7]针对传统群智能算法结构复杂、参数多、全局搜索能力不足等问题,将飞蛾火焰算法引入水下航行器全局路径规划模型,以期降低路径总能耗。
本文提出一种差分-灰狼算法,该算法将差分算子引入灰狼算法头狼群体的更新中,在保留灰狼算法局部搜索能力的同时有效增强了其全局探索能力,降低了停滞于局部最优的可能性。此外,本文采用B样条曲线对水下航行器的路径进行参数化建模,可生成更易于路径跟踪控制的平滑路径。仿真实验结果表明,本文所提出的改进算法能够有效规避各种环境障碍物,为水下航行器规划出高安全、低能耗的路径,并在平均值、最优值以及最劣值等指标方面表现明显优于等差分进化算法和灰狼算法。
1 水下航行器路径规划优化模型 1.1 路径参数化方法B样条曲线具有易于生成、灵活多样以及线条平滑等优点,能够有效贴合水下航行器的运动轨迹,可为路径跟踪控制提供很大便利[8]。鉴于B样条曲线的诸多优势,本文以其为基础对水下航行器路径进行参数化建模。
B样条曲线的定义如下:
| $ P(u) = \sum\limits_{i = 0}^n {{d_i}} {N_{i,k}}(u)。$ | (1) |
式中:
| $ \left\{\begin{split} & {N}_{i,k}(u)=\left\{\begin{array}{l}1,\text{ }若{u}_{i}\leqslant u\leqslant {u}_{i+1},\\ 0,\text{ }其他情况,\end{array}\right.\\ & {N}_{i,k}(u)=\displaystyle \frac{u-{u}_{i}}{{u}_{i+k}-{u}_{i}}{N}_{i,k-1}(u)+\frac{{u}_{i+k+1}-u}{{u}_{i+k+1}-{u}_{i+1}}{N}_{i+1,k-1}(u),\\& \displaystyle \frac{0}{0}\text=0,\end{split} \right.\\[-1pt]$ | (2) |
式中,基函数取决于一系列非递减的参数化节点
| $ \sum\limits_{i = 0}^n {{N_{i,k}}(t) \equiv 1} 。$ | (3) |
路径总长度不仅关系着水下航行器沿迹能量以及时间消耗,还直接体现了路径规划算法的优劣。本文以路径总长度最小化为目标函数构建约束优化模型,具体步骤如下:
将B样条曲线离散化为若干个等距路径点
| $ L = \sum\limits_{i = 2}^n {\sqrt {{{({p_{i,x}} - {p_{i - 1,x}})}^2} + {{({p_{i,y}} - {p_{i - 1,y}})}^2}} }。$ | (4) |
式中:
为了保证路径的安全性,路径点
| $ {C}_{si}=\left\{\begin{array}{l}1,\text{ }\sqrt{{({p}_{i,x}-Ob{s}_{x})}^{2}+{({p}_{i,y}-Ob{s}_{y})}^{2}}\leqslant{d}_{{\mathrm{safe}}},\\ 0,\text{ }其他情况。\end{array}\right. $ | (5) |
式中:
基于各个路径点的安全性,可以计算整条路径安全性
| $ {C_{\rm safe}} = \sum\limits_{i = 1}^n {{C_{si}}}。$ | (6) |
当
以B样条曲线控制点坐标为设计变量,路径总长度最短为目标函数,路径安全性为约束条件,可以得到如下的水下航行器路径规划优化模型:
| $ \begin{gathered} {\mathrm{Minimize}}:L(X) \\ S.t.{\text{ }}{C_{\rm safe}}(X) = 0。\\ \end{gathered} $ | (7) |
式中:
差分进化算法(DE)[9]是一种经典的群智能算法,具有易于实现、参数简单、高效稳定等优点,却面临着进化算子相对简单、求解效果欠佳的缺点。灰狼算法(GWO)[10]模拟了狼群捕食这一群体行为,对连续优化问题具有出色的求解效果,并在各类工程优化问题中得到了广泛应用。然而,灰狼算法进化算子对头狼群体(
步骤1 初始化
设置种群规模PopSize,最大迭代次数MaxIter并按下式生成初始种群Pop:
| $ Pop(Iter) = ({X_{ub}} - {X_{lb}}) \cdot ran{d_{[0,1]}} + {X_{lb}} 。$ | (8) |
式中:Iter为当前迭代计算的次数;Xlb=[lb1,lb2,…,lbdim] ;Xub=[ub1,ub2,…,ubdim];ubi(i=1,…,dim)和lbi(i=1,…,dim)分别为第i维设计变量的上下界;dim为问题的维数;rand[0,1]表示区间[0,1]中的一个随机数。
步骤2 差分引导
灰狼算法(GWO)中头狼群体所处位置会直接影响整个种群前进的方向,进而影响最终规划效果。为了增强灰狼算法的全局探索能力,将差分算子引入到头狼位置中以改善相关个体质量。记当前种群中最优的3个个体为头狼,并依次记为
| $ \left\{ {\begin{array}{l} {{X_{\alpha *}}(Iter) = {X_\alpha }(Iter) + F * ({X_\beta }(Iter) - {X_\gamma }(Iter))}, \\ {{X_{\beta *}}(Iter) = {X_\beta }(Iter) + F * ({X_\gamma }(Iter) - {X_\alpha }(Iter))}, \\ {{X_{\gamma *}}(Iter) = {X_\gamma }(Iter) + F * ({X_\alpha }(Iter) - {X_\beta }(Iter))} 。\end{array}} \right. $ | (9) |
步骤3 个体竞优
为了使头狼群体具有更优位置并加快收敛速度,差分-灰狼算法引入了个体竞优机制,具有更优适应度值的个体将被保留下来,其具体操作步骤如下:
| $ \left\{\begin{array}{{l}}{X}_{\alpha }(Iter) = {X}_{\alpha *}(Iter),f({X}_{\alpha *}(Iter)) \leqslant f({X}_{\alpha }(Iter)) ,\\ {X}_{\beta }(Iter) = {X}_{\beta *}(Iter),\text{ }f({X}_{\beta *}(Iter)) \leqslant f({X}_{\beta }(Iter)) ,\\ {X}_{\gamma }(Iter) = {X}_{\gamma *}(Iter),f({X}_{\gamma *}(Iter)) \leqslant f({X}_{\gamma }(Iter)) 。\end{array} \right. $ | (10) |
步骤4 更新种群位置
灰狼算法(GWO)具有性能出色的种群进化算子,差分-灰狼算法借鉴灰狼算法的进化算子进行种群位置的更新,其具体操作方法如下:
| $ {D_i} = \left| {{C_i} \cdot {X_p}(Iter) - {X_i}(Iter)} \right|, $ | (11) |
| $ {X_i}(Iter + 1) = {X_p}(Iter) - {A_i} \cdot {D_i} 。$ | (12) |
式中:Xi为当前种群第i个个体所在位置;Xp为猎物所在位置。Ai和Ci为系数向量,计算式为:
| $ {A_i} = 2a \cdot {r_1} - a ,$ | (13) |
| $ {C_i} = 2 \cdot {r_2} ,$ | (14) |
| $ a = 2 - 2Iter/{\text{Max}}Iter 。$ | (15) |
其中:r1与r2是[0,1]之间的随机参数;a从2线性减少至0。
步骤5 迭代求解
按步骤1~步骤4循环进行直到达到预设最大迭代次数,并输出全局最优个体作为求解结果。
3 仿真实验与讨论 3.1 实验设定为了测试差分-灰狼算法(DGWO)的性能,本文设计了仿真对比试验,每个算例独立重复运行30次,并绘制等权均值收敛曲线。此外,每个测试算例统计了均值、最优值以及最劣值3项指标,并将每项指标中最优表现的算法进行了额外标注。
3.2 仿真实验 3.2.1 仿真算例1仿真算例1的路径起点设置为(5,45),路径终点设置为(45,5),在起点与终点之间随机分布16个半径为2的圆柱形障碍物。表1汇总了该算例下差分进化算法(DE)、灰狼算法(GWO)以及差分-灰狼算法(DGWO)3种算法的统计运行结果。图1为3种算法所规划的行驶路线,图2为3种算法的等权均值收敛曲线。
|
|
表 1 算例1测试结果 Tab.1 Test results of case 1 |
|
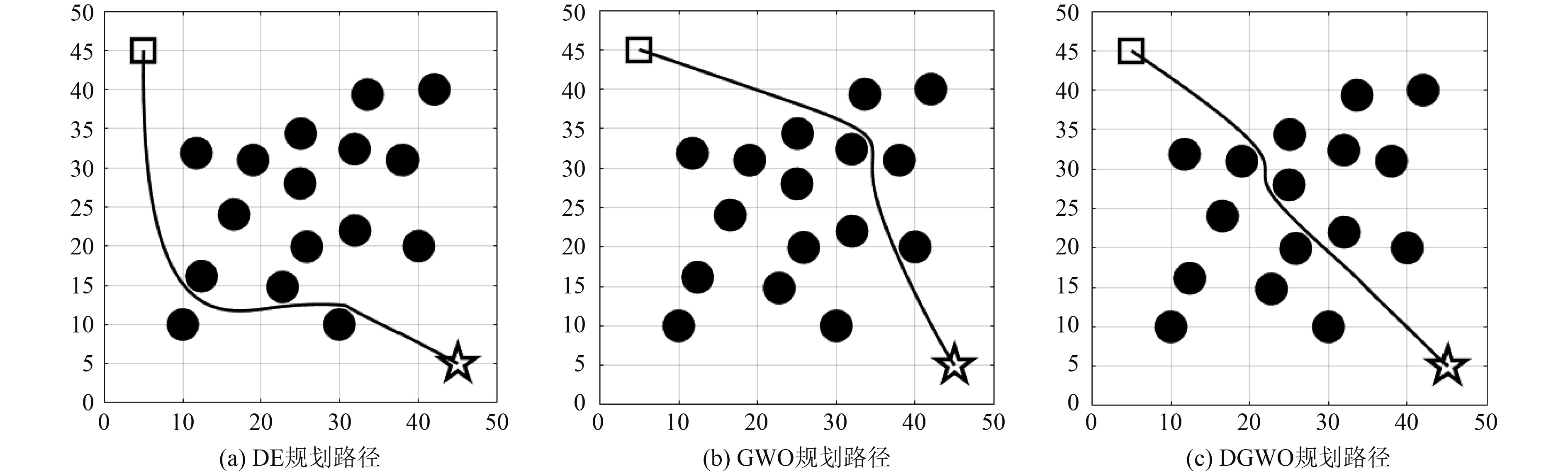
图 1 算例1 路径规划图 Fig. 1 Path planning results of case 1 |
|
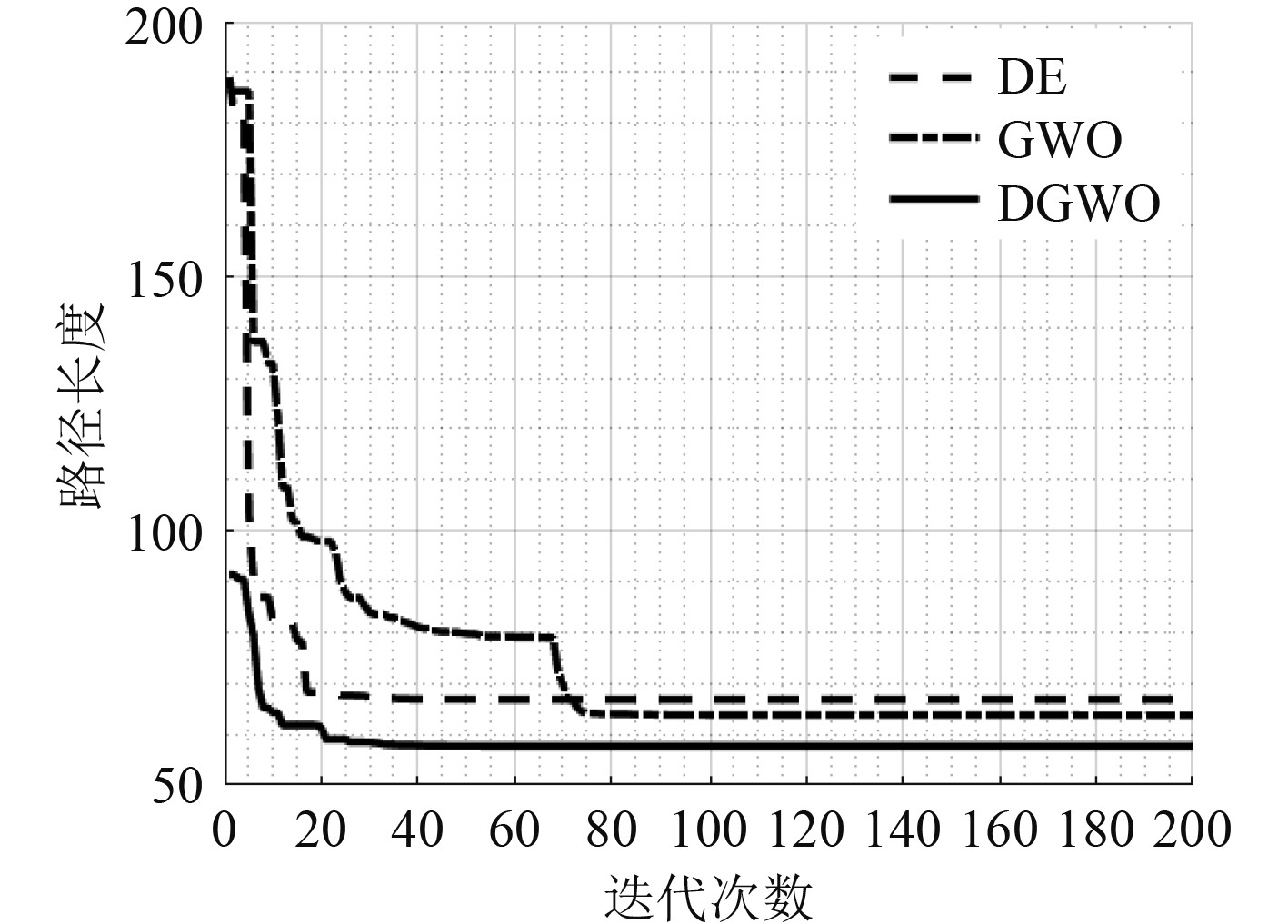
图 2 算例1收敛曲线 Fig. 2 Convergence curves of case 1 |
如表1所示,在平均值、最优值以及最劣值3项指标中,差分-灰狼算法均表现最佳。其中,在平均值以及最劣值2项指标中,差分-灰狼算法有着明显优势,这充分表明了该算法有效结合了原有2种算法的优势并有着稳定出色的求解效果。在最优值方面,由于群智能算法搜索算子存在一定的随机性,差分-灰狼算法并未展示出明显优势。如图1所示,3种算法均可在保证路径安全性的前提下导引水下航行器行驶至路径终点,但差分-灰狼算法所规划路径的平直程度明显优于其余2种算法,并且有着最短的路径总长度。如图2所示,差分-灰狼算法的收敛曲线始终位于其余2种算法相应曲线之下,差分-灰狼算法在第60轮迭代已经趋于收敛,灰狼算法在第80轮才趋于收敛,差分进化算法在3种算法中收敛速度是最快的(第20轮迭代),但是却陷入了局部最优解无法跳出,以至于影响最终的规划效果。
3.2.2 仿真算例2仿真算例2的路径起点设置为(5, 5),路径终点设置为(45,45),在起点与终点之间随机分布20个半径为2的圆柱形障碍物。表2汇总了该算例下差分进化算法(DE)、灰狼算法(GWO)以及差分-灰狼算法(DGWO)3种算法的统计运行结果。图3为3种算法所规划的行驶路线,图4为3种算法的等权均值收敛曲线。
|
|
表 2 算例2测试结果 Tab.2 Test results of case 2 |
|
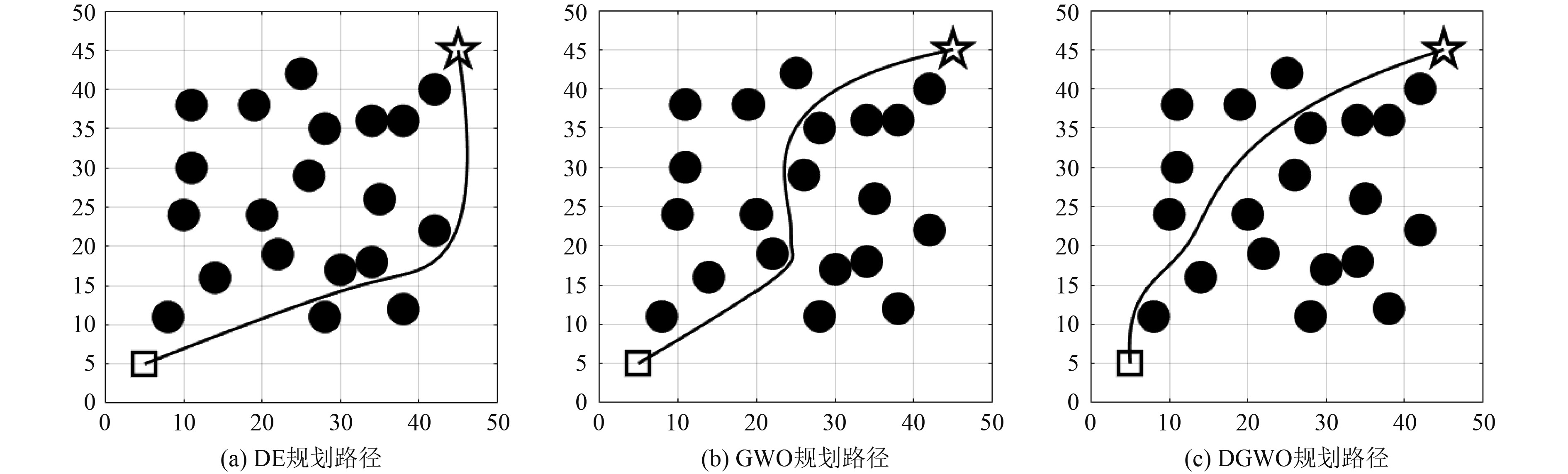
图 3 算例2路径规划图 Fig. 3 Path planning results of case 2 |
|
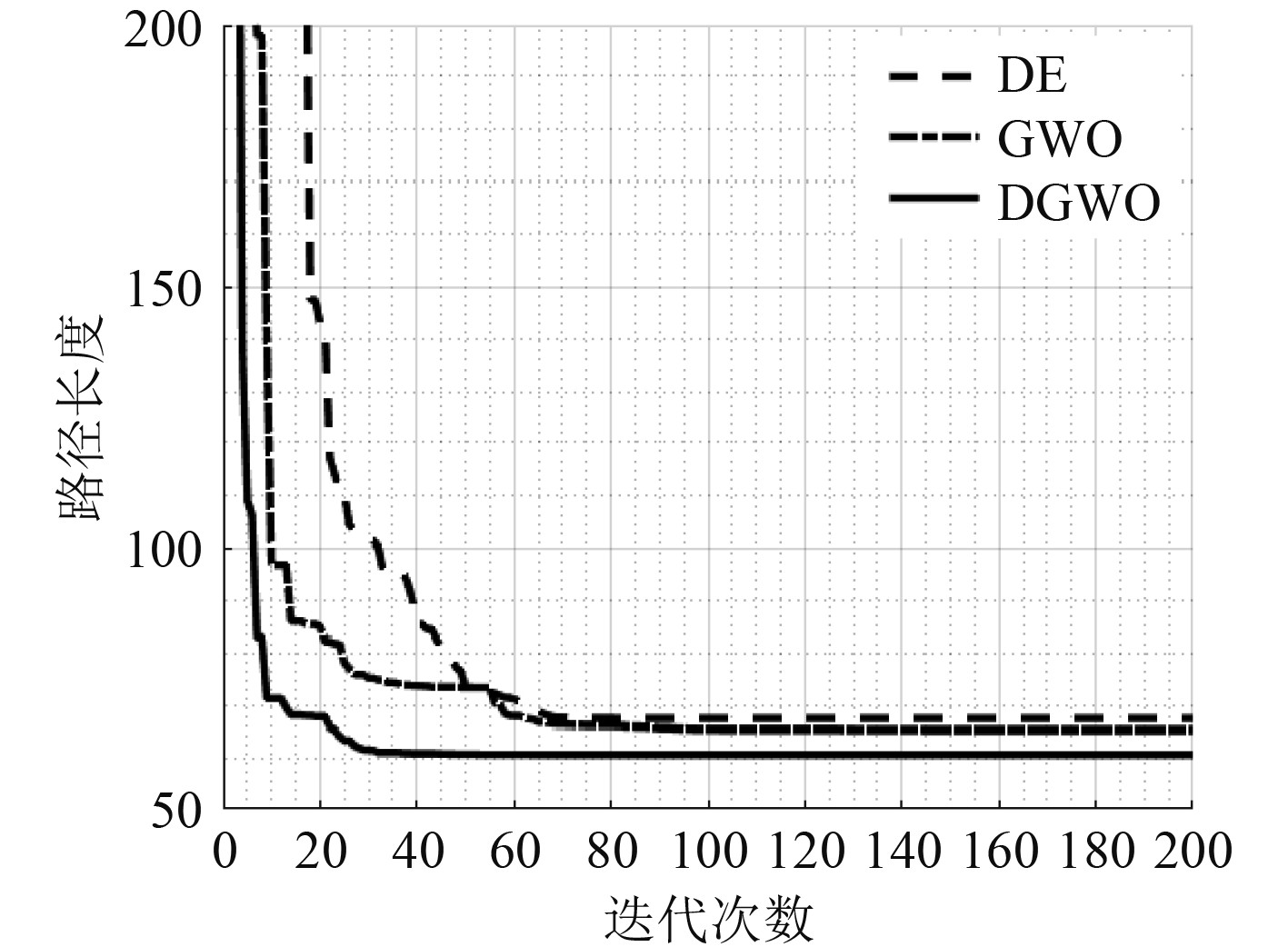
图 4 算例2收敛曲线 Fig. 4 Convergence curves of case 2 |
如表2所示,差分-灰狼算法在平均值与最劣值方面较差分进化算法与灰狼算法有较为明显的优势,这充分证明了差分搜索算子有效改善了灰狼算法的全局搜索能力;在最优值方面,差分-灰狼算法也获得了该项指标的最优表现,但其优势并不明显,这是由于群智能算法的搜索算子具备一定的随机性,在30次独立重复运行的状态下,差分进化算法与灰狼算法也会产生表现优异的个体。如图3所示,无论是差分进化算法、灰狼算法还是差分-灰狼算法,都可以在不与障碍物发生碰撞的情况下最终到达路径终点,但差分-灰狼算法所规划路径的平滑程度以及路径总长度仍表现出了明显优势。如图4所示,差分-灰狼算法的收敛曲线始终位于差分进化算法与灰狼算法的下方,这种现象既表明差分-灰狼算法有着最优的求解效果,也表明差分-灰狼算法的收敛速度相较其余2种算法更快。
3.3 分析与讨论根据表1与表2中的统计结果,差分-灰狼算法在平均值以及最劣值2项指标中优势明显,在最优值这项指标中也有着一定的优势,这表明将差分算子引入灰狼算法可以有效改善灰狼算法全局搜索能力并。如图1与图3所示,相较于差分进化算法以及灰狼算法,差分-灰狼算法所规划路径的弯折现象明显少了很多,并且在总路径长度方面显示出了明显优势。如图2与图4所示,差分-灰狼算法的收敛曲线始终位于其余2种算法下方,这表明在搜索的任何阶段,差分-灰狼算法均能规划出更优的路径方案,充分证明了其在全局搜索以及局部开发方面均有出色表现。最重要的是,差分-灰狼算法可以为水下航行器规划出安全、经济的全局路径,具有广泛工程应用价值。
4 结 语以B样条曲线对路径进行参数化建模,提出一种差分-灰狼优化算法,并通过仿真实验研究其在水下航行器路径规划问题方面的表现,结论如下:
1) 本文所提出的差分-灰狼算法可有效改善水下航行器路径规划求解效果。根据仿真实验统计结果,差分-灰狼算法在平均值、最优值以及最劣值方面表现较差分进化算法与灰狼算法有明显优势。
2) 本文所提出的差分-灰狼算法具有强大的全局搜索能力。根据仿真实验统计结果,差分-灰狼算法的收敛曲线始终位于差分进化算法与灰狼算法收敛曲线的下方,这既表明差分-灰狼算法有着最优的规划效果,也表明其具有最快的收敛速度。
3) 本文所提出的差分-灰狼算法可以为水下航行器规划出安全、经济的全局路径,具有广阔的工程应用价值。
水下航行在执行任务时往往会遇到各种类型的动态障碍物并受到时变洋流等环境的影响,因此,后续还可针对规避动态障碍物以及洋流环境下的实时路径规划方法开展进一步研究。
| [1] |
ZHANG W, WANG N, WU W. A hybrid path planning algorithm considering AUV dynamic constraints based on improved A* algorithm and APF algorithm[J]. Ocean Engineering, 2023, 285(1): 115333.
|
| [2] |
LI Y, WEI W, GAO Y, et al. PQ-RRT*: An improved path planning algorithm for mobile robots[J]. Expert Systems With Applications, 2020, 152: 113425.
|
| [3] |
刘涛, 贾立校, 曹翔. 动态人工势场法的无人船避障路径规划[J]. 舰船科学技术, 2023, 45(5): 89-92. LIU Tao, JIA Lixiao, CAO Xiang. Research on obstacle avoidance path planning of unmanned vehicle based on dynamic artificial potential field method[J]. Ship Science and Technology, 2023, 45(5): 89-92. DOI:10.3404/j.issn.1672-7649.2023.05.016 |
| [4] |
QU C, GAI W, ZHANG J, et al. A novel hybrid grey wolf optimizer algorithm for unmanned aerial vehicle (UAV) path planning[J]. Knowledge-Based Systems, 2020, 194: 105530.
|
| [5] |
黄鹤, 李潇磊, 杨澜, 等. 引入改进蝠鲼觅食优化算法的水下无人航行器三维路径规划[J]. 西安交通大学学报, 2022, 56(7): 9−18.
|
| [6] |
刘兴盛, 王俊雄. 基于改进蚁群算法的水下机器人路径规划算法[J]. 舰船科学技术, 2022, 44(21): 80−87. LIU X, WANG J. Research on path planning algorithm for underwater robots based on improved ant colony algorithm [J]. Ship Science and Technology, 2022, 44(21): 80−87. |
| [7] |
徐炜翔, 朱志宇. 基于飞蛾火焰算法的AUV三维全局路径规划[J]. 上海理工大学学报, 2021, 43(2): 148−155.
|
| [8] |
CHEN Y, MEI Y, YU J, et al. Three-dimensional unmanned aerial vehicle path planning using modified wolf pack search algorithm[J]. Neurocomputing, 2017, 266: 445-457. DOI:10.1016/j.neucom.2017.05.059 |
| [9] |
YU X, LI C, YEN G. A knee-guided differential evolution algorithm for unmanned aerial vehicle path planning in disaster management[J]. Applied Soft Computing Journal, 2021, 98: 106857.
|
| [10] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014: 46–61.
|
 2024, Vol. 46
2024, Vol. 46
