2. 武汉工程大学 电气信息学院,湖北 武汉 430205;
3. 武汉第二船舶设计研究所,湖北 武汉 430064
2. College of Electrical Information, Wuhan Institute of Technology, Wuhan 430205, China;
3. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
近年来,随着新能源技术与储能技术的发展,我国“十四五”节能减排综合工作方案提出,要“加强船舶清洁能源动力推广应用,推动舰船岸电受电设施改造”[1],使得越来越多的电能储存技术运用于舰船电力系统中,如超级电容、飞轮储能、超导磁电能储存等[2 − 4]。而三相四线制储能变流器(Three-phase Four-wire Power Conversion System, 3P4W-PCS)以其可提供单相电源和带不平衡负载的特点,在舰船电力系统中应用广泛。
在船用3P4W-PCS中,T型三电平结构相较于中点钳位型结构具有器件数量更少、损耗分布更均匀等优点而应用广泛[5]。该系统通常会接入不平衡负载,在这种工况下变流器的输出中包含了正序、负序和零序分量。根据对零序分量控制方法的不同,3P4W-PCS分为了三桥臂和四桥臂2种拓扑结构[6 − 7],其中四桥臂结构包含远多于其他结构的开关状态,成本更高且控制更为复杂。因此,本文的研究对象为T型三电平三桥臂三相四线制储能变流器。
三桥臂结构直流母线电容中点与负载侧中性点直接相连,在接入不平衡负载时变流器产生的零序电流直接流过母线电容会加剧中点电位的波动[8]。为解决中点电位波动问题,唐健等[9]在abc坐标系下使用3D-SVPWM调制算法,并加入中点平衡因子对中点波动进行控制,该方法的抑制能力较强,但抑制程度不可控。Wang等[10]提出一种重构O状态作用时间的中点电位平衡方法即零电平分解法,该方法根据检测的中点电压偏移值,对其定量补偿,在低不平衡度负载下抑制效果显著,但缺点是在高不平衡度负载下效果不佳。
在上述研究的基础上,本文拟对3P4W系统中点波动机理进行分析,给出零电平分解法运用在高不平衡度负载下中点难以控制的本质问题,并进一步提出一种基于零电平分解改进的中点平衡优化控制方法,验证所提控制策略在低不平衡度和高不平衡度负载下对中点波动均具备良好抑制能力。
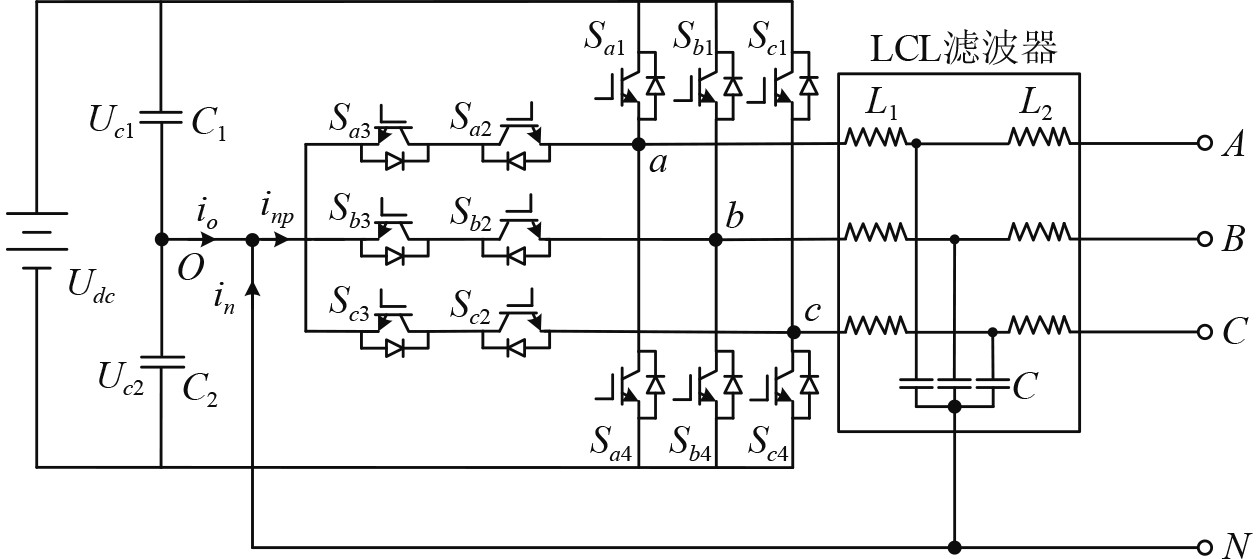
1 三相四线制三电平储能变流器中点波动控制原理 1.1 变流器中点电位波动机理图1为T型三电平三桥臂3P4W-PCS的拓扑图。在该拓扑中,中性点N与直流侧中点O直接相连,定义相电流的正方向为桥臂输出侧流向负载侧的方向。
|
图 1 T型三电平三桥臂3P4W-PCS拓扑图 Fig. 1 T-type three-level three-leg 3P4W-PCS topology |
当开关管箝位使桥臂输出O电平时,单位周期内变流器的中点流出电流inp可定义为:
| $ {i_{{{np}}}} = {d_{{ {a0}}}}{i_{ {a}}} + {d_{{ {b0}}}}{i_{ {b}}} + {d_{{ {c0}}}}{i_{ {c}}} 。$ | (1) |
式中:ix为变流器输出电流;dx0为单位周期内开关管箝位到O电平的占空比,x=a,b,c。
dx0与输出相电压ux的关系可表示为:
| $ {d_{x0}} = 1 - \left| {{{{u_x} / }{({{{U_{{{dc}}}}} \mathord{\left/ {\vphantom {{{U_{{\text{dc}}}}} 2}} \right. } 2})}}} \right|。$ | (2) |
式中:ux为变流器输出相电压;Udc为储能电池提供的直流电压。
已知中线电流in,结合式(1)可得中点流出电流io:
| $ \begin{aligned}[b] {i_{{o}}} = &{i_{{{np}}}} - {i_{{n}}} = \\ &{d_{{{a0}}}}{i_{{a}}} + {d_{{{b0}}}}{i_{{b}}} + {d_{{{c0}}}}{i_{{c}}} - {i_{{a}}} - {i_{{b}}} - {i_{{c}}} =\\ &\sum\limits_{x{{ = a,b,c}}} {(({d_{x0}} - 1){i_x})}= - ({2 \mathord{\left/ {\vphantom {2 {{U_{{{dc}}}}}}} \right. } {{U_{{{dc}}}}}})\sum\limits_{x{{ = a,b,c}}} {(\left| {{u_x}} \right|{i_x})}。\end{aligned} $ | (3) |
可知,当桥臂仅输出O电平时,单个周期内中点流出电流io=0,因此当且仅当各桥臂输出P或N电平时,相电流ix才会对io造成影响,进而引起中点电位的波动。
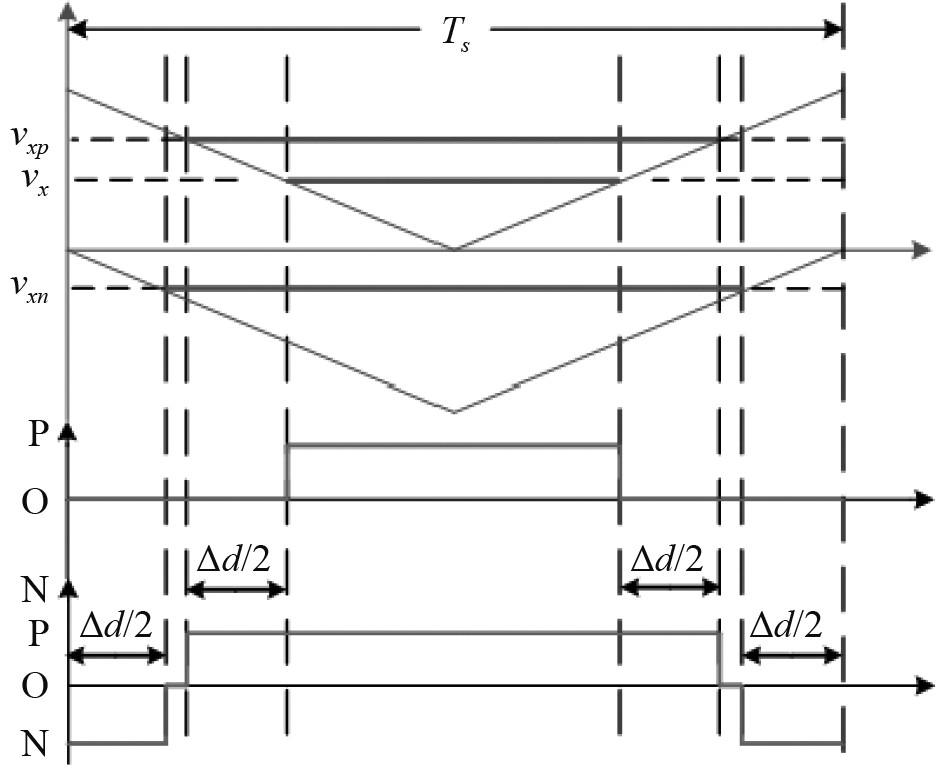
1.2 传统零电平分解中点控制方法传统零电平分解中点控制方法是通过改变单位周期内O电平的占空比,使得对中点电位无影响的O状态向抑制中点电位偏移的P或者N状态转化,以此来达到对中点电压的控制。文献[10]在双调制波的基础上实现零电平分解,双调制波方式如图2所示,调制波vx在满足伏秒平衡原理的前提下被分解为vxp和vxn。
|
图 2 基于零电平分解的双调制波方式 Fig. 2 Double modulation method based on the disassembly of zero level |
记被分解的O电平占空比为∆d,零电平分解法将∆d与中点电压偏移量Unp_off相联系,使其能够根据偏移量对O电平进行定量分解。Unp_off由两部分组成,一部分是下一载波周期内将会产生的中点电压变化量∆Unp,另一部分是下一载波周期开始前的中点电压偏移量Unp。若此时为第k次载波周期,则中点电压变化量为:
| $ \begin{aligned} \Delta {U_{{{np}}}}(k) = &\frac{{{T_s}}}{C}{i_{\text{o}}}(k) = h\sum\limits_{x = {{a,b,c}}} {(\left| {{u_x}(k)} \right|{i_x}(k))} 。\end{aligned} $ | (4) |
式中:
∆Unp与Unp需满足
| $ \overline {{U_{{{np}}}}(k + 1)} = {U_{{{np}}}}(k) + \Delta {U_{{{np}}}}(k) 。$ | (5) |
式中:
则Unp_off直接可表示为:
| $ {U_{{{np\_{\text{off}}}}}}(k) = \overline {{U_{{{np}}}}(k + 1)}。$ | (6) |
进一步确定分解的O电平占空比∆d,为减少开关损耗,只对一相进行分解,因此有
| $ \Delta d = C\frac{{{U_{{{np\_{\text{off}}}}}}}}{{{i_x}{T_s}}}。$ | (7) |
要确定∆d的值,还需判断应该对哪一相进行分解,因此引入中点控制裕量NPCM进行判断。NPCMx表征的是x相电流对中点电压波动的抑制能力,其表达式为:
| $ NPC{M_x} = {\text{sign}}({U_{{{np\_{\text{off}}}}}}){i_x}{d_{x0}} 。$ | (8) |
取NPCM最大的一相进行分解,将∆d平分到对应相的调制波vxp和vxn,其取值分别为:
| $ {v_{xp}} = \left\{ \begin{split} & {v_x} + {{\Delta d} \mathord{\left/ {\vphantom {{\Delta d} 2}} \right. } 2},{\text{ }}{v_x} \geqslant 0 ,\\ & {{\Delta d} \mathord{\left/ {\vphantom {{\Delta d} 2}} \right. } 2},{\text{ }}{v_x} < 0 , \end{split} \right. $ | (9) |
| $ {v_{x{{n}}}} = \left\{ \begin{gathered} {{ - \Delta d} \mathord{\left/ {\vphantom {{ - \Delta d} 2}} \right. } 2},{\text{ }}{v_x} \geqslant 0 , \\ {v_x} - {{\Delta d} \mathord{\left/ {\vphantom {{\Delta d} 2}} \right. } 2},{\text{ }}{v_x} < 0 。\\ \end{gathered} \right. $ | (10) |
最后基于双调制波方法进行调制,发出PWM脉冲,完成对中点波动的控制。记分解后的中点流出电流为io',以及中点电压变化量为∆Unp',经过零电平分解后的∆Unp'与Unp都应满足:
| $ \left|{U}_{{np}}(k)+\Delta {U}_{{np}}{}'(k)\right| < \left|\overline{{U}_{{np}}(k+1)}\right| 。$ | (11) |
变流器接入平衡负载时,全范围内均可进行分解,中点电压波动的抑制效果显著。但在不平衡负载接入时,根据负载不平衡程度的不同,零电平分解法的抑制效果会被不同程度地减弱,下面对这种情况进行说明。定义不平衡度px表征各相负载的不平衡程度,可表示为:
| $ {p_x} = (1 - {i_x}/{i_{a}}) \times 100\text% 。$ | (12) |
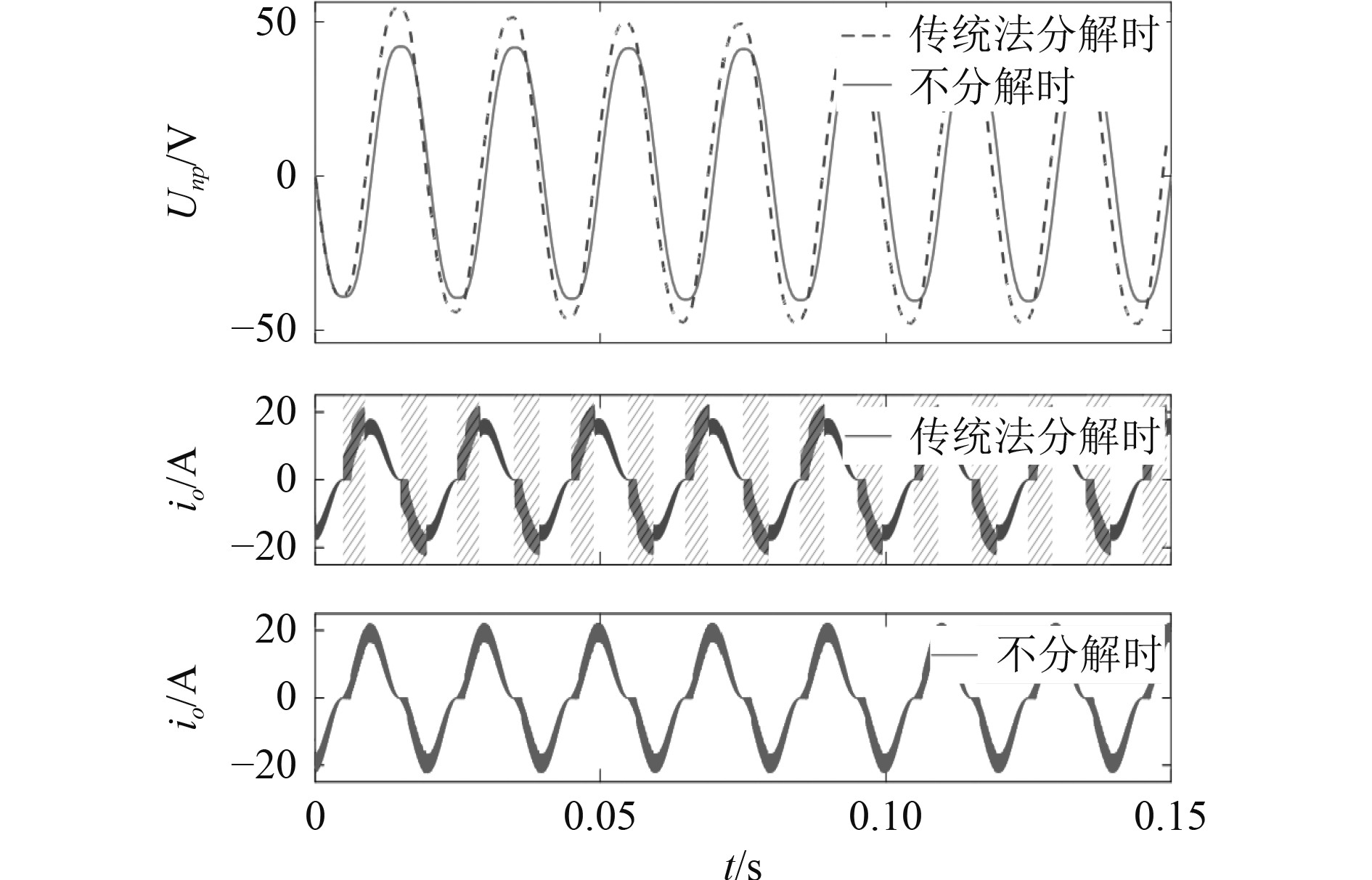
图3以pa=0%、pb=100%、pc=100%的极端不平衡工况为例,对比不分解和零电平分解时中点电压的波动。可以看出,进行零电平分解后,中点电压偏移量没有被抑制,其峰值也被增加。根据文献[11]对3P4W变流器输出不同电流时中点电压的分析可知,当输出基波电流时,Unp会产生工频纹波,仅当三相都输出对称的基波电流时,Unp会产生3倍频纹波。
|
图 3 高不平衡度下零电平分解与不分解时中点电压和中点电流波形 Fig. 3 Waveforms of neutral-point voltage and current during zero level decomposition and non decomposition under high imbalance |
对于图3这种仅有一相输出基波电流的情况,Unp满足:
| $ {U_{{{np}}}}(\theta ) = {U_{{{np}}}}(\theta + 2{\text{π}})。$ | (13) |
同时,在该工况下中点流出电流io为:
| $ {i_{o}} = - ({2 \mathord{\left/ {\vphantom {2 {{U_{{{dc}}}}}}} \right. } {{U_{{{dc}}}}}})\left| {{u_{{a}}}} \right|{i_{{a}}}。$ | (14) |
因此,根据函数的周期性与对称性可得在不分解时io在[θ,θ+π]的积分:
| $ \int_\theta ^{\theta + {\text{π }}} {{i_{\text{o}}}{\text{d}}} \theta = \int_\theta ^{\theta + {{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} {\text{2}}}} \right. } {\text{2}}}} {{i_{o}}{\text{d}}} \theta + \int_{\theta + {{\text{π}} \mathord{\left/ {\vphantom {{\text{π}} 2}} \right. } 2}}^{\theta + {\text{π}}} {{i_{o}}{\text{d}}} \theta = 0。$ | (15) |
图3中阴影区域为零电平分解区域,记每个阴影中零电平分解持续时间为t。进一步的,可以得到iox与io的积分值关系如表1所示。
|
|
表 1 iox与io的积分值关系 Tab.1 The relationship between the integral values of iox and io |
不分解时产生的中点电压偏移量为Unp0和分解时产生的中点电压偏移量为Unp1分别为:
| $ \left\{ \begin{split} & {U_{{{np}}0}} = \frac{1}{C}\int {{i_{o}}{\mathrm{d}}\theta } ,\\ & {U_{{{np}}1}} = \frac{1}{C}\int {{i_{o}}^{'}{\mathrm{d}}\theta } 。\end{split} \right. $ | (16) |
结合表1,当θ∈(π/2, π/2+ωt)时,|Unp1|<|Unp0|,此时io'的积分为:
| $ {\displaystyle {\int }_{0}^{\text{π}/2}{i}_{o}{}'\text{d}\theta }+{\displaystyle {\int }_{\text{π}/2}^{\text{π}/2+\omega t}{i}_{o}{}^{{'}}\text{d}\theta }=0 。$ | (17) |
式中:0<ωt<π/2,因为在分解时需满足式(11),所以io'能够在(0,π)内使积分值重新回到0。
进一步的,当θ=3π/2时,Unp0和Unp1满足:
| $ \left\{\begin{aligned} &{U}_{{np}0}=\frac{1}{C}{\displaystyle {\int }_{0}^{3\text{π}/2}{i}_{o}\text{d}\theta },\\ &{U}_{{np1}}=\frac{1}{C}{\displaystyle {\int }_{0}^{3\text{π}/2}{i}_{o}{}^{{'}}\text{d}\theta },\\ &{U}_{{np1}} > {U}_{{np}0}。\end{aligned}\right. $ | (18) |
结合式(17)和式(18)可知,虽然分解后Unp能更快的回到平衡点,但io与Unp同号时的积分区间也因此变大,最终使Unp峰值变化。此外,中点电压不可控区域也是导致Unp峰值变化的另一原因。
因此,传统零电平分解中点控制在高不平衡度负载工况下,中点电位的波动峰值会因分解而增大。
2 基于零电平分解改进的中点平衡优化控制方法 2.1 高不平衡度下零电平分解改进方法根据上节分析,在高不平衡度负载工况下,传统零电平分解方法会造成中点输出电流积分区间变化,加剧中点电位波动。且在负载缺相等极端工况下,还存在着中点电压不可控区域。针对传统零电平分解方法存在的问题,有必要对该方法进行进一步分析和改进。
记a、b、c各相O电平被完全分解后的中点流出电流为iox,根据式(3)可得:
| $\left\{ \begin{split} & {i_{{\ {oa}}}} = - {i_{\ {a}}} - ({2 \mathord{\left/ {\vphantom {2 {{U_{{\ {dc}}}}}}} \right. } {{U_{{\ {dc}}}}}})({i_{\ {b}}} \cdot \left| {{u_{\ {b}}}} \right| + {i_{\ {c}}} \cdot \left| {{u_{\ {c}}}} \right|), \\& {i_{{\ {ob}}}} = - {i_{\ {b}}} - ({2 \mathord{\left/ {\vphantom {2 {{U_{{\ {dc}}}}}}} \right. } {{U_{{\ {dc}}}}}})({i_{\ {a}}} \cdot \left| {{u_{\ {a}}}} \right| + {i_{\ {c}}} \cdot \left| {{u_{\ {c}}}} \right|) , \\& {i_{{\ {oc}}}} = - {i_{\ {c}}} - ({2 \mathord{\left/ {\vphantom {2 {{U_{{\ {dc}}}}}}} \right. } {{U_{{\ {dc}}}}}})({i_{\ {a}}} \cdot \left| {{u_{\ {a}}}} \right| + {i_{\ {b}}} \cdot \left| {{u_{\ {b}}}} \right|) 。\end{split} \right.$ | (19) |
若分解前的io和分解后的iox符号相异,则说明必然能够通过分解某相一定量的O电平占空比,使中点电流的偏移被完全补偿。因此,中点电流完全补偿需满足:
| $ {i_{{o}}} \cdot {i_{{{o}}x}} < 0 。$ | (20) |
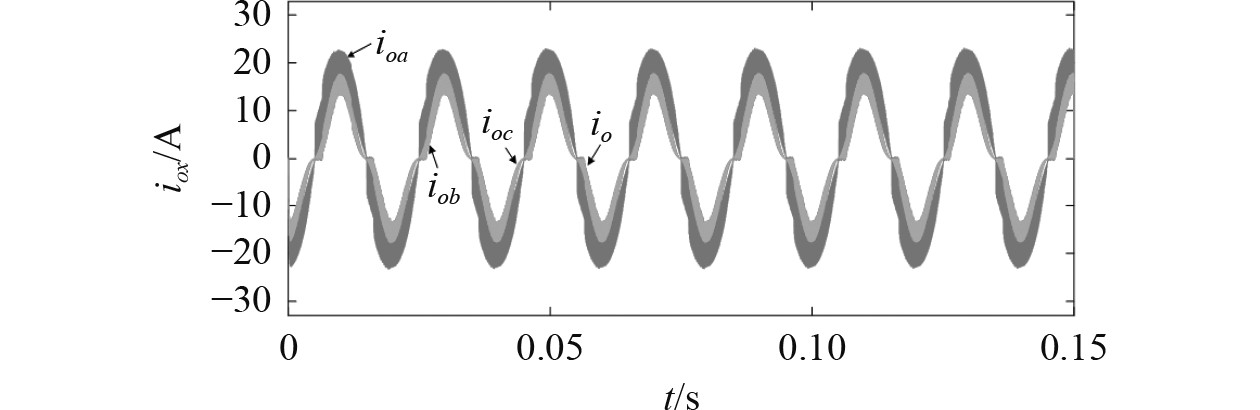
根据式(20)可以将io的积分区域也即Unp对应区域划分为可控区域和不可控区域。图4为变流器在pa=0%、pb=100%、pc=100%的工况下iox和io的输出波形,因为该工况下仅有A相输出电流,因此io、iob、ioc的波形重合。结合图3中Unp的波形并分析可知,图4中几乎没有满足式(20)的区域,这表明在全范围内中点电流几乎不可能被完全补偿,Unp完全处于中点电压不可控区域之中。
|
图 4 高不平衡负载工况下iox与io波形 Fig. 4 iox and io under under high unbalanced condition |
综上,在高不平衡度负载工况时,中点电压不可控区域过大,大部分区域中无法对中点电流完全补偿,此时对零电平进行分解,虽然可使Unp以较快速率回归平衡点即过零点,但改变了io的积分区间,最终对中点波动产生了不利影响。
因此,针对这一问题,这里提出的改进方案是在高不平衡度工况下对零电平分解作用区域和分解量进行控制,在分解零电平的同时尽量不改变Unp的平衡点,减小io的积分区间变化带来的影响。
零电平分解法作用区域可分为三类,具体分类条件及对应的零电平分解量见表2。其中类型I和II都可能会改变Unp的平衡点,需要对分解量进行控制。
|
|
表 2 零电平分解作用区域分类及相应零电平分解量 Tab.2 Classification of the disassembly area of zero level and disassembly amount |
确定改进的零电平分解法需遵循以下规则:对于类型I,不进行分解;对于类型II,计算出使io被抑制为零所需分解的O电平占空比∆do,并与∆d比较,选择较小值作为分解量;对于类型III,零电平分解正常作用即可。其中∆do的表达式如下:
| $ \Delta {d_{{o}}} = {T_s}\frac{{{i_{{o}}}}}{{{i_x}}}。$ | (21) |
在零电平分解改进方法中,根据负载不平衡度对零电平分解作用区域和分解量进行控制是进行中点平衡控制的关键。而负载不平衡度可用单个基波周期内中点电压可控范围因子Kcnp来衡量。
定义中点电压可控开关函数Snp为:
| $ {S_{{{np}}}} = \left\{ \begin{gathered} 1,{i_{{o}}} \cdot {i_{{{o}}x}} < 0, \\ 0,{i_{{o}}} \cdot {i_{{{o}}x}} \geqslant 0,\\ \end{gathered} \right.x = a,b,c 。$ | (22) |
io和iox都是以2π为周期,因此在一个基波周期内对Snp进行积分即可得中点电压可控范围因子:
| $ {K_{cnp}} = \frac{1}{{2{\text{π }}}}\int_{2k{\text{π }}}^{{\text{(2}}k+ 1){\text{π}}} {{S_{{{np}}}}{\text{d}}\theta } \times 100{\text{% }} 。$ | (23) |
图5分别为不同调制比和负载不平衡度下对应的Kcnp,其中图5(b)~图5(f)分别为m=0.4、0.5、0.77时Kcnp的等高线在pb-pc平面上的投影。易知,在pb-pc平面上,平面区域越靠近右上方代表负载的不平衡程度越高,且平面上的每一条等高线均标明了Kcnp的值。图中可见,Kcnp的等高线逐渐向平面右上方区域扩散,其值随之减小,这表明Kcnp与负载的不平衡度呈现一种反比例关系。

|
图 5 不同调制比下不平衡度与Kcnp关系 Fig. 5 Comparison of Kcnp under different m and unbalance factor |
而从图5(a),图5(c),图5(e)中观察到,随着调制比的增加,Kcnp的空间波动区域逐渐较少。这表明单位周期内的可分解O电平占空比由于调制比的增加而不断减小,中点电压不可控范围逐渐增大,导致Kcnp的波动范围减小。
因此Kcnp能够反映零电平分解法在不同调制比与不同不平衡程度下的作用能力,可对负载不平衡度进行衡量。本文通过计算Kcnp来表征负载不平衡度,并以此确定何时应该对零电平分解作用区域和分解量进行控制。
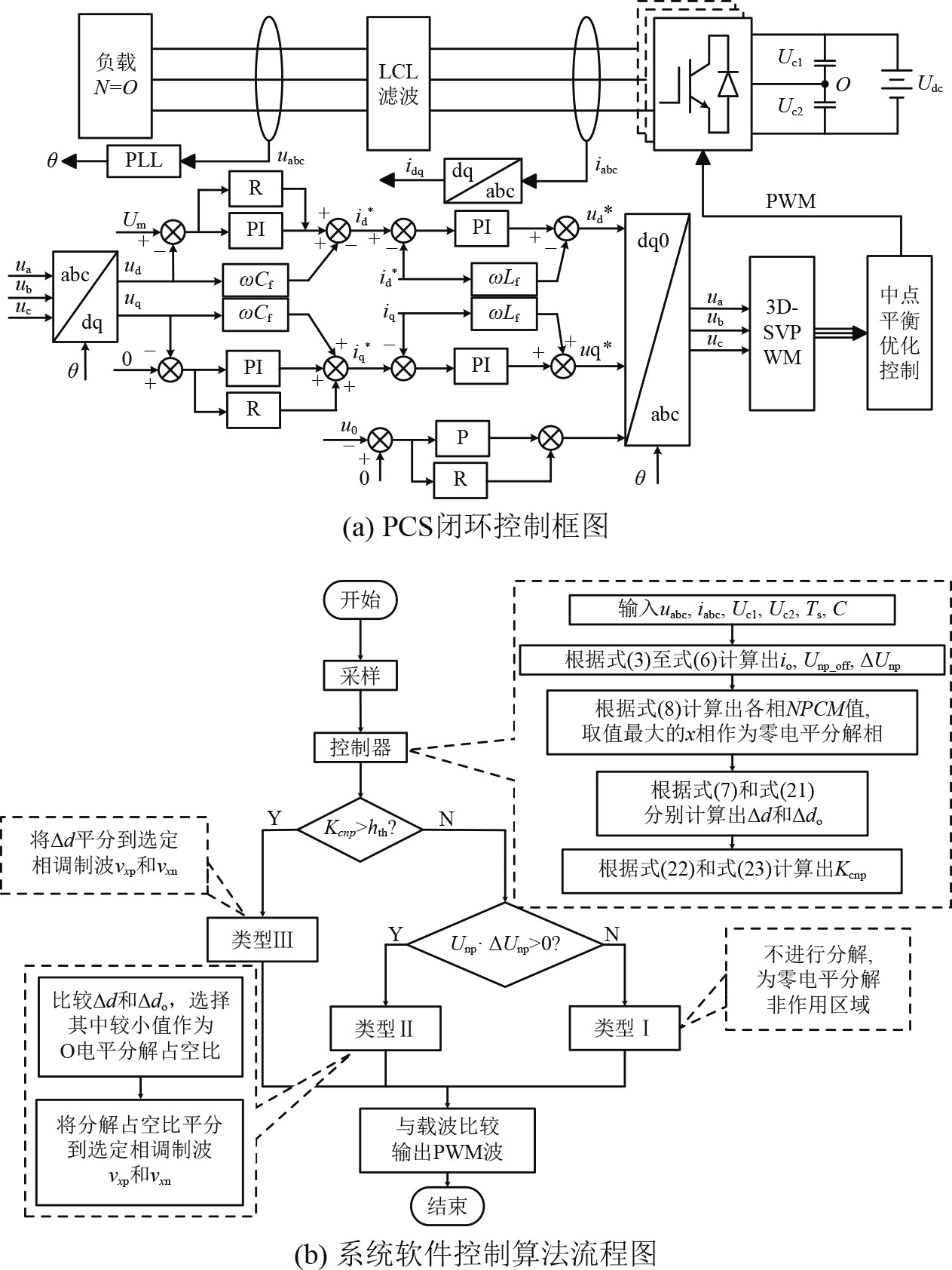
2.3 不同负载工况下中点控制优化策略结合前文分析,给出如图6所示的PCS总体控制框图以及中点优化控制方法的流程图。图6(a)为PCS的闭环控制框图,图6(b)为系统软件控制算法流程图,输入uabc、iabc、Uc1、Uc2、Ts和C,计算出Unp、∆Unp和Kcnp并判断,若Kcnp>hth则为类型III,零电平正常分解,不对分解作用区域进行控制;若异号则为类型I,不进行分解,并令∆d=0;若同号则为类型II,比较∆d与∆do值的大小,若∆do<∆d,说明此时有能力使io完全抑制,但为了不影响io的积分区间,仅需将io抑制到零,从而使中点优化控制方法能够在高不平衡度工况下也能够起到抑制作用。
|
图 6 变流器总体控制框图与中点控制方法流程图 Fig. 6 Control diagram of the inverter and flowchart of neutral-point control strategy |
为验证所提出中点控制方法的可行性和有效性,按照图6(a)的结构,在Matlab/Simulink中搭建T型三电平三桥臂3P4W-PCS模型进行仿真实验,具体仿真参数如表3所示。
|
|
表 3 仿真参数 Tab.3 Simulation parameters |
通过系统仿真,图7和图8分别为低不平衡度和高不平衡度负载下未加算法、加入传统零电平分解法和加入改进零电平分解法的仿真结果,图9为2种中点控制方法在负载突变时的仿真结果。
|
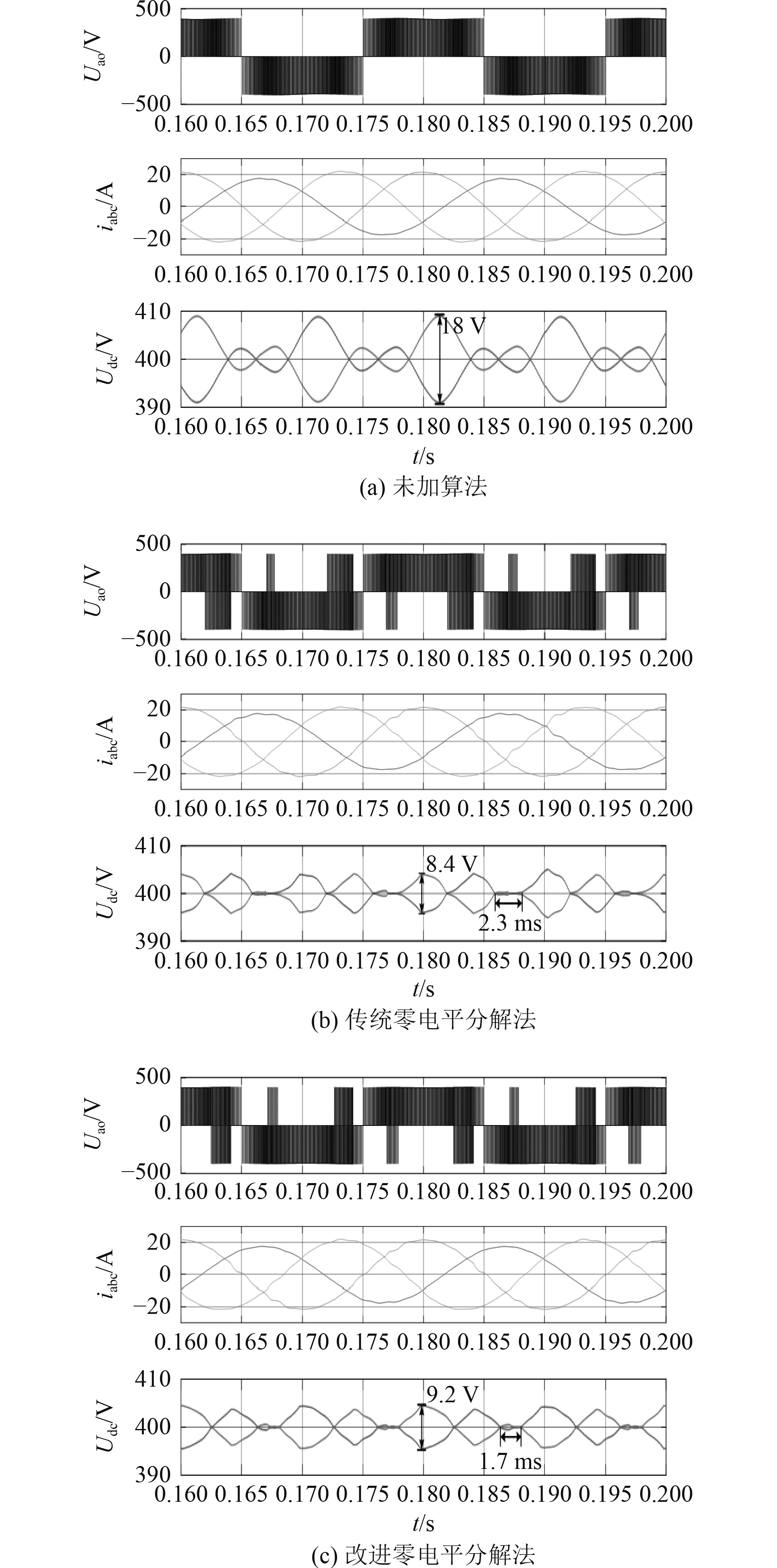
图 7 pa=0%,pb=20%,pc=0%,Kcnp=62%时仿真结果 Fig. 7 The simulation result when pa=0%,pb=20%,pc=0%,Kcnp=62% |
|
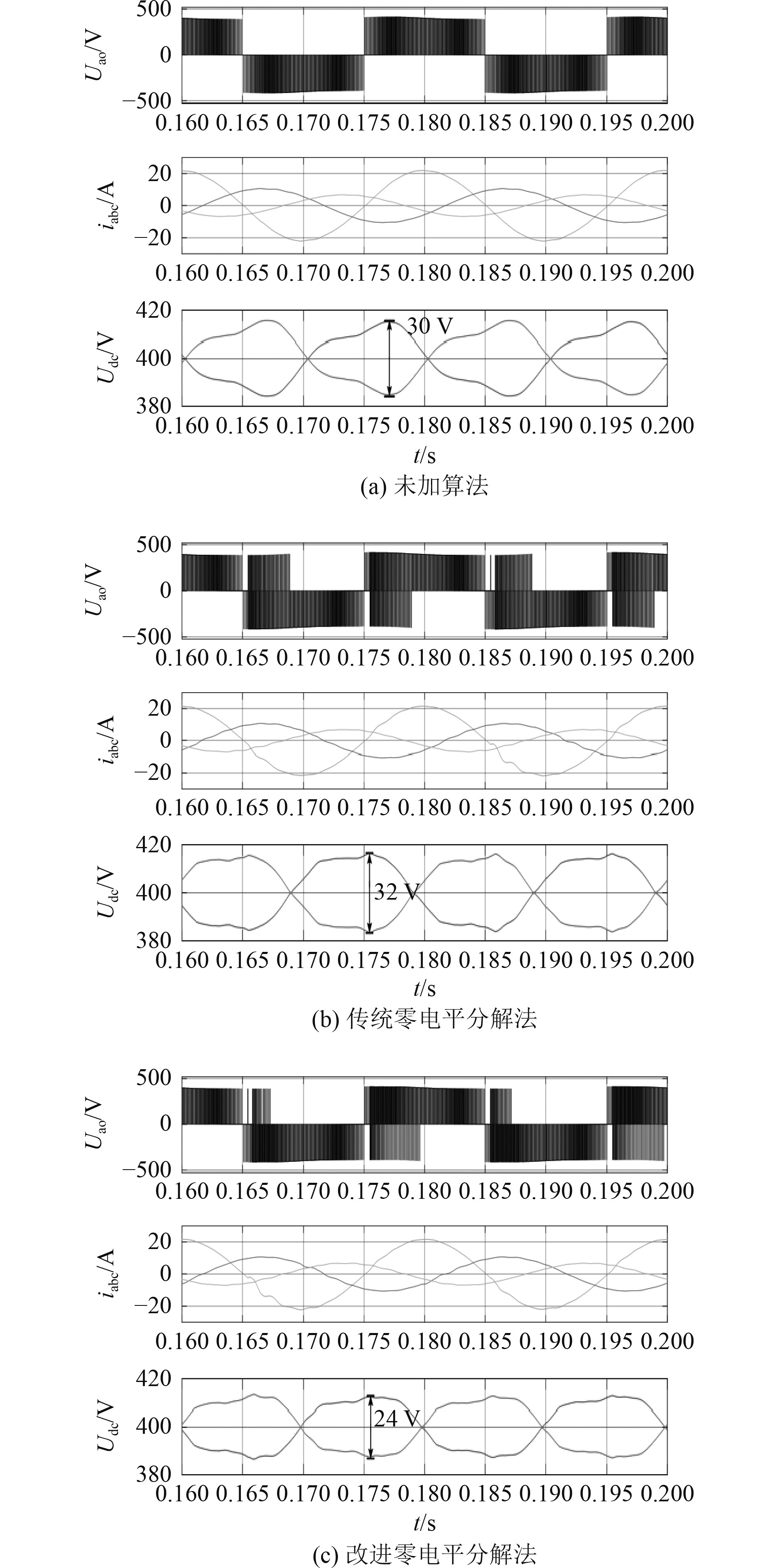
图 8 pa=0%,pb=50%,pc=70%,Kcnp=39%时仿真结果 Fig. 8 The simulation result when pa=0%,pb=50%,pc=70%,Kcnp=39% |

|
图 9 负载突变时不同中点控制方法仿真结果 Fig. 9 The simulation result of different neutral-point voltage suppression strategies when load changing |
从图7可知,与未加算法时相比,加入传统零电平分解法和改进零电平分解法对中点波动均起抑制作用,但是传统零电平分解法能够更持久的将中点电压维持在直流母线电压的1/2,这是因为在此工况下中点电压可控范围因子Kcnp较高,传统零电平分解法有能力对中点电压波动进行完全抑制,与所提出优化控制方法中在该工况下对零电平分解作用区域不进行控制的结论一致。
而在高不平衡度负载工况下,对比图8(a)和图8(b),与未加算法时对比,传统零电平分解法对中点电压波动并没有起到抑制作用,波动峰值反而加剧;而图8(c)中,改进的零电平分解法可对此工况下中点电压波动起到抑制作用。
为验证所提改进算法的负载突变适应性,在0.1 s时各相负载的不平衡度由pa=0%、pb=0%、pc=0%变化到pa=0%、pb=90%、pc=60%。从图9中仿真结果可以看到,在0.1 s负载变化之前,2种控制方法下的中点电压波动相同,而在负载变化之后,相较于传统控制方法,优化控制方法的中点电压波动得到明显改善,验证了所提方法的适应性。
4 结 语针对三电平三桥臂3P4W-PCS的中点电压波动问题,文中提出了一种中点平衡优化控制改进方法。该控制方法能够实时衡量负载不平衡程度,控制零电平分解的作用区域与分解量,以实现在不同不平衡负载工况下良好的中点波动抑制能力。仿真实验结果验证了所提出中点控制方法的可行性和有效性,解决了传统零电平分解方法在高不平衡度时不能对中点电压波动有效抑制的问题。
| [1] |
国务院印发《“十四五”节能减排综合工作方案》[J]. 节能与环保, 2022(2): 6.
|
| [2] |
付荣. 超导磁储能系统在船舶电力系统中的应用[J]. 舰船科学技术, 2018, 40(18): 76-78. FU Rong. Application of superconducting magnetic energy storage system in ship power system[J]. Ship Science and Technology, 2018, 40(18): 76-78. |
| [3] |
方斯顿, 王鸿东, 张军军. 船舶大容量储能系统应用研究综述[J]. 中国舰船研究, 2022, 17(6): 22-35. |
| [4] |
XU L, GUERRERO J M, LASHAB A, et al. A review of DC shipboard microgrids—Part I: Power architectures, energy storage, and power converters[J]. IEEE Transactions on Power Electronics, 2021, 37(5): 5155-5172. |
| [5] |
李敏裕, 马晓军, 魏曙光, 等. T型逆变器中点电压全范围精确平衡研究[J]. 电工技术学报, 2018, 33(8): 1814-1826. |
| [6] |
陈瑶, 金新民, 童亦斌. 三相四线系统中SPWM与SVPWM的归一化研究[J]. 电工技术学报, 2007(12): 122-127. DOI:10.3321/j.issn:1000-6753.2007.12.020 |
| [7] |
王晓刚, 谢运祥, 黄少辉, 等. 四桥臂逆变器SPWM和SVPWM的归一化研究[J]. 电机与控制学报, 2010, 14(1): 23-28+34. DOI:10.3969/j.issn.1007-449X.2010.01.005 |
| [8] |
GUO L, LIU R, LI X, et al. Neutral point potential balancing method for three‐level power converters in two‐stage three‐phase four‐wire power conversion system[J]. IET Power Electronics, 2020, 13(12): 2618-2627. DOI:10.1049/iet-pel.2019.1211 |
| [9] |
唐健, 邹旭东, 何英杰, 等. 三相四线制三电平变换器新型三维矢量调制策略[J]. 中国电机工程学报, 2009, 29(36): 9-17. DOI:10.3321/j.issn:0258-8013.2009.36.002 |
| [10] |
WANG C, LI Z, SI X, et al. Control of neutral-point voltage in three-phase four-wire three-level NPC inverter based on the disassembly of zero level[J]. CPSS Transactions on Power Electronics and Applications, 2018, 3(3): 213-222. DOI:10.24295/CPSSTPEA.2018.00021 |
| [11] |
WANG J, WANG J, MA M, et al. Neutral point voltage analysis for three-phase four-wire three-level grid-connected converter based on CBPWM strategy[J]. IEEE Access, 2020, 8: 165583-165592. DOI:10.1109/ACCESS.2020.3022691 |
 2024, Vol. 46
2024, Vol. 46
