定子绕组的铜耗由直流铜耗和交流附加铜耗两部分组成,交流附加铜耗可以分为由趋服效应及临近效应所引起的股线内部电流密度分布不均以及股线间环流效应所引起的电流分布不均产生的损耗,对于多股线并绕的绕组,股线间的环流引起的环流损耗也属于附加铜耗[1]。股线间环流效应主要是由于导线的并绕结构导致导线的交链漏磁通不同所引起,表现为并绕导线间的电流有差异。对于高速电机来说,高频引起的交流铜损耗非常可观,甚至大于直流铜损耗[2],绕组环流损耗对电机效率及温升等都有很大影响,准确计算绕组环流损耗是高速电机电磁性能分析及优化设计的重要前提[3 − 5]。
为抑制绕组高频附加铜耗,通常可通过减小导体直径的方法来抑制股线内部电流分布不均[6],电机制造过程中常采用多根直径较小的股线并绕的方式来代替单一直径较大的导体作为定子绕组。由于绕组内部的交变电流会在槽内引起交变的漏磁通,且漏磁在槽内分布不均匀,越靠近槽口位置的漏磁越大[7],为此可通过绕组换位的方式来抑制漏磁分布不均的现象。
绕组换位的原理是通过重新排列绕组的电气连接方式,改变绕组的串并联关系,重新布置绕组的接线方式,从而调整电流在绕组中的流动路径,使得电流在绕组内的分布更加均匀[8 − 10] ,避免出现一些导体只承受较大电流而其他导体承受较小电流的情况,进而减小了局部电阻损耗,达到降低环流损耗的目的[11]。本文以一台集中式绕组定子为研究对象,针对绕组端部换位与不换位2种情况,采用无转子模型模拟有转子情况下的环流效应,通过对比换位前后的环流损耗系数与不同股线间电流的相位差进而验证绕组换位对环流损耗抑制的有效性。
1 环流附加铜耗数学模型在忽略导线内部电流分布不均的前提下,由环流效应引起的交流电阻系数kcirc可以表示为存在环流效应时的直流铜耗与不存在环流效应时的直流铜耗的比值[12],即
| $ {k_{circ}} = {n_p}{\sum\limits_{n = 1}^{{n_p}} {{ {\dot I} _n^2\Bigg/\left( {\sum\limits_{n = 1}^{n_p} {{\dot I}_n}} \right)} } ^2}。$ | (1) |
式中:np为并绕导线根数;
在若忽略铁芯饱和效应的条件下交流铜耗满足频域叠加原理,各次谐波铜耗之和即为总的交流铜耗,为不失一般性,以单一频率下的交流电流为激励建立数学模型进行解析。
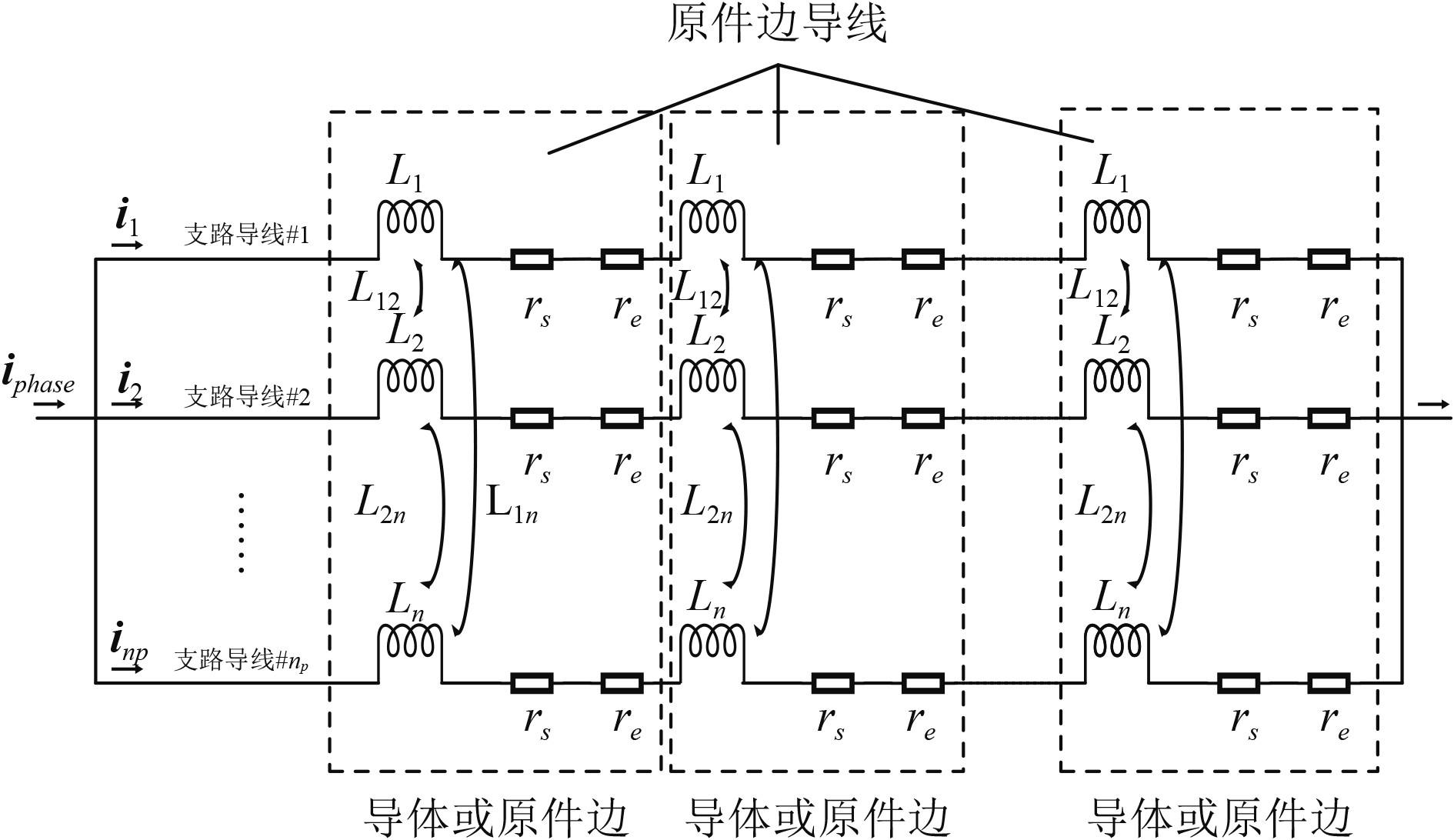
以单一并联支路绕组为研究对象,其结构示意图如图1所示。
|
图 1 单一并联支路绕组结构示意图 Fig. 1 Single parallel branch winding structure diagram |
以三相电机为例,假设并联支路数npr为1,则所有相所含并绕股线一共为3×np,且各支路均满足电压方程:
| $ \dot U = \dot E + j\omega L\dot I + j\omega {L_\sigma }\,\dot I + R\dot I。$ | (2) |
其中:
向量
| $ \dot U = {\left[ {({{\dot U}_a}......{{\dot U}_a}\;\;{{\dot U}_b}......{{\dot U}_b}\;\;{{\dot U}_c}......{{\dot U}_c}} \right]^{\text{T}}}。$ | (3) |
式中:向量
向量
| $ \dot I = {\left[ {{{\dot I}_{a1}}\;\;{{\dot I}_{a2}}...{{\dot I}_{a{n_p}}}\;\;{{\dot I}_{b1}}\;\;{{\dot I}_{b2}}...{{\dot I}_{b{n_p}}}\;\;{{\dot I}_{c1}}\;\;{{\dot I}_{c2}}...{{\dot I}_{c{n_p}}}} \right]^{\text{T}}}。$ | (4) |
式中:
| $ \dot E = \left[ {{{\dot E}_a}...{{\dot E}_a}{{\dot E}_b}...{{\dot E}_b}{{\dot E}_c}...{{\dot E}_c}} \right] 。$ | (5) |
式中:
L代表股线的主电感矩阵,其表达式为:
| $L = \left[ \begin{gathered} {L_{aa}}\;\;{\text{ }}\;\;{L_{ab}}\;\;{\text{ }}\;\;{L_{ac}} \\ {L_{ba}}\;\;{\text{ }}\;\;{L_{bb}}\;\;{\text{ }}\;\;{L_{ba}} \\ {L_{ca}}\;\;{\text{ }}\;\;{L_{cb}}\;\;{\text{ }}\;\;{L_{cc}} \\ \end{gathered} \right] 。$ | (6) |
其中,对角线上的矩阵
| $ L = \left[ \begin{gathered} {L_{aa}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{ab}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{ac}}{{\text{l}}_{{n_p} \times {n_p}}} \\ {L_{ba}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{bb}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{ba}}{{\text{l}}_{{n_p} \times {n_p}}} \\ {L_{ca}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{cb}}{{\text{l}}_{{n_p} \times {n_p}}}{\text{ }}{L_{cc}}{{\text{l}}_{{n_p} \times {n_p}}} \\ \end{gathered} \right] 。$ | (7) |
式中:
| ${L_\sigma } = \left[ \begin{gathered} {L_{\sigma aa}}{\text{ }}{L_{\sigma ab}}{\text{ }}{L_{\sigma ac}} \\ {L_{\sigma ba}}{\text{ }}{L_{\sigma bb}}{\text{ }}{L_{\sigma ba}} \\ {L_{\sigma ca}}{\text{ }}{L_{\sigma cb}}{\text{ }}{L_{\sigma cc}} \\ \end{gathered} \right]。$ | (8) |
| $ {L_{\sigma ik}} = \left[ \begin{gathered} {L_{\sigma ik}}{\text{(1,1) }}{L_{\sigma ik}}{\text{(1,2) }}\cdots{\text{ }}{L_{\sigma ik}}{\text{(1,}}{{{n}}_p}{\text{)}} \\ {L_{\sigma ik}}{\text{(2,1) }}{L_{\sigma ik}}{\text{(1,1) }}\cdots{\text{ }}{L_{\sigma ik}}{\text{(1,}}{{{n}}_p}{\text{)}} \\ {\text{ }} \vdots \quad\quad\quad{\text{ }} \vdots \quad\quad{\text{ }} \ddots \quad\quad {\text{ }} \vdots \\ {L_{\sigma ik}}{\text{(}}{{{n}}_p}{\text{,1) }}{L_{\sigma ik}}{\text{(}}{{{n}}_p}{\text{,2) }}\cdots{\text{ }}{L_{\sigma ik}}{\text{(}}{{{n}}_p}{\text{,}}{{{n}}_p}{\text{)}} \\ \end{gathered} \right]。$ | (9) |
股线p、q之间的互漏感用
用矩阵R来表示股线的电阻矩阵,其表达式为:
| ${\boldsymbol{R}} = \left[ \begin{gathered} {r_1}{\text{ }} \qquad \qquad \\ \qquad{\text{ }} \ddots \qquad \\ \qquad\qquad{\text{ }}{r_{3{n_p}}} \\ \end{gathered} \right] 。$ | (10) |
通常认为每条支路的导线电阻值无差别,且第i条股线的电阻用ri表示。
由以上推导可得出结论,求解各股线电流时可忽略反电动势和主电感,故可以利用无转子模型模拟有转子情况下的环流效应,为定子绕组环流抑制实验设计提供了基础。
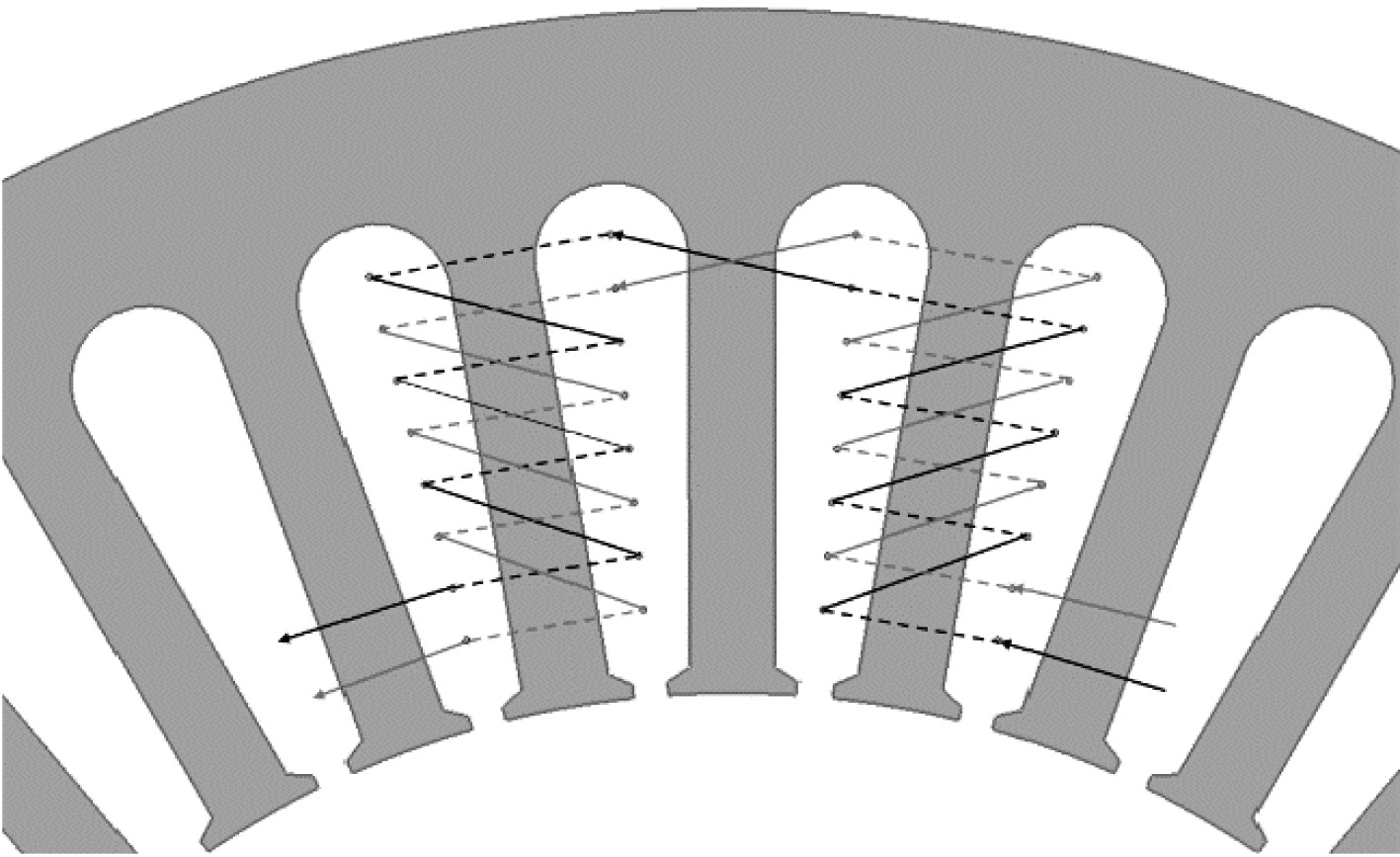
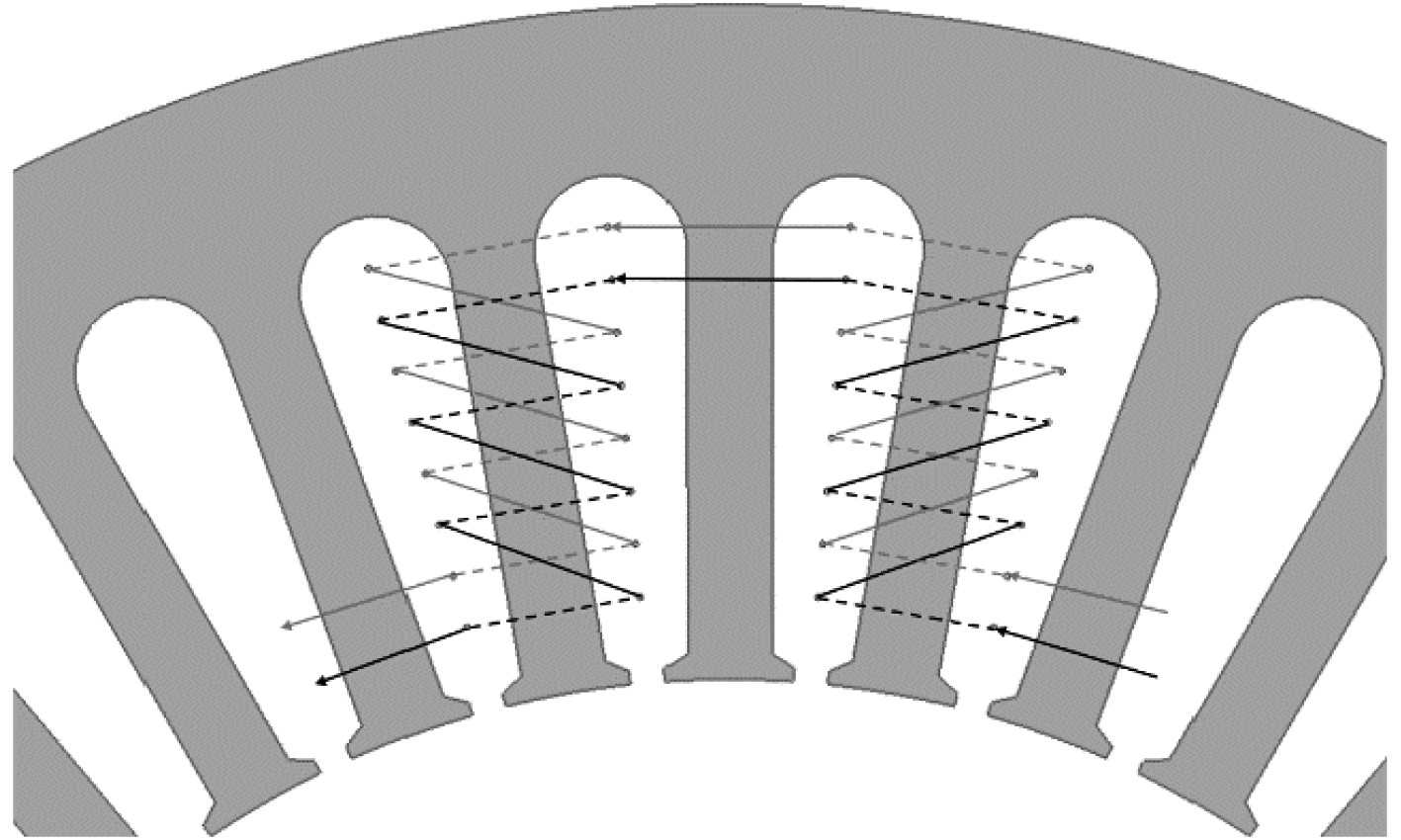
2 定子绕组换位模型为验证绕组换位对环流损耗的抑制作用,分别建立了换位与不换位的2个定子模型其换位方式如图2和图3所示,实线部分为上层,虚线部分为下层,图中导线电流方向如箭头所示。每个槽内共有4根导线,每根导线绕成两股,其连接方式如图4和图5所示,定子主要参数如表1所示。
|
图 2 换位绕组示意图 Fig. 2 Transposition winding diagram |
|
图 3 不换位绕组示意图 Fig. 3 Diagram of untransposed winding |

|
图 4 换位绕组等效电阻示意图 Fig. 4 Equivalent resistance diagram of transposition winding |

|
图 5 不换位绕组等效电阻示意图 Fig. 5 Diagram of equivalent resistance of untransposed winding |
|
|
表 1 定子及绕组主要参数 Tab.1 Main parameters of stator and winding |
该计算样例含有2条股线,分别标记为1号股线与2号股线,且每条支路可等效为16根导线串联组成,即16个等效电阻串联而成,图1与图2的导线编号顺序均为槽间按从左至右的顺序,槽内按从槽口至槽底的顺序编号,其等效连接如图3和图4所示。
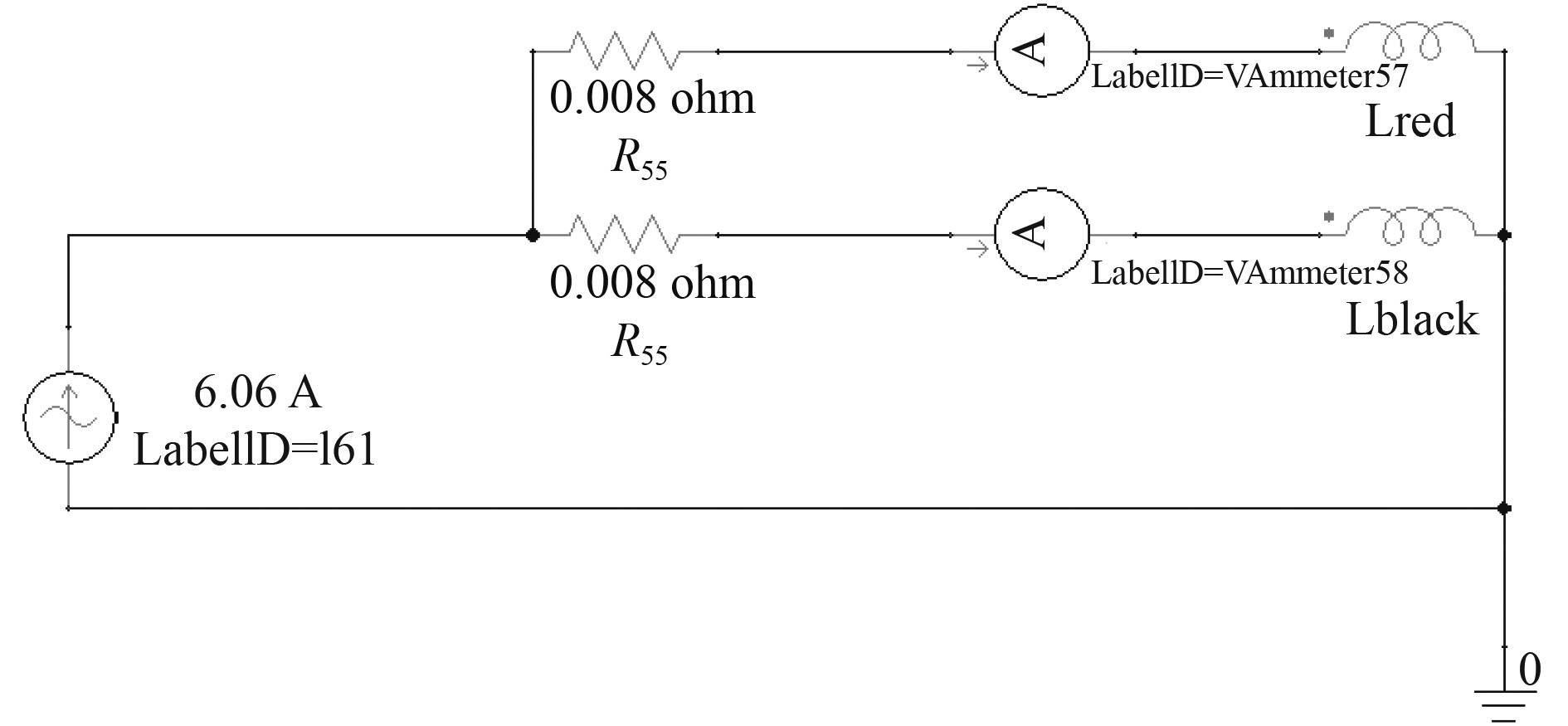
3 绕组换位对环流影响验证 3.1 有限元模型计算结果针对如图2和图3所示计算模型,采用有限元方法进行验证,激励源为幅值6.06 A的正弦电流,电流频率为20、200、400、600、800、
|
图 6 模型外电路 Fig. 6 External model circuit |
当电流频率为1 kHz时,有限元计算得到换位绕组与不换位绕组的电流密度分布如图7所示。
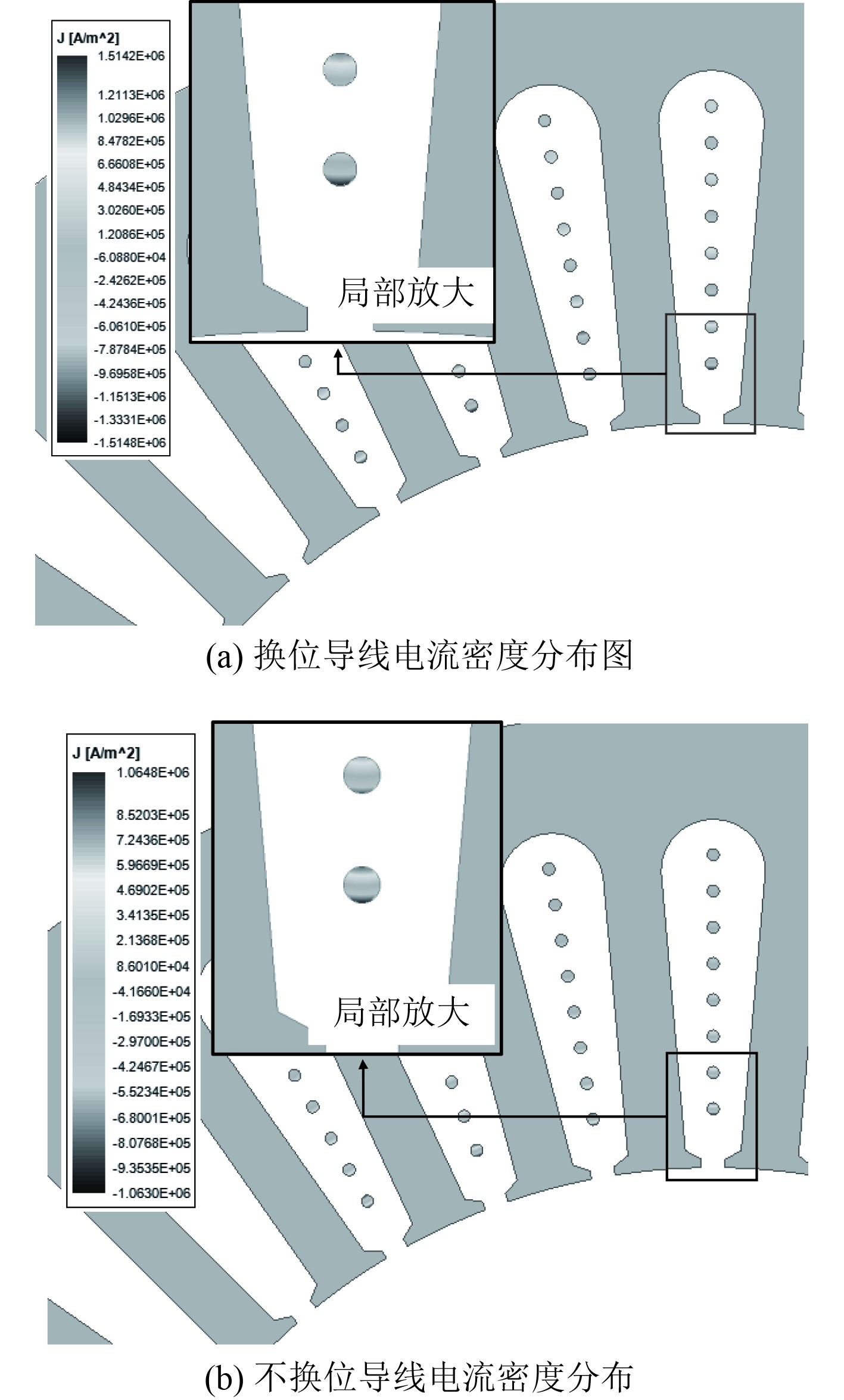
|
图 7 电流密度分布(1 kHz) Fig. 7 Current density distribution (1 kHz) |
不同频率下换位与不换位绕组由环流引起的交流电阻系数对比如图8所示,各股线电流相位差值如图9所示。
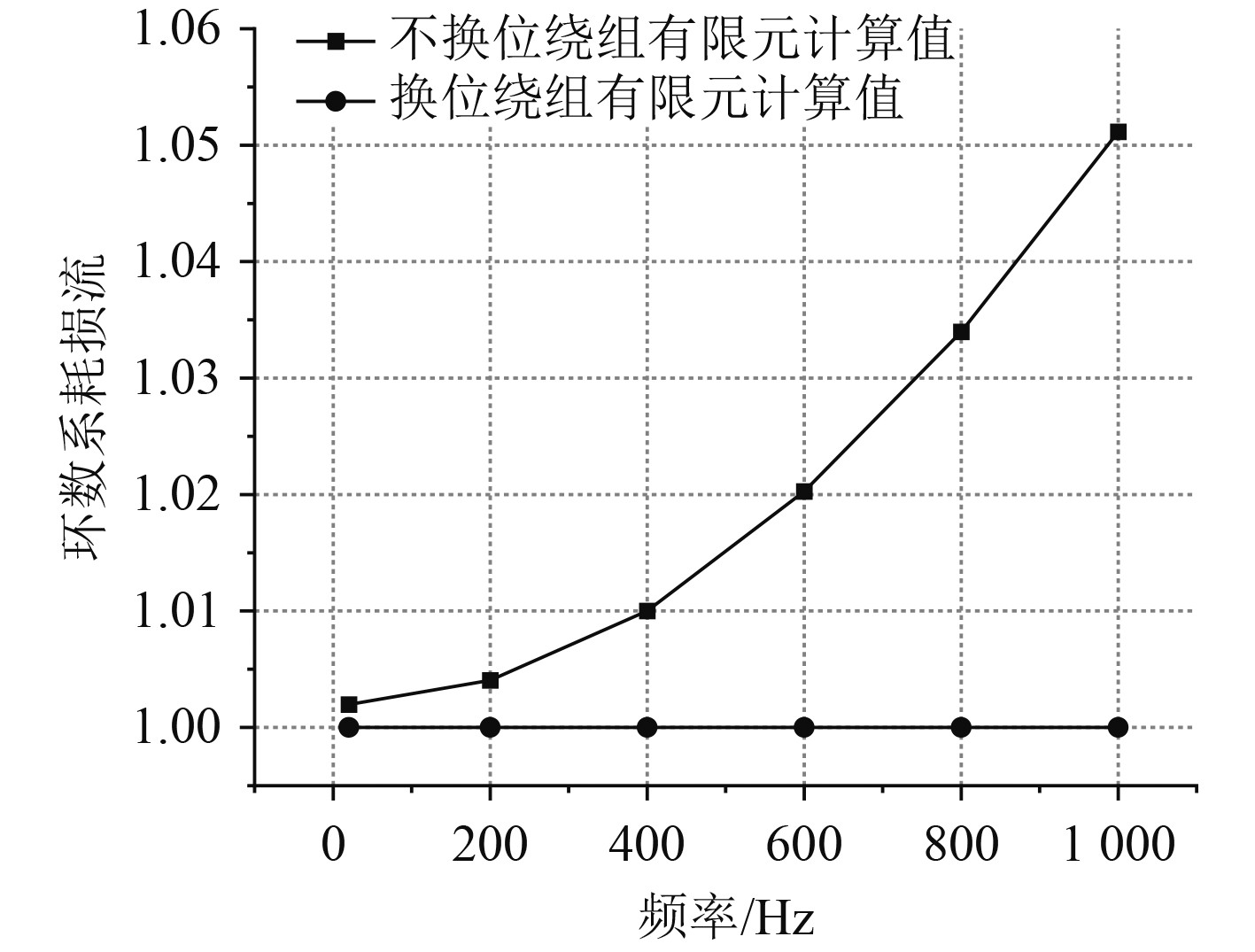
|
图 8 环流损耗系数 Fig. 8 Circulation loss coefficient |
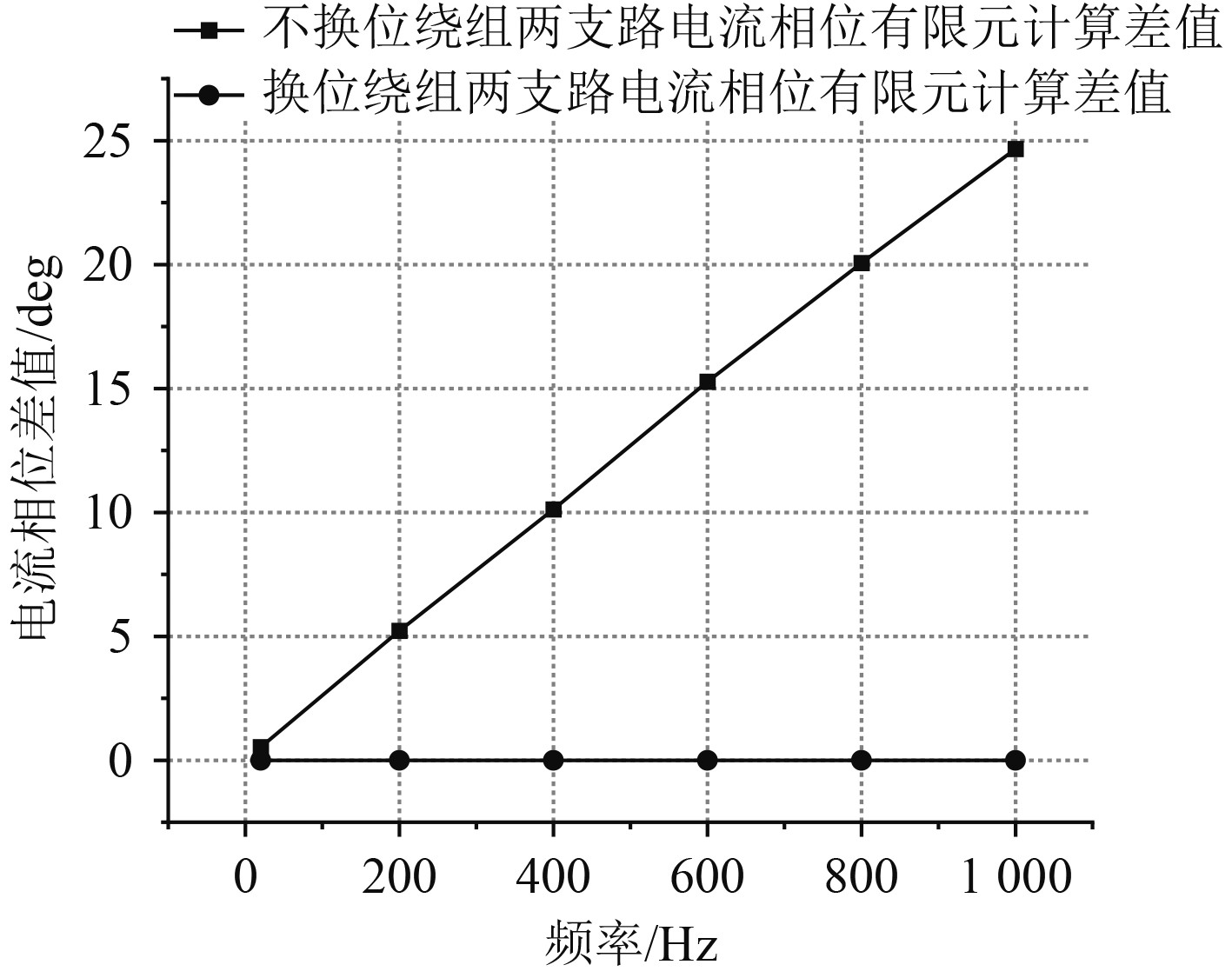
|
图 9 相位差值 Fig. 9 The phase difference |
将换位的绕组与不换位的绕组绕在同一个定子铁心的不同位置中,将图1和图2中的1号绕组与2号绕组并联,对其通入不同频率的正弦交流电。
实验分为2组测量,分别使用2个电流探头测量定子绕组换位与不换位2种工况下的实验数据,分别采集工况为20、200、300、500、600、
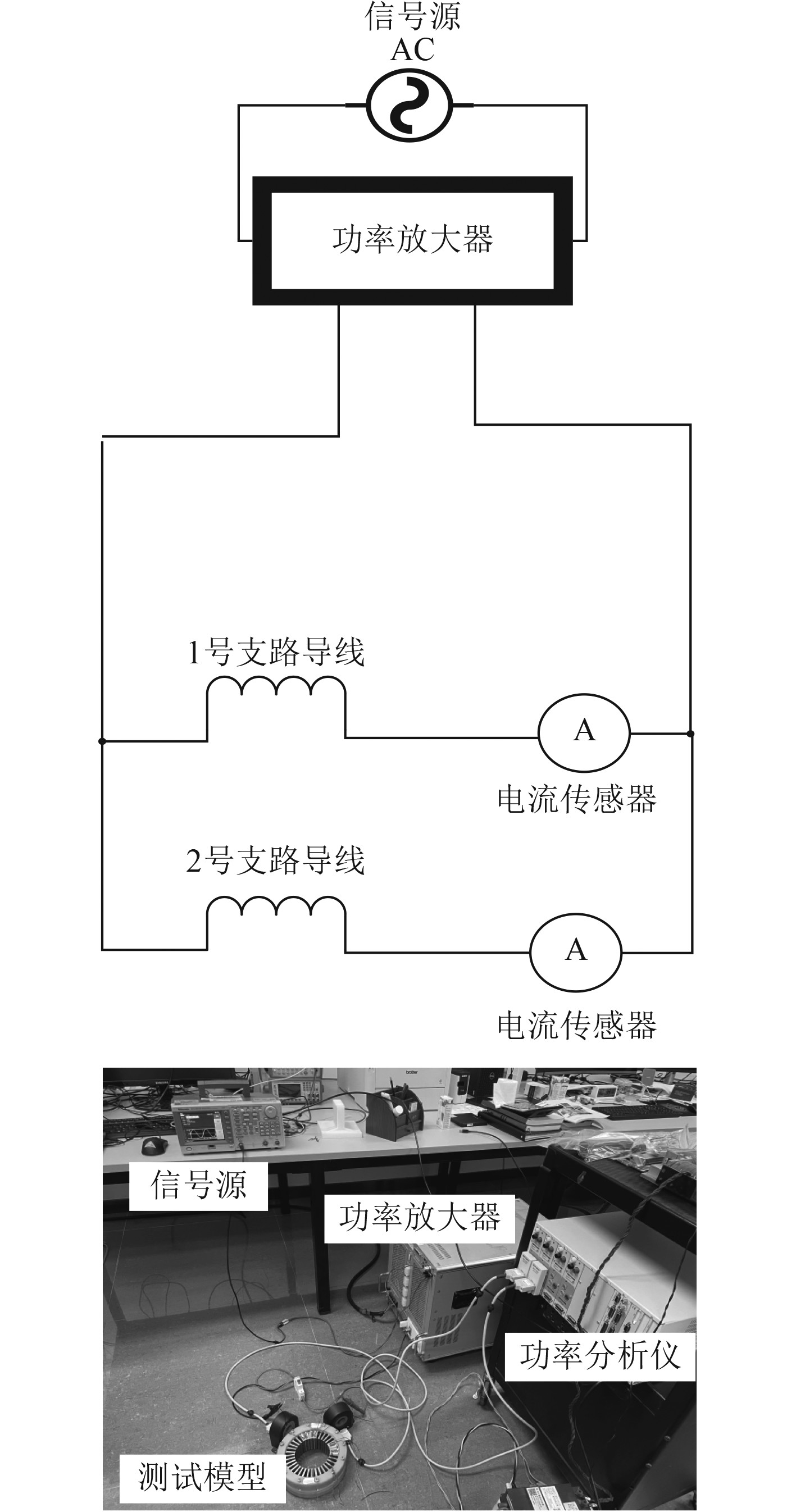
|
图 10 绕组环流抑制实验平台 Fig. 10 Winding circulation suppression experiment platform |
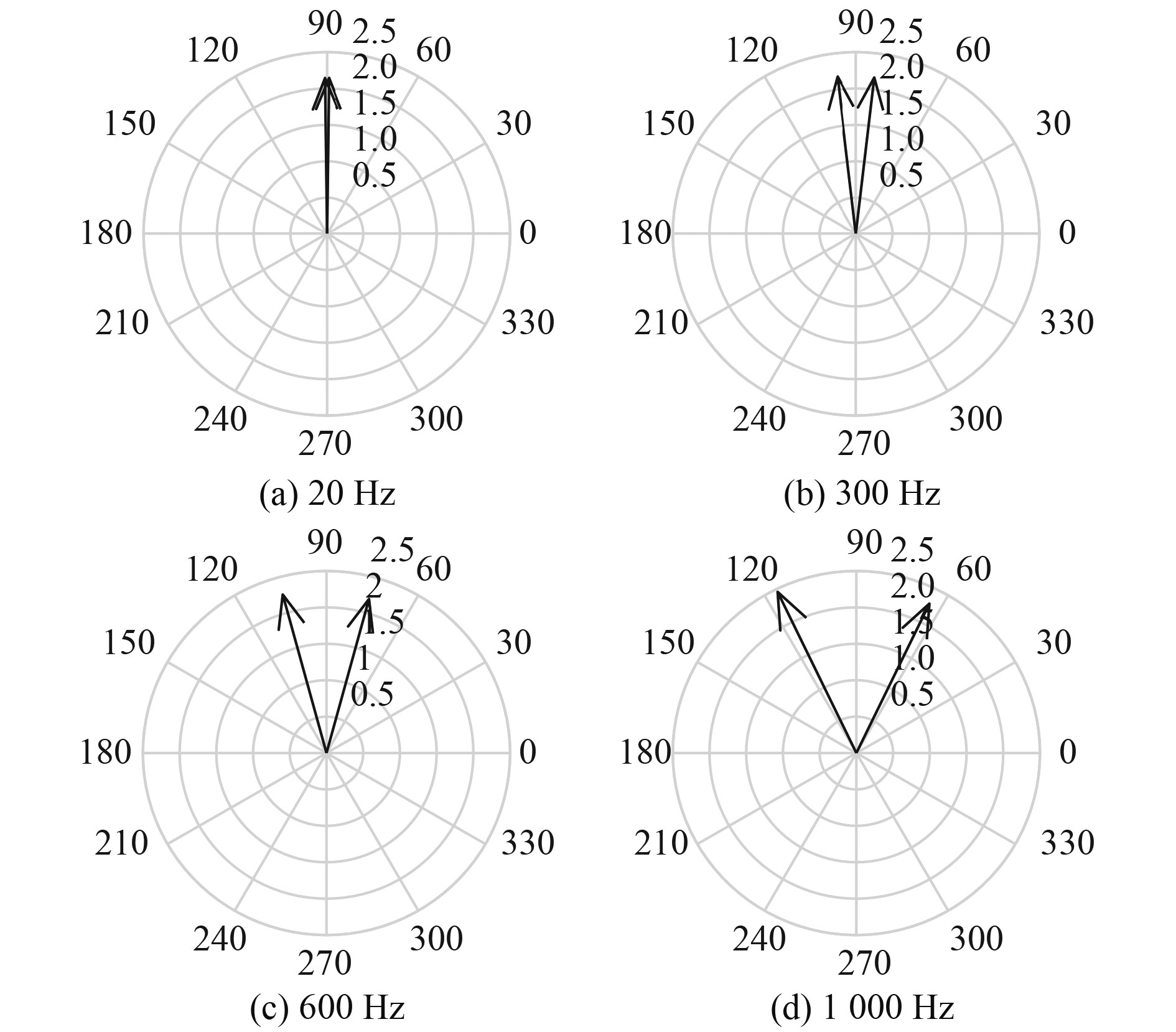
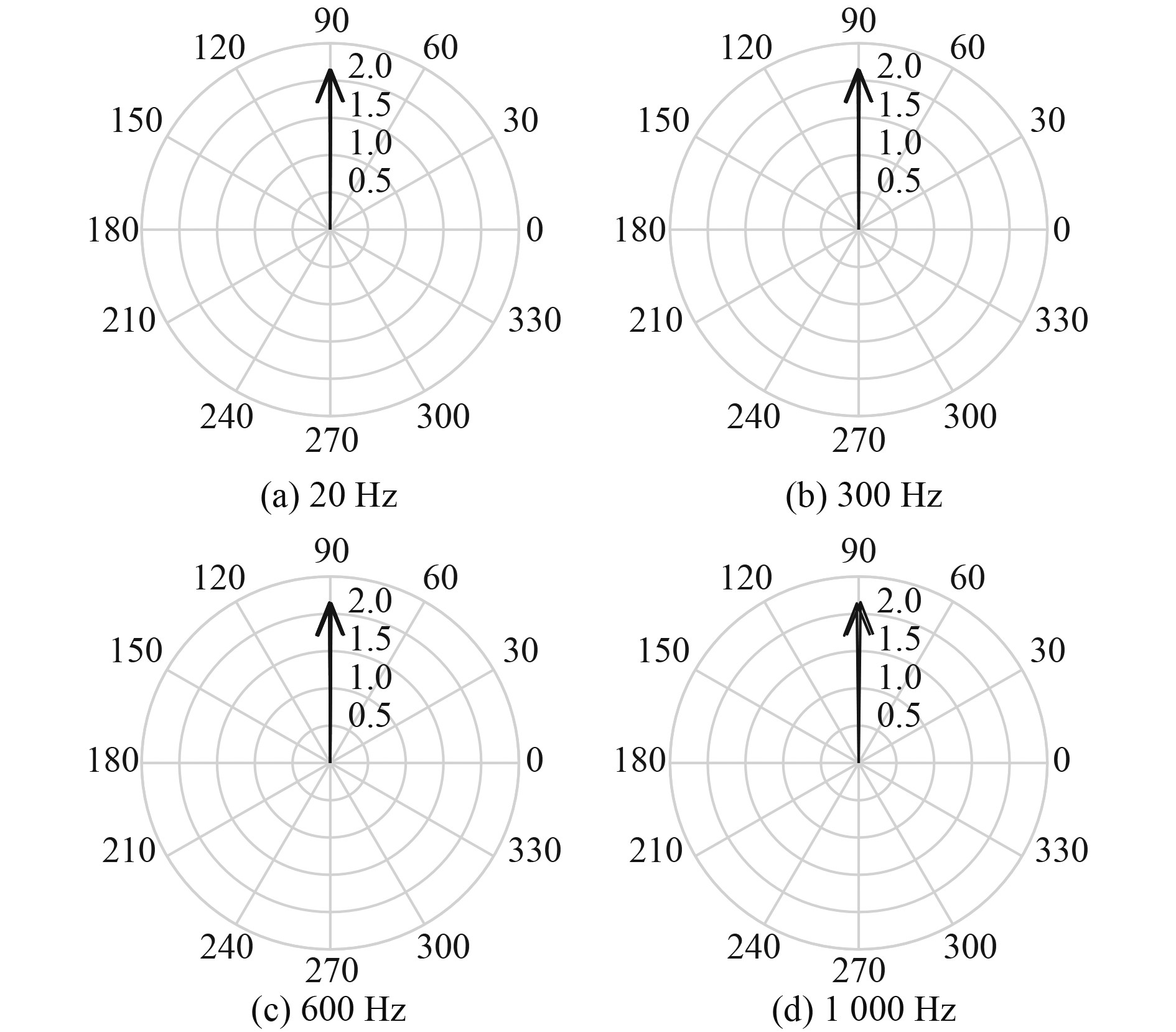
对采集的电流电压数据进行处理,为简化对比,取20、300、600、
|
图 11 换位前电流矢量图 Fig. 11 Vector diagram of current before transposition |
|
图 12 换位后电流矢量图 Fig. 12 Current vector diagram after transposition |
|
|
表 2 换位前电流相位参数 Tab.2 Pre-transposition current phase parameter |
|
|
表 4 环流损耗系数 Tab.4 Circulation loss coefficient |
由表4及图8可知,在有限元仿真结果及实验测量中,换位绕组与不换位绕组环流损耗系数均随电流频率升高而增大,且换位绕组环流损耗系数在20~
|
|
表 5 环流损耗系数增幅百分数对比 Tab.5 Comparison of percentage increase of circulation loss coefficient |
|
|
表 6 环流损耗系数差值百分数对比 Tab.6 Comparison of percentage difference of circulation loss coefficient |
由表2、表3及图9可知,在有限元仿真结果及实验测量中,换位及不换位绕组两支路电流相位差均随电流频率升高而增大,且在20~
|
|
表 3 换位后电流相位参数 Tab.3 Phase parameter of current after transposition |
|
|
表 7 相位差值增幅对比 Tab.7 Comparison of phase difference value increase |
|
|
表 8 相位差值对比 Tab.8 Contrast of phase difference values |
|
|
表 9 1 kHz工况下环流损耗系数有限元与实验误差 Tab.9 Finite element analysis and experimental error of circulation loss coefficient under 1 kHz condition |
由上述对比结果可知,换位绕组与不换位绕组在有限元和实验测量中环流损耗系数及两支路相位差均随频率升高而增大,说明了在高频条件下环流损耗会增加,而从环流损耗系数与两支路电流相位差增幅对比来看,在有限元和实验测量中换位绕组的环流损耗系数及两支路电流相位差相较于不换位绕组增幅更小,换位绕组环流损耗系数及两支路相位差值在各频率工况下均低于不换位绕组,且在高频条件下效果更明显,验证了绕组换位对环流损耗的抑制作用。
针对有限元与实验结果误差进行了分析,由于有限元外电路中所设置的电阻与实际电机定子端部外加引线的总电阻值有偏差,此为造成有限元仿真与实验数据测量存在差异的主要原因,此外电机定子在制作过程中工艺的误差及实验过程中由于电源输出的不稳定性也是造成实验测量误差的原因之一。
4 结 语本文通过永磁电机绕组端部换位的方式抑制导线间交链漏磁通从而达到抑制环流的目的,基于理论分析可使用无转子模型模拟有转子时的环流效应,通过仿真和实验结果对比换位绕组与不换位绕组不同股线电流相位、有效值及环流损耗系数差值,验证了绕组端部换位对环流损耗的抑制作用,为高速电机高频环流损耗的抑制提供了绕组设计参考。
| [1] |
LEHIKOINEN A, CHIODETTO N, LANTTO E, et al. Monte Carlo analysis of circulating currents in random wound electrical machines[J]. IEEE Transactions on Magnetics, 2016, 52(8): 1-12. |
| [2] |
HAMALAINEN H, PYRHONEN J, NERG J. Ac resistance factor in one layer form-wound winding used in rotating electrical machines[J]. IEEE Transactionson Magnetics, 2013, 49(6): 2967−2973.
|
| [3] |
薛继印, 杨在葆, 刘永, 等. 变压器绕组并联支路不等匝引起环流问题的分析与探讨[J]. 变压器, 2021, 58(8): 21-23. |
| [4] |
任亚军, 韩军锋, 张峰. 电力变压器不同绕组导线换位方式下环流损耗对比分析[J]. 电工电气, 2021(1): 30-34. DOI:10.3969/j.issn.1007-3175.2021.01.006 |
| [5] |
王泰丽. 多工况下同步调相机定子线棒环流损耗计算[D]. 哈尔滨: 哈尔滨理工大学, 2019.
|
| [6] |
冯慈璋. 工程电磁场导论[M]. 北京: 高等教育出版社, 2000.
|
| [7] |
武岳, 张志锋. 轴向磁通永磁电机扁铜线交流铜耗的混合解析计算及抑制[J]. 电工技术学报: 2023, 38(24): 6609−6618.
|
| [8] |
ROEBEL L. Electrical Conductor: US19130751640[P]. US1144252A.
|
| [9] |
梁艳萍, 柳杨, 王晨光. 大型水轮发电机定子绕组新型组合换位方法分析[J]. 中国电机工程学报, 2016, 36: 3092-3100. |
| [10] |
XIA Sheng, YAO Yingying. Optimization of transposition in stator bars of hydro-gcncrators[C]//2012 Sixth International Conference on ElcctromagncticFicld Problcms and Applications, 2012: 1−4.
|
| [11] |
梁艳萍, 乔雪, 边旭, 等. 改进漏感电动势法计算换位线棒股线电流及环流损耗[J]. 电工技术学报, 2017, 32(17): 164-171. |
| [12] |
JIANG Yapeng, CHEN Junquan, WANG Hanghang, et al. Semi-analytical method of form-wound windig loss considering circulating current effect[J]. IEEE Transactionson Magnetics, 2021, 58(2): 1−4.
|
 2024, Vol. 46
2024, Vol. 46
