0 引　言

船舵作为舰船操纵机构的核心组成部分，其主要功能是控制船舶的航向和转向，确保船舶能够按照预定的航线安全航行^[1]。然而，在实际操作中，船舵的稳定性往往受到多种因素的影响，包括舵机本身的质量和设计、使用环境、系统的维护和保养，以及操作者的技能和经验等^[2]。这些因素若处理不当，极易导致船舵在避撞过程中出现不稳定现象，通过对船舵进行不稳定性分析，可以提升船舶的操纵精度和灵敏度，降低碰撞风险。

国内外学者对降低舰船碰撞风险的相关研究有很多，例如，黄宠平等^[3]以舰船舵角误差以及舵角变化率为控制目标，建立非线性模型预测控制模型；为提升舵角控制效果，在控制模型内引入避碰因数，并由粒子群算法，求解该模型，得到舵角控制方案^[3]。粒子群算法需要多个迭代步骤来找到近似最优解，这会导致实时性不足，特别是在模型复杂或者计算资源有限的情况下。王文新等^[4]通过鲁棒神经网络，完成舵角控制，该方法通过设计自适应学习参数，实时地、动态地补偿舰船中难以预知的增益变化以及舵机可能遭遇的故障情况，确保舰船在面对不确定性和故障时仍能维持稳定性能和可靠操作。虽然通过结合鲁棒神经阻尼技术和自适应方法减少了神经网络权值的计算量，但是自适应方法的参数调整过程需要一定的时间来响应环境变化，特别是在快速变化的海况中，这种调整不够迅速。Kim等^[5]通过建立船舶在不规则波浪作用下的数学模型，并利用计算流体动力学（CFD）方法对船舶在波浪中的运动特性进行数值模拟。通过对船舶航向控制系统进行分析和设计，提出一种适用于不规则波浪中的船舶航向控制方法。利用CFD方法对船舶在不规则波浪中的运动特性进行数值模拟是一个非常计算密集的过程，难以在实时控制系统中应用。CFD模拟通常需要较长的计算时间，这对于需要快速响应的船舶航向控制系统来说是一个限制因素。张显库等^[6]以三阶闭环增益成形算法为基础，构建舵角控制器。为了克服该控制器在处理复杂非线性动态时的不足，在其内部引入适当的非线性函数，微调控制信号，以更好地适应舰船在不同航行状态下的舵角响应特性；为确保控制信号在控制时的连续性和稳定性，在控制器的输出端添加零阶保持器，避免因信息采样和量化过程而可能引入的抖动或误差。非线性修饰和零阶保持器的引入会增加系统复杂性，这可能会影响控制器的实时响应能力。

尽管上述方法都在不同程度上提高了舵角控制的性能，但在实际应用中均存在实时性不足的问题。为此，本文研究舰船避撞过程中船舵不稳定性分析方法，以期为舰船舵角控制提供更加实时、有效的解决方案。

1 船舵不稳定性分析 1.1 舰船避撞过程中船舵数学模型构建

舰船避撞过程中，舰船包含4个自由度^[6,7]，分别是纵荡、横荡、横摇、首摇，表达公式分别如下：

$ \sigma \left( {\dot \xi - v\omega - {x_g}{\omega ^2} + {z_g}p\omega } \right) = F ，$

(1)

$ \sigma \left( {\dot v - {z_g}\dot p + {x_g}\dot \omega + \xi \omega } \right) = X ，$

(2)

$ {I_{xx}}\dot p - \sigma {z_g}\dot v - \sigma {z_g}\xi \omega = Y，$

(3)

$ {I_{zz}}\dot \omega + \sigma {x_g}\dot v + \sigma {x_g}\xi \omega = N 。$

(4)

式中：$ \sigma $为舰船质量；v为横漂速度；$ \dot v $为v的一阶导数；$ \omega $为艏摇角速度；$ \dot \omega $为$ \omega $的一阶导数；g为舰船质心；在x、z轴上，g至附体坐标系的距离为$ {x_g} $、$ {z_g} $；在x、z轴上，$ {I_{xx}} $为舰船的转动惯量、$ {I_{zz}} $；p为横摇角速度；$ \dot p $为p的一阶导数；$ \xi $为航速；$ \dot \xi $为$ \xi $的一阶导数；F、X、Y为不同方向上的外力，N为外力矩。

舰船避撞过程中，舰船的状态变量是$ x = \left[ {v\mathop {}\nolimits_{} p\mathop {}\nolimits_{} \omega \mathop {}\nolimits_{} \alpha \mathop {}\nolimits_{} \theta } \right] $。式中：横摇角为$ \alpha $；航向角为$ \theta $；$ \theta = r\cos \alpha $。整合式（2）~式（4）得到舰船避撞过程非线性模型，具体如下：

$ \dot x = Mf(x) + B\delta。$

(5)

为降低船舵不稳定性分析的复杂性，将式（5）的非线性模型变更成线性模型，公式如下：

$ \dot x = Ax + B\delta 。$

(6)

式中：$ A = {M^{ - 1}}\frac{{\partial f\left( x \right)}}{{\partial x}} $；$ B = {M^{ - 1}}{R^{\rm T}} $；R为舰船避撞过程中相关参数的欧式空间。

依据式（6）获取舰船避撞过程中，船舵的输入舵角为：

$ \delta = Kx 。$

(7)

式中：K为舰船避撞过程中的增益。

此时，式（6）变更成：

$ \dot x = Ax + BKx 。$

(8)

$ K $的计算公式如下：

$ K = \left( {\frac{v}{L}} \right)\frac{{{N_{\dot v}}{Y_\delta } - {N_\delta }{Y_{\dot v}}}}{S} 。$

(9)

式中：$ {N_\delta } $为船舵受到的外力矩；$ S = {Y_{\dot v}}{N_{\dot \omega }} - {N_{\dot v}}\left( {{Y_{\dot \omega }} - \sigma } \right) $；L为船长。

1.2 舰船避撞过程中船舵不稳定性分析过程

针对式（8）计算获取的$ K $，令$ {A_1} = HK $，则变更式（8）得到舰船避撞过程中，包含时变延迟的线性模型，公式如下：

$ \dot x = Ax + {A_1}x 。$

(10)

分析舰船避撞过程中，船舵不稳定性分析时需要以下引理：

引理1　已知矩阵$ {\boldsymbol P} > 0 $，针对在$ R $内全部不间断可微函数$ \varphi $，成立以下不等式：

$ \begin{gathered} - \int {{{\dot \varphi }^{\rm T}}\left( \varepsilon \right)} P\dot \varphi \left( \varepsilon \right){\text{d}}\varepsilon \geqslant \\ - \frac{{{{\left[ {\varphi \left( {{R_{\max }}} \right) - \varphi \left( {{R_{\min }}} \right)} \right]}^{\rm T}}P\left[ {\varphi \left( {{R_{\max }}} \right) - \varphi \left( {{R_{\min }}} \right)} \right]}}{{{R_{\max }} - {R_{\min }}}}，\\ - \frac{{3{{\left[ {\varphi \left( {{R_{\max }}} \right) + \varphi \left( {{R_{\min }}} \right) + \frac{{2\int {\varphi \left( \varepsilon \right){\text{d}}\varepsilon } }}{{{R_{\max }} - {R_{\min }}}}} \right]}^{\rm T}}}}{{{R_{\max }} - {R_{\min }}}} \\ \times P\left[ {\varphi \left( {{R_{\max }}} \right) + \varphi \left( {{R_{\min }}} \right) + \frac{{2\int {\varphi \left( \varepsilon \right){\text{d}}\varepsilon } }}{{{R_{\max }} - {R_{\min }}}}} \right] 。\\ \end{gathered} $

(11)

式中：$ \dot \varphi $为$ \varphi $的一阶导数；$ {R_{\max }} $、$ {R_{\min }} $为R的上界、下界；$ \varepsilon $为复变量。

引理2　针对随机向量$ {\alpha _1} $与$ {\alpha _2} $，给出合理的二阶矩阵$ W $、$ C $与正数$ {\beta _1} $、$ {\beta _2} $，若$ \left[ \begin{gathered} W\mathop {}\nolimits_{} C \\ {0_{}}\mathop {}\nolimits_{} W \\ \end{gathered} \right] \geqslant 0 $，$ {\beta _1} + {\beta _2} = 1 $，则存在以下不等式：

$ \frac{{\alpha _1^{\rm T}W{\alpha _1}}}{{{\beta _1}}} + \frac{{\alpha _2^{\rm T}W{\alpha _2}}}{{{\beta _2}}} \leqslant {\left[ \begin{gathered} {\alpha _1} \\ {\alpha _2} \\ \end{gathered} \right]^{\rm T}}\left[ \begin{gathered} W\mathop {}\nolimits_{} C \\ {0_{}}\mathop {}\nolimits_{} W \\ \end{gathered} \right]\left[ \begin{gathered} {\alpha _1} \\ {\alpha _2} \\ \end{gathered} \right] 。$

(12)

依据引理1与引理2，结合李雅普诺夫稳定性判定理论，得到以下定理。

定理　若包含正定矩阵$ {{\boldsymbol G}_1} $、$ {{\boldsymbol G}_2} $，2个矩阵均是对称的，大小均为$ 5 \times 5 $。矩阵$ {\boldsymbol{\chi}} = \left[ \begin{gathered} {{\boldsymbol{\chi}} _{11}}\mathop {}\nolimits_{} {{\boldsymbol{\chi}} _{12}} \\ {{\boldsymbol{\chi}} _{21}}\mathop {}\nolimits_{} {{\boldsymbol{\chi}} _{22}} \\ \end{gathered} \right] $的大小是$ 10 \times 10 $；矩阵$ {\boldsymbol{\chi}} $左上角的元素为$ {{\boldsymbol{\chi}} _{11}} $；矩阵$ {\boldsymbol{\chi}} $左下角的元素为$ {{\boldsymbol{\chi}} _{12}} $；矩阵$ {\boldsymbol{\chi}} $右上角的元素为$ {{\boldsymbol{\chi}} _{21}} $；矩阵$ {\boldsymbol{\chi}} $右下角的元素为$ {{\boldsymbol{\chi}} _{22}} $。则存在以下不等式：

$ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol G}_2} & 0 & {{\boldsymbol \chi} _{11}} & {{\boldsymbol \chi} _{12}} \\ 0 & 3{{\boldsymbol G}_2} & {{\boldsymbol \chi} _{21}} & {{\boldsymbol \chi} _{22}} \\ {\boldsymbol \chi} _{11}^{\rm T} & {\boldsymbol \chi} _{21}^{\rm T} & {{\boldsymbol G}_2} & 0 \\ {\boldsymbol \chi} _{12}^{\rm T} & {\boldsymbol \chi} _{22}^{\rm T} & 0 & 3{{\boldsymbol G}_2} \\ \end{array} }\right] < 0 。$

(13)

因此，式（10）的舰船避撞过程中，包含时变延迟的线性模型，在式（7）的输入舵角作用下是不稳定的。

2 结果与分析

以某舰船为实验对象，利用本文方法对该舰船避撞过程中的船舵进行不稳定性分析，提升舰船避撞效果，并确保避撞过程舰船能够稳定航行。该舰船的相关参数如表1所示。

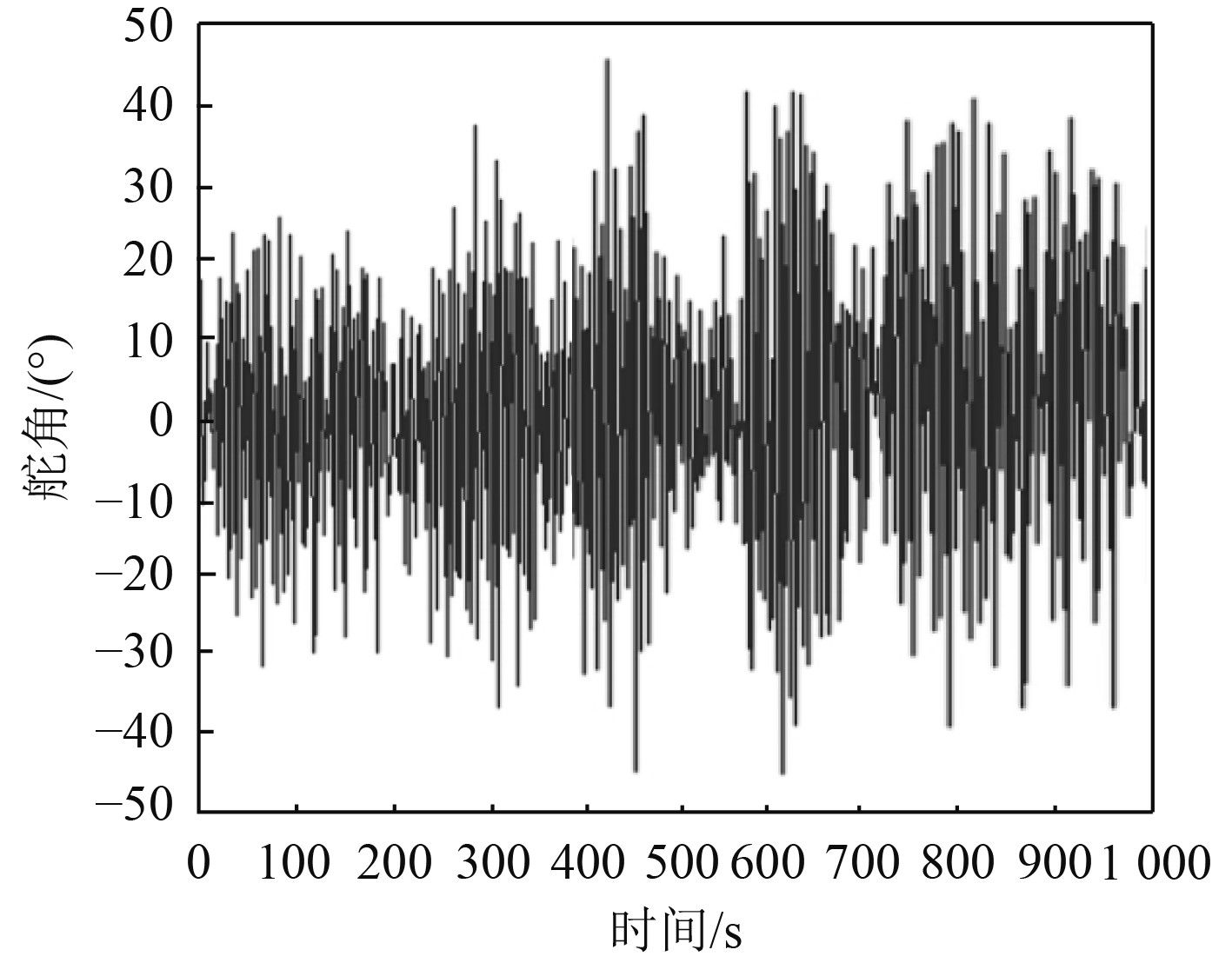
利用本文方法对该舰船避撞过程中，进行船舵不稳定性分析，分析结果如图1所示。可知，本文方法可有效完成舰船避撞过程中船舵不稳定性分析。从分析结果中了解到，该舰船在避撞过程中，其舵角的操舵幅度在±50°之间，操舵幅度较大，舵角的大幅变化可能导致舰船在短时间内经历急剧的航向变化，提升其不稳定性，增加与障碍物或其他船舶碰撞的风险。

给定该舰船避撞过程中的时滞下界，利用本文方法确定舰船避撞过程中船舵的最大时滞上界，确定结果如表2所示。可知，本文方法可有效依据时滞下界，确定舰船避撞过程中船舵的最大时滞上界。从表中还可以看出，随着时滞下界的增加，最大时滞上界也有所增加，这表明时滞下界的选择会影响最大时滞上界的确定，原因是时滞下界代表舰船避撞过程中的最小时间延迟要求，而最大时滞上界则是为了确保足够的避撞空间。观察表格中的数据，可以发现它们在数值上呈现出一致的增长趋势。每个时滞下界的增加都导致最大时滞上界相应地增加，这表明本文方法确定最大时滞上界的过程是可靠的。

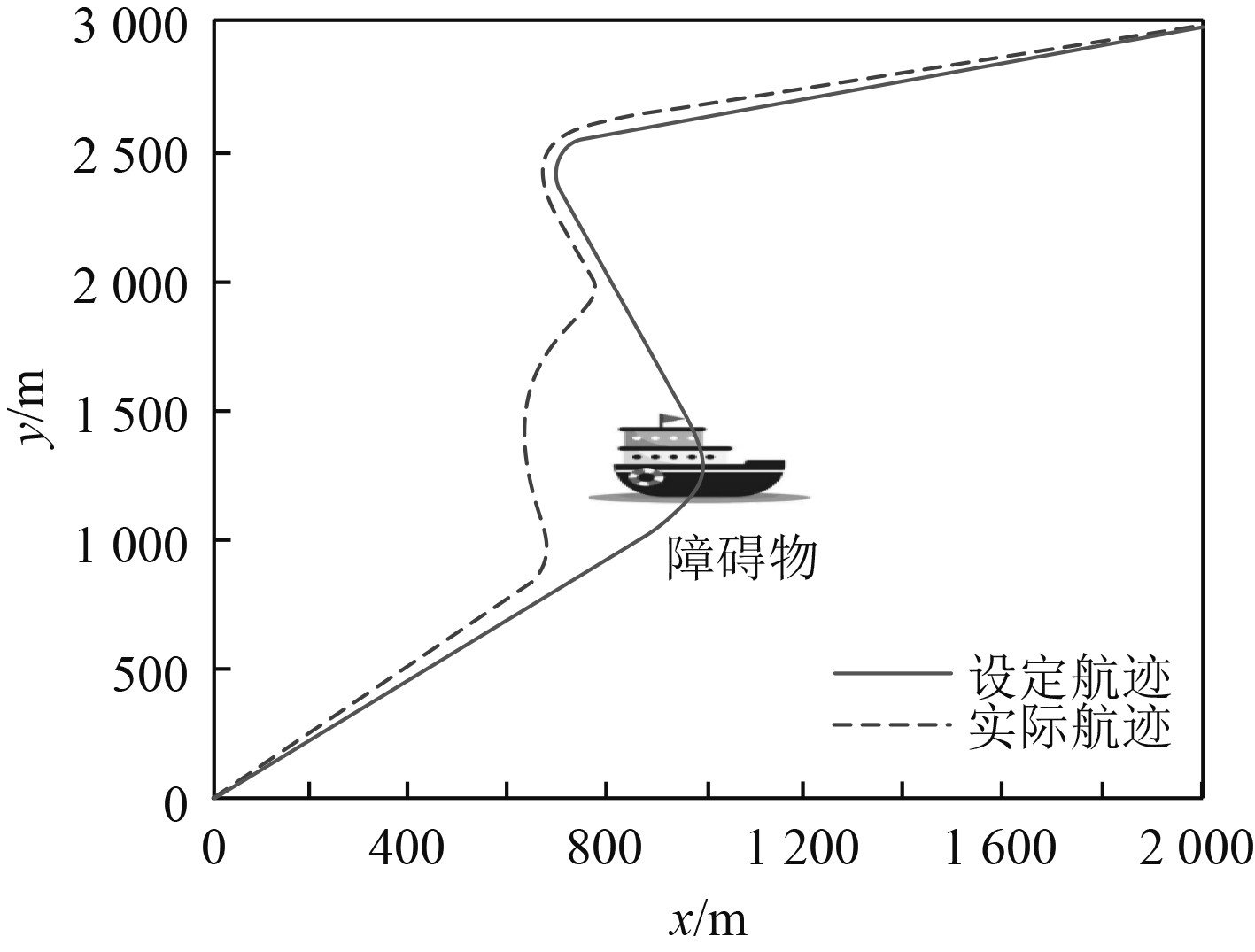
分析该舰船应用本文方法后，其避撞过程中的航行轨迹，分析结果如图2所示。可知，应用本文方法后，在未发生碰撞风险前，该舰船的实际航迹与设定航迹非常接近，在即将发生碰撞危险时，该舰船可有效完成避撞，且舰船的航迹调整是平滑且连续的，这表明应用本文方法后，舰船可根据实时环境动态调整避碰策略，这种实时性确保舰船在复杂多变的海洋环境中能够灵活应对，减少因突然转向或急停造成的航行不稳定。完成避撞后，该舰船的实际航迹与设定航迹也非常接近。实验证明：经过本文方法分析船舵不稳定性后，可有效提升舰船避撞过程中航行的稳定性，增强整体航行的安全性。

3 结　语

船舵作为船舶操纵机构的核心部分，其稳定性直接影响船舶的操纵性能和避撞效果。因此，研究舰船避撞过程中船舵不稳定性分析方法，有助于提升船舶在复杂航行环境中的安全性和可靠性。实验结果表明：应用本文方法分析船舵的不稳定性，可以提升船舶执行避撞指令的精度，降低碰撞风险。