0 引　言

由于减振降噪和隐身材料技术的发展，传统的声呐探潜技术受到了极大的限制。因此各国将目光转向了非声学的潜艇探测方法^[1]。非声学潜艇探测技术包含尾迹探测技术^[2]，而尾迹探测技术中包含对热尾迹的探测技术。水下的潜艇航行时所排出的冷却水形成的热尾流，热尾流消失缓慢并逐渐扩散上浮，当潜艇的潜深较浅时，热尾流会浮升到海面并形成数百米的“热斑”，此即热尾迹，通过红外探测设备和蓝绿激光雷达均可对热尾流进行探测。

1997年Wren和May对是否可以利用潜艇排放的冷却水对潜艇进行探测的问题进行了研究。潜艇航行过程中为了保证关键设备的冷却等正常工作条件，会通过冷却系统向海水中传递大量热量。据推算，1台拥有190 MW有用功的核潜艇，最终会约有188 MW的能量都被释放到了海水中，当该潜艇以5 kn速度航行时，这些热量大约会让其尾部海水温度升高0.2℃^[3]。CHEN^[4]对水下航行体的热水排放过程进行了仿真和实验，对比了水下航行体的不同运动状态下热尾流，仿真结果发现在水深14 m水下航行体直航速度为0.2 m/s时，当排放的冷却水比环境水温度高50 K时，在水面上会形成高温区，即“热斑”现象，当水下航行体运动速度加快时，“热斑”逐渐后移，且与周围水面的温差会减小，当水下航行体的速度超过4 m/s时，热尾流的浮升作用变弱，很难在水面形成“热斑”。为了对仿真结果进行验证，其团队利用热成像仪拍摄了水下航行体排出热水时水面的热像图，并在水池中布置了测点进行温度测量。胡日查等^[5]更进一步在水池的水中及水池壁面布设大量测温传感器进行实验，对低航速下的潜艇热尾流在水中的浮升规律进行了测量研究。戴天奇等^[6]对二维潜艇缩比模型排水过程进行了仿真，使用了来流法和动网格法2种仿真方法，并对比了2种方法的结果，发现动网格方法的尾流的浮升现象强度大于来流法的，而且动网格法的结果有很明显的震荡。王平等^[7]使用来流法和重叠网格法对三维潜艇缩比模型进行了排水仿真，并进行了水池验证实验，结果显示使用重叠网格法水面热斑出现的比来流法早且温度更高，同时与实验结果相对更吻合。

由于潜艇属于高敏感度的武器装备，目前已有的热尾流仿真与实验研究多是基于缩比模型进行，但是缩比模型无法做到满足所有的相似准则，目前的缩比模型研究多采用弗劳德相似准则，而无法满足传热学上的格拉晓夫相似准则，因此，采用缩比模型对热尾流进行研究存在一定缺陷。

目前主要海军强国的核潜艇很多都能达到万吨以上的排水量，为了探索潜艇排放的冷却水所造成的影响，本文建立了一个10000吨级的全尺寸潜艇模型，采用来流法对该模型冷却水排放过程进行了数值仿真，规避了采用缩比模型应该遵循何种相似准则的问题，仿真场景更贴近实际情况。

1 热尾流浮升仿真理论 1.1 热尾流理想模型

水的密度会受多种因素影响，如气压、温度以及水的纯度等，而潜艇排放的冷却水形成热尾流，并进一步扩散、浮升乃至在水面引起温度变化属于流动传热问题，其中的主要影响因素为温度，因此后文的仿真工作中仅考虑温度对水密度的影响。对已有的水的温度-密度测量数据的拟合，将水的密度与温度关联，得到水的密度和温度的关系，如下式：

$ \rho {\text{ = }}767.18 + 1.7841T - 0.003\ 4{T^2} 。$

(1)

若假定尾流扩散空间区域为圆锥形^[8]，设海水的温度、密度和比热分别为t₁、ρ₁、c_p，释放到尾流中的总热量为Q₀，设圆锥形尾流区底部半径为r、高度为s，排出冷却水温度为t_w，当潜艇航行τ秒时尾流扩散区的热平衡方程为：

$ {Q_0} = m{c_p}({t_{{w}}} - {t_1}) = \frac{{{\text π} {\rho _1}{{{r}}^2}s}}{3} 。$

(2)

式中，$s \approx {u_1}\tau $，其中u₁为潜艇的航速，由此尾流平均温升为：

$ {t_{{w}}} - {t_1} = \frac{{3{Q_0}}}{{{\text π} {\rho _1}{{{r}}^2}{u_1}{c_p}}}。$

(3)

式（2）中尾流区底部半径r可取值为：

$ \frac{{{r}}}{D} = 0.47{\left(\frac{s}{D}\right)^{0.293}}。$

(4)

1.2 热尾流浮升仿真控制方程 1.2.1 控制方程

本文采用基于雷诺平均的N-S方程（RANS方程），由于还涉及流动传热问题，因此需要在质量连续方程、动量方程的基础上补充能量方程，构成本文的控制方程组^[9]:

$ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0 ，$

(5)

$ \rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = \rho {\overline F _i} - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left( {\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {u_i^\prime u_j^\prime } } \right)。$

(6)

式中：$ \overline {{u_i}} $与$ u_i^\prime $分别为雷诺平均速度和脉动速度；$ \rho \overline {u_i^\prime u_j^\prime } $为雷诺应力项；$ {\overline F _i} $为质量力；$ \rho $为流体密度。

因为本文中还涉及到传热过程，所以控制方程需要增加能量守恒定律，能量守恒定律的方程如下式：

$\begin{aligned}[b] &\frac{\partial }{{\partial t}}\left( {\rho E} \right) + \frac{\partial }{{\partial {x_j}}}\left( {{u_i}\left( {\rho E + P} \right)} \right) = \\ &\frac{\partial }{{\partial {x_i}}}\left( {{K_{eff}}\frac{{\partial T}}{{\partial {x_i}}} - \mathop \sum \limits_{j'} {h_{j'}}{J_{j'}} + {u_i}{\tau _{ij}}} \right) + {S_h} 。\end{aligned}$

(7)

1.2.2 湍流模型

RANS方程组中有关湍流脉动值的雷诺应力项$ \rho \overline {u_i^\prime u_j^\prime } $是未知的。为了使方程封闭，选用适当的湍流模型十分必要。

由Yakhot及Orzag提出的RNG k-epsilon模型^[10]，通过修正大尺度运动的粘度项来体现小尺度运动的影响，将这些小尺度运动系统性地从控制方程中去除。与常用的Standard k-epsilon模型相比，RNG k-epsilon主要有以下优势：1）RNG模型在epsilon方程中有一项附加项，可以提高急变流的精度；2）RNG模型在计算时纳入了涡流对湍流的影响，当流动包含涡流时，可以提高仿真计算精确性；3）在Standard k-epsilon模型中，普朗特数是一个常数，而RNG理论对湍流普朗特数提出了自己的解析公式；4）RNG k-epsilon模型包含低雷诺数场景下有效粘度的计算公式，而标准k-epsilon模型仅适应高雷诺数场景。

RNG k-epsilon模型的输运方程为：

$\begin{aligned}[b] &\frac{{\partial \rho }}{{\partial t}}\left( {\rho {{k}}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {{k}}{u_i}} \right) = \\ &\frac{\partial }{{\partial {x_i}}}\left( {{\alpha _k}{\mu _{eff}}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {{{G}}_k} + {{{G}}_b} - \rho \varepsilon - {Y_M} + {S_k}，\end{aligned}$

(8)

$\begin{aligned} &\frac{{\partial \rho }}{{\partial t}}\left( {\rho{\text{ε}}} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho {\text{ε}}{u_i}} \right) =\\ &\frac{\partial }{{\partial {x_i}}}\left( {{\alpha _\varepsilon }{\mu _{eff}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right) + {{C}_{1\varepsilon }}\frac{\varepsilon }{k}\left( {{{{G}}_k} + {C_{3\varepsilon }}{G_b}} \right) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - {R_\varepsilon } + {S_\varepsilon }。\end{aligned}$

(9)

式中：${{{C}}_{1\varepsilon }} = 1.42$；${C_{2\varepsilon }} = 1.68$。

${\alpha _k}$和${\alpha _\varepsilon }$分别为湍动能和湍流耗散率的普朗特数的倒数，${\alpha _k}$和${\alpha _\varepsilon }$的计算公式为：

$ {\left| {\frac{{\alpha - 1.3929}}{{{\alpha _0} - 1.3929}}} \right|^{0.6321}}{\left| {\frac{{\alpha + 2.3929}}{{{\alpha _0} + 2.3929}}} \right|^{0.3679}} = \frac{{{\mu _{mol}}}}{{{\mu _{eff}}}}。$

(10)

其中，${\alpha _0} = 1.0$，在高雷诺数下（$\displaystyle\frac{{{\mu _{mol}}}}{{{\mu _{e f f}}}} \ll 1$），${\alpha _k} = {\alpha _\varepsilon } = 1.393$。

${R_\varepsilon }$为附加项，其计算公式为：

$ {R_\varepsilon } = \frac{{{C_\mu }\rho {\eta ^3}\left( {1 - \eta /{\eta _0}} \right)}}{{1 + \beta {\eta ^3}}}\frac{{{\varepsilon ^2}}}{k} 。$

(11)

式中：$\eta = \displaystyle\frac{{{S_k}}}{\varepsilon }$；${\eta _0} = 4.38$；$\beta = 0.012$。

${u_t}$为有效湍流粘度，其计算公式为：

$ {u_t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon } 。$

(12)

式中：${C_\mu }$=0.0854。

1.2.3 VOF模型

潜艇的热尾流数值仿真，包含空气和海水的流动传热；同时潜艇在水下航行时，会在水面形成兴波尾迹。为了捕捉水面的温度分布、兴波尾迹等现象，需要使用多相流模型。本文仿真涉及空气与水2种流体，忽略空气在水中的溶解性问题，假定空气与水互不相溶。由于VOF模型能很好地求解2种及以上的互不相溶的流体之间形成的自由分界面，因此本文采用VOF多相流模型。在VOF模型中，所有流体共用相同的动量方程，追踪计算域中每个网格内某一相流体所占的体积百分数会^[11]。进一步，相与相之间的自由分界面是通过求解整个计算域所有网格中某一相流体的体积百分数而实现，例如第q相流体，方程如下：

$ \frac{{\partial {{\text{α }}_q}}}{{\partial t}} + {u_i}\frac{{\partial {{\text{α }}_q}}}{{\partial {x_i}}} = 0。$

(13)

当α_q=0时，说明该网格内不含第q相流体；当α_q=1，即该网格内全都为第q相流体；当0<α_q<1，该网格存在不同流体的分界面，通过求解的体积分数的输运方程跟踪流体之间的分界面。

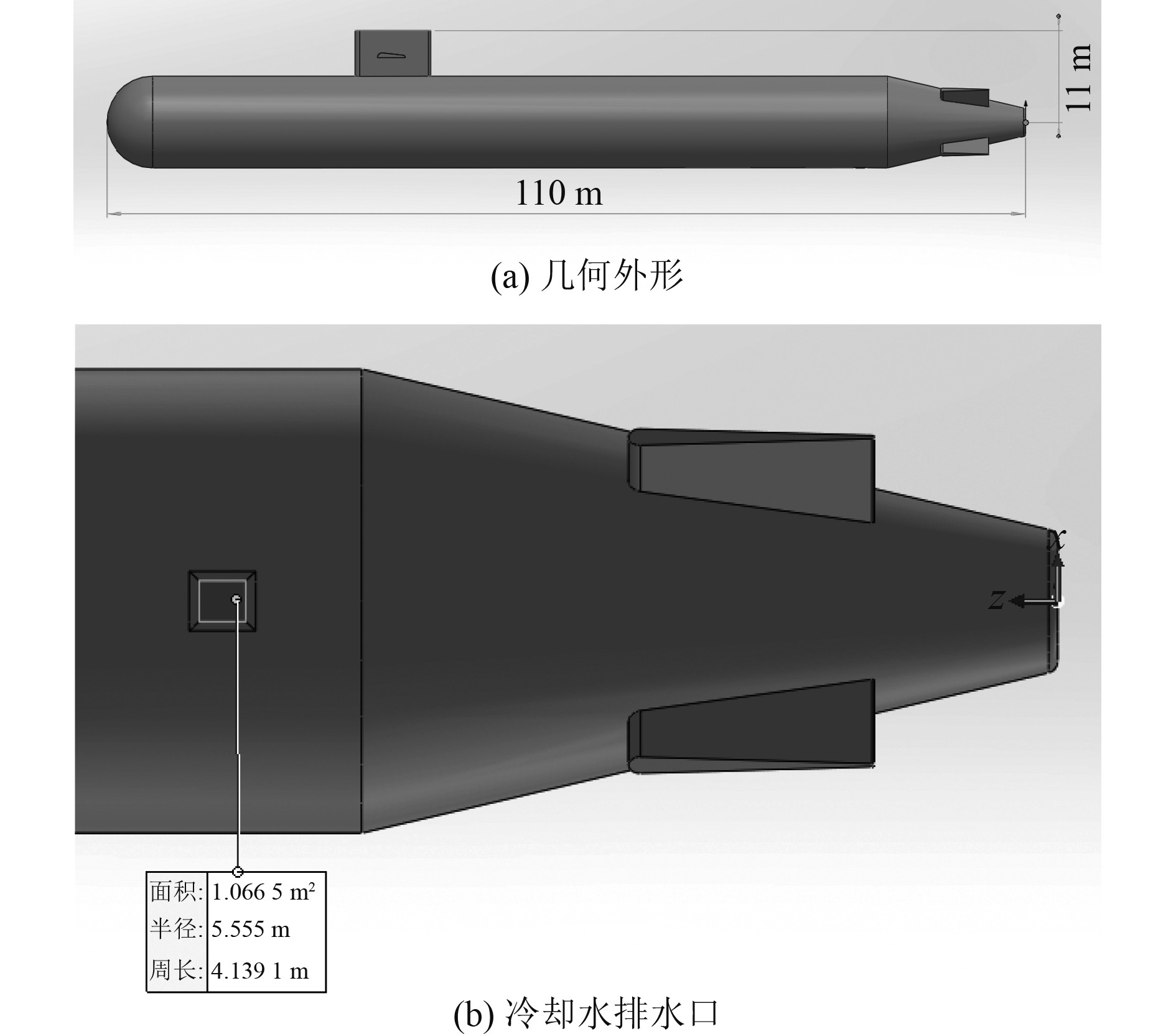
2 仿真设置 2.1 几何模型

图1为本文仿真对象的几何外形，主要结构包括艇身、围壳、围壳舵及x尾舵等；艇长110 m，艇身直径11 m，排水口形状如图1(b)所示，其位于艇身后部腹部，排水口面积约1.067 m²。

2.2 计算域及边界条件

由于潜艇大部分时间都是以较低的航速和较深的潜深进行巡航，以最大程度减小自身噪声，从而实现声学上的隐身^[12]。因此后文仿真专门针对较大的潜深和较低的航速的场景下，潜艇排放冷却水所产生的热尾流对水面的温度分布的影响进行分析。

本文的计算域宽为200 m，长为1000 m，其中计算域入口距离艇首90 m，计算域的出口距艇尾800 m如图2所示。环境水温有均匀温度和线性温度梯度2种情况，其中均匀温度环境水温为293.15 K，线性温度梯度的温度分布规律如式(14)所示^[13]；排出的冷却水温度设为333.15 K；本文中，潜深定义为潜艇模型最高点至水面的距离，潜深设置为50 m；采用来流法进行计算，则计算域入口的速度即为潜艇的航速，计算域入口速度设为5 kn；冷却水排水口为速度出口，流速为1.116 m/s。

$ T = 293.15 - 0.166\ 67H。$

(14)

式中：H为水深。

根据排水口面积，可推得排水的体积流速约为1.191 m³/s，水的比热容为4.2×10³ J/(kg·K)，此处暂时假定水的密度为1000 kg/m³的恒定值，可以推算出排出的冷却水可以带走的热功率约为200 MW。

2.3 网格划分

针对计算域的网格划分，采用混合网格方法，其中潜艇模型周围使用四面体非结构网格，并在模型表面进行了附面层加密以更好地贴合模型较为复杂的几何外表面；其余计算域采用六面体结构网格，对水-空气交界面附近的网格进行了局部加密，提高对水面特征的计算精度。如图3所示。

3 结果分析

本文采用来流法，对潜艇冷却水排放的过程进行了仿真，排放过程持续了300 s。

3.1 冷却水排放对水面温度分布的影响

潜艇排放冷却水时，因为冷却水温度比环境水温高，所以冷却水会与周围的水进行热量传递。图4为第300 s时，均匀环境水温下的水面温度云图和计算域纵剖面的温度云图；图5为第300 s时，线性温度梯度环境水温下的水面温度云图和计算域纵剖面的温度云图。

可以看出，潜艇排出的冷却水所形成的热尾流主要向潜艇后方进行扩散，而向上浮升的趋势较为微弱，因此在均匀环境水温下水面未形成明显的温差区域。

而在线性温度梯度环境水温下，由图5可知，潜艇在水面产生的主要温差现象为：由于艇体对水体的扰动，使得深处较冷的水上涌，进而使得水面出现一块温度相对较低的“冷斑”。

3.2 艇体扰动对水面温度分布的影响

本节对线性温度梯度环境水温条件下，艇体扰动对水面温度分布的影响，即“冷斑”进行仿真计算分析，仿真包含潜艇无排放冷却水动作和由排放冷却水动作2种情况。

图6为潜艇无排放冷却水动作时，第300 s时的水面温度分布和计算域纵剖面温度云图；图7为时潜艇有排放冷却水动作时，第300 s时的水面温度分布和计算域纵剖面温度云图。

通过对是否有排放冷却水动作的结果分析，可以粗略得到，在线性温度梯度环境水温下，即使此时冷却水与周围水体温差更大，即密度差更大，但其本身的浮升趋势仍然很微弱。通过对纵剖面温度云图中潜艇后方等温线分析可以发现：潜艇后方等温线出现了较长的上抬区域，这说明深处较冷的水上涌到了较浅处，这就是出现“冷斑”的原因。同时可以发现潜艇航行所产生的“冷斑”的基本特征是：位于潜艇正后方的水面上，呈细长条状分布。

对比2种情况下“冷斑”和周围水面的温差：当不存在排放冷却水动作时，水面“冷斑”比周围低0.001 K；当存在排放冷却水动作时，水面“冷斑”比周围低0.0015 K。

4 结　语

本文针对潜艇在水下航行的过程中所排放的冷却水得扩散和自身对周围水体的扰动，建立了三维潜艇热尾流扩散模型，对热尾流自身的扩散和潜艇的扰动作用进行了数值仿真计算，主要结论如下：

1） 通过对不同环境下的潜艇冷却水排放过程的仿真研究可以知道，在50 m潜深、5 kn航速条件下，潜艇的热尾流虽然与周围海水存在一定密度差，自身有上浮的趋势，但潜艇航行过程中热尾流更主要的是与周围冷的海水掺混并向艇身后方扩散，而不足以在水面形成明显的温度差现象；

2）在线性温度梯度环境水温下，潜艇航行对水体的扰动会促使深处较冷的海水上涌，并最终在水面形成温度较低的“冷斑”区域；

3）通过对是否有冷却水排放动作的比较研究，发现在当前的航行状态下，潜艇自身的排放冷却水对水面“冷斑”的影响比较微弱。

本文工作中研究的航行条件仅包括小部分情况，后期需要对更多航行条件下的结果进行计算并对比分析；现有的结果为今后的红外波段探潜技术研究和潜艇在红外波段隐身技术研究提供了一定的基础。