单点系泊中油轮使用缆绳系泊在浮筒的台柱上,在特定海域长期作业的单点系泊油轮,其受到的环境载荷会发生不断变化。在真实海况环境中,风、浪、流载荷较大且方向不一致有较大夹角,这种复杂实际环境下的船舶运动与受力和单一外载作用下的情况会产生较大偏差,因此研究不同环境条件下单点系泊系统受力性能的变化规律,确定系泊载荷的影响因素,对确定油轮单点系泊的设计环境条件、预测单点系泊系统所能承受的最大载荷,具有十分重要的意义。
有许多研究者从理论、数值以及试验方面提出了在波流、风浪流等作用下对船舶单点系泊系统动力响应进行研究。Chen等[1]利用时域势分解为线性分量和相互作用分量,对定常流在低速条件与波浪衍射的相互作用进行研究,得出结论,浪流之间耦合作用对包括波浪漂移阻尼在内的一阶、二阶载荷有重要影响。黄国樑等[2]开展了单点系泊船舶的水池试验,探究了风和潮流对于单点系泊船舶运动的影响。许鑫等[3]应用数值模拟方法对比分析单点系泊系统在考虑波流耦合作用和不考虑波流耦合作用下油轮的受力情况,得出考虑波流耦合作用下油轮系泊力和运动幅值均会增大,同时发现在波流同向时波流耦合作用最大。孙玉柱等[4]应用MOSES软件计算分析了8个典型的波浪入射方向下船舶的系泊能力能否满足该环境载荷工况的要求。周楠[5]针对油轮单点系泊系统在风浪流作用油船鱼尾运动的控制方法进行分析,提出在油船尾部施加拉力以抑制鱼尾运动的方案。刘孟琦等[6]基于物理模型试验,对悬链式单点系泊系统动力响应进行研究,探讨了单点系泊系统在风、浪、流的联合作用下油轮的运动规律和系泊力影响因素。通过研究表明,风速和波高的增大对船舶系泊力影响显著。陆阳[7]基于数值模拟对LNG船的系泊响应进行计算,分析了船体运动响应以及缆绳张力在不同浪向下的变化,发现在南向 90°波浪作用下,船舶的纵摇角最小,横摇角最大。葛帅等[8]针对悬链锚腿系泊(CALM)单点系泊系统实例,利用时域仿真方法对在风、浪、流作用下的单点系泊(SPM)系统进行动态稳定性分析,并使用时域仿真验证动稳性分析的有效性。
综上,由于现实海况多为波流不同向,且油轮单点系泊系统在实际海况作用下运动的复杂性。需要对系泊油轮在不同风浪流条件下的运动响应进行分析,同时要结合运动情况对油轮运动姿态进行调整,以确保单点系泊系统的安全以及海上施工作业的正常进行。本文主要研究油轮单点系泊在海浪、海流和风作用下的动力响应。
1 数值模型介绍 1.1 模型建立本计算为风、浪、流3种动力条件综合作用下的系泊系统数值模型,首先基于MOSES软件建立了8×104 t油轮及6根缆绳系泊系统的数值模型。表1 为该油轮的基本参数,表2为系泊系统参数。
|
|
表 1 船舶参数 Tab.1 Ship parameters |
|
|
表 2 系泊系统参数 Tab.2 Ship parameters |
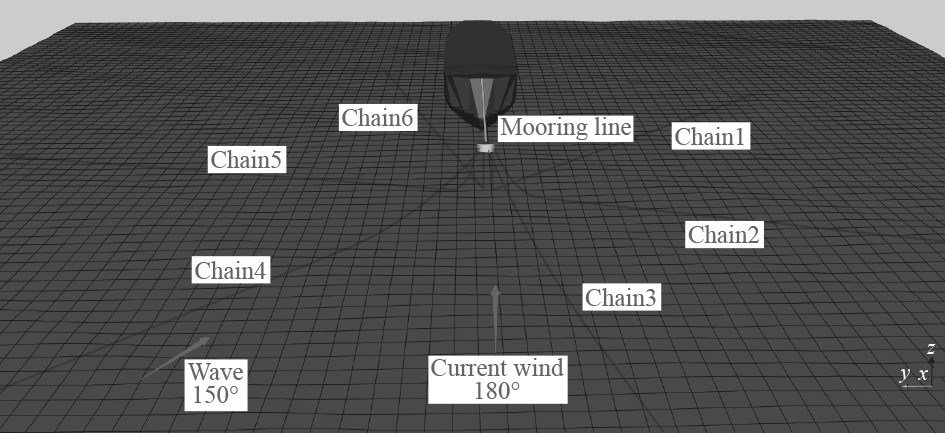
在船型尺寸和浮筒尺寸参数确定后,对锚索和缆绳布置完毕后。为探讨动力响应变化规律,需要对初始波、流、风参数进行设置,参照表3。油轮单点系泊系统布置模型见图1。
|
|
表 3 环境参数 Tab.3 Environmental parameters |
|
图 1 油轮单点系泊系统模型初始状态 Fig. 1 Initial state of model |
风、浪、流不同方向的组合会对油轮的运动性能产生影响,实际工况中,风、浪、流往往呈一定夹角。根据设计和工程实践经验,分析表3环境条件下,波浪和海流呈30°夹角下,船体的六自由度运动,以及所受系泊力。
根据图2船体六自由度运动横荡来说,船体横荡的时间变化历程周期很长,几乎没有波频率成分,说明其横荡运动响应以低频响应为主要运动方式。在波流出现夹角的情况下,船体横荡和首摇幅值较大,船体鱼尾现象明显。

|
图 2 船体六自由度运动 Fig. 2 Six degree of freedom motion of ship hull |
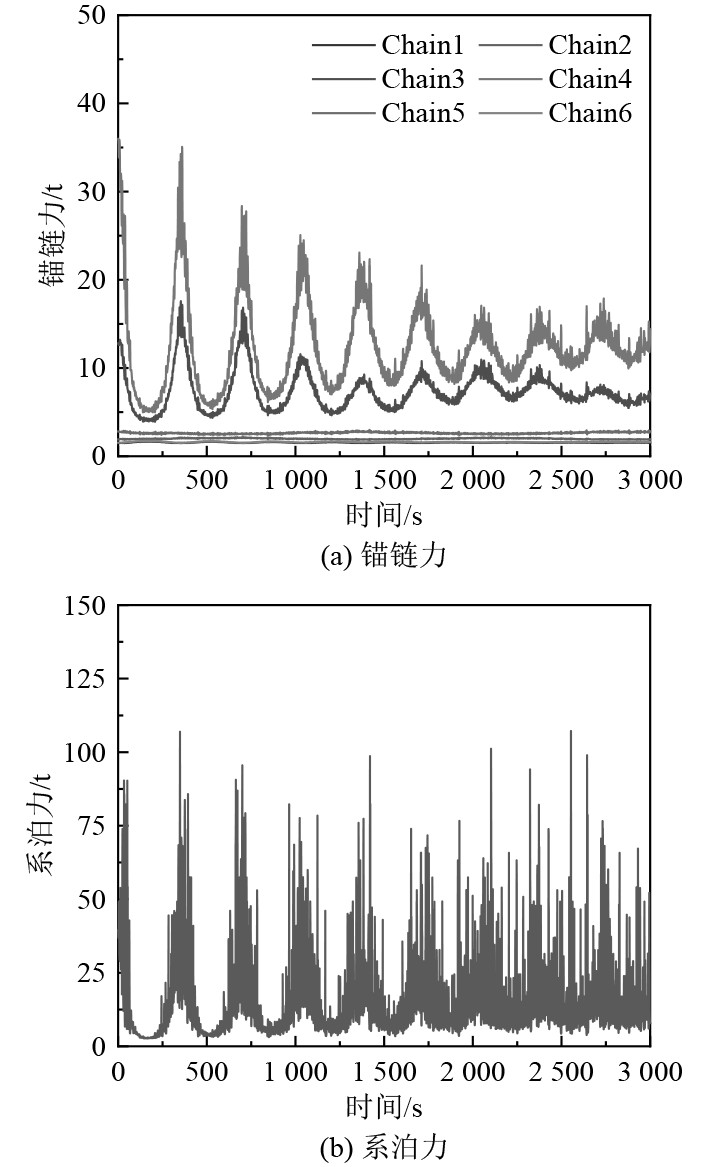
根据图3系泊和锚链力随时间变化的曲线可以看出在波动载荷下,锚索和系泊都在一个均值张力附近往复振动。对于锚链,chain4数值最大,主要原因是该锚链更靠近波流方向,使浮筒产生该方向位移,造成更大的锚链力。
|
图 3 锚链和系泊力时间历程 Fig. 3 Time history of anchor chains and mooring forces |
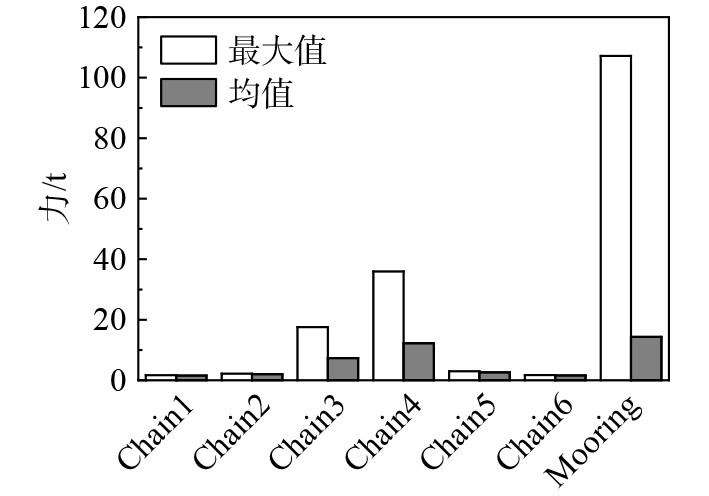
将系泊缆和锚链力的最大值和均值统计在图4中,可以看出系泊缆瞬时张力最大达107 t,锚链最大张力达40 t。系泊缆张力稳定维持在14 t附近。
|
图 4 锚链和系泊力最大值和均值统计值 Fig. 4 Maximum and mean statistical values of anchor chains and mooring forces |
风、浪、流不同的方向组合会使具有风标效应的油轮指向不同的首向,受到风、浪、流的作用力也不同,因而不同工况下油轮的水平偏移也不相同。现比较波流同向和波流30°夹角两工况下的船体运动和锚链、系泊缆受力大小。
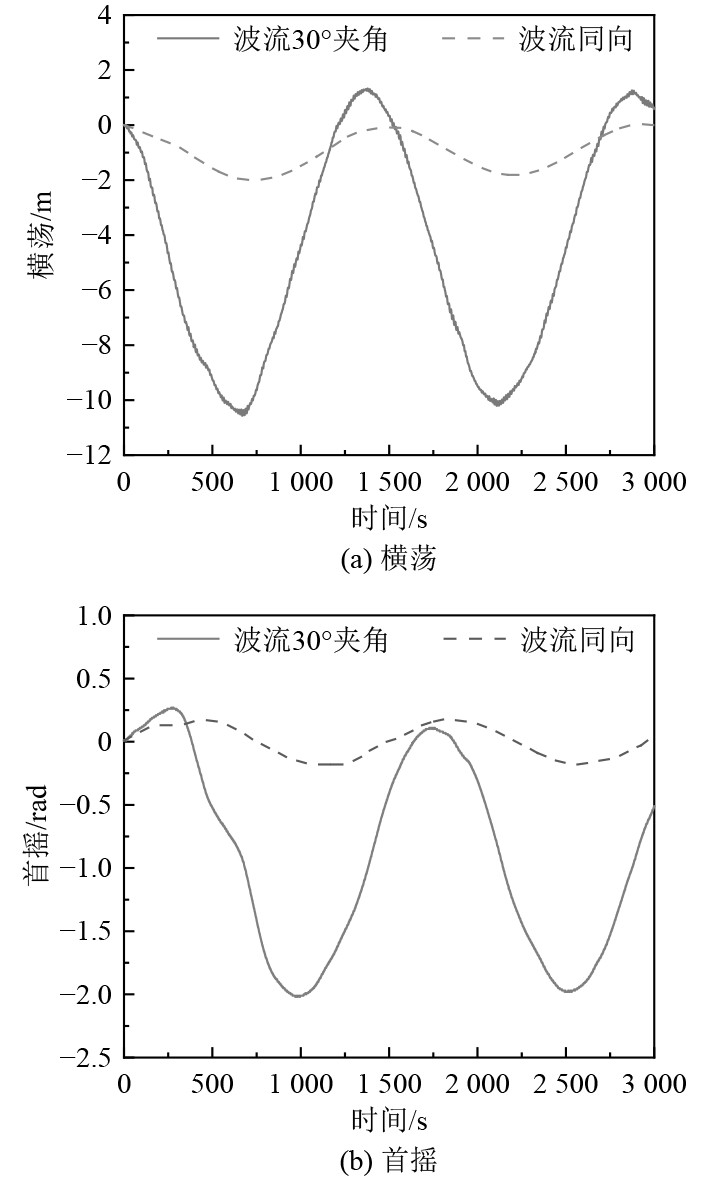
根据图5,随着波流夹角改变为波流同向,可以看出横荡和首摇幅值降低。因此,波流夹角使船体“鱼尾运动”明显,同时由于鱼尾运动导致的艏摇角度剧烈增大,也使得船体水动力增大。
|
图 5 波流夹角不同船体运动对比 Fig. 5 Comparison of ship motion with different wave current angles |
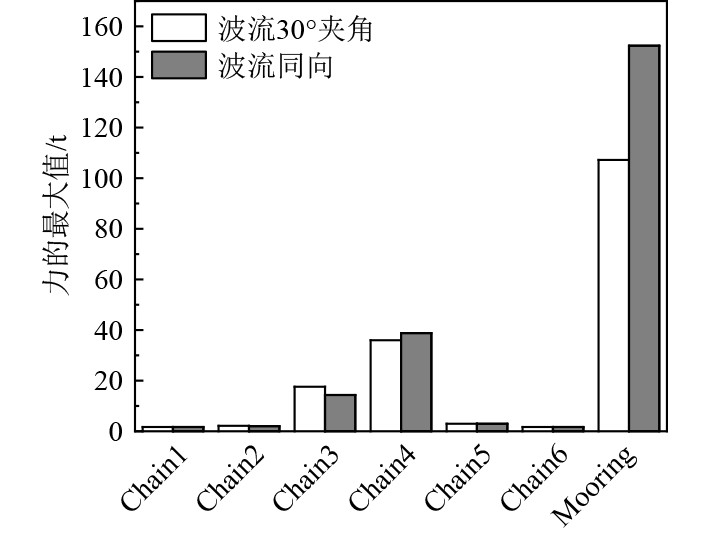
如图6所示,进一步分析锚链和系泊缆时间历程曲线可以看出改变波流方向,系泊力增长较大,这是由于由于风浪流同向引起了更大的漂移,较有夹角时动态响应剧烈,从而导致拉力增长较大;对于锚链,chain3更靠近波流30°波的方向,此时有夹角时受力更大,而chain4更靠近波流同向的方向,此时同向方向受力更大。
|
图 6 锚链力和系泊力最大值统计 Fig. 6 Statistics of maximum anchor and mooring forces |
根据上述分析,看以看出在初始海况条件下,油轮纵荡和横荡方向会产生较大位移,为保证正常作业环境,现对船舶的运动姿态进行控制。首先在原有系泊系统的基础上,在船尾处施加不同方向的后拉力,环境参数见表3,计算工况见表4。
|
|
表 4 计算工况 Tab.4 Calculate case |
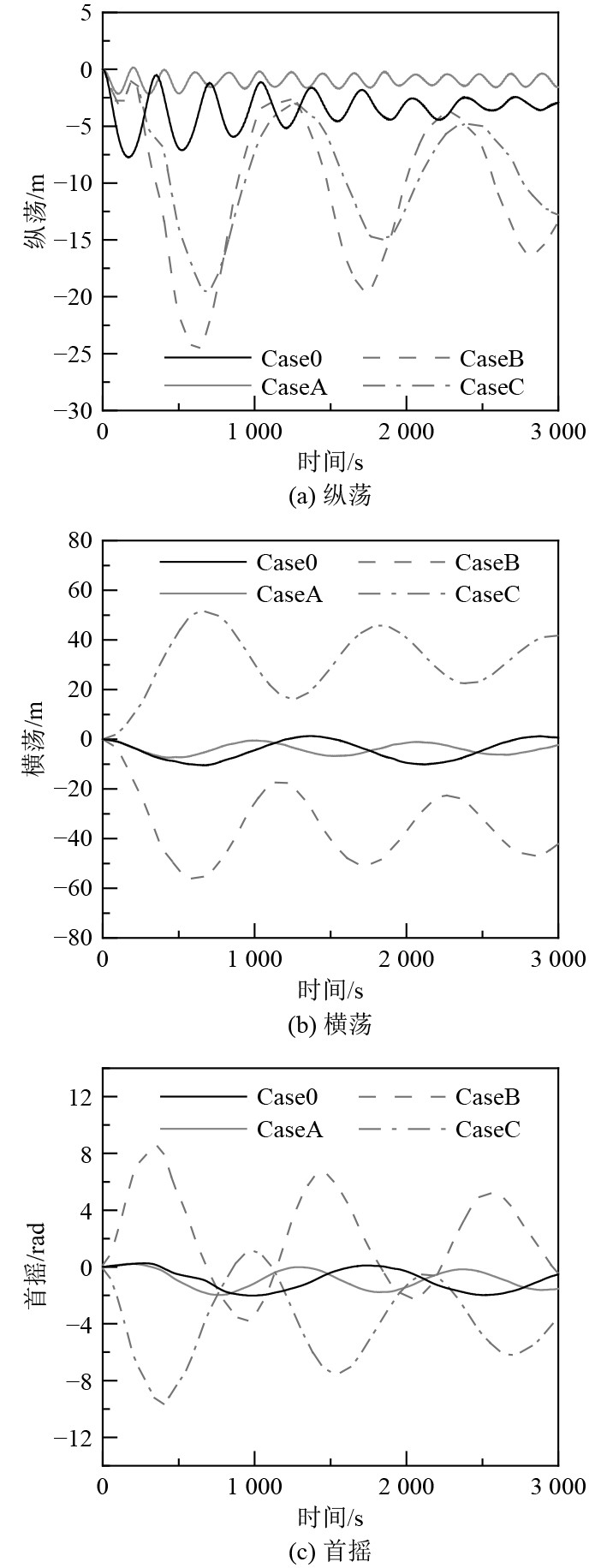
根据图7可以看出,在施加外力后,对于工况A,施加0°水平拉力时候,各自由度幅值降低,对船体运动具有抑制作用;对于工况B、工况C,施加具有角度的拉力时,船体运动幅值增大。且根据横荡和首摇时间历程图可以看出,此时两工况下船体运动具有对称趋势。
|
图 7 不同工况下船体运动 Fig. 7 Ship motion under different working conditions |
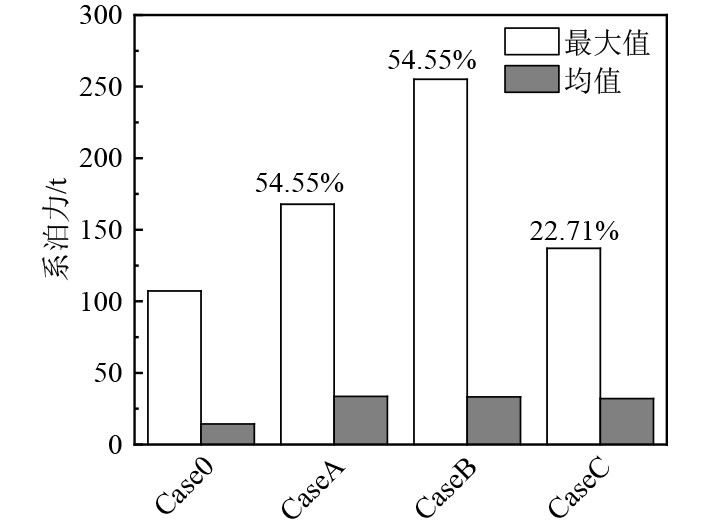
图8为4种工况下系泊力最大值和均值统计图,可以看出施加后拉力,会增大系泊力,特别是系泊力方向与波浪方向夹角越大时(工况B),系泊所受的拉力最大。同时,后拉力方向改变对系泊力影响主要体现在峰值上,波浪方向与拉力方夹角越大,系泊力峰值更大。
|
图 8 不同工况下系泊力统计值 Fig. 8 Statistical values of mooring force under different working conditions |
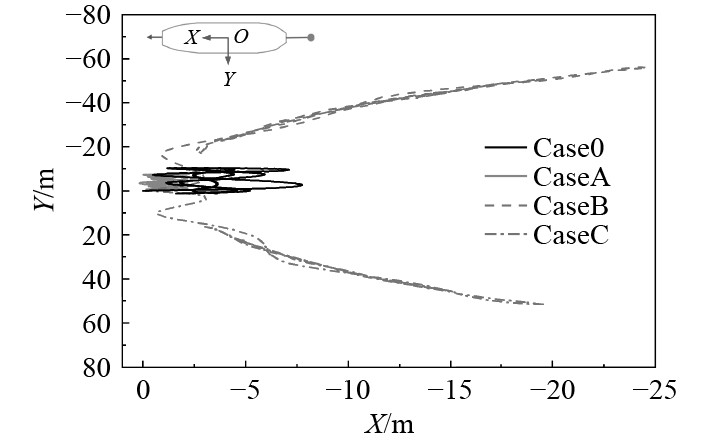
绘制船体XOY平面运动轨迹(见图9),可以看出在工况A条件下,船体运动幅值降低。在工况B、工况C条件下,增加外力后船体绕浮筒摆动的幅值更大,且两者具有对称绕浮筒运动的趋势。
|
图 9 船体运动轨迹 Fig. 9 Ship motion trajectory |
对船体运动姿态进一步进行调整,在右舷处施加拉力。此时选择较恶劣工况对系泊系统进行数值模拟,波高1.4 m,周期7.0 s,流速2 m/s。计算工况见表5。
|
|
表 5 计算工况 Tab.5 Calculate case |
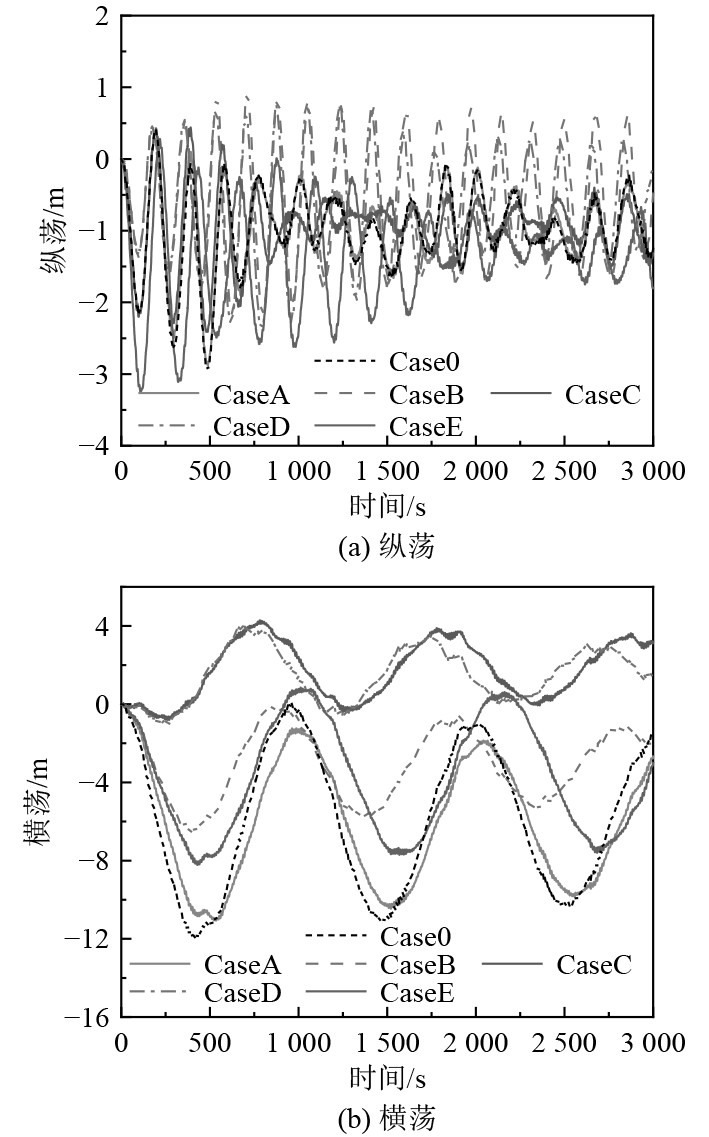
根据图10位移曲线,可以看出工况C、工况E减小了船体位移。工况C横荡位移降低了67%,工况E横荡位移降低了33%。
|
图 10 船体运动位移 Fig. 10 Ship movement displacement |
对系泊拉力进行分析(见图11),可以看出工况A、工况C、工况E均减小了系泊拉力。工况C降低了系泊力峰值7.93%,工况E降低了系泊力峰值16.92%。综上,工况E对船舶控制效果更好。

|
图 11 不同工况下系泊力统计值 Fig. 11 Statistical values of mooring force under different case |
对工况E控制效果进一步优化,更改侧拉力大小,以控制船舶运动位移更小。计算工况如表6。
|
|
表 6 计算工况 Tab.6 Calculate case |
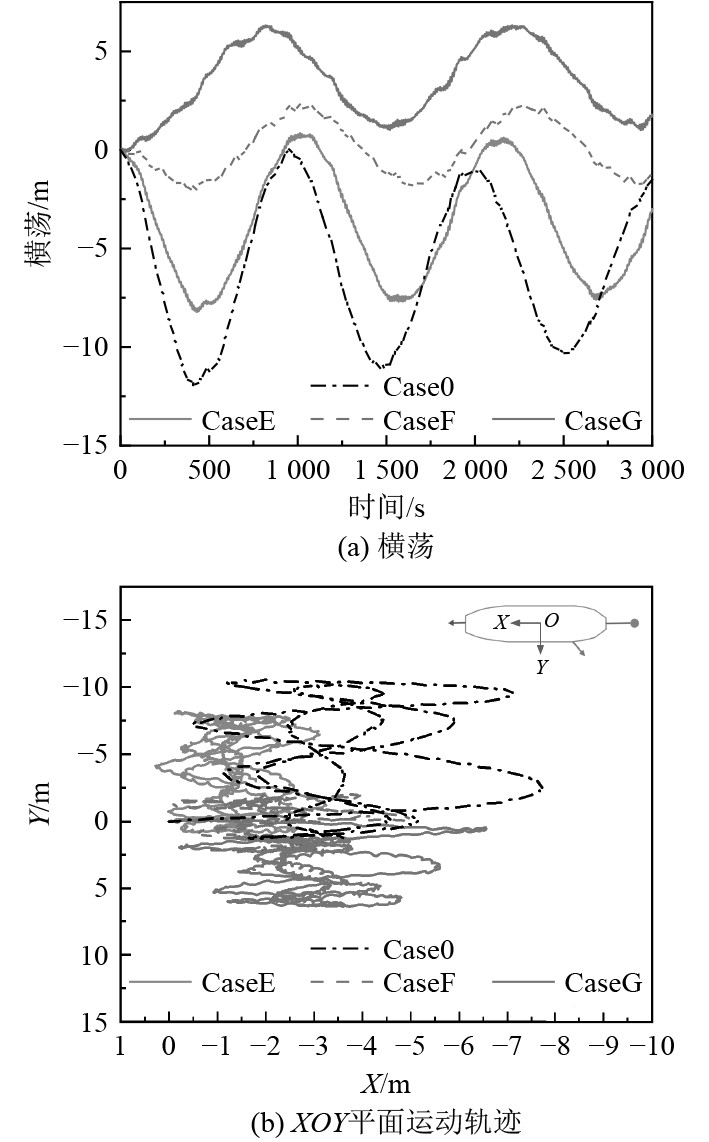
根据图12,可以看出拉力增大船体横荡位移会发生变化,随着拉力增大船体的横荡位移逐步向Y轴正向偏,在15 t时达到平衡状态。当拉力大于15 t时,横荡向Y轴正向进一步偏移。工况F横荡的振幅相对更小,比原始工况降低了67.86%,对船体控制效果更明显。
|
图 12 船体运动位移及运动轨迹 Fig. 12 Ship movement displacement and trajectory |
本节讨论各物理量对系泊力影响敏感性的差异,在不规则波和风流作用下,波高、周期和流速等因素对系泊力的影响。通过控制其它条件不变,改变某一参数,设计几种典型工况对比分析,简单讨论各影响因素的敏感性。
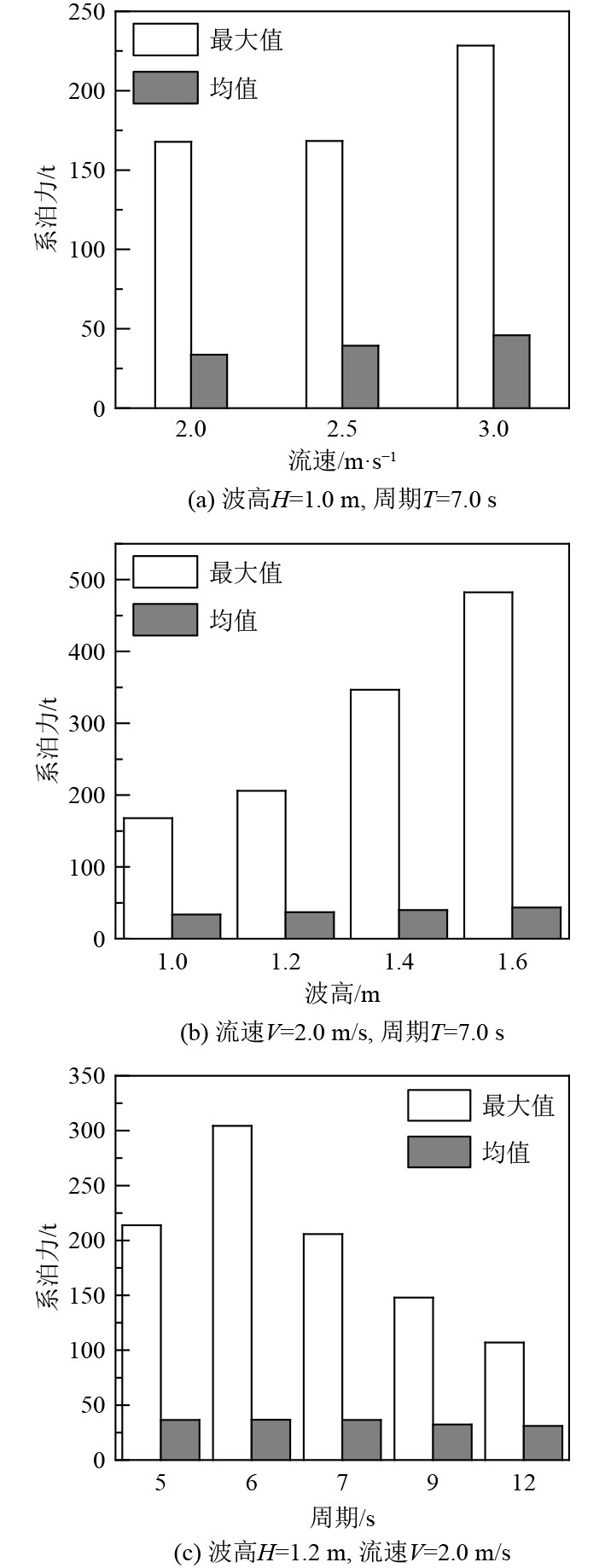
对于图13(a),控制波高周期不变,只改变流速,此时流速改变对系泊力改变不明显。但随着流速进一步增大,系泊力的最大值会突然增大,此时流速对系泊力影响会随之增大;对于图13(b),只改变波高,系泊力稳步增大;对于图13(c),周期的改变会使系泊力降低,对于T=6 s时,系泊力突增,分析原因是由于随着谱峰周期增大,接近船舶横摇和纵荡的固有周期,会产生一定程度的共振,从而造成系泊缆张力升高。
|
图 13 参数敏感性分析 Fig. 13 Parameter sensitivity analysis |
根据上述分析可得,波高和流速增大会导致系泊力不断增大。由于这些参数的改变会影响系泊受力大小以及船体的六自由度运动,从而对海上作业产生影响。现分析不同波高和流速下系泊缆的最大值,选出极限作业海况。
系泊索张力安全系数[1 − 2]取决于设计工况及所采用的系泊分析方法,在分析时应考虑系泊索的腐蚀裕量和磨损。张力安全系数F:
| $ F=P_B/t_{\rm{max}} 。$ |
式中:PB为系泊索的最小额定破断负荷;tmax为按本章要求计算得到的系泊索最大张力
本算例中张力安全系数F=1.67,tmax=600 t。则最小破断负荷PB=359 t。
在初始状态只有系泊力无外拉力时,横荡和系泊力峰值见表7。此时波高在大于1.4 m时,系泊力都大于300 t,此时较为危险;流速变化,系泊力变化不单调,流速值超过2.5 m/s时,系泊力峰值会突然增大,此时也较为危险。
|
|
表 7 不同波高和流速下系泊力峰值统计值(无外拉力) Tab.7 Statistical values of peak mooring force under different wave heights and flow velocities (without external tension) |
为控制船舶运动,在船体后施加后拉力,会导致系泊力增大。如表8所示,在系泊系统中增加后拉力条件下,系泊力峰值相对于无拉力情况增大,此时波高大于1.4 m时,仍是危险工况;在波高小于1.4 m时,流速的改变对系泊力峰值有更大的影响,流速大于2.5 m/s时,系泊峰值变化更加剧烈,且会超过PB,属于危险工况。
|
|
表 8 不同波高和流速下系泊力峰值统计值(船尾施加后拉力) Tab.8 Statistical values of peak mooring force under different wave heights and flow velocities (tension applied to the stern) |
综上,波高大于1.4 m时,系泊力峰值过大,均属于危险工况;流速大于2.5 m/s时,系泊力峰值会出现突变,也较为危险。
5 结 语1)波流不同向时,油轮横荡和首摇幅值增大,船体稳定性降低;系泊缆拉力相对减小,主要是由于波流同向会引起更大的纵荡位移,系泊运动响应更剧烈;对于锚链来说,在靠近波浪方向的锚链受力更大;
2)在船尾处施加控制船体运动的后拉力时,水平后拉力会降低船体运动幅值,斜拉力均会使运动幅值增大;船尾后拉力会造成系泊缆受力峰值和均值增大;
3)继续在船侧施加测拉力,可以发现135°方向测拉力的控制效果最好,有效降低船体横荡位移;对拉力大小进一步优化,可以进一步提升船体运动控制效果;
4)分析波高和流速对系泊力的影响,可以得出随着波高和流速的增大,系泊力不断增大,得出本系泊系统极限作业海况为波高1.4 m,流速2.5 m/s。
| [1] |
CHEN X B , MALENICA B . Interaction effects of local steady flow on wave diffraction-radiation at low forward speed[J]. International Journal of Offshore and Polar Engineering, 1998, 8(2).
|
| [2] |
黃国樑, 藤野正隆. 关于风和潮流作用下单点系泊船体的鱼尾状摆动的研究[J]. 海洋工程, 1987, 5(3): 1-13. |
| [3] |
许鑫, 申辉, 杨凯东, 等. 波流耦合作用对单点系泊系统的影响[C]// 2015 年深海能源大会, 2015.
|
| [4] |
孙玉柱, 任小伟. 利用MOSES软件进行施工船系泊分析[J]. 中国水运(下半月), 2016, 16(3): 13-15. |
| [5] |
周楠. CALM单点系泊油船“鱼尾效应”[J]. 中国海洋平台, 2018, 33(5): 70-74. DOI:10.3969/j.issn.1001-4500.2018.05.010 |
| [6] |
刘孟琦, 张宁川. CALM系泊30万吨级油轮动力响应试验研究[J]. 中国水运(下半月), 2020, 20(9): 4-5+8. |
| [7] |
陆阳. 基于MOSES的LNG船舶系泊运动响应分析[J]. 中国水运(下半月), 2020(10): 6-8. |
| [8] |
葛帅, 潘选任, 王冬姣, 等. 单点系泊稳定性分析与鱼尾运动对策[J]. 舰船科学技术, 2022, 44(2): 70-77. DOI:10.3404/j.issn.1672-7649.2022.02.014 |
 2024, Vol. 46
2024, Vol. 46
