2. 上海船舶工艺研究所 市场部,上海 200030
2. Marketing Department, Shanghai Shipbuilding Technology Research Institute, Shanghai 200030, China
党的十八大提出我国应由发展战略海洋大国转向建设海洋强国的战略目标以来,我国积极推动海洋实体经济向高效质量型转变,大力发展海洋科技技术来突破制约海洋发展和海洋生态保护的瓶颈。船舶作为海上交通运输的重要载体,在远洋运输、海上开采以及海洋勘探中都扮演着至关重要的角色。船舶在海上航行作业过程中,经常会受到外部环境扰动、系统内部扰动以及网络传输带宽受限而导致船舶偏离预定航向,从而改变作业船舶的运动状态,造成不可忽视的经济损失。因此,如何设计出鲁棒性较强的控制方法实现对作业船舶航向的精准控制一直是国内外科研人员研究的热门课题[1 − 5]。
船舶航向控制问题不仅关系到船舶的操控性能,而且还影响海上航行的安全性能和经济性能。从20世纪80年代开始,国内外就已经针对航向控制进行大规模的研究并已取得一定的成果。安顺等[6]针对船舶航向控制理论运动数学模型的非线性以及不确定性问题进入了深入研究,利用反馈线性化理论和反向递推思想成功的将状态向量替代了系统误差的变量线性,并以此设计出了基于反步法的通用控制器。Zhang等[7]在现有的通用运动学模型上提出了一种基于径向基函数神经网络(RBF-NNs)的自适应滑模控制算法,通过使用RBF-NN来估算侧滑角并引入线性扩张状态观测器(LESO)来估计路径跟随过程中的总扰动干扰项,从而解决了模型中外部扰动和内部不确定性的问题。Chu等[8]在Zhang的模型上提出一种侧滑角的补偿方法并对超扭转滑模控制算法进行了优化改进,通过有限时间扩张状态观测器(FTESO)来估算时变侧滑角、外部扰动以及内部不确定性,同时通过侧滑角来补偿航向误差,使得模型更加贴合于实际航行情况。Liu等[9] 基于复杂流域的动态水面控制和Nussbaum增益技术提出一种自适应性反步控制算法,这种控制算法通过优化处理船舶转弯时产生的非零漂移角来改善工作船舶因转弯惯性而引起的偏移航向问题,保持水面运输船和舰船的航向跟踪性能。以上均是考虑如何设计更有效的控制策略实现船舶航向的跟踪控制,默认系统的被控输入信号直接传送到控制器。但在实际航海实践中,船舶航向控制系统中的传感器、执行器以及控制器等都是通过网终相连,也就是意味着控制输入信号需要通过网络传输时可能存在缺失、乱码以及传输速度缓慢等问题,一个连续信号要想在网络中传输必须进行采样量化,把连续信号变成有限序列的离散信号,为保证系统在给定的带宽内正常运行,考虑带有输入量化的船舶航向控制更具有航海实践意义。
近年来由于船舶航向控制方法受到广泛关注,关于量化反馈控制及量化误差的研究得到了飞速的发展。Hao等[10 − 12]为解决基于状态和信号量化的无人水面飞行器(USV)编队航向跟踪及输出反馈控制等问题,提出一种自适应滑模技术与动态量化参数调整策略相结合的新型无人船容错航向控制方法模型,该模型可提供更大的量化参数的调整范围,更弥补了量化误差和时延影响,同时还能够减少偏航速度误差带来的震荡幅度,为后续的船舶航向控制系统研究拓宽了一种新思路。同时Wu等[13]研究了在严格控制输入量化信号反馈非线性系统在多个未知控制方向下的自适应渐近船舶航向跟踪控制的问题,研究人员在控制器中纳入了正积分时变函数和滞环量化器来实现渐近船舶航向跟踪控制。Fang等[14]基于博弈论对多艘无人水面舰艇(USV)的航向分布问题进行了深入研究,针对每个USV都赋予其独立个体使成为单独的研究目标,并制定了多个方位的定位博弈,同时为每个USV都设计了基于博弈的控制器。最后考虑到海上实际带宽通信有限,采用了均匀量化器对所有USV的传输信息进行了量化处理。Guo等[15]研究了具有推进器故障和非线性的海洋无人潜航器量化滑模控制的问题,研究团队为了消除无人船(UMV)输出和控制输入与遥控站之间的通信信道所引起的量化误差过程,提出了一种量化滑模控制器和动态量化参数相结合的优化策略,以减小推进器故障时横摆速度产生的误差和横摆角的振荡幅度误差。然而此研究是将量化后的变量视作未量化变量的扰动,利用量化器所产生扰动来分析量化对系统性能的影响。
以上研究对于具有输入量化的船舶航向控制系统,并不能提供一种既有系统兼容性又有常规通用性的量化误差估量和闭环系统稳定性的鉴定方法。本文针对具有输入量化的船舶航向控制系统,提出一种量化神经网络自适应运动控制方法。基于RBF神经网络无限逼近航向控制系统中的不确定项,采用均匀量化器去描述控制系统中的控制输入,通过Lyapunov稳定性理论[16]验证了闭环控制系统的稳定性,同时采用Matlab Simulink仿真模块证明了量化神经网络自适应运动控制方法的有效性。
1 问题描述在传统的船舶航向控制系统中,研究人员一般采用线性的一阶Nomoto模型来描述船舶航向的数学模型,但此模型只适合于船舶航行处于小扰动或低频的状态下。然而船舶实际在海上航行的过程中通常会受到较大的干扰以及因航向改变操作时大舵角突变的情况,此时一阶Nomoto模型无法将船舶真实的运动状态准确的描述出来。为建立更贴合实际情况的控制模型来提高船舶航向的控制精度,1963年Norrbin等[17]提出在Nomoto模型的基础上用逆旋螺优化实验产生的非线性项
根据Norrbin和Bech等提出的优化模型,用
| $ T\dot r + f(r) = K\delta。$ | (1) |
通过坐标变换,将式(1)写成状态方程的形式可以表示为:
| $ \left\{ \begin{split}& \dot \varphi = r ,\\& \dot r = b\delta (t) - \frac{1}{T}f(r) 。\end{split} \right. $ | (2) |
式中:
考虑输入量化后的船舶航向控制系统的结构框图如图1所示。
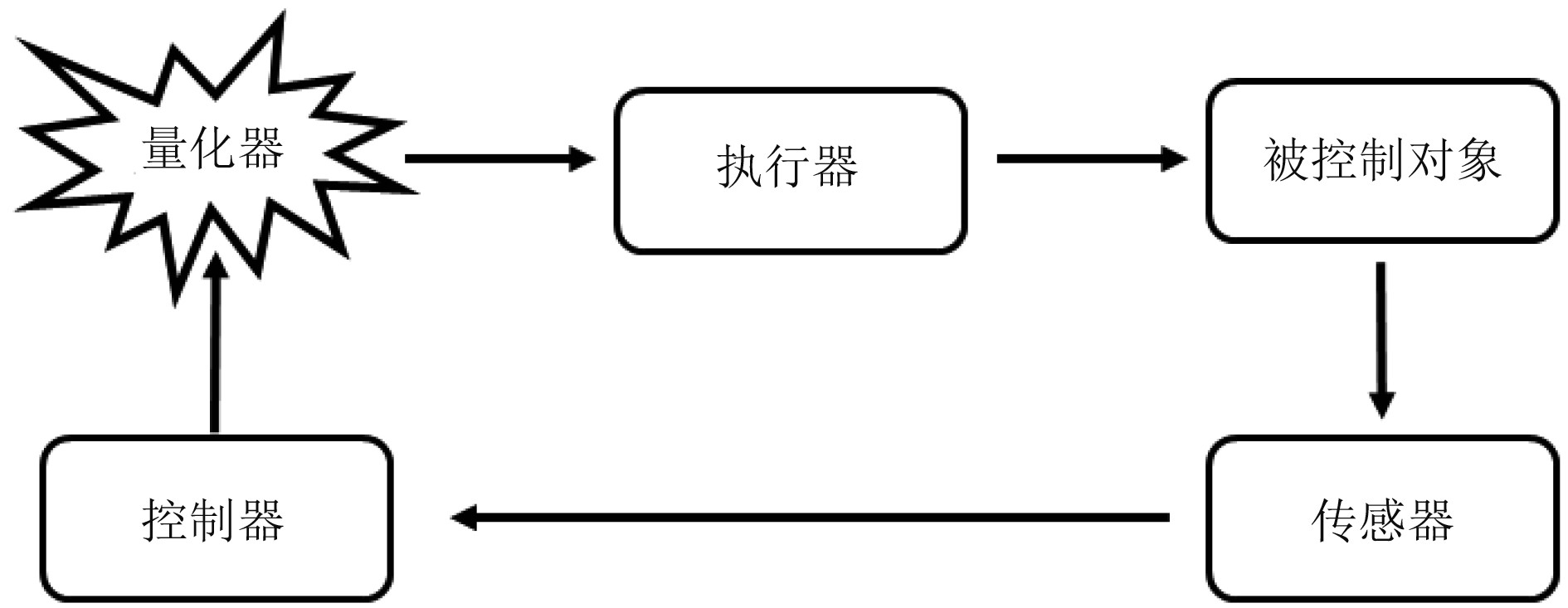
|
图 1 输入量化控制系统结构图 Fig. 1 Structure of the quantitative control system |
在此过程中,控制输入
| $ \left\{ \begin{gathered} {{\dot x}_1} = {x_2} , \\ {{\dot x}_2} = Q(u) + f(x) 。\\ \end{gathered} \right. $ | (3) |
式中:
| $ Q(u) = k\;{\rm round}\left( {\frac{u}{k}} \right)。$ | (4) |
式中:
在实际船舶航向控制系统中,船舶运动数学模型中的不确定项
| $ \begin{gathered} {h_j} = g\left(\frac{{\left\| {x - {c_{ij}}} \right\|}}{{b_j^2}}\right) , \\ f = {W^{*{\text T}}}h(x) + \varepsilon。\\ \end{gathered} $ | (5) |
式中:
故利用RBF神经网络逼近船舶的未知函数
| $ \hat f(x) = {\hat W^{\text T}}h(x) 。$ | (6) |
式中,
| $ \tilde f(x) = f(x) - \hat f(x) = {W^{ * {\text T}}}h(x) + \varepsilon - {\hat W^{\text T}}h(x) = {\tilde W^{\text T}}h(x) + \varepsilon 。$ | (7) |
式中,
本文设计的船舶航向控制器的目标是寻找一个合适的控制律
首先,令
| $ {q_1}(t) = \left\{ \begin{gathered} \frac{{Q(u(t))}}{{u(t)}}{\text{ }},\left| {u(t)} \right| \geqslant a , \\ 1{\text{ }},\left| {u(t)} \right| < a 。\\ \end{gathered} \right. $ | (8) |
| $ {q_2}(t) = \left\{ \begin{gathered} 0{\text{ }},\left| {u(t)} \right| \geqslant a, \\ Q(u(t)) - u(t){\text{ }},\left| {u(t)} \right| < a 。\\ \end{gathered} \right. $ | (9) |
其中,
其次,取滑模函数为:
| $ s = ce + \dot e ,$ | (10) |
其中,
则
| $ \dot s = c\dot e + \ddot e = Q(u) + f(x) - {\ddot x_{d}} + c\dot e = {q_1}u + {q_2} + f(x) - {\ddot x_{d}} + c\dot e ,$ | (11) |
| $ \begin{split} s\dot s =& s\left[ {{q_1}u + {q_2} + f(x) - {{\ddot x}_{d}} + c\dot e} \right] = s{q_1}u + s{q_2} + sf(x) +\\ & s\left( {c\dot e - {{\ddot x}_{d}}} \right) \leqslant s{q_1}u + \frac{1}{2}{s^2} + \frac{1}{2}\bar q_2^2 + sf(x) + s\left( {c\dot e - {{\ddot x}_{d}}} \right) =\\ & s\left[ { - ls - \eta {\text{sgn}}s + ls + \eta {\text{sgn}}s + \frac{1}{2}s + f(x) + c\dot e - {{\ddot x}_{d}}} \right] +\\ & s{q_1}u + \frac{1}{2}\bar q_2^2。\\[-1pt] \end{split} $ | (12) |
取
| $ \bar u = ls + \eta {\text{sgn}}s + \frac{1}{2}s + \hat f(x) + c\dot e - {\ddot x_{{d}}}。$ | (13) |
其中,
则
| $ \begin{split} s\dot s &\leqslant - l{s^2} - \eta |s| + s\bar u + s\left[ {f(x) - \hat f(x)} \right] + s{q_1}u + \frac{1}{2}\bar q_2^2 = \\ & -l{s^2} - \eta |s| + s\bar u + s\left[ { - {{\tilde W}^{\text{T}}}h(x) + \varepsilon } \right] + s{q_1}u + \frac{1}{2}\bar q\; _2^2 \leqslant \\ &-l{s^2} - {\eta _{d}}|s| + s\bar u + s\left[ { - {{\tilde W}^{\rm T}}h(x)} \right] + s{q_1}u + \frac{1}{2}\bar q_2^2。\\ [-3pt] \end{split} $ | (14) |
针对量化控制律
设计控制律和自适应律为:
| $ u = - \frac{{s{{\hat \mu }^2}{{\bar u}^2}}}{{|s\hat \mu \bar u| + \rho }} ,$ | (15) |
| $ \dot \hat \mu = {\gamma _2}s\bar u - {\gamma _2}\sigma \hat u, $ | (16) |
| $ \dot \hat W = {\gamma _1}sh(x) 。$ | (17) |
其中,
自适应律(16)用于对量化参数进行估计,使得所设计的动力学底层控制率(15)不依赖于量化信息,无需预知量化程度,量化参数可以根据系统性能需要自行调整。
3 稳定性分析稳定性是系统的一个基本特性也是检验控制系统质量的一个重要指标,本文采用的是Lyapunov理论[18]对所设计的控制系统的进行稳定性分析,设计一个Lyapuno函数
| $ V = \frac{1}{2}{s^2} + \frac{1}{{2{\gamma _2}\mu }}{\tilde \mu ^2} + \frac{1}{{2{\gamma _1}}}{\tilde W^{\text{T}}}\tilde W 。$ | (18) |
其中,
| $ \begin{split} \dot V = & s\dot s + \frac{1}{{{\gamma _2}\mu }}\tilde \mu \dot {\hat \mu} + \frac{1}{{{\gamma _1}}}{{\tilde W}^{\text{T}}}\dot {\hat W} \leqslant - l{s^2} - {\eta _{d}}|s| + s\bar u + s\left[ { - {{\tilde W}^{\text{T}}}h(x)} \right] +\\ & s{q_1}u + \frac{1}{2}\bar q_2^2 + \frac{1}{{{\gamma _2}\mu }}\tilde \mu \dot {\hat \mu} + \frac{1}{{{\gamma _1}}}{{\tilde W}^{\text{T}}}\dot {\hat W} = - l{s^2} - {\eta _{d}}|s| +\\ & s\bar u + s{q_1}u + \frac{1}{2}\bar q_2^2 + \frac{1}{{{\gamma _2}\mu }}\tilde \mu \dot {\hat \mu} + {{\tilde W}^{\text{T}}}\left[ { - sh(x) + \frac{1}{{{\gamma _1}}}\dot {\hat W}} \right] 。\\[-10pt] \end{split} $ | (19) |
由式(15)~式(17)可得:
| $\begin{split} \dot V \leqslant & - l{s^2} - {\eta _{\text{d}}}|s| + s\bar u - {q_1}\frac{{{s^2}{{\hat \mu }^2}{{\bar u}^2}}}{{|s\hat \mu \bar u| + \rho }} + \frac{1}{2}\bar q_2^2 +\\ &\frac{1}{{{\gamma _2}\mu }}\tilde \mu \left( {{\gamma _2}s\bar u - {\gamma _2}\sigma \hat \mu } \right)。\end{split}$ | (20) |
由于
| $ - \frac{{{{(s\hat \mu \bar u)}^2}}}{{\rho + |s\hat \mu \bar u|}} \leqslant \rho - s\hat \mu \bar u。$ | (21) |
考虑到
| $ - {q_1}\frac{{{s^2}{{\hat \mu }^2}{{\bar u}^2}}}{{|s\hat \mu \bar u| + \rho }} \leqslant \frac{1}{\mu }(\rho - s\hat \mu \bar u) 。$ | (22) |
| $ \begin{split} \dot V \leqslant & - l{s^2} - {\eta _d}|s| + s\bar u + \frac{1}{\mu }(\rho - s\hat \mu \bar u) + \frac{1}{2}\bar q_2^2 + \frac{1}{\mu }\tilde \mu s\bar u - \frac{1}{\mu }\tilde \mu \sigma \hat \mu =\\ & - l{s^2} - {\eta _{\text{d}}}|s| + s\bar u + \frac{1}{2}\bar q_2^2 + \frac{1}{\mu }\rho - \frac{1}{\mu }(\hat \mu s\bar u - \tilde \mu s\bar u) - \frac{1}{\mu }\tilde \mu \sigma \hat \mu =\\ &- l{s^2} - {\eta _{\text{d}}}|s| + \frac{1}{2}\bar q_2^2 + \frac{1}{\mu }\rho - \frac{1}{\mu }\tilde \mu \sigma \hat \mu 。\\[-10pt] \end{split} $ | (23) |
由于
| $\begin{split} - \bar \mu \hat \mu =& - \bar \mu (\bar \mu + \mu ) = - {\bar \mu ^2} - \bar \mu \mu \leqslant - {\bar \mu ^2} +\\ &\frac{1}{2}{\bar \mu ^2} + \frac{1}{2}{\mu ^2} = - \frac{1}{2}{\bar \mu ^2} + \frac{1}{2}{\mu ^2} 。\end{split}$ | (24) |
则
| $ \begin{split} \dot V \leqslant & - l{s^2} - {\eta _d}|s| + \frac{1}{2}\bar q_2^2 + \frac{1}{\mu }\rho - \frac{1}{{2\mu }}\sigma {{\bar \mu }^2} + \frac{1}{2}\sigma \mu \leqslant \\ &- l{s^2} - \frac{1}{{2\mu }}\sigma {{\tilde \mu }^2} - {\eta _d}|s| + d \leqslant - {\eta _d}|s| + d 。\\ \end{split} $ | (25) |
其中,
可得满足
| $ \mathop {\lim }\limits_{t \to \infty } \left| s \right| \leqslant \frac{d}{{{\eta _d}}}。$ | (26) |
当
以某远洋船作为模拟仿真对象,假定工作船舶运动的初始速度为
|
|
表 1 某远洋船参数表 Tab.1 Parameters of the X ocean vessel |
该船的相关模型参数为:
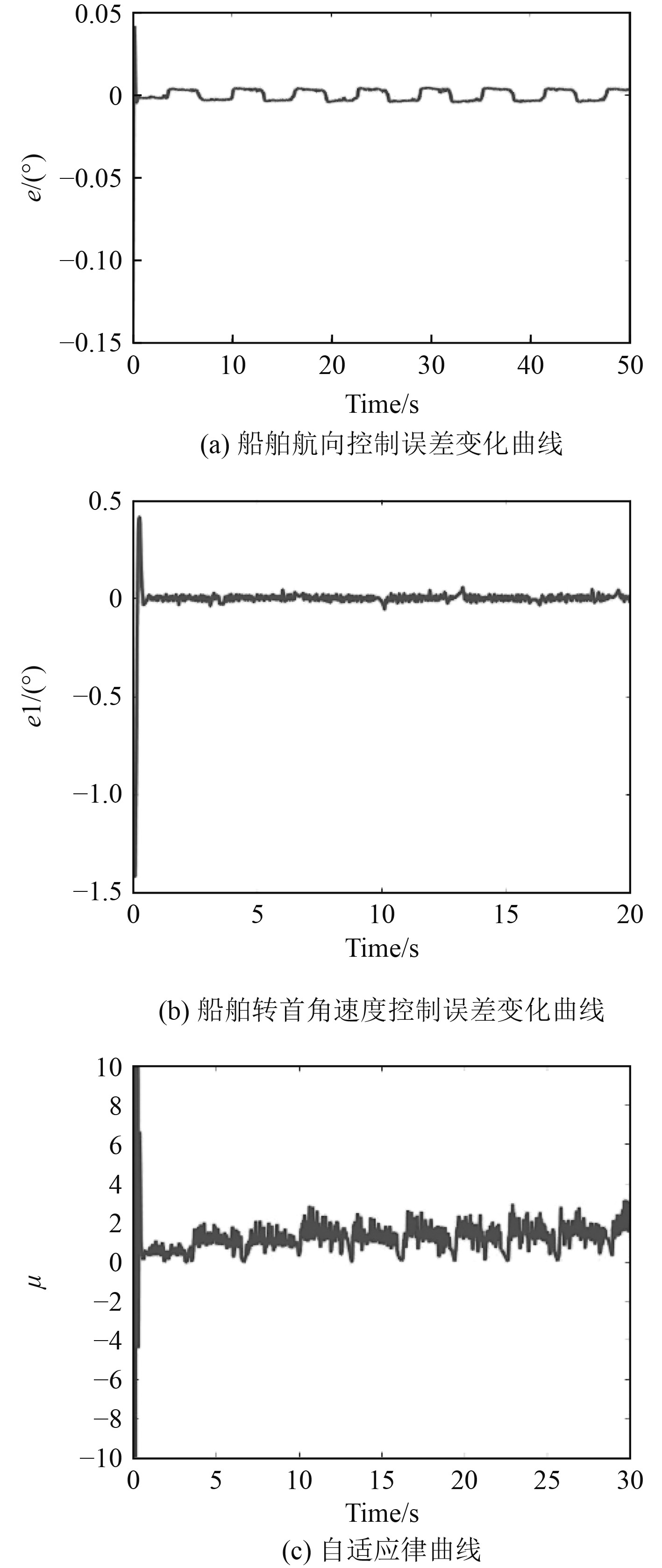
|
图 4 船舶航向控制误差、船舶转首角速度控制误差和自适应律曲线图 Fig. 4 Curves of vessel course control error, vessel bow angle speed error and adaptive law |
如图2(a)所示,在考虑输入信号量化的情况下,船舶实际航向依旧和期望航向高度吻合,从侧面证明了设计思路的合理性。如图2(b)所示,期望转首角速度和实际转首角速度图,在0~0.5 s为设计的里量化控制系统的反应调节时间,0.5 s后实际转首角速度和期望转首角速度高度吻合,进一步证明了本文设计的模型量化器以及控制方法的合理性和准确性。
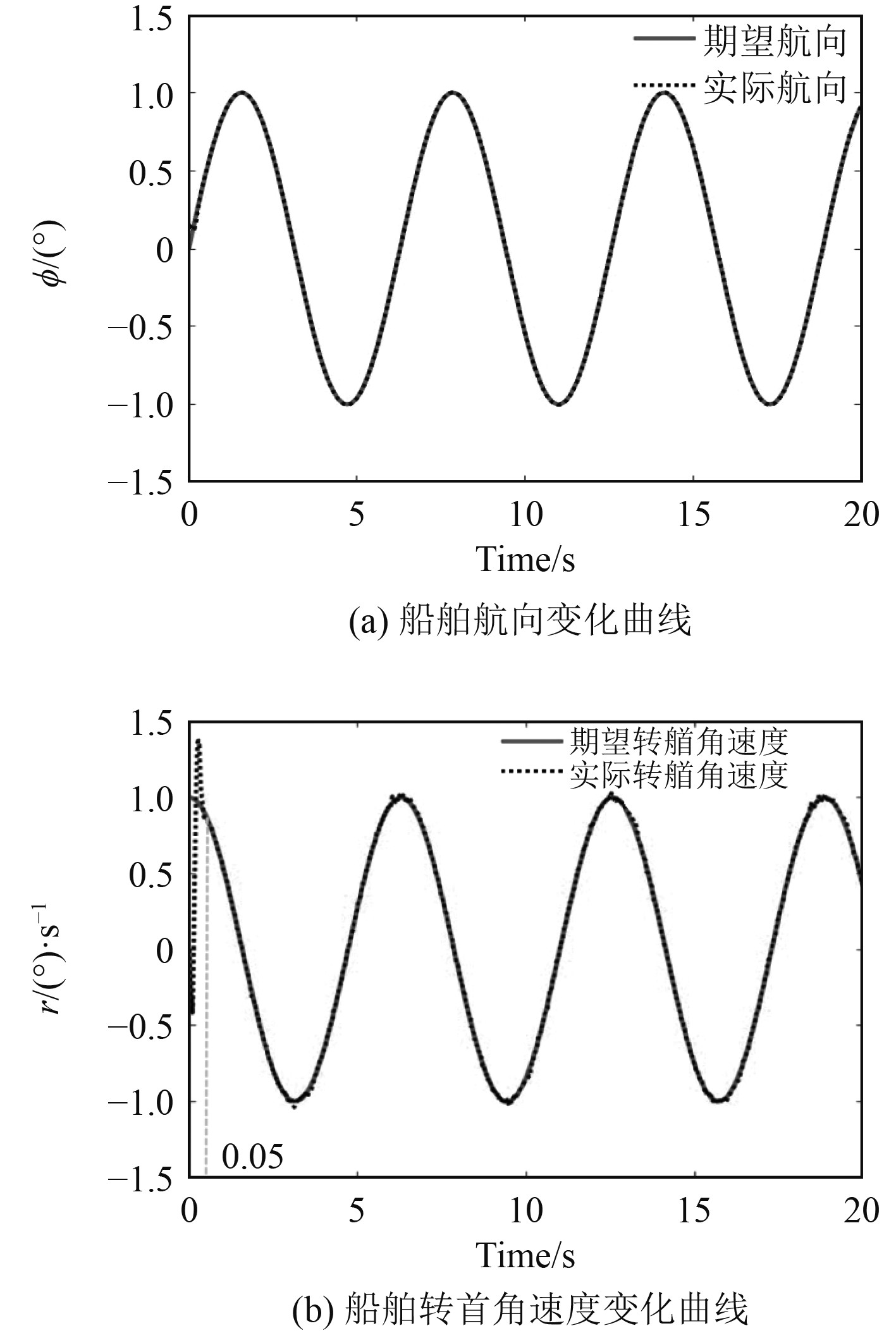
|
图 2 船舶航向和转首角速度变化曲线 Fig. 2 Curve of ship course change and bow rocking angular velocity |
图3(a) 为无量化的控制输入和量化后的控制输入曲线对比图。可以看出,考虑输入量化后的船舶航向自适应神经网络控制策略具有较强的鲁棒性,控制系统也能够在短时间内跟踪上船舶的期望航向以及期望角速度。图3(b)为神经网络的逼近未知函数的结果图。可以看出,经过一段反应和调整时间后,2条曲线基本吻合,RBF逼近效果显著。
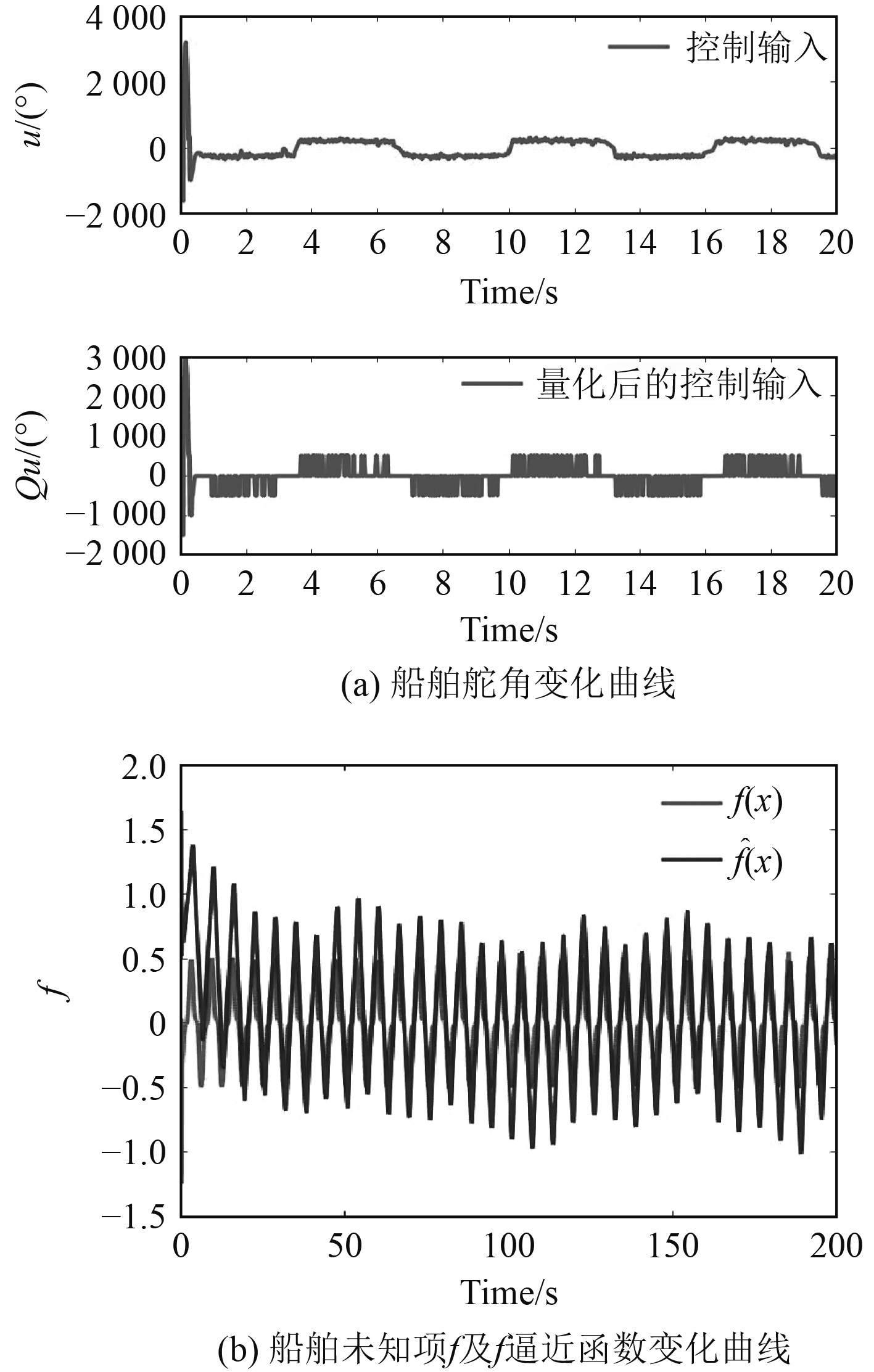
|
图 3 船舶舵角和船舶未知项逼近函数变化曲线图 Fig. 3 Curves of ship rudder angle and ship unknowns f and f approximation Functio |
图4分别为航向控制误差、转首角速度控制误差以及自适应律曲线。从图4(a)和图4(b)中可以看出,航向跟踪误差以及转首角速度跟踪曲线都很稳定,结果都收敛于残差集内。从图4(c)中可看出,自适应律曲线在一个极小的范围内波动,模型控制方法在考虑输入量化的约束情况后,依旧可以保持船舶航向的精准控制,并未明显牺牲过渡过程中的控制品质,证明了本文所提出的控制算法的有效性。
5 结 语本文探讨带有模型不确定项和输入量化的船舶航向控制问题,利用RBF神经网络逼近航向控制系统中的未知非线性项,从而消除不确定项对控制系统的影响。同时考虑了船舶航海实际过程中通讯带宽受限的问题,构造了时变非线性解析模型来描述船舶航向控制系统的输入量化过程,所构造的RBF神经网络自适应量化控制器能够有效的跟踪运动学制导律,且不需要量化参数的先验信息。最后通过Matlab Simulink仿真模块验证了本文提出的船舶类量化神经网络自适应运动控制方法的有效性。
| [1] |
朱丽燕, 李铁山, 单麒赫. 船舶航向非线性离散系统自适应模糊最优控制[J]. 哈尔滨工程大学学报, 2019, 40(9): 1576-1581. |
| [2] |
JIA F, CHEN M. Design of a nonlinear course control system for ocean going ships based on backstepping technique[J]. Journal of Coastal Research, 2019, 94(SI): 515-519. |
| [3] |
李蕊, 朱喜梅, 周民, 等. 基于虚拟现实技术的船舶航向自动跟踪控制方法[J]. 舰船科学技术, 2020, 42(S1): 67-69. |
| [4] |
PARK B S, YOO S J. Quantized-communication-based neural network control for formation tracking of networked multiple unmanned surface vehicles without velocity information[J]. Engineering Applications of Artificial Intelligence, 2022, 114: 105160. DOI:10.1016/j.engappai.2022.105160 |
| [5] |
NING J, LI T, CHEN C L P. Neuro-adaptive distributed formation tracking control of under actuated unmanned surface vehicles with input quantization[J]. Ocean Engineering, 2022, 265: 112492. DOI:10.1016/j.oceaneng.2022.112492 |
| [6] |
安顺, 何燕, 王龙金. 基于反步自适应控制算法的船舶航向控制方法[J]. 机电设备, 2020(6): 65−69.
|
| [7] |
ZHANG H, ZHANG X, BU R. Sliding mode adaptive control for ship path following with sideslip angle observer[J]. Ocean Engineering, 2022, 251: 111106. DOI:10.1016/j.oceaneng.2022.111106 |
| [8] |
CHU R, LIU Z, CHU Z. Improved super-twisting sliding mode control for ship course with sideslip angle compensation[J]. Ocean Engineering, 2022, 260: 111996. DOI:10.1016/j.oceaneng.2022.111996 |
| [9] |
LIU Z, CHU R. Robust adaptive course control for a surface vessel with drift angles[J]. Ocean Engineering, 2020, 205: 107310. DOI:10.1016/j.oceaneng.2020.107310 |
| [10] |
HAO L Y, ZHANG H, LI H, et al. Sliding mode fault-tolerant control for unmanned marine vehicles with signal quantization and time-delay[J]. Ocean Engineering, 2020, 215(5): 107882. |
| [11] |
HAO L Y, ZHANG H, LI T S, et al. Fault tolerant control for dynamic positioning of unmanned marine vehicles based on TS fuzzy model with unknown membership functions[J]. IEEE Transactions on Vehicular Technology, 2021, 70(1): 146-157. DOI:10.1109/TVT.2021.3050044 |
| [12] |
HAO L Y, YU Y, LI T S, et al. Quantized output-feedback control for unmanned marine vehicles with thruster faults via sliding-mode technique[J]. IEEE Transactions on Cybernetics, 2021, 52(9): 9363-9376. |
| [13] |
WU J, SUN W, SU S F, et al. Adaptive asymptotic tracking control for input-quantized nonlinear systems with multiple unknown control directions[J]. IEEE Transactions on Cybernetics, 2022.
|
| [14] |
FANG X, ZHOU J, WEN G. Location game of multiple unmanned surface vessels with quantized communications[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 69(3): 1322-1326. |
| [15] |
HAO L Y, ZHANG H, GUO G, et al. Quantized sliding mode control of unmanned marine vehicles: Various thruster faults tolerated with a unified model[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, 51(3): 2012-2026. |
| [16] |
罗胜琪. 基于Lyapunov稳定性理论的模型参考自适应控制[J]. 硅谷, 2011(17): 27-29. |
| [17] |
NORRBIN N. On the design and analysis of the zig-zag test on base of quasi-linear frequency response[J]. Processing of the 10th I.T.T.C., 1963: 355−374.
|
| [18] |
廖晓昕. 稳定性的理论、方法和应用[M]. 武汉: 华中理工大学出版社, 1999.
|
 2024, Vol. 46
2024, Vol. 46

