2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
振动问题是船舶营运过程中的一大难题,船体振动不仅容易引起结构的疲劳损伤,影响设备寿命,还会影响船员的正常工作生活甚至危害健康。为了抑制有害的振动,人们提出了源头消振、缓冲隔振、阻尼减振、动力吸振等多种振动控制技术。其中动力吸振技术是指通过在主系统上附加由弹簧、阻尼器、质量块组成的子系统以吸收主系统的能量,从而抑制主系统振动的方法。
动力吸振器按照对外界能源的输入需求可以分为被动式、半主动式和主动式三大类。被动式动力吸振器结构简单、使用成本低,但其有效吸振频带较窄,普遍适用性差。尽管已有许多关于拓宽被动式动力吸振器有效吸振频带的研究,但仍无法对较宽激励频带内的多个共振峰进行有效抑制[1]。主动式动力吸振器通过在主系统和子系统之间直接施加作用力,可以在附加质量较小的情况下获得良好的吸振效果,但其结构复杂、能耗大、使用成本过高,在实际工程应用中受限较大。半主动式动力吸振器即通过改变吸振器的质量、阻尼和刚度,使其固有频率跟随激振频率的变化而变化,从而最大限度地提升动力吸振器的性能[2]。半主动式动力吸振器耗能少、控制简单、稳定性好,随着控制理论以及计算机技术的发展,近年来得到了广泛研究。陈文华等[3]提出可调频悬臂梁式动力吸振器;马强等[4]提出一种通过改变刚度和动态质量来实现自调频的动力吸振器;邢昭阳等[5]将基于频率识别的控制策略应用到负刚度动力吸振器,改善了其低频减振性能;Shen等[6]采用平均法研究了4种半主动式动力吸振器的参数优化问题并分析了时滞对半主动控制的影响;郎君等[7]对半主动控制接地阻尼动力吸振器进行了参数优化和性能分析。
本文以动力吸振器的弹性元件为出发点,将齿轮基胞元结构应用到动力吸振器中,构建了一种新型动力吸振器,并对其动力学特性开展了一系列分析。将齿轮基动力吸振器应用在某中型邮轮尾部舱段结构上,经有限元计算验证了新型吸振器的减振效果,并探究了吸振器质量变化对减振效果的影响。研究结果可为新型半主动式动力吸振器的设计及应用提供参考。
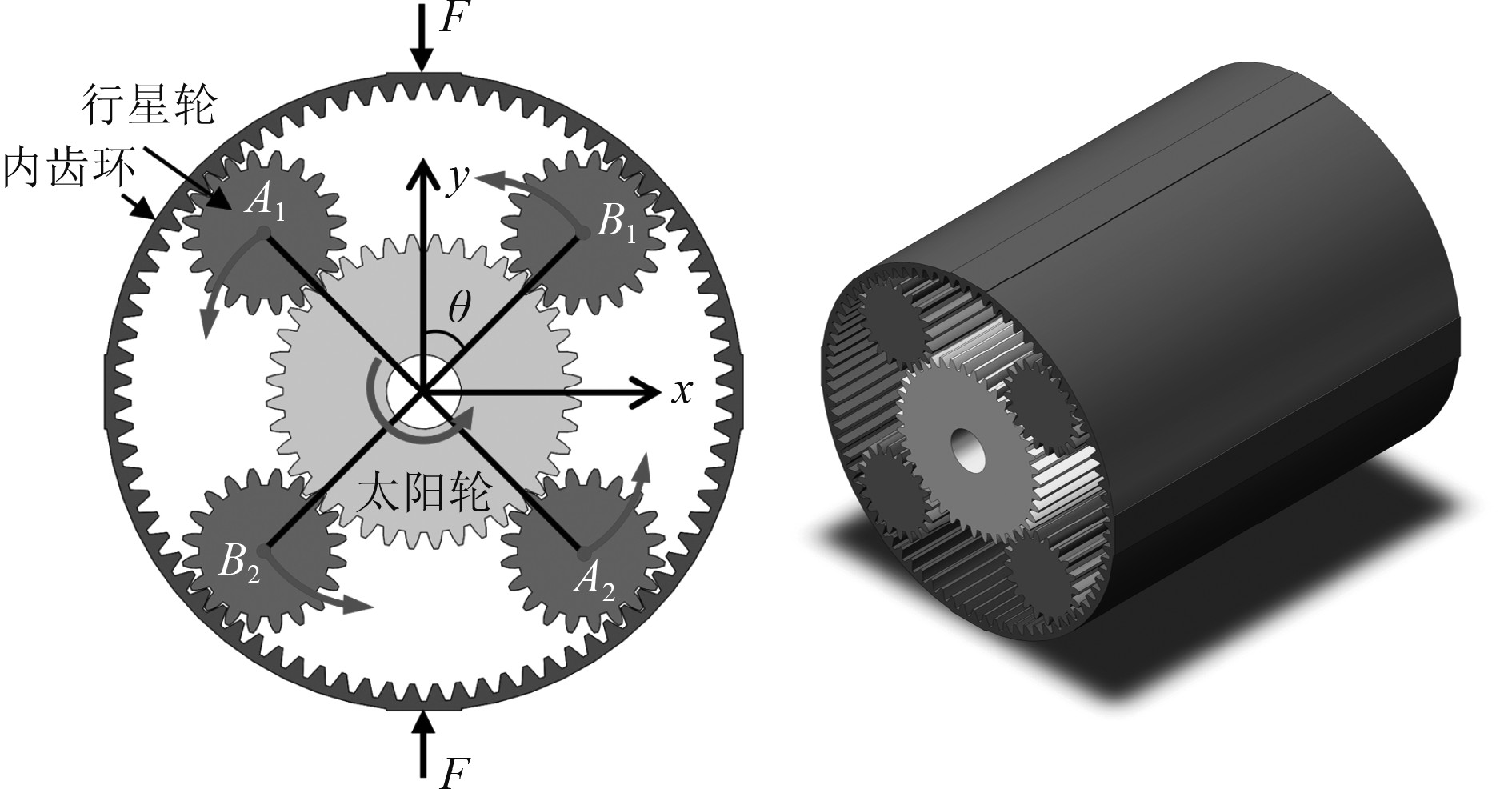
1 新型动力吸振器的构建 1.1 齿轮基胞元结构齿轮基胞元结构由1个内齿环、2对行星齿轮和1个太阳中心轮组成[8],如图1所示。坐标(x,y)的原点是太阳轮的中心点,y向定义为垂向,x向定义为水平。Ai和Bi表示行星齿轮的中心点,且A1A2⊥B1B2。将胞元结构内齿环固定,通过调节每个胞元中太阳轮的角度,带动行星轮旋转,可实现齿轮基胞元的垂向(y向)刚度调节。
|
图 1 齿轮基胞元 Fig. 1 The gear-based metacell |
本文齿轮基胞元概念来源于齿轮基机械超材料[8],机械超材料力学性能主要由其内部微结构的几何、拓扑及空间密度决定[9 − 11]。齿轮基超材料的刚度可调特性事实上与材料本身的结构大小尺度无关,因此将齿轮基超材料的微结构放大制造成为宏观胞元结构,该结构仍具有刚度可调特性。本文齿轮基胞元内行星轮系的基本参数见表1,各齿轮的齿宽一致。
|
|
表 1 标准直齿圆柱齿轮参数 Tab.1 Standard spur gear parameters |
该新型动力吸振器由6×4齿轮基胞元阵列及顶端质量块构成,如图2所示,顶端质量块的长度为680 mm,高度为250 mm,宽度与胞元齿宽一致。通过使每个胞元中太阳轮转动相同的角度,调节单个胞元的垂向刚度,进而改变整个吸振器的刚度,实现对动力吸振器固有频率的调节。

|
图 2 齿轮基动力吸振器模型 Fig. 2 Mechanical model of gear-based DVA |
本新型动力吸振器的齿轮基胞元阵列部分采用碳纤维增强聚醚醚酮复合材料(PEEK-CF),其基本力学参数如表2所示[12−13]。聚醚醚酮材料具有良好的啮合承载性,是一种优异的自润滑材料,在高温下仍具有较高的拉伸强度和弯曲模量,并表现出可靠的耐蠕变和抗疲劳性能,是模塑齿轮中的顶级工程材料之一。碳纤维增强聚醚醚酮复合材料的强度、弹性模量等机械特性获得进一步提升,抗疲劳、抗冲击、耐磨损性能极好,且在潮湿或高温条件下强度损失更少。采用该材料制作零部件,可有效避免金属或陶瓷材料表面裂纹等缺陷[14−15]。
|
|
表 2 PEEK-CF (550 CA30)基本力学参数表 Tab.2 Basic mechanical parameters of PEEK-CF (550 CA30) |
本动力吸振器顶端质量块采用密度为19 g/cm3的钨基高密度合金。钨基高密度合金的高密度、高强度、高硬度、低热膨胀系数等特性,使其作为配重和平衡元件在交通运输、武器装备等领域得到广泛应用。
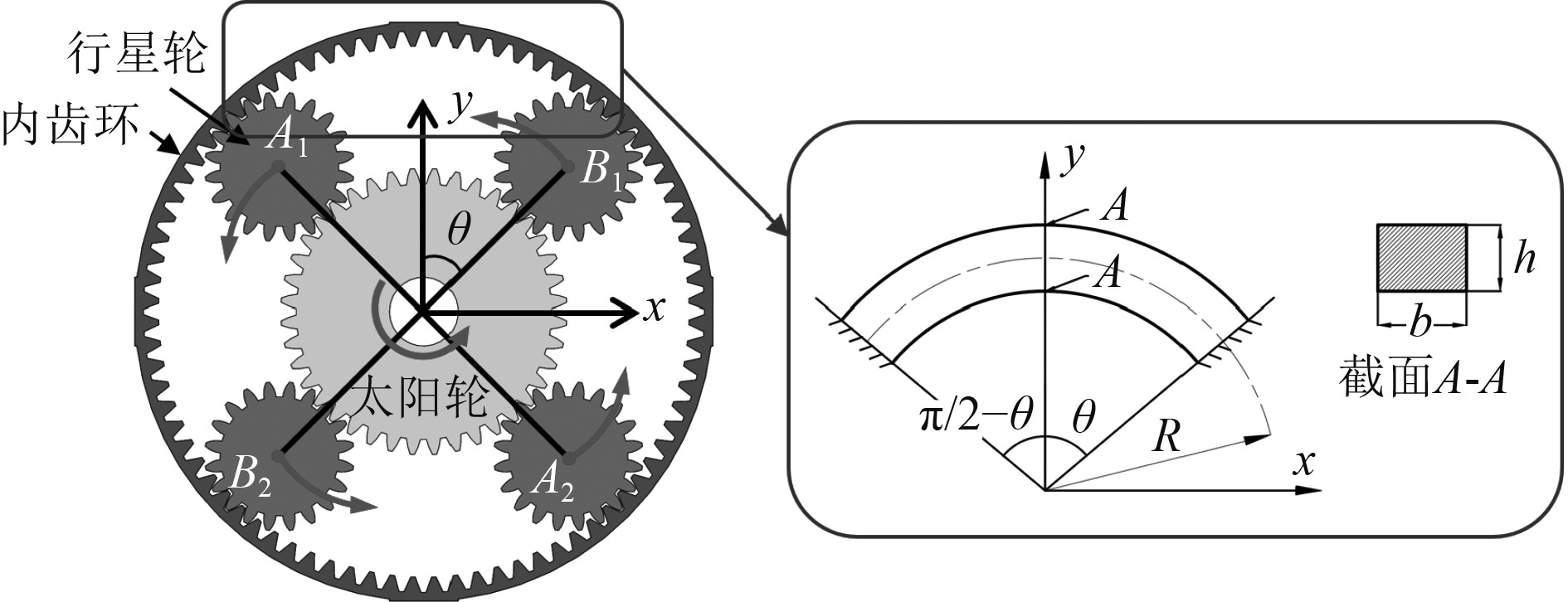
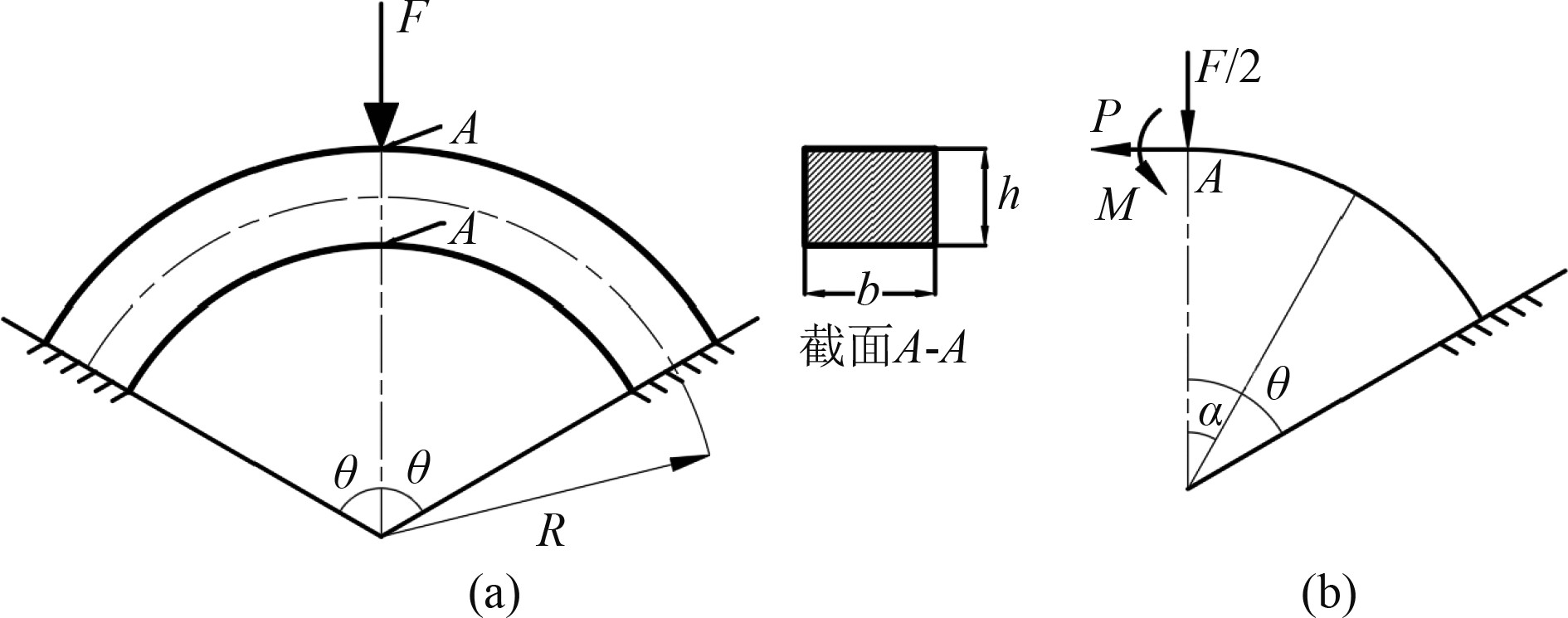
2 齿轮基动力吸振器动力学特性 2.1 齿轮基胞元刚度理论解析模型本文提出的动力吸振器在工作过程中,垂向刚度主要由A、B两行星轮支撑点之间的内齿环提供。内齿环刚度计算力学模型可简化为横截面为矩形的平面曲杆,如图3所示,首先考虑行星轮A1和B1关于y轴对称支撑的情况,如图4(a)所示。
|
图 3 内齿环简化示意图 Fig. 3 Simplified model of gear ring |
|
图 4 内齿环刚度计算简化力学模型 Fig. 4 Simplified mechanical model for calculating the stiffness of gear ring |
在图4(a)模型中,内齿环中性层的曲率半径为:
| $ r = \frac{h}{{\ln ({R_1}/{R_2})}}。$ | (1) |
横截面对中性轴的静矩为:
| $ S = Ae = A(R - r)。$ | (2) |
式中:R1为内齿环外缘曲率半径;R2为内齿环内缘曲率半径(考虑齿的影响,令内齿环内径等于内齿环齿根圆直径乘以系数
由于结构对称,取其一半进行研究,如图4(b)所示。曲杆任意截面的内力方程为:
| $ {M_\alpha } = M + PR(1 - \cos \alpha ) + \frac{{{F}}}{2}R\sin \alpha,$ | (3) |
| $ {F_{\text{N}}} = P\cos \alpha - \frac{{{F}}}{2}\sin \alpha,$ | (4) |
| $ {F_{\text{Q}}} = - P\sin \alpha - \frac{{{F}}}{2}\cos \alpha。$ | (5) |
式中:Mα为任意截面弯矩;FN为任意截面轴力;FQ为任意截面剪力;α为任意截面与y轴夹角;F为垂向外力;M为截面A-A处弯矩;P为截面A-A处轴力。
曲杆的变形能:
| $ U = \int\limits_l {\left(\frac{{{M_\alpha }^2}}{{2ESR}} + \frac{{{M_\alpha }{F_{\text{N}}}}}{{EAR}} + \frac{{{F_{\text{N}}}^2}}{{2EA}} + \frac{{{\text{c}}{F_{\text{Q}}}^2}}{{2GA}}\right)} {\mathrm{d}}l。$ | (6) |
式中:E为弹性模量;G为剪切模量;c为与横截面形状有关的因数,矩形截面取1.2。
根据变形协调条件,即截面A-A的转角和水平位移为0,根据卡式定理可得:
| $ {\theta _{\text{A}}} = \frac{{\partial U}}{{\partial M}} = 0,$ | (7) |
| $ {\delta _{\text{A}}}_x = \frac{{\partial U}}{{\partial P}} = 0。$ | (8) |
联立式(6)~式(8),求解可得内齿环截面A-A处弯矩M和轴力P:
| $ \begin{aligned}[b] M = &{{F}}R[{{G}}{R^2}(3\sin 2\theta - 6\sin \theta + 3\theta - \theta \cos 2\theta - 2\theta \cos \theta ) + \\ &{{ G}}{e^2}(3\sin 2\theta - 6\sin \theta + 2\theta - 2\theta \cos \theta ) + \\ &{{ E}}{e^2}c(\sin 2\theta - 2\theta - 2\sin \theta + 2\theta \cos \theta ) + \\ &{{ G}}eR(12\sin \theta - 6\sin 2\theta - 5\theta + \theta \cos 2\theta + 4\theta \cos \theta ) + \\ &{{ E}}eRc(\theta - \sin 2\theta + 2\sin \theta - 2\theta \cos \theta + \theta \cos 2\theta )]/ \\ &{{ }}2[{{G}}{R^2}(2 - 2\cos 2\theta - 2{\theta ^2} - \theta \sin 2\theta ) +\\ & 2{{G}}{e^2}(1 - \cos 2\theta ) + {{ G}}eR(2{\theta ^2} + 4\cos 2\theta + \theta \sin 2\theta - 4) + \\ &{{E}}eRc(\theta \sin 2\theta - 2{\theta ^2})],\end{aligned} $ | (9) |
| $ \begin{aligned}[b] P = &{{F}}\sin \theta [{{G}}{R^2}(2 - 2\cos \theta - \theta \sin \theta ) + 2{{G}}{e^2}(1 - \cos \theta ) + \\ &{{ G}}eR(4\cos \theta - 4 + \theta \sin \theta ) + {{E}}eRc\theta \sin \theta ]/ \\ &[{{G}}{R^2}(4{\sin ^2}\theta - 2{\theta ^2} - \theta \sin 2\theta ) + 4{{G}}{e^2}{\sin ^2}\theta + \\ &{{ G}}eR(2{\theta ^2} - 8{\sin ^2}\theta + \theta \sin 2\theta ) + \\ &{{E}}eRc(\theta \sin 2\theta - 2{\theta ^2})]。\end{aligned} $ | (10) |
由卡式定理和胡克定律可知:
| $ {\delta _{{\text{A}}y}} = \frac{{\partial U}}{{\partial \displaystyle\frac{{{F}}}{2}}} ,$ | (11) |
| $ \frac{{{F}}}{2} = {k_\theta }{\delta _{Ay}}。$ | (12) |
式中:δAy为截面A-A处垂向位移。
联立求解上述公式即可求得如图4(b)所示圆心角为θ的平面曲杆的垂向等效刚度:
| $ {\begin{gathered}[b] {k_\theta } = A{\text{E}}/\left\{ 2\left[\frac{R}{4}\left(\frac{R}{e} - 1\right)\left(\theta - \frac{{\sin 2\theta }}{2}\right) + \frac{R}{4}\frac{{{{E}}c}}{{{G}}}\left(\theta + \frac{{\sin 2\theta }}{2}\right) - \right.\right. \\ \left.\left.{\text{ }}\frac{1}{2}\sin {\theta ^2}QR\left(\left(\frac{R}{e} - 1\right) - \frac{{{{E}}c}}{{{G}}}\right) - \left(N + QR)(\frac{R}{e} - 1\right)\left(\cos \theta - 1\right)\right]\right\}。\\ \end{gathered}} $ | (13) |
式中:N=M/F;Q=P/F。
综上,齿轮基胞元单侧内齿环刚度k的理论解析公式如下:
| $ k = {k_\theta } + {k_{{\text{π }}/2 - \theta }}。$ | (14) |
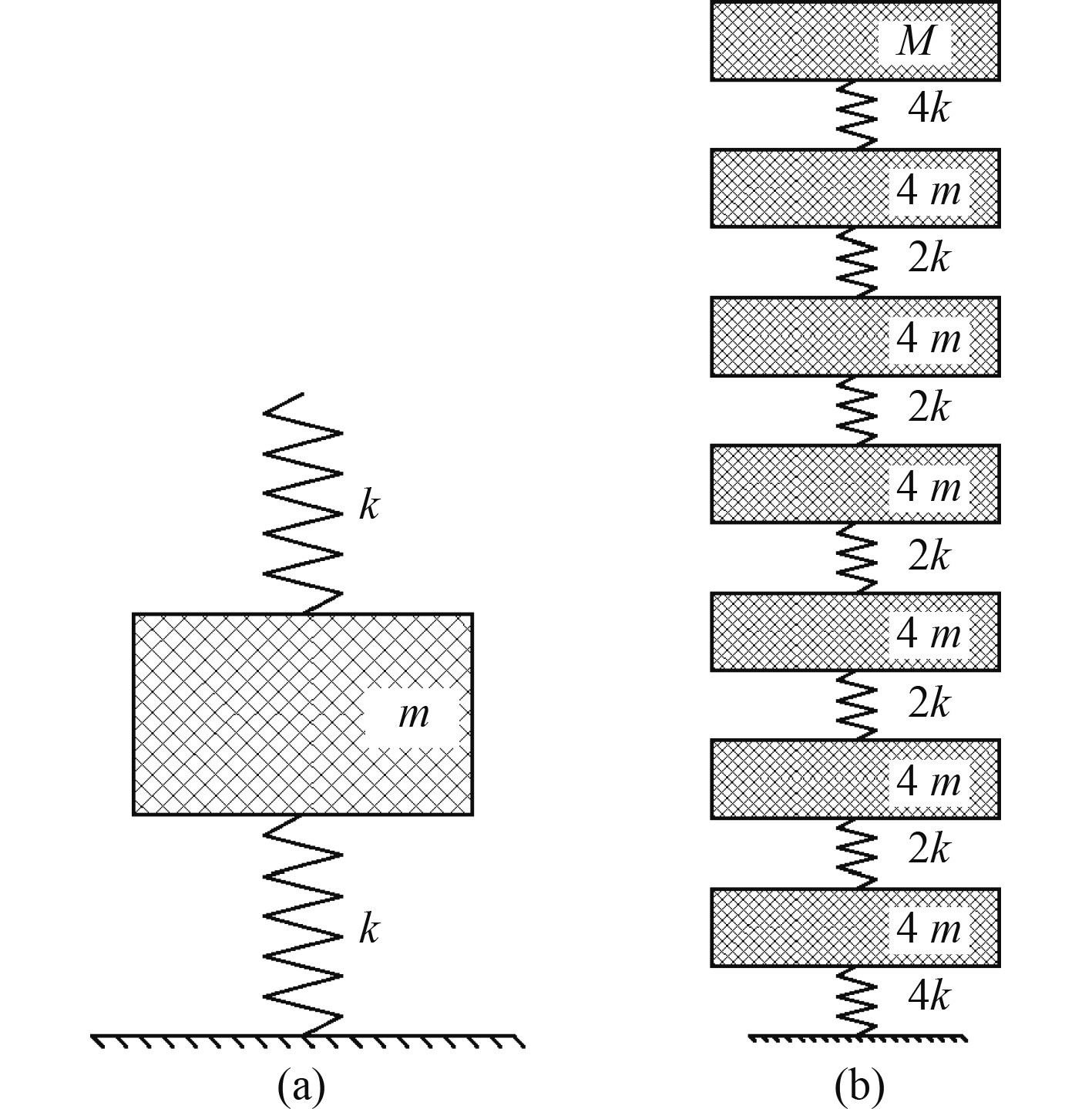
单个胞元的质量弹簧模型如图5(a)所示,根据弹簧串并联理论,整个吸振器的质量弹簧模型如图5(b)所示。图中,M为顶端质量块质量,m为单个胞元质量,k为单个胞元的单侧内齿环刚度。
|
图 5 动力学简化模型 Fig. 5 Simplified dynamical model of DVA |
该吸振器的动力学方程如下:
| $ M\ddot u + Ku = 0 。$ | (15) |
式中:
| $\begin{aligned} & M{\text{ = }}\left[ {\begin{array}{*{20}{c}} m&0&0&0&0&0&0 \\ 0&m&0&0&0&0&0 \\ 0&0&m&0&0&0&0 \\ 0&0&0&m&0&0&0 \\ 0&0&0&0&m&0&0 \\ 0&0&0&0&0&m&0 \\ 0&0&0&0&0&0&M \end{array}} \right],{\text{ }}\\ & K = \left[ {\begin{array}{*{20}{c}} {6k}&{ - 2k}&0&0&0&0&0 \\ { - 2k}&{4k}&{ - 2k}&0&0&0&0 \\ 0&{ - 2k}&{4k}&{ - 2k}&0&0&0 \\ 0&0&{ - 2k}&{4k}&{ - 2k}&0&0 \\ 0&0&0&{ - 2k}&{4k}&{ - 2k}&0 \\ 0&0&0&0&{ - 2k}&{6k}&{ - 4k} \\ 0&0&0&0&0&{ - 4k}&{4k} \end{array}} \right] 。\end{aligned}$ |
设位移矩阵为:
| $ \boldsymbol u = \left[ {\begin{array}{*{20}{c}} {{u_1}} \\ {{u_2}} \\ {{u_3}} \\ {{u_4}} \\ {{u_5}} \\ {{u_6}} \\ {{u_7}} \end{array}} \right] = \boldsymbol A\cos (\omega t + \varphi ) = \left[ {\begin{array}{*{20}{c}} {{A_1}} \\ {{A_2}} \\ {{A_3}} \\ {{A_4}} \\ {{A_5}} \\ {{A_6}} \\ {{A_7}} \end{array}} \right]\cos (\omega t + \varphi )。$ | (16) |
式中:A1~A7为图5(b)吸振器简化模型中各质量块的振幅。
将位移矩阵代入动力学方程,使特征值方程有非零解,则系数行列式为0,得频率方程:
| $\begin{aligned} \left| {\begin{array}{*{20}{c}} {6k - {\omega ^2}m}&{ - 2k}&0&0& \\ { - 2k}&{4k - {\omega ^2}m}&{ - 2k}&0& \\ 0&{ - 2k}&{4k - {\omega ^2}m}&{ - 2k}& \\ 0&0&{ - 2k}&{4k - {\omega ^2}m}&\\ 0&0&0&{ - 2k}& \\ 0&0&0&0&\\ 0&0&0&0& \end{array}} \right. \\ \left.{\begin{array}{*{20}{c}} 0&0&0\\ 0&0&0\\ 0&0&0\\ { - 2k}&0&0 \\ {4k - {\omega ^2}m}&{ - 2k}&0\\ { - 2k}&{6k - {\omega ^2}m}&{ - 4k} \\ 0&{ - 4k}&{4k - {\omega ^2}M} \end{array}}\right| = 0。\end{aligned} $ | (17) |
求解上述固有频率方程即可得到动力吸振器的各阶固有频率。通过观察解析公式和理论模型可知该吸振器的固有频率与胞元的齿宽参数无关,这是因为齿宽变化伴随着整个吸振器的刚度和质量等比例变化。
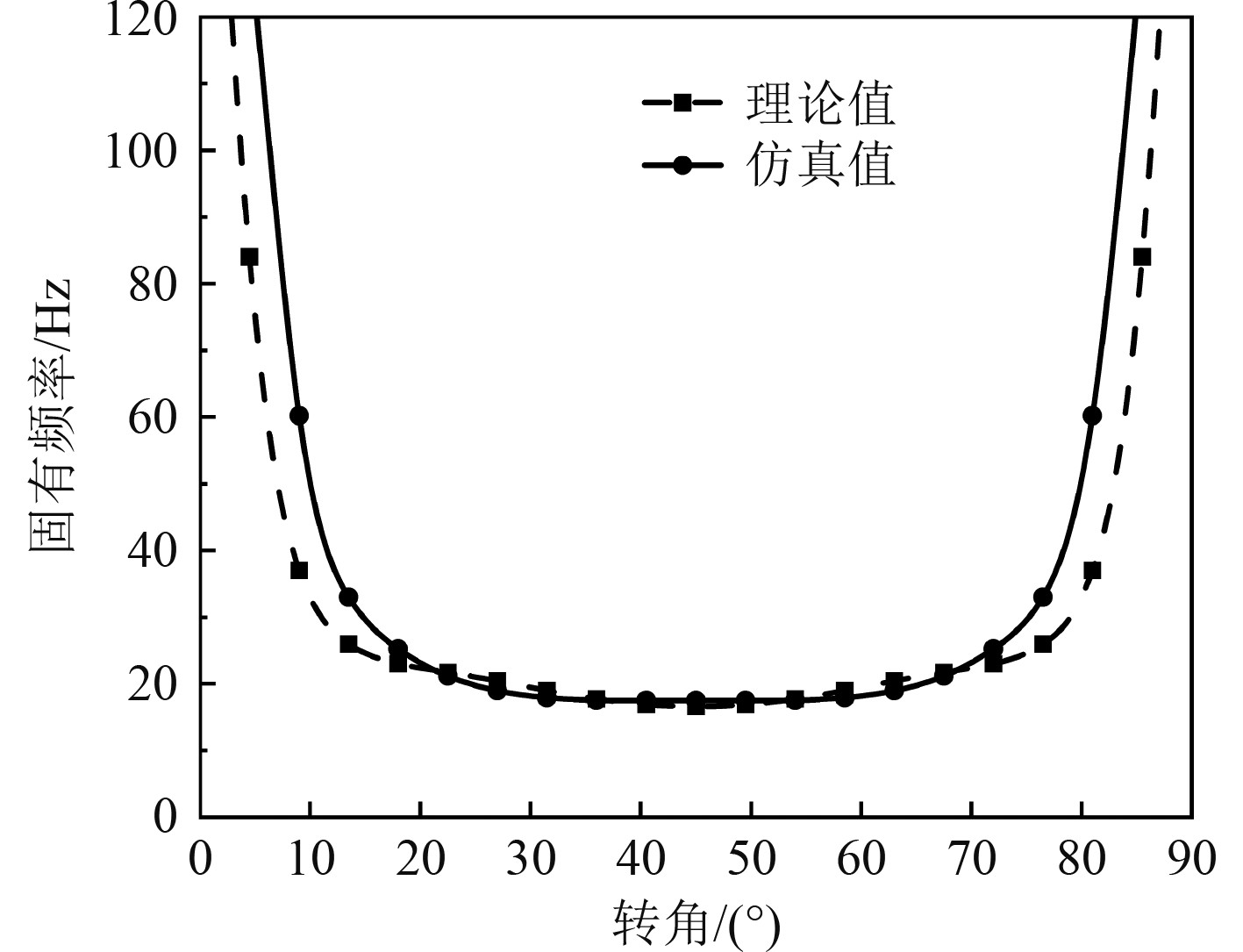
2.3 齿轮基动力吸振器移频特性利用Ansys Workbench模态计算模块求解动力吸振器在调频过程中的垂向固有频率(以齿宽取200 mm为例),计算过程中行星轮系的内齿环贡献了吸振器的主要刚度,齿轮间啮合的接触面简化为绑定状态进行模拟[8, 16],行星轮转角θ在4.5°~85.5°范围内调整时,动力吸振器的调频区间为17.47~130.85 Hz,有限元仿真及理论计算结果对比如图6所示。
|
图 6 动力吸振器移频特性 Fig. 6 Frequency shift characteristics of DVA |
可知,动力吸振器调频过程中,行星轮与y轴夹角θ越接近0°和90°,固有频率变化率越大,θ角越接近45°,固有频率变化越平缓,这是齿轮基胞元的结构形式导致的,行星轮位置越接近y轴,胞元刚度变化越快。行星轮转角θ越接近45°,固有频率理论计算值与仿真值的拟合效果越好,而θ越趋近于0°或90°,其拟合效果越差。这是因为2.1节中理论刚度的计算是按照压缩时的受力开展的,即压缩刚度。而本例中内齿环在受压缩和拉伸时刚度不同,二者的差异随着行星轮转角θ趋于0°或90°而愈发明显。采用压缩刚度作为系统振动时的等效刚度在有限范围内合理。
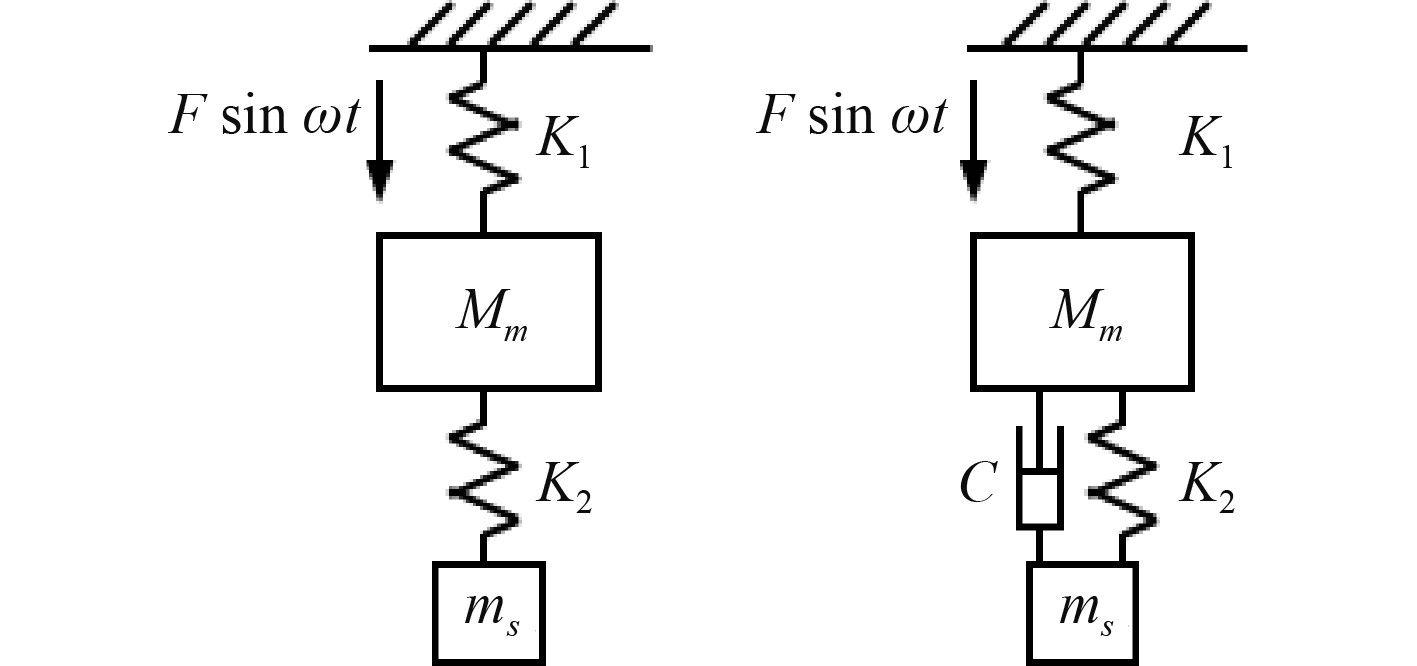
3 船体减振应用分析 3.1 动力吸振器反共振消振原理图7为两自由度质量-弹簧-阻尼主从系统中,对于主质量Mm施加简谐激振力,在某个频率点(反共振点),主系统Mm虽然受到激振但是却保持不动,只有从质量ms发生剧烈振动,这就是反共振现象。动力吸振器即利用反共振原理实现消振。从力平衡角度分析,该反共振频率等于从系统的固有频率,从系统ms通过共振运动的惯性力,由弹簧传递到主系统Mm,该惯性力大小与激振力相等,而方向相反,抵消了外界激振力,导致主系统质量Mm处于静止状态。弹簧、阻尼器及从系统ms构成动力吸振器。
|
图 7 无阻尼/有阻尼动力吸振原理 Fig. 7 Principle of DVA without/with damping |
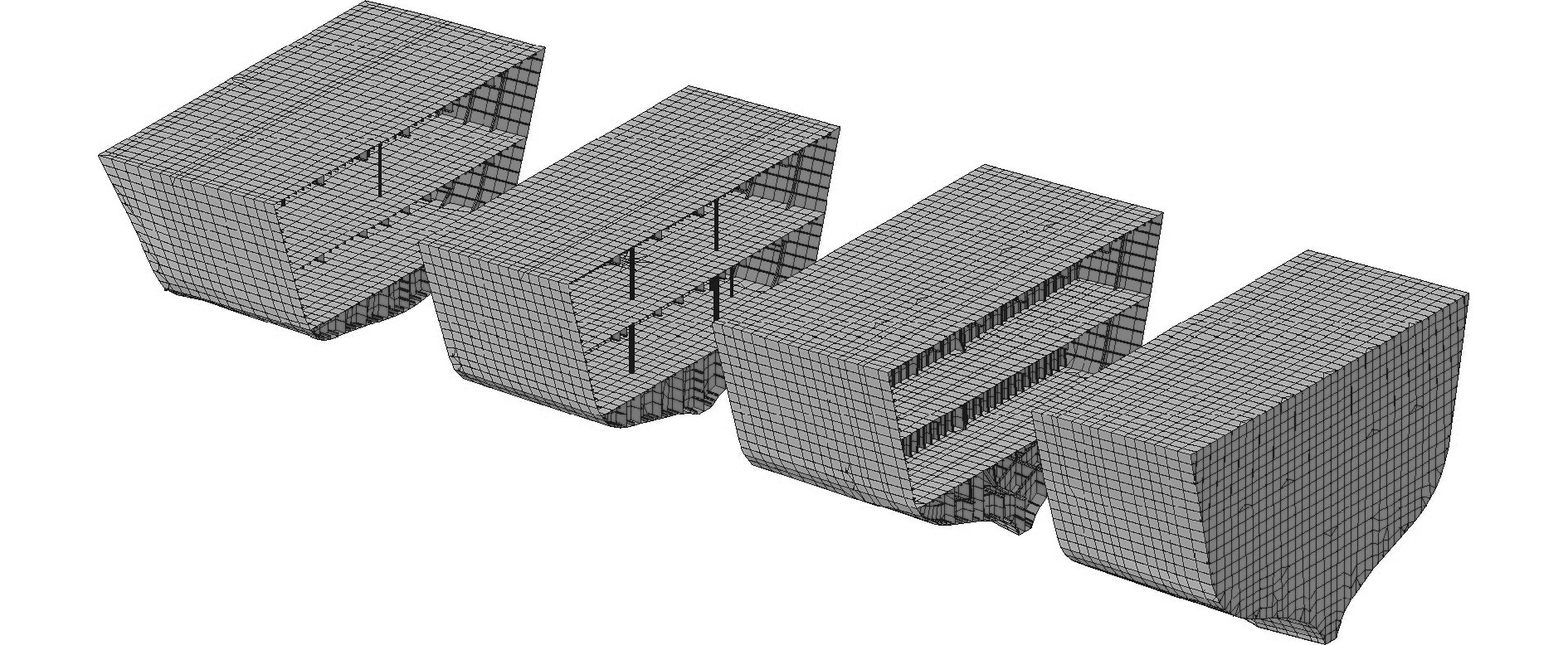
某中型邮轮尾部结构有限元模型分段展示如图8所示,该船包含3层甲板,采用单机单桨推进,其常态运营和最高航速工况下螺旋桨表面力激励频率和大小见表3。将动力吸振器布置于螺旋桨直接作用于船底板架上,如图9所示,通过调节动力吸振器的固有频率,使之与各工况激励频率一致,对整个船体尾部进行吸振。
|
图 8 船尾有限元模型 Fig. 8 Finite element model of stern |
|
|
表 3 螺旋桨表面力汇总表 Tab.3 Propeller exciting forces |
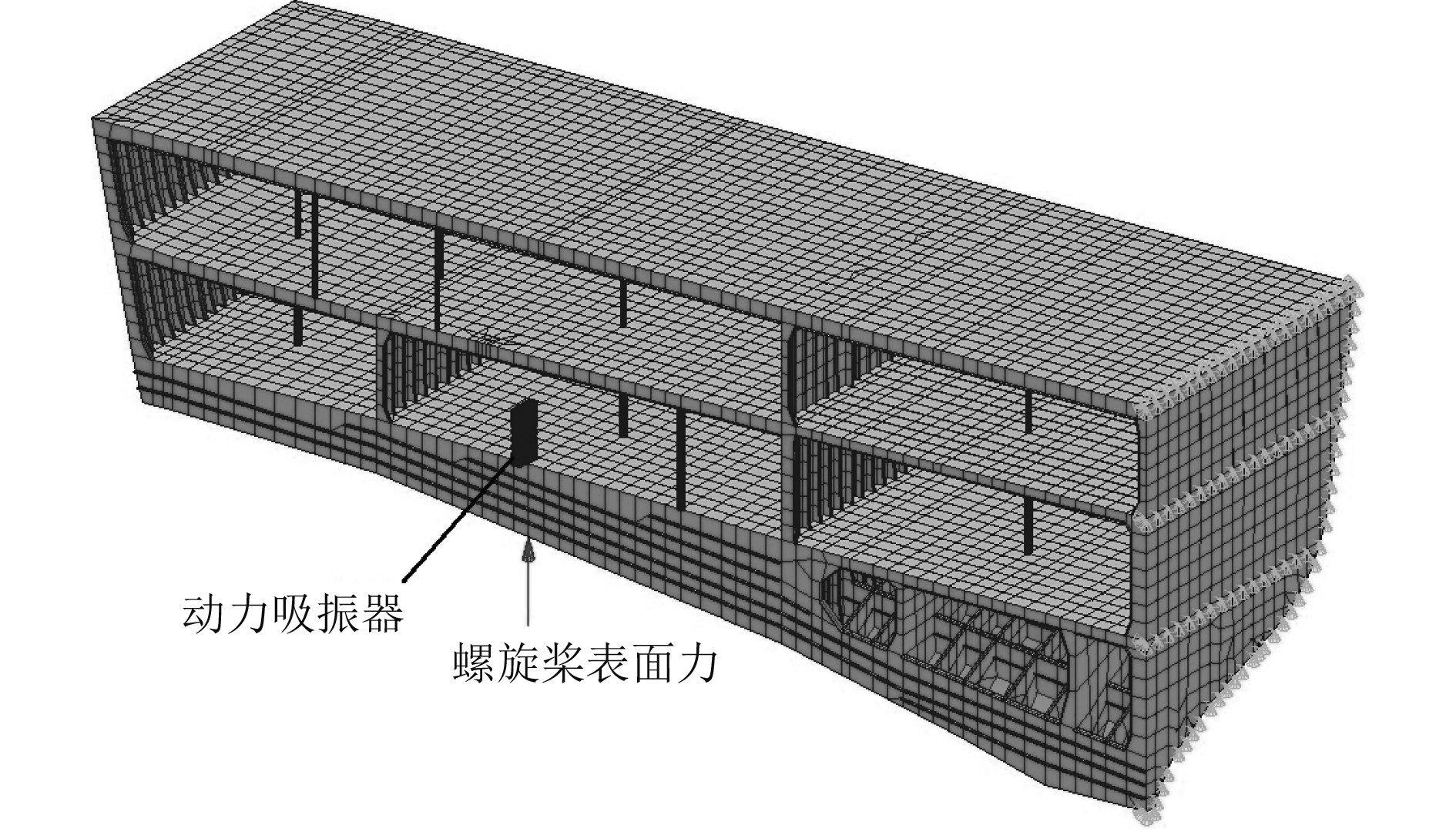
|
图 9 安装动力吸振器的船尾振动响应计算模型图 Fig. 9 Stern modal of FEM simulation |
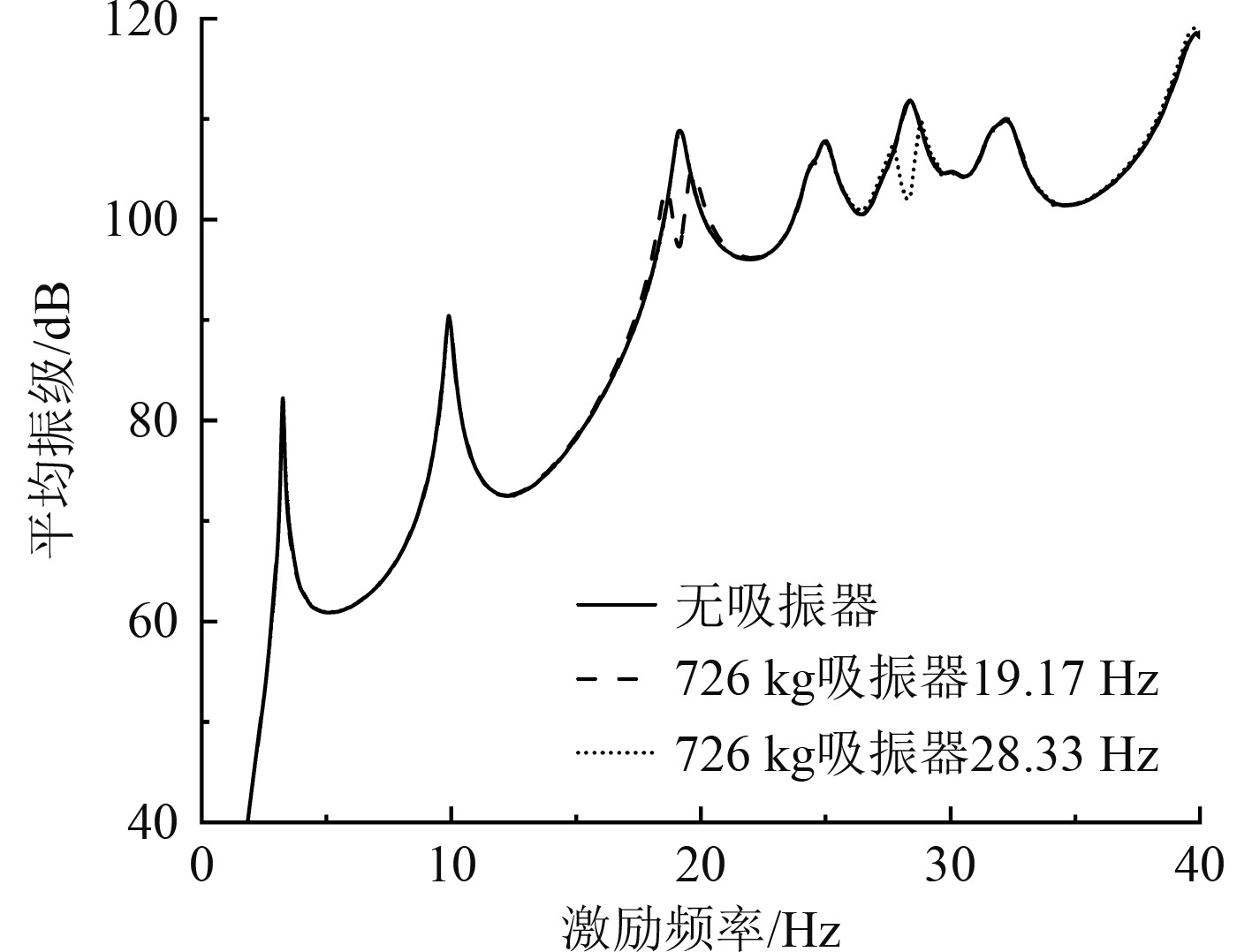
将动力吸振器质量设置为726 kg,此时齿轮齿宽为200 mm,结合有限元软件MSC Patran/Nastran对安装吸振器前后的船体尾部振动响应进行对比计算,在船尾截断处设置简支边界条件,螺旋桨表面力施加在沿螺旋桨轴线方向螺旋桨盘面之前 0.1倍桨径处,如图9所示,计算阻尼采用ABS推荐阻尼取值0.015,振级响应曲线如图10所示,利用分贝值对振动响应进行评估,振动加速度级计算公式如下:
|
图 10 振级响应曲线 Fig. 10 Vibration level response curve |
| $ {L_a} = 20\lg ({a_{\text{e}}}/{a_{{\text{ref}}}})。$ | (18) |
式中:
在尾部舱段甲板、舷侧、船底板、舱壁结构上等间距选取响应计算点,针对船尾所有计算点的平均振级计算公式如下:
| $ {\bar L_a} = 10\lg (\frac{1}{M}\sum\limits_{i = 1}^M {{{10}^{{L_{ai}}/10}}} )。$ | (19) |
式中:尾部舱段选取的响应计算点数量M=88。
由计算结果可知,齿轮基动力吸振器使常态运营工况船尾加速度振级降低了10.83 dB,使最高航速工况船尾加速度振级降低了9.79 dB,具有良好的减振效果。
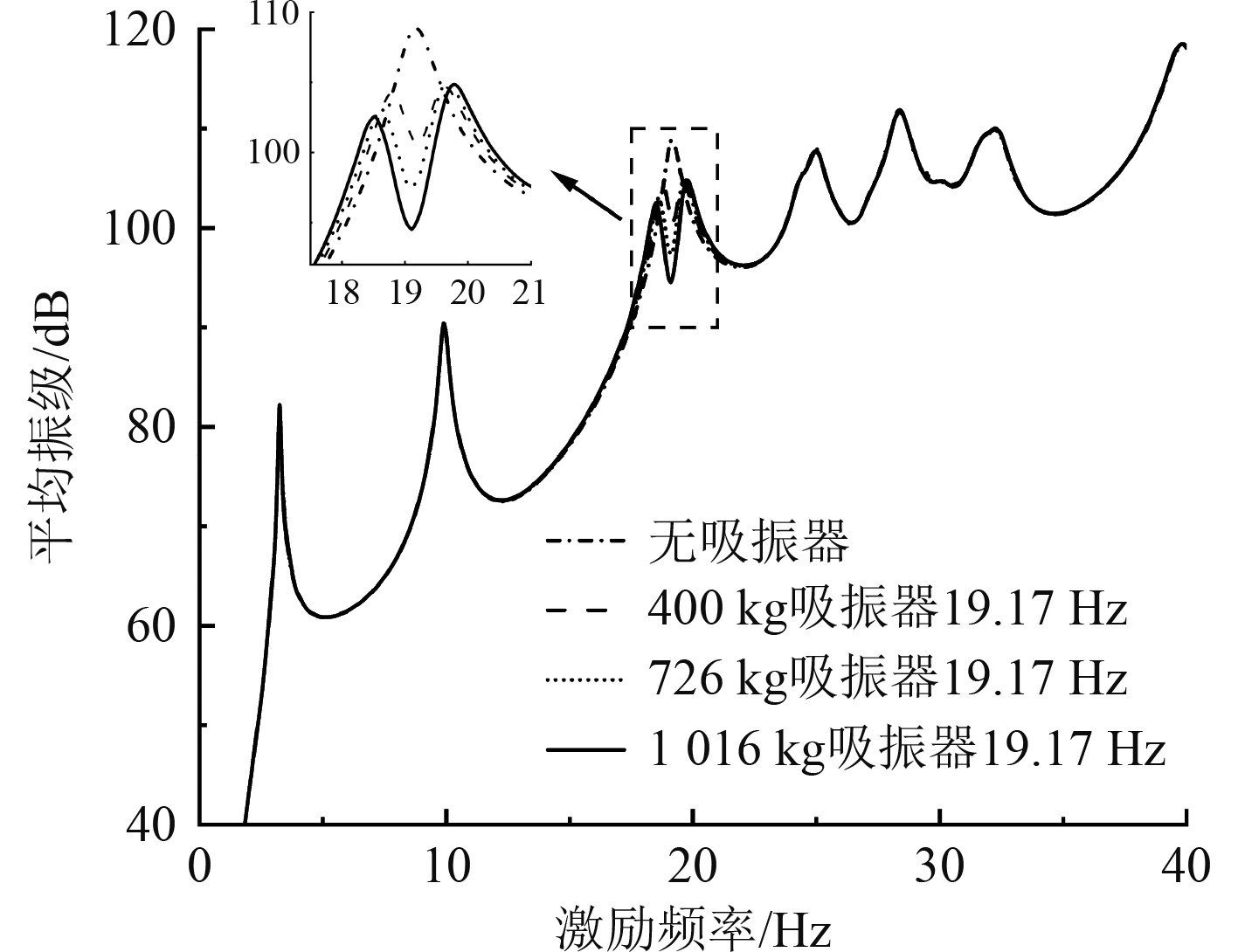
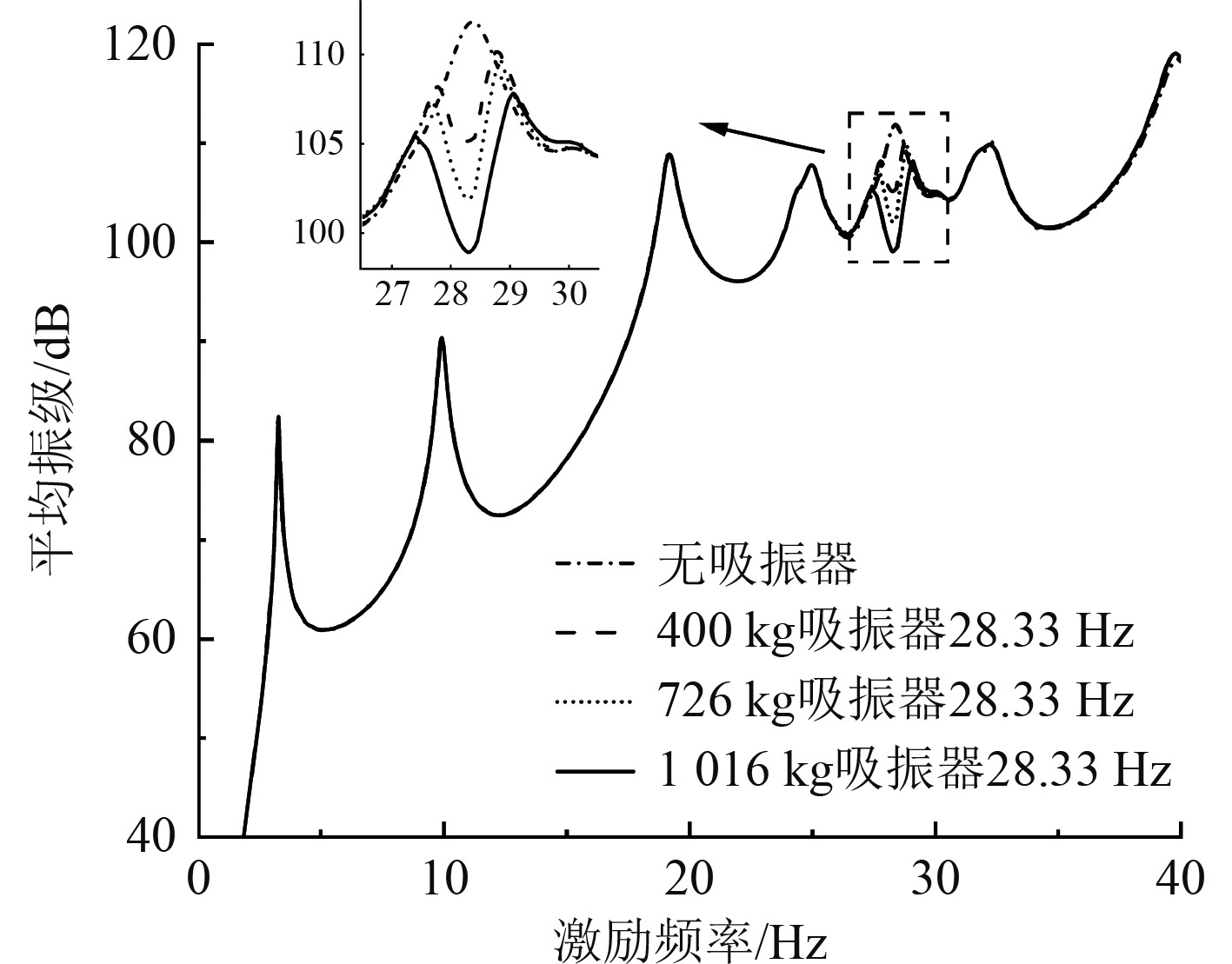
3.3 吸振器质量对减振效果的影响根据2.1节理论推导,齿轮基动力吸振器胞元内齿轮的齿宽是固有频率的无关参数,基于此将齿宽作为动力吸振器的质量调节参数。结合3.2节计算结果,分别选取更重和更轻的动力吸振器进行船尾振动响应计算,探究质量对减振效果的影响,振级响应曲线见图11~图12,计算结果汇总见表4。
|
图 11 常态运营工况下不同质量动力吸振器的吸振效果 Fig. 11 Vibration absorption effect of DVAs with different masses under normal condition |
|
图 12 最高航速工况下不同质量动力吸振器的吸振效果 Fig. 12 Vibration absorption effect of DVAs with different masses under the maximum speed condition |
|
|
表 4 吸振器质量对减振效果的影响 Tab.4 Influence of mass on vibration absorption |
可知,在常态运营工况下,将动力吸振器调频至19.17 Hz,吸振器质量设置在400~
本文基于齿轮基胞元构建了一种新型半主动式动力吸振器,结合理论模型和有限元计算分析了该型式动力吸振器的移频特性及减振效果,主要结论如下:
1)齿轮基动力吸振器调频范围广,可实现超宽频带吸振,为传统动力吸振器无法抑制激励频带内多个共振峰的问题提供了新的研究思路。
2)胞元内行星轮系的齿宽是该类型动力吸振器固有频率的无关参数,这是因为齿宽变化伴随着整个吸振器的刚度和质量等比例变化。
3)受齿轮基胞元结构形式的影响,动力吸振器调频过程中,行星轮与y轴夹角θ越接近0°和90°,固有频率变化率越大,θ角越接近45°,固有频率变化越平缓,这为齿轮基动力吸振器固有频率的调节提供了指导。
4)对不同质量动力吸振器的船体减振效果进行对比分析,结果显示齿轮基动力吸振器具有良好的减振效果,且吸振器质量越大减振效果越好,即同等条件下,动力吸振器的减振效果与其齿宽参数正相关。研究结果为后续新型吸振器的设计应用提供了参考。
| [1] |
徐鉴. 振动控制研究进展综述[J]. 力学季刊, 2015, 36(4): 547-565. XU Jian. Advances of research on vibration control[J]. Chinese Quarterly of Mechanics, 2015, 36(4): 547-565. |
| [2] |
贾富淳, 孟宪皆. 基于功率流理论的主动式动力吸振器控制方法[J]. 机械设计与制造, 2020(3): 72-75,80. JIA Fuchun, MENG Xianjie. The method of active dynamic vibration absorber control based on power flow[J]. Machinery Design & Manufacture, 2020(3): 72-75,80. DOI:10.3969/j.issn.1001-3997.2020.03.017 |
| [3] |
陈文华, 牛军川. 可调频悬臂梁式动力吸振器多频减振研究[J]. 噪声与振动控制, 2021, 41(1): 188-193. CHEN Wenhua, NIU Junchuan. Study on multi-frequency vibration reduction of cantilever type dynamic vibration absorbers with tunable resonant frequency[J]. Noise and Vibration Control, 2021, 41(1): 188-193. DOI:10.3969/j.issn.1006-1355.2021.01.034 |
| [4] |
马强, 狄杰建, 赵全亮, 等. 一种自调频动力吸振器及其吸振特性研究[J]. 应用力学学报, 2014, 31(4): 626-630,13. MA Qiang, DI Jiejian, ZHAO Quanliang, et al. Research of a dynamic vibration absorber with tunable resonant frequency and its damping effect[J]. Chinese Journal of Applied Mechanics, 2014, 31(4): 626-630,13. DOI:10.11776/cjam.31.04.C044 |
| [5] |
邢昭阳, 申永军, 邢海军, 等. 一种半主动负刚度动力吸振器[J]. 振动与冲击, 2021, 40(15): 123-128,36. XING Zhaoyang, SHEN Yongjun, XING Haijun, et al. A semi-active negative stiffness dynamic vibration absorber[J]. Journal of Vibration and Shock, 2021, 40(15): 123-128,36. |
| [6] |
SHEN Y J, WANG L, YANG S P, et al. Nonlinear dynamical analysis and parameters optimization of four semi-active on-off dynamic vibration absorbers[J]. Journal of Vibration and Control, 2012, 19(1): 143-160. |
| [7] |
郎君, 申永军, 杨绍普. 半主动控制接地式动力吸振器参数优化及性能比较[J]. 动力学与控制学报, 2019, 17(2): 168-177. LANG Jun, SHEN Yongjun, YANG Shaopu. Parameter optimization and performance comparison of semi-active ground-hook control dvas[J]. Journal of Dynamics and Control, 2019, 17(2): 168-177. DOI:10.6052/1672-6553-2018-048 |
| [8] |
FANG X, WEN J, CHENG L, et al. Programmable gear-based mechanical metamaterials[J]. Nat Mater, 2022, 21(8): 869-876. DOI:10.1038/s41563-022-01269-3 |
| [9] |
LEVINE D J, TURNER K T, PIKUL J H. Materials with electroprogrammable stiffness[J]. Advanced Materials, 2021, 33(35): 2007952. DOI:10.1002/adma.202007952 |
| [10] |
OZTEMEL E, GURSEV S. Literature review of Industry 4.0 and related technologies[J]. Journal of Intelligent Manufacturing, 2020, 31: 127-182. DOI:10.1007/s10845-018-1433-8 |
| [11] |
WOLF S, GRIOLI G, EIBERGER O, et al. Variable stiffness actuators: Review on design and components[J]. IEEE/ASME Transactions on Mechatronics, 2015, 21(5): 2418-2430. |
| [12] |
陆承志, 赵乐, 杨雪勤, 等. 碳纤维增强聚醚酮酮模压复合材料结构与性能调控[J]. 复合材料学报, 2022, 39(8): 3684-3694. LU Chengzhi, ZHAO Le, YANG Xueqin, et al. Study on structure and performance control of carbon fiber reinforced poly(ether ketone ketone) molding composites[J]. Acta Materiae Compositae Sinica, 2022, 39(8): 3684-3694. |
| [13] |
宋海蓝, 刁英洁, 郑榆槿, 等. 油润滑下短碳纤维强化PEEK齿轮接触疲劳试验研究[J]. 实验与技术管理, 2023, 40(5): 18-23,30. SONG Hailan, DIAO Yingjie, ZHENG Yujin, et al. Investigations on the contact fatigue performance of short carbon fibers reinforced PEEK gears under oil-injected lubrication[J]. Experimental Technology and Management, 2023, 40(5): 18-23,30. |
| [14] |
MAO J, PAN Y, DING J. Tensile mechanical characteristics of CF/PEEK biocomposites with different surface modifications[J]. Micro & Nano Letters, 2019, 14(3): 263-268. |
| [15] |
PAN L, YAPICI U. A comparative study on mechanical properties of carbon fiber/PEEK composites[J]. Advanced Composite Materials, 2016, 25(4): 359-374. DOI:10.1080/09243046.2014.996961 |
| [16] |
李强, 闫月, 闫洪波. 基于Ansys的对数螺旋锥齿轮装配体的模态分析[J]. 机械设计与制造, 2013(5): 194-196. LI Qiang, YAN Yue, YAN Hongbo. Modal analysis of the logarithm spiral bevel gear assembly based on the Ansys[J]. Machinery Design & Manufacture, 2013(5): 194-196. DOI:10.3969/j.issn.1001-3997.2013.05.059 |
 2024, Vol. 46
2024, Vol. 46
