随着全球变暖,北极海冰融化范围增加,运输船舶在北极航行的可能性得到提高,从而带来了巨大的经济效益和社会效益。北极航道冰况复杂多变,覆盖着大量不规则浮冰,运输船舶在航行过程中难免会与浮冰发生碰撞,受到浮冰的多次冲击和挤压等作用,造成船首结构的累积损伤,对船舶安全产生较大的损害[1]。近年来,在考虑船舶在冰区通行时的船碰撞冰累计损伤研究时,都没有考虑船在冰区航行时船外板的附着冰层对于船冰碰撞的影响,然而冰区船舶在北极航道航行时船外板的附着冰是常见现象。尹群等[2]认为在船冰碰撞时外板是碰撞的主要吸能材料,所以与外板直接接触的船外板附着冰也应得到考虑。本文针对运输船舶在极地多次航行过程考虑船外板附着冰造成船首结构的累积损伤变形、碰撞力大小及分布等一系列问题展开研究,并且对受到浮冰载荷作用后的船舶的运动响应进行分析。
1 船冰碰撞相关理论 1.1 接触算法LS-DYNA软件是一种优秀的显式分析软件,在处理各类碰撞问题有着很大的优势,可以准确合理地模拟出实际情况下碰撞过程的结构力学行为[3]。该软件重启动处理碰撞分析问题时需要定义发生接触的主从接触、接触类型和相关参数,保证在后续计算中程序可以识别发生接触的表面。有对称罚函数法、动态约束法和分配参数法3种算法用于处理接触表面。
动态约束法是最早的接触算法,目前只适用于固连界面的接触问题。其原理主要是在每一个时间步内,分析判断主表面是否存在被与其相互接触的从节点穿过的情况,若主表面出现被穿透的现象,将时间步长调小使贯穿节点停止贯穿。在下一时间步中,在刚到主节面的从节点位置施加碰撞条件[4]。
分配参数法是将每个接触单元从单元的一般质量施加到主表面区域上,且接触过程中主表面上的压力主要是由每个单元的内应力决定的一种算法,比较适合处理过程中主从表面没有分离而有相对滑动的问题。通过及时更新主表面的加速度并约束从节点的速度和加速度,确保它们沿主表面运动,因此此方法主要用于滑动接触方式研究。
1.2 接触定义在研究船舶结构碰撞问题时,除了考虑接触算法,还需要考虑结构界面接触类型。在接触可能发生的结构之间定义接触面,可以有效模拟碰撞结构之间的接触情况,允许结构之间存在不断的接触、摩擦和滑动,同时,需要保证模型在计算之前不能有初始接触以及接触部位不能有重叠区域。LS-DYNA程序目前有40多种接触类型求解不同接触问题,一般接触定义主要包括3种基本类型:单面接触、节点-表面接触和表面-表面接触。一个物体表面自我接触或与另一物体表面接触时采用单面接触;2个表面接触,接触节点穿透主表面时采用节点-表面接触;表面-表面接触通常应用于一个物体的表面穿透另一个物体表面的接触问题。
在船舶与冰碰撞过程中,冰材料模型会因碰撞而失效,这类问题一般采用侵蚀接触类型进行研究。因此本文采用侵蚀表面-表面接触(*CONTACT_ERODING_SURFACE_TO-SURFACE)定义船首与冰体之间的接触,考虑发生碰撞后碎冰单元也会发生自我接触,出现失效删除的情况,所以采用侵蚀单面接触(*CONTACT_ERODING_SINGLE_SURFACE)来定义碎冰发生的自我接触问题[3]。
2 仿真模型的建立 2.1 基于元胞自动机构建碎冰模型元胞自动机是一组规则排布在元胞空间上且具有有限多个状态量的元胞根据自身及其邻居上一时刻的状态量在离散的时间步上按照指定的演变规则进行状态更新的系统,拥有模拟复杂系统的时空演化能力[1]。元胞自动机的构建没有固定的数学公式,构成方法复杂,分类难度也很大,一般将其分为4类:平稳型、周期型、混沌型和复杂型。
构建元胞自动机有2种方法:Hoopsnake法和VB脚本法,VB脚本基于蚂蚁规则,利用横纵坐标表示位置,利用0、1表示网格颜色,将问题数值逻辑化,对比Hoopsnake法可以大大减少计算时间。因此本文利用VB脚本的方法构建元胞自动机,构建流程如图1所示[5]。

|
图 1 VB脚本法构建元胞自动机流程图 Fig. 1 The flow chart of building cellular automata with VB script method |
最终建立的实体碎冰区域模型俯视图和主视图如图2所示,该碎冰模型可以较好地模拟真实冰区情况。

|
图 2 碎冰实体模型 Fig. 2 The solid model of crushed ice |
利用Hypermesh软件对碰撞区碎冰模型以0.5 m的大小进行网格划分,对碰撞区外的碎冰模型以1 m的网格大小进行网格划分,以节省算力和时间,结果如图3所示,并生成K文件为后续船-冰碰撞做准备。

|
图 3 碎冰有限元模型 Fig. 3 Finite element model of crushed ice |
本文研究的对象箱型梁是一种典型的加筋板组合起来的结构,本身拥有节省材料、强度优秀等优点,在船舶工程结构中箱型梁结构被普遍应用,箱型梁的极限强度素来被船舶行业工作者重视。因本文旨在研究船外板附着冰对于船冰碰撞有何影响,主要比较有无船外板附着冰,所以典型箱型梁代替船体简化模型具有可行性。
本文所用箱型梁模型的剖面结构如图4所示,箱型梁结构的有效跨长为540 mm,型深及型宽均为720 mm,在箱型梁内部一共设置有12个加强筋,其中面板厚度为3.05 mm,加强筋尺寸为50 mm×3.05 mm。

|
图 4 箱型梁剖面结构形式 Fig. 4 Box girder section structure |
Coon等[6]在北极冰动力学联合实验(Arctic Ice Dynamics Joint Experiment,AIDJEX)中对北极海域的海冰进行分析,提出一种弹塑性海冰本构模型。这种本构模型把海冰看作一种大尺度的二维连续体,将海冰力学问题转化为平面应力问题。海冰在弹性阶段的应力应变关系满足广义胡克定律,如下式:
| $ \sigma = K{D_{el}}G + 2D_e^{'}。$ | (1) |
式中:
体积弹性模量K和剪切弹性模量G的计算式为:
| $ K = \frac{E}{{3\left( {1 - 2v} \right)}},$ | (2) |
| $ G = \frac{E}{{2\left( {1 + v} \right)}} 。$ | (3) |
式中:
这种弹塑性海冰本构模型基于Von-Mises屈服准则,在海冰发生弹性变形即将屈服时,海冰模型的应变能为:
| ${ W = \displaystyle\frac{1}{2}{\sigma _{i j}}{\varepsilon _{i j}} = \frac{1}{{2E}} \left[ {\sigma _1^2 + \sigma _2^2 + \sigma _3^2 - 2v\left( {{\sigma _1} {\sigma _2} + {\sigma _2}{\sigma _3} + {\sigma _1} {\sigma _3}} \right)} \right] 。}$ | (4) |
应变能可以拆分为形状变化能
| $ W = {W_v} + {W_s} 。$ | (5) |
其中,形状变化能如下式:
| $ {W_v} = \frac{{1{\sigma _m}}}{{2K}},{\sigma _m} = \frac{1}{3}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)。$ | (6) |
滑动变形跟体积变化能没有关系。假设形状变化能达到临界值,海冰模型随之达到屈服,则体积变化能如下式:
| $ {{W_s} = W - {W_v} = \displaystyle\frac{{1 + v}}{{6E}}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}} \right] = C。} $ | (7) |
若考虑单向拉伸:
| $ C = \frac{{1 + v}}{{3E}}\sigma _Y^2 ,$ | (8) |
综上所述:
| $ {\sigma _e} = \sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}} \right]} = {\sigma _Y} 。$ | (9) |
式(9)是Von-Mises屈服条件。其中,
| $ {\sigma _Y} = \sqrt 3 {\tau _Y} 。$ | (10) |
海冰模型在处于塑性阶段时,其总应变为弹性应变
| $ \varepsilon = {\varepsilon _e} + {\varepsilon _p}。$ | (11) |
其增量形式为:
| $ {\mathrm{d}}D = {\mathrm{d}}{D_e} + {\mathrm{d}}{D_p} 。$ | (12) |
式中:
海冰模型在达到塑性阶段前,
| $ {\mathrm{d}}{D_p} = {\mathrm{d}}\lambda \frac{{\partial \Psi }}{{\partial \sigma }} 。$ | (13) |
其中:
综上所述,在本文有限元仿真模拟当中,海冰本构模型采用各向同性的弹塑性失效破坏模型,具体为LS-DYNA软件材料库中的13号材料,且将VP设置为1,并插入自定义材料*MAT_THERMAL_ISOTROPIC*,比热容为
| $ \left\{\begin{array}{c}{p}^{n+1}<{p}_{t},\\ {\epsilon }_{eff}^{p}<{\varepsilon }_{\mathrm{max}}^{p}。\end{array} \right.$ | (14) |
其中:
本文选择有限元软件LS-DYNA对箱型梁结构进行数值仿真分析,分析箱型梁在冰载荷作用以及低温环境下的极限强度,建立箱型梁结构时选用具有4个节点的壳单元(shell1),海冰采用具有8个节点的实体单元。在有限元分析中箱型梁结构的材料Q235钢,海冰材料特性具体如表1所示。
|
|
表 1 冰材料参数 Tab.1 Ice material parameter |
对于箱型梁结构的极限强度分析来说,边界条件的设置非常重要。对其直接计算可能会产生较大的误差,为了消除误差的影响,其中最常用的手段是延长箱型梁结构的两端,并在箱型梁结构的两端设置边界条件,此种方法是运用St·Venant原理修正边界条件产生的误差。延长区域的纵向长度可以选取1跨长,即建模时在纵向采用1+1+1的模型,故此箱型梁模型的总体长度为
为了简化计算,碰撞过程采用元胞机生成的碎冰,且碎冰的位置位于箱型梁的下方处。碰撞过程对箱型梁结构左端3个方向的线位移进行约束,对绕x、z轴方向的角位移进行约束,右端对y、z两个方向的线位移进行约束,对绕x、z轴的角位移进行约束,约束冰体沿x、z两个方向的线位移以及绕x、z轴的角位移,并给冰体一个初始速度使其向箱型梁移动。
在有限元分析中,网格大小的选取对箱型梁结构的极限强度可能会产生较大影响,从而导致模拟结果误差较大。因此,分别选取100 mm×100 mm、200 mm×200 mm、300 mm×300 mm的网格大小进行收敛性研究,从而验证网格大小对极限强度的影响,进而减小误差。综上所述,箱型梁-冰有限元模型如图5所示。
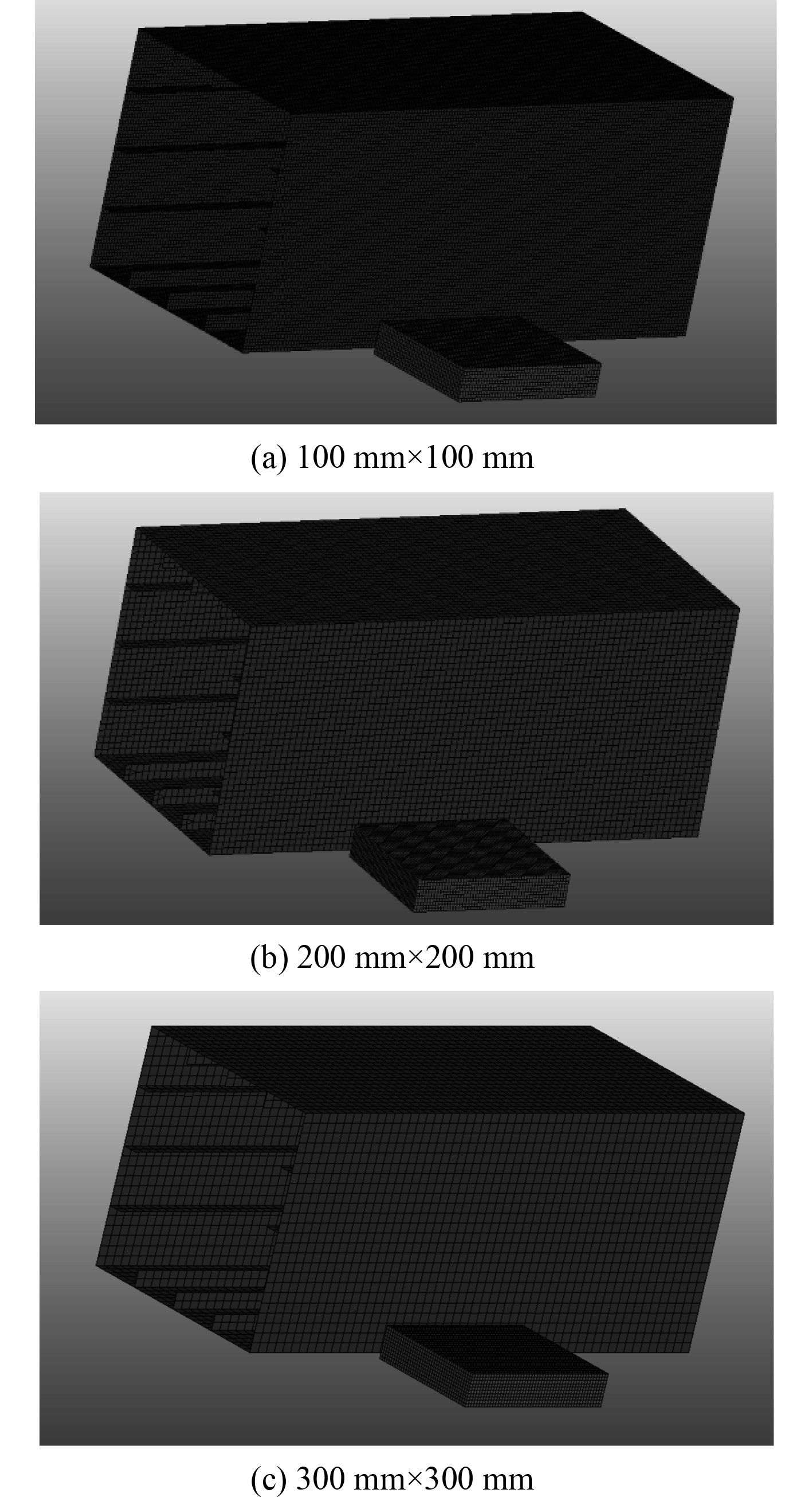
|
图 5 箱型梁-冰数值仿真模型 Fig. 5 Box girder - ice numerical simulation model |
在有限元仿真分析中网格尺寸的大小对结果的准确性有很大的影响,粗糙的网格会使模拟结果不准确,而精密有效的网格尺寸不但可以节省大量计算时间,而且可以提高计算模拟的准确性。选取船速为3.89 kn,冰厚为1 m,碎冰网格为0.5 m的工况进行模拟,对箱型梁网格分别为0.1、0.2、0.3 m 等尺寸进行数值计算,得到表2不同网格尺寸下箱型梁模型网格数量及冰阻力大小。可以看出,随着网格尺寸的减小,冰载荷趋于稳定,冰阻力逐渐增加。当网格尺寸为0.2 m时,数值模拟既满足精度要求又可以节省计算时间,提高计算效率。
|
|
表 2 网格无关性验证结果 Tab.2 Result of the mesh independence verification |
使用有限元软件LS-DYNA在常温下对箱型梁-冰碰撞进行数值仿真,考虑到一般货船速度5~8 m/s之间;一般大型集装箱船的航行速度为8~14 m/s,所以仿真的速度选取为5、8、14 m/s,不同工况在冰厚1 m的情况下仿真航行150 m的箱型梁损伤变形及冰区应力云图,具体如图6所示。

|
图 6 不同速度工况下箱型梁结构损伤变形及冰区应力云图 Fig. 6 Damage and deformation of box girder structures and stress cloud map in ice zone under different velocity conditions |
可知,箱型梁结构的损伤变形随着航行速度的增大呈现出更加严重的趋势,速度14.0 m/s,航行11 s时,可以清楚地观察到箱型梁由于碰撞产生的大变形凹槽;速度5 m/s和8 m/s的变形和应力情况大致相似,只在碰撞区域稍有变形。综上所述,箱型梁结构在该150 m冰区行驶后的损伤变形在对于货船速度(5~8 m/s)来说差别不大,对于集装箱船的速度(8~14 m/s)来说,高速相较低速航行变形差距较大。
图7为不同工况下的箱型梁结构碰撞力时历曲线。可以看出,箱型梁结构的碰撞力峰值随着航行速度的增大呈现出线性增大的趋势。为了更好地定量比较各个速度下的具体数据,对碰撞力时历曲线进行积分,得到各个工况下的冲量值,5 m/s曲线积分后得到冲量为
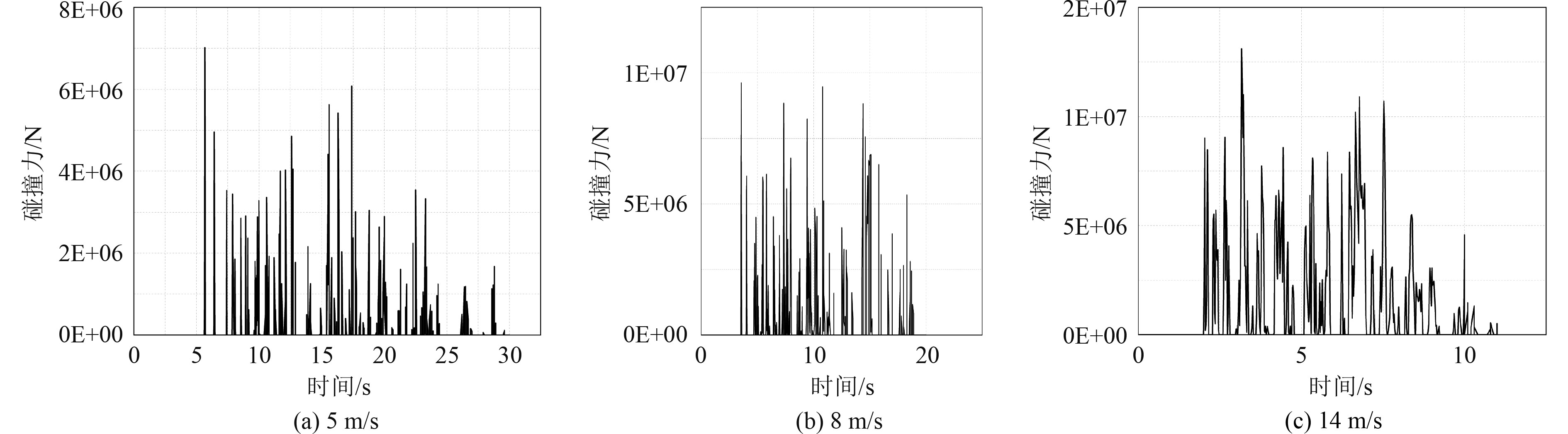
|
图 7 不同速度下箱型梁结构-冰碰撞力时历曲线 Fig. 7 Time-history curve of box girder structures -ice impact force under different velocities |
根据图8可知,不同速度工况下,普通货船的速度区间内(5~8 m/s)箱型梁内能的增长曲线颇为相似,但普通集装箱船的速度区间内(8~14 m/s)箱型梁在高速和低速2种工况下的曲线线形相差较大。所以对于普通货船在碎冰区的累计损伤来说在速度区间内可以一起研究,集装箱船在碎冰区的累计损伤需考虑高速和低速2种情况。
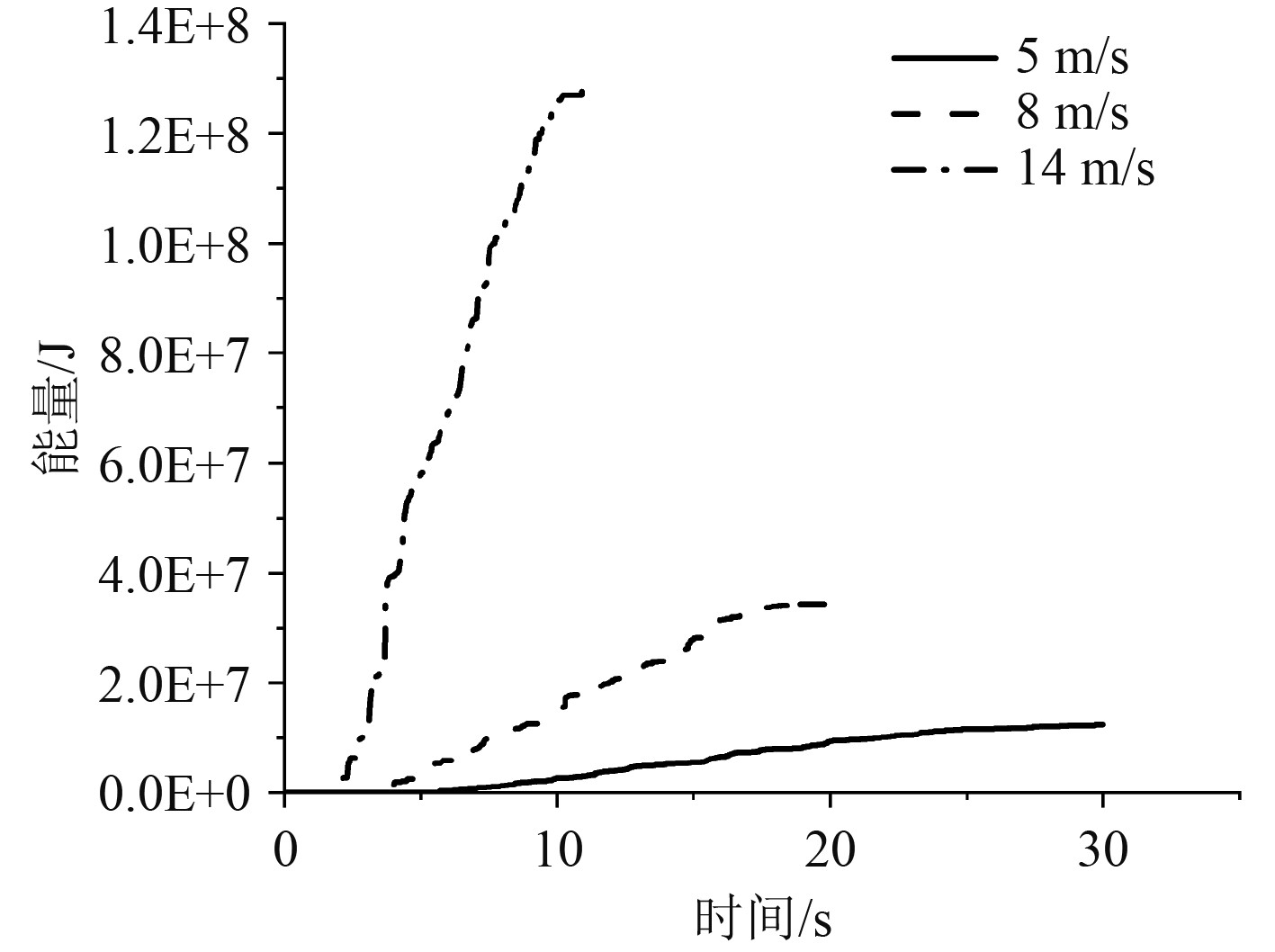
|
图 8 不同速度下箱型梁结构内能曲线 Fig. 8 Internal energy curve of box girder structure under different velocities |
近年来,在考虑船舶在冰区通行时的船冰碰撞研究时,都没有考虑船在冰区航行时船外板的附着冰层对于船冰碰撞的影响,张健等[8-9]得到了在船冰碰撞时外板作为碰撞的主要吸能材料,所以与外板直接接触的船外板附着冰也应得到考虑,碎冰区域继续用前文提到的元胞机随机生成,下文将用dyna重启动模块对考虑船外板附着冰情况下的船冰碰撞累计损伤研究。
碎冰区分为第1次碰撞区域与第2次碰撞区域2块区域。在5 m/s的航速下,箱型梁通过第1个碎冰区域后,删除第1碎冰区域,导出变形stl模型文件,为外板变形后的箱型梁外板添加附着冰模型,保证附着冰与通过第1次碰撞区域后变形后的外板面紧密接触,运用重启动模块,保留其塑性变形及应力应变的情况下分别考虑有附着冰与无附着冰情况下的碰撞响应。
图9为5 m/s时2种工况下的箱型梁累计损伤及碎冰区应力云图。可以看出在通过第1次碰撞区域后,直接保留应力应变后运用重启动在第2次碰撞区域进行仿真,60 s结束后塑性应变为0.47;若是通过第1次碰撞区域后,船体在保留塑性变形后外板附着有冰,在60 s仿真结束后塑性应变为0.40。综上可知,船冰碰撞时附着冰能大幅降低船外板的塑性应变。船舶在北极碎冰区航行时前期船冰碰撞后船体变形后加上温度下降,船外板通常附着有冰,所以外板的附着冰应在船冰碰撞中得到考虑。
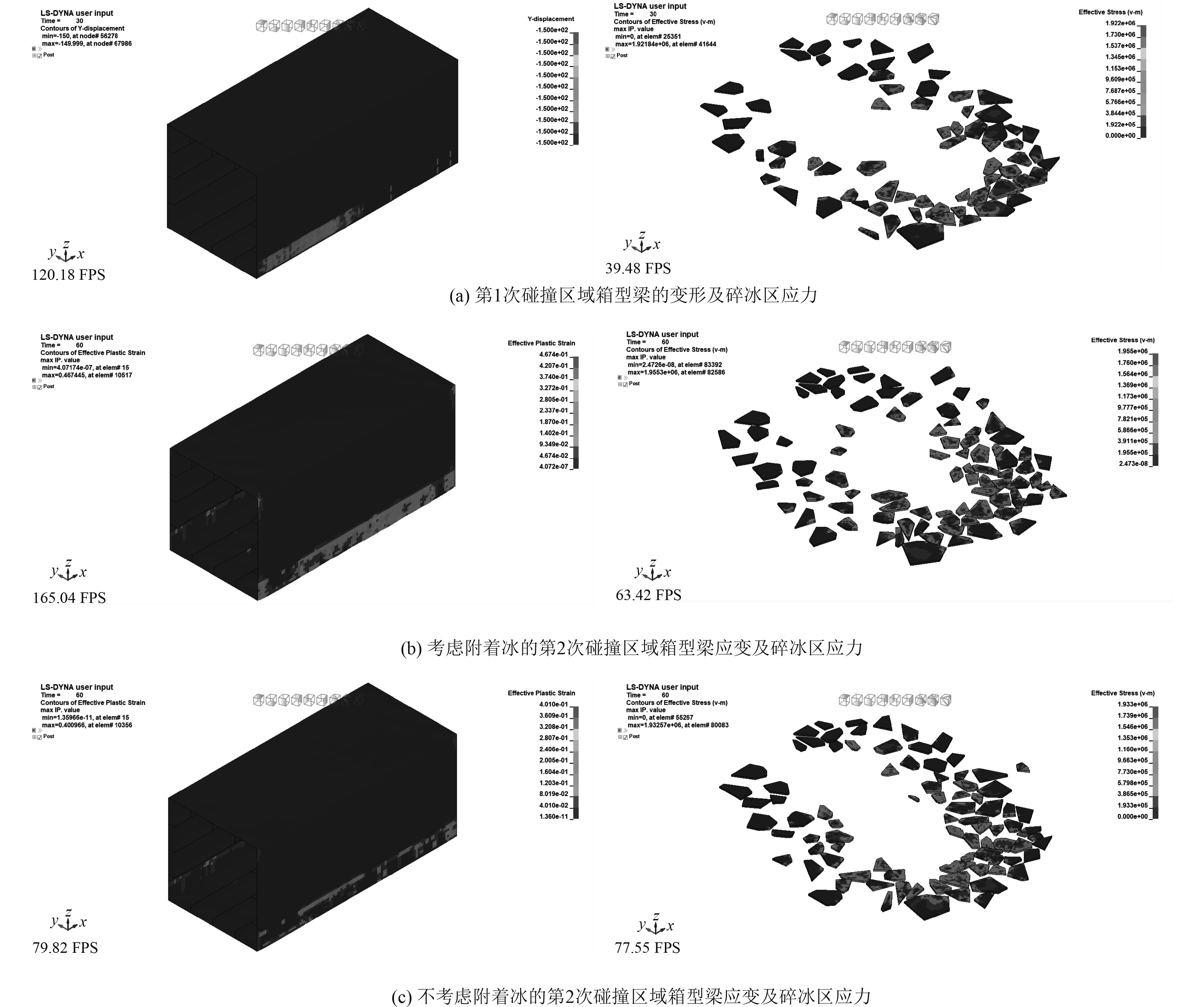
|
图 9 5 m/s时2种工况下的箱型梁累计损伤及碎冰区应力云图 Fig. 9 Accumulated damage and stress cloud map in the fragmented ice zone for two different scenarios of box girder at a velocity of 5 m/s |
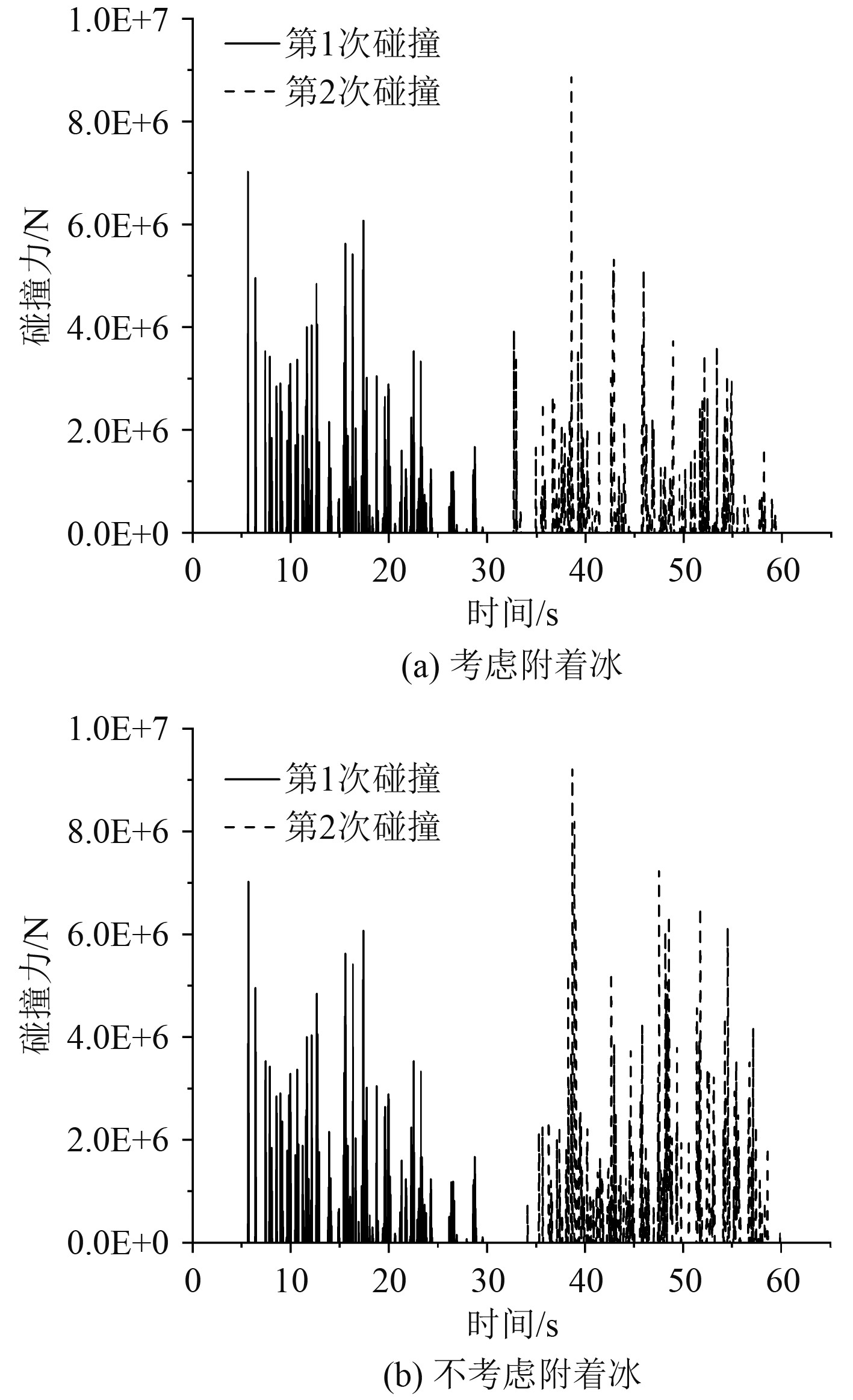
图10为2种工况下的箱型梁结构碰撞力时历曲线。可以看出,箱型梁结构的碰撞力在考虑附着冰的影响后碰撞力峰值大幅降低。为了更好地定量比较2种工况的具体数据,对重启动后的第2次碰撞区域碰撞力时历曲线进行积分,得到2个工况下的冲量值,考虑船外板附着冰碰撞力曲线积分后得到冲量为7.29 MN·s;不考虑船外板附着冰碰撞力曲线积分后得到冲量为12.03 MN·s。综上可以得到考虑附着冰对于船冰碰撞碰撞力峰值是不考虑附着冰的96%;但冲量却只是不考虑附着冰的60.6%。所以考虑外板附着冰情况下的船冰碰撞碰撞力峰值降低不多,但船外板吸能降低了很大一部分。
|
图 10 2种工况下的箱型梁结构-冰碰撞力时历曲线及其面积积分 Fig. 10 Time-history curve and its area integral of ship-ice impact force on box girder structure for two different scenarios |
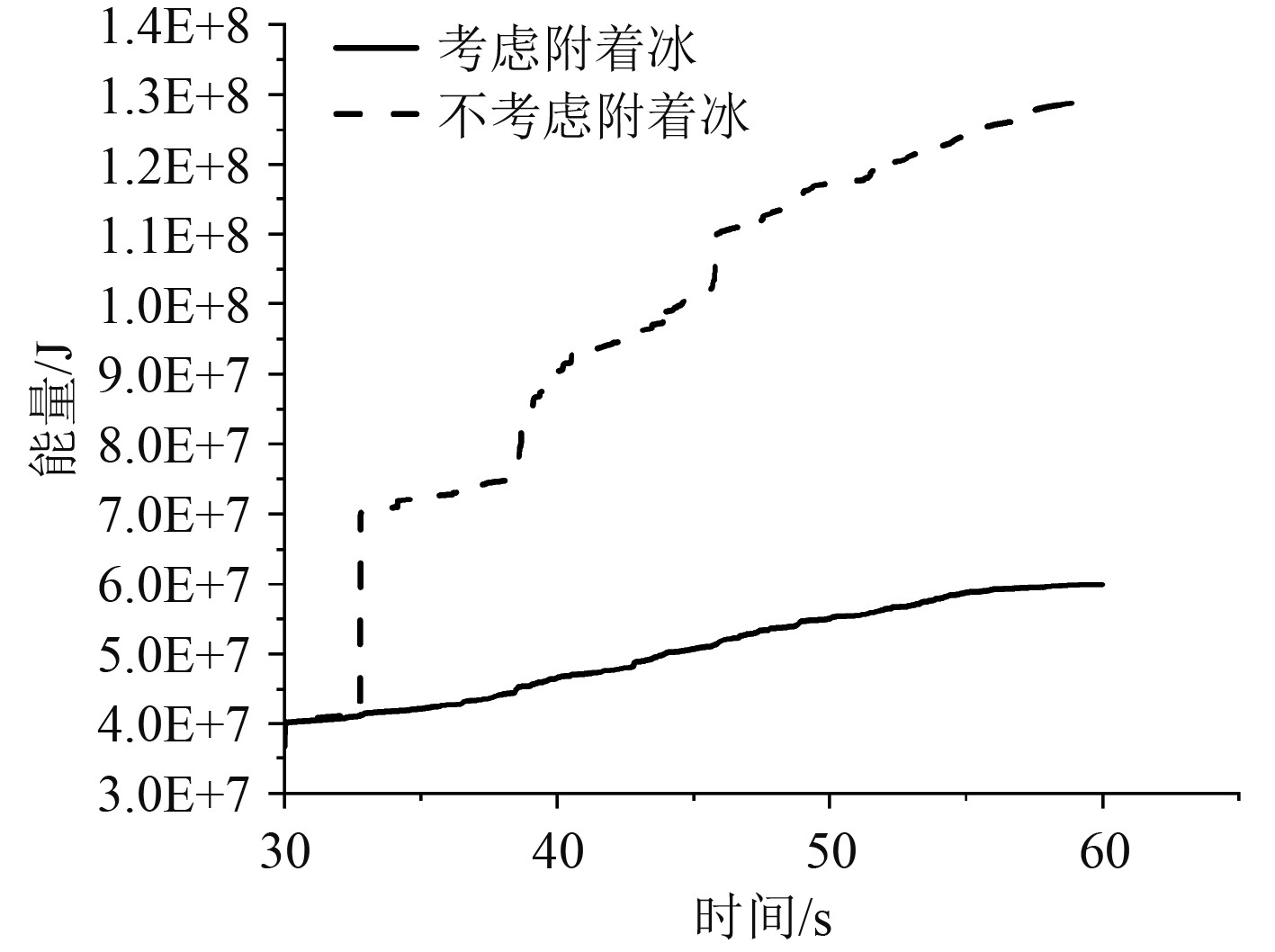
由图11可知,在考虑外板附着冰的情况下,船外板内能增长比较平滑,不考虑外板附着冰的情况下,碰撞力曲线存在阶跃点,船外板内能随发生碰撞的瞬间急剧增大,碰撞发生后其内能又平滑增长,增涨幅度与考虑船外板附着冰情况相近。由此可以看出外板附着冰能一定程度的改善船舶在碎冰区航行的荷载不规律激增,能让冰阻荷载能平稳的作用在船体结构上,并且大幅减少船体外板对于碰撞荷载的能量吸收。
|
图 11 2种工况下的箱型梁结构内能量曲线 Fig. 11 Energy curve of box girder structure for two different scenarios |
本文利用LS-DYNA对船冰碰撞进行模拟仿真,因本文旨在研究船外板附着冰对于船冰碰撞有何影响,主要比较有无船外板附着冰,所以典型箱型梁代替船体简化模型,借助LS-DYNA中的重启动技术以及元胞自动机生成的碎冰区对典型箱型梁在碎冰区2次航行过程开展数值仿真模拟研究,通过比较有无船外板附着冰,对每种方案下不同工况的典型箱型梁结构累积损伤变形和碰撞力-时间曲线等结果加以对比分析,得到以下结论:
1)考虑船外板附着冰的情况下,典型箱型梁的塑性应变与吸收能量都大幅降低,碰撞力峰值没有太大的改变,但对碰撞力的时间积分(冲量)大幅减少。由此可以推断,船舶在北极航行时船外板附着冰,对于船冰碰撞的累计损伤来说是有利的。
2)根据本文的仿真数据,船外板附着冰的情况下,船体结构的累计损伤能大幅减小,因冰碰撞破碎后可以再生,所以如果能利用这一特点,主动控制冰层厚度,将能吸收大量碰撞能量,进而保护船舶在北极航行时的安全,比加厚钢板更经济。这能够为以后普通商船进入北极航道的结构优化做出一定的指导意见。
3)本文通过对普通商船行驶速度工况在碎冰区进行模拟,普通货船的速度(5~8 m/s)累计损伤不是很严重,对于集装箱船的速度(8~14 m/s)来说,全速14 m/s时,航行通过碎冰区的仿真结构损伤较为严重,在模拟中能看到明显的碰撞凹痕。所以普通商船经北极航道运输时为保证经济性,还需进行结构优化。
| [1] |
李锐, 碎冰和层冰联合作用下船首结构动态响应研究[D]. 镇江: 江苏科技大学, 2021.
|
| [2] |
尹群, 陈永念, 张健, 等 碎冰和层冰联合作用下船首结构动态响应研究[J]. 中国造船. 2007, (4): 42−52 YIN Qun, CHEN Yongnian, ZHANG Jian, et al. Study on the dynamic response of ship's bow structure under the combined action of fragmented ice and level ice[J]. Chinese Shipbuilding, 2007, (4): 42−52. |
| [3] |
虞亦伟, 碎冰区船—冰碰撞数值仿真研究[D]. 大连: 大连理工大学, 2021.
|
| [4] |
都巍巍, 惯性振动落砂机动态特性研究[D]. 合肥: 合肥工业大学. 2012.
|
| [5] |
张健, 王蓓怡, 李兰岚, 基于元胞机技术的碎冰模型构建优化方法[J]. 舰船科学技术, 2022, 44 (20): 1−6. ZHANG Jian, WANG Beiyi, LI Lanlan. Optimization method for constructing fragmented ice models based on cellular automaton technology[J]. Ship Science and Technology, 2022, 44(20): 1−6. |
| [6] |
COON M, MAYKUT G, PRITCHARD R. Modeling the pack ice as an elastic-plastic material[J]. AIDJEX Bulletin, 1974, 24: 100-105. |
| [7] |
俞同强, 刘昆, 刘俊杰, 等. 船-冰碰撞中考虑温度影响的冰体材料本构模型研究[J] 船舶力学. 2023, 27(2), 250−259. YU Tongqiang, LIU Kun , LIU Junjie, et al. Study on ice material constitutive model considering temperature effect in ship-ice collision[J]. Ship Mechanics, 2023, 27(2): 250−259. |
| [8] |
张健, 万正权, 陈聪. 船-冰碰撞载荷下球鼻艏结构动态响应研究[J]. 船舶力学, 2014(1): 106-114. ZHANG Jian, WAN Zheng-quan, CHEN Cong. Dynamic response study of spherical-nose bow structure under ship-ice collision load[J]. Ship Mechanics, 2014(1): 106-114. DOI:10.3969/j.issn.1007-7294.2015.h1.012 |
| [9] |
张健. 冰载荷作用下船舶结构动态响应及损伤机理 [M]. 北京: 国防工业出版社. 2015
|
 2024, Vol. 46
2024, Vol. 46
