2. 中南大学 数学与统计学院,湖南 长沙 410083
2. School of Mathematics and Statistics, Central South University, Changsha 410083, China
船舶在航行过程中,其主机、辅机等设备的运转、螺旋桨、船体的振动等都会产生噪声,这些噪声不仅容易使得船体出现结构性的疲劳损坏,同时也会降低仪器设备的使用寿命。船舶在远洋航行过程中,很多时候船员在舱外活动的时间受到限制,因而舱室中的噪声水平在很大程度上影响船员的休息和生活质量。对船舶噪声进行预测的方法有多种,包括有限元法(Finite Element Method, FEM)、边界元法(Boundary Element Method, BEM)以及统计能量分析法(Statistical Energy Analysis, SEA)[1 − 2]。有限元法适用于复杂几何形状和边界条件的结构分析,可以精确模拟结构的局部细节和应力分布。但是对于大型复杂模型,计算量可能非常大,需要较长的计算时间和高性能的计算资源,同时对高频噪声的预测可能不够精确,因为FEM在高频区域的模态密度处理上存在限制。边界元法只需要对结构的边界进行离散化,减少了计算量。对于复杂形状的边界,建立边界积分方程可能较为困难,这就意味着需要较高精度的边界信息,对模型的精确度要求较高[3]。统计能量分析法适用于预测和分析复杂系统的宽带噪声,能够处理各种不同尺度和不同频率的模态。对于舱室噪声的分布规律和整体特性分析较为有效[4]。
通过分析可以发现,虽然以上3种方法都能够对船舶噪声进行预测,但是在舱室噪声预测方面统计能量分析法具有非常大的优势,通过对噪声的精确预测可以为船舶优化设计以及舱室噪声防护提供有效辅助。
1 统计能量分析法原理分析 1.1 SEA简介统计能量分析法(Statistical Energy Analysis, SEA)是一种用于预测和控制结构传播噪声的分析技术。它在船舶、汽车、建筑和其他工业领域中被广泛用于噪声预测和控制。SEA的核心思想是将一个复杂的系统分解为多个子系统,这些子系统在能量上相互耦合。通过分析这些子系统之间的能量交换,可以预测整个系统的噪声响应。
SEA基于能量守恒原理,认为能量在系统中的传递和转换遵循能量守恒定律。系统可以被视为由多个模态(振动模式)组成,每个模态具有特定的能量密度和阻尼特性。使用SEA对船舶噪声进行预测的流程如图1所示。

|
图 1 SEA噪声预测流程 Fig. 1 SEA noise prediction process |
对船舶机舱的预测首先需要将船舶机舱系统分解为多个子系统,这些子系统包括房间、舱室或结构部件,然后需要确定每个子系统的模态频率和模态密度,计算子系统之间的能量传递,包括直接传递和通过结构的传递,同时对系统的阻尼和能量损耗进行计算。最后根据能量平衡方程预测不同子系统的噪声响应[5]。可以发现,能量传递、模态密度、模态频率的计算是研究的重点。
SEA能高效地预测复杂系统在高频随机激励下的动力反应,是因为它能够将这些系统分解为多个能量模式。尽管SEA无法精确地预测单个子系统的具体反应,但它能够在统计层面上预测整个系统的反应。当SEA应用于复杂的船舶噪声预测模型时,一个关键的步骤是合理地简化模型,将复杂的船舶舱室结构系统划分为相互连接的独立子系统。对这些舱室系统的子系统进行分类和划分的首要任务是识别模型中具有相似或相同动态特性的部分,相似的耦合损耗系数或类似的结构阻尼能量模式,然后将这些能量模式相近或结构相似的部分合并为一个子系统。
1.2 SEA能量传递模型SEA能量传递模型通常采用线性方程组来描述。根据能量传递方程可以对能量随时间的变化进行描述,同时还可以对能量在不同子系统之间的流动进行数学表达,从而为后续的噪声预测提供基础。
设Ei为第i个子系统的能量,Cij为子系统i和j之间的耦合系数,则能量平衡方程可以表示为:
| $ \frac{{{\rm d}{E_i}}}{{{\rm d}t}} = \sum\limits_{j = 1}^n {{C_{ij}}} ({E_j} - {E_i}) - {\eta _i}{E_i} \text{。} $ |
式中:n为船舶机舱建模时子系统的总数;ηi为子系统i的损耗因子。损耗因子的计算和船舶整体运动的频率以及不同结构采用的材料有关。阻尼和损耗是影响能量传递和噪声预测的关键因素,主要是由于船舶和空气或其他介质的摩擦而产生。损耗因子可以表示为:
| $ \eta (f) = \frac{{4\xi w}}{{1 + {{\left({w}/{{{w_c}}}\right)}^2}}} \text{。} $ |
式中:w为角频率;
SEA通常用于复杂的振动和噪声问题,尤其是在船舶和建筑声学等领域。通过建立系统的统计模型,可以预测和控制噪声和振动。为了推导出船舶舱室所有子系统之间的能量传导情况,作出如下假设:
1)保守耦合系统。假设船舶舱室系统保守,即没有能量的输入和输出损耗。这意味着系统的能量是守恒的,能量不会凭空消失也不会无故增加。在SEA中,双向功率流(即能量从子系统i流向子系统j,以及反向)是相等的,但这种流动并不是一个可逆过程,即能量流动的方向性是存在的。
2)弱耦合连接。假设舱室的所有子系统之间是弱耦合的,即耦合损耗因子小于子系统的内损耗因子。这种假设允许忽略边界条件对子系统的影响,并且认为子系统间的振动能量流与平均耦合模态能量差成正比,系统的不同部分之间的能量交换不会显著影响各自的能量水平。
3)不相关性。假设系统中的各个子系统的声源激励是相互独立的,并且模态间存在不相干性。每个激励对舱室系统的影响是独立的,并且不同模态之间的能量可以线性相加。这简化了系统的分析,因为可以分别考虑每个激励对系统的影响,而不是必须考虑它们之间的相互作用[6]。
为了描述子系统振动能量分布,需要为每个子系统定义模态密度,建立子系统之间的耦合矩阵,描述能量在子系统之间的传递。模态密度是指在一定频率范围内,子系统中模态的数量,它可以用来衡量系统的储存能量的能力,模态密度可以通过模态数与带宽的比值来表示。模态密度p的计算公式为:
| $ p = \frac{P}{{\Delta \omega }} \text{。} $ |
式中:P为模态总数;△w为带宽。
船舶舱室中的子系统主要为梁系统、标准平板等,对梁系统、标准平板等进行模态密度计算。
1)梁弯曲振动模态密度计算
| $ {p_1}(f) = \frac{{2{\text π} RC_S^2f}}{{{C_l}}} \text{。} $ |
式中:l为梁的长度;Cs为弯曲波的传播速度;f为频率;Cl为纵向波速;R为梁的半径。
2)梁纵向振动模态密度计算
| $ {p_2}(f) = \frac{{2{\text π} f}}{{cl}} \text{。} $ |
3)梁的扭转振动模态密度计算
| $ {p}_{3}(f)=\frac{2\mu (1+\mu )}{{C}_{l}} \text{。} $ |
式中:μ为泊松比。
4)平板的弯曲振动模态密度计算
| $ {p_4}(f) = \frac{{{V_3}S}}{{{C_l}{{h}}}} \text{。} $ |
式中:S为平板面积;h为平板厚度。
2 船舶噪声预测的实现 2.1 噪声来源分析船舶舱室噪声的来源可以多种多样,主要来源于船舶自身噪声和环境噪声。这些噪声都会成为船舶舱室噪声的输入,即噪声激励源。
1)自身噪声
船舶主机(通常是柴油发动机或燃气轮机)在运行时会产生大量的机械噪声和空气动力噪声,辅机包括发电机、风机、压缩机、螺旋桨等,结构振动导致的噪声可以在船舱内部传播,并且通过金属结构传播到舱室中。与此同时一些大功率作战设备也会产生噪声,如雷达、导航系统、武器系统等。
2)环境噪声
当船舶结构的自然频率与激励频率相匹配时,可能会发生共振,导致噪声水平增加。
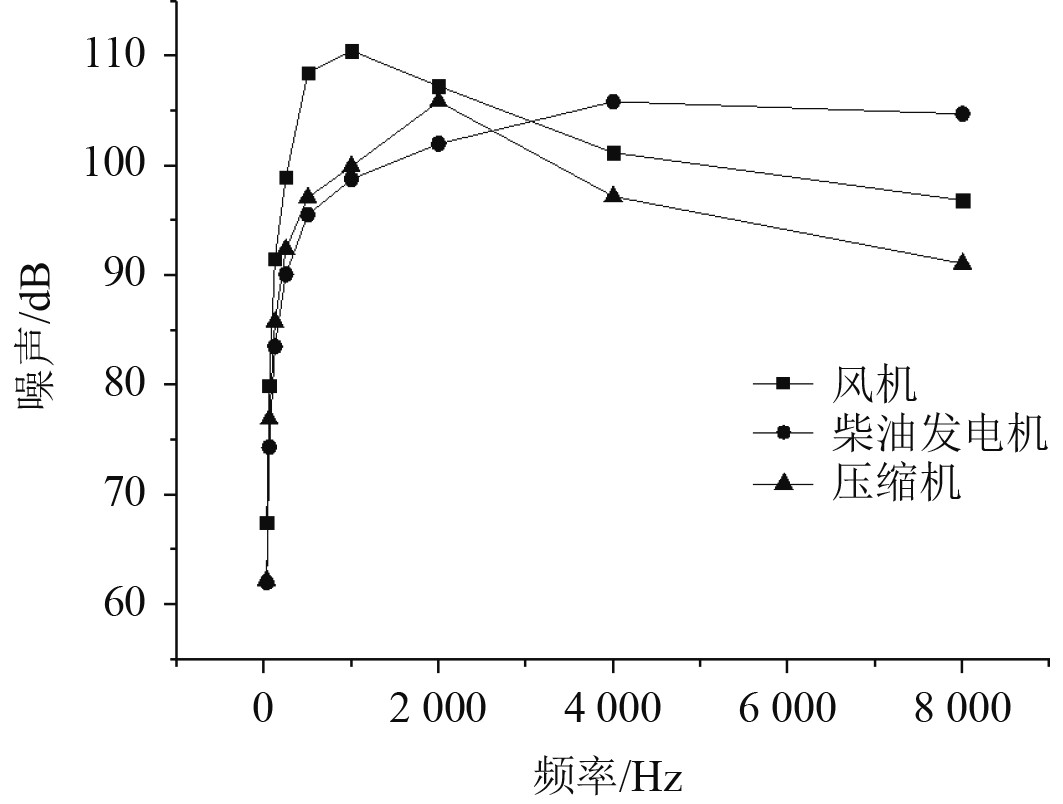
图2为风机、柴油发电机、压缩机等不同噪声激励源产生的噪声随频率的变化情况。可知,在
|
图 2 不同噪声激励随频率变化情况 Fig. 2 Different noise excitation changes with frequency |
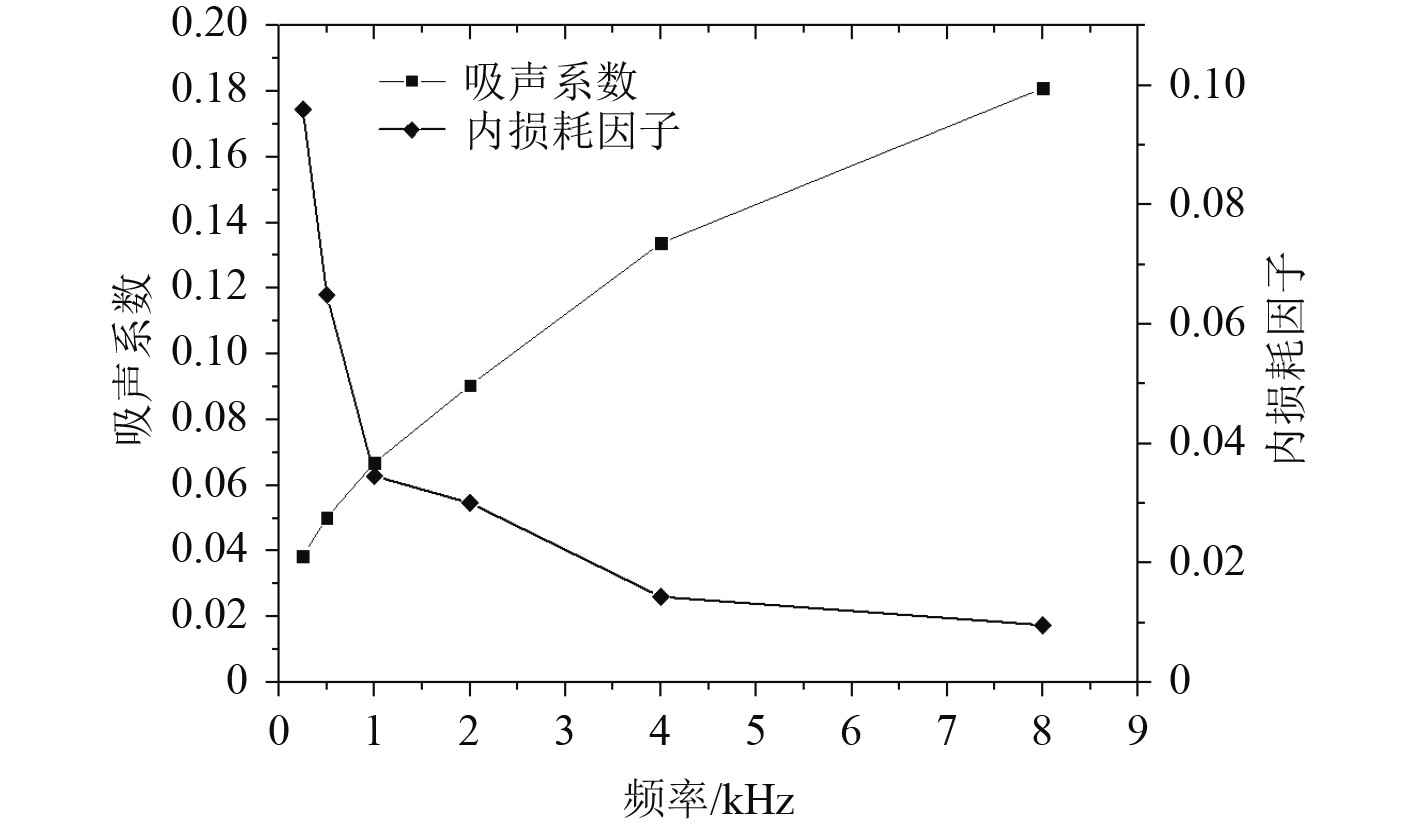
在确定噪声来源后需要将这些声源进行分类,并对这些噪声源影响舱室的位置、功率等进行确定。同时对舱室四周墙壁、地板等所采用材料的声学特性进行研究,不同材料、厚度等对噪声的能量传递均具有较大影响。在本文的分析中,船舶舱室四周墙壁均采用0.01 m厚度的钢板,密度为7.8 g/cm3,噪声传播速度为343 m/s。图3为舱室钢板吸声系数和内损耗因子随频率变化曲线,这些参数为后续预测船舶舱室噪声预测中不同子系统对噪声吸收的情况进行分析提供基础。
|
图 3 舱室钢板吸声系数和内损耗因子随频率变化曲线 Fig. 3 The variation curve of sound absorption coefficient and internal loss factor of cabin steel plate with frequency |
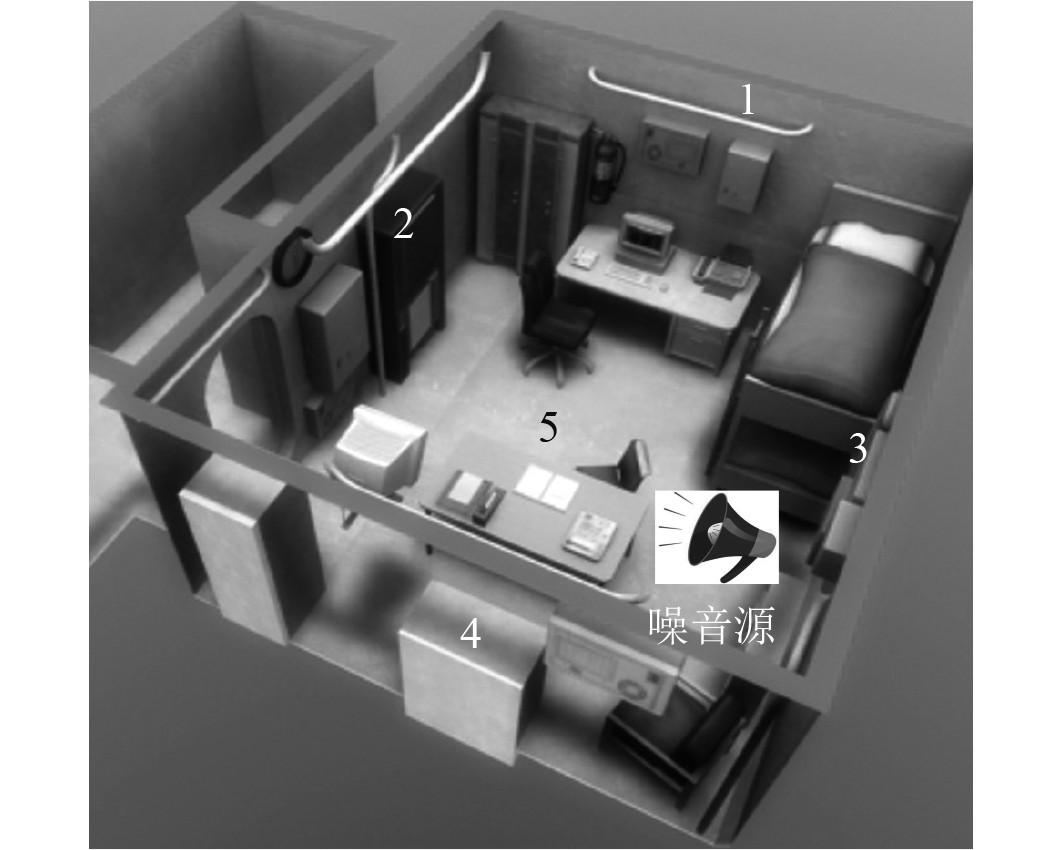
为了更好地对噪声在舱室内的能量传递进行研究和分析,需要对舱室进行划分,如图4所示。图中1~4为舱室的四面墙,5为地板,将舱室考虑为一个密闭系统,子系统之间会互相耦合,且会存在能量传递,不考虑天花板对噪声能量的传递和影响。
|
图 4 舱室子系统划分 Fig. 4 Cabin subsystem division |
VA One是一款专业的声学模拟软件,它提供了多种声学分析工具,包括统计能量分析(SEA)和有限元分析。使用VA One软件对船舶舱室噪声进行预测。首先确定船舶舱室的结构参数,包括尺寸、材料属性(密度、弹性模量、阻尼比等),本文船舶基本数据如表1所示。
|
|
表 1 舰船基本参数 Tab.1 Ship basic parameters |
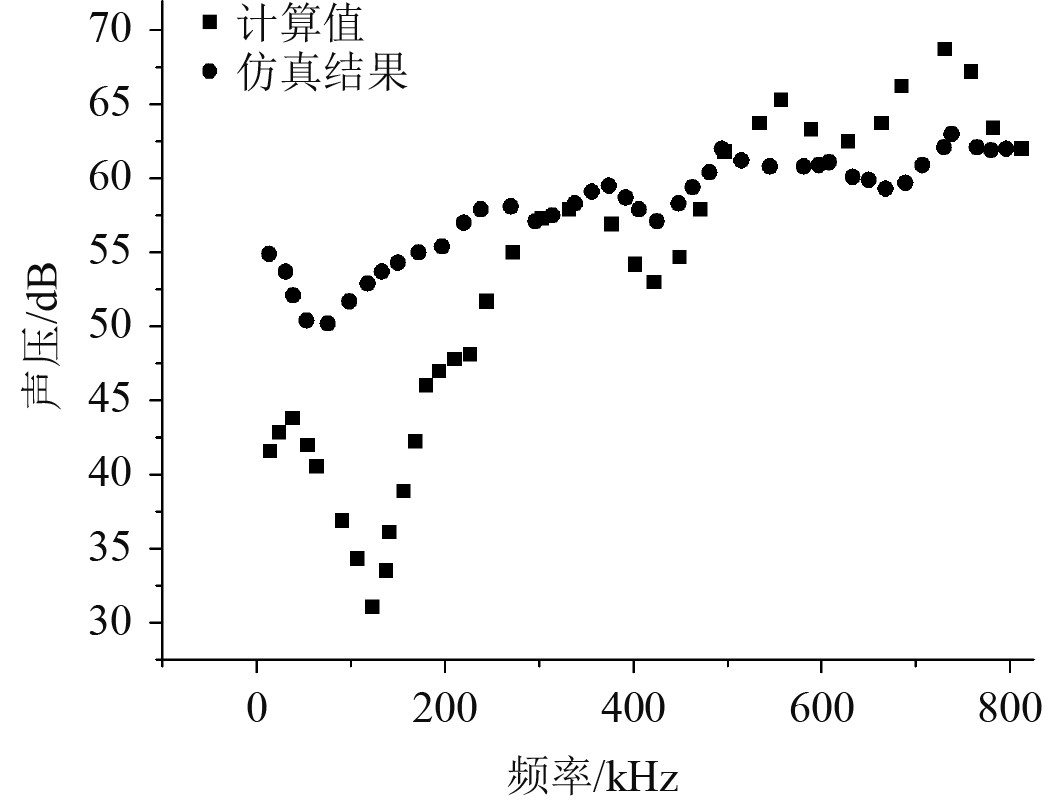
在模型中放置声源,并设置其特性,如声功率、频率等。确定舱室内的接收点,这些点用于测量和分析噪声水平。使用VA One软件对建立的模型进行仿真,并将其和计算值与实际值进行对比,得到的结果如图5所示。计算值在初始时小于仿真结果,这是由于在计算模型中没有考虑舱室中一些常用物件对声波吸收的可能,如床、桌椅等,随着频率的增加,计算结果和仿真结果开始趋近,说明使用SEA可以对船舶舱室噪声进行较为准确的预测。
|
图 5 仿真结果和计算结果对比 Fig. 5 Comparison of simulation results and calculation results |
对船舶舱室进行噪声预测可以为船舶结构设计提供有效辅助,同时也能够为船舶人员提供舒适的生活环境创造有利条件。本文使用统计能量方法对船舶舱室噪声预测进行研究,本文得到的结论主要包括:
1)研究了SEA能量传递模型,给出了梁系统、标准平板等的模态密度计算公式;
2)分析了船舶的噪声来源,并研究了不同噪声激励随频率变化情况,确定了舱室钢板吸声系数和内损耗因子随频率变化的规律;
3)对舱室子系统进行了划分,在此基础上进行了船舶舱室噪声预测仿真,结果表明使用SEA能够较为准确的对噪声进行预测。
| [1] |
张晓再, 杨红超. 基于RBF神经网络的船舶辐射噪声预测[J]. 价值工程, 2011, 30(14): 62-63. ZHANG Xiaozai, YANG Hongchao. Prediction of ship radiated noise based on rbf neural network[J]. Value Engineering, 2011, 30(14): 62-63. DOI:10.3969/j.issn.1006-4311.2011.14.039 |
| [2] |
敖庆章, 聂建栋, 吴晖. 统计能量分析法在船舶噪声预测中的应用综述[J]. 舰船电子工程, 2009, 29(4): 140-144. AO Qingzhang, NIE Jiandong, WU Hui. A review of the application of statistical energy analysis in ship noise prediction[J]. Ship Electronic Engineering, 2009, 29(4): 140-144. DOI:10.3969/j.issn.1627-9730.2009.04.041 |
| [3] |
刘成才. 非线性回归预测技术在船舶上层建筑振动噪声预报中的应用[J]. 舰船科学技术, 2023, 45(22): 210-213. LIU Chengcai. Application of nonlinear regression prediction technology in the forecast of vibration and noise of ship's superstructure[J]. Ship Science and Technology, 2023, 45(22): 210-213. |
| [4] |
李婷婷. 船舶舱室内部噪声精细化预报研究[D]. 大连: 大连理工大学, 2019.
|
| [5] |
樊红, 丁许聪, 秦欢. 船舶机舱集控室声能量分析与降噪设计[J]. 噪声与振动控制, 2018, 38(3): 110-114. FAN Hong, DING Xucong, QIN Huan. Acoustic energy analysis and noise reduction design of ship engine control room[J]. Noise and Vibration Control, 2018, 38(3): 110-114. DOI:10.3969/j.issn.1006-1355.2018.03.020 |
| [6] |
王云龙. 船舶舱室全频段噪声预测与控制技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
 2024, Vol. 46
2024, Vol. 46
