0 引　言

在海洋运输、海洋探索以及海上军事行动等领域，船舶的航迹精确性和安全性至关重要。然而，由于海洋环境的复杂性，如海洋流、风浪、潮汐等自然因素，以及船舶自身的传感器误差、执行机构误差等人为因素，船舶在航行过程中难以保持预设的航迹^[1]。因此，对船舶航迹进行自适应修正成为了海洋工程领域的一个重要研究方向。

王海等^[2]提出了一种融合航位推算、运动状态识别以及修正点信息的低成本、高精度车辆定位方法，旨在解决仓库内固定线路货运车辆在无GPS环境下使用低精度惯性传感器时的定位精度问题。然而，由于传感器误差、车轮打滑或车辆非直线运动等因素，航位推算算法会产生误差，并且这些误差会随时间累积，导致航迹修正效果降低。甄绪等^[3]提出了一种基于改进的模糊C均值和信息熵修正的航迹融合算法，通过交互式多模型滤波修正聚类数据质量，并利用信息熵和隶属度选择并融合局部航迹，以在局部航迹信息质量不均衡条件下提高系统的跟踪性能。使用模糊C均值算法对局部航迹进行聚类过程中参数设置不合理会导致局部航迹被错误地分配到不同的聚类中，从而影响航迹修正的效果。张天舒等^[4]提出一种基于对等结构的多传感器目标数据关联算法，通过时间精同步和高低精度节点间的误差修正模型，有效修正低精度节点的系统误差，并利用灰关联法实现稳定且高精度的航迹关联。时间精同步是算法的基础，时间差异可能导致数据错位，使得修正和关联失去意义。

通过三维重建技术，可以获取船舶周围环境的精确三维模型，包括地形、障碍物、海岸线等信息。这些信息对于船舶航迹修正具有重要价值^[5]。在此基础上，剔除三维重建中的外点，可以减少噪声和异常值对航迹修正的影响，提高修正结果的准确性和可靠性。因此，提出基于三维重建外点剔除的船舶航迹自适应修正，提升船舶目标航行的安全性。

1 船舶航迹自适应修正 1.1 船舶三维点云数据滤波

在复杂场景下，船舶的三维点云数据通常包含大量的噪声，严重影响对船舶航迹的准确分析和修正效果。为了保证船舶三维点云数据的准确性，采用均值限差法对船舶三维点云数据进行滤波。均值限差法在去除噪声的同时，能够较好地保留点云数据的细节和特征，有助于更直观地分析和理解船舶的航迹。

围绕船舶中的随机一点设定任意窗口，在二维平面上投影窗口中的点，确定中心点外的点云高程均值^[6]，在此基础上，获取中心点同高程均值间的差值，对比该差值与阈值实现点云滤波。通过下式描述窗口尺寸：

$ W = \left( {{W_{\min }}} \right) \times {2^{m - 1}}。$

(1)

式中：$ W $和$ {W_{\min }} $分别为窗口尺寸与其下限值；$ m $为滤波迭代次数。

以$ {D_s} $和$ {D_x} $分别表示中心点高程均值以上点和以下点的差值，其对应阈值可以表示为：

$ {t_h} = \frac{{{t_{h,c}}\left( {{D_s} - {D_x}} \right)}}{W} 。$

(2)

式中：$ {t_{h,c}} $为初始阈值。此时，通过调整$ {D_s} - {D_x} $的差值状态，即令$ {D_s} - {D_x} > 1 $、$ {D_s} - {D_x} < 1 $、$ {D_s} - {D_x} = 1 $，使得$ {t_h} = 1 $，即点云分布相对均匀，实现船舶三维点云数据滤波。

1.2 船舶三维重建剔除

基于均值限差法的点云滤波算法可以有效地去除噪声，但它独立于点云的实际形状和分布，可能会把一些表面特征复杂的物体表面上的点过滤掉，这就导致了信息丢失和点云不完整的问题。八叉树自适应网格可以根据点云数据的密度和分布特性，自动调整网格的大小和形状，从而更准确地拟合船舶的表面形状。因此，在船舶航迹自适应修正过程中，通过实时获取和处理船舶的三维点云数据，结合八叉树自适应网格的三维重建方法，可以实现对船舶航迹的实时监测和修正。当船舶航迹偏离预设航线时，系统可以自动调整修正策略，确保船舶能够按照正确的航线航行。

针对船舶曲面$ Q $，以船舶外轮廓为起始，将$ Q $划分成8个立方体空间，不同空间大小一致，以$ O $和$ {Q_O} $分别表示八叉树节点和八叉树细分立方体约束的$ Q $的局部表面。若$ {Q_O} $不为空，则可通过简单的表面描述$ {Q_O} $，因此可通过平面构建八叉树。基于式（3）能够获取同$ {Q_O} $最为相似的最优平面P：

$ P = {t_h}{\left( {n \cdot p + y} \right)^2} 。$

(3)

式中，$ n $和$ y $分别为船舶平面的三维法向量和偏移量。

以确保令法线方向和基础平面法线方向相同为目的，判断$ n $同$ {Q_O} $的平均法线间角度是否小于$ {90^ \circ } $，若大于$ {90^ \circ } $需将$ n $同$ y $同时与−1相乘。

若受O所在立方体区域约束的$ P $平面补丁和船舶局部形状近似补丁的质量分别为$ {P_O} $和$ {\beta _O} $，则依照豪斯多夫距离理论能够得到：

$ {\beta _O} = di{s_H}\left( {{P_O},{\beta _O}} \right)。$

(4)

式中，$ di{s_H}\left( {} \right) $表示2个平面的豪斯多夫距离。通过$ di{s_H}\left( {} \right) $能够表示2组船舶点云集合间的一致度。

针对全部非最大深度级别的子节点O，若$ {Q_O} $为非空同时$ {\beta _O} $与设定阈值$ \beta ' $相比较大，即可对O实施细分，逐步构建出整个船舶的曲面模型，完成三维重建。

但重建出的船舶三维模型中仍然包含一些冗余数据和噪声点。因此，对八叉树自适应网格节点实施多点拾取，通过定义一个或多个多边形区域，确定哪些点云数据点位于这些区域内，从而区分出属于船舶曲面的内点和不属于的外点^{[7 − 8]}。不在拾取多边形内的点被定义为外点并被剔除，这样可以进一步减少数据冗余和噪声，提高模型的精度和准确性。

船舶三维重建外点剔除的具体步骤如下：

步骤1　在屏幕上投影八叉树自适应网格节点的包围盒，生成凸多边形$ {P_i} $。判断凸多边形$ {P_i} $与用户确定的矩形包围盒$ M $是否有交互（即是否重叠或相交）。

步骤2　如果凸多边形$ {P_i} $完全在矩形包围盒M外部，那么该八叉树自适应网格节点中的船舶图像三维点云均被认为是外点，直接剔除。如果凸多边形$ {P_i} $与矩形包围盒$ M $有交互（即部分重叠或完全包含），则将该八叉树自适应网格节点中的船舶图像三维点云暂存在一个查找集合中。

步骤3　对于查找集合中的每个三维点云，判断该三维点是否处于矩形包围盒$ M $内。如果不在$ M $内，说明该点为外点，直接剔除。

步骤4　剔除所有被判定为外点的三维点云后^{[9 − 10]}，更新船舶的三维模型。

步骤5　重复上述步骤，直到所有八叉树自适应网格节点中的点云都被处理完毕。

步骤6　结束剔除流程，得到优化后的船舶三维模型。

综上，经过外点剔除的三维模型，减少了由于噪声和冗余数据导致的误差，使得船舶位置、姿态、速度等关键参数的计算更加准确。这有助于船舶更精确地执行航迹修正，确保按照预定的航线航行。

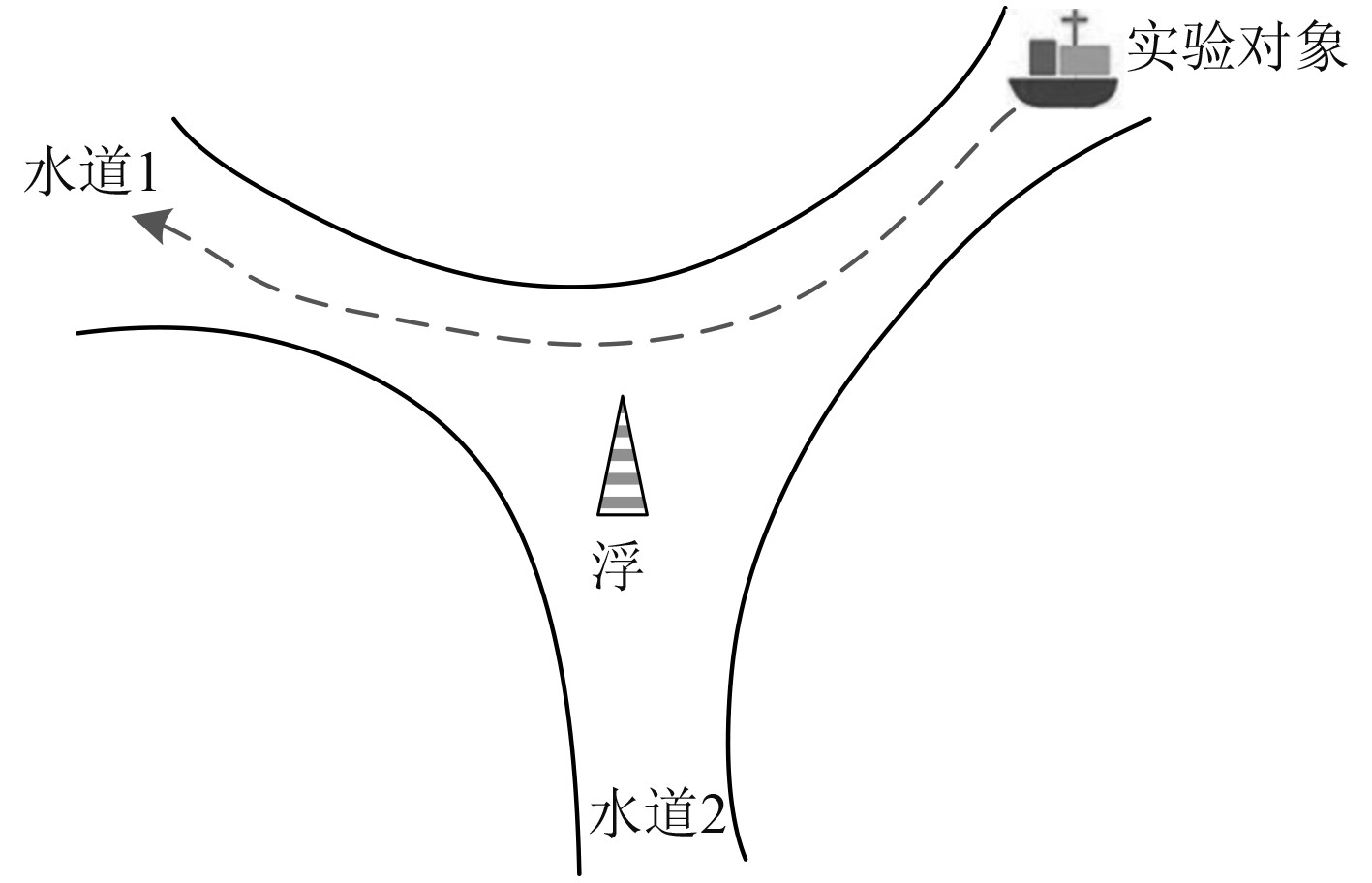
2 实验与分析 2.1 实验设置

为验证基于三维重建外点剔除的船舶航迹自适应修正方法在实际外点剔除中的应用效果，以海域中某型号船舶的航行轨迹为实验对象，实验对象的预设航迹路线如图1所示。

通过IBEO激光雷达获取实验对象的三维点云信息生成实验集，表1为IBEO激光雷达的相关技术参数。

在实验集利用本文技术对所选点云数据实施滤波处理。实验过程中的相关参数设置如表2所示。

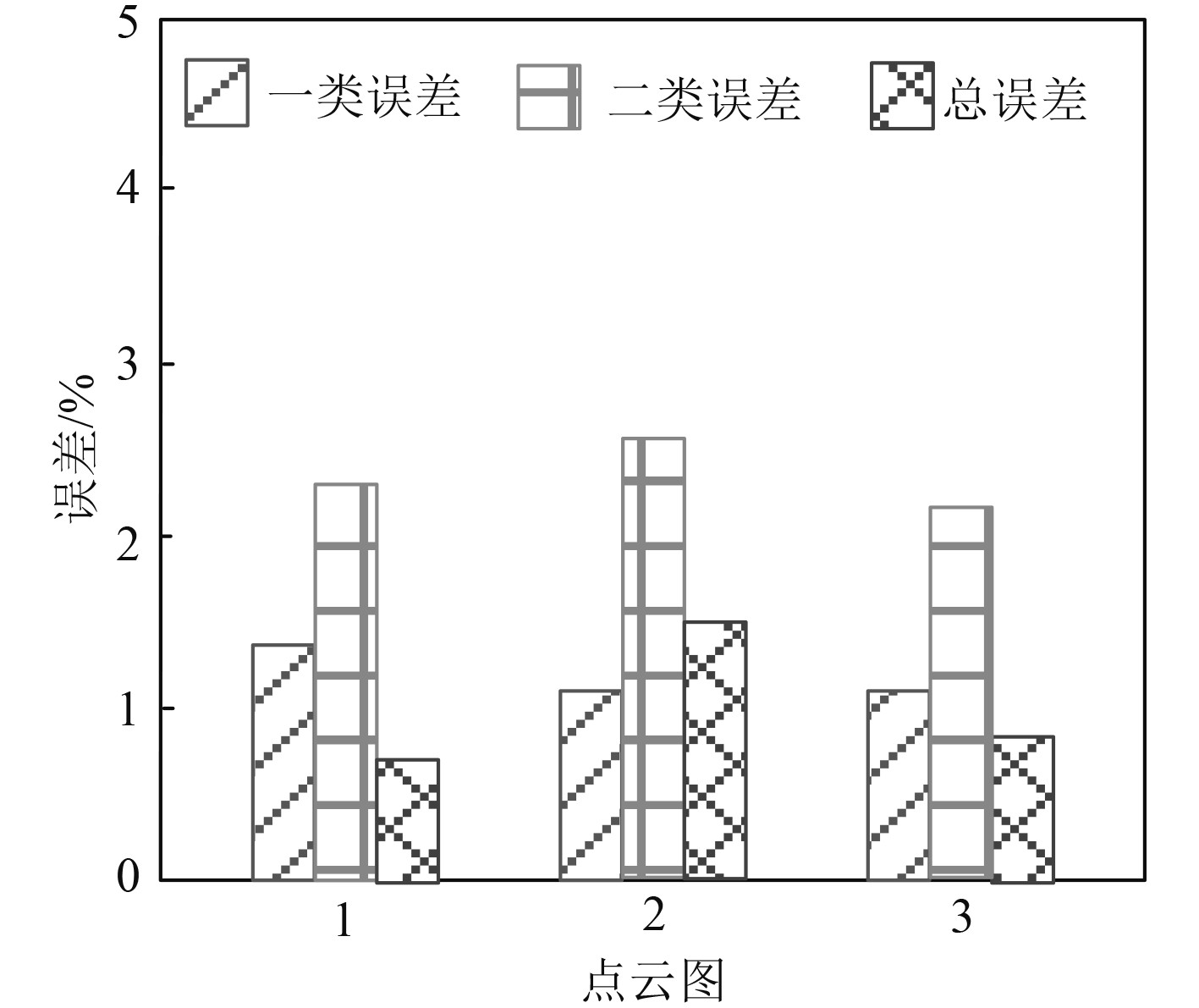
在此基础上，选取相关领域普遍认同的滤波误差定量评价标准（见表3）评价本文技术滤波性能，所得结果如图2所示。

可知，采用本文技术对实验对象点云点实施滤波时，二类误差高于一类误差，但均控制在3%以内，总误差则控制在1.5%以内，由此说明本文技术针对点云图进行滤波时具有较高的滤波性能。

2.2 结果与分析

采用本文技术对实验对象进行图像三维重建中的外点剔除，对比采用本文技术前后，实验对象的三维重建结果，结果如图3所示。

分析可知，采用本文技术对实验对象图像三维重建过程中的点云进行外点剔除后，实验对象的三维重建图像质量更高，能够有效抑制复杂海况条件下海面杂波等因素造成的外点影响。

在此基础上，对船舶航迹自适应修正效果进行测试，得到的结果如图4所示。可以看出，实验船在航行过程中遇到占用预定航行轨迹的船时，可以自适应地重新规划合理航线，且规划的航线与原定航线一致性较高。表明所提方法可以有效修正船舶航迹，保证船舶的运行安全。

3 结　语

为了保证船舶的航行安全，本文基于三维重建外点剔除完成船舶航迹自适应修正。实验结果表明本文技术可以根据船舶的实时航行状态和环境变化，动态调整航迹规划，实现船舶的精确控制和高效航行。