0 引　言

目标跟踪技术主要是根据假定的目标运动模型，结合获得不同时刻的离散量测信息，采用某种目标跟踪算法，从而估计目标的连续运动状态。纯方位目标跟踪是指结合不同时刻观测到的方位信息，采用算法并估计出目标的位置、速度等参数的过程^[1]，由于纯方位目标跟踪具有隐蔽性好的特点，其在目标跟踪领域内具有重要的研究价值，一直是学术和工程领域内的研究热点和难点^[2]。由于方位信息是目标运动参数的不完全描述，机动目标可观测的必要非充分条件是观测站平台运动或至少2台静态观测站同时观测^[3]。

在目标跟踪领域中最为经典、应用广泛的算法是卡尔曼滤波算法^[4]（Kalman Filter,KF），适用于线性、高斯系统。为解决实际应用的非线性与非高斯系统的目标跟踪问题，出现了经典的改进算法，如扩展卡尔曼滤波算法（Extended Kalman Filter,EKF）、无迹卡尔曼滤波算法（Unscented Kalman Filter,UKF）等。另一类解决非线性滤波问题的方法是序列蒙特卡罗方法，即粒子滤波算法（Particle Filter,PF），该算法对噪声的高斯性依赖不强，常用于纯方位水下目标跟踪^[5]。但粒子滤波算法运算量大，且容易产生粒子退化和多样性匮乏的问题，因此有学者提出扩展粒子滤波算法（Extended Kalman Particle Filter,EPF），即使用EKF算法生成粒子滤波的重要性函数，从而提升算法性能。近年来对粒子滤波在目标跟踪中的应用研究中，多集中在对算法的改进^{[6 − 9]}，李晓花等^[10]对比分析了扩展卡尔曼滤波EKF算法和PF算法的估计精度，张程振等^[11]对比分析了PF、EPF算法的性能，但不是纯方位目标跟踪系统，并且主要研究不同噪声对算法性能的影响。本文主要研究静止双观测站的水下纯方位目标跟踪问题，利用EPF算法和PF算法进行双观测站纯方位水下目标运动分析，并结合UKF、EKF算法进行对比，观察不同条件下的跟踪效果，同时分析了目标运动速度、粒子数目对跟踪精度的影响。

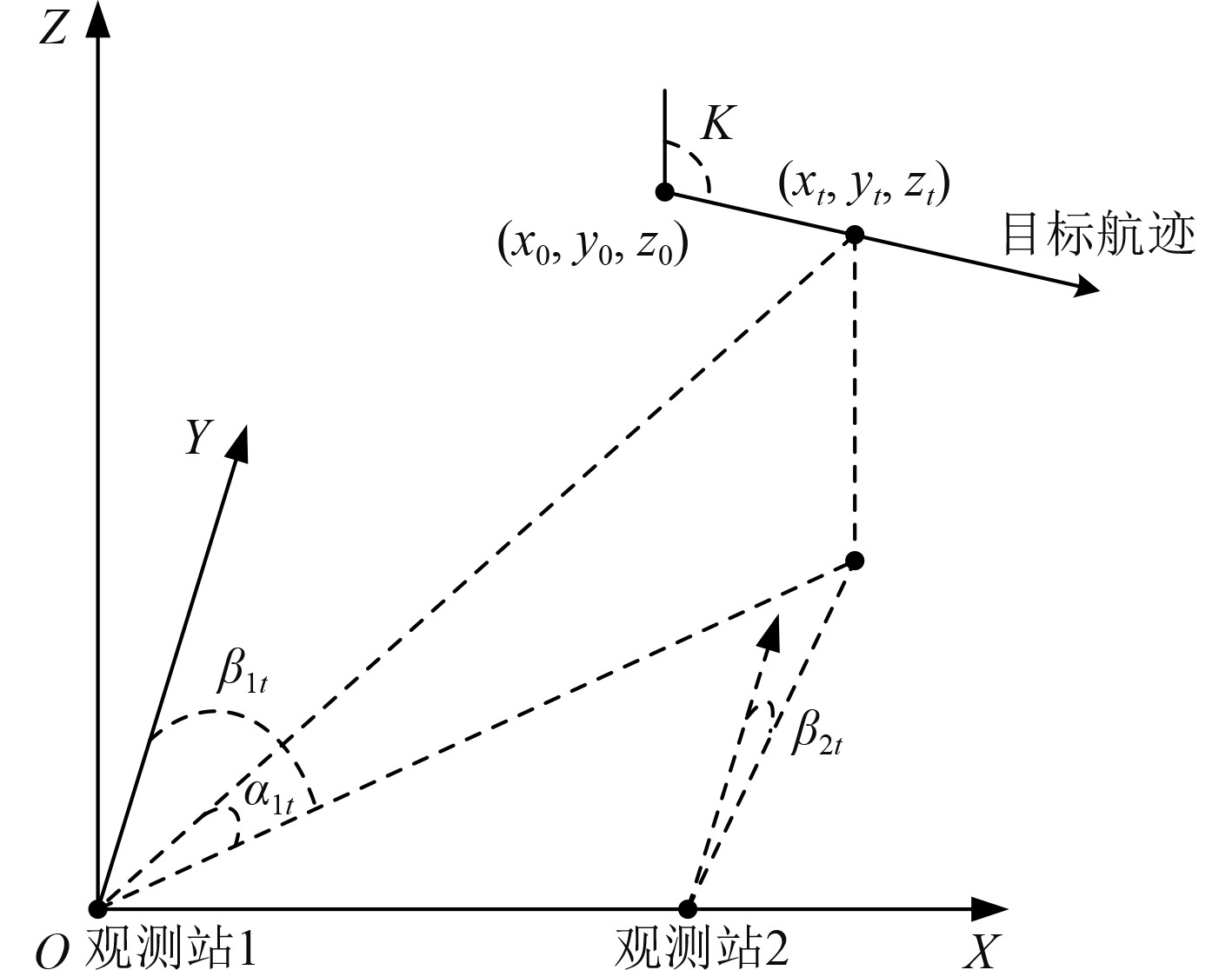
1 三维双观测站纯方位跟踪系统模型 1.1 目标运动模型和状态方程

本文考虑静止双观测站的三维纯方位目标跟踪问题。双观测站与机动目标在三维坐标系下的几何关系如图1所示，设观测站1的位置在原点，则观测站1的坐标$ ({x_1},{y_1},{z_1}) = (0,0,0) $，以观测站2与观测站1的连线作$ X $轴，则观测站2的坐标为$ ({x_2},{y_2},{z_2}) = ({x_2},0,0) $。假设初始时刻目标所在的位置为$ ({x_0},{y_0},{z_0}) $，目标以恒定的速度$ ({v_x},{v_y},{v_z}) $作直线运动，$ K $为目标航向角。设$ t $时刻目标所在的位置为$ ({x_t},{y_t},{z_t}) $，观测站1在$ t $时刻对目标观测的方位角为$ {\beta _{1t}} $、观测站2在$ t $时刻对目标观测的方位角$ {\beta _{2t}} $，观测站1在$ t $时刻对目标观测的俯仰角为$ {\alpha _{1t}} $。

设目标在$ t $时刻的状态向量为$ {X}(t) = {\left[ {\begin{array}{l} {{x_t}}\;{{y_t}}\;{{z_t}}\;{{v_x}}\;{{v_y}}\;{{v_z}} \end{array}} \right]^{\text{T}}} $，$ T $为采样间隔，目标在$ t + T $时刻的状态向量为$ {X}{\text{(}}t + T{\text{)}} = {\left[ {\begin{array}{*{20}{c}} {{x_{t + T}}}\;{{y_{t + T}}}\;{{z_{t + T}}}\;{{v_x}}\;{{v_y}}\;{{v_z}} \end{array}} \right]^{\text{T}}} $。由于目标做匀速直线运动，则系统的状态方程可表示为：

$ X{\text{(}}t + T{\text{)}} = {\boldsymbol{F}}X{\text{(}}t{\text{)}} + Gw{\text{(}}t{\text{)}}。$

(1)

其中，$ {\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&T&0&0 \\ 0&1&0&0&T&0 \\ 0&0&1&0&0&T \\ 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \end{array}} \right] $是目标的系统状态转移矩阵，表示将目标当前时刻的状态映射到目标下一时刻的状态；$ {\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {0.5{T^2}}&0&0 \\ 0&{0.5{T^2}}&0 \\ 0&0&{0.5{T^2}} \\ T&0&0 \\ 0&T&0 \\ 0&0&T \end{array}} \right] $为噪声转移矩阵，表示在模型中引入加速度作为随机扰动；$ w(t) $为系统噪声，假设其为0均值的高斯白噪声。

1.2 量测方程

观测站传感器获得的量测信息有观测站1在$ t $时刻对目标观测的俯仰角$ {\alpha _{1t}} $、观测站1在$ t $时刻对目标观测的方位角$ {\beta _{1t}} $、观测站2在$ t $时刻对目标观测的方位角$ {\beta _{2t}} $。

考虑测量误差，则$ t $时刻三维双观测站的量测方程可表示为：

$ \begin{aligned}[b] Z(t) = \left[ {\begin{array}{*{20}{c}} {{\alpha _{1t}}} \\ {{\beta _{1t}}} \\ {{\beta _{2t}}} \end{array}} \right] + &V(t) = \left[ {\begin{array}{*{20}{c}} {\arctan \displaystyle\frac{{{z_t} - {z_1}}}{{\sqrt {{{({x_t} - {x_1})}^2} + {{({y_t} - {y_1})}^2}} }}} \\ {\arctan \displaystyle\frac{{{x_t} - {x_1}}}{{{y_t} - {y_1}}}} \\ {\arctan \displaystyle\frac{{{x_t} - {x_2}}}{{{y_t} - {y_2}}}} \end{array}} \right] + \\ &V(t) = \left[ {\begin{array}{*{20}{c}} {\arctan \displaystyle\frac{{{z_t}}}{{\sqrt {{x_t}^2 + {y_t}^2} }}} \\ {\arctan \displaystyle\frac{{{x_t}}}{{{y_t}}}} \\ {\arctan \displaystyle\frac{{{x_t} - {x_2}}}{{{y_t}}}} \end{array}} \right] + V(t) 。\end{aligned}$

(2)

式中：$ V(t) $为观测误差噪声，假设其为0均值、方差为R的高斯白噪声。

2 粒子滤波算法（PF）与扩展粒子滤波算法（EPF） 2.1 粒子滤波算法（PF）

粒子滤波是在随机采样的基础上建立起来的一种滤波算法，主要通过采用蒙特卡罗随机抽样的方式实现，适用于非线性非高斯系统。其具体实现过程为：首先从状态空间中抽取一系列随机抽样，然后估计得到系统的后验概率分布，从而实现贝叶斯滤波。

粒子滤波算法采用序贯重要性采样（SIS），使用先验概率密度函数作为重要性密度函数，在序贯重要性采样中加入重采样步骤。用$ {f_{k - 1}}( \cdot ) $表示系统的状态转移函数，$ {x_k} \in {R^n} $表示系统的状态向量，$ {w_k} \in {R^p} $表示系统的过程噪声，$ {h_k}( \cdot ) $表示系统的量测函数，$ {z_k} \in {R^m} $表示系统的量测向量，$ {v_k} \in {R^q} $表示系统的量测噪声，且与系统的过程噪声互不相关，对于该系统状态空间，其数学模型可表示为：

$ \left\{ {\begin{array}{*{20}{l}} {{x_k} = f({x_{k - 1}},{w_{k - 1}})}，\\ {{z_k} = h({x_k},{v_k})} 。\end{array}} \right. $

(3)

粒子滤波算法的实现流程如下：

步骤1　初始化粒子和权值。$ k = 0 $时，$ i = 1, \cdots ,N $，$ N $为粒子数目。首先进行采样，产生$ N $个服从先验概率$ p({x_0}) $分布的样本$ x_0^i = p({x_0}) $，然后令所有的样本点权值$ w_0^i = {1 \mathord{\left/ {\vphantom {1 N}} \right. } N} $。

步骤2　重要性采样。令$ x_k^i\ \sim p({x_k}|x_{k - 1}^i) $。

步骤3　计算粒子重要性权值并归一化重要性权值。

$ \left\{ \begin{array}{l} \displaystyle {w}_{k}^{i}={w}_{k-1}^{i}\frac{p\left({z}_{k}\mid {x}_{k}^{i}\right)p\left({x}_{k}^{i}\mid {x}_{k-l}^{i}\right)}{q\left({x}_{k}^{i}\mid {x}_{k-l}^{i},{z}_{k}\right)}，\\ {\tilde{w}}_{k}^{i}={w}_{k}^{i}/\displaystyle{\sum_{i=1}^{N}}{w}_{k}^{i}。\end{array} \right.$

(4)

步骤4　重采样。若从$ x_k^i $中根据重要性权值重新采样得到新的$ N $个粒子$ \tilde x_k^i $，并重新分配权值$ \tilde w_k^i = 1/N $。

步骤5　返回状态估计值。

$ {\hat{x}}_{k}=\sum _{i=1}^{N}{\tilde{w}}_{k}^{i}{x}_{k}^{i} 。$

(5)

在粒子滤波算法中，粒子退化是一种无法避免的现象。经过很多次循环后，除极少数粒子之外，其余大部分粒子的权重均小到可以忽略。粒子退化不仅占用了大量的计算资源，而且对状态估计的帮助不大。为此，有必要对粒子的退化问题开展研究。通过增加粒子数目$ N $可以最有效地减少退化现象，但是这样做会增加算法的运算量，导致滤波算法的运算速度降低，滤波器的实时性变差。为避免该现象的出现，常从2个方面对粒子滤波算法进行改进，一是改进重要性函数法，二是重采样法。改进重要性函数法的其中一种方法就是EPF算法。

2.2 扩展粒子滤波算法（EPF）

扩展粒子滤波算法EPF是结合扩展卡尔曼滤波EKF算法对粒子滤波进行改进的算法。EPF算法与PF算法的不同之处在于，PF算法的重要性概率密度函数是采用先验概率密度函数，而EPF的重要性概率密度函数则使用EKF算法来生成。EPF算法在状态预测阶段通过采用EKF算法来更新采样粒子，使其能够及时地将最新的量测信息融入到系统，从而使与量测值相关粒子的权重增大，在重釆样步骤后，与量测值相关粒子的数量大幅增加，同时未利用量测信息粒子的权重大幅减小，从而提高了整个算法的效率和精度。

扩展粒子滤波算法的实现流程如下：

步骤1　初始化粒子和权值。$ k = 0 $时，$ i = 1, \cdots ,N $，$ N $为粒子数目。首先进行采样，产生$ N $个服从先验概率$ p({x_0}) $分布的样本$ x_0^i = p({x_0}) $，然后令所有的样本点权值$ w_0^i = {1 \mathord{\left/ {\vphantom {1 N}} \right. } N} $。

步骤2　重要性采样。根据EKF滤波递推公式更新采样粒子，得到$ x_k^i $、$ P_k^i $。

状态一步预测值：

$ x_{k,k - 1}^i = f(x_{k - 1}^i)，$

(6)

一步预测误差方差阵：

$ P_{k,k - 1}^i = F_k^iP_{k - 1}^iF_k^{{\text{T}}i} + G_k^iQ_{k - 1}^iG_k^{{\text{T}}i}，$

(7)

滤波增益：

$ K_k^i = P_{k,k - 1}^iH_k^{{\text{T}}i}{(H_k^iP_{k,k - 1}^iH_k^{{\text{T}}i} + {R_k})^{ - 1}}，$

(8)

状态估计值：

$ x_k^i = x_{k,k - 1}^i + K_k^i(Z_k^i - h(x_{k,k - 1}^i))，$

(9)

估计误差方差阵：

$ P_k^i = (I - K_k^iH_k^i)P_{_{k,k - 1}}^i 。$

(10)

步骤3　计算粒子重要性权值并归一化重要性权值。

$ \left\{\begin{array}{l} \displaystyle{w}_{k}^{i}={w}_{k-1}^{i}\frac{p\left({z}_{k}\mid {x}_{k}^{i}\right)p\left({x}_{k}^{i}\mid {x}_{k-l}^{i}\right)}{q\left({x}_{k}^{i}\mid {x}_{k-l}^{i},{z}_{k}\right)}，\\ {\tilde{w}}_{k}^{i}={w}_{k}^{i}/\displaystyle{\sum _{i=1}^{N}}{w}_{k}^{i}。\end{array} \right.$

(11)

步骤4　重采样。若从$ x_k^i $中根据重要性权值重新采样得到新的$ N $个粒子$ \tilde x_k^i $，并重新分配权值$ \tilde w_k^i = 1/N $。

步骤5　返回状态估计值。

$ \left\{\begin{array}{l} \displaystyle{\hat{x}}_{k}=\sum _{i=1}^{N}{\tilde{w}}_{k}^{i}{x}_{k}^{i}，\\ {P}_{k}=\displaystyle{\sum_{i=1}^{N}}{\tilde{w}}_{k}^{i}\left({\tilde{x}}_{k}^{i}-{\hat{x}}_{k}\right){\left({\tilde{x}}_{k}^{i}-{\hat{x}}_{k}\right)}^{\text{T}}。\end{array}\right. $

(12)

EPF算法利用EKF产生系统的重要性密度函数的优势在于，将最新的观测信息实时融入系统，保证先验分布向着高似然区域移动，增大了与量测值相关的粒子的权值，从而大幅增加有效粒子数，减少无效粒子数，从而提高了算法整体的效率和精度。

3 仿真结果及分析

本节使用Matlab仿真比较PF和EPF滤波算法的机动目标跟踪性能，使用均方根误差RMSE反映不同条件下2种算法的跟踪误差。考虑非线性非高斯系统模型，过程噪声和观测噪声都为零均值高斯噪声。本实验的仿真条件为：最大采样次数为150次，采样间隔为1 s，进行50次蒙特卡洛实验，观测站1的位置为原点，观测站2的位置坐标为（1000，0，0） ，初始时刻，观测站1与目标距离为2375 m，观测站1对目标观测的方位角为$ 39^\circ $，俯仰角为$ 57^\circ $，方位角、俯仰角观测误差方差均为$ 1^\circ $，目标以航向角$ K = 150^\circ $做匀速直线运动，对目标速度分别为20、30、50 kn的情况下进行仿真，并结合经典的卡尔曼滤波算法中的EKF和UKF算法进行对比。

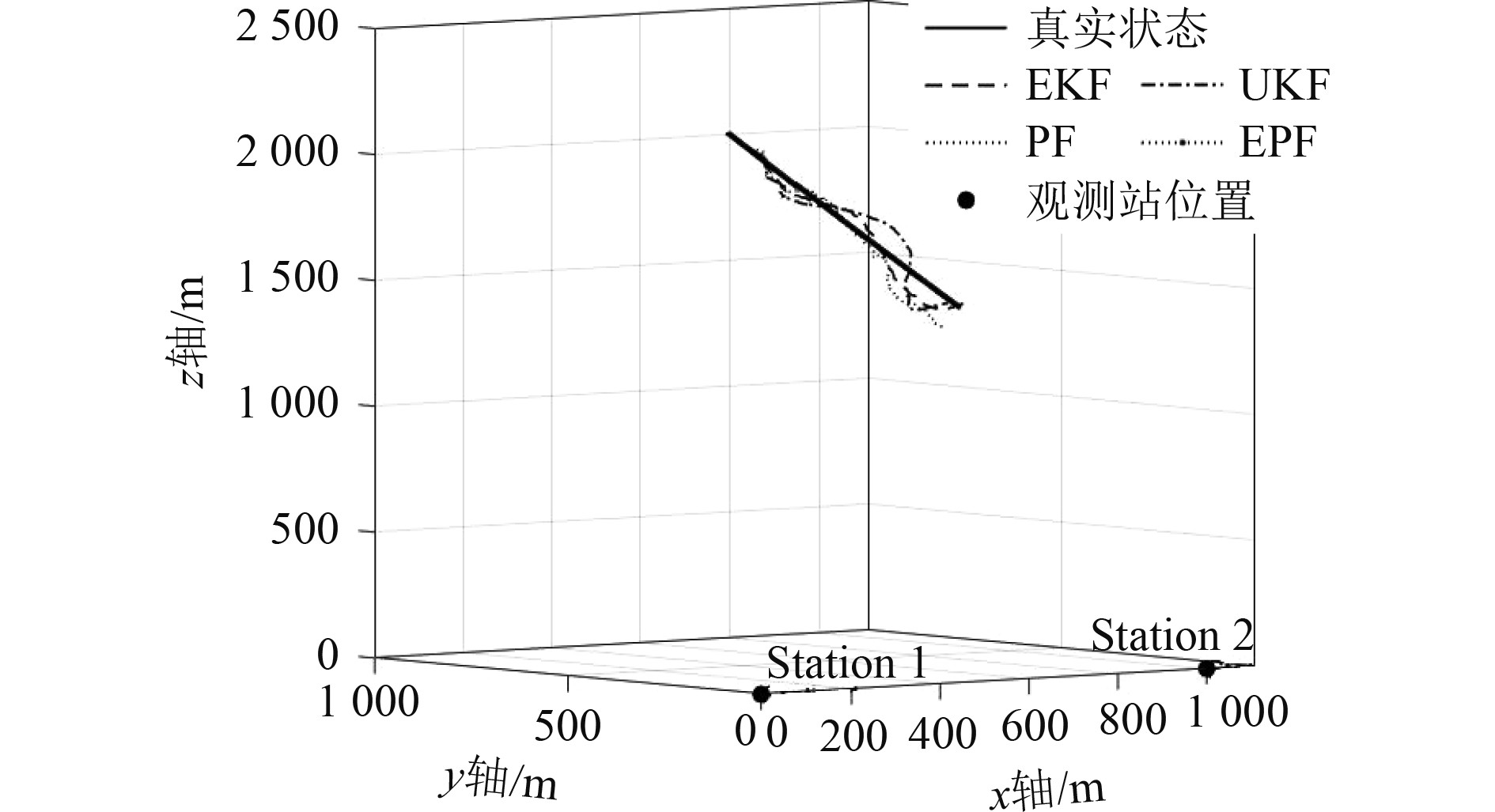
实验1　目标速度为20 kn时，选取粒子数目为200对PF和EPF粒子滤波算法进行仿真，真实轨迹和跟踪效果如图2所示，相比于其他算法，EPF算法的跟踪效果最好。

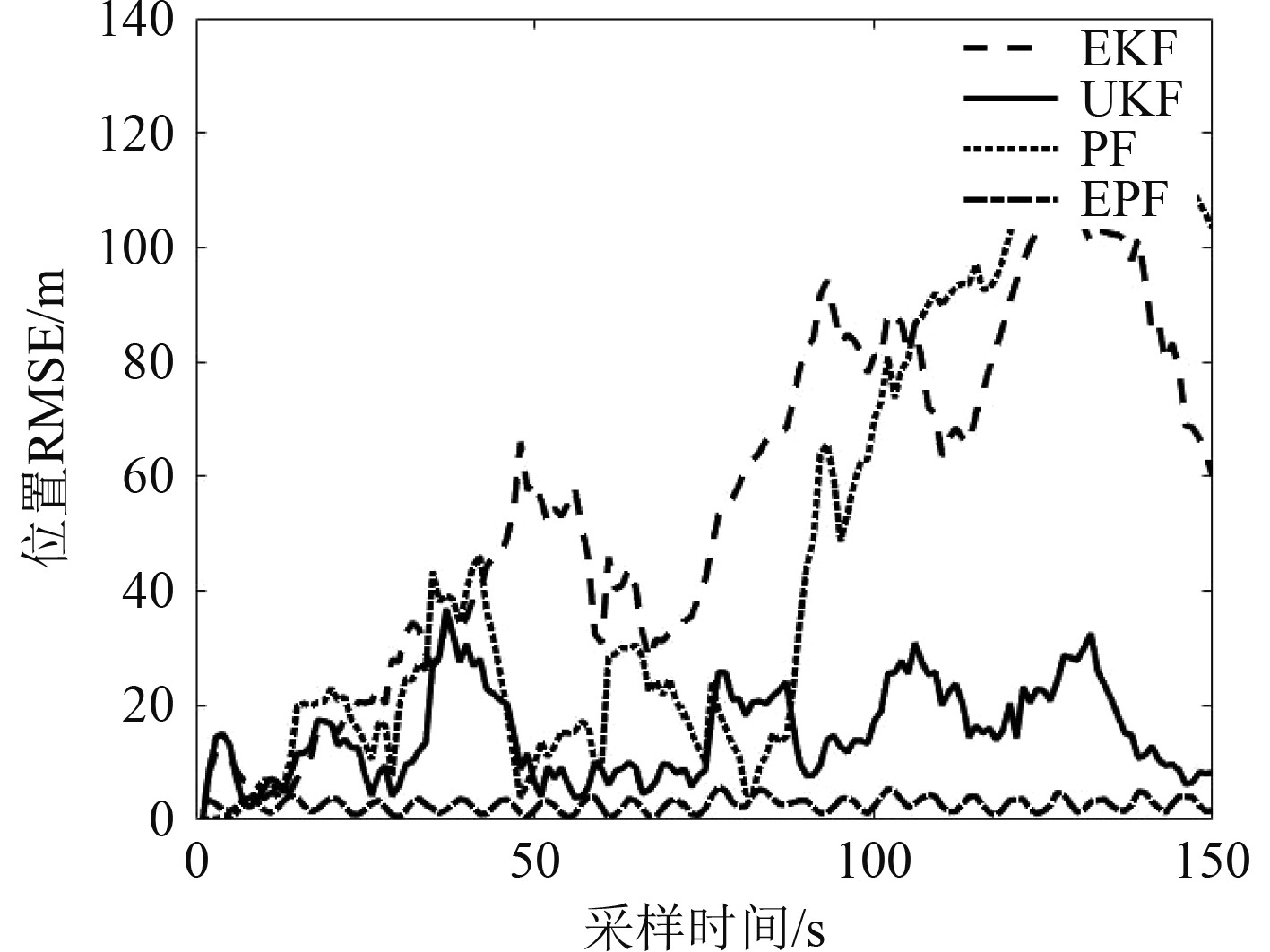
图3为4种算法的位置均方根误差图，PF和UKF的位置均方根误差一直维持在较小的水平，EPF的位置均方根误差最小，具有收敛快、精度高的特点。EKF算法和PF算法前期位置均方根误差较小，随着时间的增大，误差增大，后期难以准确跟踪目标。

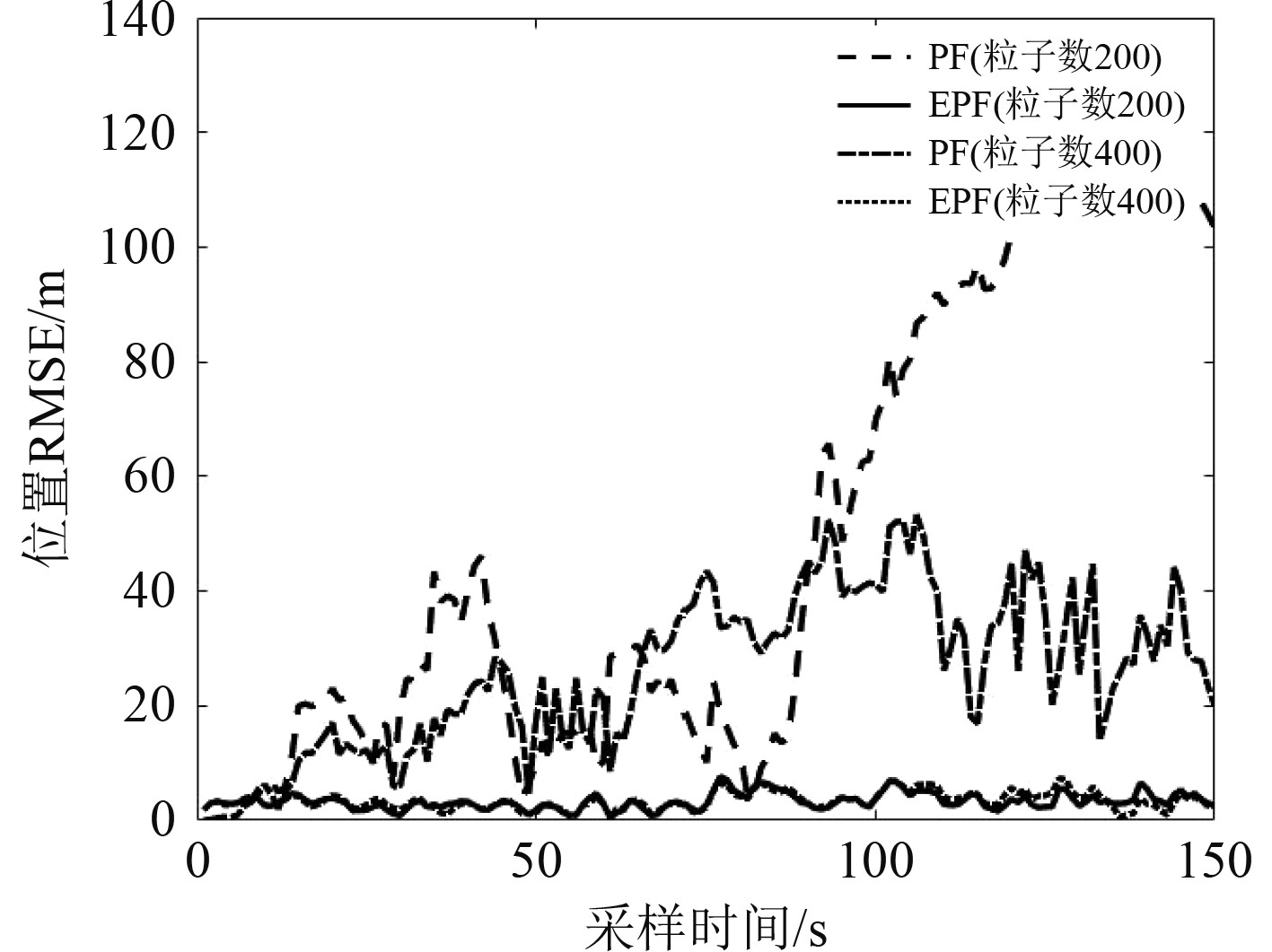
图4为粒子数为400和200时2种算法的位置均方根误差。PF算法在粒子数为200时，误差随着采样时间的增加而增大，当增加粒子数至400时，有效地避免粒子退化现象，PF算法能较好地跟踪目标。但相比于EPF算法，PF算法的误差更大，精度更低。EPF算法在粒子数为200和400时均方根误差都很小，都能表现出较好的跟踪效果。对于PF算法，需要增加粒子数目从而改善其性能，而EPF算法不依赖于粒子数目，无需太多粒子数就能表现出较好的跟踪效果。

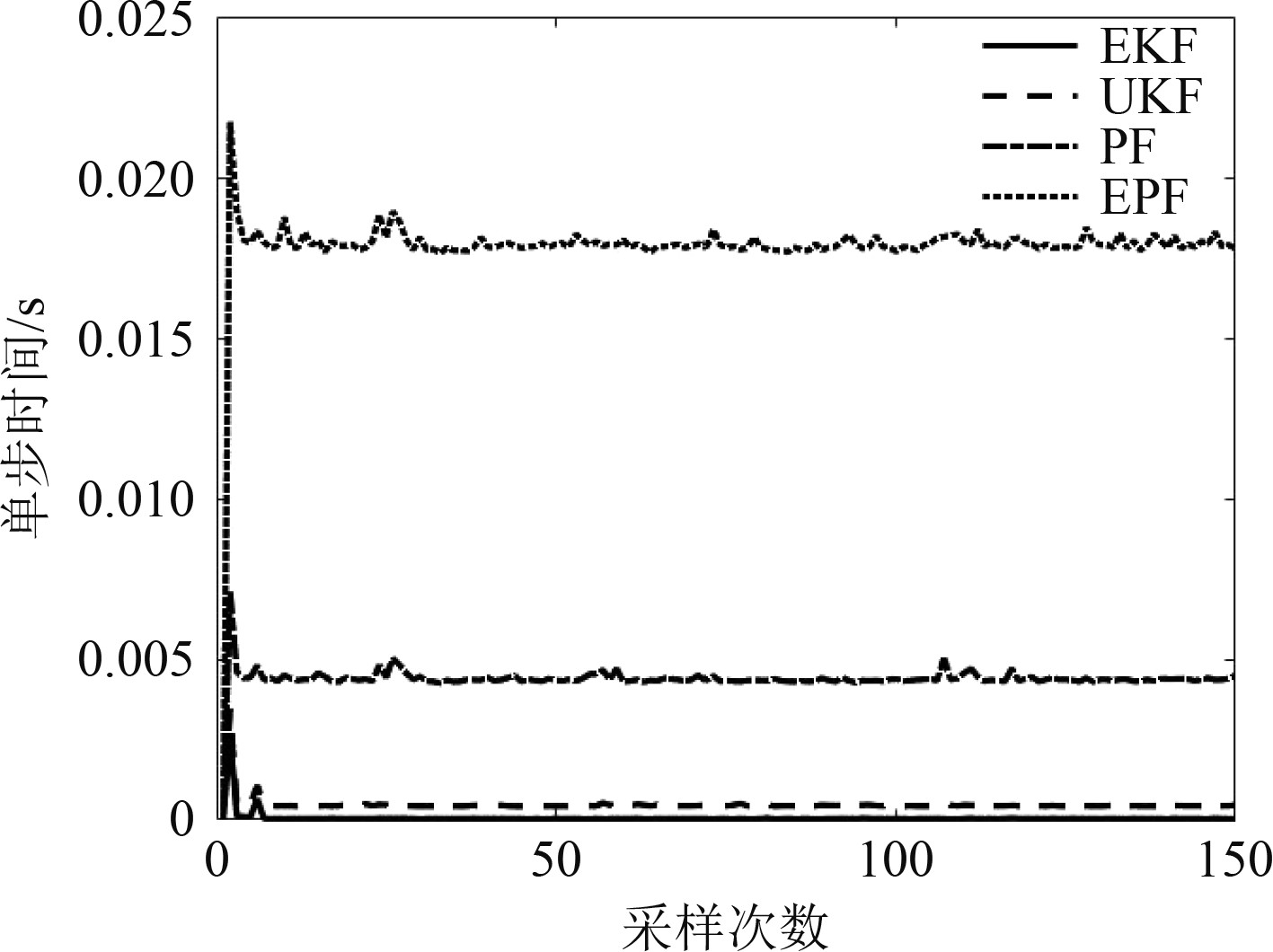
图5为粒子数为200时4种算法的单步时长，相比于EKF和UKF，PF进行一次滤波的时间较长，EPF进行一次滤波的时间最长。在粒子滤波算法中，选取的粒子数量过少会导致无法收敛，但选取的粒子数量过多可能会导致实时性下降，结合图4对不同粒子数目时的误差对比可知，PF算法需要选取的粒子数目为400以保证跟踪精度，实时性会降低，因此在本仿真实例中，EPF算法选取粒子数200非常合适，不会降低精度，也保障了实时性。

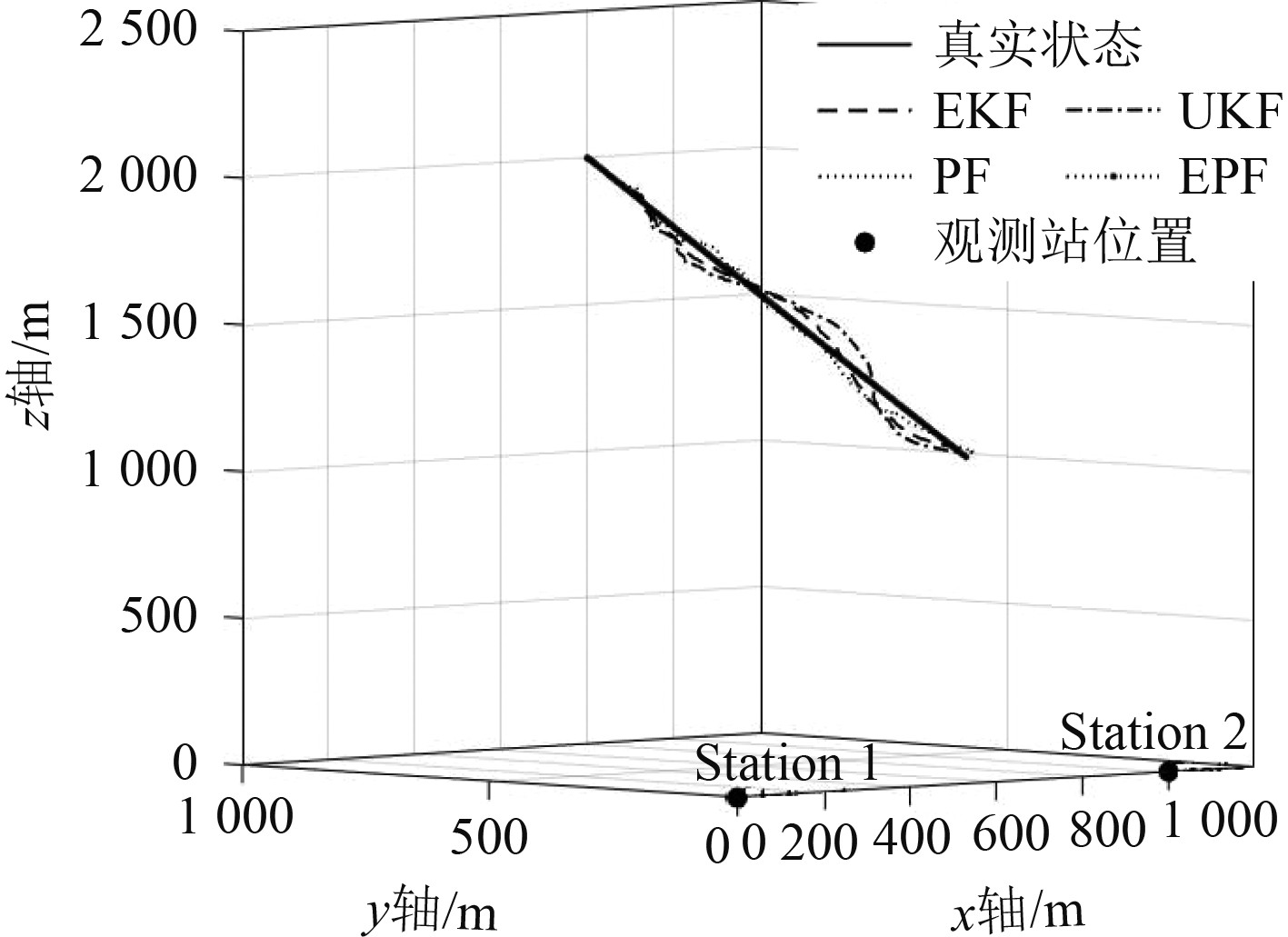
实验2　目标速度为30 kn时，选取粒子数目为200对PF和EPF算法进行仿真，真实轨迹和跟踪效果如图6所示，EPF算法表现出了非常优秀的跟踪性能。UKF算法的跟踪效果较好，PF和EKF的跟踪效果次之。

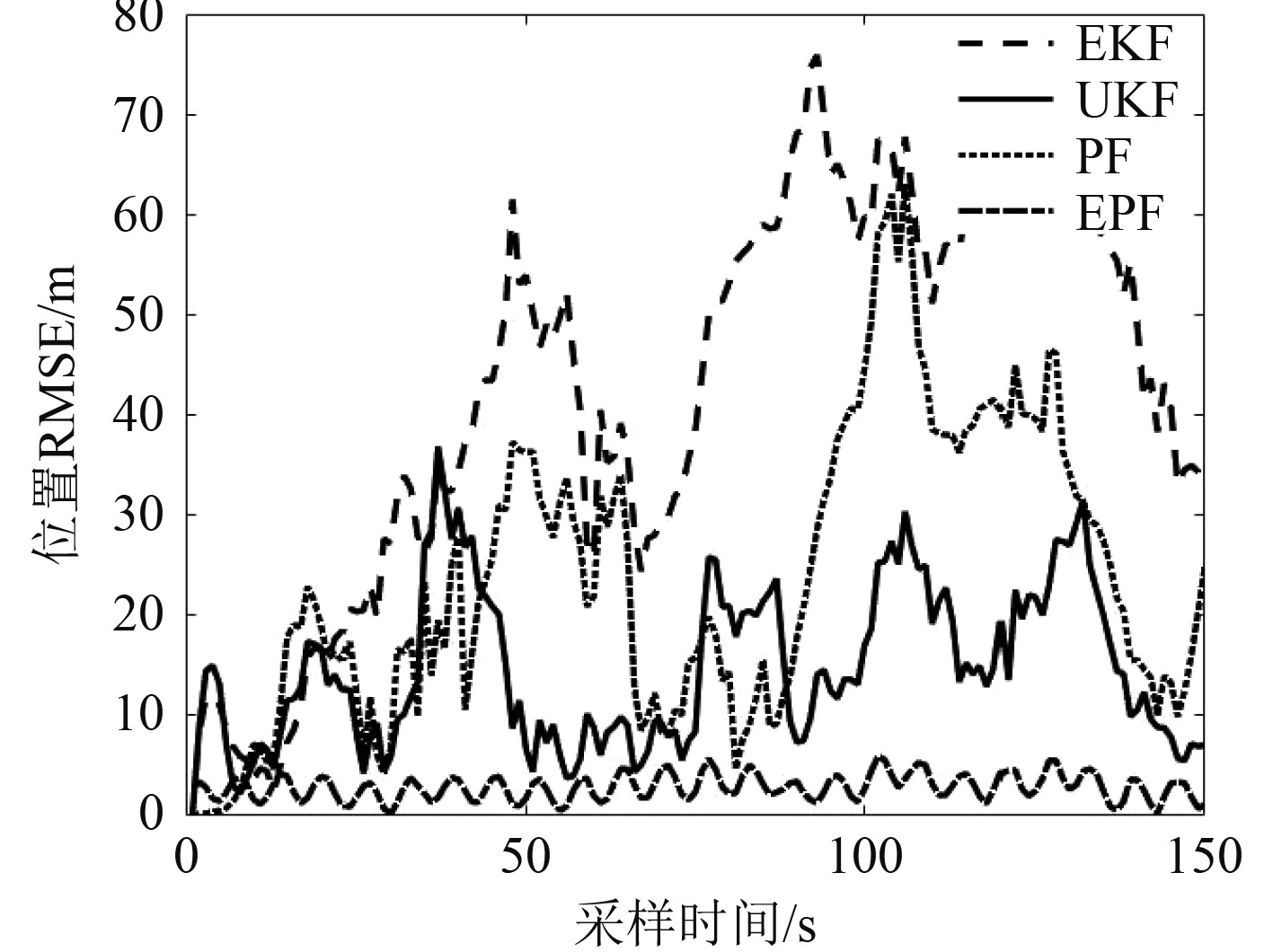
图7为4种算法的位置均方根误差图，EKF算法的位置均方根误差最大，PF算法和UKF算法的误差较小，EPF算法的均方根误差最小。

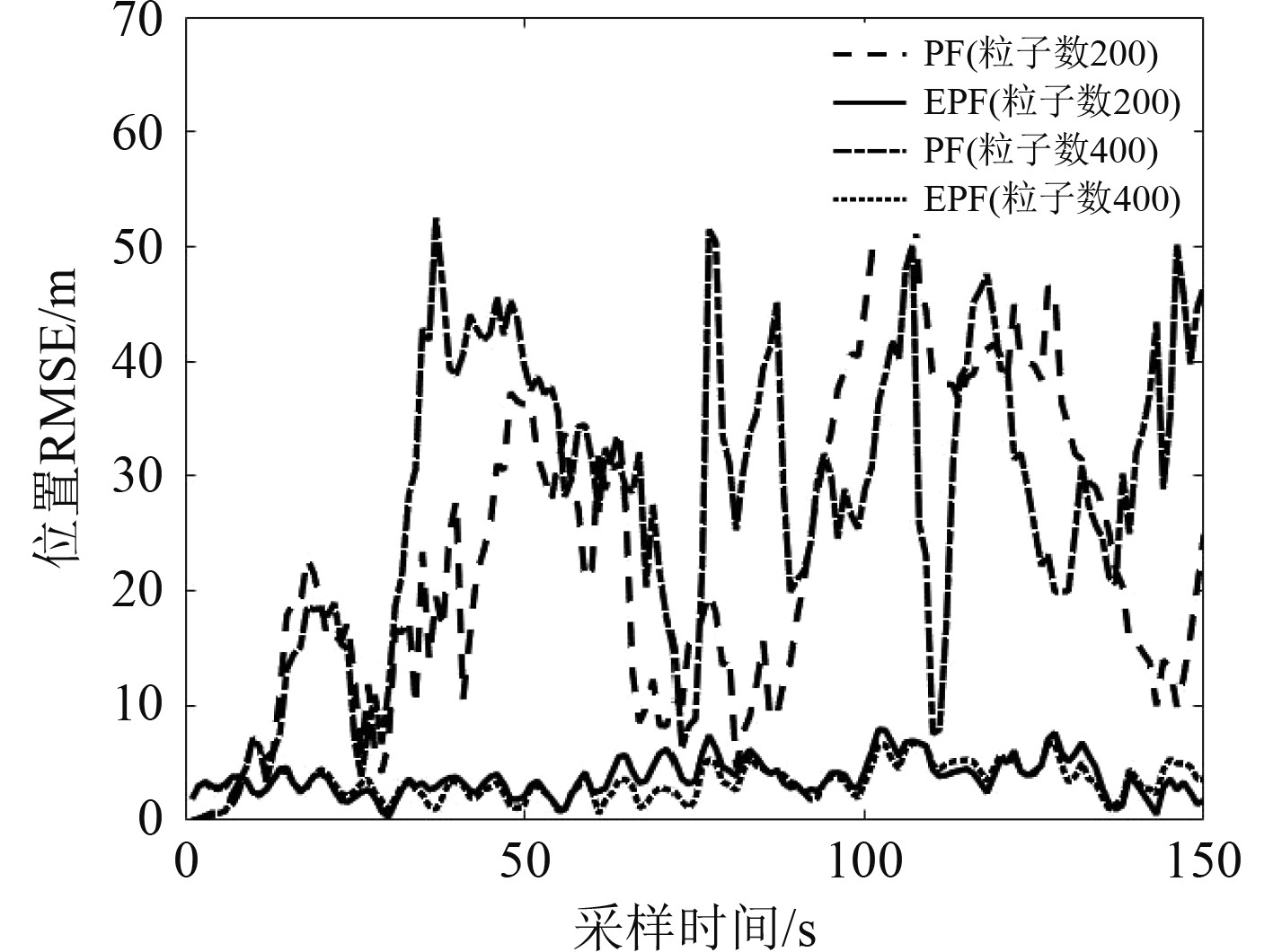
图8为粒子数为400和200时2种算法的位置均方根误差。PF算法在粒子数为200和400时误差都能维持在较小水平，能有效跟踪目标，但跟踪精度比EPF算法低，EPF算法在粒子数为200和400的均方根误差都较小。

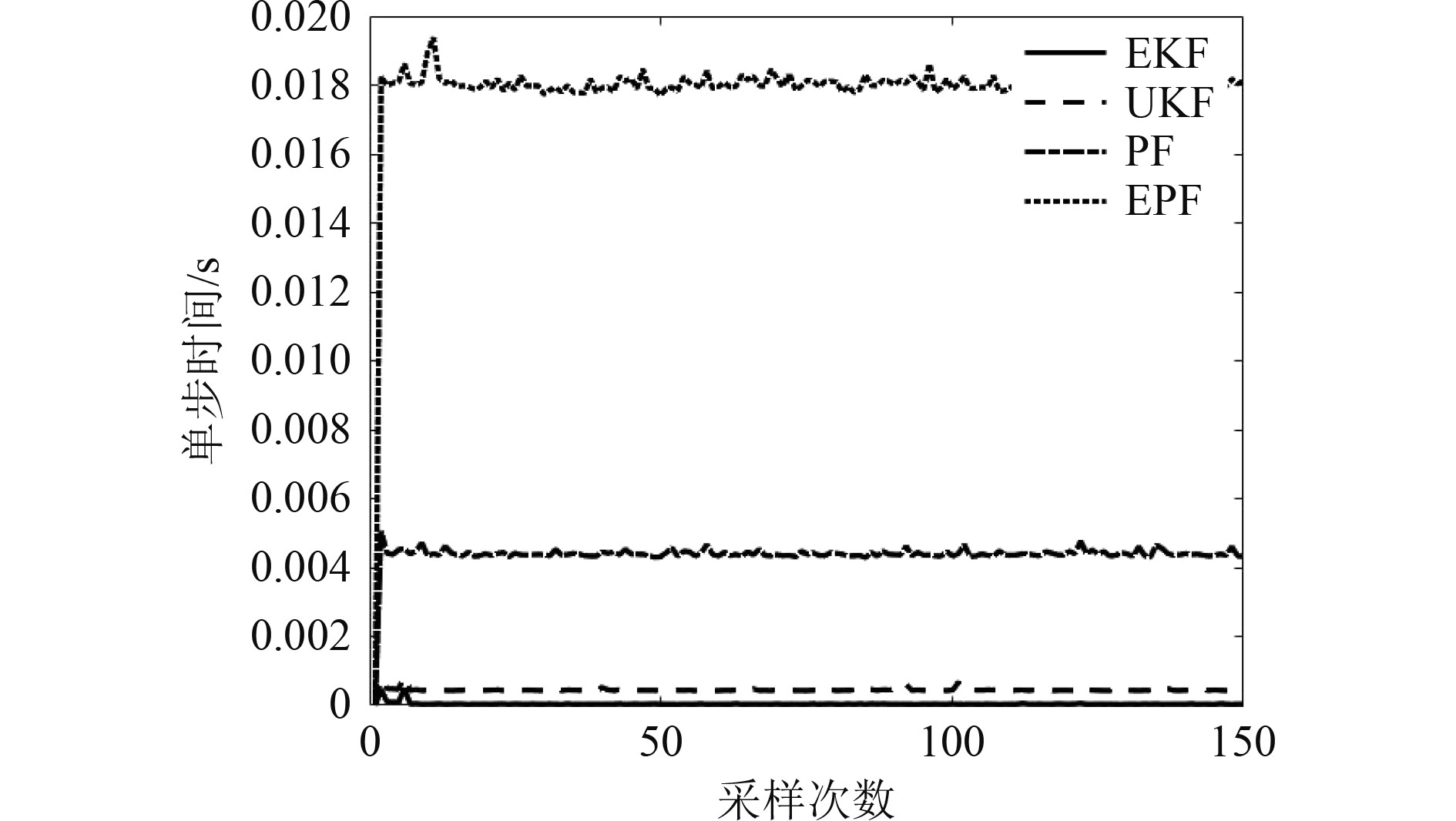
图9为4种算法的单步时长，与实验1一样，在目标以30 kn速度进行匀速直线运动时，相比于EKF和UKF，PF进行一次滤波的时间较长，EPF进行一次滤波的时间最长。结合图8对不同粒子数目时的均方根误差对比可知，在本仿真实例中选取粒子数200非常合适，精度要求较高的系统中优先选择EPF算法，在对实时性要求较高、精度要求不高的系统中可选择PF算法。

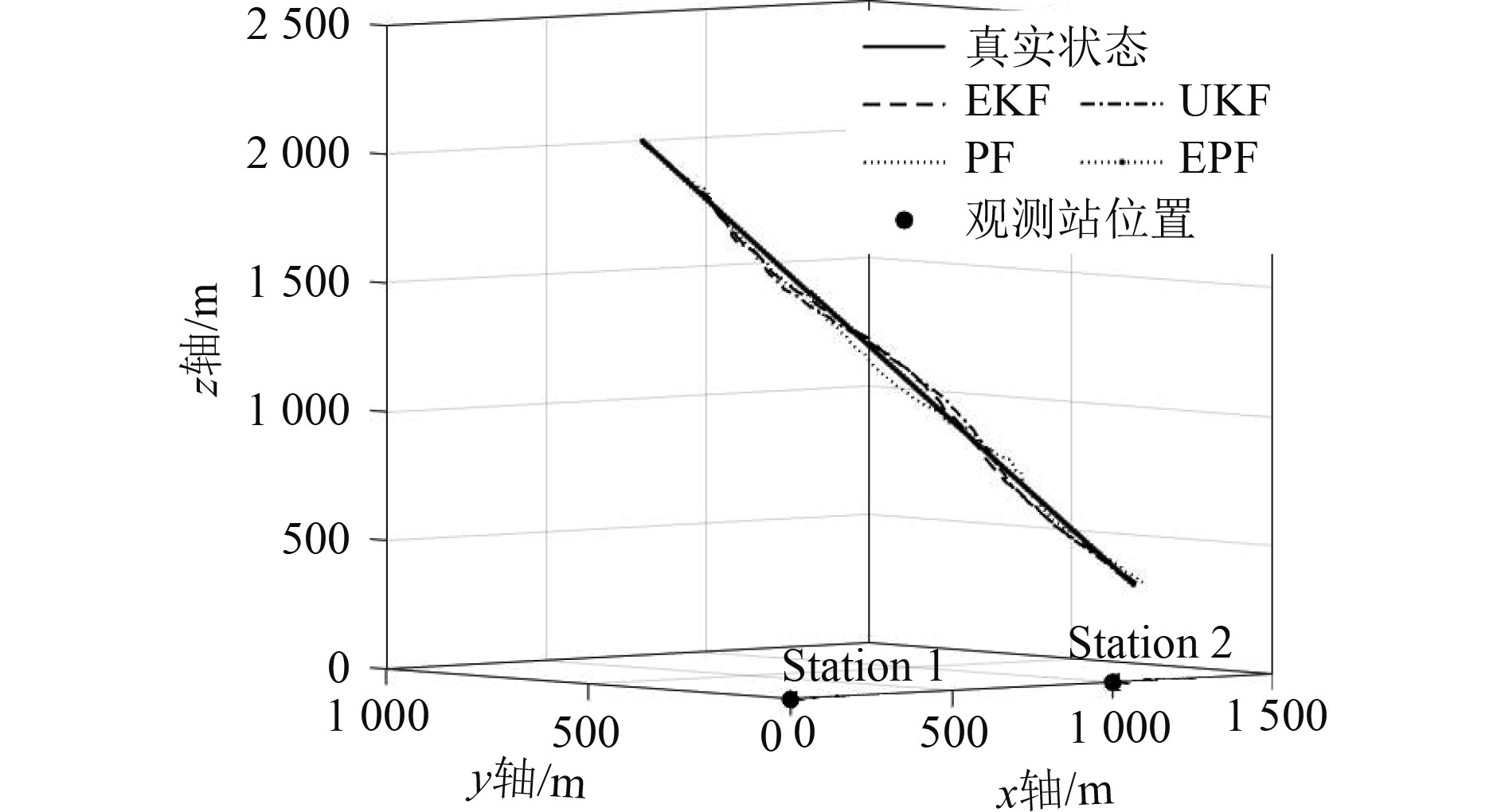
实验3　目标速度为50 kn时，选取粒子数目为200对PF和EPF算法进行仿真，真实轨迹和跟踪效果如图10所示，4种算法的跟踪效果都很好，其中EPF算法表现出了非常优秀的跟踪性能。

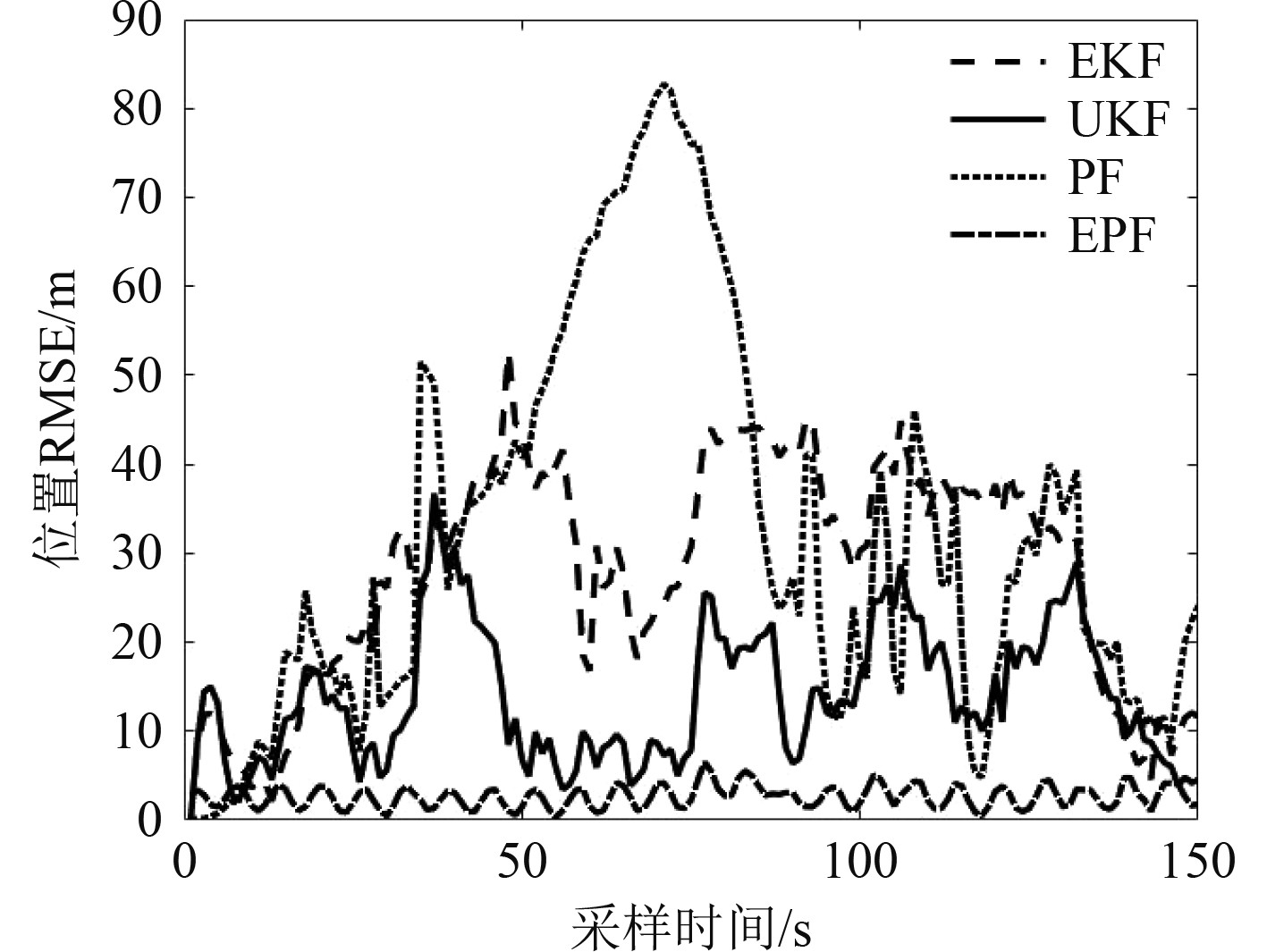
图11为4种算法的位置均方根误差图，PF算法的位置均方根误差最大，EKF算法、UKF算法的误差较小，EPF算法的位置均方根误差最小。

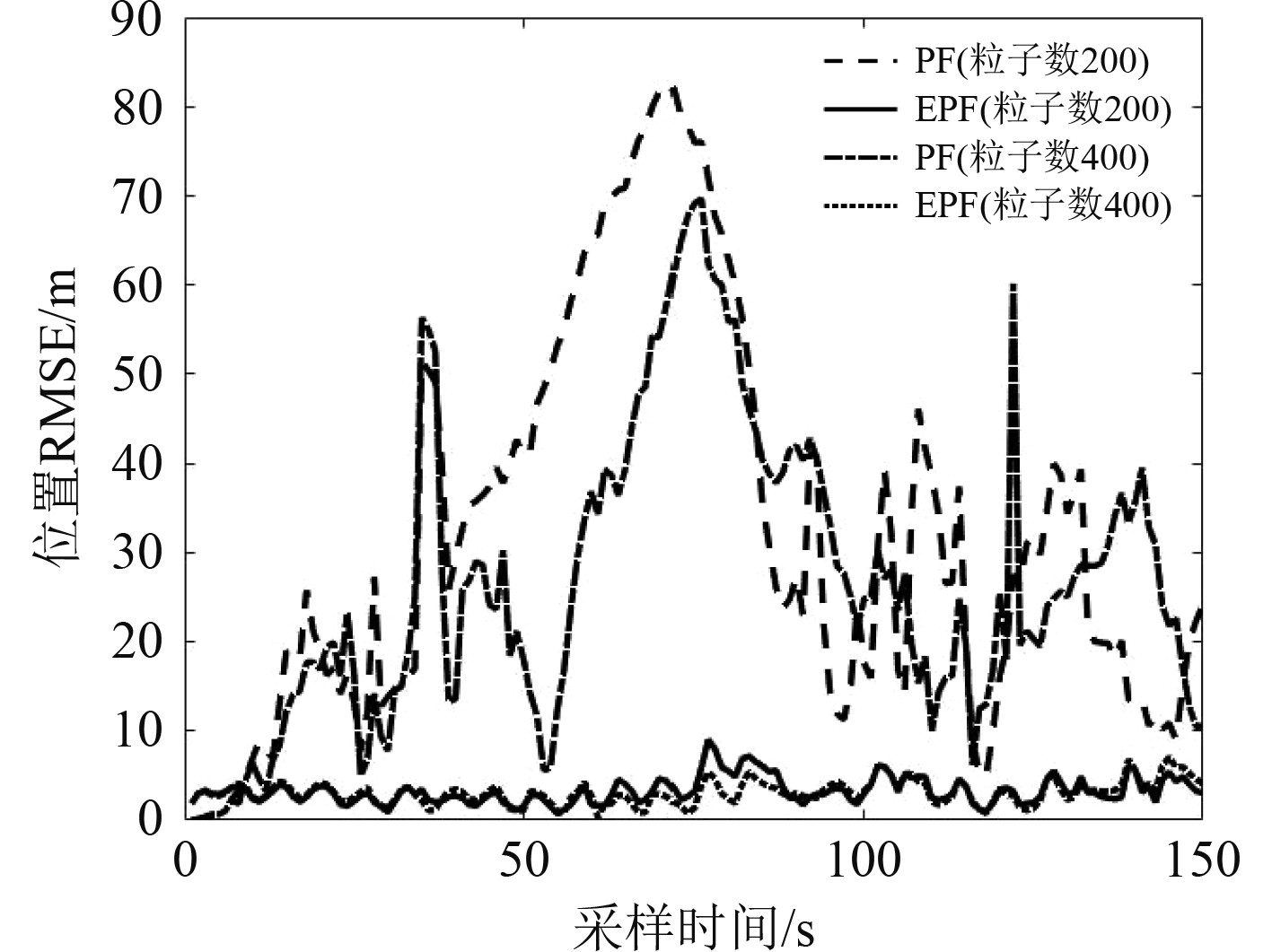
图12为粒子数为400和200时2种算法的位置均方根误差。PF算法在粒子数为200和400时误差都能维持在较小水平，能有效跟踪目标，但跟踪精度比EPF算法低，EPF算法在粒子数为200和400的均方根误差都较小。

图13为4种算法的单步时长，与实验1、实验2一样，在目标以50 kn速度进行匀速直线运动时，相比于EKF和UKF，PF进行一次滤波的时间较长，EPF进行一次滤波的时间最长。结合图12对不同粒子数目时的均方根误差对比也可知得出，在本仿真实例中选取粒子数200非常合适，精度要求较高的系统中优先选择EPF算法，在对实时性要求较高、精度要求不高的系统中可选择PF算法。

由3组仿真结果对比分析可知，EPF算法相较于其他算法有更好的跟踪效果，但是单步时长较长，适用于对实时性要求不高，但对跟踪精度要求高的系统。在本研究中还发现，在追求更好的跟踪效果时，无需选取过多的粒子数目，EPF算法本身有较好的性能，选取过多粒子数目对提高跟踪效果裨益不大，却可能增加大量的计算时间，因此只需选取恰当粒子数目即可。

4 结　语

本文针对水下目标跟踪问题，以静止双观测站三维纯方位目标跟踪系统为研究对象，介绍了粒子滤波（PF）和扩展粒子滤波（EPF）的基本思想和算法实现步骤，对基于这2种算法的双观测站三维纯方位跟踪系统进行了仿真分析与比较。通过对比分析发现，在不同目标运动速度情况下，EPF算法相较于其他算法都有更好的跟踪效果，但是单步时长较长，适用于对实时性要求不高，但对跟踪精度要求高的系统。在本研究中还发现，在追求更好的跟踪效果时，无需选取过多的粒子数目，EPF算法本身有较好的性能，选取过多粒子数目对提高跟踪效果裨益不大，却可能增加大量的计算时间。在使用EPF算法时选取恰当的粒子数目，寻找实时性更高的改进方法将是今后研究的重要方向。