2. 海军装备部装备项目管理中心,北京 100010;
3. 哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001
2. Project Management Office, Naval Equipment Department, Beijing 100010, China;
3. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
离心泵具有使用工况广、运行稳定、结构与操作简单、维护方便等诸多优点,在海洋平台中有广泛应用,是海洋核动力平台动力系统的重要组成设备,其运行状况直接关系海洋核动力平台管网的匹配关系及安全稳定性。离心泵内部由于流体被加速至较高流速,工质绝对压力下降。当其降低至对应温度的汽化压力以下时,水等液体介质将发生汽化,形成汽泡。这些汽泡被输运至高压区后溃灭,恢复至液体状态,由于流体高速填充气穴等过程的体积剧烈变化,伴随产生明显的压力波动,即发生汽蚀。离心泵汽蚀一方面会使水泵性能明显下降,另一方面将产生振动和噪声,甚至破坏固体壁面,故如何抑制离心泵汽蚀是学术界以及工业界长期关注的热点问题[1 - 2]。
黄建德等[3]利用水泵汽蚀试验台和涂漆法对具有不同叶片进口角和叶片进口位置的5种离心泵进行了汽蚀性能试验,明晰了3%扬程点汽蚀状态下叶轮形状、流量、运行时间等对叶轮内汽蚀损伤位置等的影响。刘忠等[4]采用小波分析方法对离心泵空化试验过程中不同状态下的声发射信号进行能量特征提取,结果表明汽蚀不同发展阶段、不同位置处声发射信号小波能量特征有明显不同,可为离心泵空化状态判别提供参考。
近年来,随着计算能力、多相流模型以及求解算法等的飞速发展,计算流体动力学(CFD)方法越来越多应用于各学科分析,离心泵汽蚀的CFD仿真分析研究也日益增加。王秀礼等[5 - 6]采用均质多相模型及Rayleigh-Plesset模型对离心泵内的汽蚀过程进行仿真分析,揭示了离心泵汽蚀发生后流量-扬程曲线下降的原因,初步分析了泵内部汽-液两相流场分布规律。同时结合仿真与试验结果,分析了船用离心泵不同汽蚀余量时叶轮内部压力和两相含率分布规律,提出低速漩涡区与空腔的存在将影响蜗壳内部流动速度和稳定性,进而影响振动噪声[7]。张宁[8]采用数值模拟结合振动试验,构建了泵内压力脉动能量和涡结构特性内在关联,分析了空化对压力脉动、振动频谱的影响机理,得出可以从空化诱导振动角度出发提前判断空化发生,避免离心泵空化,以达到预防空化对泵系统安全稳定性和叶轮的破坏的目的。崔宝玲[9]采用CFD对带诱导轮离心泵进行了汽蚀仿真分析,提出采用串联等螺距诱导轮及引射器等方法提升离心泵抗汽蚀性能,并对叶片数目及叶轮形式进行仿真分析,为离心泵抗汽蚀设计提供支撑。
可以看出,采用数值分析开展离心泵汽蚀过程分析,提升离心泵抗汽蚀性能,已经逐渐成为主流方法。然而当前绝大多数研究仅考虑固定平台中离心泵的汽蚀过程,海洋平台离心泵汽蚀及热力特性研究当前还相对不足。相较于固定平台,海洋平台离心泵布置空间十分有限,导致其实际灌注高度小,容易发生汽蚀,同时,在摇摆、晃动等海洋条件作用下,其入口条件、内部工质受力等均会发生变化,进一步对离心泵内汽蚀现象和热力特性产生影响。
本文通过不同模型计算结果对比分析,选择合适模型,结合动网格等技术模拟海洋摇摆条件下离心泵空间位置动态变化,构建了海洋条件下离心泵汽蚀过程仿真分析模型,以此模型模拟了不同参数海洋摇摆条件下离心泵的汽蚀过程,相关模型及结果等可为海洋条件下离心泵的抗汽蚀设计提供技术支撑。
1 计算模型本文采用仿真软件Fluent对离心泵内汽蚀过程进行仿真分析。重点对两相模型、汽蚀模型以及网格技术等三方面进行分析,以构建摇摆条件下离心泵汽蚀仿真模型。
1.1 湍流模型由于离心泵汽蚀过程,尤其是汽蚀初生阶段气泡尺径较小,气相跟随性较好,故本文多相流模型决定采用Mixture模型进行模拟。其假设汽、液两相之间互相渗透掺混,引入滑移速度,各相共享同一压力场引入相体积分数得到描述多相流动的控制方程:
| $ \frac{\partial }{{\partial t}}\left( {{\rho _m}} \right) + \nabla \cdot \left( {{\rho _m}{v_m}} \right) = 0,$ | (1) |
| $\begin{split} \frac{\partial }{{\partial t}}\left( {{\rho _m}{v_m}} \right) + & \nabla \cdot \left( {{\rho _m}{v_m}{v_m}} \right) = - \nabla p + \nabla \cdot \left[ {{\mu _m}\left( {\nabla {v_m} + \nabla v_m^{\text T}} \right)} \right] +\\ &{\rho _m}g + F + \nabla \cdot \left( {\sum\limits_{k = 1}^n {{\alpha _k}{\rho _k}{v_{dr,k}}{v_{dr,k}}} } \right) ,\end{split}$ | (2) |
| $\begin{split} \frac{\partial }{{\partial t}}\sum\limits_{k = 1}^n &{\left( {{\alpha _k}{\rho _k}{E_k}} \right) + \nabla \cdot \sum\limits_{k = 1}^n {\left[ {{\alpha _k}{v_k}\left( {{\rho _k}{E_k} + p} \right)} \right]} } =\\ &\nabla \cdot \left( {{k_{eff}}\nabla T} \right) + {S_E}。\end{split}$ | (3) |
式中:vm为质量平均速度;ρm为混合密度;α为相体积分数;n为相数量,取n=2;F为体积力;μm为混合物粘度,vdr,k为滑移速度;keff为有效传热系数;SE为体积热源,对于不可压流体,有Ek=hk。
1.2 汽蚀模型绝大多数汽蚀模型均是基于Rayleigh-Plesset方程导出:
| $ \frac{{{P_\nu } - P}}{{{\rho _l}}} = \frac{{{{\rm d}^2}R}}{{{\rm d}{t^2}}} + \frac{3}{2}{\left(\frac{{{\rm d}R}}{{{\rm d}t}}\right)^2} + \frac{1}{{{\rho _l}}}\left(4{\mu _l}\frac{{{\rm d}R}}{{{\rm d}t}} + \frac{{2\sigma }}{R}\right),$ | (4) |
| $ \frac{\partial }{{\partial t}}(\alpha {\rho _\nu }) + \nabla (\alpha {\rho _\nu }{u_\nu }) = {R_e} - {R_c} 。$ | (5) |
式中:Pv为空泡内的压力;P为当地大气压力;R为空泡直径;ρl为液相密度;ρv为气相密度;σ为表面张力系数;μx为液体的湍动能粘度;Re和Rc分别为空泡产生及溃灭相变率。
当前在水动力机械流动这一方面的数值模拟中,使用较为广泛的空化模型有Schnerr-Sauer模型(简称SS模型)以及Zwart-Gerber-Belamri(简称ZGB模型)模型等。
SS模型:
| $ {R}_{e}=3\frac{{\rho }_{\nu }{\rho }_{l}}{{\rho }_{m}}\frac{{\alpha }_{\nu }(1-{\alpha }_{\nu })}{{R}_{B}}\sqrt{\frac{2}{3}\frac{{P}_{\nu }-P}{{\rho }_{l}}}\text{,}P < {P}_{\nu } ,$ | (6) |
| $ {R}_{c}=3\frac{{\rho }_{\nu }{\rho }_{l}}{{\rho }_{m}}\frac{{\alpha }_{\nu }(1-{\alpha }_{\nu })}{{R}_{B}}\sqrt{\frac{2}{3}\frac{P-{P}_{\nu }}{{\rho }_{l}}}\text{,}P > {P}_{\nu },$ | (7) |
| $ {R_B} = {(3{\alpha _\nu }/(4{\text π} {n_0}(1 - {\alpha _\nu })))^{1/3}} 。$ | (8) |
式中:n0为单位液体体积空泡个数,即空泡数密度,取值一般为1013。
ZGB模型:
| $ {R}_{e}={F}_{\text{vap}}\frac{3{\alpha }_{\text{ruc}}(1-{\alpha }_{\nu }){\rho }_{\nu }}{{R}_{B}}\sqrt{\frac{2}{3}\frac{{P}_{\nu }-P}{{\rho }_{l}}}\text{,}P < {P}_{\nu },$ | (9) |
| $ {R}_{c}={F}_{\text{cond}}\frac{3{\alpha }_{\nu }{\rho }_{\nu }}{{R}_{B}}\sqrt{\frac{2}{3}\frac{P-{P}_{\nu }}{{\rho }_{l}}}\text{,}P > {P}_{\nu }。$ | (10) |
式中:αruc取5×10−4;RB为空泡半径,取1.0×10−6 m;P、Pv分别为流场压力和汽化压力,Pa;Fvap、Fcond分别为对应于蒸发和凝结过程2个经验校正系数,分别取值50、0.01,Fvap和Fcond不相等的原因是凝结过程通常要比蒸发过程慢得多。
本文主要分析海洋条件下泵汽蚀余量影响,其中汽蚀余量定义如下:
| $ NPSHa = \frac{{{P_m} - {P_v}}}{{\rho g}} 。$ | (11) |
式中,Pm为泵进口压力。
1.3 网格技术对于离心泵这类旋转机械,常见的旋转仿真方法为多参考坐标系模型(Multiple Reference Frame, MRF)、滑移网格模型(Sliding Mesh, SM)或动网格模型(Dynamic Mesh, DM)。其中由于SM模型不能满足绝对坐标系下的摇摆运动仿真需求,所以本项目主要将MRF模型与DM模型的仿真结果进行对比。
MRF模型采用定常计算方法来替代非定常流动,将离心泵叶轮流场和蜗壳流场,即旋转流动与和静流域,分别定义在2个不同坐标系中。动静流域间通过交界面interface传递计算数据,保证流场连续性,其中动区坐标性附着在叶轮部件上,该区域边界相对于旋转坐标系静止,从而实现定常计算。
DM模型对于存在运动边界的任意控制单元,某一标量守恒型积分形式如下:
| $ \frac{{\rm d}}{{{\rm d}t}} \int\limits_v {\rho \phi {\rm d}V + \int\limits_{\partial V} {\rho \phi \left( {v - {v_g}} \right) \cdot {\rm d}A = \int\limits_{\partial V} {\Gamma \nabla \phi \cdot {\rm d}A + \int\limits_V {{S_\phi }{\rm d}V} } } } 。$ | (12) |
式中:v为流体运动矢量;vg为运动边界处网格速度;Γ为扩散系数;Sϕ为标量ϕ的源项;V为控制单元。
关于时间微分项可写成一阶向后差分形式:
| $ \frac{{\rm d}}{{{\rm d}t}}\int_V {\rho \phi {\rm d}V = \frac{{{{\left( {\rho \phi V} \right)}^{n + 1}} - {{\left( {\rho \phi V} \right)}^n}}}{{\Delta t}}} 。$ | (13) |
式中:n、n+1分别代表第n和第n+1时间步上的数值。
对于海洋摇摆条件,泵在绕自身转轴旋转同时,受环境影响,还将绕摇摆中心发生位置变化,即在离心泵自转域内包含泵内的流动包括绕泵转轴的自转运动以及公转运动(见图1),对于离心泵非自转域,则仅包含公转运动。本文通过用户自定义函数UDF实现计算过程中自转及公转[10]。

|
图 1 海洋摇摆条件下离心泵自转公转示意图 Fig. 1 A schematic of the rotation and revolution of the centrifugal pump under rolling conditions |
本文计算过程中,压力-速度耦合求解方法为COUPLED方法,压力项采用Body Force Weighted方法,体积分数项采用QUICK方法离散,其余皆为一阶迎风格式进行数学离散。计算时间步长设为
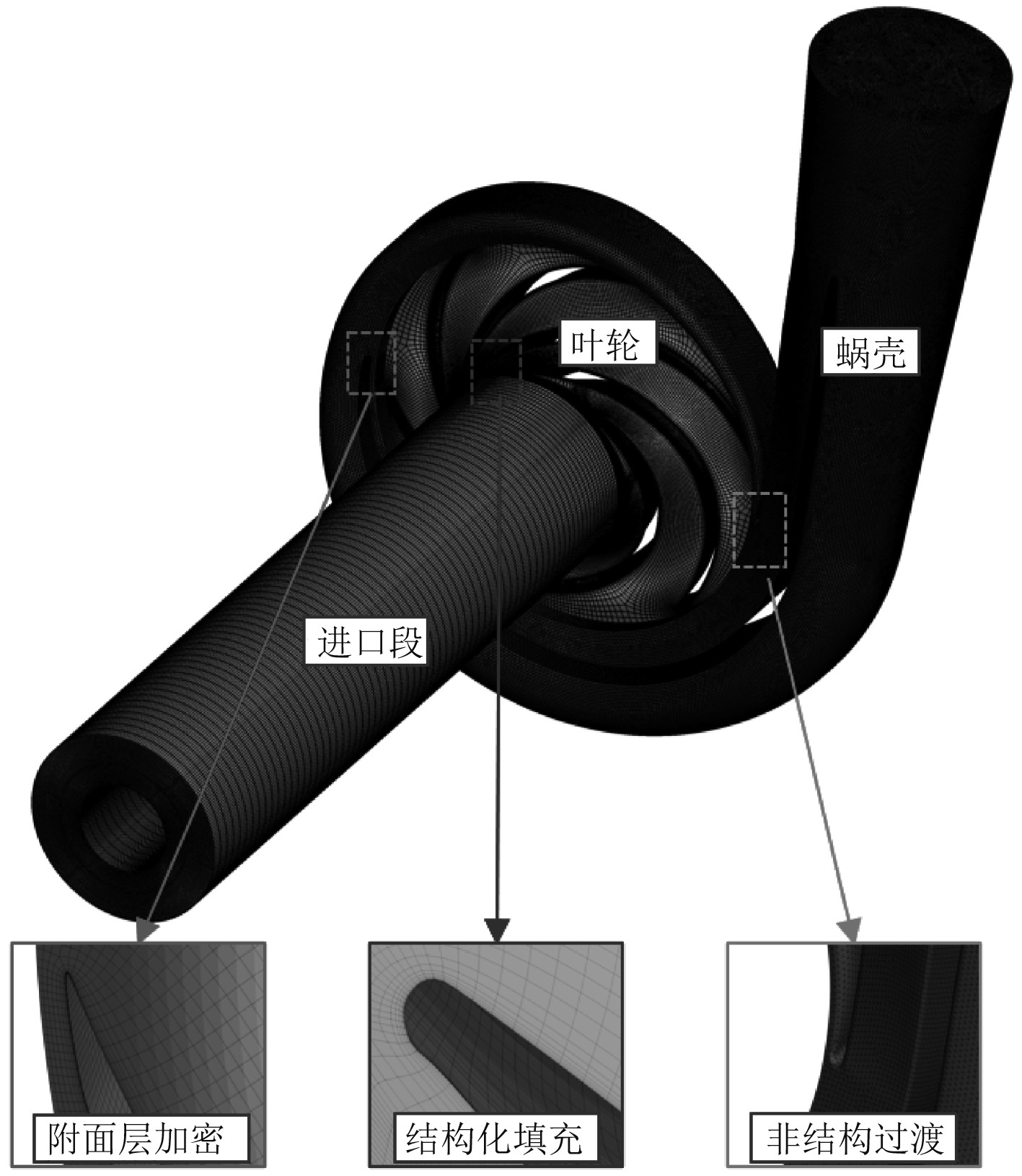
为验证模型准确性,选用文献中单级离心泵试验结果进行对比,该泵设计参数详见表1[11]。计算域网格由非结构网格划分的蜗壳、结构化网格划分的进口以及叶轮组成(见图2)。根据试验实际进行适当简化,为保证计算稳定性,将出口段延长500 mm。
|
|
表 1 离心泵设计参数 Tab.1 Designed parameter for the centrifugal pump |
|
图 2 验证模型网格划分 Fig. 2 Meshes for model validation |
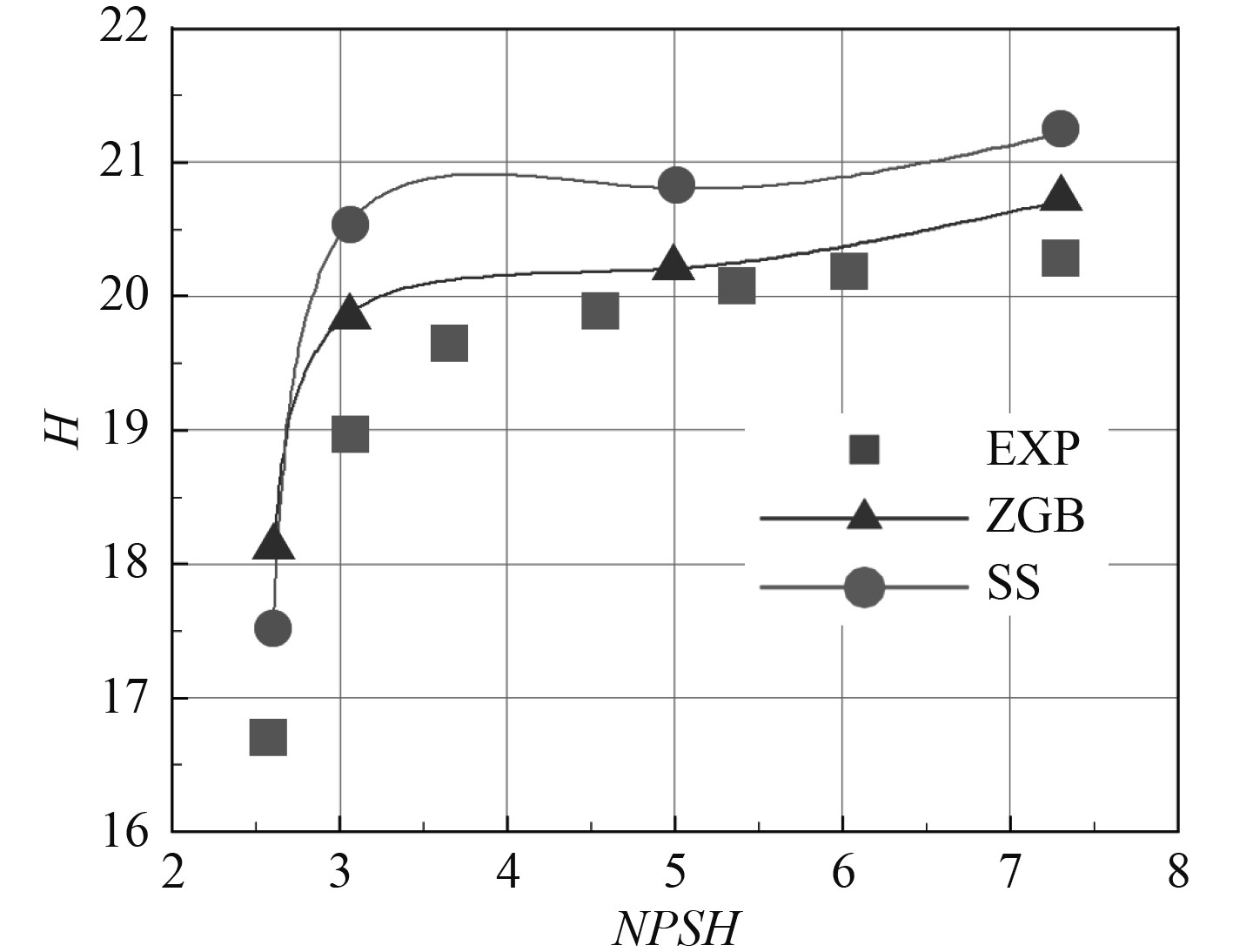
首先对汽蚀模型进行验证考核,为比较不同汽蚀模型适用性,通过调整出口静压系数更改出口静压,从而保证在进口流量一定的条件下改变汽蚀余量的数值,相应的离心泵的工况发生改变,扬程大小也会发生变化。图3给出了不同汽蚀模型在进口流量一定时扬程随汽蚀余量的变化曲线。可以看出2种汽蚀模型扬程变化趋势均与试验接近,相较而言ZGB模型仿真精度更高。故后续的仿真将采用ZGB模型对离心泵汽蚀过程的仿真过程进行分析。
|
图 3 不同汽蚀模型预测的扬程随汽蚀余量曲线对比 Fig. 3 Head-NPSH curves predicted by different cavitation models |
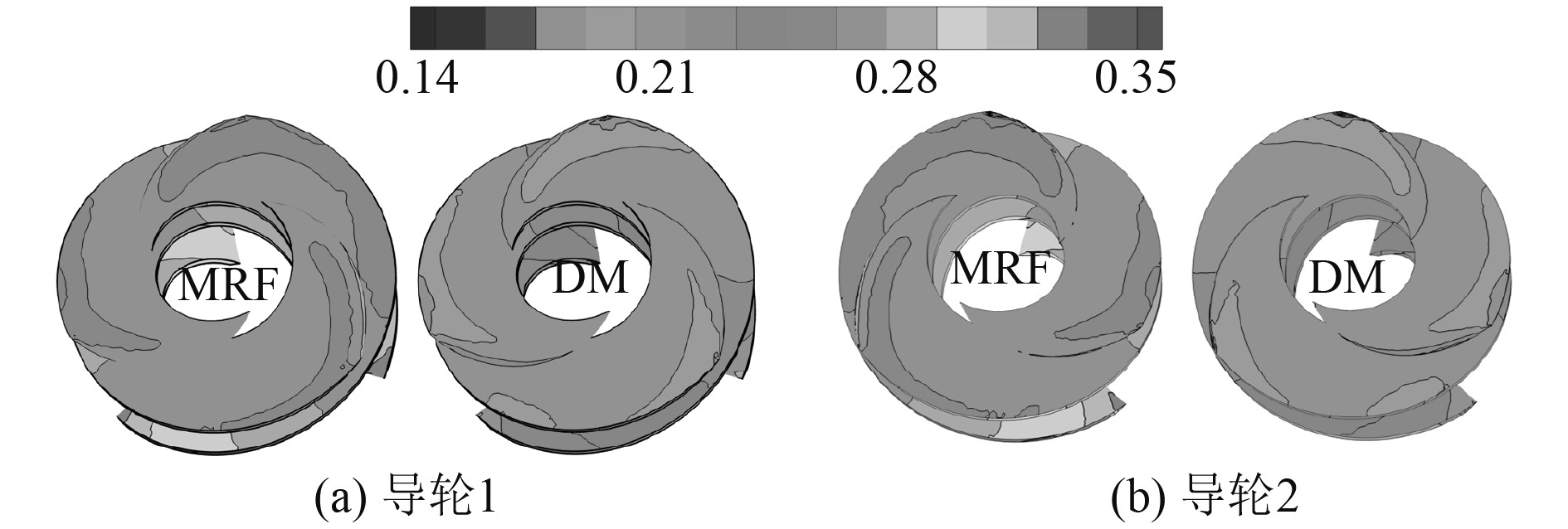
本部分以双级离心泵为对象,对比MRF与DM两种网格技术对离心泵汽蚀过程的预测分析结果。相较DM方法,MRF方法将旋转机械做准稳态处理,计算量明显减少。2种网格技术预测导轮旋转叶片表面压力分布如图4所示,通过MRF方法仿真得到的导轮叶片表面压力明显高于DM方法得到的仿真结果。
|
图 4 不同网格技术导轮叶面压力结果对比 Fig. 4 Pressure distributions on inducers predicted by MRF and DM |
进一步分析工作轮叶片表面压力也能发现类似结果,即一级工作轮中MRF方案得到表面压力较DM方案高,二级工作轮压力分布两者接近。由于MRF在计算过程中仅考虑旋转部件内均速相对运动,所得结果更偏向于时均值,与真实物理运动存在一定偏差。DM方案尽管计算量较大,但能较准确捕捉对象真实运动瞬时流场信息。故在计算条件允许情况下采用DM方法进行摇摆条件下离心泵汽蚀分析。
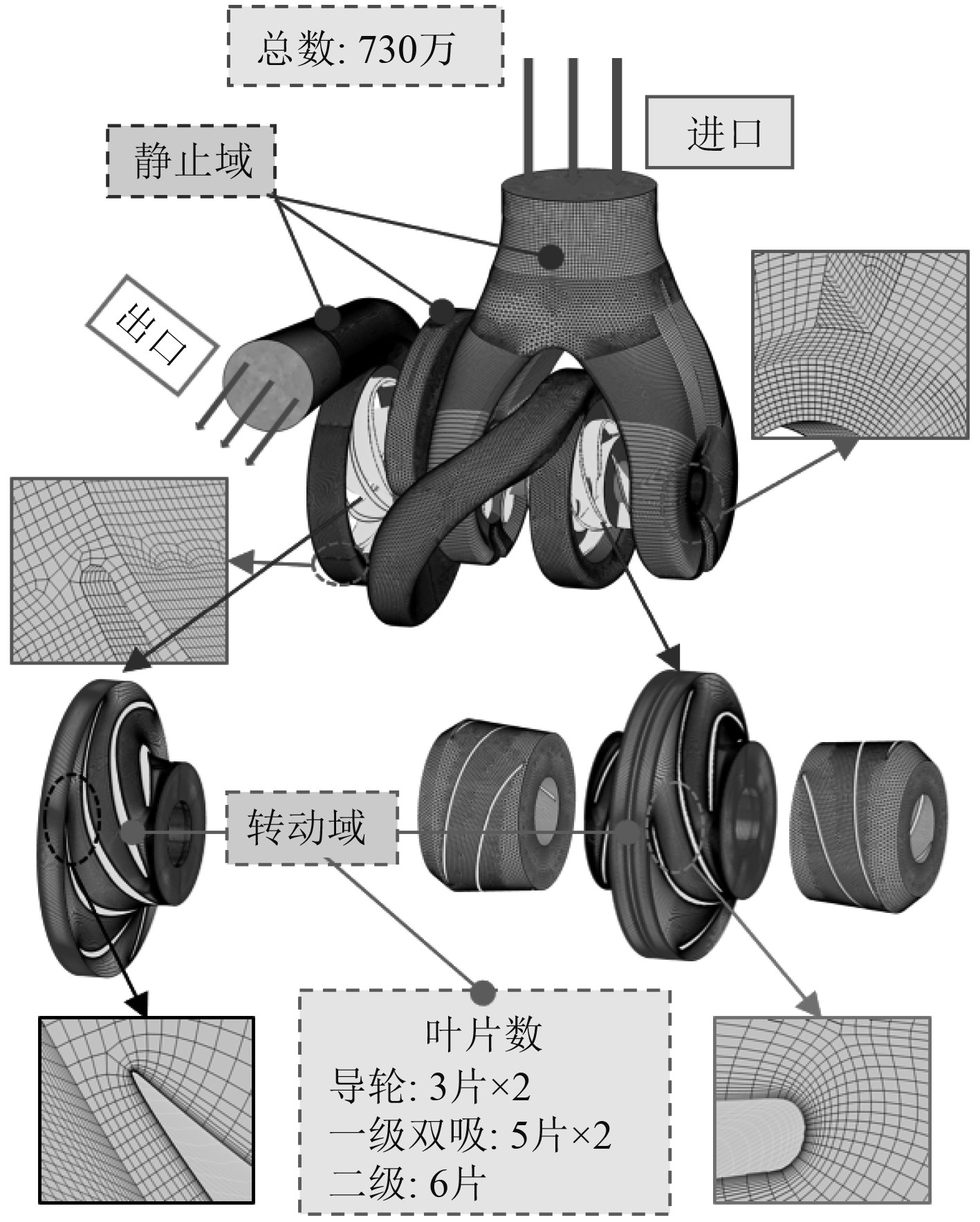
3 海洋摇摆条件在研究海洋摇摆条件影响过程中,本文以具有两级叶片及诱导轮的离心泵为研究对象。图5为全局网格划分示意图,按照各部分运动规律的不同可将全局划分为静止域和运动域。静止计算域局部区域采用非结构网格划分,转动计算域采用分区结构化网格进行划分。静止计算域由吸水室、级间过渡段及出口蜗壳、加密各导轮、工作轮叶片等部分组成,壁面y+小于10,由于该部分形状变化复杂,需要在局部变形较大区域采用非结构网格填充。转动计算域包括2个对称导轮、一级双吸工作轮及二级工作轮,整体网格尺寸约730万。
|
图 5 带导轮离心泵网格划分 Fig. 5 Meshes for the centrifugal pump with inducer |
静止计算域进出口边界设置为流量入口与压力出口,转动计算域的各部件间采用交界面(interface)连接。除此之外,转动计算域与静止计算域也采用交界面(interface)连接,其余各部件的外表面均为无滑移壁面,转速约
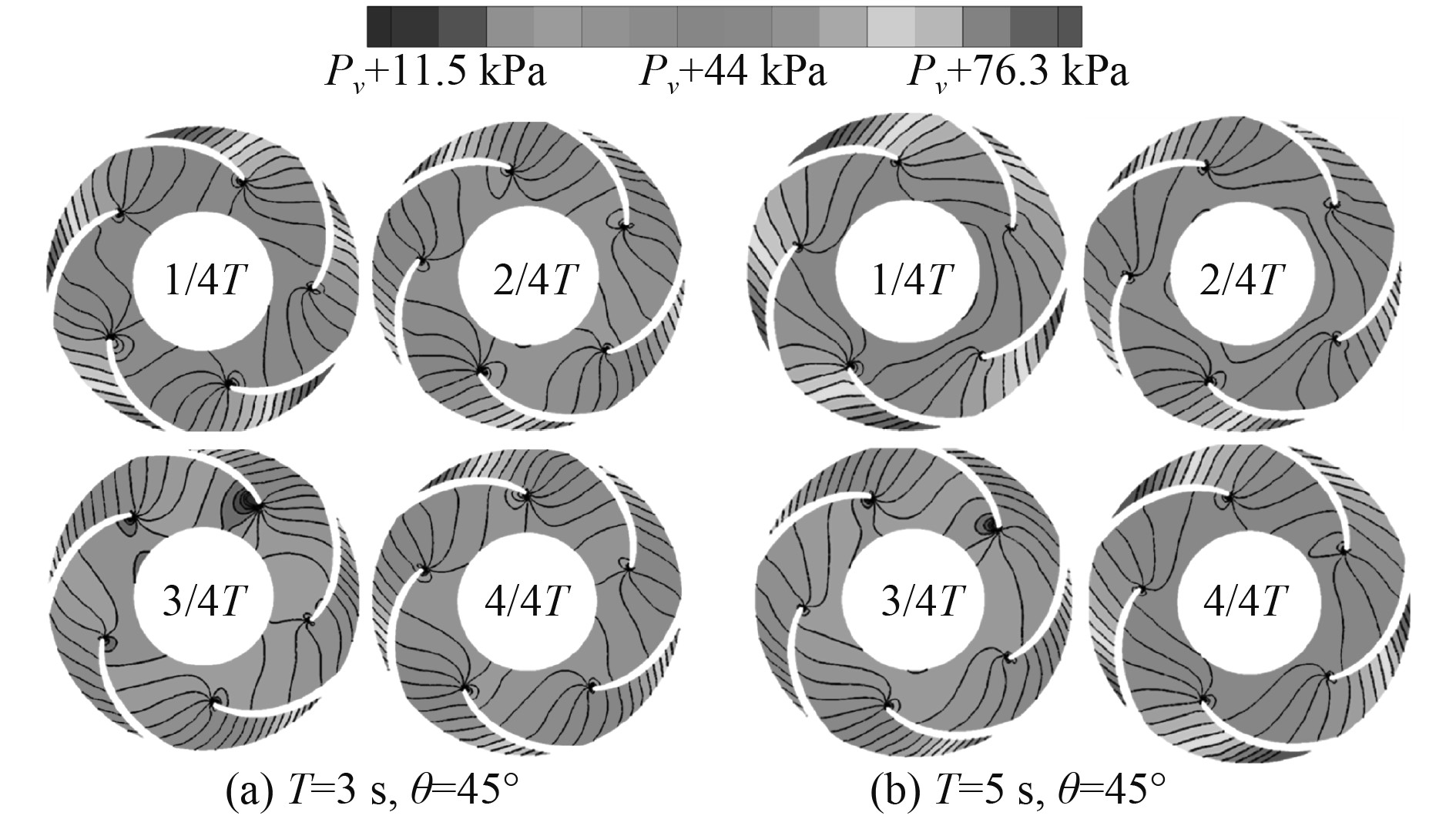
为研究不同摇摆周期对离心泵汽蚀特性影响,本节对2种特定摇摆工况(方案1:摇摆周期T=3 s,摇摆幅值θmax=45°;方案2:摇摆周期T=5 s,摇摆幅值θmax=45°)进行了三维非定常数值仿真分析。由于汽蚀发生与离心泵内压力分布密切相关,所以本文首先分析工作轮及导轮附近压力分布情况。一级及二级工作轮内截面压力分布如图6和图7所示。
|
图 6 不同摇摆周期下一级工作轮截面压力分布云图 Fig. 6 Pressure distribution of the first stage working wheel for different rolling period |

|
图 7 不同摇摆周期下二级工作轮截面压力分布云图 Fig. 7 Pressure distribution of the second stage working wheel for different rolling period |
可以看出,一级工作轮最小压力值高于汽化压力,并无汽蚀现象产生,不同摇摆周期下压力场均随摇摆周期呈现先减小后增大的变化规律。从公转角度考虑,单周期内摇摆运动分速度最大值在1/4T及3/4T处达到,结合工作轮自转运动,离心泵单周期内速度最大时刻出现在3/4T附近,此时压力场数值也相应最低。此外,对比不同摇摆周期方案相同特征时刻的压力云图可知,摇摆周期越大,相同时刻的压力场参数值越大,越难形成空化,表明其受摇摆运动的影响越弱,抗汽蚀性能更强。
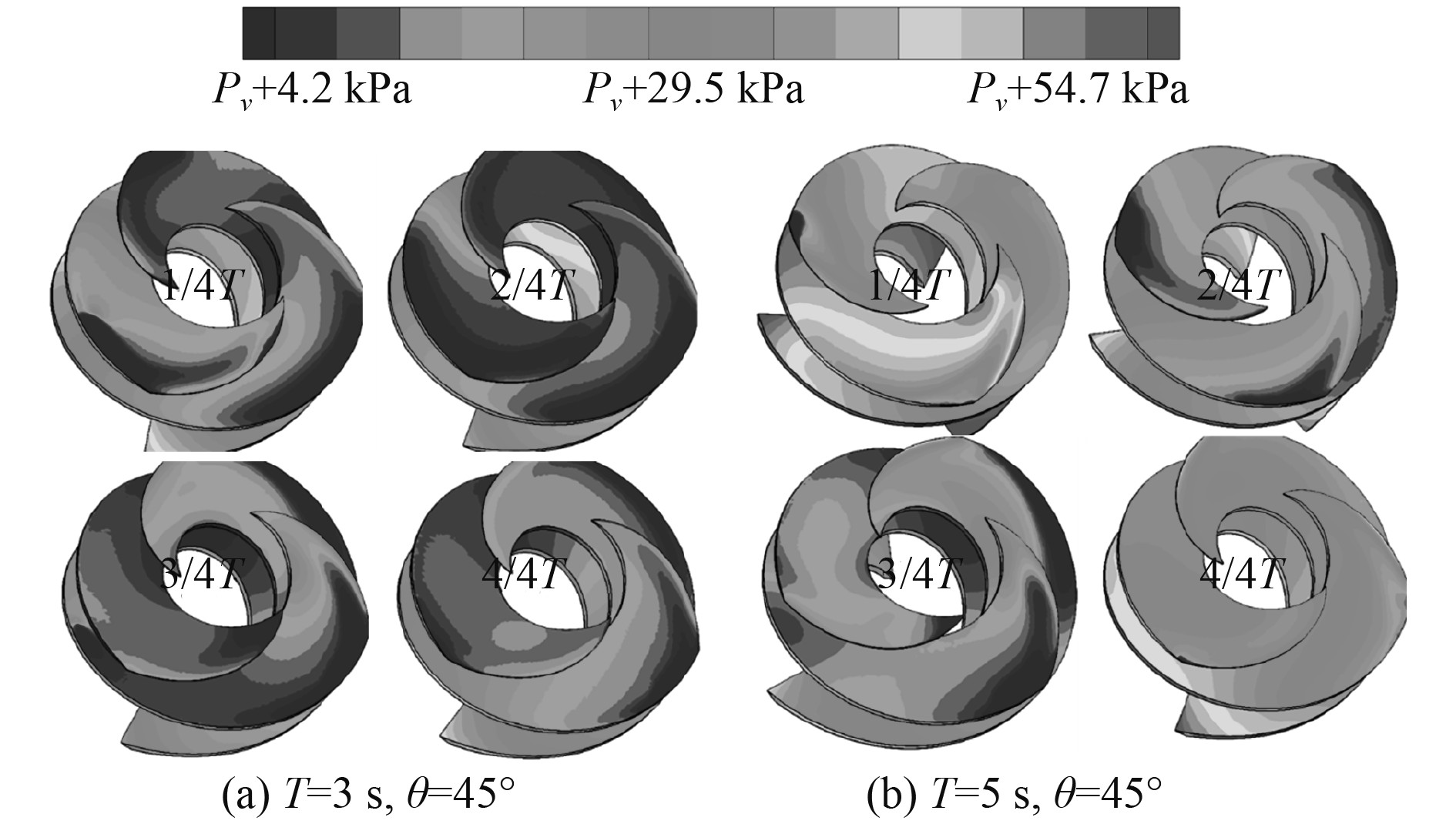
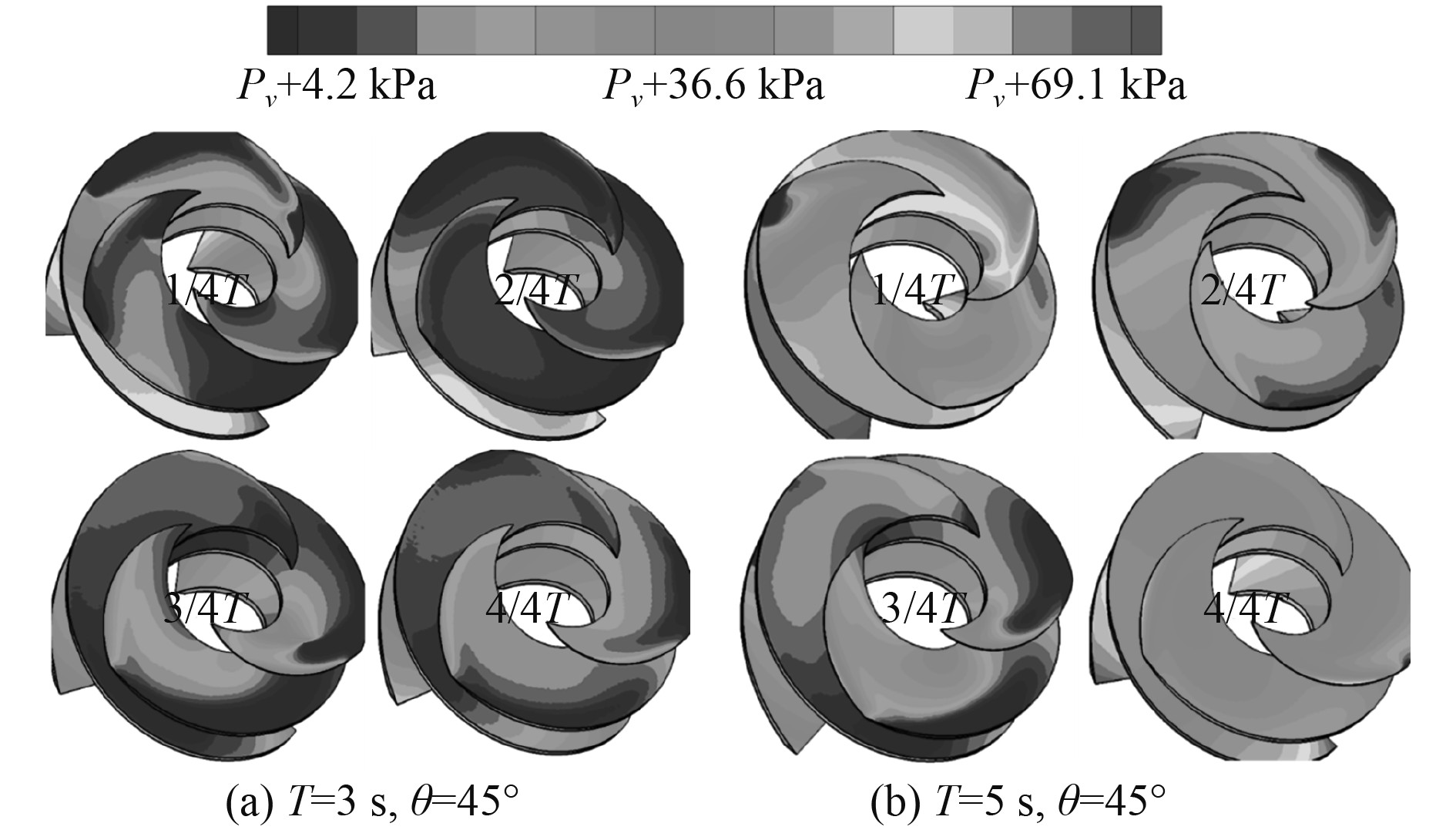
整个离心泵内低压区主要分布在进入一级双吸工作轮前的2个导轮内。研究离心泵汽蚀形成区流场时变特性规律对整个摇摆运动中物理现象背后机制的理解十分重要。图8及图9分别为导轮1和导轮2叶片表面的压力分布云图。与前文2个工作轮不同,导轮附近的压力场数值最小值达到了工质特定温度下的饱和蒸汽压力,能够发生汽蚀,且2个导轮关于双吸工作轮1对称,2个导轮的流场参数分布大致对称。但由于关键部件整体做摇摆运动,导轮叶片表面的局部压力仍略有差别。2个导轮叶片表面的压力场分布时变规律遵循上文所述的摇摆运动规律,压力场数值均先减小后增大,但整个摇摆周期内最低压力值始终存在。此外,与工作轮中低压区所处位置不同,导轮叶片表面的低压区分布在叶片吸力面边缘处。摇摆周期越大,2个导轮叶片表面的压力场参数值显著更大,越不易形成空化现象。
|
图 8 不同摇摆周期下导轮1压力分布云图 Fig. 8 Pressure distribution of inducer 1 for different rolling period |
|
图 9 不同摇摆周期下导轮2压力分布云图 Fig. 9 Pressure distribution of inducer 2 for different rolling period |
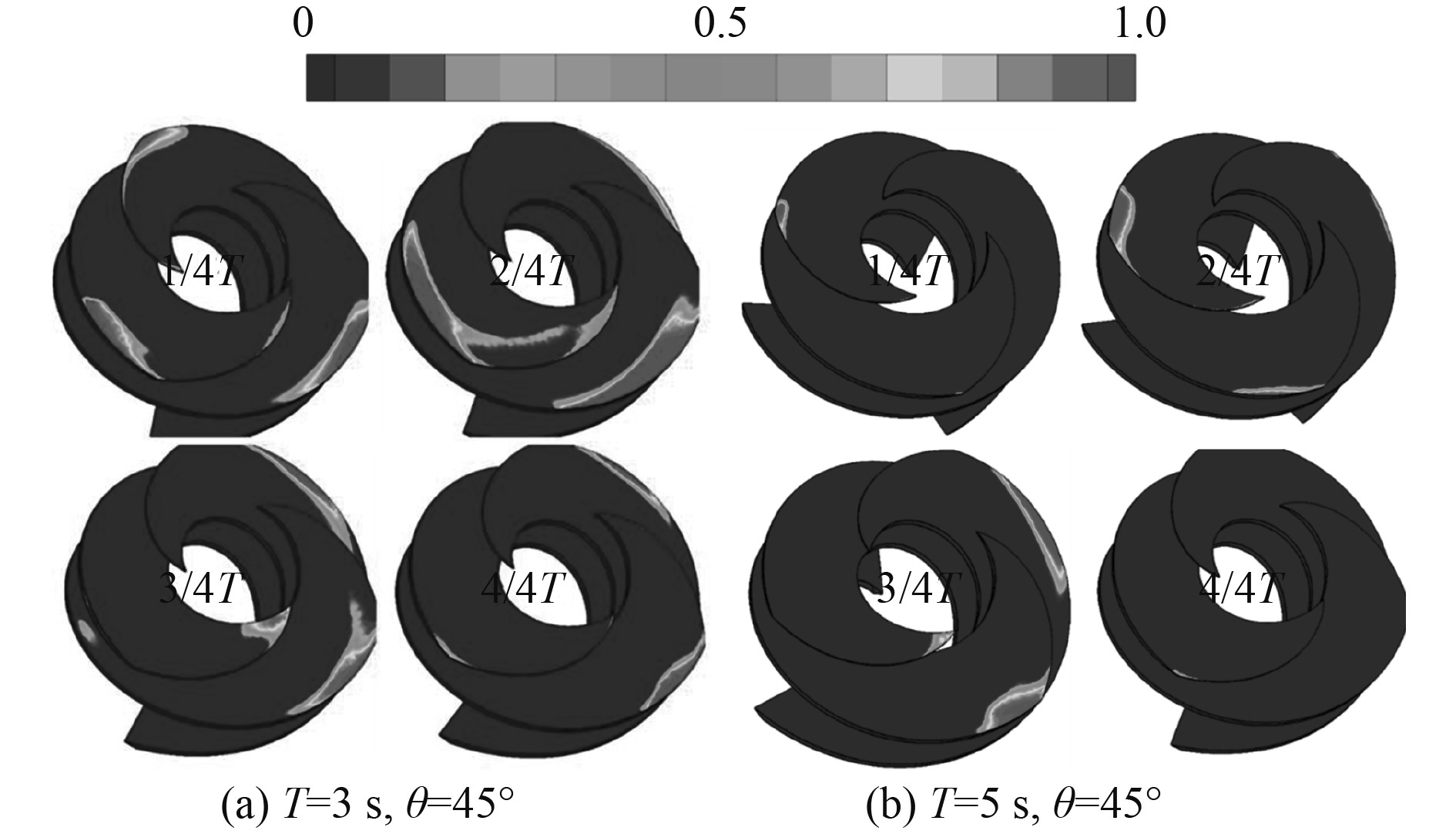
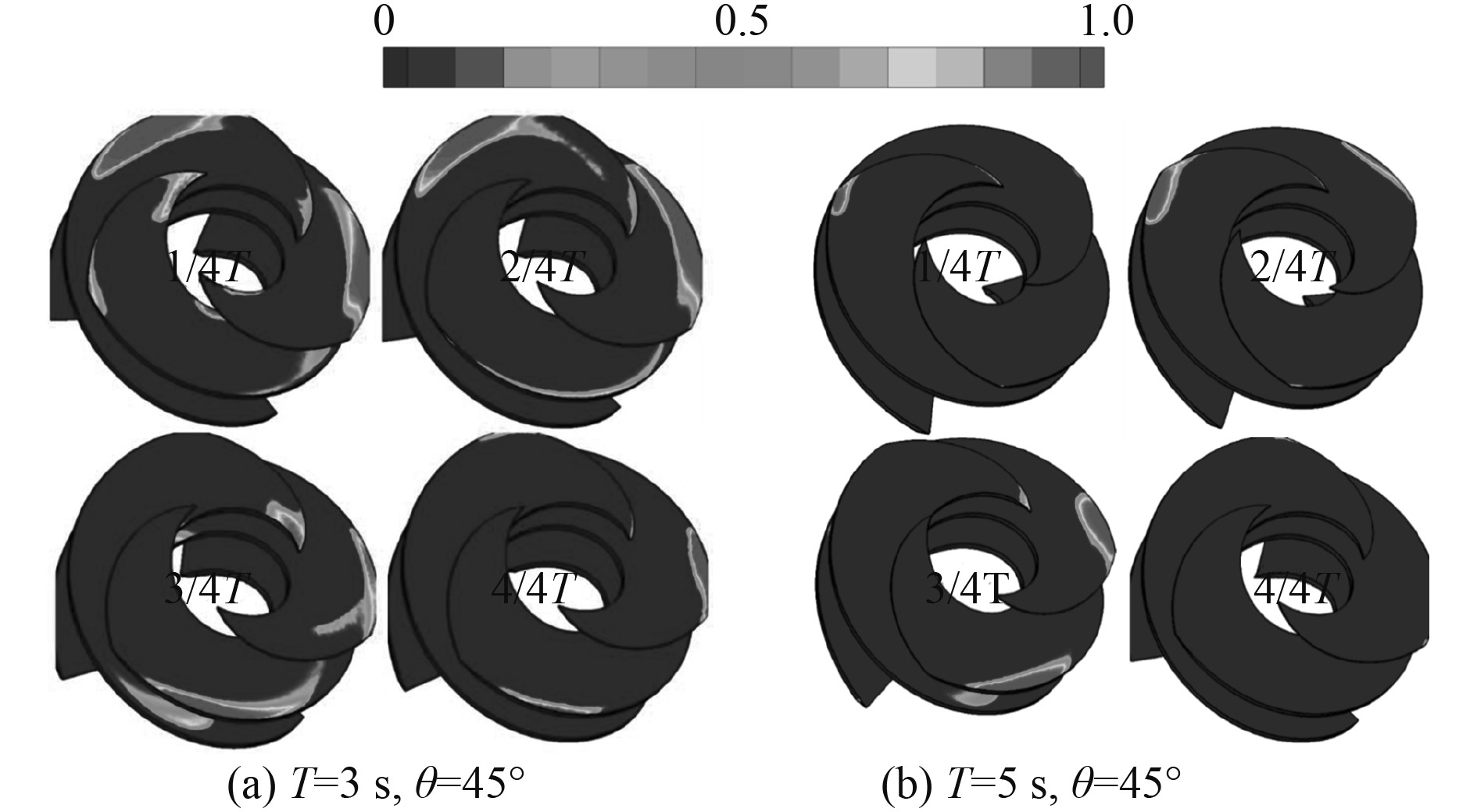
图10和图11更直观地给出了导轮叶片表面形成的空化影响范围,不难发现,出现空化的区域与图8和图9中低压区的影响范围一致。具体来看,单周期内导轮叶片表面的空化现象源于叶片吸力面边缘,随后向压力面扩散,在3/4周期时刻影响范围最大,而后降低,但导轮叶片表面的空化影响范围十分有限。空化现象的形成主要在前1/4周期内,而后大体上保持稳定,存在于2个导轮叶片表面吸力面边缘,随着关键部件继续做摇摆运动而略有变化。此外,摇摆周期越大,2个导轮叶片表面形成的空化现象范围越小,与上文分析导轮叶片压力场具有高度对称性结果类似,空化影响范围出现了高度的对称性。
|
图 10 不同摇摆周期下导轮1汽含率分布云图 Fig. 10 Vapor fraction distributions of inducer 1 for different rolling period |
|
图 11 不同摇摆周期下导轮2汽含率分布云图 Fig. 11 Vapor volume fraction distributions of inducer 2 for different rolling period |
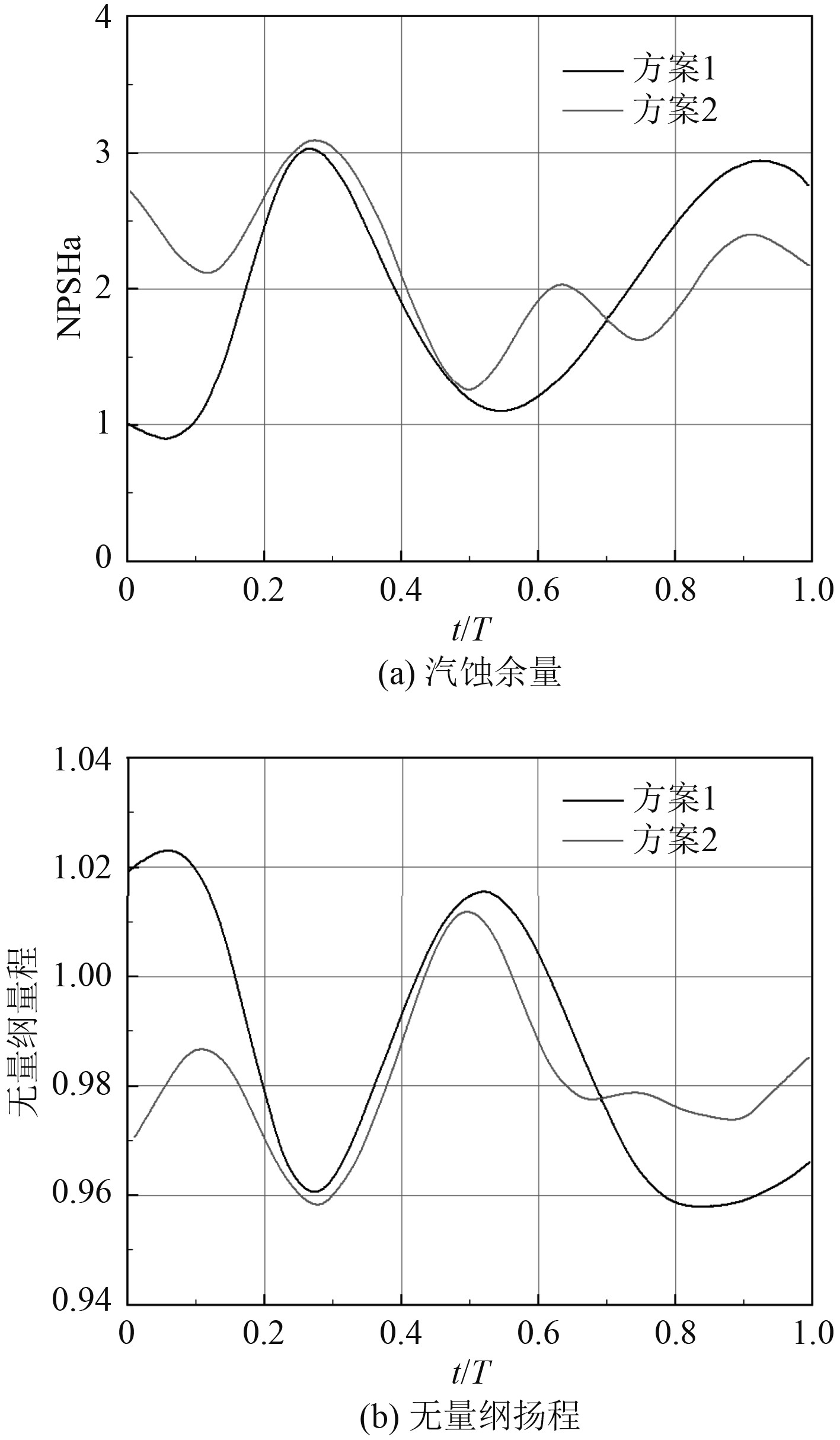
图12所示为不同摇摆周期下汽蚀余量及无量纲扬程的动态演化规律。可以看出,在经历5个摇摆周期后,依然未达到完全的周期性稳定工况。不同摇摆周期下扬程均为先减再增再减的规律,均在1/4及3/4周期时刻扬程达到最小值,而2/4及4/4周期时刻扬程最高。结合上文对空化影响范围的时变规律可知:空化的影响范围与扬程的大小呈现显著的负相关性,汽蚀余量这个性能参数通常用来描述系统特定时刻状态与空化形成的临界状态间的距离。汽蚀余量越大表明系统中的空化越难形成,观察图12中汽蚀余量的时变曲线可知:2个摇摆周期方案中汽蚀余量先增后减再增再减,但与实际的空化形成规律相反,这是由于该汽蚀余量指标为装置汽蚀余量,反映的是正常工况下的系统的抗汽蚀性能,但在摇摆条件下不能准确衡量复杂系统内部的空化程度,需要结合实际流场来进行判断。整体而言,摇摆周期越大,汽蚀余量的时变波动范围越小,表明空化现象的影响时间段越短。
|
图 12 不同摇摆周期下汽蚀余量及无量纲扬程变化情况 Fig. 12 The influences of rolling period on the NPSHa and head |
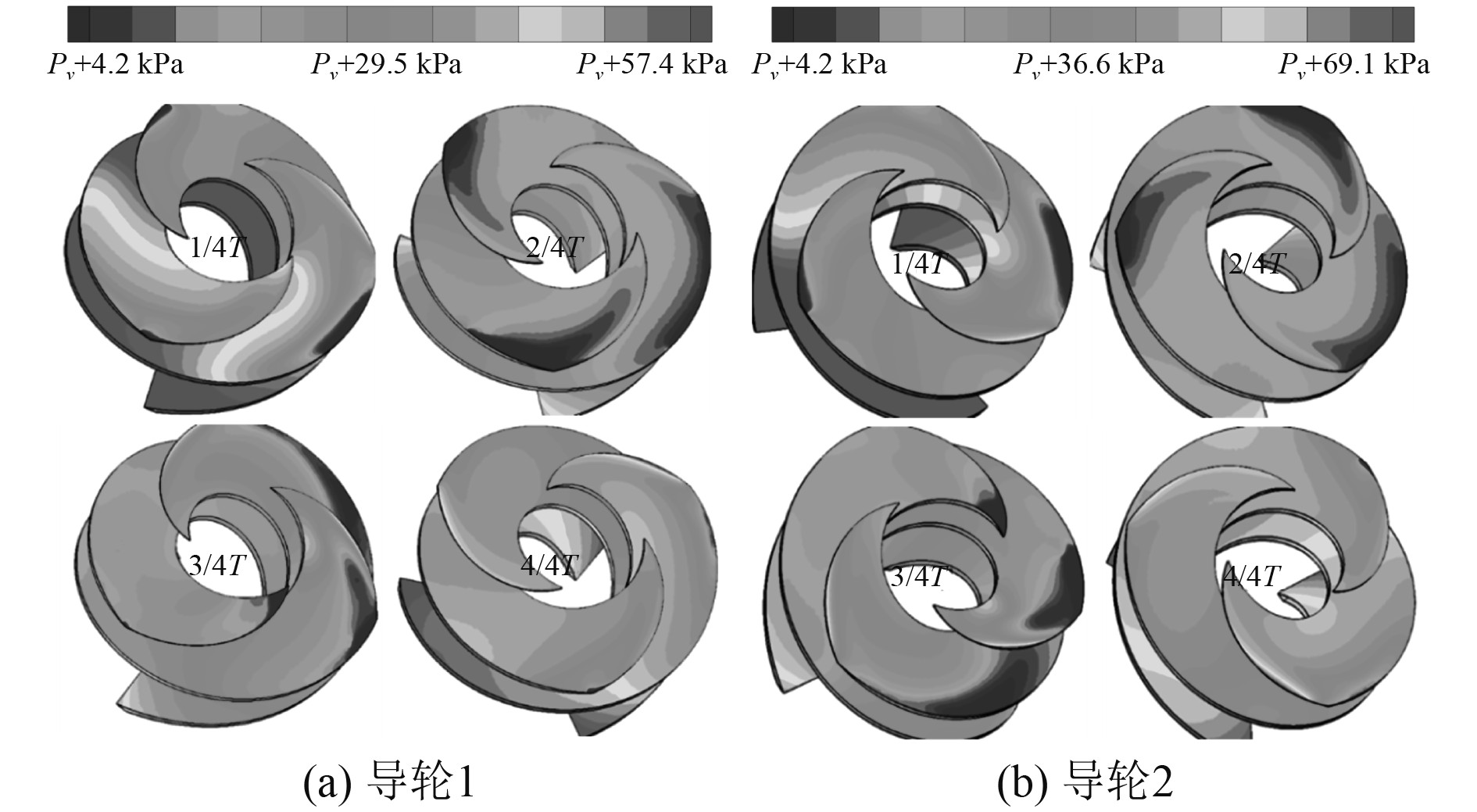
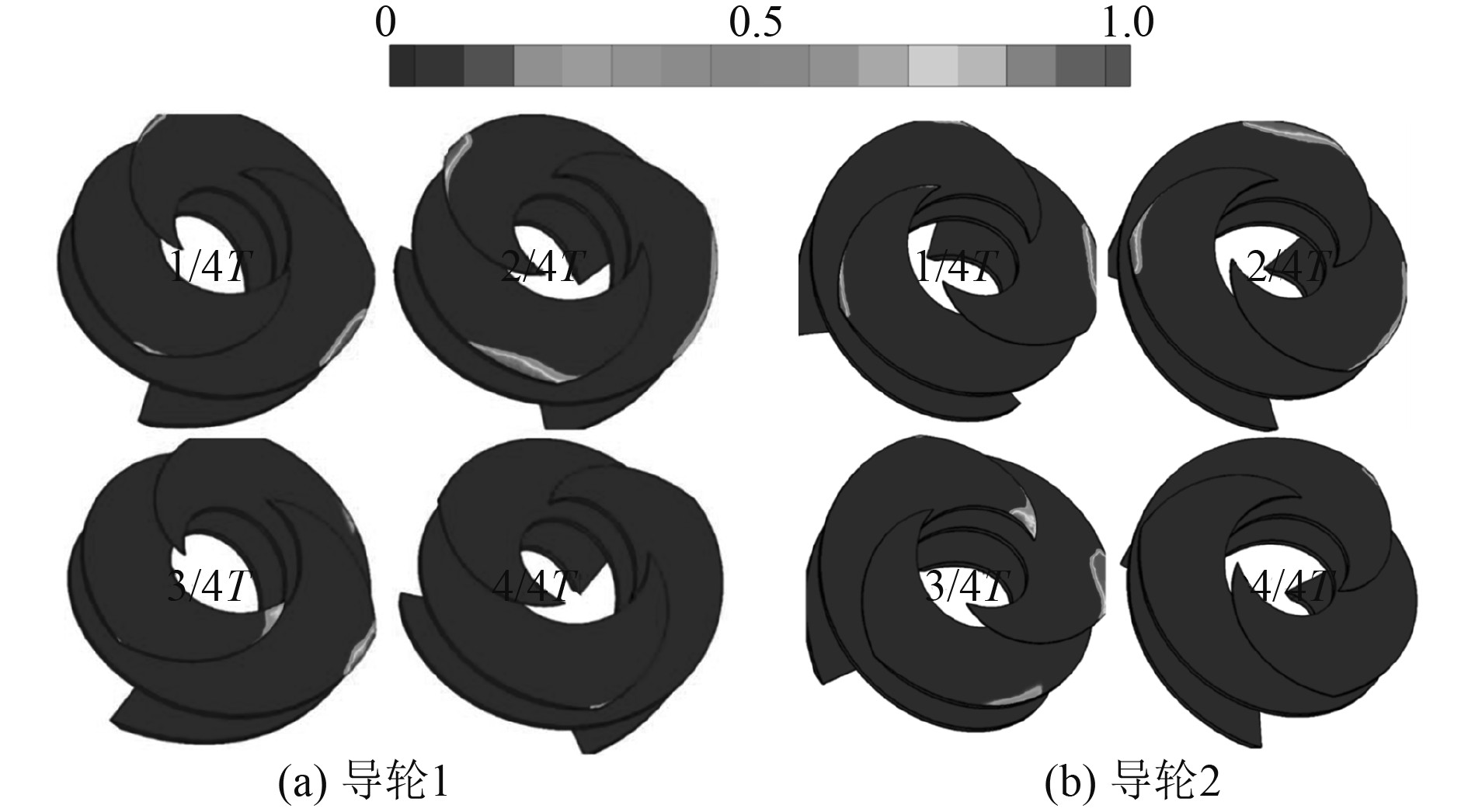
为研究摇摆幅值的影响,本文开展了2种不同摇摆幅值下的离心泵数值模拟(方案1:摇摆周期T=3 s,摇摆幅值θmax=45°;方案3:摇摆周期T=3 s,摇摆幅值θmax=30°)。与摇摆周期影响研究结果类似,在一级工作轮与二级工作轮中压力最小值均大于饱和蒸汽压力,未曾出现空化现象。图13和图14分别给出了方案3两个导轮叶片表面的压力分布云图和汽含率分布图,对比图8(a)和图9(a)可以看出,摇摆幅值越大2个导轮叶片表面的压力值更小,越容易形成空化现象,意味着其受摇摆运动的影响越大,抗汽蚀性更弱。
|
图 13 导轮1及导轮2叶面压力分布(T=3 s,θmax=30°) Fig. 13 Pressure distributions on the inducer 1 and 2 (T=3 s,θmax=30°) |
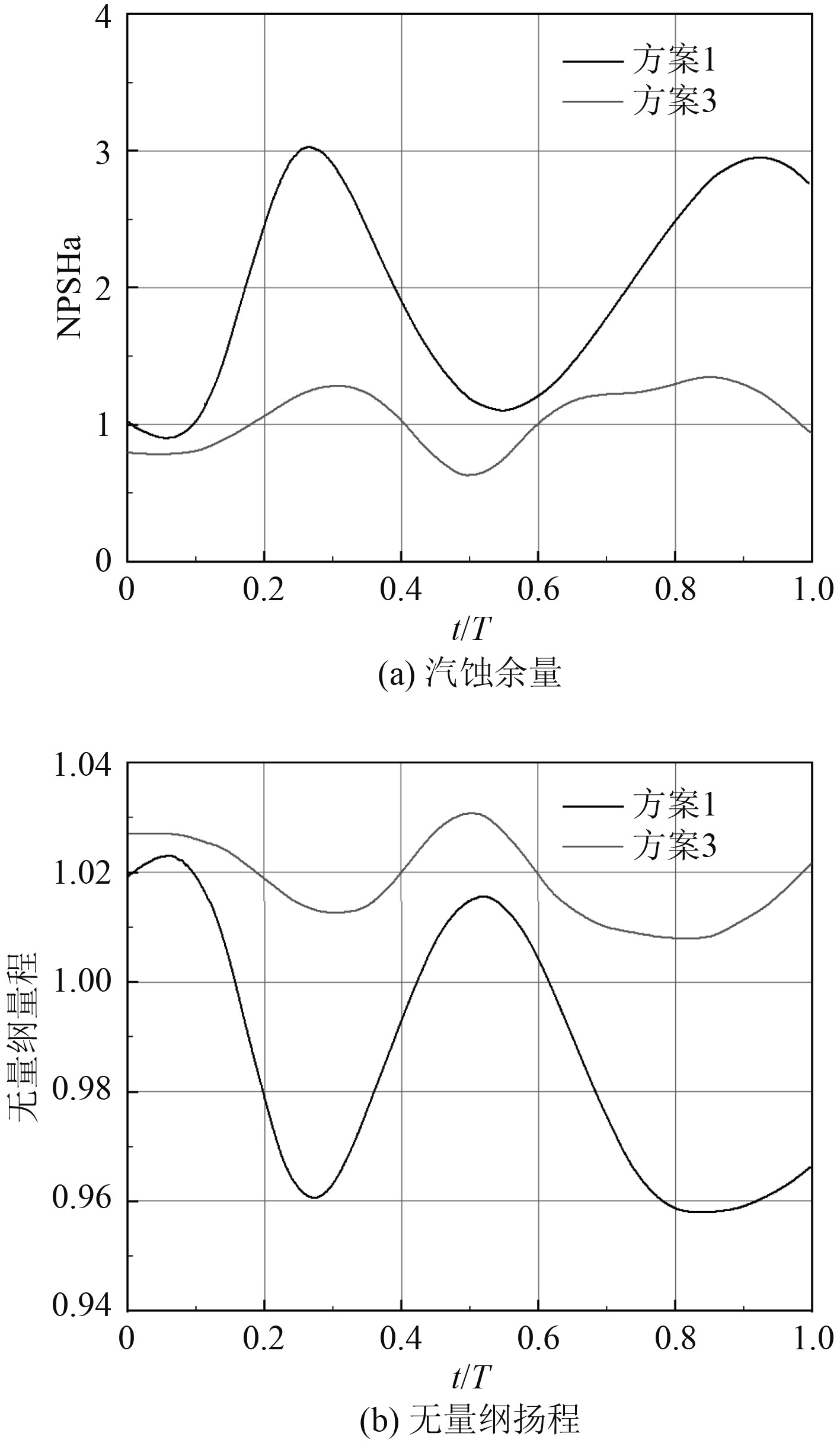
图15所示为不同摇摆幅值下汽蚀余量及扬程变化的规律。其规律与前文类似,同时可以看到,随着摇摆幅值的减小,汽蚀余量与扬程的波动量也越小,扬程有所增加。这表明摇摆幅值越小,空化影响范围越小,而汽蚀余量规律与之相反。可知,仅从汽蚀余量数值分析并不能准确衡量离心泵内部空化现象,必须结合实际流场进行判断。
|
图 14 导轮1及导轮2叶面汽含率分布(T=3 s,θmax=30°) Fig. 14 Vapor volume fraction distributions on the inducer1 and 2 (T=3 s,θmax=30°) |
|
图 15 不同摇摆幅值下汽蚀余量及无量纲扬程变化情况 Fig. 15 The influences of rolling amplitude on the NPSHa and head |
本文对海洋摇摆条件下的离心泵内汽蚀特性以及总体特性开展了数值仿真研究,结论如下:
1)构建了海洋条件下离心泵汽蚀仿真模型,通过与文献试验数据对比分析,汽蚀模型采用ZGB模型,旋转机械仿真采用动网格技术,离心泵摇摆公转采用动网格技术能较准确预测摇摆条件下离心泵汽蚀过程;
2)摇摆过程中导轮吸力面边缘出现汽蚀,并向压力面扩散,工作轮区域未发现明显汽蚀发生,通过对流量、扬程、功率以及效率等整体特性值分析可以发现时均值与固定平台相差并不大,然而部分时刻(1/4T及3/4T)与时均值存在较大偏差;
3)采用时均量衡量摇摆条件对离心泵汽蚀过程影响并不足够,针对海洋条件诱发的摇摆、晃荡等工况,还需综合考虑瞬态因素,识别离心泵汽蚀风险。
| [1] |
郭晓梅. 高速诱导轮离心泵抗汽蚀特性的数值计算与试验研究[D]. 杭州: 浙江理工大学, 2013.
|
| [2] |
潘中永, 袁寿其, 编著. 泵空化基础[M]. 镇江: 江苏大学出版社, 2013.
|
| [3] |
黄建德, 邓强, 黄炜. 离心泵叶轮形状对汽蚀损伤的影响[J]. 核动力工程, 2002, 23(4): 45-49. DOI:10.3969/j.issn.0258-0926.2002.04.012 |
| [4] |
刘忠, 邹淑云, 李志鹏, 等. 离心泵空化状态下声发射信号的小波能量特征[J]. 农业工程学报, 2015, 31(8): 99-103. |
| [5] |
王秀礼, 袁寿其, 朱荣生, 等. 离心泵汽蚀断裂工况原因的数值模拟分析[J]. 核动力工程, 2012, 33(6): 101-104. DOI:10.3969/j.issn.0258-0926.2012.06.022 |
| [6] |
王秀礼, 袁寿其, 朱荣生, 等. 离心泵汽蚀过渡过程瞬态特性分析[J]. 西安交通大学学报, 2012, 46(7): 38-43. |
| [7] |
王秀礼, 姜大连, 俞志君, 等. 船用离心泵汽蚀性能数值模拟与试验研究[J]. 热能动力工程, 2011, 26(5): 588-592. |
| [8] |
张宁. 离心泵内部非稳态流动激励特性研究[D]. 镇江: 江苏大学, 2016.
|
| [9] |
崔宝玲. 高速诱导轮离心泵的理论分析与数值模拟[D]. 杭州: 浙江大学, 2006.
|
| [10] |
申晓慧. 摇摆条件下凝水泵三维汽蚀仿真模拟[D]. 哈尔滨: 哈尔滨工业大学, 2020.
|
| [11] |
赵希枫. 基于CFD技术改善离心泵内部空化性能的研究[D]. 兰州: 兰州理工大学, 2009.
|
 2024, Vol. 46
2024, Vol. 46
