0 引　言

环境驱动无人船通常指的是依靠海洋自然能源驱动的水面航行器，例如波浪滑翔机、saildrone等，它们具有航速低、欠驱动、机动性差等特点，使其在大洋远距离航行时面临着诸多困难。首先，欠驱动无人船航速较低，使其对海洋流场更为敏感，在部分强洋流海域甚至会出现失控的情况，因此在其路径规划问题上需要充分考虑洋流的影响；此外，大洋远距离航行需要充分考虑海洋流场的季节效应，不同时间出发的无人船抵达目标所用时间有所不同，即需要在时间维度上等待有利洋流，选择合适的出发时间。

近年来，针对大规模复杂海洋环境下无人船的路径规划问题，涌现出诸多研究。KULARAINE等^[1]通过图搜索算法在流场中生成无人船可行路径，同时在路径规划过程中考虑了如距离和时间代价等，利用最小生成树算法寻找到了一条具有最小代价的路径。ALVAREZ等^[2]针对AUV进行路径规划，充分考虑变化的海洋环境，利用演化算法在全局上搜索出适应海洋变化的可行路径集，以避障和路径距离最短为目标对路径进行优化。GARAU等^[3]基于${\mathrm{A}^*}$算法搜索出了一条能耗最小的路径，并分析了不同启发式函数对${\mathrm{A}^*}$算法性能的影响。姚褚梁等^[4]基于双层规划算法提出了一种时变洋流场环境下的路径规划方法，考虑洋流场的时变性特征，以能耗最小为目标建立了AUV路径规划数学模型，同时利用粒子群算法来求解最优路径。王斐然^[5]针对复杂海洋环境下无人船的自主决策系统展开研究，提出了基于种群超启发式算法的路径规划方法。KRUGER等^[6]提出了基于能量最优的路径规划方法，并且建立了多维代价函数作为衡量路径最优指标，但其考虑的模型是一个较为简单的静态水流和障碍物的河口人工模型。WITT和ZHANG等^[7-8]在此基础上做了改进，使用真实的洋流数据，同时在具有动态障碍物的时变环境中研究更加复杂的规划案例。

上述研究大多假定流场环境是稳定静态的，流场由多个漩涡公式叠加形成，不适用实际动态变化的流场环境；同时传统的路径规划方法通常将路径离散成若干个点，点和点之间通过直线连接，忽略了环境特性，并且路径在路径点之间出现突然转折，缺乏光滑性，而使用B样条曲线可以很好解决上述问题；相较于其他路径搜索算法，遗传算法收敛速度快，鲁棒行强，适用于求解复杂的优化问题。鉴于此，本文首先将我国国家海洋科学数据中心（NMDC）提供的洋流数据进行可视化处理，建立了动态变化的洋流场模型。然后通过B样条控制点随机生成无人船路径，计算每一条可行路径在动态洋流中的路径距离、洋流代价以及路径光滑度等综合代价函数，基于遗传算法迭代搜索最优控制点组合，使其满足综合代价值最小。同时，考虑到大洋长航程路径规划中时间跨度长的特点，对比分析了出发时间对航行时间的影响。

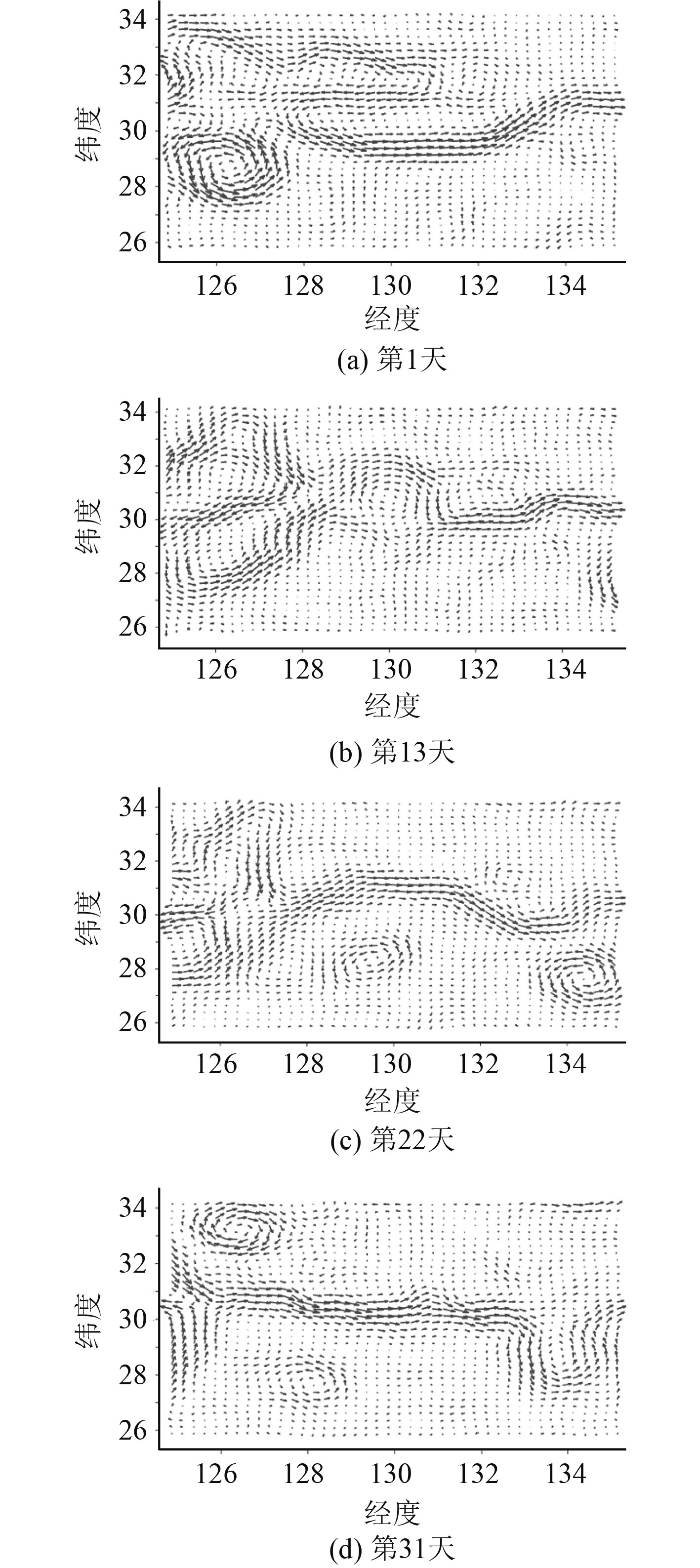
1 路径规划基本问题陈述 1.1 洋流场模型

洋流又称海流，是指海水沿着一定方向有规律的具有相对稳定速度的流动^[9]，其随着时间和地点的变化而变化，同时受到多种因素诸如风、地球偏转力等影响。现如今，随着科技的迅猛发展，已经可以通过多种渠道比如卫星观测、高频雷达探测等手段获取实时洋流信息^[4]。目前，我国国家海洋科学数据中心通过台站、浮标、调查船等观测手段获取并统计了历年的洋流数据，覆盖了全球海域，同时针对洋流流动做了可视化处理，该数据已经广泛应用于海洋学界，为船舶路径规划提供了重要的数据支撑。本文流场信息是先验、可用的，流场时间跨度为2019年1月1日−2019年12月31日，时间维度上以天为单位更新，地点跨度为从(0.125 S,98.875 N)～(45.125 N,162.62 E)，数据来源于国家海洋科学数据中心。图1所示为2019年9月1日−2019年10月1日从(26 N, 125 E)～(34N, 135E)海域可视化之后的流场，箭头长度为流速大小，箭头方向为流的方向。

针对该先验可用的洋流数据，将其处理为如下数学模型：

$ {V_f}(L,t) = \left[ \begin{gathered} \mathop x\limits^ \bullet \\ \mathop y\limits^ \bullet \\ \end{gathered} \right] = \left[ \begin{gathered} {V_{fx}}(x,t) \\ {V_{fy}}(y,t) \\ \end{gathered} \right]，L \in {\bf{Z}},t \in \left[ {{t_s},{t_f}} \right] \in {\bf{R}}。$

(1)

式中：$x$为东西经度方向；$y$为南北纬度方向；$L$为某个具体经纬度坐标下的位置；${V_f}(L,t)$为洋流的流速，表示在$L \in {\bf{Z}}$处、$t \in [{t_s},{t_f}] \in {\bf{R}}$时刻的洋流，是同时具有大小、方向和时间3个维度的物理量。洋流的流速大小为${V_f}(L,t) = \left\| {{V_f}(L,t)} \right\|$，且流速最大值${V_{fm}}(L,t)$为：

$ {V_{fm}}(L,t) = \mathop {\max }\limits_{L \in {\text{Z}},t \in [{t_s},{t_f}]} {V_f}(L,t) 。$

(2)

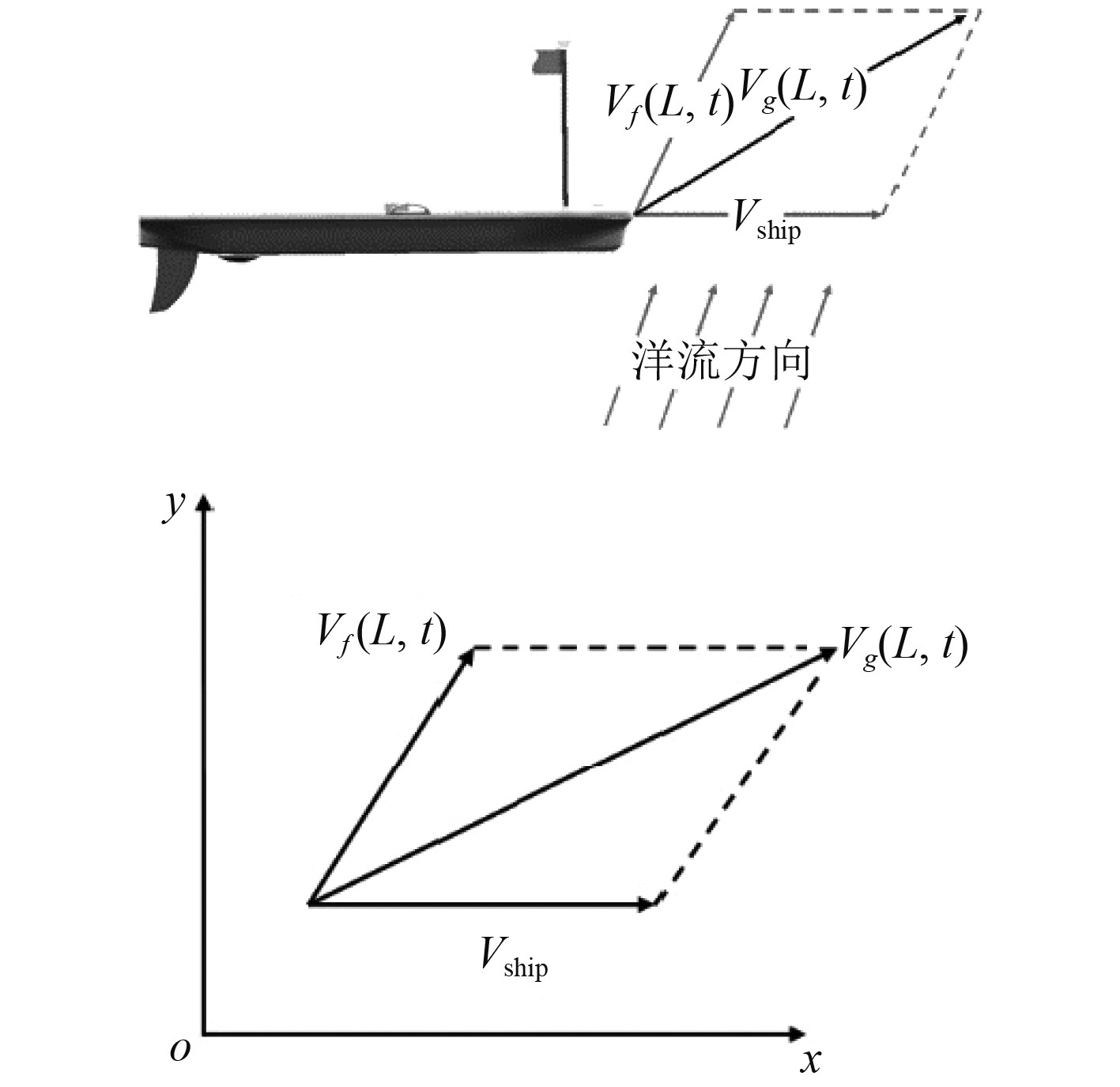
同时假定欠驱动无人船在静水中的船速${V_\mathrm{ship}}$为常数。图2所示为船在静水中的船速和洋流流速的合速度${V_g}(L,t)$，通过二维平行坐标法建立流场模型，箭头方向为洋流指向，箭头长度为洋流流速大小。

$ {V_g}(L,t) = {V_f}(L,t) + {V_\mathrm{ship}}。$

(3)

1.2 路径形式

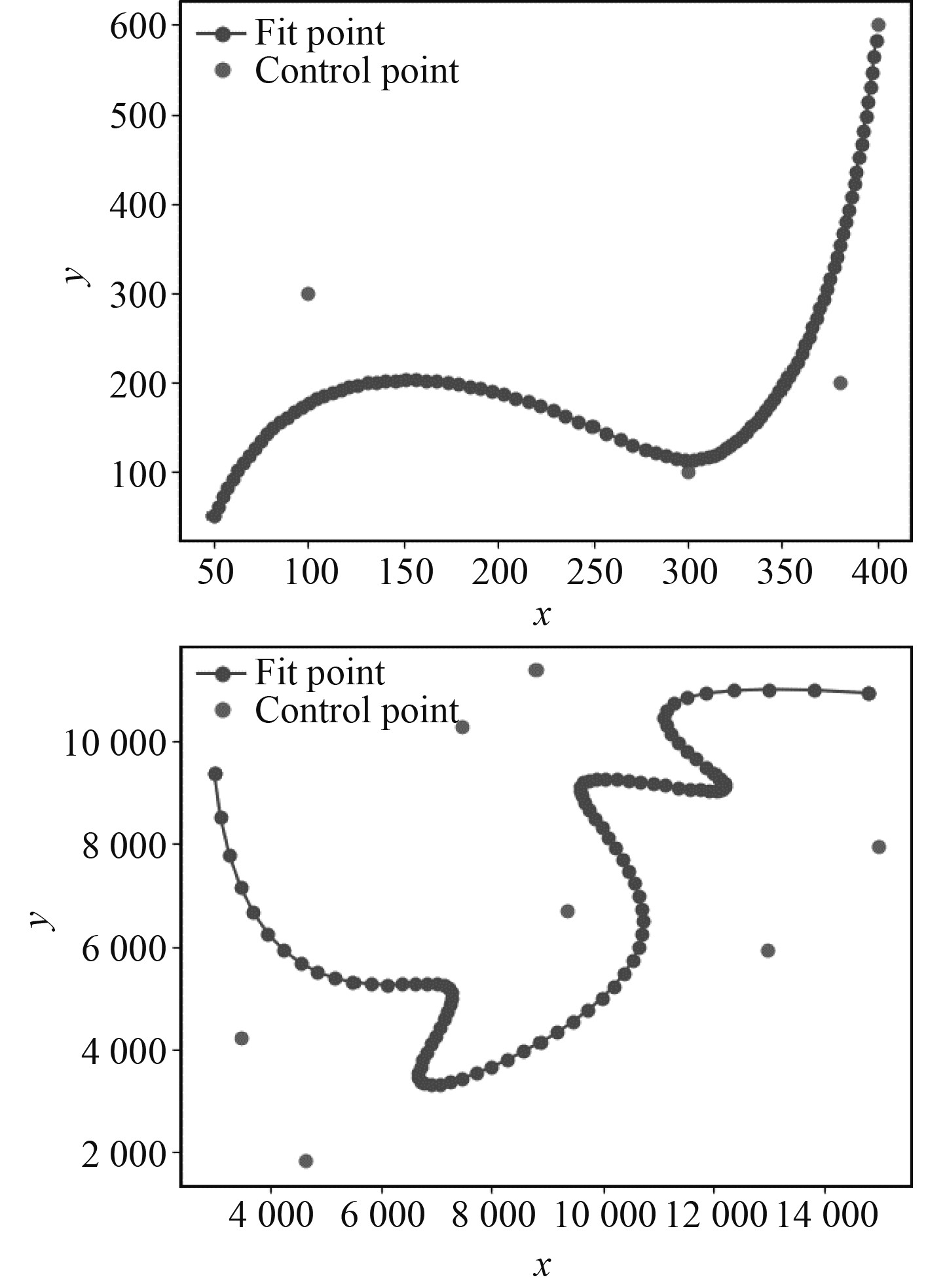
由于环境驱动的欠驱动无人船在大洋中航行时始终在海面上航行，则整个路径形式可表示为一条二维路径^[5]。许多传统的路径规划方法将连续的路径空间离散化成有限路径点，路径点之间通过直线连接，这就会导致生成的路径在路径点之间出现突然转折，同时忽略了中间障碍物和环境特性，导致路径无法适应环境的变化，缺乏光滑性。而在路径规划问题中使用B样条曲线可以很好解决上述问题。样条即为通过一组指定点集而生成的平滑曲线柔性带^[10]，而B样条曲线是由一组控制点来定义的，如图3所示。通过调整这些控制点的位置，可灵活调整曲线形状，同时可以利用最优化方法来优化控制点的位置，以满足特定的运动需求及环境约束条件，从而得到更优的路径规划结果。因此，本文使用B样条曲线来表示无人船路径，设时间域为$[{t_s},{t_f}] \in {\bf R}$，控制点数量为n的B样条曲线轨迹可以定义为如下式：

$ z(t) = \sum\limits_{i = 1}^n {{P_i}{B_{i,k,\delta }}(t),t \in [{t_s},{t_f}]}。$

(4)

式中：${P_i} = [{P_1},...,{P_n}]$为B样条曲线的控制点，且${P_i} \in {{\bf R}^m}(i \in \{ 1,...,n\} ,n \geqslant k + 1)$，这些控制点用于调整样条曲线的形状和走向，且第一个控制点和最后一个控制点分别为样条曲线轨迹$z(t)$的起点和终点，即$z({t_s}) = {P_1}、z({t_f}) = {P_n}$；${B_{i,k,\delta }}(t)$包含了B样条的k次基函数，与控制点${P_i}$相对应，阶次k≥1，基函数的计算可根据de Boor-Cox递推公式^[11]:

$ {B_{i,0,\delta }}(t) = \left\{ \begin{gathered} 1,{\text{ }}{\tau _i} \leqslant t \leqslant {\tau _{i + 1}}，\\ 0,{\text{ }}{\mathrm{else}}。\\ \end{gathered} \right. $

(5)

$ {B_{i,k,\delta }}(t) = \frac{{t - {\tau _i}}}{{{\tau _{i + k}} - {\tau _i}}} {B_{i,k - 1,\delta }}(t) + \frac{{{\tau _{i + k + 1}} - t}}{{{\tau _{i + k + 1}} - {\tau _{i + 1}}}} {B_{i + 1,k - 1,\delta }}(t),k \geqslant 1。$

(6)

式中：

$ \delta = \{ {\tau _1} \leqslant {\tau _2} \leqslant ,..., \leqslant {\tau _{n + k + 1}}\}，$

(7)

$ {\tau _j} = \left\{ \begin{gathered} {t_s},{\text{ }}1 \leqslant j \leqslant k，\\ {t_s} + (j - k - 1)\frac{{{t_f} - {t_s}}}{{n - k}},{\text{ }}k + 1 \leqslant j \leqslant n + 1，\\ {t_f},{\text{ }}n + 2 \leqslant j \leqslant n + k + 1。\\ \end{gathered} \right. $

(8)

将B样条曲线引入到欠驱动无人船路径表示中，则一组控制点坐标可表达为：

$ \{ {{P = (P}}_{{i}}^{{x}}{{,P}}_{{i}}^{{y}}{{)|i = }}1,2,3,...,n\}。$

(9)

同时欠驱动无人的一条路径形式可以表达为：

$ z(t) = \left\{ \begin{gathered} X(t) = \sum\limits_{i = 1}^n {P_i^x{B_{i,k,\delta }}(t)}，\\ Y(t) = \sum\limits_{i = 1}^n {P_i^y{B_{i,k,\delta }}(t)}。\\ \end{gathered} \right. $

(10)

2 基于遗传算法的路径规划策略

遗传算法是一种自适应全局优化的元启发式搜索算法，其受到基于适者生存原则的达尔文进化论和孟德尔遗传学理论启发，通过模仿自然选择和繁殖的过程，使用合理的适应度函数对种群性能进行评估，从而不断迭代和保留优势种群，通常分为生成初始种群、选择、交叉、突变遗传和计算个体适应度值等步骤^[12]。由于遗传算法收敛速度较快同时复杂度更低，具有较强鲁棒性，因此目前该算法已成功运用于解决包括路径规划在内的许多涉及到搜索、学习、优化的问题。

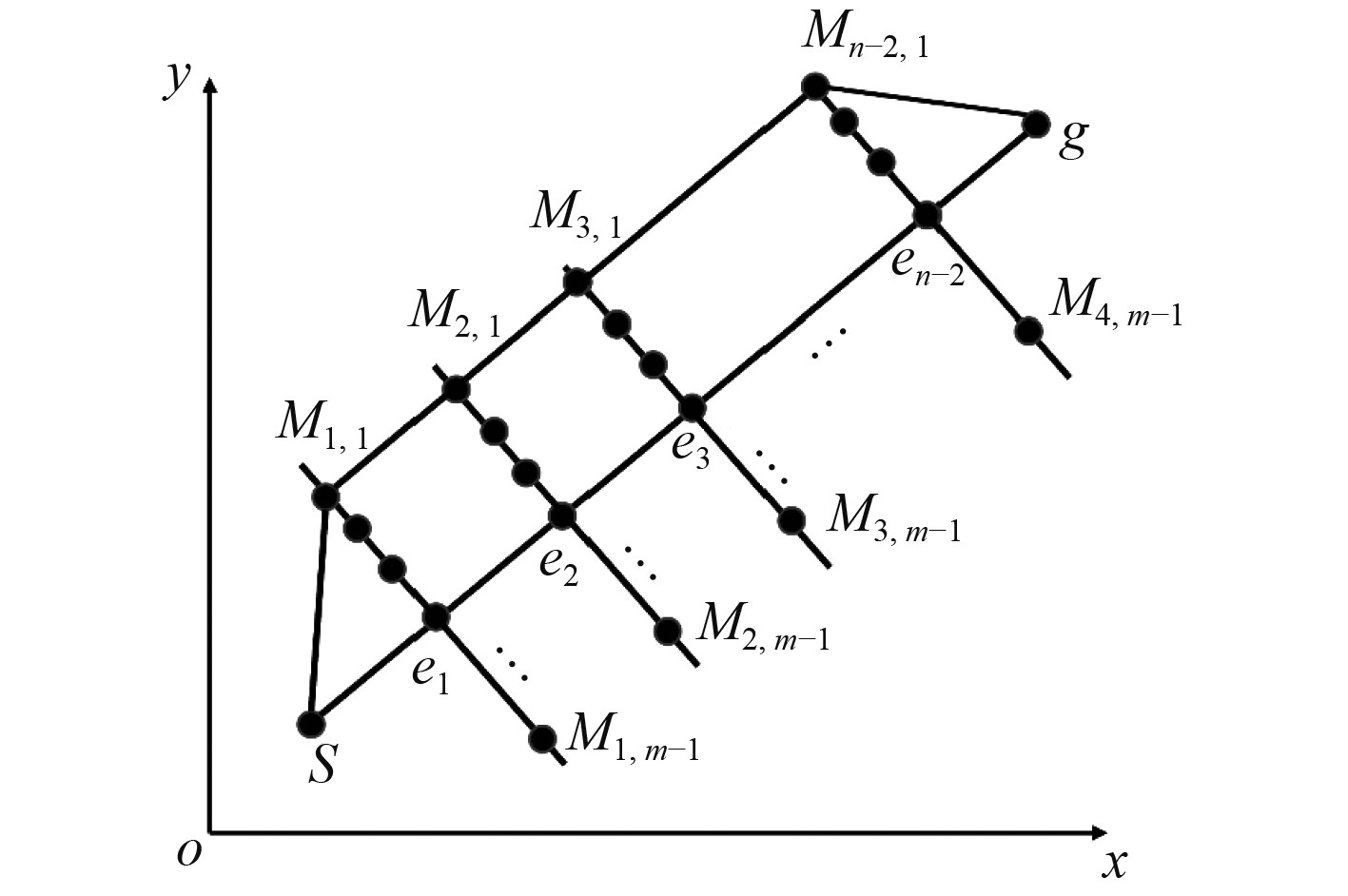
2.1 编码方式

基于上述路径形式的讨论，整个路径规划问题就转化为了搜索一组控制点，种群中每一个个体都为一组控制点$\{ P = (P_i^x,P_i^y|i = {{1,2,3,}}...{{,\mathit{n}}})\} $，代表着一条可行路径。如图4所示，设控制点的数量为n，起点s为第一个控制点${P_1}$，终点g为最后一个控制点${P_n}$，连接起点与终点得到直线sg，在直线sg之间取n-2个等分点，等分点设为$\{ {e_i}|{e_1},{e_2},{e_3},...,{e_{n - 2}}\} $，过每一个等分点${e_i}$作直线sg的垂线，得到n-2条垂线段，再在每一条垂线上随机生成m-1个点，则任意一组控制点P为：$[{P_1},{P_2},...,{P_n}] = [s,{M_{1,1}},{M_{2,1}},...,{M_{n - 2,1}},g]$，这样一组控制点存放在一个个体中，个体维度为n；由于每条垂线上随机生成了m-1个点，再加上等分点，则在初始状态下共可以产生m组控制点，从而得到了初始状态的种群，且种群规模为m。

控制点坐标计算如下，如图5所示，由于已知起点s的经纬度坐标为$(la{t_s},{{lng}}_s)$和终点g的经纬度坐标$(la{t_s},{{lng_s}})$，则可以通过经纬度换算式（11）求出sg之间的距离${d_{sg}}$。

$\begin{split} &{d_{sg}} = 2\arcsin \\ &\sqrt {{{\sin }^2} \frac{{la{t_g} - la{t_s}}}{2} + \cos ( la{t_s} )\cos ( la{t_g} ){{\sin }^2} \frac{{{{ln}}{{{g}}_g} - {{ln}}{g_s}}}{2}} \times {{r}}。\end{split} $

(11)

式中：r为地球半径；${k_{sg}}$为直线sg的斜率。

则控制点坐标(${{M}_{i,k,x}},{{M}_{{i}{.k}{.y}}}$)为：

$ \left\{ \begin{gathered} {M_{i,k,x}} = {e_{i,x}} + {d_{sg}} \times rand，\\ {M_{i,k,y}} = {e_{i,y}} - \frac{{{d_{sg}} \times rand}}{{{k_{sg}}}}。\\ \end{gathered} \right. $

(12)

因为${d_{sg}}$可以通过经纬度换算公式求出，又因为${e_i}$为${d_{sg}}$的等分点，因此$({e_{i,x}},{e_{i,y}})$可以求出，rand为随机数且$rand \in [ - 0.5,0.5]$，则一组控制点坐标就全部可以求出。

通过上述编码方式，可以将B样条曲线的控制点表示为遗传算法的个体，即一组控制点代表一条可行路径，一条无人船路径代表一个遗传个体，并通过遗传算法的进化过程来搜索最佳的控制点配置，以实现时间最优的路径规划目标。

2.2 适应度函数设计

适应度函数是衡量遗传算法收敛和有效性的重要指标^[13]。在本文中，种群中每一个个体都代表一组控制点，即每个个体都代表着一条路径，然后计算个体的适应度，再进行遗传迭代优化。过程中淘汰劣质个体和保留遗传优质个体的依据便是适应度函数，因此，应根据实际问题的要求选择合适的适应度函数。欠驱动无人船在大洋中航行时的路径规划问题应满足3个条件：1）限制路径距离尽可能短；2）限制船和洋流的合速度尽可能高；3）限制路径尽可能光滑。3个限制条件共同作用的结果是搜索出一条距离尽可能短、方向上尽可能顺流且光滑的路径。对以上3项指标取不同的权重，形成最终的适应度函数，通过该适应度函数筛选出来的个体满足综合代价值最小。

2.2.1 路径距离

该限制条件主要是为了约束路径距离，即在满足船舶与洋流合速度尽可能大的情况下，搜索出一条距离尽可能短的路径。

$ f(d) = \sum\limits_{i = 1}^h {z_{i + 1}^{x,y} - z_i^{x,y}}。$

(13)

式中，h为离散点数量。

2.2.2 洋流代价

欠驱动无人船由于自身航速低以及弱机动性等特点，导致其在航行过程中会显著的受到洋流的影响，因此合理利用洋流可以使船以更快的平均航速到达目的地，即在路径选择上，应该尽可能的贴近洋流的方向^[14]。洋流代价可以通过路径上每个离散点处洋流向量和路径方向向量的点乘累加来表示。

$ f(w) = \sum\limits_{i = 1}^h {\left| {\overrightarrow {{V_f}(L,t)} } \right|} \cdot \alpha (\overrightarrow {{V_f}(L,t)} ,\overrightarrow {{\tau _{z_i^{x,y}}}} )。$

(14)

式中：$\overrightarrow {{\tau _{z_i^{x,y}}}} $为点$z_i^{x,y}$处路径的单位方向向量，$\alpha $为该向量与洋流向量的夹角。

2.2.3 路径光滑度

路径光滑度可按照欠驱动无人船在大洋中航行时的曲率来计算，为了使得路径尽可能光滑，则曲率应该越小越好，曲率可通过船的偏航角来进行计算，即：

$ f(\rho ) = \sum\limits_{i = 1}^{h - 1} {\frac{{\left| {z_{i + 1}^\theta - z_i^\theta } \right|}}{{\left| {z_{i + 1}^{x,y} - z_i^{x,y}} \right|}}} 。$

(15)

式中，$\theta $为无人船的偏航角。

$ \theta (t) = \arctan (\frac{{\left| {{Y_{i + 1}}(t) - {Y_i}(t)} \right|}}{{\left| {{X_{i + 1}}(t) - {X_i}(t)} \right|}})。$

(16)

3个指标赋予权重进行加权求和，则最终的适应度函数为:

$ F = {\omega _1}f(d) + {\omega _2}f(w) + {\omega _3}f(\rho ) 。$

(17)

迭代优化准则为使适应度函数最小，即min F。

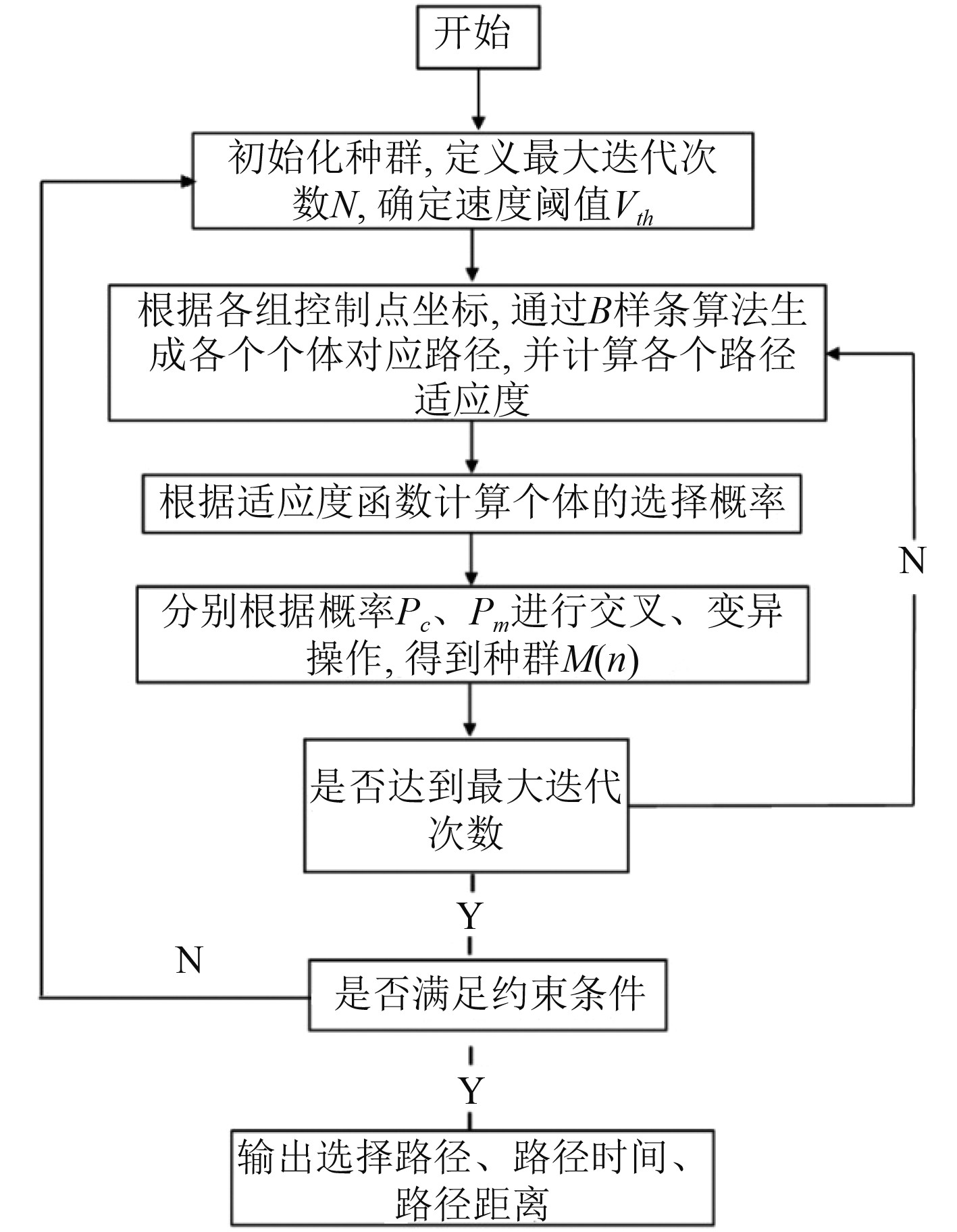
2.3 算法寻优步骤

图6所示为基于遗传算法的大范围动态流场中欠驱动无人船的路径规划流程。

该算法模型寻优步骤如下：

步骤1　随机生成19组坐标和1组等间距数量为13的控制点坐标；同时确定交叉概率为${P_c}$、变异概率为${P_m}$以及迭代次数等参数；

步骤2　根据起点和终点位置以及各组控制点的坐标，使用B样条插值算法生成欠驱动无人船在流场中的路径；

步骤3　计算各个路径的适应度函数值，记为各个个体的适应度；

步骤4　根据20个个体的适应度值进行赌轮盘选择操作，得到子代，同时20个个体中适应度最高的个体不参与选择，直接进入子代；

步骤5　进行交叉、变异操作，得到n+1代个体；

步骤6　计算n+1代个体的适应度；

步骤7　判断n是否大于设定的迭代次数，如果大于最大迭代次数，进入下一步，否则返回上述操作；

步骤8　根据得到的最优个体，进行B样条插值得到最优路径。

3 路径规划仿真实验 3.1 仿真参数设置

采用上述遗传算法进行欠驱动无人船的路径规划仿真实验。算法参数设置如下：种群规模$M = 20$，最大迭代次数$N = 1\,200$，交叉概率${P_c} = 0.7$，变异概率${P_m} = 0.1$。B样条曲线的基函数阶次$k = 3$，控制点$P$的数量为15。流场数据为先验已知的，流场时间跨度为2019年1月1日−2019年12月31日，地点跨度为从(0.125 S,98.875 N)～(45.125 N,162.62 E)，数据来源于中国国家海洋科学数据中心，本文通过多个子图来表示流场的变化。

3.2 考虑洋流和不考虑洋流的路径规划对比实验

仿真中，欠驱动无人船的起点经纬度位置选取为(38 N,150 E)，终点坐标为(45 N,160 E)，东西方向为$X$轴，南北方向为$Y$轴，通过经纬度换算公式计算出实际距离，出发时间为2019年5月1日，船舶设定航速${V_\mathrm{ship}} = 0.5\ \mathrm{m/s}$，子图按照时间分段，以天为单位输出。

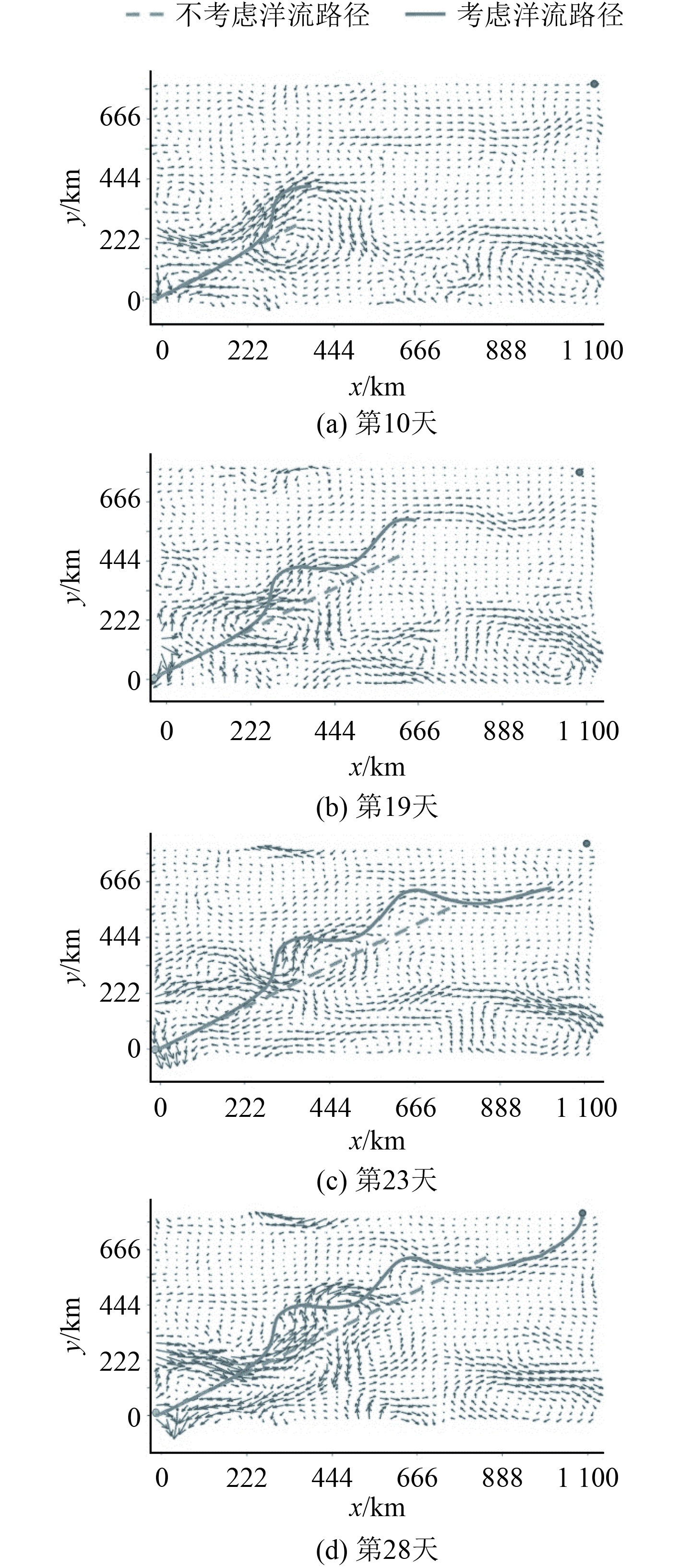
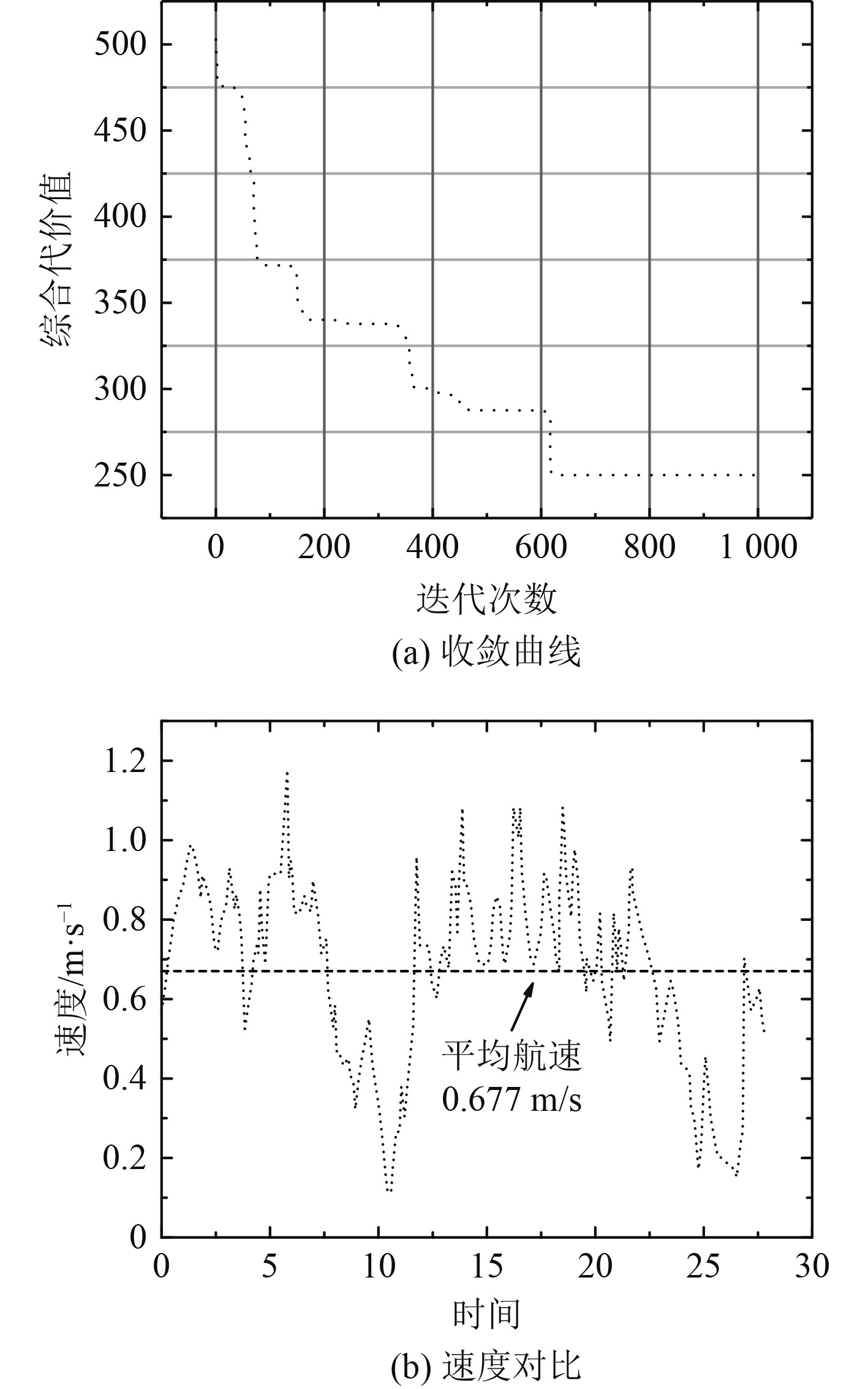
如图7所示，实线代表的是考虑洋流信息时迭代搜索出来的最优路径，虚线代表的是不考虑洋流时规划的路径，即船舶以0.5 m/s的恒定航速从起点直线走向终点。从图7(d)中可以看出，考虑洋流信息时规划出来的路径更早的到达了目的地。图8(a)所示为遗传算法收敛曲线，当迭代次数达到600次左右的时候，模型趋近于收敛。如图8(b)所示，欠驱动无人船叠加洋流之后的平均航速为0.677 m/s，大于船舶初始设定航速为0.5 m/s，证明真正利用了洋流。此外，仿真结果表明所提出的路径规划方法可以有效解决动态流场环境下欠驱动无人船目标抵达时间最短的路径规划问题。

3.3 不同出发时间的仿真对比

大洋远距离航行过程中，由于欠驱动无人船的航速较低，因此需要充分利用洋流的季节效应，即在时间维度上等待有利洋流，选择合适的出发时间。在本次仿真中，将出发时间作为路径优化参数，则路径形式变为：

$ z({t_{{t_d}}}) = \left\{ \begin{gathered} X({t_{{t_d}}}) = \sum\limits_{i = 1}^n {P_i^x{B_{i,k,\delta }}({t_{{t_d}}})}，\\ Y({t_{{t_d}}}) = \sum\limits_{i = 1}^n {P_i^y{B_{i,k,\delta }}({t_{{t_d}}})}。\\ \end{gathered} \right. $

(18)

式中：t_d为出发时间，且${t_d} \in [1,360]$，欠驱动无人船的起始点经纬度坐标为从(26 N,125 E)～(34 N,135 E)，总航程超过1000 km，出发时间工况分别选取为2019年1月1日、2019年5月1日和2019年9月1日，即t_d取值为1、150、270 。

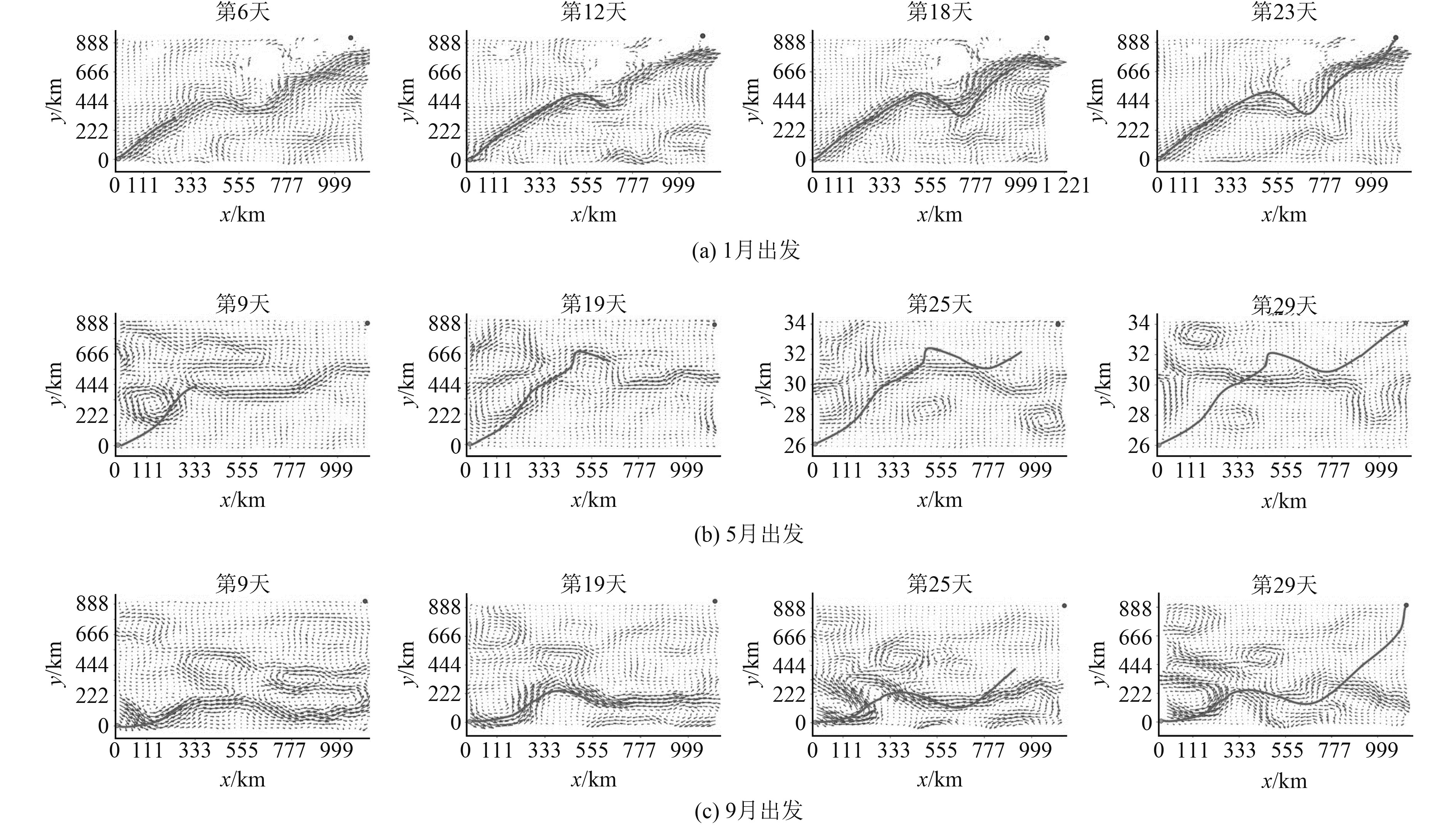
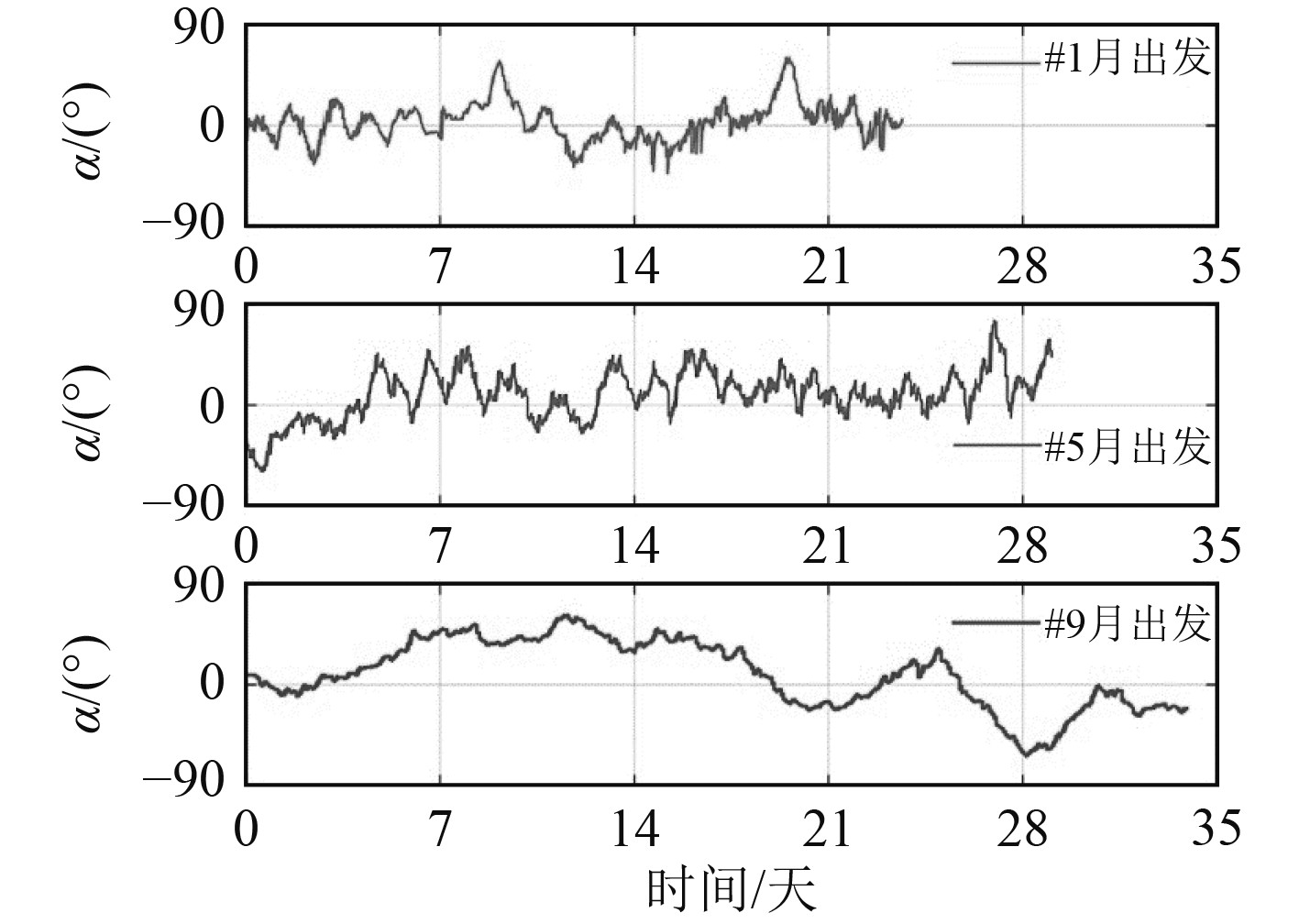
欠驱动无人船在先验已知动态流场中以不同时间出发的路径规划仿真结果如图9所示。从图9(a)可以看出1月份的洋流流向与路径方向最为拟合，图9(c)展示了当洋流流向与起始点到目标点方向向量差距过大时，此时规划出来的路径洋流代价较高，最终收敛得到的适应度值也相应更高，适应度值为251.04，平均航速也相应更低，为0.57 m/s。从图9中可以看出，选择不同出发时间最终搜索出来的最优路径也不同。分析原因如下：大洋远距离航行需要充分考虑洋流的时空动态性，即不同月份的洋流流速、流向都差距较大，在出发点和终点确定时，如果洋流流向与欠驱动无人船路径方向向量高度一致，则此时出发最为有利。如图10所示，$\alpha $为欠驱动无人船路径方向向量与洋流向量的夹角。从图中可以看出1月份出发时$\overline \alpha $最小，9月份出发时的$\overline \alpha $最大。

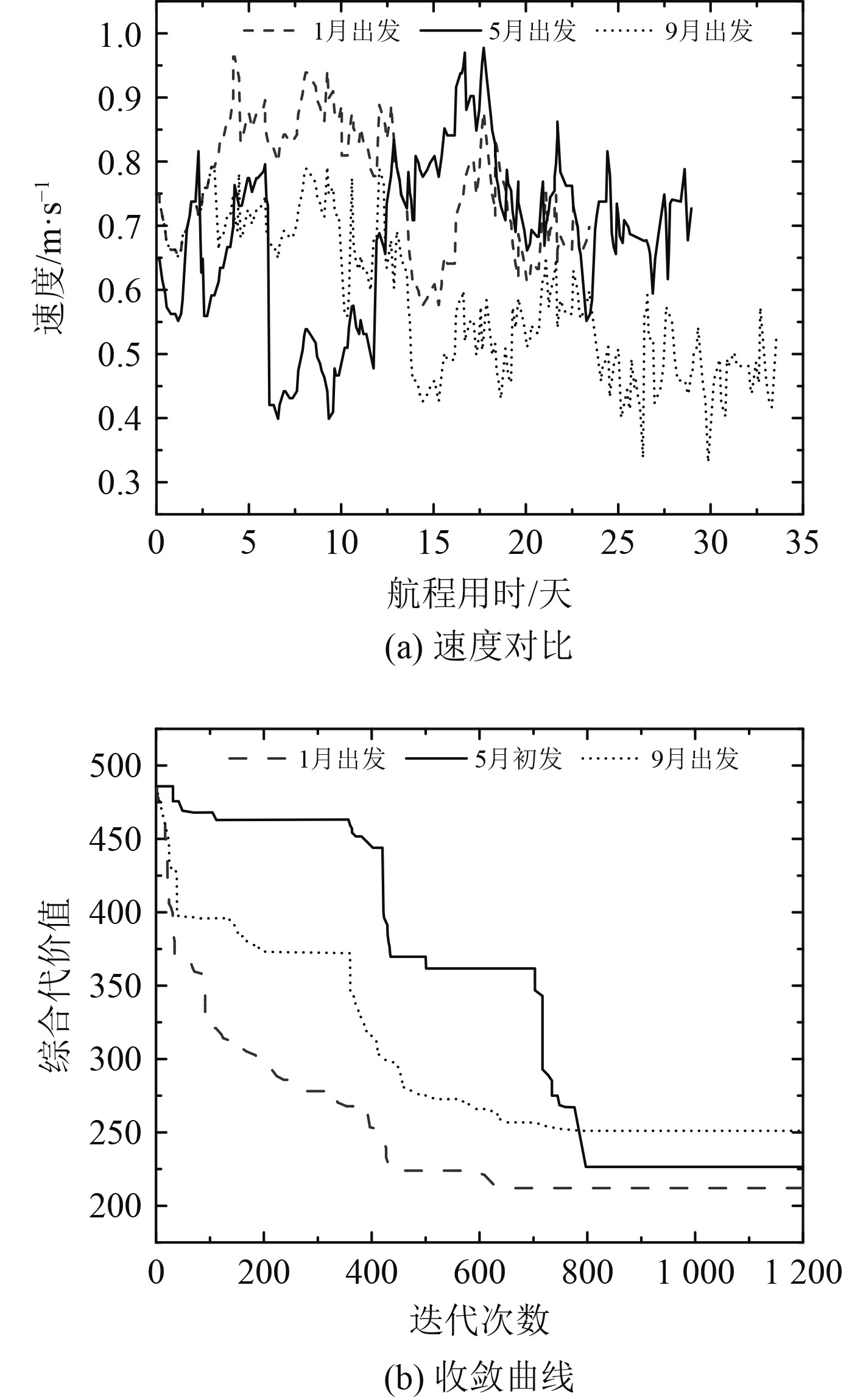
速度和适应度对比如图11所示，1月份出发可以最快速到达目的地，用时23.4天，且平均航速最高，为0.77 m/s。同时，1月份出发时最后迭代收敛的适应度值最低，为212.1。5月出发时的路径距离虽比9月出发时的路径更长，但是由于其路径方向更加贴近洋流且5月份的洋流整体流速更大，所以5月出发能比9月出发更快到达目的地，适应度值也更低。仿真结果证明在大范围长时序航行的情况下，需要考虑在时间维度上等待利洋流，选择合适的出发时间。

4 结　语

本文通过分析先验已知的流场数据，以路径时间最优为目标，提出了一种适用于环境驱动无人船在大范围动态变化流场中的路径规划策略。首先，通过B样条控制点随机生成无人船路径，再计算每一条可行路径在动态洋流中的代价，最后基于遗传算法迭代搜索最优控制点组合，该组合生成的路径即为时间最优路径。仿真结果表明，考虑动态变化洋流信息时所规划的路径比不考虑洋流信息时规划的路径更优，到达目标地的时间更短，航时由34天缩短到29天，航速由0.5 m/s提高到0.677 m/s，验证了算法的有效性和高效性。同时，在大范围长时序航行的情况下，将出发时间作为路径优化参数，考虑在时间维度上等待有利洋流，选择合适的出发时间，能够进一步缩短达到目的地的时间，航行时间从33天缩短为23天。因此本文所提出的路径规划策略能够有效解决欠驱动无人船在大范围动态流场中的时间最优路径规划问题，对于其在复杂海洋海洋环境中的路径规划具有重要的指导意义。