2. 江苏现代造船技术有限公司,江苏 镇江 212000;
3. 浙江省海洋开发研究院,浙江 舟山 316021
2. Jiangsu Modern Shipbuilding Technology Co., Ltd., Zhenjiang 212000, China;
3. Zhejiang Marine Development Research Instiute, Zhoushan 316021, China
滑行艇在水面高速运动时处于滑行状态,因其阻力小、速度快的特点而被广泛应用[1]。为了能够更好地掌握阻力对船艇的影响,现今滑行艇阻力性能的预报方法有很多,但是迄今未止,没有能够完全依靠理论基础的预报方法。所以高速滑行艇阻力性能的研究相较于常规排水船显得十分复杂。除此之外,高速航行状态下的滑行艇在受到流体动力及其他表现出来运动响应会变得十分复杂,这也是相对常规排水船艇的一个复杂问题,这对船的阻力性能、稳定性、安全性都产生了至关重要的影响[2]。为了能让高速滑行艇处于最佳的航行状态,对其阻力性、耐波性还需要更加深入的研究。这也是世界各国研究人员和国际海事组织关注的内容。
在国外,Hajme等 [3]运用边界元的方法对滑行艇艇体表面的流体进行数值仿真模拟,试验结果发现艇体表面压力分布、阻力、升力以及滑行艇周围水域的波形,这些因素对滑行艇的运动响应有巨大联系。Sun[4]基于更精确的数值解求解艇体剖面入水问题,在此基础上进行了静水中强迫升沉与纵摇运动的滑行艇水动力求解,计算中满足了非线性自由表面条件与瞬时湿表面条件。在国内,董文才等[5]针对深V型滑行艇模型在波浪中的纵向运动开展试验研究,揭示了相同航速下滑行艇在波浪中航行的纵向运动是相对于静水浮态的升沉纵摇运动。王硕等[6]为验证滑行艇模拟的真实性,将模拟计算值与实验值进行比较,结果表明,计算流体动力学技术可以准确且高效地模拟滑行艇在静水以及波浪中高速航行时的运动姿态和水动力特性,为滑行艇设计提供可靠的参考依据。
本文主要对自主设计的滑行艇进行了阻力预报和运行响应预报仿真试验,通过分析试验数据,得到该艇在波浪中的运动性能,为进一步研究提供依据。
1 波浪作用下滑行艇阻力和运动响应数值分析方法 1.1 方法及理论 1.1.1 八叉树计算法八叉树是一种树枝分叉的思想,形象的表达如同树枝一样,层层细化,每个节点被分解成8个相互连接的数据结构,octri的建模是一种功能强大、有效的建模方法,具有简单的存储形式,计算简单等优点,八叉树的深度可以根据需要进行动态调整,在处理三维空间数据和进行空间查询时具有显著的优势,因此在计算机图形学、CAD等领域得到了广泛应用。
1.1.2 RANS方程的数值方程雷诺平均N-S方程是流场平均变量的控制方程,其相关的模拟理论被称为湍流模式理论。耐维-司托克斯方程,即是粘性流体的力学基本方程。对于湍流而言一般都求解完整的雷诺平均N-S方程,即所谓的RANS方程。这是一个复杂的非线性偏微分方程,低雷诺数时可以认为是层流,高雷诺数时流体就会进入湍流状态。湍流的计算基于雷诺张力与应变之比(湍流粘滞系数)的计算。该方程是统计平均的,不需要计算每个尺度上湍流的起伏,只需要计算平均运动,从而减少了空间时间分辨率和减少计算负担。
RANS时均方程:
1)连续方程
| $\begin{split} \frac{\overline{\partial \left(\overline{{u}}+{{u}'}\right)}}{\partial {x}}&+\frac{\overline{\partial \left(\overline{{v}}+{{v}'}\right)}}{\partial {y}}+\frac{\overline{\partial \left(\overline{{w}}+{{w}'}\right)}}{\partial {y}}=\\ &\frac{\partial \overline{{u}}}{\partial {x}}+\frac{\partial \overline{{v}}}{\partial {y}}+\frac{\partial \overline{{w}}}{\partial {y}}+\frac{\partial \overline{{{u}'}}}{\partial {x}}+\frac{\partial \overline{{{v}'}}}{\partial {y}}+\frac{\partial \overline{{{w}'}}}{\partial {y}}=0。\end{split}$ | (1) |
其中,
| $ \frac{\partial \overline{{{u}'}}}{\partial {x}}+\frac{\partial \overline{{{v}}'}}{\partial {y}}+\frac{\partial \overline{{{w}}'}}{\partial {y}}=0,$ | (2) |
| $ \frac{\partial \overline{{u}}}{\partial {x}}+\frac{\partial \overline{{v}}}{\partial {y}}+\frac{\partial \overline{{w}}}{\partial {y}}=0。$ | (3) |
如式(2)与式(3)所示,两方程依然满足连续方程。
2)动量方程
以x方向模仿上式,可得:
| $\begin{aligned}[b] \frac{\overline{\partial \left(\overline{{u}} + {{u}'}\right)}}{\partial {t}} +&\frac{\overline{\partial {\left(\overline{{u}} + {{u}'}\right)}^{2}}}{\partial {x}} + \frac{\overline{\partial \left(\overline{{u}} + {{u}'}\right)\partial \left(\overline{{v}} + {{v}'}\right)}}{\partial {y}}+\\ &\frac{\overline{\partial \left(\overline{{u}} + {{u}'}\right)\partial \left(\overline{{w}} + {{w}'}\right)}}{\partial {z}} = -\frac{1}{{\rho }}\frac{\overline{\partial \left(\overline{{p}} + {{p}'}\right)}}{\partial {x}}+\\ &{v}\left[\frac{\overline{{\partial }^{2}\left(\overline{{u}} + {{u}'}\right)}}{{\partial }^{2}{x}}+\frac{\overline{{\partial }^{2}\left(\overline{{v}} + {{v}'}\right)}}{{\partial }^{2}{y}}+\frac{\overline{{\partial }^{2}\left(\overline{{w}} + {{w}'}\right)}}{{\partial }^{2}{y}}\right]。\end{aligned}$ | (4) |
利用式(4)给出的关系式,可得:
| $\begin{aligned}[b] \frac{\partial \overline{{u}}}{\partial {t}}+&\frac{\partial \left({\overline{{u}}^{2}}\right)}{\partial {x}}+\frac{\partial \left(\overline{{u}{v}}\right)}{\partial {y}}+\frac{\partial \left(\overline{{u}}\overline{{w}}\right)}{\partial {z}}+\frac{\overline{\partial {\left({{u}'}\right)}^{2}}}{\partial {x}}+\displaystyle\frac{\overline{\partial \left({{u}'}{{v}'}\right)}}{\partial {y}}+ \\ &\displaystyle\frac{\overline{\partial \left({{u}'}{{w}'}\right)}}{\partial {x}} =-\frac{1}{{\rho }}\frac{\partial \overline{{p}}}{\partial {x}}+{v}(\frac{{\partial }^{2}\overline{{u}}}{\partial {{x}}^{2}}+\frac{{\partial }^{2}\overline{{u}}}{\partial {{y}}^{2}}+\frac{{\partial }^{2}\overline{{u}}}{\partial {{z}}^{2}}) 。\end{aligned}$ | (5) |
把左端时均值项移放到等于号的右端形成新的方程式,如下式:
| $\begin{aligned}[b] \frac{\partial \overline{{u}}}{\partial {t}} +& \frac{\partial \left({\overline{{u}}}^{2}\right)}{\partial {x}} + \frac{\partial \left(\overline{{u}{v}}\right)}{\partial {y}} + \frac{\partial \left(\overline{{u}}\overline{{w}}\right)}{\partial {z}} + \frac{\overline{\partial {\left({{u}'}\right)}^{2}}}{\partial {x}} + \frac{\overline{\partial \left({{u}'}{{v}'}\right)}}{\partial {y}} +\\ & \frac{\overline{\partial \left({{u}'}{{w}'}\right)}}{\partial {x}} = - \frac{1}{{\rho }}\frac{\partial \overline{{p}}}{\partial {x}} + \frac{\partial }{\partial {x}}\left[{v}\frac{\partial \overline{{u}}}{\partial {x}} - \overline{{\left({{u}'}\right)}^{2}}\right] +\\ & \frac{\partial }{\partial {y}}\left[{v}\frac{\partial \overline{{u}}}{\partial {y}} - \overline{{{u}'}{{v}'}}\right] + \frac{\partial }{\partial {x}}\left[{v}\frac{\partial \overline{{u}}}{\partial {x}} - \overline{{{u}'}{{w}'}}\right]。\end{aligned}$ | (6) |
对其他y方向和z方向作类似的推导。可得下列时均形式的Navier-Stokes方程,即Reynolds方程,如下:
| $ \frac{\partial \left({\rho } \overline{{u_i }}\right)}{\partial {t}}+\frac{\partial \left({\rho }{\overline{{u_i}}}\overline{{u_j}}\right)}{\partial {{x}}_{{j}}} = -\frac{\partial \overline{{p}}}{\partial {{x}}_{{i}}} + \frac{\partial }{\partial {{x}}_{{j}}}\left({\mu }\frac{\partial \overline{{{u}}_{{i}}}}{\partial {{x}}_{{j}}} - {\rho }\overline{{{u}'}_{{i}}{{u }'}_{j}}\right),(i = 1,3)。$ | (7) |
3)其他变量方程
| $ \frac{\partial \left({\rho } \overline{{\varphi }}\right)}{\partial {t}} + \frac{\partial \left({\rho }{\overline{{u}}}_{{j}}\overline{{\varphi }}\right)}{\partial {{x}}_{{j}}} = -\frac{\partial \overline{{p}}}{\partial {{x}}_{{j}}} + \frac{\partial }{\partial {{x}}_{{j}}}\left({\Gamma }\frac{\partial \overline{{{u}}_{{i}}}}{\partial {{x}}_{{j}}} - {\rho }\overline{{{u}'}_{{j}}{{\varphi }'}}\right) + {s}。$ | (8) |
动态网格技术就是通过动态网格的模型对艇体表面周围的流场形状进行实时模拟。针对所设置的边界条件,如速度和角速度等,可以通过层层迭代,通过Fluent自动完成网格的更新,一层一层连续性的更新数据,但是起初的网格边界条件需要提前设置完成,随后是自动连续性的改变。当使用移动网格模型时就会用边界移动的方式在指定移动区域自行移动。
本文用FINE/MARINE软件对艇体表面进行数值模拟,得到滑行艇在静水中的阻力和较为真实的尾流分布情况。同时针对重心位置的不同,进行艇之间的对比,模拟相同的条件和环境,分析重心对滑行艇阻力的影响。在运用FINE/MARINE软件,选用三维非定常分离隐式求解器,SST k-ω湍流模型,基于全六面体非结构化网格技术求解粘性雷诺平均方程的自由液面捕捉法,探讨艇体在静水中的速度场和压力场信息。同时考虑规则波对阻力的影响,取4个不同波浪周期的规则波进行对比。
1.2 计算模型和网格划分针对滑行艇艇体模型,采用Solidworks软件完成三维实体建模,主尺度如表1所示。
|
|
表 1 滑行艇模型的主要参数 Tab.1 Key parameters of the surfboard model |
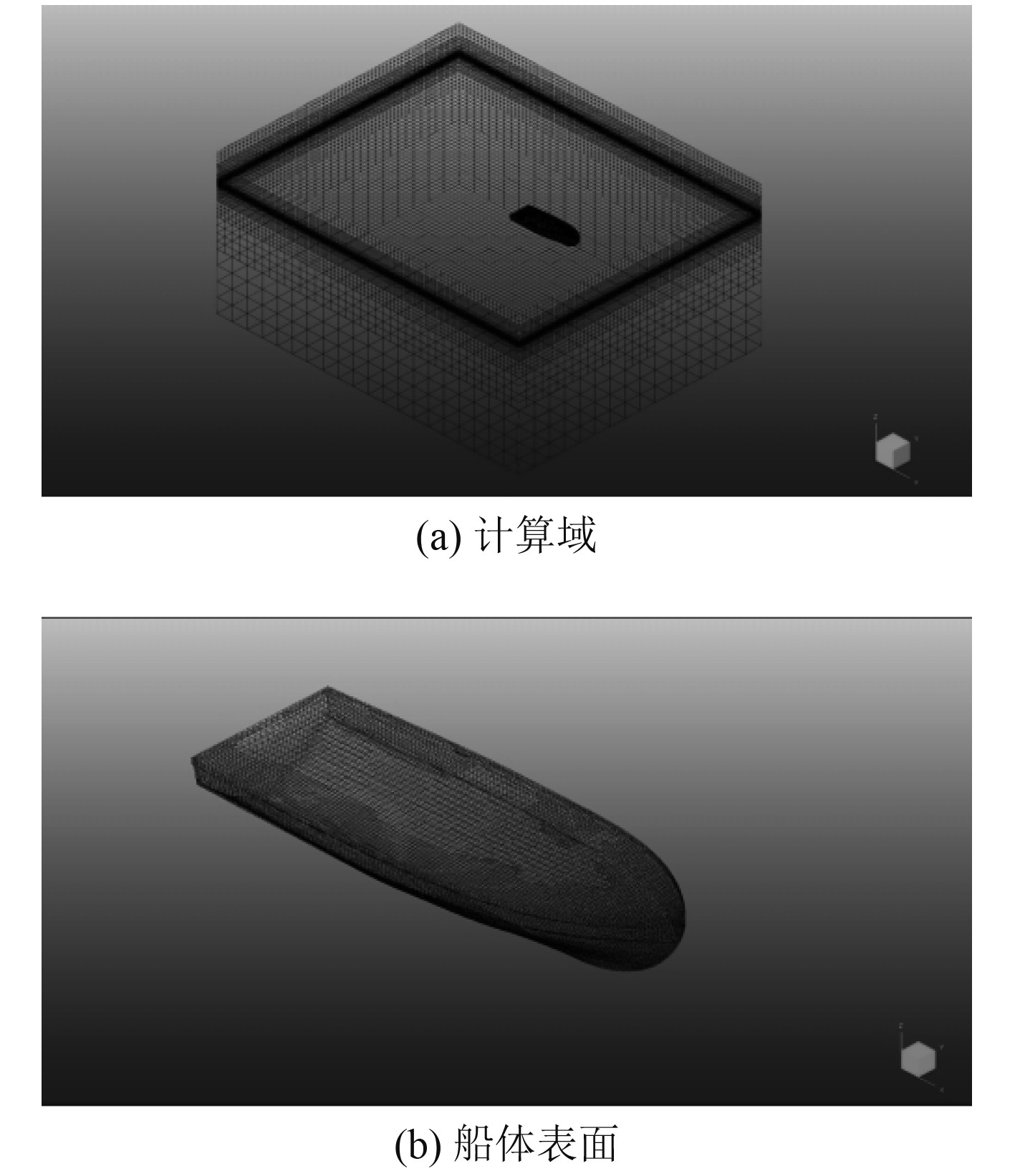
随后将所建立好的模型导入HEXPRESS中进行网格划分,运用八叉树计算方法将网格细化,对六面体进行结构化网格划分,将网格划分136万个。计算域和船体表面网格划分如图1所示。
|
图 1 网格划分 Fig. 1 Grid division diagram. |
从水动力学的观点出发,根据
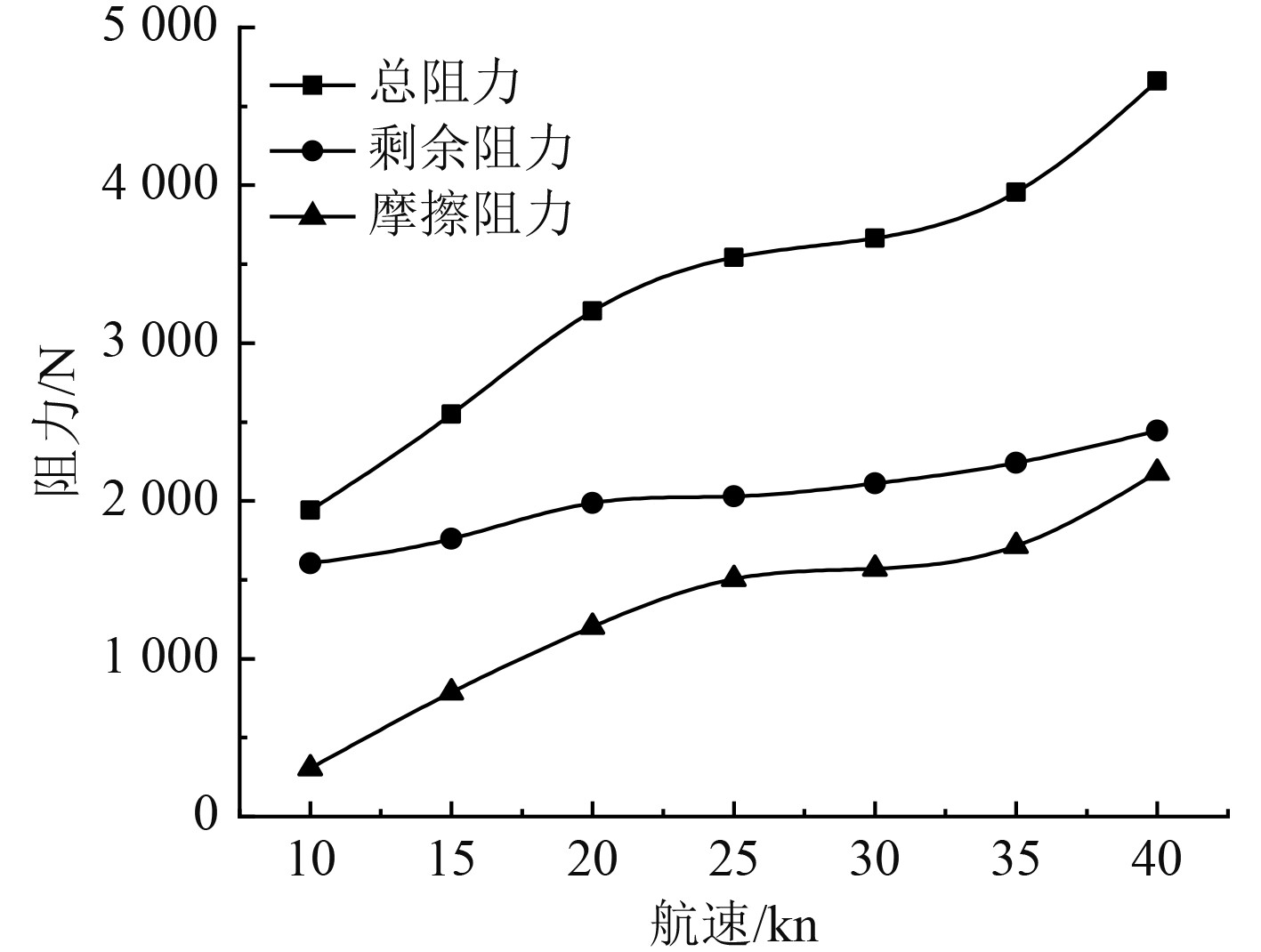
图2为滑行艇航速在10~40 kn时的阻力曲线,可以看出,滑行艇总阻力随航速的增加而增加。当航速<10 kn时,滑行艇处于预滑行状态,艇体的浸湿面积较大,随速度的增加而增加;当航速≥25 kn时,滑行艇处于完全滑行状态,艇首抬高,所接触的艇体表面主要处于艇身的尾部区域,艇体浸湿面积减少,主要都是艇体水线面以下为锲形的表面与水接触,所以形状阻力较小,剩余阻力中占主导地位的是兴波阻力,并随速度的增加而增加。
|
图 2 静水中滑行艇各阻力曲线 Fig. 2 Resistance curves of coasting boats in still water |
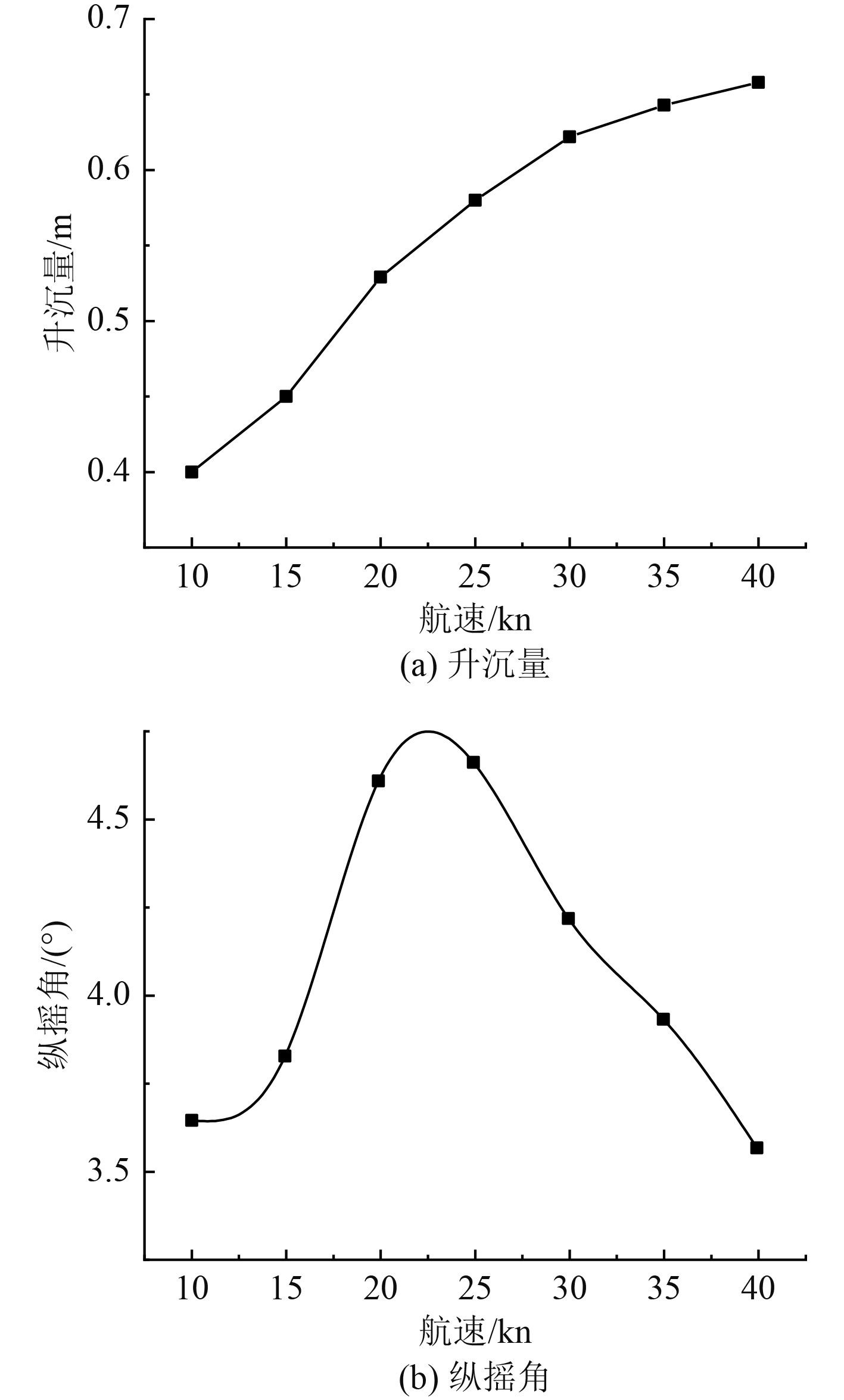
从图3(a)可以看出,滑行艇的升沉量随着速度的增加而增加,由于滑行艇的速度基数大,所以上升的幅度不是很大,但可以根据曲线图的趋势来判断,滑行艇升沉量上升的幅度不断减小并趋于稳定。
|
图 3 不同航速滑行艇升沉量和纵摇角 Fig. 3 Heave and pitch angle of coasting boat at different speed |
从图3(b)可以看出,当航速<20 kn时,滑行艇的动升力不断增加,由于其幅度较小,压力中心点的变化也很小,同时基于尾倾的条件下,其抬首力矩不断增加,直到航速达到22 kn时,达到了一个顶峰,其纵倾角开始下降,这是由于航速的增加并没有改变动升力的减小,但改变了压力的中心点位置,压力中心点开始不断后移,从而使抬首力矩不断地减小。
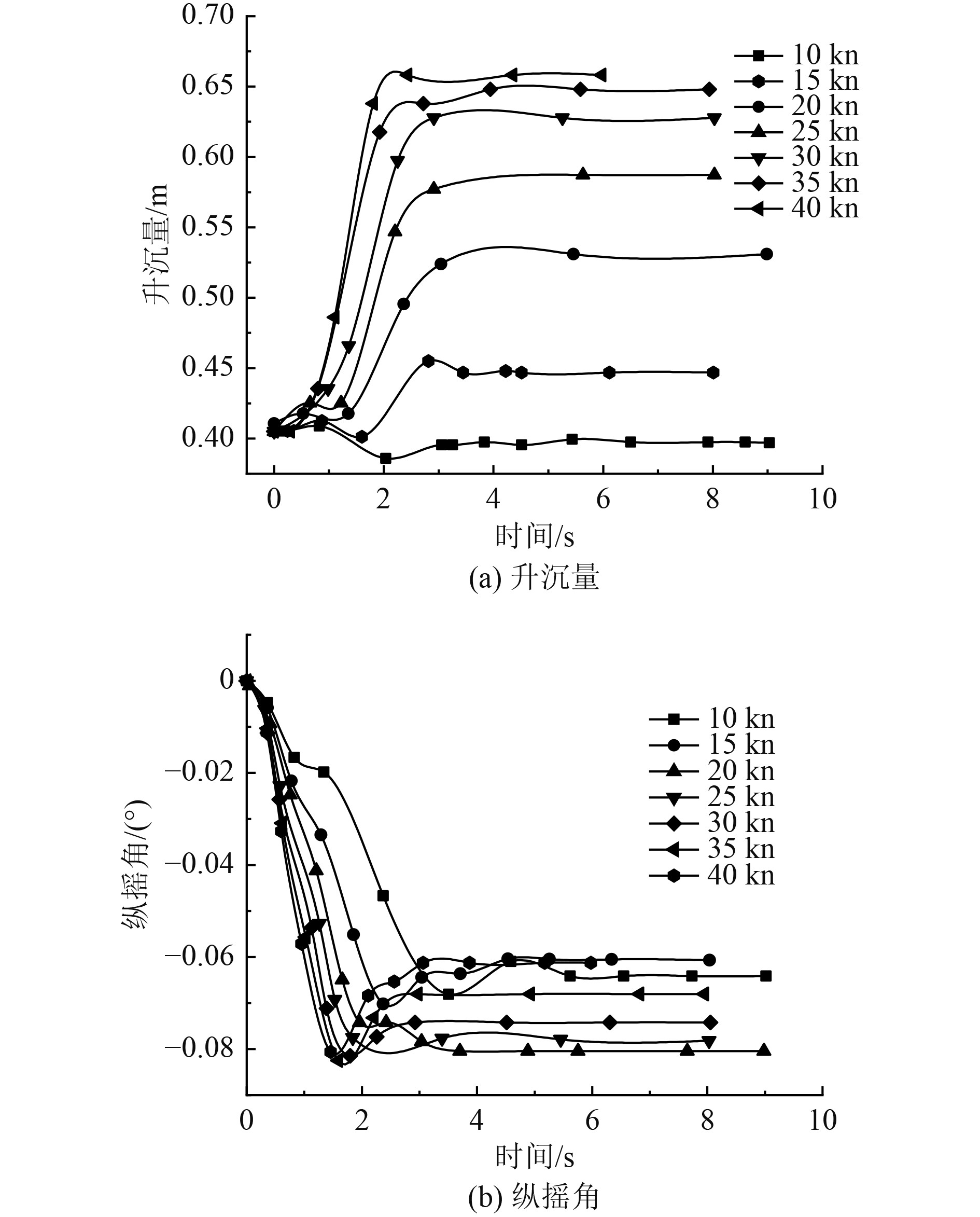
滑行艇在静水中不同航速下的运动响应如图4所示。可以看出,不管是纵摇角还是升沉量,随着时间的推移都趋于稳定,当然从纵向的角度来看,升沉量随着航速的增加,从剧烈增长到缓慢增长最后区域一个峰值。而从纵摇角曲线图的纵向分析来看,其曲线的拐点随着航速的增加,出现的越来越早,可知压力中心点的位置在不断后移。
|
图 4 不同航速下的运动响应 Fig. 4 Motion response at different speeds |
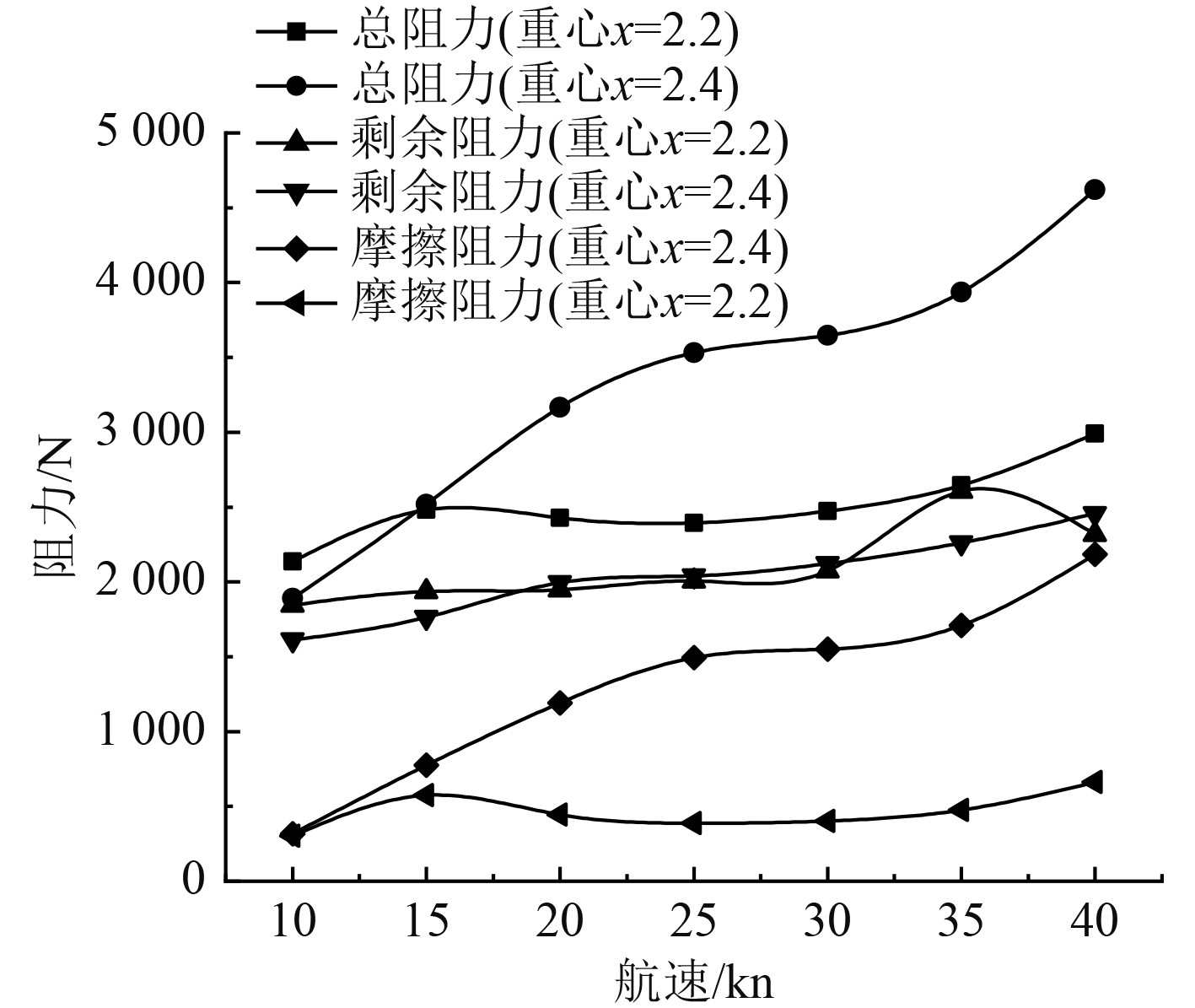
在考虑滑行艇阻力性能时,重心位置也会对滑行艇产生很大影响,相对于之前的重心,艇体重心纵向坐标向后移动,由图5可知,重心后移的船体尽管总阻力也是呈现上升的趋势,但相对于原来的船艇总阻力小且缓和,可见重心纵向位置的后移可以有效改善滑行艇的阻力性能。由于重心纵向位置的后移相对原来艇体更加容易发生尾倾,抬首力矩加大,浸湿面积将减少,所以可以看出粘性阻力相对减少,但是剩余阻力相对没有明显变化,仍然是兴波阻力占主导。
|
图 5 重心位置对阻力的影响 Fig. 5 Influence of center of gravity position on resistance |
从图6(a)的升沉量对比曲线可以看出,相对原来的滑行艇垂荡来说,重心后移将导致升沉量成比例的增加,所呈现的趋势相一致,增幅不断减小并且趋于平稳。
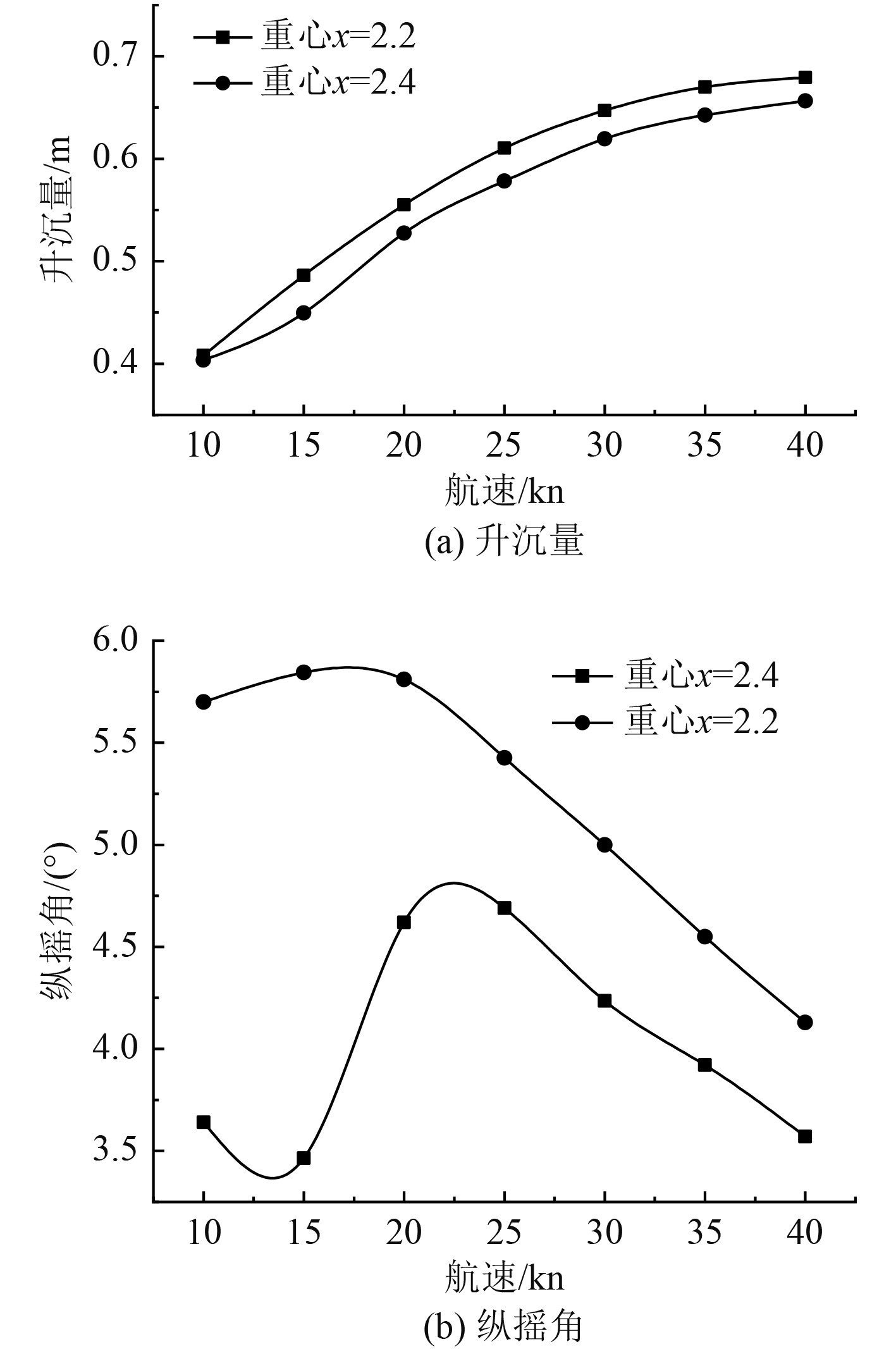
|
图 6 不同位置重心的运动响应 Fig. 6 Motion response with different center of gravity positions |
从图6(b)的纵摇角对比曲线可以看出,压力中心点的变化相较于之前一直在变化,动升力不断增加,压力中心不断后移,抬首力矩不断减少。不同于先前的滑行艇纵摇运动特性,抬首力矩转折点并没有在图上明显显示,但按照曲线的趋势,其转折点应小于原滑行艇力矩转折点所对应的航速。
2 规则波中滑行运动响应数值预报与分析 2.1 滑行艇在规则波下的工况计算为了研究滑行艇在规则波下的阻力性能,同时考虑规则波对阻力的影响,取不同波浪周期的规则波进行对比,所以选取了4个工况进行计算,计算工况见表2。
|
|
表 2 滑行艇规则波中运动响应计算工况表 Tab.2 Calculation conditions for motion response of surfboard in regular waves |
如图7(b)所示,在不同规则波的作用下,总阻力随着波浪周期的增加呈现近似正弦曲线的趋势,呈现周期性变化。结合图7(a)来看,由于摩擦阻力时按线性缓和下降的,所以产生骤然变化是剩余阻力,其中占主导作用的则是兴波阻力,由于规则波是周期性变化的,所以波峰和波谷对艇体作用有所不同,可见当波浪周期在T=8 s时,剩余阻力和总阻力最低,随滑行艇航行十分有利。
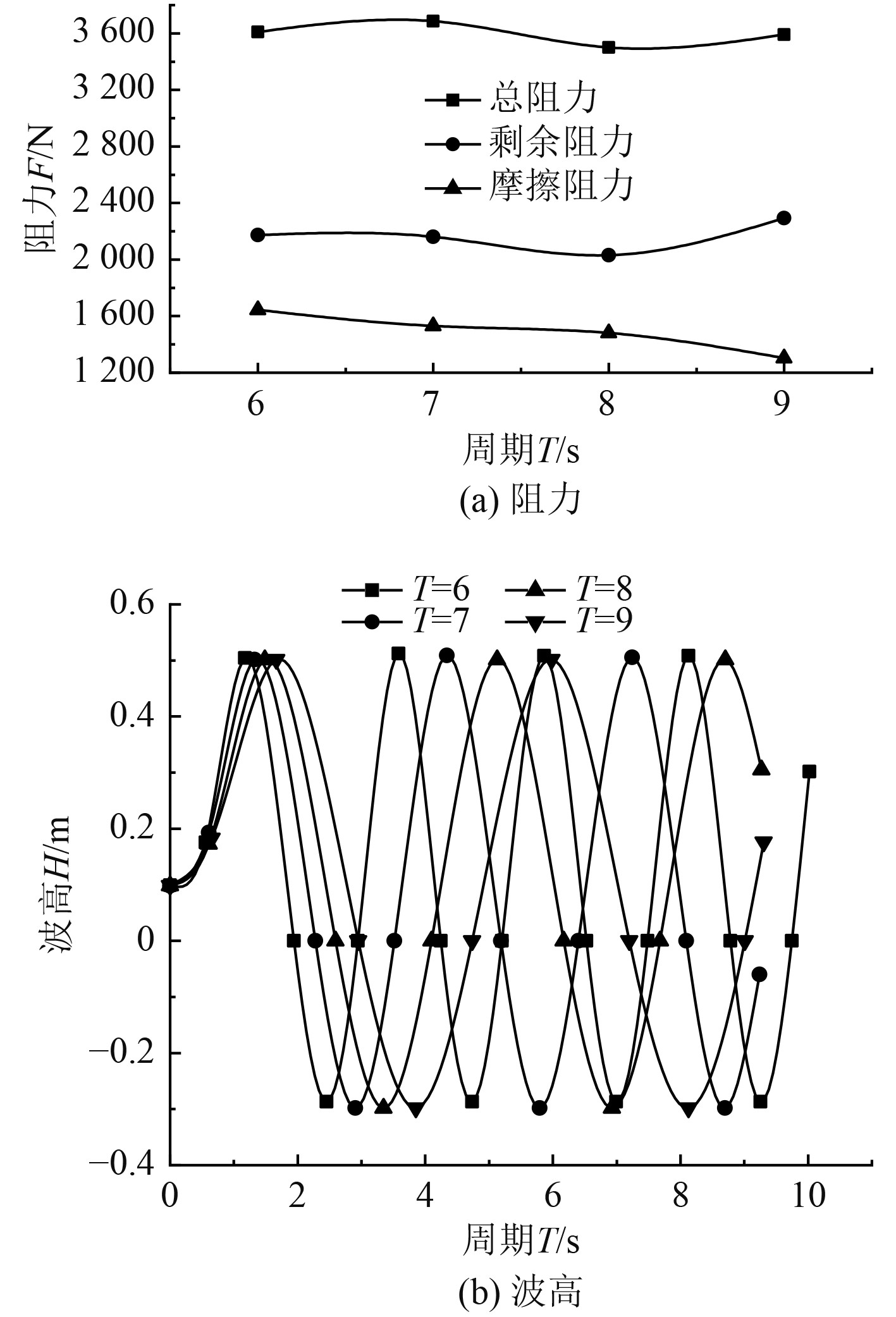
|
图 7 不同周期下的运动响应 Fig. 7 Motion response at different wave periods. |
图8给出了升沉量与纵摇角幅值随λ/L的变化曲线,可以看出,升沉量与纵摇角随着波长先增大后减小,在λ/L=16的时,运动响应最明显。
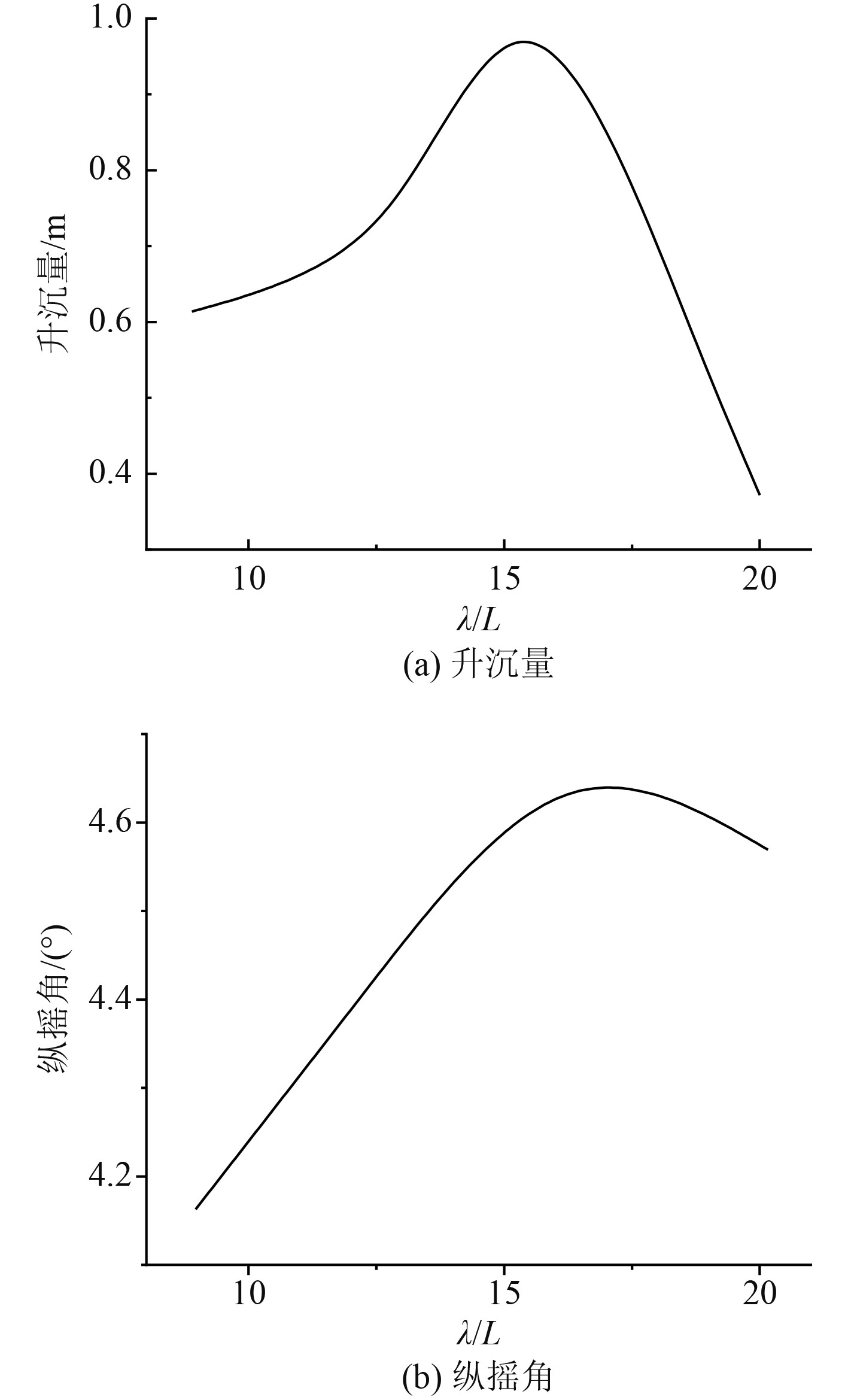
|
图 8 不同波长下的运动响应 Fig. 8 Motion response at different wave lengths |
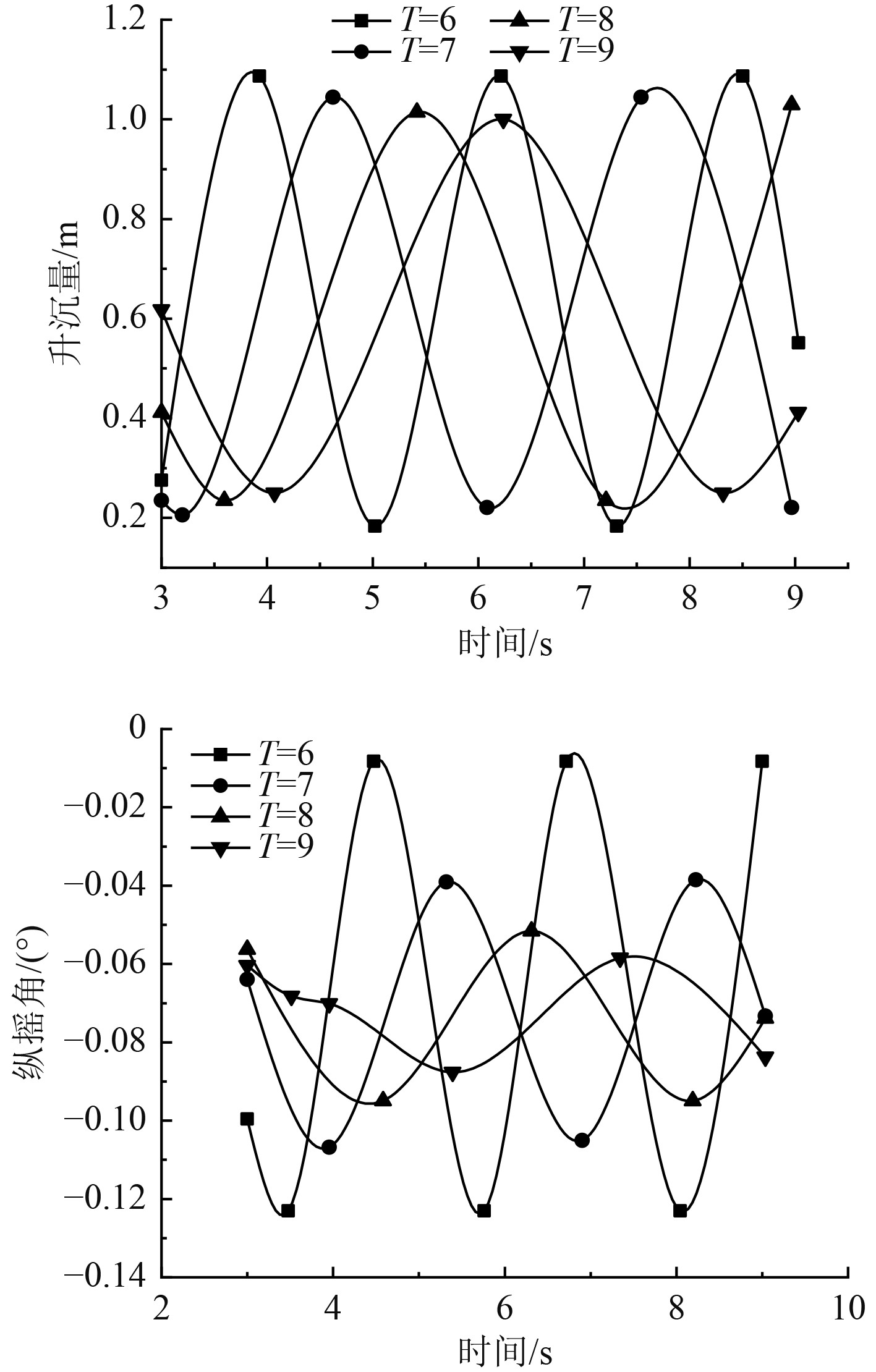
根据图9所看到各不同周期下的升沉量与纵摇角,其都是周期性而且随时间的变化区域稳定,再对比不同周期下的升沉量与纵摇角,随着周期的增加,其变化的幅度也随之减小。可以看出,当波浪周期为6~7 s时,升沉量与纵摇角有明显的高频部分,当波浪周期为8~9 s时,升沉量与纵摇角运动量中以波频成分为主。
|
图 9 不同波浪下历时的运动响应 Fig. 9 Duration of motion response under different wave conditions |
本文基于RANS粘流理论,利用SST k-ω湍流模型,并且应用了FINE/MARINE软件,对高速滑行艇在静水中、不同重心下以及不同规则波中的数值进行研究,得到以下结论:
1)滑行艇在静水中的阻力特性
滑行艇在到达越峰阻力前,随着航速的不断增加阻力不断增加,越过阻力峰后出现随着航速增加阻力下降的情况,当该艇航速在24~32 kn之间阻力上升相对较缓。因此在航行中时,该艇航速为32 kn最佳。
2)重心对滑行艇静水阻力的影响
只改变重心纵向坐标,将原艇重心x=2.4 m(lg=0.38L)改为x=2.2 m(lg=0.35L),重心总线坐标向船尾后移,总阻力小于原艇阻力,在运动响应上进行对比,升沉值虽大于原艇但是趋势相差不大。重心后移的纵摇角基数也是大于原艇纵摇角,其曲线趋势大致一致,可见适当移动重心能够一定程度影响该艇的阻力性能。
3)不同规则波下阻力特性及运动响应
根据规则波所得到不同周期规则波的阻力曲线首先单独分析可得,当波浪周期为8 s时,剩余阻力和总阻力最低,随滑行艇航行十分有利。在运动响应方面,升沉值和纵摇角都会随λ/L的增加,在某一处达到顶峰最后就下降。当λ/L=16时,该艇运动响应最为明显,在航行中应尽可能避开该频率段。
| [1] |
高双, 朱齐丹, 李磊. 滑行艇高速运动建模与姿态控制仿真[J]. 系统仿真学报, 2008, 20(16): 4461−4465. GAO Shuang, ZHU Qidan, LI Lei. Modeling and attitude control simulation of high-speed sailing boats[J].Journal of System Simulation, 2008, 20(16):4461−4465. |
| [2] |
朱鑫, 段文祥, 马山, 等. 棱柱波滑行艇在规则波中迎浪运动响应的频域解[J]. 哈尔冰工程大学学报, 2012, 11(33): 1326-1333. ZHU Xin, Duan Wenxiang, MA Shan, et al. Frequency domain solution of the head wave motion response of a prismatic wave-piercing boat in regular waves[J]. Journal of Harbin Engineering University, 2012, 11(33): 1326-1333. |
| [3] |
WU Gongxing, ZOU Jin, WEI Lei, et al. Design of the basic motion control system for water-jet-propelled unmanned surface vhicle[J]. Control Theory and Application, 2010, 27(2): 257−262.
|
| [4] |
SUN Hui. A boundary element method applied to stronglynonlinear wave-body interaction problems[D]. Trondheim: Norwegian University of Science and Technology, 2007: 103−142.
|
| [5] |
董文才, 岳国强. 深V型滑行艇纵向运动试验研究[J]. 船舶工程, 2004, 26(2): 14−16. DONG Wencai, YUE Guoqiang. Experimental study on the longitudinal motion of deep-V planing boats[J]. Ship Engineering, 2004, 26(2): 14−16. |
| [6] |
王硕, 苏玉民, 庞永杰, 等. 高速滑行艇在规则波中的纵向运动数值研究[J]. 哈尔滨工程大学学报, 2014, 35(1): 45-52. WANG Shuo, SU Yumin, PANG Yongjie, et al. Numerical study on the longitudinal motion of high-speed planing boats in regular waves[J]. Journal of Harbin Engineering University, 2014, 35(1): 45-52. |
 2024, Vol. 46
2024, Vol. 46
