0 引　言

随着全球变暖，极地冰层融化加速，极地航线的开通逐渐成为可能。开通极地航线可大幅缩短航程，所带来的经济效益非常可观，因此越来越多的人开始关注冰区航行船舶，冰区加强型商船的研发热度也逐渐上升。但目前对于冰区加强型船舶的设计能力发展非常不均衡，仅少数科研院所或企业具备相应的设计研发能力。然而在冰区加强型船舶设计研发过程中，船体线型的设计优化是其中很重要的一环，而能够对冰阻力进行准确评估是进行冰区加强型船舶线型设计优化的前提。考虑到冰水池试验成本高、周期长，开展对于冰区航行船舶冰阻力的数值模拟方法研究势在必行。

近年来，对碎冰条件下冰区船水动力性能的数值模拟研究日渐增多，其中有相当比例为应用离散元方法（Discrete Element Method，DEM）进行模拟。Sorsimo^[1]模拟了实尺度船舶在碎冰航道内航行的船-冰相互作用情况，并将阻力的数值计算结果与经验公式计算结果进行对比，表明数值模拟中的碎冰模型及其材料属性对数值计算结果影响很大；Seo等^[2]探究了碎冰条件下船体复杂尾部区域的船-冰相互作用情况，并且验证了其数值模型中冰摩擦系数设置的有效性；骆婉珍等^[3]计算了某型冰区加强型散货船的船舶阻力，并研究了不同碎冰粒子形状及采用单/双向耦合对于计算结果的影响；国威等^[4]研究了船舶航速和碎冰区粒子厚度对船体所受冰力的影响规律；齐江辉等^[5]对船舶在碎冰区航行过程进行了数值模拟，对碎冰在船体周围的运动状态进行了分析；金强等^[6]模拟了船舶与浮/碎冰之间的接触碰撞过程，比较了几种不同接触模型对于船-冰相互作用形式及冰阻力数值计算结果的影响。目前，对冰区航行船舶冰阻力的研究大多集中在对不同航速、不同碎冰密集度等条件下冰阻力变化趋势的分析，也因碎冰阻力试验公开资料较少，仅极少数研究者将对其计算结果与模型试验结果进行对比，评估该数值模拟方法能够达到何种精度。

本文对冰区航行船舶冰阻力数值模拟方法开展研究，旨在提出一套能够准确模拟船舶在碎冰航道中航行时船-冰相互作用现象，且阻力计算精度满足工程应用需要的数值模拟方法。依托本公司某型液化天然气（Liquid Natural Gas，LNG）加注船项目，参照冰池试验，建立该船在碎冰航道内航行的数值模拟流程。为与试验结果进行对比，计算采用模型尺度，分别计算了该船在不同吃水、不同冰级条件（冰厚）下的碎冰航行阻力，并将计算结果与模型试验结果进行对比，评估计算精度，分析误差产生原因。

1 数值计算理论

采用拉格朗日-欧拉模型来模拟船舶在碎冰航道中航行的运动问题。使用拉格朗日模型描述离散相碎冰粒子，满足动量守恒方程和角动量守恒方程；使用欧拉模型描述连续相，满足连续性方程和动量守恒方程。

1.1 拉格朗日-欧拉模型

离散相为碎冰粒子。取单一粒子进行分析，根据牛顿第二定律，粒子的运动方程为：

$ F_{\mathrm{drag}} + F_{\mathrm{buoyancy}} + F_{\mathrm{virtualmass}} + F_{\mathrm{gravity}} + F_{\mathrm{contact}} = \frac{{\mathrm{d}}(mv)}{{\mathrm{d}}t}，$

(1)

$ I\frac{{\text d}\omega}{{\text d}t}=M_{\mathrm{drag}}+M_{\mathrm{contact}}。$

(2)

式中：${{F}_{{{\mathrm{drag}}}}}$为拖曳力；${{F}_{{{\mathrm{buoyancy}}}}}$为压力梯度力；${{F}_{{{\mathrm{virtualmass}}}}}$为虚拟质量力；$ F\mathrm{_{gravity}} $为重力；${{F}_{{{\mathrm{contact}}}}}$为接触力；$m$为粒子质量；$v$为粒子瞬时速度；${I}$为粒子转动惯量；$\omega $为粒子的转动角速度；${{M}_{{{\mathrm{drag}}}}}$为拖曳力矩；${{M}_{{{\mathrm{contact}}}}}$为接触力矩。

$ F {_\text{drag}}=\frac{1}{2}C_{ {d}}\rho_{ {c}}A_{ {p}}\left|v {_c}-v\right|(v {_c}-v)。$

(3)

式中：$ {{C}}_{{d}} $为拖曳力系数；$ {\rho _{{{c}}}} $为连续相的密度；$ {A_{{{p}}}} $为粒子投影面积；$ {v_{{{c}}}} $为连续相的瞬时速度。

$ F_{\mathrm{buoyancy}}=-\nabla p_{\mathrm{static}}=\rho_{{c}}g ，$

(4)

$ F_{\mathrm{virtualmass}}=C_{{vm}}\rho V\left(\frac{Dv}{Dt}-\frac{{\mathrm{d}}v}{{\mathrm{d}}t}\right)。$

(5)

式中：$ {{C}_{{{{vm}}}}} $为附加质量系数；$ V $为粒子体积。

$ F\mathrm{_{gravity}}=mg，$

(6)

$ {{M}_{{{\mathrm{drag}}}}} = \frac{{{\rho _{{\mathrm{c}}}}}}{2}{\left(\frac{d}{2}\right)^5} {C_{{{R}}}}\left| \Omega \right|\Omega ，$

(7)

$ C_{ R}=\left\{\begin{gathered}\frac{12.9}{Re_{ R}^{0.5}}+\frac{128.4}{Re_{ R}},32\leqslant Re_{ R}\leqslant1000，\\ \frac{64\text{π}}{Re_{ R}},Re_{ R}\leqslant32。\\ \end{gathered}\right. $

(8)

$ Re_{{R}}=\frac{\rho d^2\left|\Omega\right|}{\nu} ，$

(9)

$ {\Omega } = \frac{1}{2}\nabla \times {v_c} - {\omega _p}。$

(10)

式中：$ d $为粒子直径；$ {C_{R}} $为旋转拖曳系数；$ {\Omega } $为相对旋转角速度；$ \nu $力粘性系数；$ {\omega _p} $为粒子转动角速度。

$ M\mathrm{_{contact}}=(r_{\mathrm{contact}}\times F\mathrm{_{contact}}+M_{\mathrm{rolling}})。$

(11)

式中：${r_{{{\mathrm{contact}}}}}$为粒子重心距接触点的位置矢量；${{M}_{{{\mathrm{rolling}}}}}$为转动阻力作用于粒子上的力矩。

对连续相：

$ \frac{\partial(\alpha_{c}\rho_{c})}{\partial t}+\nabla\cdot(\alpha_{c}\rho_{c}v_{c})=0 ，$

(12)

$\begin{aligned}[b] \frac{{\partial ({\alpha _c}{\rho _c}{v_c})}}{{\partial t}} &+ \nabla \cdot \left[ {{\alpha _c}{\rho _c}({v_c} \otimes {v_c})} \right] - \nabla \cdot ({\alpha _c}{\rho _c}{\tau _c}) =\\ &- {\alpha _c}\nabla {p_c} + {\alpha _c}{\rho _c}g - F。\end{aligned}$

(13)

式中：${\alpha _{{{c}}}}$为连续相的相分数；${p_{{c}}}$为压力；$ {\tau _{{{c}}}} $为雷诺应力；$ F $为界面交换力，表示每单位体积的两相之间的传递。

$ \alpha_{{c}}=1-\alpha_{{p}}，\alpha_{{p}}=\sum\limits_{i=1}^{n_{{p}}}V_{{p}i}/\Delta V 。$

(14)

本次计算中采用单向耦合计算，即不考虑粒子对所在连续相的影响，仅考虑连续相对粒子运动的影响，上述方程简化为单向流动方程：

$ \frac{{\partial ({\rho _c}{v_c})}}{{\partial t}} + \nabla \cdot \left[ {{\rho _c}({v_c} \otimes {v_c})} \right] - \nabla \cdot ({\rho _c}{\tau _c}) = - \nabla {p_c} + {\rho _c}g 。$

(15)

1.2 拖曳力系数

拖曳力系数采用Haider and Levenspiel 方法计算，该方法适用于非球状固体粒子，$ {C_d} $取决于粒子雷诺数和粒子的球度。

$ C {_d}=\frac{24}{Re_{ {p}}}(1+ARe_{ {p}}^B)+\frac{C}{\left(1+\displaystyle\frac{D}{Re_{ {p}}}\right)}，$

(16)

$ Re_{ {p}}=\frac{\rho\left|v_s\right|d}{\upsilon} ，$

(17)

其中：

$\left\{\begin{gathered} A = 8.1716{{\text e}^{ - 4.0665\varphi }}，\\ B = 0.0964 + 0.5565\varphi ，\\ C = 73.690{{\text e}^{ - 5.0746\varphi }}，\\ D = 5.3780{{\text e}^{6.2122\varphi }}。\\ \end{gathered} \right.$

(18)

式中：$\varphi $为粒子的球度。

1.3 接触模型

接触模型是关系到数值模拟准确性最为关键的内容，包含碎冰粒子与粒子之间的接触，以及碎冰粒子与壁面之间的接触。

本文计算中选取Hertz Mindlin Model作为接触模型。Hertz Mindlin Model是非线性弹簧阻尼接触模型的变种，适用粒子接触但非破碎情况，粒子间接触力表示为：

$ F\mathrm{_{contact}}=F_n+F_t 。$

(19)

其中：$ {F_n} $为垂直接触面的法向力；$ {F_t} $为行接触面的切向力。

$ {F_ {n}} = - {K_ {n}}{d_ {n}} - {N_ {n}}{v_ {n}} ，$

(20)

$ K_{{n}}=\frac{4}{3}E_{{eq}}\sqrt{d_{{n}}R_{eq}}，$

(21)

$ {E_{eq}} = \displaystyle \dfrac{1}{{\dfrac{{1 - \mu _A^2}}{{{E_A}}} +\displaystyle \dfrac{{1 - \mu _B^2}}{{{E_B}}}}} ，$

(22)

$ R_{eq}=\frac{1}{\displaystyle\frac{1}{R_A}+\displaystyle\frac{1}{R_B}}，$

(23)

$ N_n=\sqrt{(5K_nM_{eq})N_{\mathrm{ndamp}}} ，$

(24)

$ {M_{eq}} = \dfrac{1}{{\dfrac{1}{{{M_A}}} + \dfrac{1}{{{M_B}}}}}，$

(25)

$ {N}_{\text{ndamp}}=\frac{-\mathrm{ln}（{C}_{\text{nrest}}）}{\sqrt{{{\text π} }^{2}+\mathrm{ln}{({C}_{\text{nrest}})}^{2}}}。$

(26)

式中：$ {d_n} $为接触点法向重叠部分；$ {v_n} $为接触点相对球面速度的法向速度分量；$ {\mu _A}、{\mu _B} $均为子泊松比；$ {E_A}、{E_B} $均为粒子杨氏模量；$ {R_A}、{R_B} $均为粒子半径；$ {M_A}、{M_B} $均为粒子质量；$ {C_{{\mathrm{{nrest}}}}} $定义法向恢复系数，且如果$ {C_{{\mathrm{{nrest}}}}} = 0，{N_{{\mathrm{{ndamp}}}}} = 1 $。

如果粒子与壁面接触，假设${R_{\mathrm{Wall}}} = \infty ，{M_{\mathrm{Wall}}} = \infty $，因此，$ R_{eq}=R_{\mathrm{particle}} $，$ M_{eq}=M_{\mathrm{particle}} $。

$ F_{ {t}}=\left\{\begin{gathered}-K_{ {t}}d_{ {t}}-N_{ {t}}v_{ {t}},\left|K_{ {t}}d_{ {t}}\right| < \left|K_{ {n}}d_{ {n}}\right|C_{ {fs}}，\\ \frac{\left|K_{ {n}}d_{ {n}}\right|C_{ {fs}}d_{ {t}}}{\left|d_t\right|}，\\ \end{gathered}\right. $

(27)

$ K {_t}=8G_{ {eq}}\sqrt{d_{ {n}}R_{ {eq}}}，$

(28)

$ G{_{eq}}=\frac{1}{\displaystyle\frac{2(2-\mu_A)(2+\mu_A)}{E_A}+\displaystyle\frac{2(2-\mu_B)(2+\mu_B)}{E_B}} ，$

(29)

$ N{_t}=\sqrt{(5K_tM_{{eq}})}N\mathrm{_{tdamp}}，$

(30)

$ N_{\mathrm{tdamp}}=\frac{-\ln(C\mathrm{_{trest}})}{\sqrt{\text{π}^2+\ln(C\mathrm{_{trest}})^2}} 。$

(31)

其中：$ {d_{{{t}}}} $为接触点切向重叠部分；$ {v_{{{t}}}} $为接触点相对球面速度的切向速度分量；$ {C_{{{{fs}}}}} $态摩擦系数；$ {C_{{\mathrm{{trest}}}}} $定义切向恢复系数，且如果$ {C_{{\mathrm{{trest}}}}} = 0，{N_{{\mathrm{{tdamp}}}}} = 1 $。

2 数值计算模型 2.1 船体模型

本文目标船为某7500 m³ LNG加注船，设计要求为满足芬兰-瑞典冰级规则（Finnish-Swedish Ice Class Rules，FSICR）1 A冰级，即要求该船主机能够提供保证该船以最小航速5 kn在1 A冰级对应碎冰航道中航行所需功率。该船在德国汉堡水池（HSVA）进行了冰池试验，模型缩尺比为15，船体数值模型见图1，其基本参数见表1。试验工况设置见表2，计算工况与试验工况相同。

2.2 碎冰模型 2.2.1 碎冰粒子形状模拟

由模型试验中的碎冰航道（见图2）可以看出，航道中的碎冰多为不规则的扁平多面体形状，如图3（a）所示。但在STAR CCM+软件中，构建非球形几何形状的粒子，需要间接由大量球形粒子对其进行几何填充而成，如图3（b）所示。在求解的过程中，这些球形粒子的数量直接影响计算时长，经测试，该种形状粒子求解过程缓慢，耗费大量时间及计算机资源，并不适合工程应用，因此在本文的数值模拟计算中，将对碎冰粒子形状进行简化。

总结目前应用于碎冰区航行船数值模拟研究中的碎冰粒子形状，有球体、等四面体、多面体、长方体、扁平圆盘型、冰排等，如图4所示。其中骆婉珍等^[3]在其研究中表明了正四面体碎冰粒子模型能够取得较好的模拟效果，因此在本次数值模拟过程中，选择正四面体模型来模拟碎冰粒子。

2.2.2 碎冰厚度模拟

FSICR中规定的碎冰航道剖面形状为基于航道中间冰厚${H_{M}}$，以坡度为2°向边缘变厚，因模型测试条件下很难获得与规范描述航道冰层相同的形状，因此，模型试验中采用航道冰层的平均厚度${H_{{av}}}$，该值与规范要求值及船宽有关，计算方法见式（32）^[7]，规范要求的冰厚见表3。

$ H_{{av}}=H_{{M}}+14\times10^{-3}B。$

(32)

鉴于碎冰航道中冰厚分布的随机性，在对碎冰航道内冰厚测量数据进行统计分析后，尝试使用某种数量密度函数NDF（Number Density Function）来描述碎冰粒子的冰厚分布。4次试验前对航道内碎冰厚度测量值得统计分析结果如图5所示，相应的统计分析结果见表4。

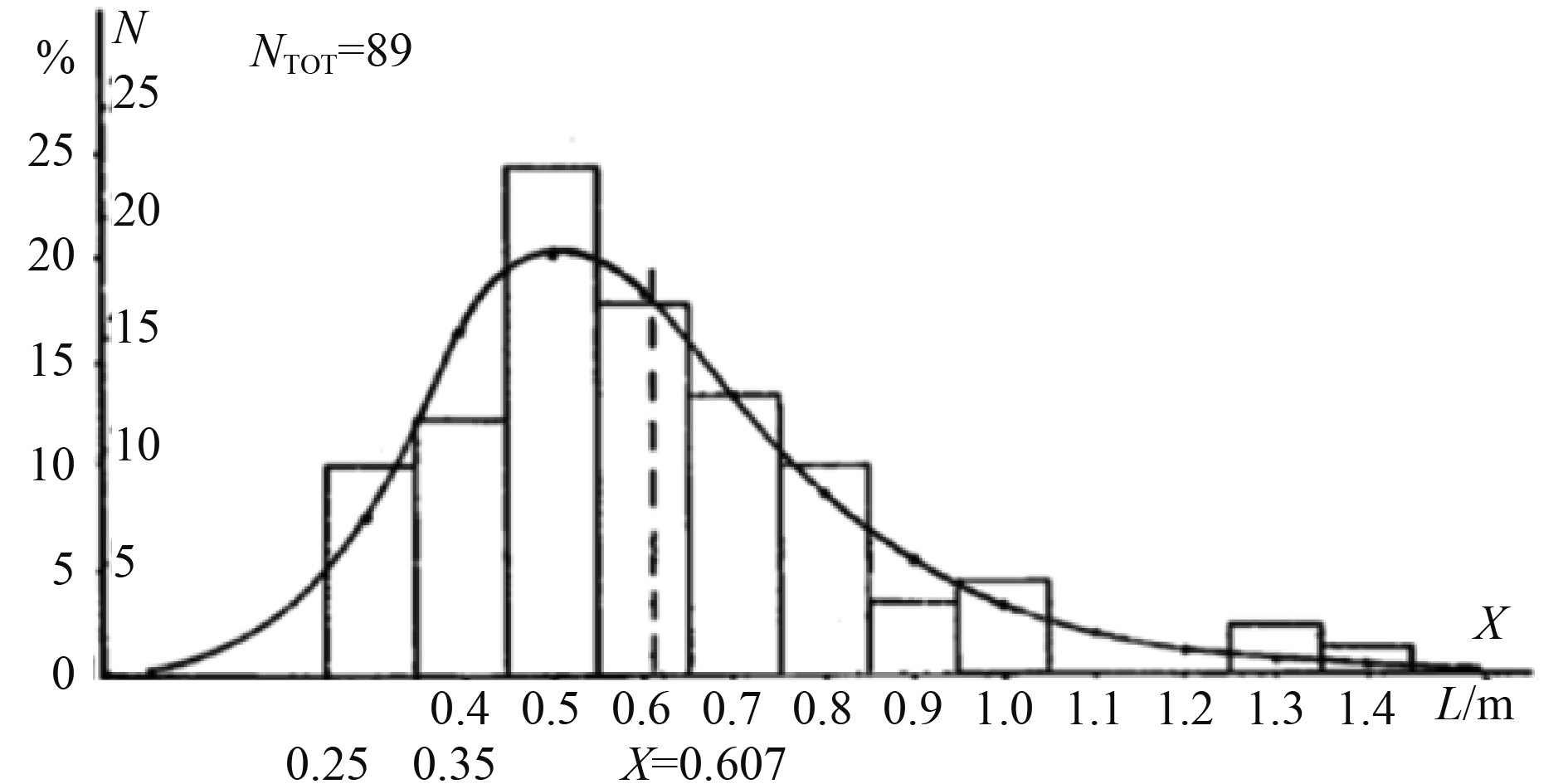
STAR−CCM+软件中，对数正态分布模型与图5所示碎冰粒子分布规律最为接近。且Arto Sorsimo^[1]曾在其计算报告中论述，波罗的海内某古航道（航道宽10 m）中的碎冰块尺寸分布可大致描述为对数正态分布，如图6所示。

其数学表达为：

$ f(x) = \frac{1}{{\sqrt {2{\text π} \varsigma x} }}{e^{\frac{1}{2}{{\left[\frac{{\ln x - \lambda }}{\varsigma }\right]}^2}}}(0 \leqslant x \leqslant \infty )，$

(33)

$ \lambda = \ln \overline x - \frac{1}{2}{\varsigma ^2}，$

(34)

$ \varsigma = \sqrt {\ln (1 + {{\left( {\frac{s}{{\bar x }}} \right)}^2})} 。$

(35)

式中：$\overline x $为均值；$s$为标准方差。

因此，在本次计算中，采用对数正态分布来描述试验中各碎冰粒子厚度分布，其值均为表4所列均值和标准差，相应的数学模型如图5中曲线所示。可以看出，图5（a）模型试验数据统计值与数学模型匹配度最高，其次为图5（b）。图5（c）与图5（d）数据统计结果有一定的相似性，对数正态分布特点不强。考虑到实际试验中，低冰级碎冰航道是由高冰级碎冰航道试验完成后未重新制冰，而是已有航道重新调整而成，随机性受到干扰。因此以初始航道状态作为碎冰粒子厚度分布模型的选择依据。

因模型试验结果会对冰厚进行修正，因此在数值模拟过程中不考虑单次试验实际冰厚与目标冰厚的差异，统一以目标冰厚为数值模拟过程中碎冰粒子的平均冰厚，其详细参数见表5。

2.2.3 碎冰粒子其他物理属性

试验中测量冰池水密度为1005.5 kg/m³（含有6.9‰的盐度），碎冰粒子密度的均值为870.17 kg/m³，数值计算中泊松比取为0.3，杨氏模量为74 MPa，因不考虑冰粒子破碎，弯曲强度系数不参与计算，所以不考虑弯曲强度值的设置。

2.3 计算域与物理模型

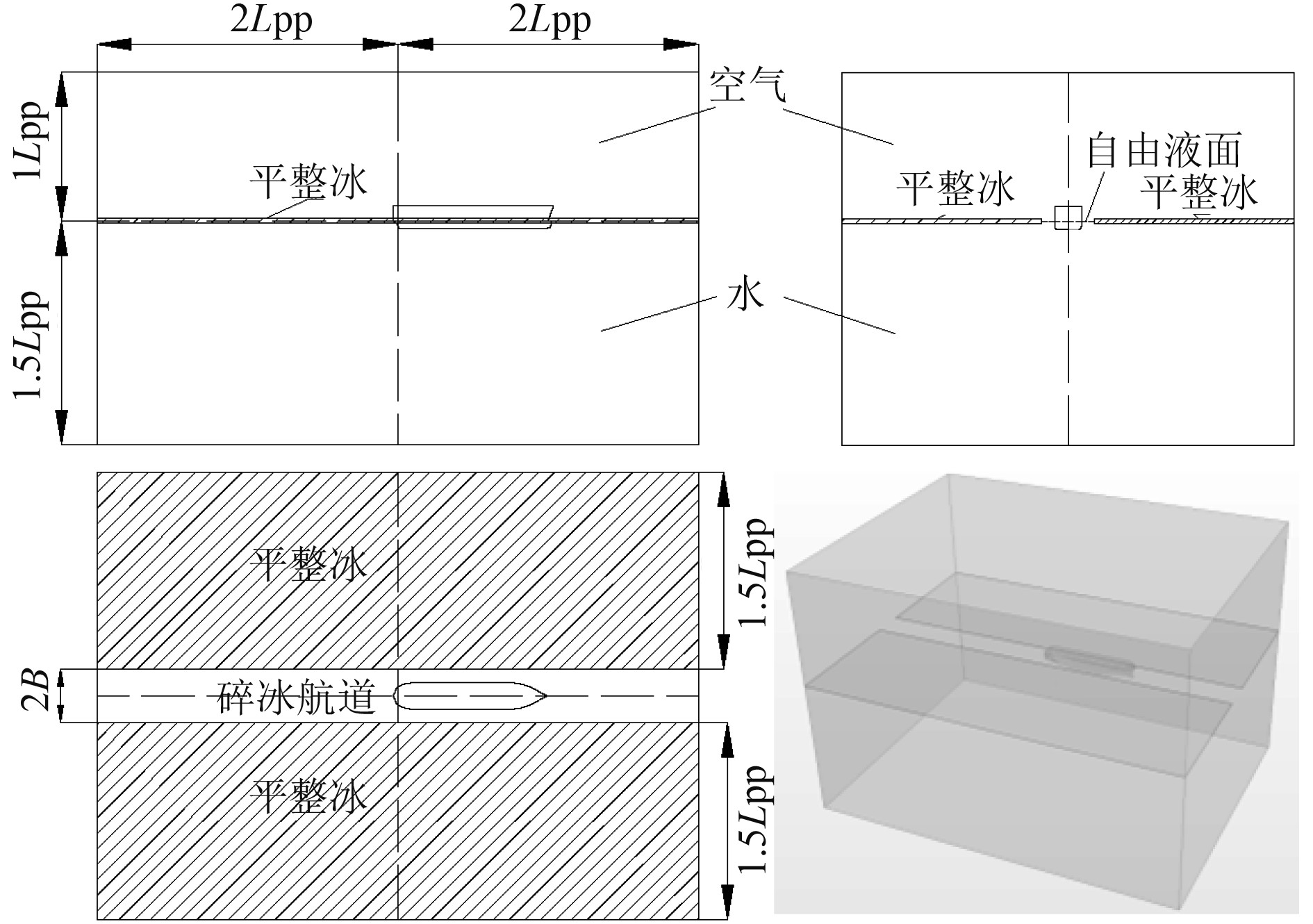
数值计算域设置如图7所示。

鉴于双向耦合较单向耦合耗时长，且在计算精度方面差别不大^[6]，因此本次数值模拟采用单向耦合，在船首、船尾、自由面等区域进行加密，网格数量在200万左右。选用K-Omega模型，Y+值控制在30～60之间，航道宽度按照规范要求为2倍船宽，两侧为平整冰。在距离船首8 m位置设置水平发射器发射碎冰粒子。粒子与粒子之间的静摩擦系数、法向恢复系数、切向恢复系数分别为0.3、0.1、0.1，粒子与船体之间分别为0.3、0.05、0.05。模型对应的设计航速为0.664 m/s。

3 数值模拟结果与分析 3.1 碎冰粒子的运动响应及船体受力分析

通过对比数值模拟结果与模型试验中观测的现象进行对比，发现该数值模拟过程可以很好地重现船体在碎冰航道中航行时，碎冰粒子与船体发生碰撞后翻转，并沿着船侧向后、向下滑移，以及船体在肩部发生堆积的现象。图8为模型试验及数值模拟过程中船体在碎冰航道中航行时碎冰粒子与船体的相互作用。可以看出，碎冰粒子的速度在船首部因与船体发生碰撞而急剧减小，在球鼻首上侧出现了轻微的碎冰堆积情况，这与模型试验中观测的现象完全相符。但在模型试验中，因碎冰粒子呈扁平片状，其平面尺寸较大，因此碎冰在与船体相互作用过程中的翻转现象较数值模拟结果会更加明显。

图9为模型试验及数值模拟过程中从水下仰视船体首部碎冰粒子的分布情况，通过两者对比进一步说明了数值模拟可以很好地描绘出碎冰粒子的运动状态。

图10为某瞬时船体受到的碎冰粒子碰撞力，从碰撞区域来看，船体两侧靠近肩部区域出现三角形的碰撞密集区，与图8和图9所展现出的现象一致。

碎冰粒子在船首与船体发生碰撞后，由于船体的存在，排开的碎冰粒子沿船体两侧向后、向下滑移、堆积。过程中与船体发生摩擦，形成了摩擦冰阻力。从图11船体与碎冰粒子接触力时历曲线（沿船长X方向）可以发现，碎冰粒子与船体的接触力具有围绕一基准值随时间震荡的特性，震荡的特性显示出了碎冰粒子与船体发生碰撞的瞬时特征，而基准值则显示出了碎冰粒子沿船体滑移的摩擦特性。

3.2 碎冰阻力数值计算结果及分析

试验中在整个碎冰航道内，对总阻力及敞水阻力各进行4次测量，如图12所示，因每次试验中无法保证碎冰厚度与目标值完全一致，因此试验最终结果考虑了对冰厚度的修正。

模型试验结果显示，同一航道内，同一吃水、同一冰级下，碎冰阻力分次测量结果波动较大。在本次试验中，同一轮试验中4次测量值与试验结果的平均值的平均偏差达到4%左右。这是因为模型试验中碎冰航道内碎冰粒子的分布具有很大的随机性，加之每轮试验单次测量距离较短，放大了这种随机性带来的阻力测量值的差异，使得每轮试验单次碎冰阻力的测量值波动较大。

在数值模拟过程中，因碎冰粒子的形状以及尺寸分布难以完全复制模型试验中碎冰航道内碎冰粒子的几何特性，仅作近似处理，因此对碎冰阻力数值计算结果的准确性进行评估应放宽要求，本次数值计算中，认为数据计算结果位于各次测量值最大值与最小值的区间内，与模型试验中各次测量值的均值相近，就认为该数值计算结果相对准确。

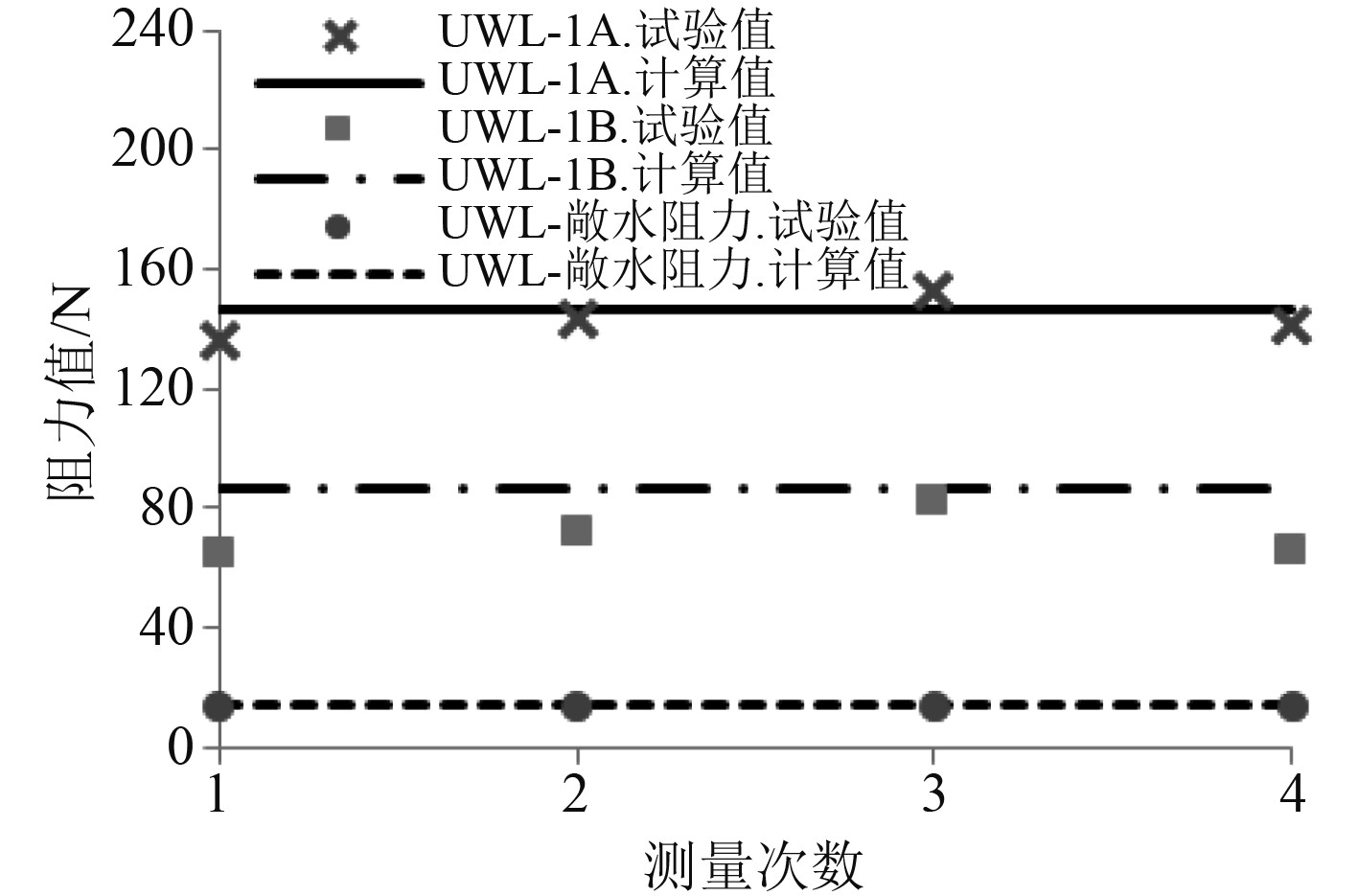
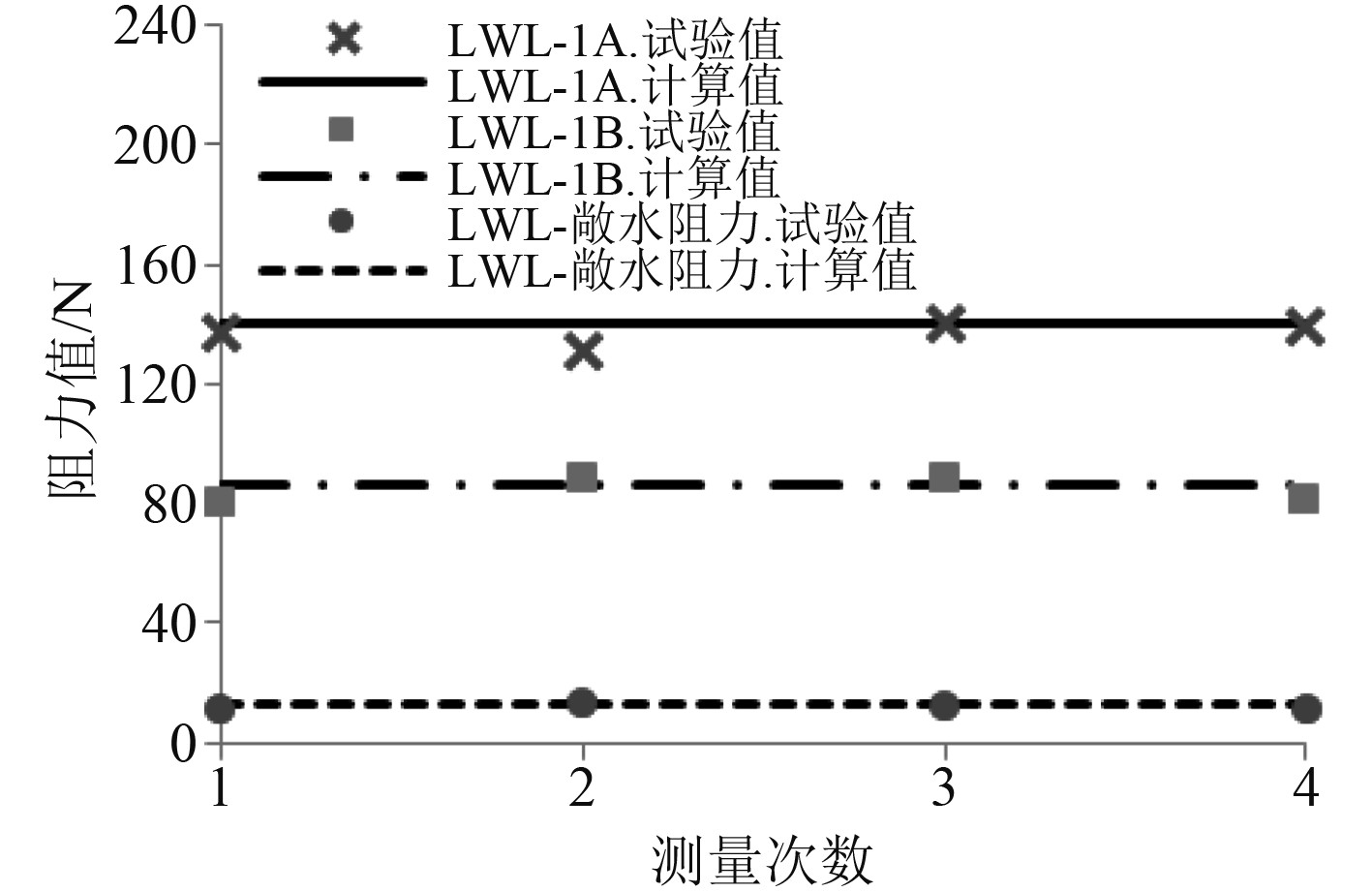
图13和图14为船体在碎冰中航行时所受总阻力的数值模拟结果与模型试验结果，其中敞水阻力代表水面无冰情况下船体所受阻力。数值模拟结果显示，除UWL-1B冰级的碎冰阻力结果与模型试验值产生较大偏差外，其余均可落在分次测量结果最大值与最小值范围内，数值计算结果与模型试验4次测量值的平均值相比，计算值会偏大2%～3%。

分析UWL-1B冰池的碎冰阻力计算结果与模型试验值产生较大偏差的原因，可能是由于模型试验中，碎冰粒子形状的差异引起的。分别提取UWL-1B、LWL-1B冰级试验航道碎冰粒子形状，如图15所示。从图15（b）可知，LWL-1B冰级试验中的碎冰粒子更接近于1A冰级试验（见图2）中不规则扁平多面体碎冰粒子形状，而UWL-1B冰级试验中的碎冰粒子更加圆润，接近于球形粒子。有研究表明，较方碎冰会比较圆碎冰导致更大的冰阻力，原因是船舶在较高覆盖率下与碎冰碰撞时会形成了力链，具有较多平行对边的四边形会形成比较稳定的力链，而椭圆等形成的力链比较脆弱^[7]；且从面接触理论来看，外形越接近于球形粒子，其与另一平面（因碎冰粒子相较于船体尺寸较小，船体与其接触面近似于平面）的接触面积越小。而低速碎冰阻力中摩擦阻力占比大，接触面积变小会直接导致碎冰阻力的测量值变小。除此之外的3种计算工况的碎冰形状类似，其计算误差也能维持在同一水平。

模型试验中无冰敞水阻力试验测量值趋于稳定。其数值模拟结果均与模型试验结果吻合较好，误差维持在1%左右。

4 结　语

采用DEM方法模拟船体在碎冰航道中航行，不仅可以描绘出碎冰与船体相互作用时的运动状态，而且通过设置适当的接触模型，其计算精度也可以满足工程应用的要求。

1）因模型试验中碎冰粒子分布的随机性，同一条件下的碎冰航道试验结果也有一定的差异性。因此数值模拟结果通常不会与试验结果完全吻合，只要维持误差在一定范围内，都可以认为准确、有效。

2）船舶在碎冰航道中的无冰敞水阻力仅占总阻力非常小的一部分，并且，当采用单向耦合方法时，无冰敞水阻力计算值与碎冰粒子-船体相互作用的数值模型无关。

3）接触模型的设置对于计算结果有非常重要的影响，选择合理的静摩擦系数及动摩擦系数，准确的模拟碎冰粒子与船体之间的接触响应，是影响数值模拟准确性的关键参数之一。

4）低航速下的碎冰阻力成分中，摩擦阻力占很大部分，除了摩擦系数的设置，碎冰粒子的形状会影响碎冰粒子与船体之间的接触面积以及力的传递，进而影响冰阻力值。本文中，同等尺寸下，若碎冰粒子为球形将使接触面积变小、力链更为脆弱，相应碎冰阻力值计算值也会减小。

5）数值计算中采用正四面体来模拟碎冰粒子，其计算结果可以满足本次计算要求。

6）本次计算中两吃水差别较小，将该数值计算模型应用于其他差别较大的吃水以及其他船型的准确性还有待进一步验证。