20世纪60年代以来,美俄两国对北极冰层下空间进行了激烈争夺。1958 年美国首艘核动力潜艇“鹦鹉螺”号、1963年苏联核潜艇K-181号先后到达北极并完成破冰上浮。进入21世纪以来,美俄两国多次在北极地区开展冰下军事演习及导弹发射实验,这也凸显了北极地区极高的战略价值。北极地区冰盖的平均厚度达3 m,冰盖能够有效阻隔水面舰船、航空、卫星等反潜兵力的对潜搜索。冰盖裂解及海水冲刷的噪声能够干扰反潜声呐探测,冰层的覆盖为潜体的航行机动及作战使用提供了极大的隐蔽性。同时,北极点向南500 km的范围内分布着北半球范围内绝大多数陆地目标。如果自北冰洋边缘算起,潜用武器射程达到
由于潜体近冰区航行敏感度较高,国内外对于潜体近冰面航行受力及操纵研究资料较少,多集中在近自由液面的航行研究。张楠等[1]对SUBOFF潜艇模型在不同浸深下的阻力特性进行数值模拟,分析了自由液面对于模型阻力的定量影响,对于SUBOFF模型在深潜与近水面状态下的艇后推力、扭矩进行了数值模拟。王陆等[2]对潜体近水面航行自由液面干扰效应进行研究,发现在近自由液面条件下(H/D≤1.3),潜艇所受阻力及垂向力系数随航速的增大均呈现明显波动现象。对于潜体近冰面航行研究,文献较少。叶礼裕等[3]对潜艇破冰上浮近场动力学模型进行了研究,分析了潜艇破冰上浮过程及冰载荷的动态特性。柏铁朝等[4]采用数值模拟方法探究潜体近冰面航行时的水动力性能,探索了潜艇的总阻力系数Ct随弗汝德数的变化规律。
潜体近冰面航行时艇体垂向受力及力矩情况是各级操艇人员最为关注的。只有掌握了近冰面航行受力特点及规律,才能给出正确的操纵方法,保障潜体航行安全。为此以美国SUBOFF为研究对象,利用STAR-CCM+软件开展潜体近冰面航行艇体受力研究,并对某一深度不同航速条件下艇体垂向力及力矩进行分析,结合潜体六自由度运动数学模型给出了定深航行操纵方法。
1 基本方程 1.1 控制方程本文研究不可压缩流体在近冰面航行潜体表明产生的力与力矩问题,以及由此产生的潜体安全操纵问题。不可压缩流体的基本方程组包括连续性方程以及动量守恒方程。质量守恒方程和动量守恒方程可表示为:
| $ \frac{\partial \rho }{\partial t}\text+\frac{\partial (\rho {u}_{i})}{\partial {x}_{i}}=0 ,$ | (1) |
| $ \begin{split}\displaystyle\frac{\partial(\rho {u}_{\text{i}})}{\partial t} + div(pu{u}_{i}) = -\displaystyle\frac{\partial p}{\partial {x}_{i}} + \displaystyle\frac{\partial {\tau }_{xi}}{\partial {x}_{}} + \displaystyle\frac{\partial {\tau }_{yi}}{\partial {y}_{}} + \displaystyle\frac{\partial {\tau }_{zi}}{\partial {z}_{}} + {F}_{i}\end{split}。$ | (2) |
式中:p为压力;ρ为流体密度;u为流体速度矢量;Fi为质量力;τ为运动粘性系数。
1.2 湍流模型在本文的计算过程中,采用湍流模型 SST k-ω两方程模型,湍流动能
| $ \begin{gathered} \frac{\partial }{{\partial t}}(\rho k) + \nabla \cdot \left[ {\rho kV} \right] = \nabla \cdot \left[ {\left(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\right)\nabla k} \right] + {G_k} - {Y_K}。\\ \end{gathered} $ | (3) |
特殊耗散率w方程为:
| $ \begin{gathered} \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \nabla \cdot \left[ {\rho \varepsilon V} \right] = \nabla \cdot \left[ {\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}\right)\nabla \varepsilon } \right] + {G_k} - {Y_\omega } + {D_\omega } 。\\ \end{gathered} $ | (4) |
式中:
本文选取的潜体计算模型为美国DARPA发表的SUBOFF全附体模型(见表1)。潜体计算域长度为 SUBOFF艇长6倍,计算域前端距离潜体首部1倍,计算域后端距潜体尾部4倍,计算域高度和宽度方向为模型艇长的2倍,艇体上表面距冰面高度为1.5倍艇体高度。
|
|
表 1 全附体模型参数 Tab.1 Parameters of SUBOFF model |
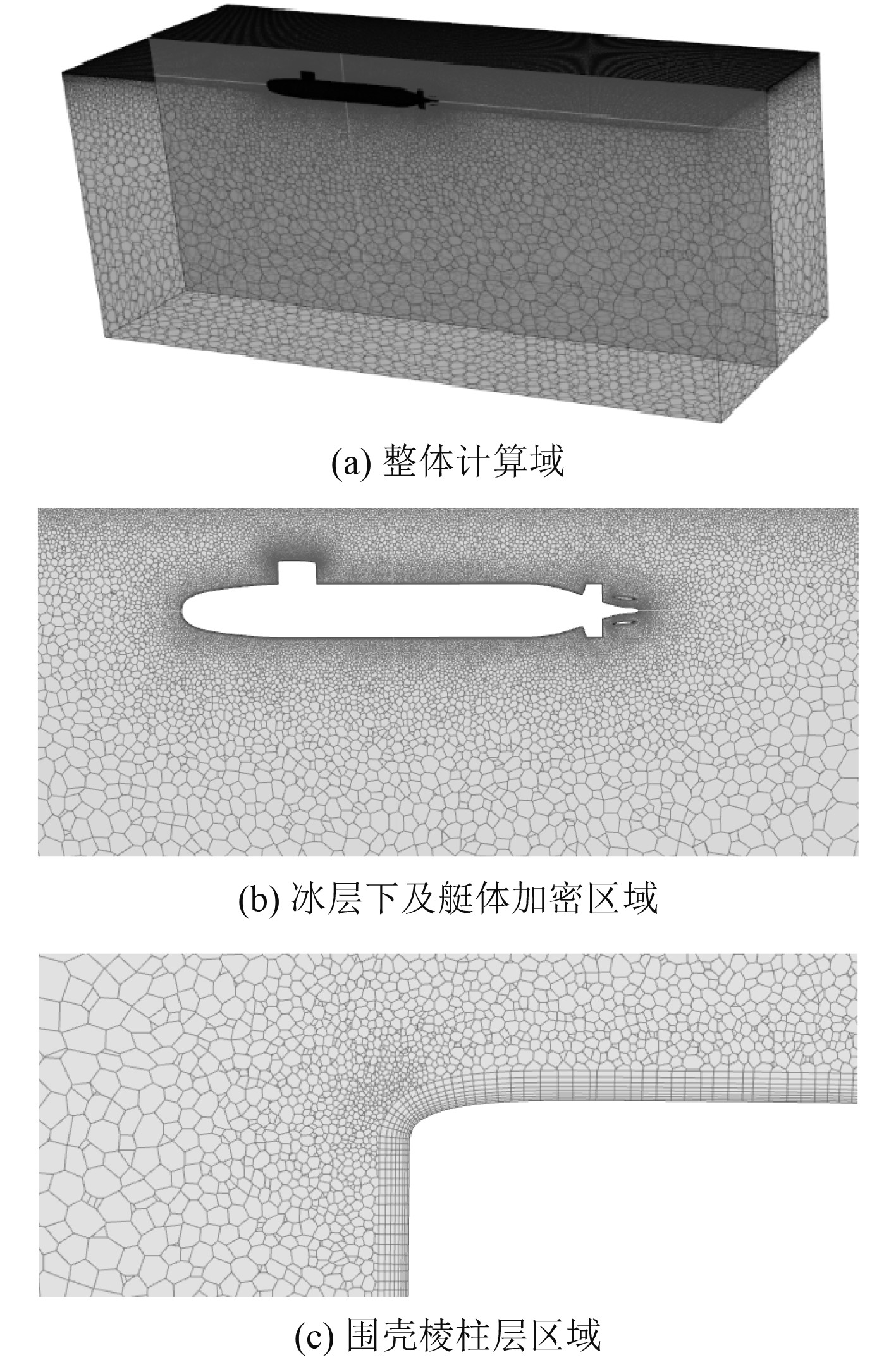
整体计算域采用六面体非结构化网格、棱柱层网格方式进行网格划分。潜体表面使用棱柱层进行网格划分,棱柱层层数设置为8层,棱柱层以外计算区域采用六面体非结构化网格。对近冰面区域、艇首、艇尾以及潜体主附体结合部位进行了局部网格加密。艇体表面y+为30,潜体计算模型约700万。计算模型网格划分如图1所示。
|
图 1 模型计算域网格划分 Fig. 1 Model grid division of computational domain |
利用 STAR-CCM +软件模拟了潜体在1.5倍艇体高度深度潜体受力情况,计算边界条件如下。
速度入口:来流速度的大小与方向,Vin=V;
压力出口:相对于参考压力点的流体静压值;
壁面:无滑移壁面条件,u=v=w=0;
外场:速度为未受扰动的主流区速度。
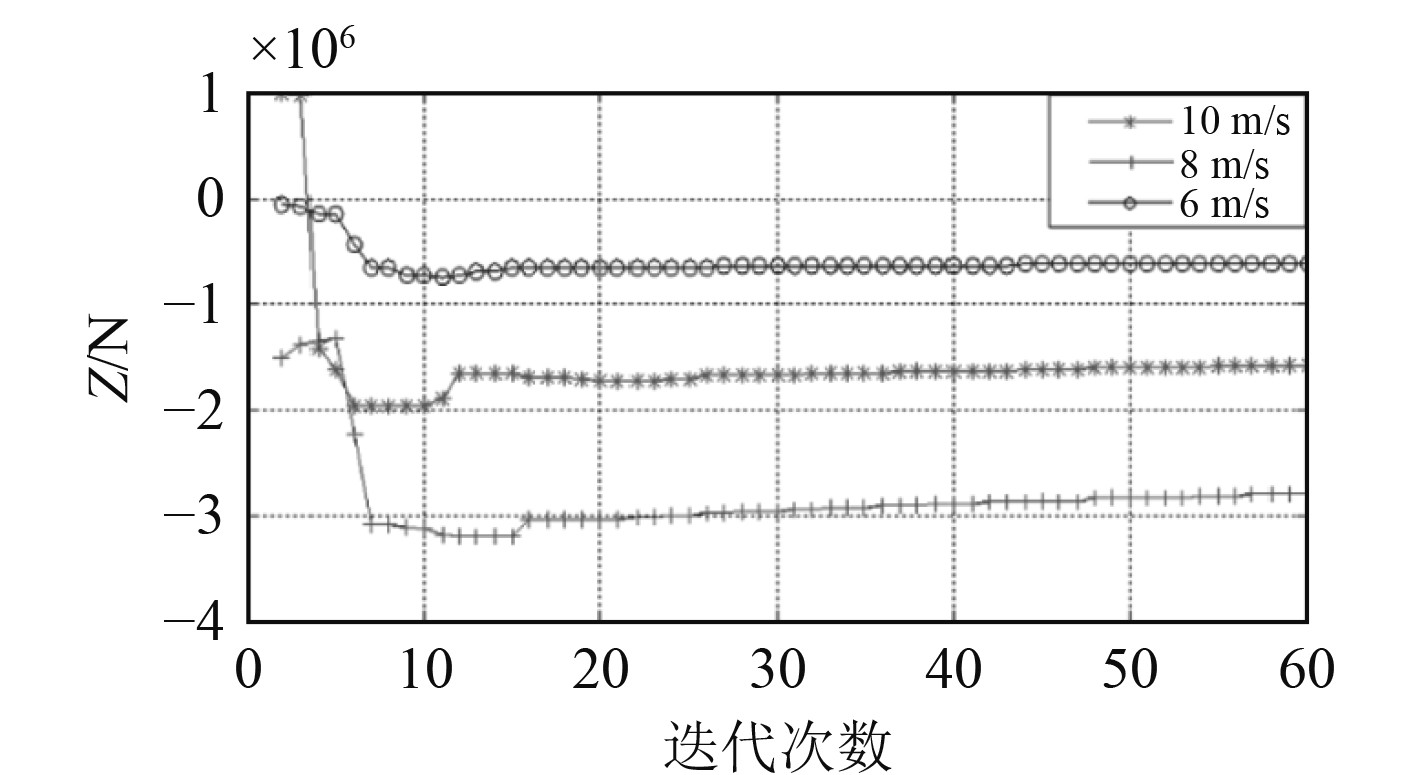
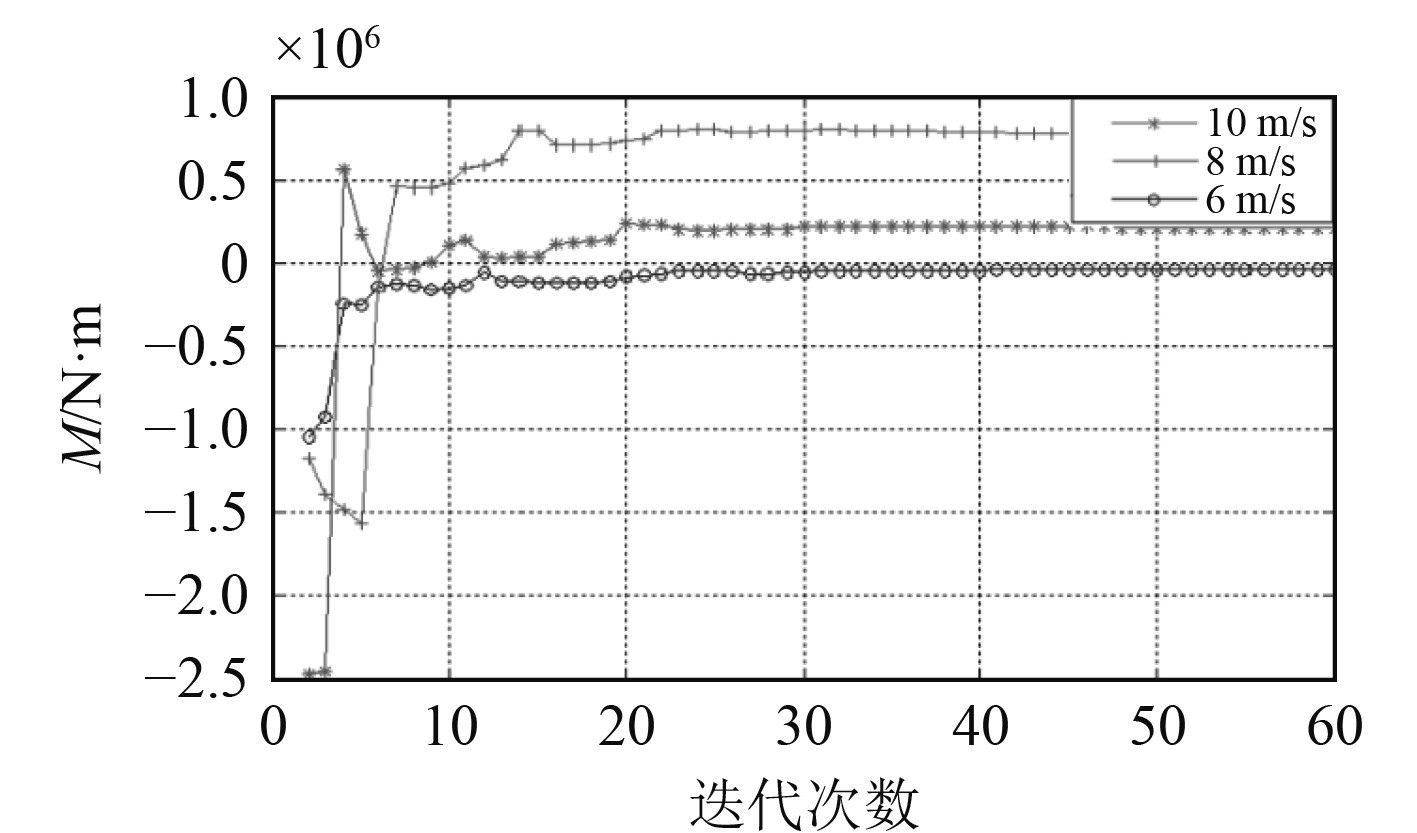
图2 所示为入口条件流速Vin分别为6、8、10 m/s时艇体速度云图;图3和图4分别给出了艇体在不同入口条件下的艇体所受垂向力和垂向力矩大小。

|
图 2 潜体近冰面航行中纵剖面速度云图 Fig. 2 The velocity distribution of mid profile near the ice layer |
|
图 3 近冰面航行潜体垂向力曲线 Fig. 3 Vertical force curve near the ice layer |
|
图 4 近冰面航行潜体力矩曲线 Fig. 4 Vertical moment curve near the ice layer |
可以看出,潜体在近冰面航行时,由于艇体上层与冰盖之间流场的变化,艇体会受到较大的垂向力和力矩,所受垂向力的大小随着航速的增加而显著增大。在初始航速6 m/s时,垂向力及力矩均较小,在零值附近。航速增至10 m/s时,垂线力达到3×106 N,垂向力矩达到0.8×106 N·m。这也表明,潜体在近冰面航行时随着航速增大,艇体会受到较大的垂向力及力矩影响,会造成深度难以保持,潜体上浮,力矩则会引起艇体产生尾倾,对于潜体操纵来说,这将引起艇首部以及围壳与冰面发生碰撞,造成操纵险情。因此,需要对潜体近冰面的安全操纵方法进行研究。
4 潜体空间运动模型本文利用格特勒潜体六自由度运动数学模型对潜体近冰面航行操纵方法进行探究。将数值计算所得潜体垂向力和力矩计入六自由度运动模型垂向速度项及纵倾力矩项,其纵向、垂向、纵倾及辅助数学模型如式(5)~式(8)所示[1 - 2]:
| $ \begin{split} m & \left[\dot{u}-vr+wq\right]=\\ &\displaystyle\frac{\rho }{2}{L}^{4}\left[{X'}_{qq}{q}^{2}+{X'}_{rr}{r}^{2}+{X'}_{rp}rp\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{3}\left[{X'}_{\dot{u}}\dot{u}+{X'}_{vr}vr+{X'}_{wq}wq\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{2}\left[{X'}_{uu}{u}^{2} + {X'}_{vv}{v}^{2} + {X'}_{ww}{w}^{2} + {X'}_{w}uw + {X'}_{\left|w\right|}u\left|w\right|\right] +\\ &\displaystyle\frac{\rho }{2}{L}^{2}{u}^{2}\left[{X'}_{{\delta }_{r}{\delta }_{r}}{\delta }_{r}{}^{2}+{X'}_{{\delta }_{b}{\delta }_{b}}{\delta }_{b}{}^{2}+{X'}_{{\delta }_{s}{\delta }_{s}}{\delta }_{s}{}^{2}\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{2}\left[{a}_{i}{u}^{2}+{b}_{i}u{u}_{c}+{c}_{i}{u}_{c}{}^{2}\right]-\Delta W\mathrm{sin}\theta ,\end{split} $ | (5) |
| $ \begin{aligned}[b] &m\left[\dot{w}-uq+vp\right]=\\ &\displaystyle\frac{\rho }{2}{L}^{4}\left[{{Z}^{\prime }}_{\dot{q}}\dot{q}+{{Z}^{\prime }}_{pp}{p}^{2}+{{Z}^{\prime }}_{rr}{r}^{2}+{{Z}^{\prime }}_{rp}rp+{{Z}^{\prime }}_{q\left|q\right|}q\left|q\right|\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{3}\left[{{Z}^{\prime }}_{\dot{w}}\dot{w}+{{Z}^{\prime }}_{vr}vr+{{Z}^{\prime }}_{vp}vp\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{3} \left[ \begin{array}{l}{Z'}_{q}uq + {Z'}_{\left|q\right|{\delta }_{s}}u\left|q\right|{\delta }_{s} + {Z'}_{w\left|q\right|}\displaystyle\frac{w}{\left|w\right|}\left|{\left({v}^{2} + {w}^{2}\right)}^{1/2}\right|\left|q\right| \\ +{Z'}_{www}w\left({v}^{2}+{w}^{2}\right)\end{array}\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{2}\left[{Z'}_{*}{u}^{2}+{Z'}_{w}uw+{Z'}_{w\left|w\right|}w\left|{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{2}\left[{Z'}_{\left|w\right|}u\left|w\right|+{Z'}_{ww}\left|w{\left({v}^{2}+{w}^{2}\right)}^{1/2}\right|\right]+\\ &\displaystyle\frac{\rho }{2}{L}^{2}\left[{Z'}_{vv}{v}^{2} + {Z'}_{\delta s}{u}^{2}{\delta }_{s} + {Z'}_{\delta b}(t){u}^{2}{\delta }_{b}\right] + \Delta W\mathrm{cos}\theta \mathrm{cos}\varphi ,\end{aligned} $ | (6) |
| $ \begin{aligned}[b] {I_y}\dot q &+ \left( {{I_x} - {I_z}} \right)rp = \\ &\displaystyle\frac{\rho }{2}{L^5}\left[ {M_{\dot q}^{'}\dot q + M_{pp}^{'}{p^2} + M_{rr}^{'}{r^2} + M_{rp}^{'}rp + {{M'}_{q\left| q \right|}}q\left| q \right|} \right] + \\ &\displaystyle\frac{\rho }{2}{L^4}\left[ {M_{\dot w}^{'}\dot w + M_{vr}^{'}vr + M_{vp}^{'}vp} \right]+ \\ &\displaystyle\frac{\rho }{2}{L^4}\left[ {M_q^{'}uq + M_{\left| q \right|{\delta _s}}^{'}u\left| q \right|{\delta _s} + M_{\left| w \right|q}^{'}\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|q} \right]+ \\ &\displaystyle\frac{\rho }{2}{L^4}\left[ {{{M'}_{www}}w\left( {{v^2} + {w^2}} \right) + {{M'}_{\left| w \right|ww}}\left| {w\left( {{v^2} + {w^2}} \right)} \right|} \right]+ \\ &\displaystyle\frac{\rho }{2}{L^3}\left[ {{{M'}_*}{u^2} + {{M'}_w}uw + {{M'}_{\left| w \right|w}}w\left| {{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|} \right]+ \\ &\displaystyle\frac{\rho }{2}{L^3}\left[ {{{M'}_{\left| w \right|}}u\left| w \right| + {{M'}_{ww}}\left| {w{{\left( {{v^2} + {w^2}} \right)}^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}} \right|} \right]+ \\ &\displaystyle\frac{\rho }{2}{L^3}[{{M'}_{vv}}{v^2} + {{M'}_{\delta s}}{u^2}{\delta _s} + {{M'}_{{\delta _b}}}{u^2}{\delta _b}] - \\ &({x_G}W - {x_B}B)\cos \theta \cos \phi - \\ &({z_G}W - {z_B}B)\sin \theta {\text{ + }}\Delta M\cos \theta ,\end{aligned} $ | (7) |
| $ q = \dot \theta。$ | (8) |
式中:
潜体操纵可以划分为正常操纵与应急操纵,其中正常操纵一般定义为潜体的常规性变深机动操纵,应急操纵则侧重于发生突发险情时可能对潜体造成潜在危害而进行的操纵。从危险程度上看,应急操纵造成的险情明显更高,因此能否在最短时间内控制潜体深度及姿态、保障潜体航行安全就显得尤为重要。对于潜体操纵方法而言,主要涉及潜体车、舵、水、气的综合应用。其中,车为潜体的动力系统,舵为潜体的首尾升降舵,水为潜体平衡水舱以及压载水舱,气为潜体的高压气。潜体近冰面航行时距离冰面较近,使用高压气对于潜体影响巨大,易造成潜体大幅变深,潜体航行深度及姿态均难以保持,此时使用高压气反而会对潜体航行安全带来不利影响。因此以下所列操纵方法不涉及高压气的使用,主要对车、舵、水的使用进行分析,比较不同操纵方法在潜体挽回时间、挽回深度以及挽回纵倾方面的效果。
潜体近冰面航行操纵方法,归纳起来可以分为2个大类,分别为采用“车+舵”操纵方法和“车+舵+水”操纵方法,具体方法如下:
方法A 采取首尾舵操舵+降速至a。
方法B 采取首尾舵操舵+降速至a+纵倾平衡水舱向首调水b。
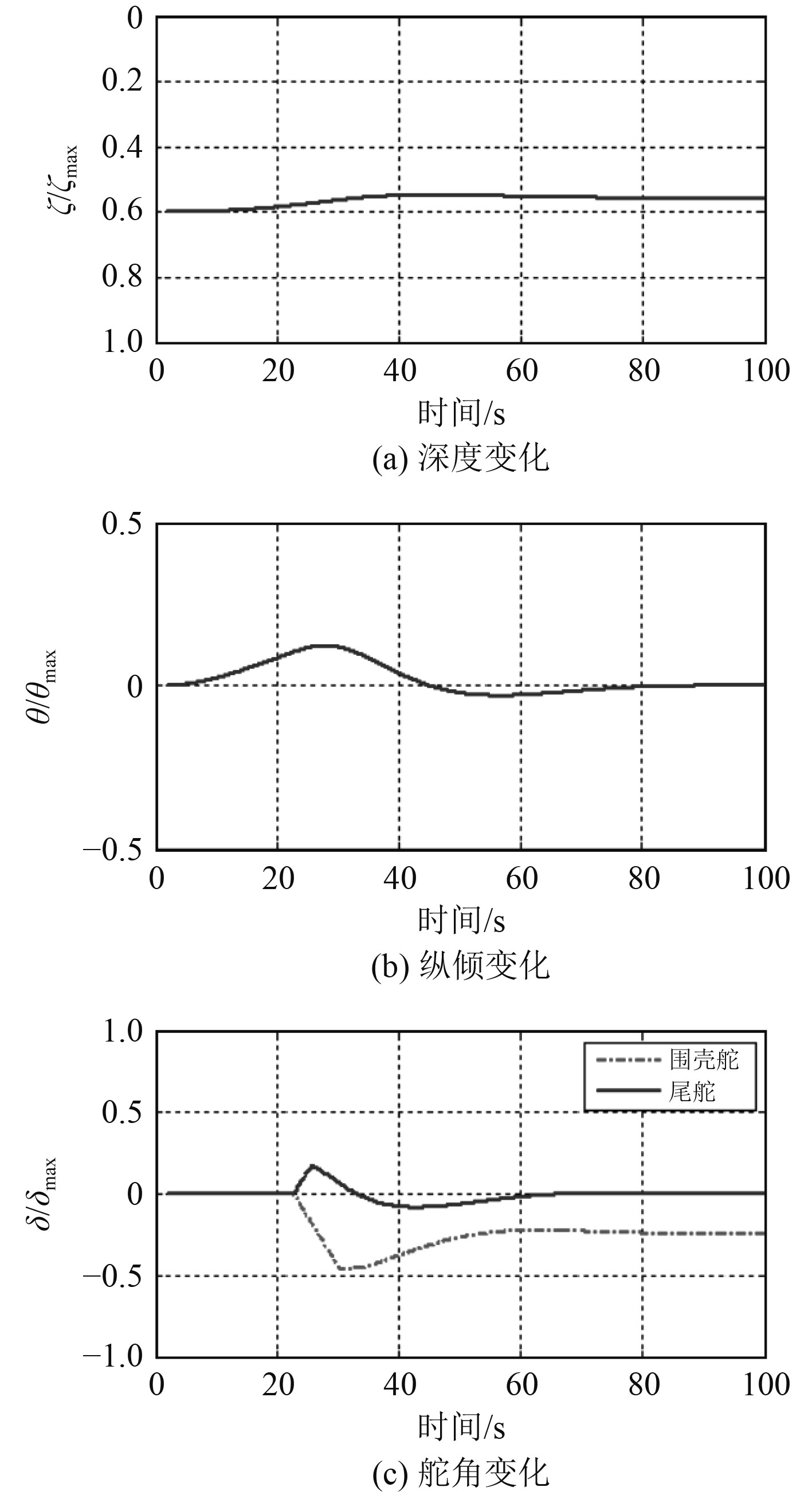
5.1 A操纵方法模拟潜体近冰面航行初始深度为H,潜体航行速度为10 m/s,首尾操舵及降速反应时间为t。图5给出了潜体深度、纵倾及首尾舵角变化曲线。
|
图 5 方法A潜体深度姿态变化曲线图 Fig. 5 Attitude and depth curve about method A |
由图5可知,潜体近冰面航行时,航行深度在未采取操舵及调水措施时会逐渐减小,潜体纵倾会逐渐增大。由于伯努利原理,流体在流经潜体上表面及冰盖之间时流速会增大,导致艇体下表面流体压力大于上表面流体压力,使艇体产生向上升力。艇首部位较宽厚,艇尾细窄,艇首压力小于艇尾压力,首尾压力不一致导致潜体产生垂直方向偏转。t时采取操舵及降速措施,艇体深度及姿态逐渐恢复,可以保持无纵倾定深航行。
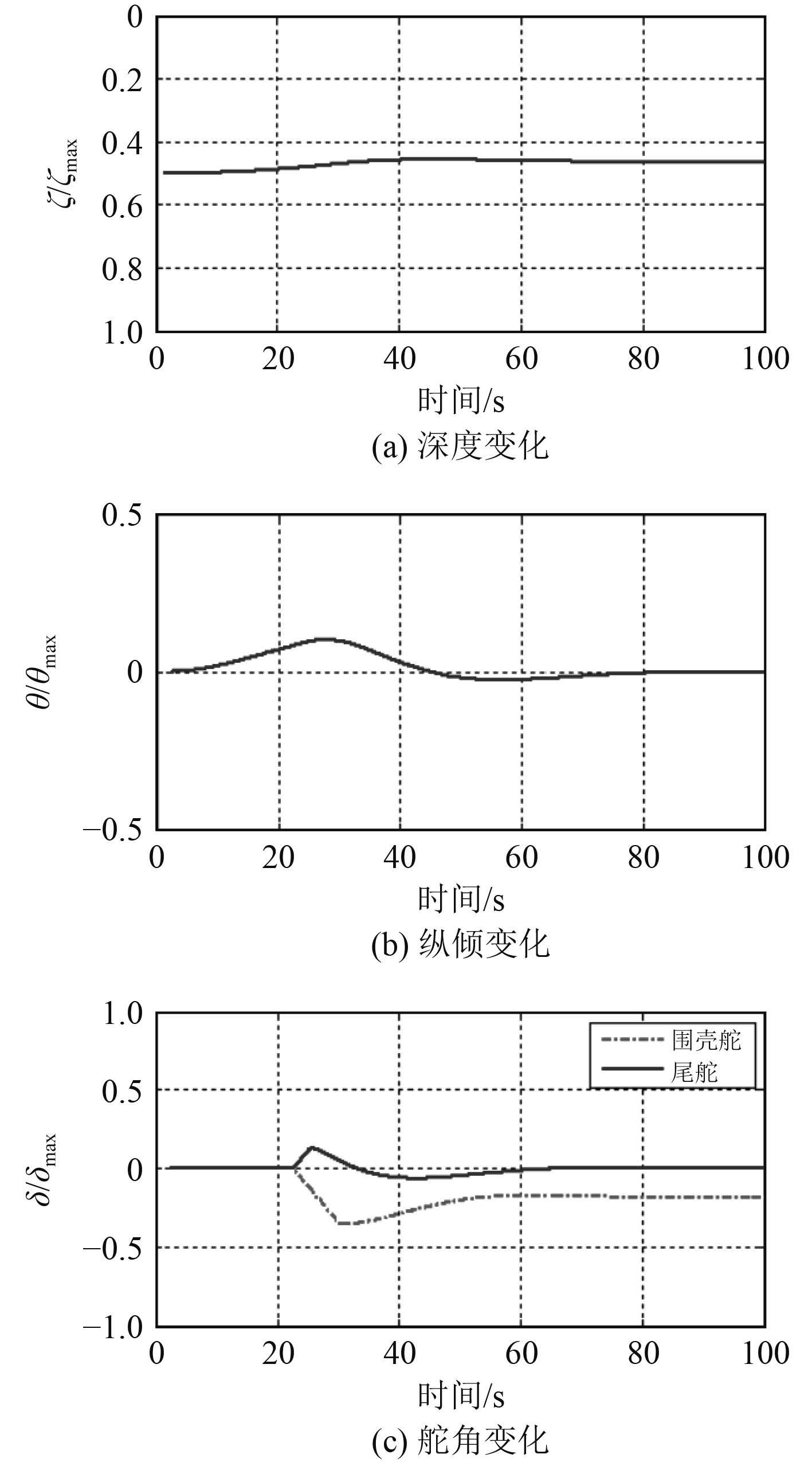
5.2 B操纵方法方法B初始条件与方法A相同,其中纵倾平衡水舱调水反应时间也为t。图6给出了潜体深度、纵倾及首尾舵舵角变化曲线。
|
图 6 方法B潜体深度姿态变化曲线图 Fig. 6 Attitude and depth curve about method B |
由图6可知,采取B 方法后,潜体稳定航行深度较方法A要小,纵倾变化值也较方法A小,围壳舵舵角稳定值也小于方法A采用舵角,潜体航行稳定时间要早于方法A。比较而言,采取纵倾平衡水舱调水措施更有利于潜体航行深度及姿态稳定。表2所示为2种方法无量纲化后的各参数。
|
|
表 2 不同操纵方法潜体响应参数值 Tab.2 Response values of different methods |
本文以近冰面航行潜体为研究对象,建立了近冰面航行数值计算模型,计算了近冰面航行时的艇体受力,结合空间六自由度运动模型对近冰面航行操纵方法进行了探讨,分析得到以下结论:
1)潜体在近冰面航行时艇体会产生升力,导致潜体向冰面变深,易造成围壳与冰面碰撞险情。
2)潜体在近冰面航行时艇体会产生尾倾,导致潜体抬首埋尾,易造成艇首与冰面碰撞险情。
3)潜体在近冰面航行时艇体所受垂向力与尾倾力矩大小与航速有关,航速越高各力(矩)越大,在6 m/s时垂向力(矩)较小。
4)航速较高时采用降速+首尾舵操舵+纵倾平衡水舱调水的方法进行操纵更有利于潜体无纵倾定深航行。
| [1] |
张楠, 张胜利, 沈泓萃, 等. 带自由液面的艇/桨干扰特性数值模拟与验证研究[J]. 水动力学研究与进展, 2012, 27(1): 94-99. ZHANG Nan, ZHANG Shengli, SHEN Hongcui, et al. Numerical simulation of hull/propeller interaction with free surface[J]. Journal of Hydrodynamics, 2012, 27(1): 94-99. |
| [2] |
王陆, 毕毅, 周广礼, 等. 潜艇近水面航行自由液面干扰效应数值研究[J]. 舰船科学技术, 2021, 43(1): 83-88. WANG Lu, BI Yi, ZHOU Guangli, et al. Numerical study on submarine's hydrodynamic performance for near-surface conditions[J]. Ship Science and Technology, 2021, 43(1): 83-88. |
| [3] |
叶礼裕, 王超, 郭春雨, 等. 潜艇破冰上浮近场动力学模型[J]. 中国舰船研究, 2018, 13(2): 51-59. YE Liyu, WANG Chao, GUO Chunyu, et al. Peridynamic model for submarine surfacing through ice[J]. Chinese Journal of Ship Research, 2018, 13(2): 51-59. |
| [4] |
柏铁朝, 许建, 王国栋, 等. 近冰面航行潜艇阻力及绕流场分析[J]. 中国舰船研究, 2021, 16(2): 37-48. BAI Tiechao, XU Jian, WANG Guodong, et al. Analysis of resistance and flow field of submarine sailing near the ice surface[J]. Chinese Journal of Ship Research, 2021, 16(2): 37-48. |
| [5] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995.
|
 2024, Vol. 46
2024, Vol. 46
