泵喷推进器作为一种性能优良的新型推进器,相较于常规螺旋桨,具有推迟空泡发生、提高推进器效率和降低辐射噪声等优势,已经在世界范围内得到广泛应用。但泵喷推进器与螺旋桨、轴流泵和涡轮机等流机装置一样,在其工作时,由于转子叶面与叶背之间存在压力差,转子梢部会发生流动分离,在叶背处形成复杂的涡结构。由于涡流的旋转特性,在梢泄涡涡核位置的压力远低于周围流体区域,当涡核压力低于饱和蒸汽压时,会产生梢泄涡空化。空化会在转子表面产生剥蚀、恶化推进器的水动力性能和引起转子叶片产生形变等,并导致推进器噪声显著增加,对水下航行体在高航速下的声隐身性能产生不利影响。因此,探究准确预测泵喷推进器转子梢涡空化方法具有重要的研究意义。
试验与数值相结合是目前较为常用的研究方法,梢涡空化试验一般以观测位置为主,以现代化测量仪器为辅。数值计算则以LES和RANS求解为主,其中,LES通过直接计算大尺度湍流结构,仅对最小尺度的湍流建模,在复杂流场计算上具有明显优势,可以准确求解复杂流体特性,Nicholas等[1]总结了LES的使用能力和限制,并提供了使用LES湍流模型的评估标准,即空间求解需要满足
空化试验是最为直观准确的研究方法,Chesnakas等[2]采用LDV技术研究了导管螺旋桨的梢涡流动,分析了其与无导管时的区别。Wu等[3]采用PIV技术研究了喷水推进泵的梢隙流动和梢泄涡的卷曲过程。Rains等[4]观测到梢泄涡空化先于面空化。Oweis等[5 - 6]发现梢涡空化最开始出现在桨叶弦长中段。但由于测量装置的限制和梢隙流场的复杂性,试验一般难以获取梢部流场信息以便于量化解释分析空化现象。
LES在许多水下结构物的梢涡空化计算方面取得了较好的实践效果。Cheng等[7]采用LES和S-S (Schnerr-Sauer)空化模型计算分析了NACA009水翼梢涡空化演化过程。You等[8]采用Smagorinsky系列亚尺度粘度湍流模型计算了转子的梢部间隙流动,讨论了LES计算中时间和空间上的布置。Asnaghi等[9 - 10]采用隐式LES(ILES)计算三维水翼的梢涡,确定了准确计算梢涡的网格布置要求,并进一步选择5叶桨中的其中一个叶片梢涡位置网格细化展开数值计算,分析了4种梢涡空化初生预测模型的适用性。Hu等[11]采用LES和S-S空化模型研究发现螺旋桨侧斜增加时空化核减小,同时分析了梢涡空化及其附近的流场特性。
本文首先对泵喷推进器进行了梢涡空化观测试验,根据试验条件布置数值计算,基于LES和WALE亚尺度涡粘度模型计算全湿流场,加入S-S空化模型后计算空化流场,分析了常用多通道周期性结构网格在梢涡空化计算上的不足,并提出新型网格划分方法,完成可行性验证,通过数值计算结果与试验结果的对比证明本文所提方法在预测梢涡空化方面的优越性。
1 空泡观测试验以图1所示的前置式定子泵喷推进器模型为研究对象,导管为加速型导管,定子为13叶,转子为7叶,转子半径R=123 mm;导管内壁与转子梢部端面之间的间隙最小值为3.7 mm,最大值为4.7 mm。

|
图 1 泵喷推进器几何模型 Fig. 1 Geometry of the pumpjet propulsor |
本试验在海军工程大学空泡水洞实验室进行,空化试验大气压力101.3 kPa,泵喷推进器转子桨轴沉深为1.2 m;水的饱和蒸汽压为3.2 kPa。根据毕托管测速仪的汞柱高度差计算各转速下导管前方流速,转速分别为900、
|
|
表 1 导管前方速度与压力 Tab.1 Velocity and pressure before the duct |
质量与动量守恒方程为:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho \overline {{u_i}} } \right) = 0 ,$ | (1) |
| $ \frac{\partial }{{\partial t}} \left( {\rho \overline {{u_i}} } \right) + \frac{\partial }{{\partial {x_j}}} \left( {\rho \overline {{u_i}} \overline {{u_j}} } \right) = - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}} \left[ { \left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} + \frac{{\partial \overline {{u_j}} }}{{\partial {x_i}}}} \right)} \right]。$ | (2) |
式中:
在WALE模型中,亚尺度粘度
| $ {\mu _t} = \rho \Delta _s^2\frac{{{{\left( {S_{ij}^dS_{ij}^d} \right)}^{\frac{3}{2}}}}}{{{{\left( {\overline {{S_{ij}}} \overline {{S_{ij}}} } \right)}^{\frac{5}{2}}} + {{\left( {S_{ij}^dS_{ij}^d} \right)}^{\frac{5}{4}}}}} 。$ | (3) |
式中,可求解的拉伸应变率
Rayleigh-Plesset方程:
| $ \frac{{{P_b} - {P_\infty }}}{{{\rho _L}}} = {R_c}\frac{{{{\text{d}}^2}{R_c}}}{{{\text{d}}{t^2}}} + \frac{3}{2}{\left( {\frac{{{\text{d}}{R_c}}}{{{\text{d}}t}}} \right)^2} + \frac{{4{v_l}}}{{{R_c}}}\frac{{{\text{d}}{R_c}}}{{{\text{d}}t}} + \frac{{2S}}{{{\rho _L}{R_{{c}}}}}。$ | (4) |
式中:
S-S(Schnerr-Sauer)空化模型简化Raleigh-Plesset方程,忽略气泡加速的影响、粘性效应和表面张力得到S-S空化模型的公式为:
| $ S = \left\{ \begin{gathered} \frac{{{\rho _v}{\rho _l}}}{{{\rho _m}}}\alpha \left( {1 - \alpha } \right)\frac{3}{{{r_b}}}\sqrt {\frac{2}{3}\frac{{{P_v} - P}}{{{\rho _l}}}} ,{P_v} \geqslant P,\\ \frac{{{\rho _v}{\rho _l}}}{{{\rho _m}}}\alpha \left( {1 - \alpha } \right)\frac{3}{{{r_b}}}\sqrt {\frac{2}{3}\frac{{P - {P_v}}}{{{\rho _l}}}} ,{P_v} \geqslant P。\\ \end{gathered} \right. $ | (5) |
本节数值计算按照空泡观测试验设置,计算区域分为导管外域、定子域和转子域。以转速为

|
图 2 外域网格及其边界条件 Fig. 2 Grid and boundary condition of external domain |
导管外域、定子域和转子域均为结构网格,定子域与转子域采用ICEM 16.0单通道网格周期性旋转所得。本文主要研究转子叶梢流场,因此,导管外域与定子域网格保持不变,网格量分别为368万和456万。
转子网格采用O型网格划分方法设置转子边界层,近壁面第一层网格厚度为0.005 mm,壁面
|
图 3
转子壁面 |
|
图 4 CFL数分布 Fig. 4 CFL distribution of the rotor |
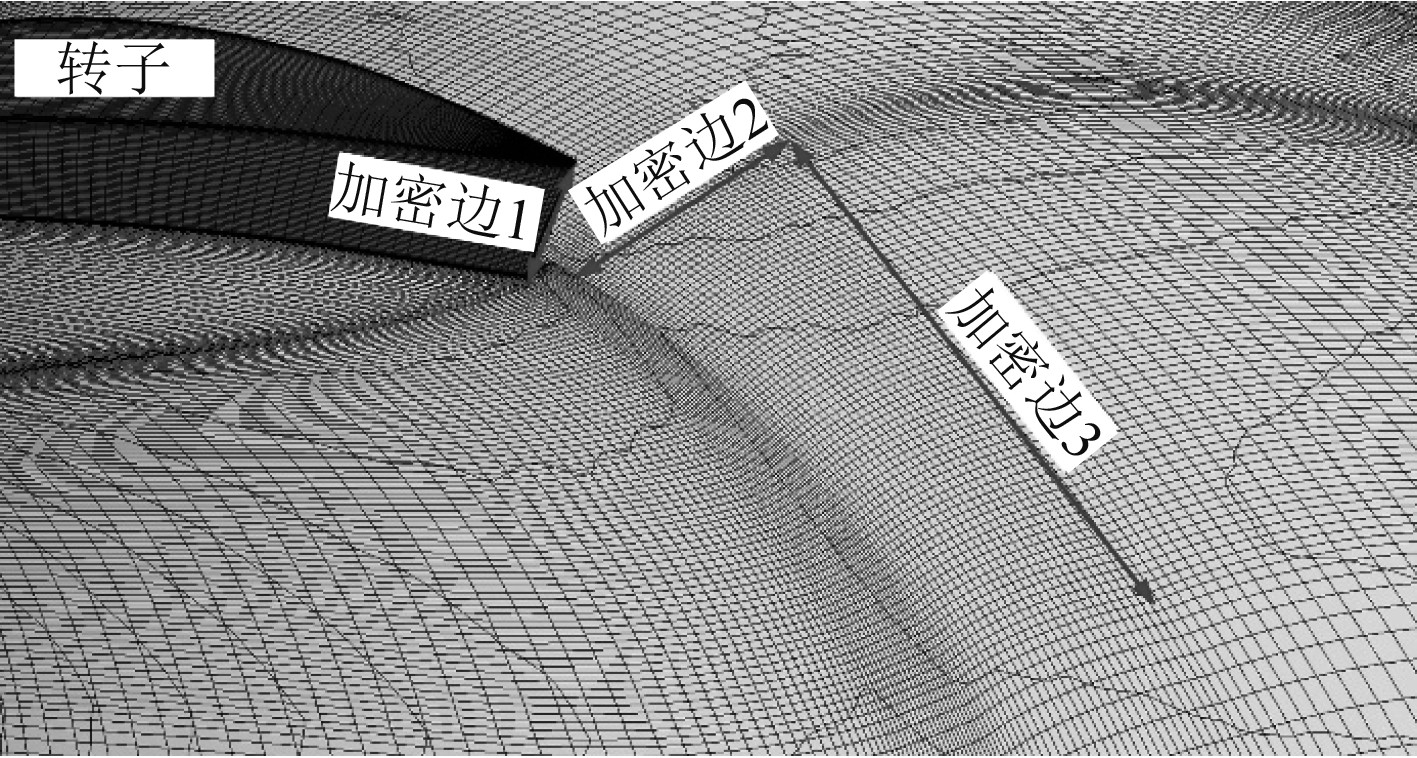
转子域网格由ICEM 16.0生成,选择转子尾缘处的1个子块上的3条边作为加密边,如图5所示。通过调整3条加密边上的网格最大尺寸可修改梢泄涡周围的网格密度,得到表2所示的3种转子域网格。
|
图 5 网格加密边定义 Fig. 5 Edges of gird refinement |
|
|
表 2 3种转子域网格的尺寸定义 Tab.2 Grid size of three rotor domain |
计算
|
图 6 监测面位置 Fig. 6 location of monitor surfaces |
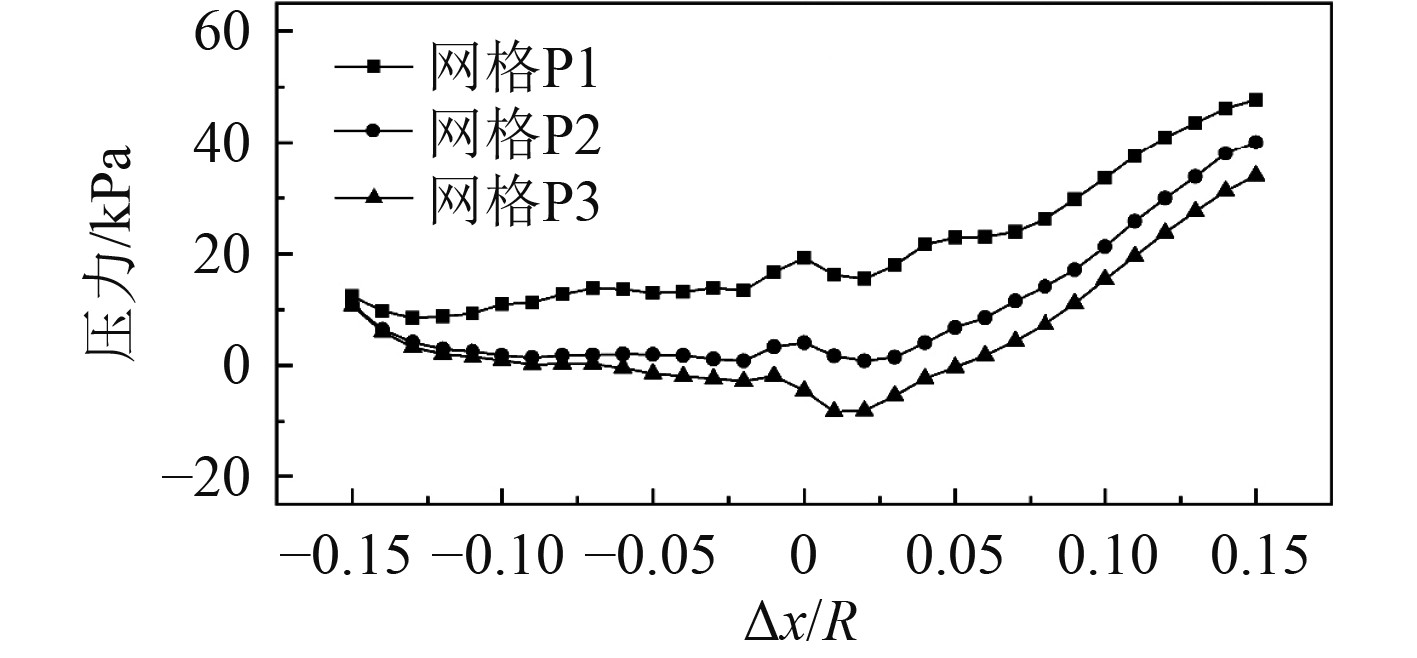
取计算稳定后的计算结果绘制时均值曲线如图7所示,由网格P2变为网格P3时,涡核压力减小比例明显缩小,但即使采用最密度的网格P3时,也仅在
|
图 7 3种转子域网格各监测面上最低压力时均值 Fig. 7 Time-averaged value of each monitoring surface in three rotor domain |
|
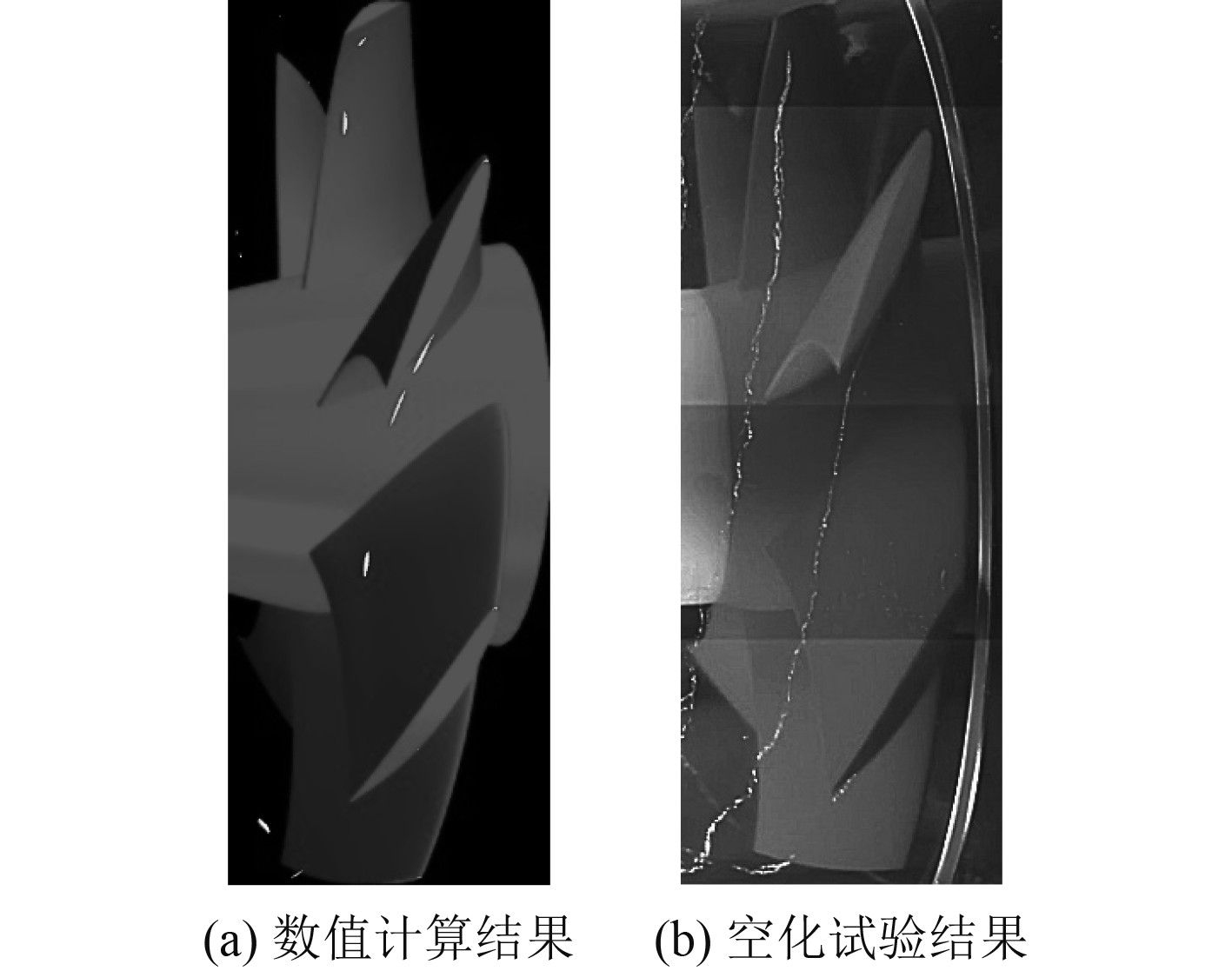
图 8 计算结果 Fig. 8 Calculation results |
分析可知,数值计算空化结果与试验结果存在较大差距。因梢泄涡一般在叶背处沿弦长向下游流动,在尾流中更多偏向于周向流动,使得在精细化梢涡位置网格时需要考虑的加密方向较多。网格密度达到一定程度后,网格尺寸的缩小对计算精确性的提升极其有限,而实际所需考虑的网格加密方向数量远超图5所示的量,如果加密转子梢涡空化区域所有相关边上的网格,将导致转子域网格量增长至难以计算的程度。
另外,因转子螺距角较大并且生成转子域网格时需要考虑周期性旋转,使得计算域网格单元正交性较差,网格边缘线的倾斜和网格节点的不合理分布使其难以充分求解流场中物理量的剧烈变化,从而出现由网格相关问题引起的计算误差,计算结果则会失真[12]。由图5可以看出,在叶背梢涡区域网格正交性良好的情况下,会牺牲其他区域网格质量,无法完全控制转子域网格的正交性,使得其难以准确计算梢涡空化。采用更精细的网格可以减少湍动能耗散,计算所得梢涡涡核压力更低,而由于常用周期性转子域网格形式难以做到梢泄涡区域网格尺寸的均匀分布,容易导致涡核压力分布不符合实际情况。由于常用多通道周期性网格存在问题,为了准确计算梢泄涡空化,需要提出新的计算方法。
2.4 新型网格划分因常用多通道周期性计算域网格在计算转子梢涡空化上存在计算成本高和准确性不足等问题,所以提出新型计算域划分方式,对转子域进行优化,在泵喷推进器转子旋转域内进行局部网格重构,将转子叶梢及其梢泄涡区域单独建域,以便更好地控制梢泄涡区域的网格质量与计算成本。
在新型计算域网格划分中,导管外域与定子域保持不变,将转子域网格分为3个部分,0.92R以下计为转子域−1,0.92R以上再分为2个部分。根据梢涡空化所在位置,选择7叶转子中的1个叶片梢部及其梢涡所处区域建立转子叶梢域,将0.92R以上转子叶梢域之外的区域设立为转子域−2。
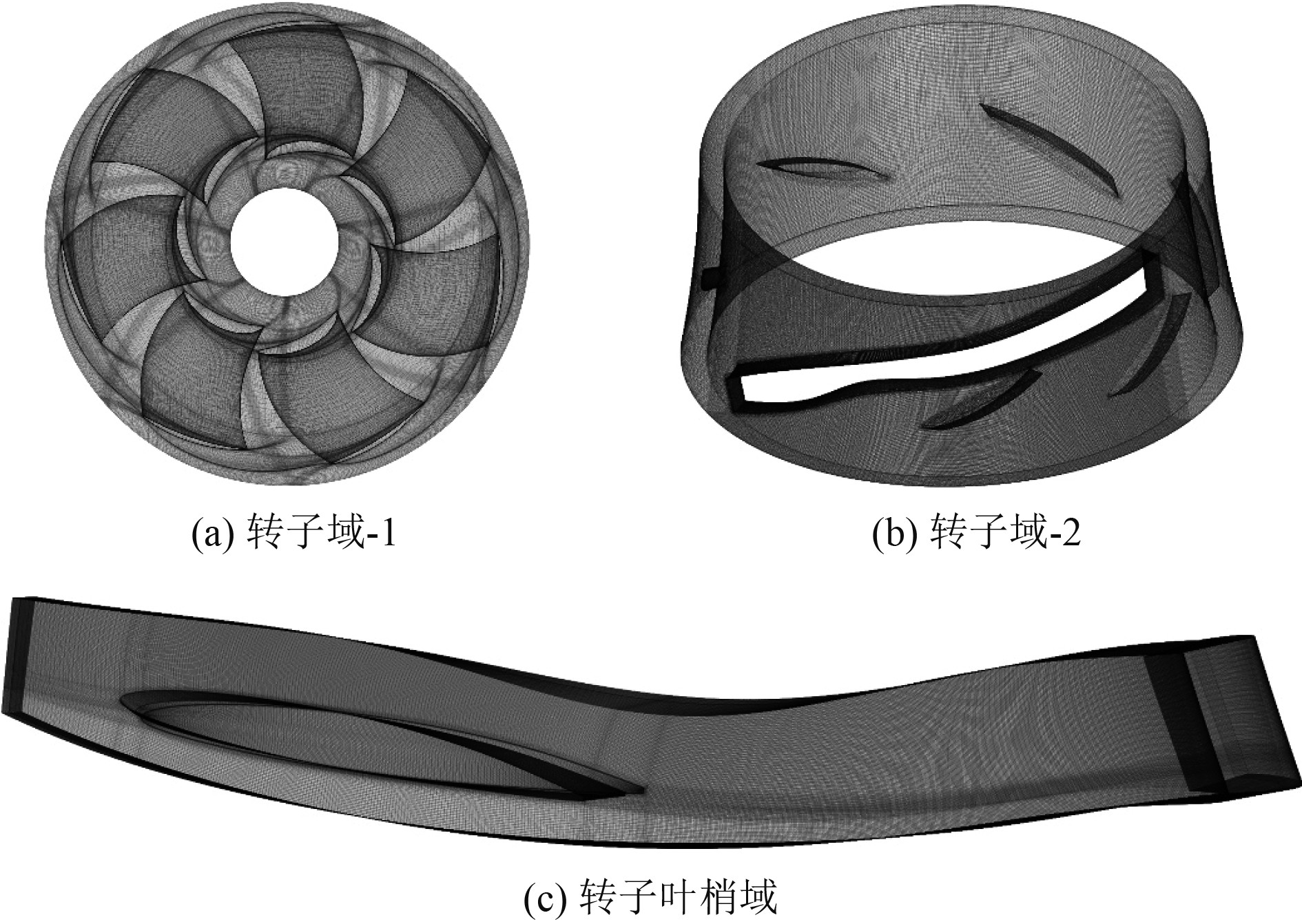
为了保持被选为研究对象的转子近壁面网格一致性,转子域−1和转子叶梢域均采用结构网格形式,转子边界层同样采用O型网格划分方法,保证2种计算域的边界层总厚度、层数和第一层网格厚度等相等。由于转子域−2形状非常不规则,不利于控制网格质量,因此采用非结构网格形式,由STAR-CCM+ 14.02生成,3个部分转子域网格如图9所示,3个转子域之间通过交界面进行数据传递。由于本文主要研究准确计算转子梢涡空化所需设置,因此仅改变转子叶梢域网格密度,而转子域−1和转子域−2网格不变,网格量分别为410万和910万。
|
图 9 转子域网格 Fig. 9 The grids of rotor domains |
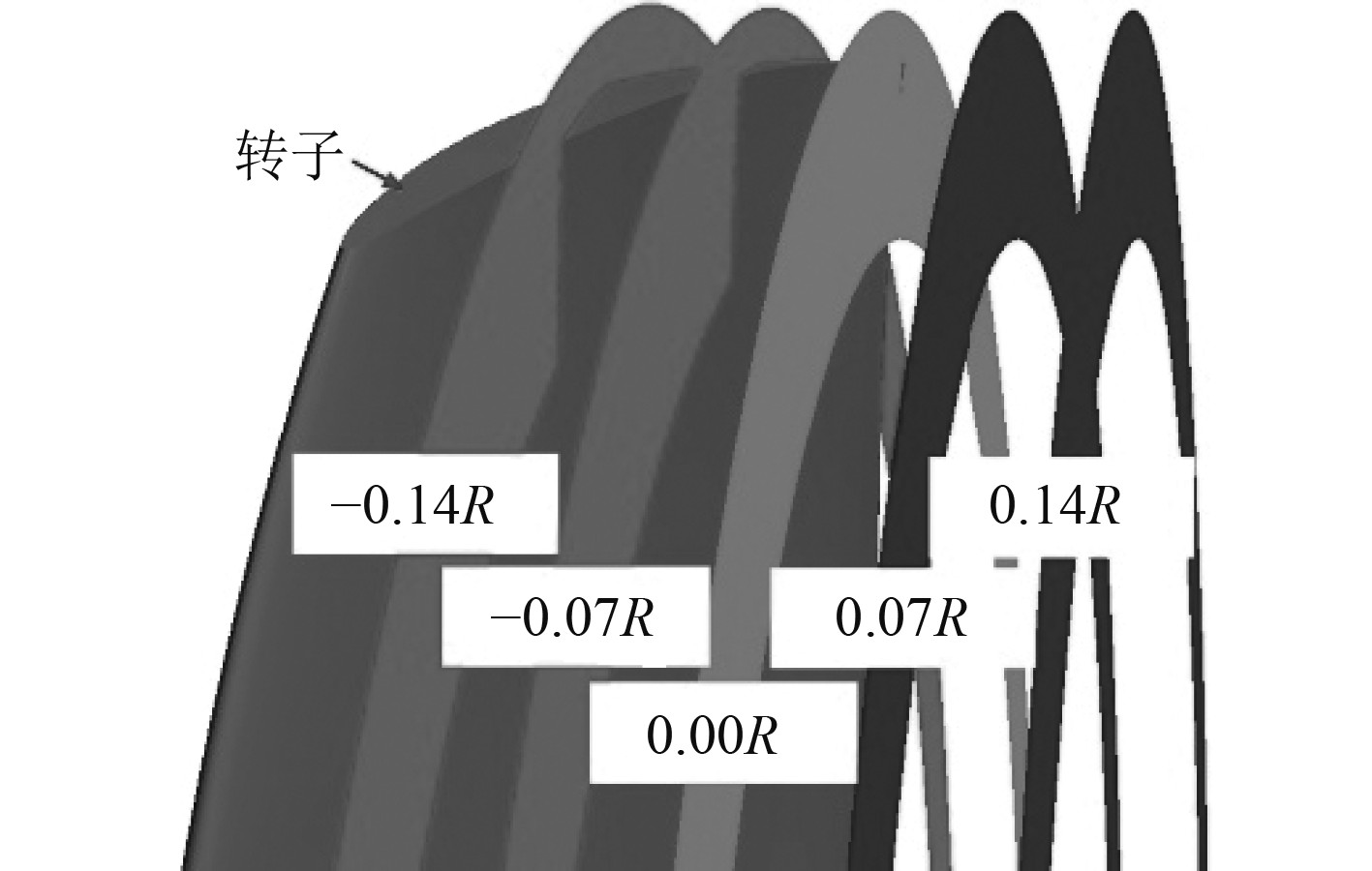
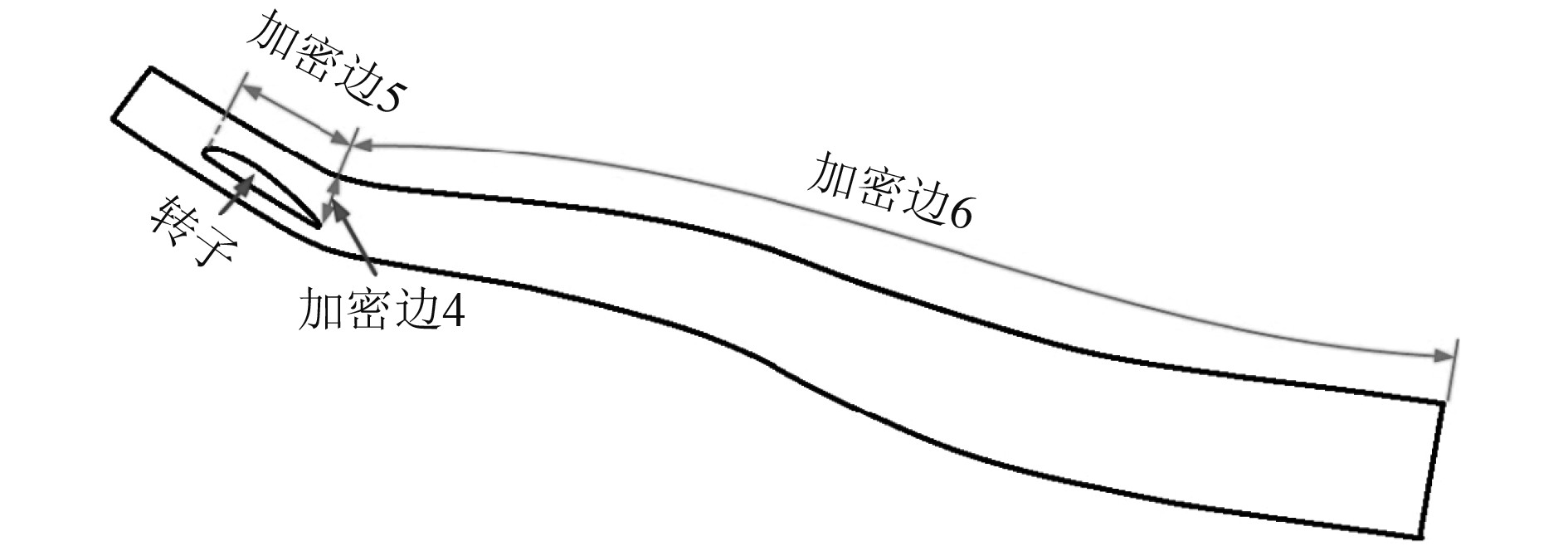
为了使梢涡空化计算效果与试验吻合,转子叶梢域大小和形状主要根据空化观测试验结果进行布置,转子梢泄涡完全可包含转子叶梢域之内,轴向长度约为100 mm、周向跨度约为125°。为了便于标识转子叶梢域加密边所在位置,将转子叶梢域中半径为0.95R的圆柱形剖面展开为二维轮廓图,加密边的位置如图10所示,转子径向加密边未在二维轮廓图中显示,其定义与图5中的加密边1相同,并且径向网格尺寸始终与加密边4相同,通过调整3条加密边上的网格尺寸,可确定梢泄涡周围所需网格密度分布。
|
图 10 网格加密边界定义 Fig. 10 Edges of gird refinement |
分别调整3条加密边上的网格最大尺寸,得到7组不同密度的转子叶梢域网格,各转子叶梢域的网格尺寸参数如表3所示。
|
|
表 3 转子叶梢域网格尺寸定义 Tab.3 Grid size of rotor tip domain |
分别采用表3中的7组转子叶梢域网格计算
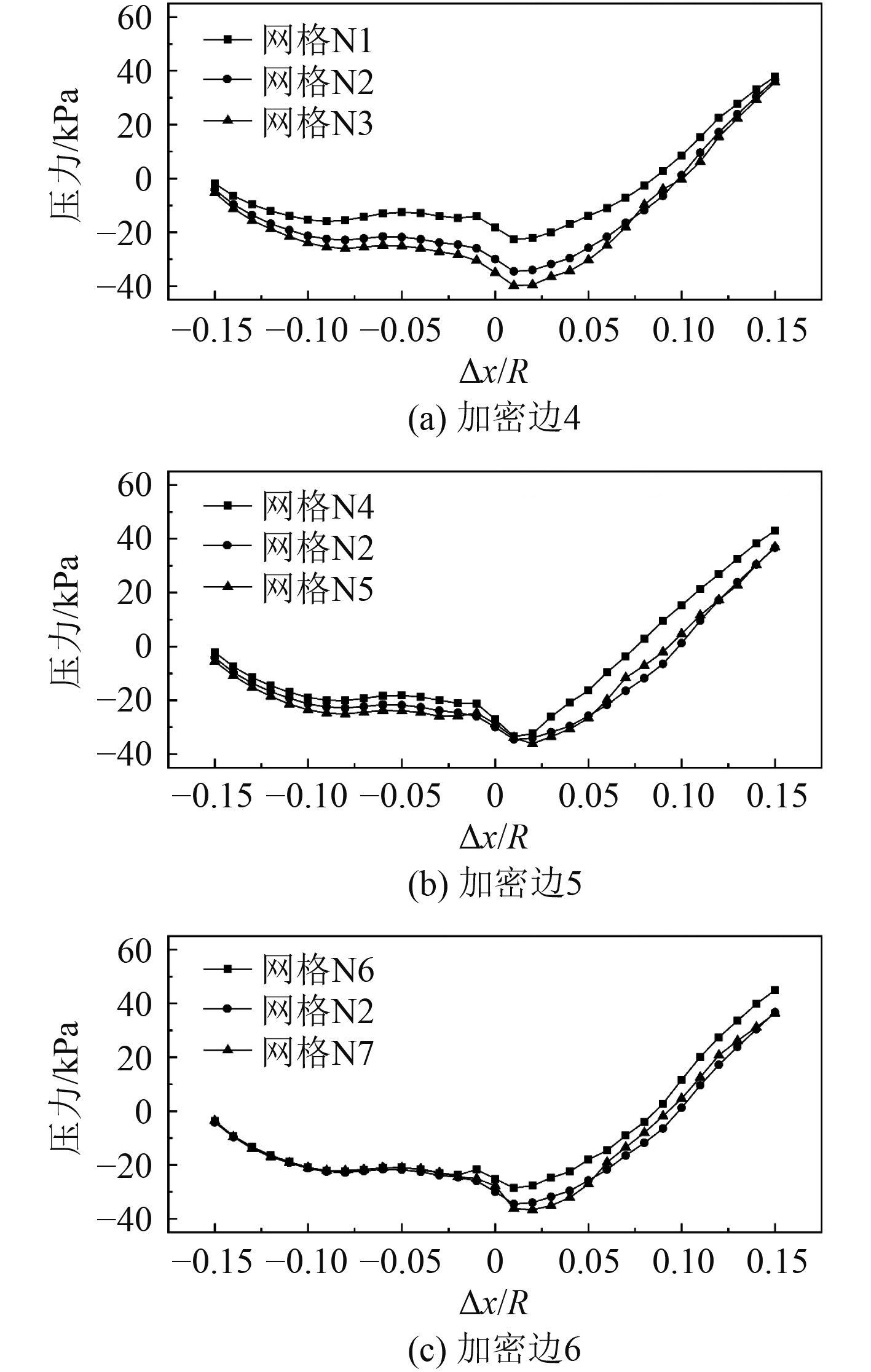
|
图 11 调整加密边上的网格尺寸后的涡核压力变化 Fig. 11 Change of vortex core pressure after adjusting the grid size |
可知,分别调整3条加密边上的网格最大尺寸后,以网格N2为基础缩小各加密边上的网格尺寸,涡核压力变化趋于稳定,且各横截面上的涡核压力最大变化率均小于2.6%(本文涡核压力变化率的定义为监测所得压力与压力出口处压力之和变化的百分比)。由此可知,采用网格N2计算梢涡流场时,再次加密网格对涡核压力计算值的影响已经很小,也就意味着梢泄涡形态和梢泄涡涡低压区所在位置趋于稳定,可以初步判定转子叶梢域网格在加密边4~6上的最大网格尺寸分别为0.1、0.4、0.2 mm时,满足计算要求。
为进一步确定计算方法可行性和转子叶梢域网格2的适用性,采用网格N2分别计算转速为900、
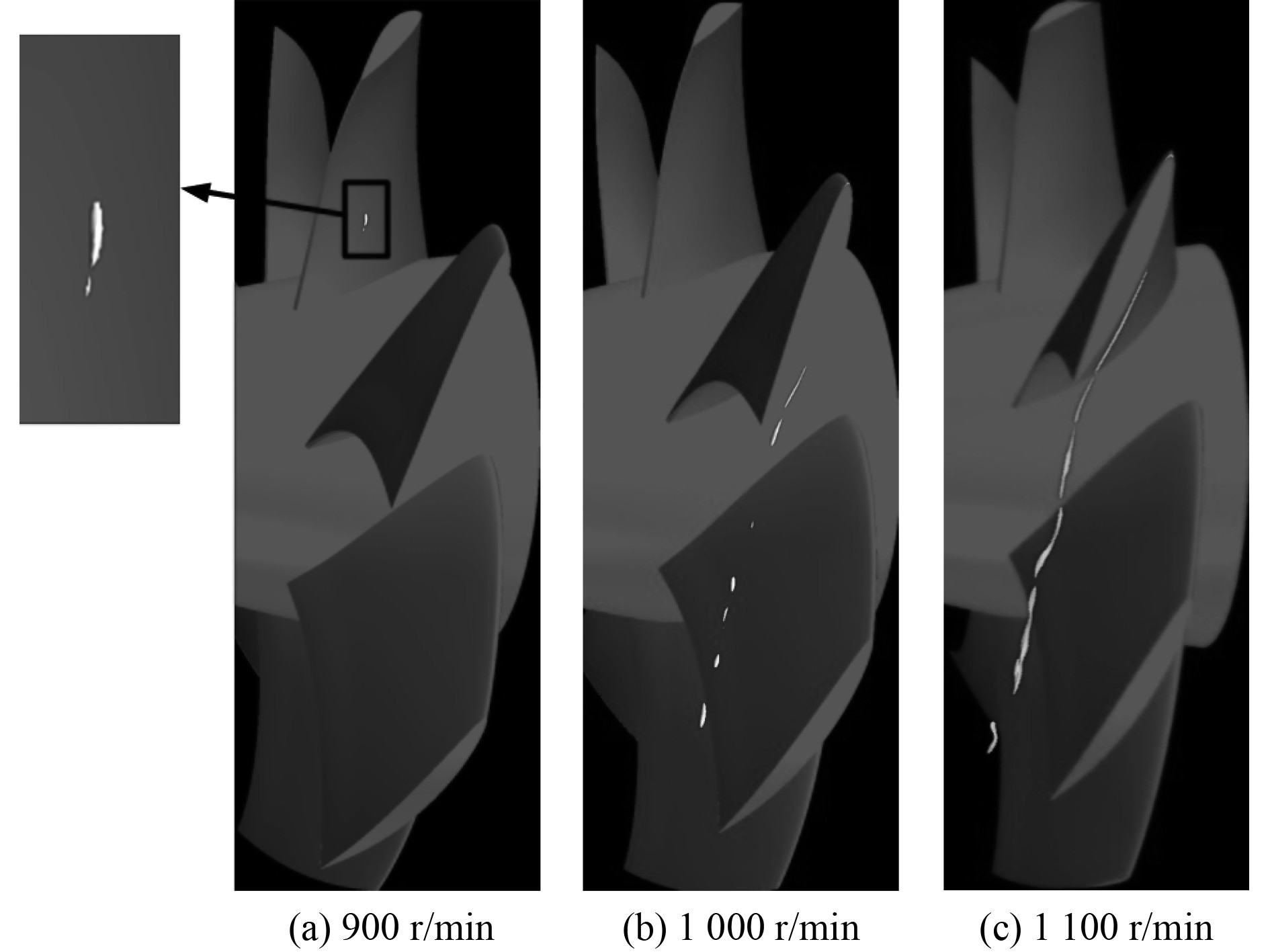
|
图 12 数值计算结果 Fig. 12 Numerical results |

|
图 13 试验结果 Fig. 13 Experiment results |
可知,在梢涡空化起始位置和梢涡空化形态等方面,数值计算结果均与空化观测试验结果精准吻合,采用本文所提出的新型网格划分方法可以较少的网格量准确计算梢涡空化。
3 结 语本文基于空化观测试验结果,以LES和S-S模型对泵喷推进器梢部流场开展数值计算,通过数值计算结果与试验结果的对比可发现:
1)由于泵喷推进器转子梢涡空化对计算域网格质量要求极高,常用多通道周期性结构网格在计算梢涡空化时,存在网格尺寸难以控制、无法完全保证网格正交性和网格密度分布不均等问题,使得其难以预测梢涡空化。
2)根据常用多通道周期性结构网格的不足之处并参照试验结果,提出了在转子域中进行局部网格重构的方法,以全湿流场中的涡核压力变化为依据,确定了计算梢涡空化所需的网格尺寸。
3)通过将空化流场中的计算结果与试验结果对比发现,本文所提出的方法完全具备准确计算梢涡空化的能力,不仅能够准确预测低转速时的梢涡初生,而且可以准确预测中高转速时的梢涡空化形态,并且所需网格量远低于常用多通道周期性结构网格。
| [1] |
NICHOLAS J G, DONALD P R. Large-eddy simulation: current capabilities, recommended practices, and future research[J]. AIAA Journal, 2010, 48(8): 1772-1784. DOI:10.2514/1.J050232 |
| [2] |
CHESNAKAS C, JESSUP S. Tip-vortex induced cavitation on a ducted propulsor[C]// Proceeding of the ASME/JSME 4th joint Fluids Summer Engineering Conference, 2003: 257−267.
|
| [3] |
WU H, SORANA F, MICHAEL T, et al. Cavitation in the tip region of the rotor blades within a waterjet pump[C]// ASME 2008 Fluids Engineering Division Summer Meeting Collocated with the Heat Transfer, Energy Sustainability, and Energy Nanotechnology Conference, 2008.
|
| [4] |
RAINS D A. Tip clearance flow in axial compressors and Pumps[R]. California Institute of technology, Hydrodynamics and Mechanical Engineering Laboratories Report No. 5, 1954.
|
| [5] |
OWEIS G, CECCIO S, CHESNAKAS C, et al. Tip leakage vortex(TLV) variability from a ductedpropeller under steady operation and its implications on cavitation inception[J]. Fukuoka University Review of Commercial Sciences, 2015, 60(6): 1229-1231. |
| [6] |
HAH C, LEE Y. Unsteady pressure field due to interactions among tip leakage vortex, trailing edge vortex, and vortex shedding in a ducted propeller[C]//ASME, 2007.
|
| [7] |
CHENG H Y, BAI X R, LONG X P, et al. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence[J]. Applied Mathematical Modelling, 2020, 77(5): 788−809.
|
| [8] |
YOU D, MITTAL R, WANG M, et al. A computational methodology for large-simulation of the tip-clearance flows[J]. AIAA Journal, 2004, 42: 271-279. DOI:10.2514/1.2626 |
| [9] |
ASNAGHI A, SVENNBERG U, RICKARD E, et al. Large eddy simulations of cavitating tip vortex flows[J]. Ocean Engineering, 2010, 195: 10670.
|
| [10] |
ASNAGHI A, SVENNBERG U, RICKARD E. et al. Analysis of tip vortex inception prediction methods[J]. Ocean Engineering, 2018, 167: 187−203.
|
| [11] |
HU J, ZHANG W, WANG C, et al. Impact of skew on propeller tip vortex cavitation[J]. Ocean Engineering, 2021, 220: 108479.
|
| [12] |
DACLES M, KWAK J, ZILLIAC D, et al, On numerical errors and turbulence modeling in tip vortex flow prediction[J]. Methods Fluids, 1999, 30 (1): 65–82.
|
 2024, Vol. 46
2024, Vol. 46

