0 引　言

当前，自主水下航行器（Autonomous Underwater Vehicle, AUV）主要的工作环境为未知海域，即没有详细环境地图的海域，加之水下无线电信号衰减过快，AUV接收不到GPS等无线电波的数据，所以如何实现水下定位就成了当前AUV的主要研究方向之一。由于声波相比于电磁波和无线电波在水下衰减更小，传播距离更远，所以一些声学定位传感器如超短基线、短基线、长基线等是当前主流的AUV外部定位方式^[1]，但由于这些传感器价格昂贵，所以通常情况下AUV依靠价格相对低廉的内部定位传感器进行自主定位的方式更加受欢迎。内部定位传感器中最重要的是惯性测量单元（IMU）等惯性传感器，但这种传感器会随着运行时长的增加产生较大的累积误差。另外还有使用视觉里程计进行导航^[2]，但水下较差的光照条件和能见度导致图像难以获得有效信息。

为了解决现有研究存在的问题，卢健等^[3]采用基于FastSLAM框架的SLAT算法用于同时定位与跟踪非合作主AUV。郑烨等^[4]引入轻量级声呐全连接网络SonarMLP，嵌入声呐参数信息，提高算法鲁棒性。简杰等^[5]提出信息增益评价标准的局部信息融合算法，通过阈值加权处理观测数据，进行局部信息滤波和优化以提高定位精度。黄聪等^[6]基于双基地声呐定位原理，提出水下目标解算方法，通过数值仿真分析定位误差分布和不同投放距离的探测范围及定位精度。上述方法虽均能实现定位目标，但不能有效适应弱纹理环境，存在轨迹误差较大的问题。

为此，本文设计一套适用于水下机器人前视图像声呐加惯性传感器的滤波里程计。后续将里程计融入图优化框架后进行验证，首先通过公开数据集验证了码头这样的结构性场景中的定位性能，进行初步评估，然后进行实验验证了其定位性能。

1 水下声呐惯性系统定位方法设计 1.1 声呐成像原理

声呐通过声波的发射和反射接收的时间差来计算声呐与物体的距离，而图像中亮度的不同则代表了声呐回波强度的不同^[7]。设置声呐成像空间是一个半径为$r \in [{r_{\min }},{r_{\max }}]$、水平开角为$\varphi $、垂直开角为$\theta $的三维空间成像，它在近距离内会有盲区，并且显示到声呐图像中时会丢失掉垂直开角信息，也就是$r$和$\varphi $相同的情况下，不同垂直开角的点显示到声呐图像中是重叠的。为了尽可能减小测量误差，需将$\theta $尽可能的设置小，当其影响足够小时就可忽略$\theta $的影响，假设声呐仅对同一平面进行测量，这一方式也称为平面假设。

1.2 声呐图像特征提取

基于声呐成像原理，提取声呐图像特征。由于声呐是声学成像，它的噪声信号强度不固定，受水下声学环境影响较大。恒定虚警率（Constant False Alarm Rate, CFAR）算法作为一种雷达信号处理技术，能稳健的对声呐图像进行特征提取。考虑到计算效果和计算复杂度之间的平衡，在CFAR算法的诸多变体中，本文选择使用最小单元平均CFAR（SOCA-CFAR）作为特征提取算法。声呐图像扇形映射如图1所示。

图1（a）为由电脑获取的原始声呐图像并不是扇形，而是以声呐波束数和距离粒度数为宽高的一个8位的内存深度图（这里使用的声呐输出图像大小为224×512）。对矩形图像进行特征提取，得到特征点云不能实现有效的点云匹配，需将矩形图像中提取的特征映射到实际扇形成像环境中的对应位置才能进行有效的点云匹配。

因此，将矩形特征点云使用声呐的角度分辨率参数$\Delta \varphi $与距离分辨率参数$\Delta r$映射成扇形点云。设原始图像上像素坐标为$(i,j)$，则对应的$\varphi $和$r$为：

$ \begin{aligned}[b] &\varphi = {\varphi _{\min }} + i \cdot \Delta \varphi，\\ & r = {r_{\min }} + j \cdot \Delta r 。\end{aligned} $

(1)

在将矩形点云映射成扇形点云后，也就得到了特征在真实世界中对应的位置，之后进行点云配准就可得到2帧图像之间的位姿变换。

1.3 声呐图像特征匹配

前面使用CFAR（恒定虚警率）算法完成了声呐图像的特征提取，并进行映射得到对应真实环境位置的特征点云，下面进行特征点云匹配工作。设${x_t}$和${x_s}$分别为目标姿态和源姿态，设${P_t}$和${P_s}$为在目标姿态和源姿态下测量的目标点和源点，2个姿态之间的相对变换包括相对旋转${R_{ts}}$和相对平移${T_{ts}}$，现使用迭代最近点（Iterative Closest Point, ICP）算法来进行声呐图像特征匹配。但ICP存在由于非凸性造成的局部最小值问题，再加上声呐成像的特征较少，噪声水平较高，导致在水下环境中使用ICP配准容易出现匹配错误的现象^[8]。为了加快收敛速度，避免局部最小值的问题，本文用到2种初始化方式，一种是在滤波里程计框架中使用IMU预积分初始化进行逐帧匹配，另一种是使用全局初始化方法进行初始化。

设${\tilde x_s}$为全局初始化的源姿态，该方法遵循共识集最大化原则，公式如下：

$ {\tilde x_s} = \mathop {{{\mathrm{argmax}}} }\limits_{{x_s}} \sum\limits_{{p_s} \in {P_s}} {\varphi r \times d\left( {{p_s}} \right)}。$

(2)

式中：$d$为到目标点的距离。

然后，将声呐图像中的特征点作为参考点集和目标点集，利用ICP算法迭代计算参考点集和目标点集之间的最佳转换，使它们尽可能拟合对齐，从而实现声呐图像的特征点匹配。

1.4 基于滤波的声呐惯性里程计

在弱纹理条件下，使用匹配结果直接添加匹配因子更新位姿容易受到ICP匹配质量的影响，产生较大的定位误差。受到视觉惯性里程计MSCKF的启发，设计了一种适用于水下环境所使用的声呐惯性滤波里程计，它使用ICP匹配数据和IMU数据维持一个动态窗口进行多个位姿优化估计，减小不稳定的匹配对位姿估计的影响。在计算前先定义坐标系，$ G $为全局坐标系；$ I $为IMU坐标系；$ S $为声呐坐标系。

1）IMU状态。将状态向量定义为：

$ {X_{{B_k}}} = {\left[ {\begin{array}{*{20}{l}} {p_I^G}&{v_I^G}&\boldsymbol{q_I^G}&{b_{{a_k}}^{}}&{b_{{g_k}}^{}} \end{array}} \right]^{\text{T}}} 。$

(3)

式中：$p_I^G$、$v_I^G$、$\boldsymbol{q_I^G}$分别为IMU在全局坐标系中的位置、速度、旋转矩阵；$ {b_{{a_k}}} $为加速度偏置；$ {b_{{g_k}}} $为陀螺仪偏置。

2）EKF状态。状态向量由当前时刻$ k $的IMU状态向量和$ M $个过去的声呐姿态表示：

$ {X_K} = {\left[ {\begin{array}{*{20}{c}} {{X_{{I_k}}}}&{{X_{{S_{k - M}}}}}&{...}&{{X_{{S_{k - 1}}}}} \end{array}} \right]^{\text{T}}}。$

(4)

其中，声呐状态定义为：

$ {X_{{S_k}}} = \left[ {\begin{array}{*{20}{c}} {p_S^G}&{q_S^G} \end{array}} \right]。$

(5)

式中：$ p_S^G $和$ q_S^G $分别为接收到图像时赋值的相机位置和方向。定义误差状态向量为：

$ {\tilde X_K} = {\left[ {\begin{array}{*{20}{c}} {{{\tilde X}_{{I_k}}}}&{{{\tilde X}_{{S_{k - N}}}}}&{...}&{{{\tilde X}_{{S_{k - 1}}}}} \end{array}} \right]^{\text{T}}}。$

(6)

3）状态传播。根据$\tilde x = \hat x - x$，IMU状态的传播即为IMU误差状态的传播，则IMU误差状态的离散传播过程如下：

$ \begin{aligned}[b] &{{\tilde X}_{{I_{{\text{k}} + 1|{\text{k}}}}}} = \boldsymbol{F_{\boldsymbol{I_k}}}{{\tilde X}_{{I_{k|k}}}}{X_{{B_k}}}{X_K} + {n_{{I_k}}}，\\ & {n_{{I_k}}} = \left[ {{n_a},{n_g},{n_{{b_a}}},{n_{{b_g}}}} \right]。\end{aligned} $

(7)

式中：$ {n_{{I_k}}} $为离散时间系统噪声向量；$\boldsymbol{F_{\boldsymbol{I_k}}}$为离散时间IMU误差状态转移矩阵，即IMU动力学模型相对于IMU状态的雅阁比矩阵。参考MSCKF的状态协方差从${t_k}$到${t_{k + 1}}$的传播可作为3个协方差矩阵的组合，如下所示：

$ \boldsymbol{P_{k + 1|k}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{P_{I{I_{k + 1|k}}}}}&{\boldsymbol{P_{I{S_{k + 1|k}}}}} \\ {{{\left( {\boldsymbol{P_{I{S_{k + 1|k}}}}} \right)}^T}}&{\boldsymbol{P_{S{S_{k|k}}}}} \end{array}} \right] $

(8)

式中：$ \boldsymbol{P_{II_{k+1|k}}} $为时间$ k + 1 $的IMU状态协方差矩阵；$ \boldsymbol{P_{S{S_{k|k}}}} $为滑动窗口状态的协方差矩阵；$ \boldsymbol{P_{I{S_{k + 1|k}}}} $为IMU状态和滑动窗口之间在时间$k + 1$的交叉协方差矩阵。

4）声呐观测模型。由前面的滑动窗口中，ICP匹配结果，可得到相邻2帧的位姿变换$\Delta {T_{ICP,k}}$，包括旋转$ {R_{ts,k}} $和${t_{ts,k}}$的观测方程为：

$ {z_k} = {\tilde X_{{I_{{\text{k}} + 1|{\text{k}}}}}}\Delta {T_{ICP,k}} \times {\tilde X_K}{P_{k + 1|k}}。$

(9)

式中：${z_k}$为观测值，然后得出观测模型：

$ h\left( {{X_k}} \right) = \left[ {\begin{array}{*{20}{c}} {{R_{ts}}\left( {{X_k}} \right)} \\ {{t_{ts}}\left( {{X_k}} \right)} \end{array}} \right]。$

(10)

式中：$ {R_{ts}}\left( {{X_k}} \right) $和$ {t_{ts}}\left( {{X_k}} \right) $分别表示从状态向量$ {X_k} $中提取的旋转和平移部分。残差计算式为：

$ {r_k} = {z_k} - h\left( {{X_k}} \right)。$

(11)

5）状态更新。

$ K = PH{r_k}{\left( {HP{H^{\mathrm{T}}} + \boldsymbol{R}} \right)^{ - 1}}。$

(12)

式中：$K$为卡尔曼增益；$H$为观测矩阵的雅阁比；$R$为观测噪声的协方差矩阵，然后更新状态估计和协方差矩阵公式如下：

$ \begin{gathered} {X_{k|k}} = {X_{k|k - 1}} + K \cdot {r_k}，\\ \boldsymbol{P_{k|k}} = \left( {I - {K_k}{H_k}} \right){P_{k|k{\text{ - 1}}}}。\\ \end{gathered} $

(13)

本方案包含3种类型的因子，分别为先验因子、滤波里程计因子、ICP关键帧匹配因子。因子图通过下式描述：

$ \begin{aligned}[b] f(\Theta ) = &{f^0}({\Theta _0})\prod\limits_i {{f_i}} ({\Theta _i}){\text{ }} \times \\ & \prod\limits_j {f_j^{ICP}} ({\Theta _j})\left( {{X_{k|k}} + {P_{k|k}}} \right)。\end{aligned} $

(14)

式中，$i、j$分别为不同姿态，公式中因子从左到右依次为先验因子、滤波里程计因子，ICP匹配因子。先验因子给出初始位姿，声呐惯性滤波里程计提供的里程计因子，使用全局初始化的关键帧ICP顺序匹配提供ICP匹配因子。关键帧的选取原则为当移动大于2 m或旋转大于20°选择为一个关键帧，对这些关键帧采取全局初始化方法进行初始化。然后将滤波里程计与ICP顺序匹配结果一起纳入图优化框架进行位姿优化，实现水下声呐惯性系统定位。

2 实验分析 2.1 开源数据集

利用开源数据集验证本文方法在港口等结构性场景中的可行性。使用Jinkun Wang团队在美国商船学院港口中使用的BlueROV2数据集进行验证。

2.2 验证结果分析

轨迹对比与轨迹均方根误差，如图2和图3所示。

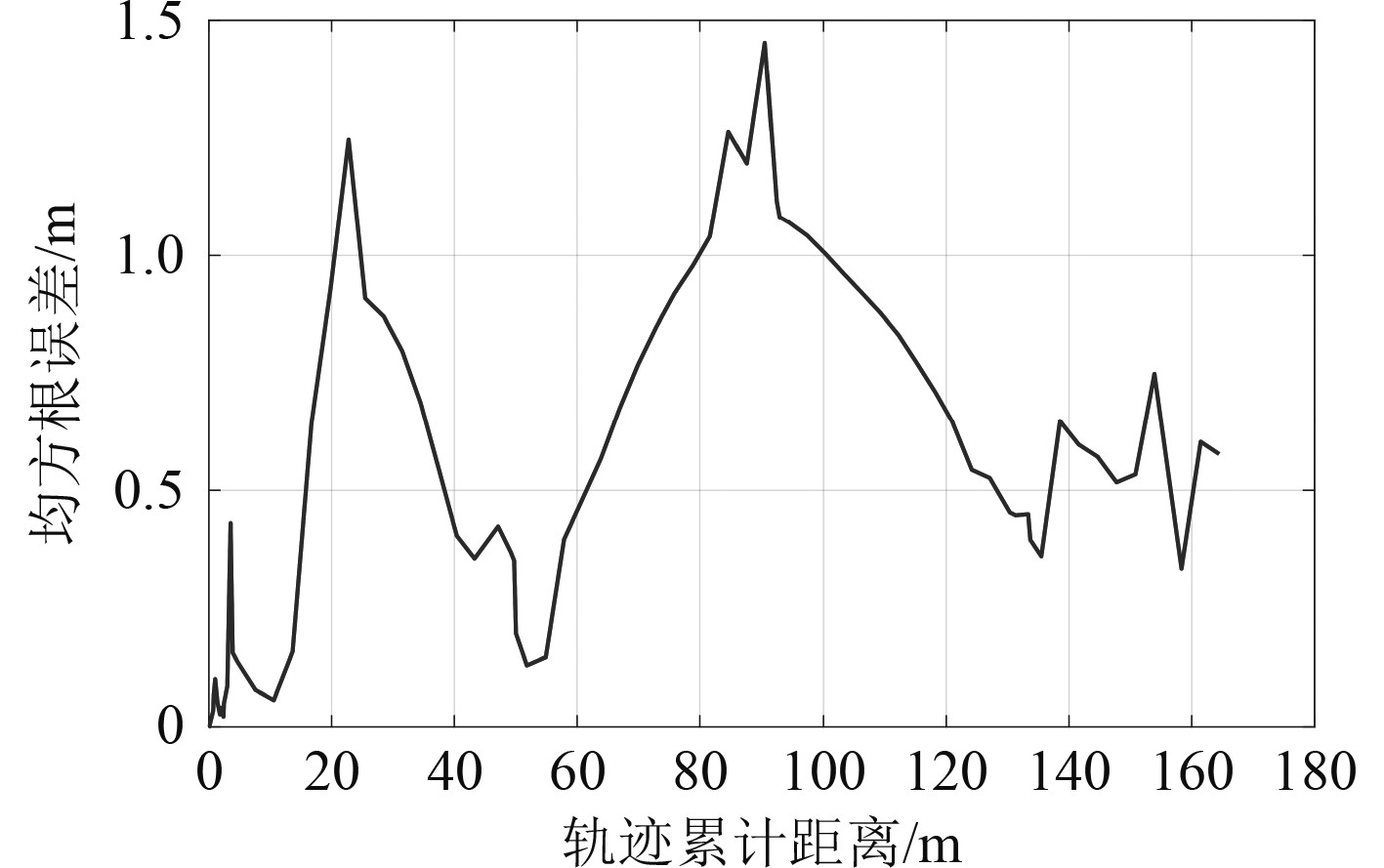
由图2可知，运行的轨迹水平运动范围小于50 m，纵向运动范围小于45 m。场景相对较小，并且由于是港口环境，其纹理特征比较丰富。由图3可知，本文的方案在结构化的港口环境中与真实轨迹之间的均方根误差最大值为1.45 m，最终的均方根误差为0.58 m，数据表明本文方法的定位误差较小能满足定位要求。

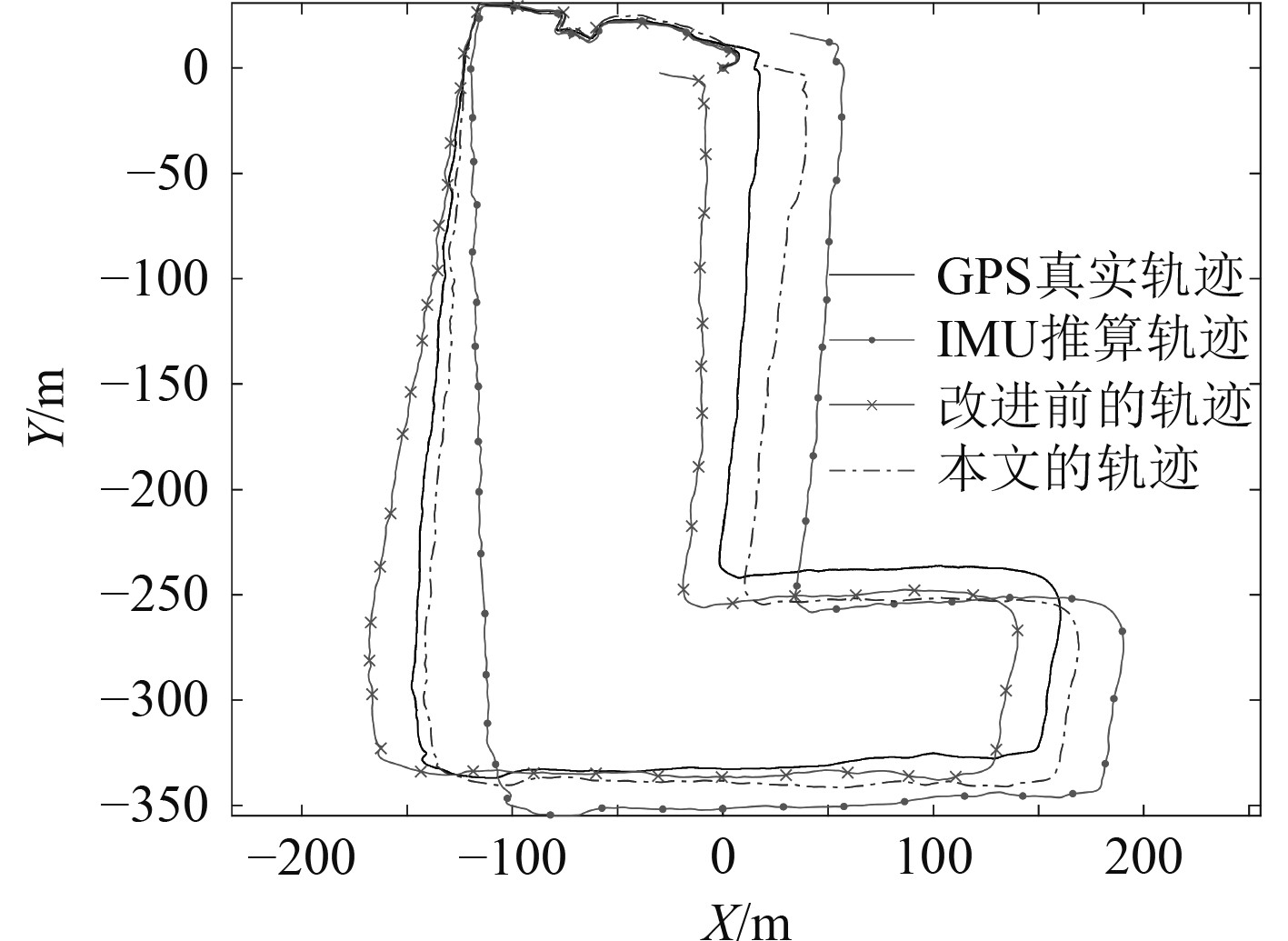
经过公开数据集的验证之后，在团队自有淡水湖泊内进行水下实验，对定位性能进行验证。实验结果如图4所示。

由于各个轨迹长度不一，并且都是与GPS真实轨迹进行计算得到，所以将横坐标统一为GPS真实轨迹的累计距离。可以看出，其余2个轨迹相较于真实轨迹的偏差较大，但本文使用滤波里程计参与图优化的轨迹相比于其他轨迹在定位精度上也具有明显优势。

计算轨迹的均方根误差（RMSE）、标准差、最大误差及平均误差，结果如表1和表2所示。

由表1可看出，本文方法轨迹的定位误差在使用均方根误差和标准差2个计算标准下，都明显优于其余2条轨迹。由表2可看出，本文轨迹的最大误差和平均误差也均小于其余2条轨迹。

3 结　语

本文提出了一种水下二维定位系统，其核心为声呐惯性滤波里程计，主要针对的是弱纹理的水下场景定位问题。通过将里程计数据与全局初始化ICP匹配数据一起纳入因子图进行优化，提高定位精度。首先使用开源数据集验证了在结构性复杂纹理场景中的适应性和定位精度，然后使用AUV在弱纹理的湖泊进行实验。结果显示在弱纹理的水下环境中，该系统能提高定位精度。