0 引　言

卫星导航由于精度高、误差不随时间积累、能全天候提供PVT信息等优势，广泛应用于军民位置服务领域，成为不可或缺的导航手段。然而卫星导航信号由于长距离传输，导致接收到的信号十分微弱，容易受到环境中各种障碍物遮挡或者其他无线信号影响，从而导致定位不稳定或长时间不工作^[1]。为此，实际使用中通过采用惯导/卫导组合方式来提供连续、高精度的位置服务。针对惯导/卫导组合，国内外学者主要从2个方面开展研究。一是惯导、卫导信息耦合度承担越来越深，从惯导/卫导松组合^[2]、惯导/卫导紧组合^[3]，发展到惯导/卫导超紧组合^{[4 − 7]}；二是针对惯导/卫导组合中的分线性问题，研究了一系列信息融合算法，从卡尔曼滤波^{[8 − 9]}、扩展卡尔曼滤波^[10]、无迹卡尔曼滤波^[11]到容积卡尔曼滤波^[12]等。这些方法在一定程度上改善了惯导/卫导组合的性能，然而在卫导长时间不可用时，仍难以持续提供高精度的位置服务。随着技术发展，无线测距被提出用于弥补惯导/卫导组合的不足，无线测距具有测距精度高、抗干扰能力强等优点，被广泛用于卫星导航信号拒止场景。Li等^{[13 − 16]}对惯导、无线测距的组合开展了研究。也有学者开展了惯导、卫导、无线电的组合研究，然而多为这3种传感器信息的松组合，这需要单卫导系统或无线电测距系统能力独立给出载体的导航信息。然而，当卫星导航可见星不足4颗或无线测距集中站不足4个时，当无法进行惯导、卫导、数据的组合导航。针对此问题，本文提出一种惯导/数据链/卫导紧组合方法，当卫导可见星不足4颗或者测距值无线测距不满足独立定位条件时，仍能对惯导起到很高的误差修正效果，从而提升卫导受限或拒止下的位置服务精度和可靠性。

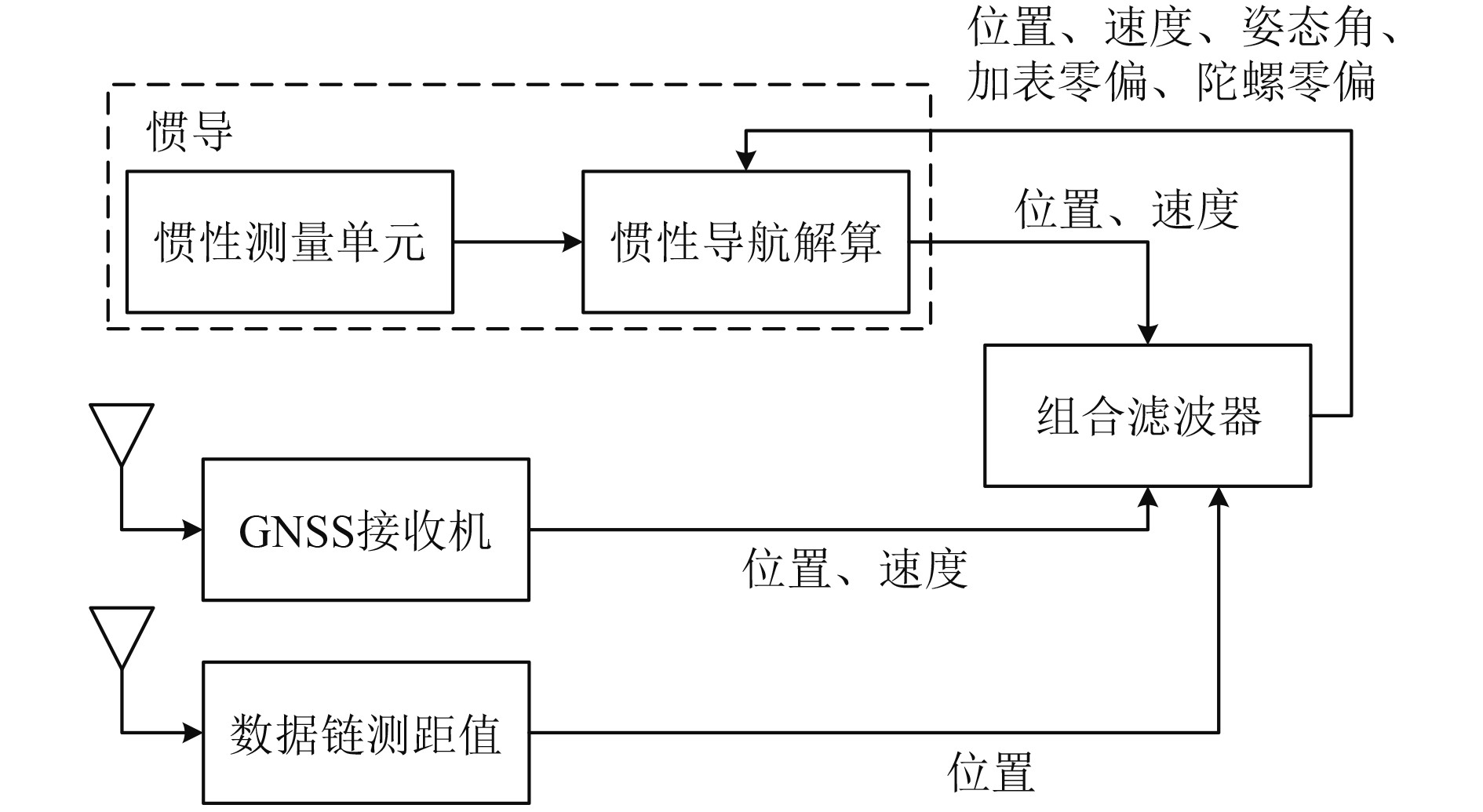
1 惯导/数据链/卫导松组合架构

图1为惯导/数据链/卫导松组合算法的架构。可知，在惯导/数据链/卫导松组合中，通过将惯导解算后的位置、速度与卫导位置、速度以及数据链得到的载体位置相融合，得到惯导解算的位置、速度、姿态角以及加表零偏、陀螺漂移误差，对惯导误差进行修正。惯导/数据链/卫导松组合中要求惯导、数据链和卫导都能独立解算载体位置，这就要求数据链的测距值不小于4个，且卫导的可见星不少于4颗。然而，当环境中卫星信号存在遮挡或干扰，或数据链信号处理弱联通状态时，可能不满足此要求，从而导致惯导/数据链/卫导松组合退化值惯导自主工作，进而导致组合系统的导航信息质量下降。

2 惯导/数据链/卫导紧组合架构

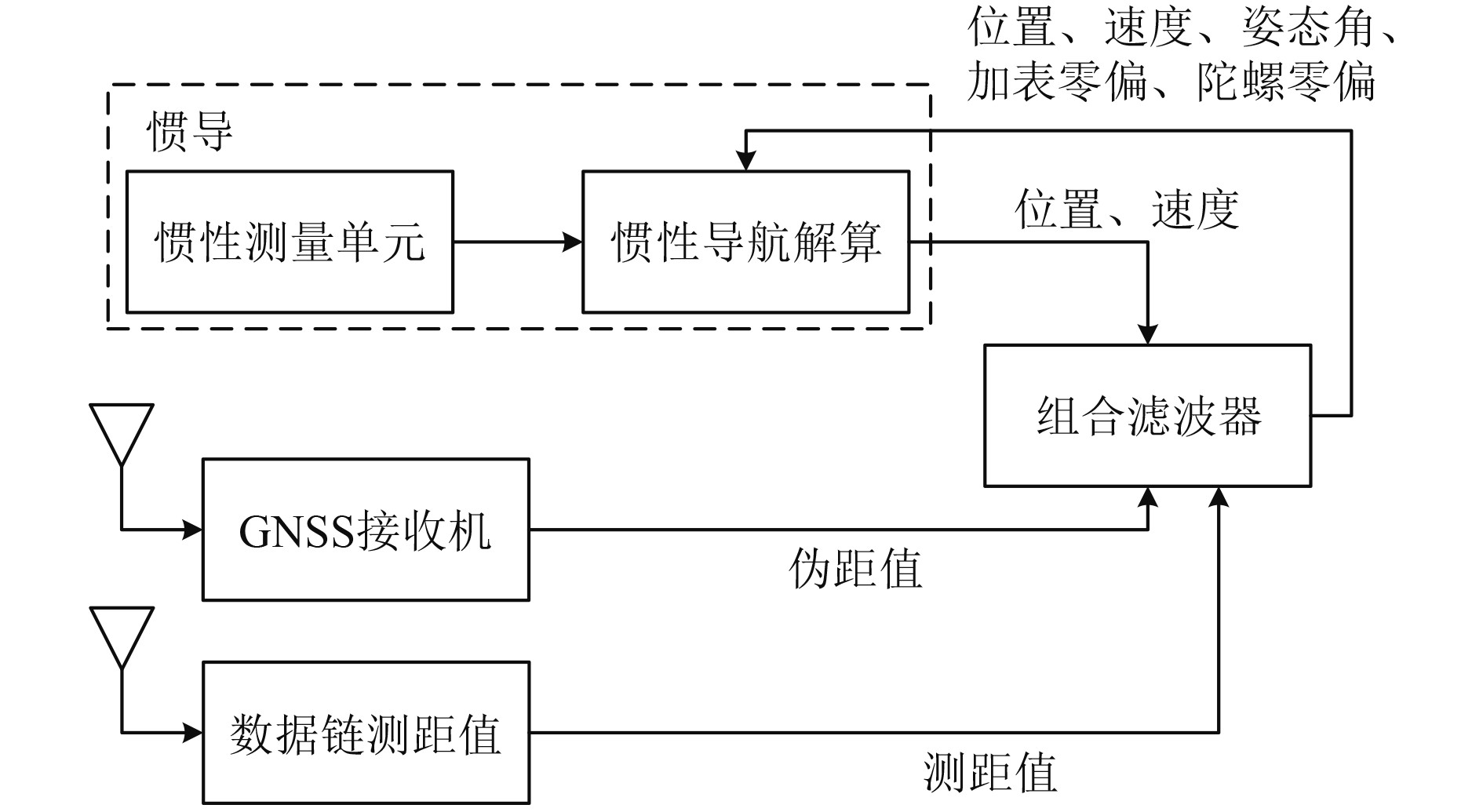
图2为惯导/数据链/卫导紧组合算法的架构。对比图1可知，在惯导/数据链/卫导紧组合中，卫导和数据链不再需要完成载体的位置解算，而是利用载体位置解算之前的伪距测量值和数据链给出的测距值与惯导解算信息，进行融合惯导的各项误差进行估计，从而提升系统的导航信息质量。这种算法结构可实现当卫导可见星数目或者数据链测距值小于4个时，仍能用卫导和数据链的观测值，对惯导误差进行估计。

3 惯导/数据链/卫导紧组合数学模型

惯导/数据链/卫导紧组合算法的状态方程主要包括15维惯导状态误差、一维数据链钟差、二维卫星导航钟差。惯导误差包括三维姿态误差、三维速度误差、三维位置误差、三维陀螺漂移误差和三维加表零偏误差。数据链误差为时钟误差等效的距离误差。接收机误差是指时钟误差等效的距离误差和时钟频率误差等效的误差，即：

$ {X_I} = \left[ \begin{array}{*{20}{c}} {{\varphi _E}} &{{\varphi _N}}&{{\varphi _U}}&{\delta {v_E}}&{\delta {v_N}}&{\delta {v_U}}&{\delta L}&{\delta \lambda } \\ &{\delta h}&{{\varepsilon _{bx}}}&{{\varepsilon _{by}}}&{{\varepsilon _{bz}}}&{{\nabla _{bx}}}&{{\nabla _{by}}}&{{\nabla _{bz}}} \end{array} \right] 。$

(1)

式中：$ {\varphi _E} $、$ {\varphi _N} $、$ {\varphi _U} $均为惯导三维姿态误差；$ \delta {v_E} $、$ \delta {v_N} $、$ \delta {v_U} $均为惯导三维速度误差；$ \delta L $、$ \delta \lambda $、$ \delta h $均为惯导三维位置误差；$ {\varepsilon _{bx}} $、$ {\varepsilon _{by}} $、$ {\varepsilon _{bz}} $均为惯导三维陀螺漂移误差；$ {\nabla _{bx}} $、$ {\nabla _{by}} $、$ {\nabla _{bz}} $均为惯导三维加表零偏误差。

$ {X_L} = {b_L}。$

(2)

式中：$ {b_L} $为数据链时钟误差等效的距离误差。

$ {X_G} = {\left[ {\begin{array}{*{20}{c}} {{b_{clk}}}&{{d_{clk}}} \end{array}} \right]^{\mathrm{T}}}。$

(3)

式中，$ {b_{clk}} $为卫导时钟误差等效的距离误差；$ {d_{clk}} $为时钟频率误差等效的误差。

从而可得到惯导/数据链/卫导紧组合算法的状态方程：

$ \dot X = FX + GW。$

(4)

式中：

$ \dot X = \left[ {\begin{array}{*{20}{c}} {{{\dot X}_I}} \\ {{{\dot X}_L}} \\ {{{\dot X}_G}} \end{array}} \right]，$

(5)

$ F = \left[ {\begin{array}{*{20}{c}} {{F_I}}&0&0 \\ 0&{{F_L}}&0 \\ 0&0&{{\boldsymbol{F_G}}} \end{array}} \right], $

(6)

$ G = \left[ {\begin{array}{*{20}{c}} {{G_I}}&0&0 \\ 0&{{G_L}}&0 \\ 0&0&{{\boldsymbol{G_G}}} \end{array}} \right], $

(7)

$ W = \left[ {\begin{array}{*{20}{c}} {{W_I}} \\ {{W_L}} \\ {{W_G}} \end{array}} \right]。$

(8)

式中：$ \boldsymbol{F_I} $、$ \boldsymbol{F_L} $、$ \boldsymbol{F_G} $分别为惯导、数据链、卫导误差方程转移矩阵；$ {G_I} $、$ {G_L} $、$ \boldsymbol{G_G} $分别为惯导、数据链、卫导系统噪声分配矩阵；$ {W_I} $、$ {W_L} $、$ {W_G} $分别为惯导、数据链、卫导噪声序列。

惯导/数据链/卫导紧组合算法的量测方程分别由数据链源节点、卫星相对载体位置的距离或者伪距差组成。

采用惯导给出的位置计算载体与源节点之间的距离$ {\rho _{Ii}} $可表示为：

$ {\rho _{Ii}} = \sqrt {{{\left( {{x_I} - {x_i}} \right)}^2} + {{\left( {{y_I} - {y_i}} \right)}^2} + {{\left( {{z_I} - {z_i}} \right)}^2}} 。$

(9)

式中：i为第i个源节点；$ {\left[ {\begin{array}{*{20}{c}} {{x_I}}&{{y_I}}&{{z_I}} \end{array}} \right]^{\mathrm{T}}} $为惯导解算的载体位置坐标。

将式（9）在$ {\left[ {\begin{array}{*{20}{c}} x&y&z \end{array}} \right]^{\mathrm{T}}} $处展开成泰勒级数，且仅取一次项，得到

$\begin{aligned}[b] {\rho _{Ii}}= &\sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}+ {{\left( {z - {z_i}} \right)}^2}} + \\ &\frac{{\partial {\rho _{Ii}}}}{{\partial x}}\delta x + \frac{{\partial {\rho _{Ii}}}}{{\partial y}}\delta y + \frac{{\partial {\rho _{Ii}}}}{{\partial z}}\delta z。\end{aligned}$

(10)

令$ {r_i} = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}} $，得到：

$ \frac{{\partial {\rho _{Ii}}}}{{\partial x}} = \frac{{x - {x_i}}}{{{r_i}}} = {e_{i1}}，$

(11)

$ \frac{{\partial {\rho _{Ii}}}}{{\partial y}} = \frac{{y - {y_i}}}{{{r_i}}} = {e_{i2}}，$

(12)

$ \frac{{\partial {\rho _{Ii}}}}{{\partial z}} = \frac{{z - {z_i}}}{{{r_i}}} = {e_{i3}}。$

(13)

将偏导数表达式代入，得到：

$ {\rho _{Ii}} = {r_i} + {e_{i1}}\delta x + {e_{i2}}\delta y + {e_{i3}}\delta z 。$

(14)

通过数据链测得的源节点与载体之间的距离值$ {\rho _{Li}} $可表示为：

$ {\rho _{Li}} = {r_j} + \delta {t_n} + {w_{Lj}} 。$

(15)

式中：$ {w_{Lj}} $为基于数据链的无线电测距随机白噪声。

联立式（14）～式（15），可得：

$ \delta {\rho _i} = {\rho _{Ii}} - {\rho _{Li}} = {e_{i1}}\delta x + {e_{i2}}\delta y + {e_{i3}}\delta z - \delta {t_n} - {w_{Lj}}。$

(16)

同理可得，卫导伪距与利用惯导解算位置计算的卫导伪距差的表达形式。

4 试验验证

为了验证惯导/数据链/卫导紧组合的性能，搭建了验证试验系统，主要包括惯导1套、数据链终端5套、卫导接收机1套，设备布放如图3所示。可知，该验证系统试验主要模拟了5个节点，将这5个节点分为4个主节点和1个从节点，每个主节点包含1个数据链终端（具有GNSS定位功能），从节点包含1个数据链终端、1个卫导接收机和1套惯导。其中，卫导接收机能输出伪距信息，卫导定位误差优于10 m，数据链测距误差优于40 m。

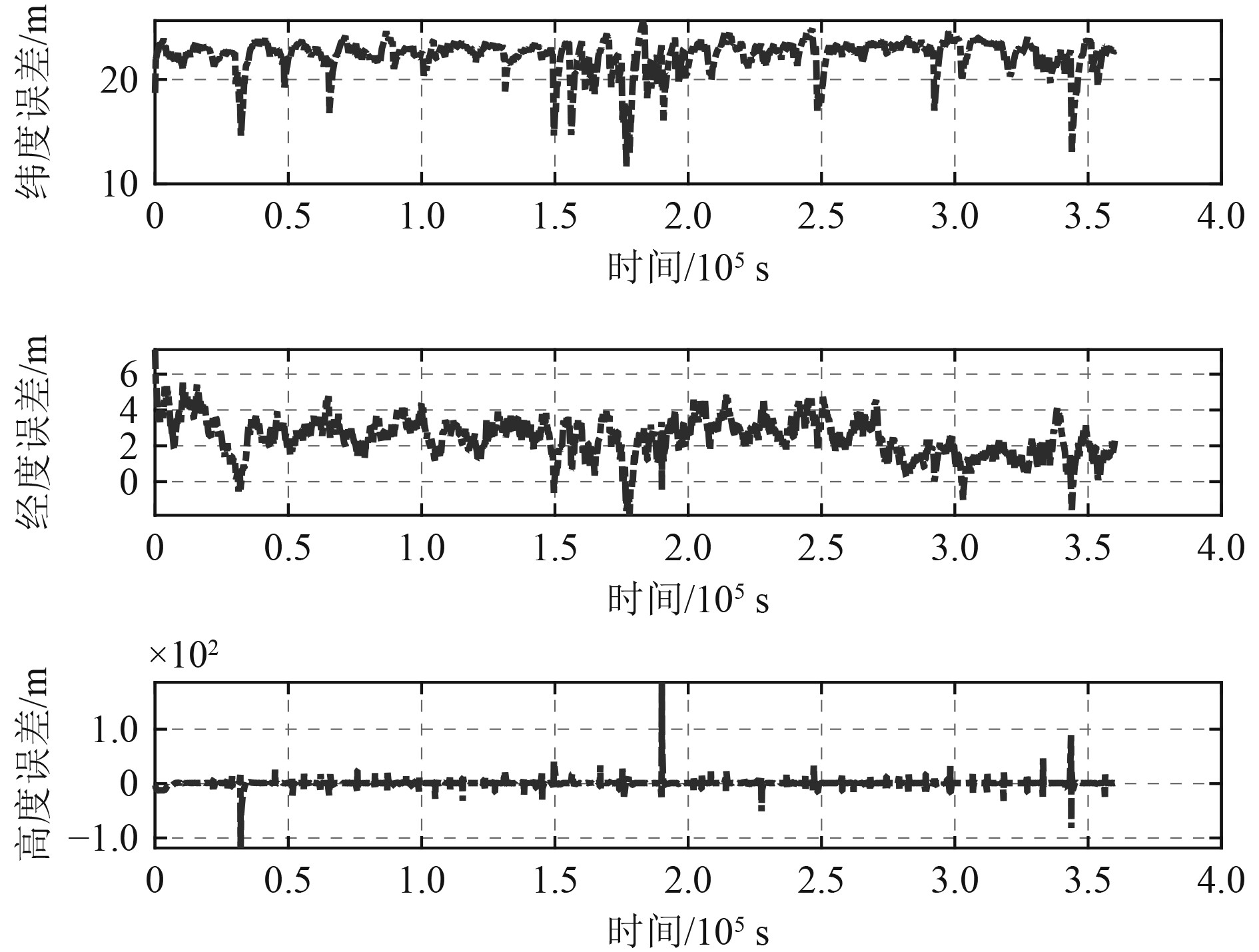
图4为从节点卫导拒止时，惯导/数据链/卫导紧组合定位三维误差。

经统计，卫导拒止时，惯导/数据链/卫导紧组合纬度方向均方根误差为22.38 m，标准差为1.53 m；经度方向均方根误差为2.69 m，标准差为1.06 m；高度方向均方根误差为6.52 m，标准差为6.47 m。

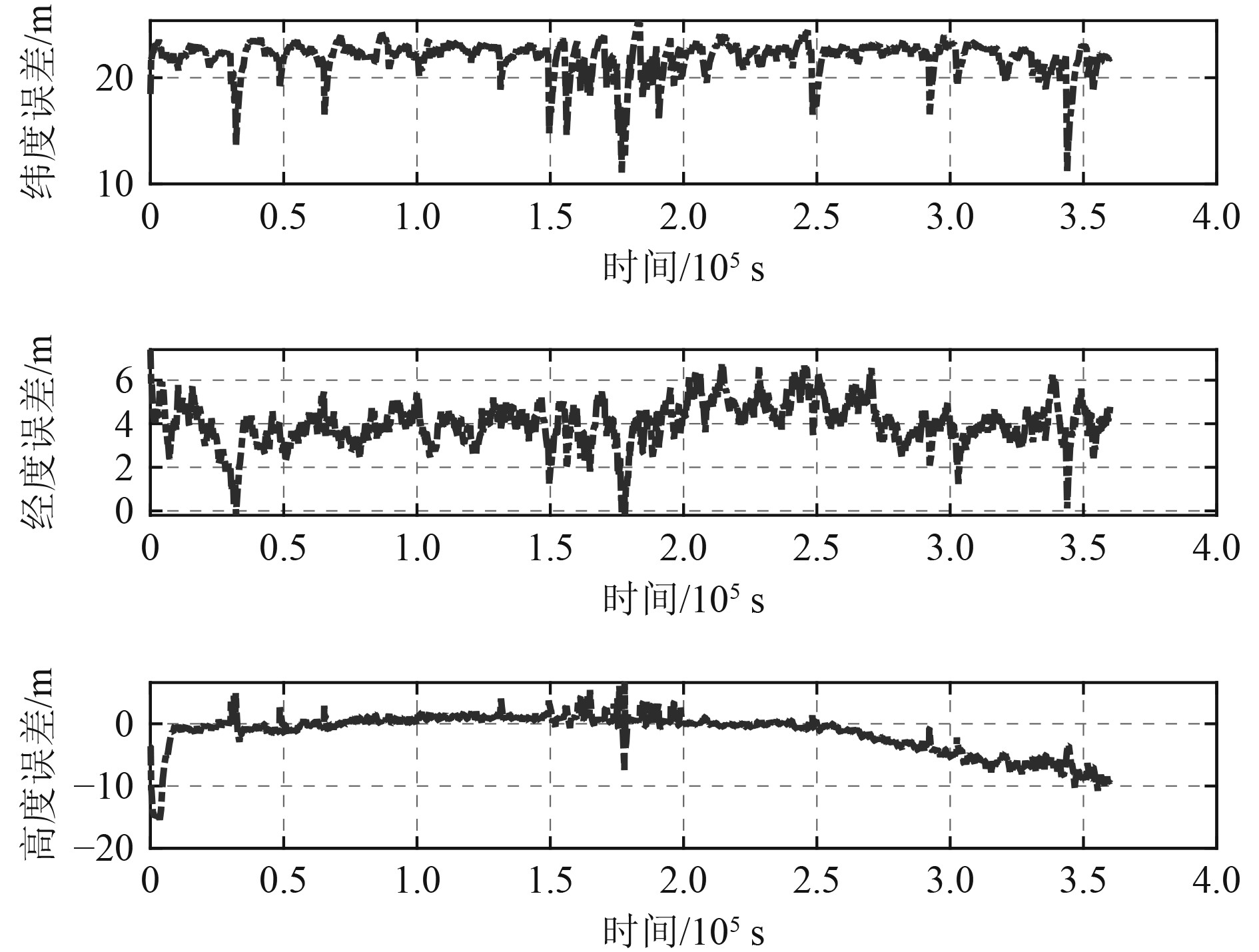
图5为卫导受限时，惯导/数据链/卫导紧组合定位三维误差。此时，数据链4个主节点可联通，同时3颗卫星可见。

本试验主要为了考察增加卫导观测信息对惯导/数据链/卫导紧组合定位性能的影响。经统计，纬度方向均方根误差为22.99 m，标准差为4.15 m；经度方向均方根误差为0.97 m，标准差为0.84 m；高度方向均方根误差为3.51 m，标准差为3.20 m。与卫导拒止情况相比，纬度方向误差略有下降，经度、高度方向误差有明显提升，分别提升了64%和45%。

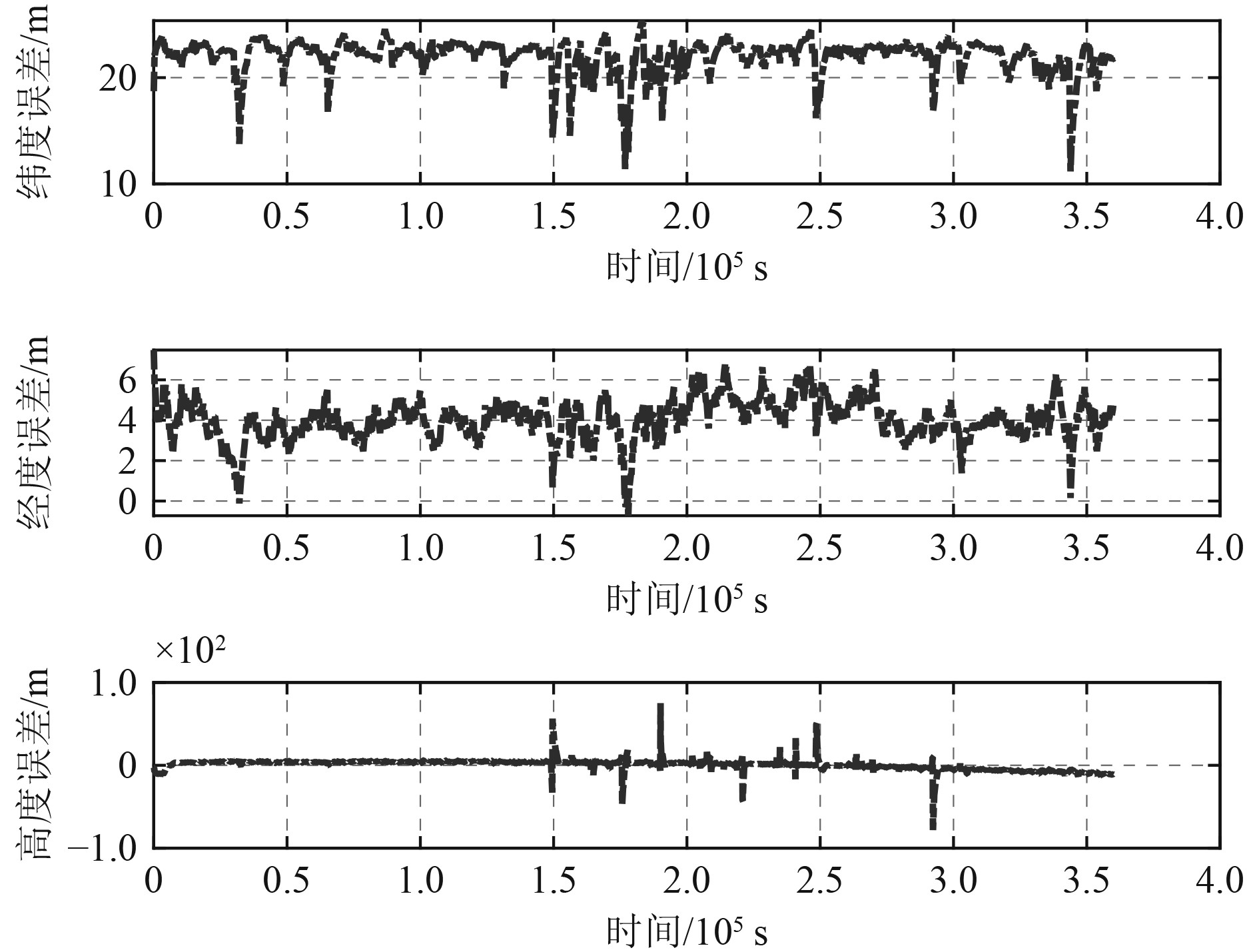
图6为数据链4个主节点可联通，同时2颗卫星可见的情况下，惯导/数据链/卫导紧组合定位存在误差。

经统计，纬度方向均方根误差为22.08 m，标准差为1.58 m；经度方向均方根误差为4.16 m，标准差为0.98 m；高度方向均方根误差为6.37 m，标准差为6.33 m。相比卫导拒止情况，通过引入卫导信息，纬度、高度方向误差略有改善，经度方向误差下降，稳定度略有提升。与图5相比，由于卫导观测信息减少，经度、高度方向的误差增大。

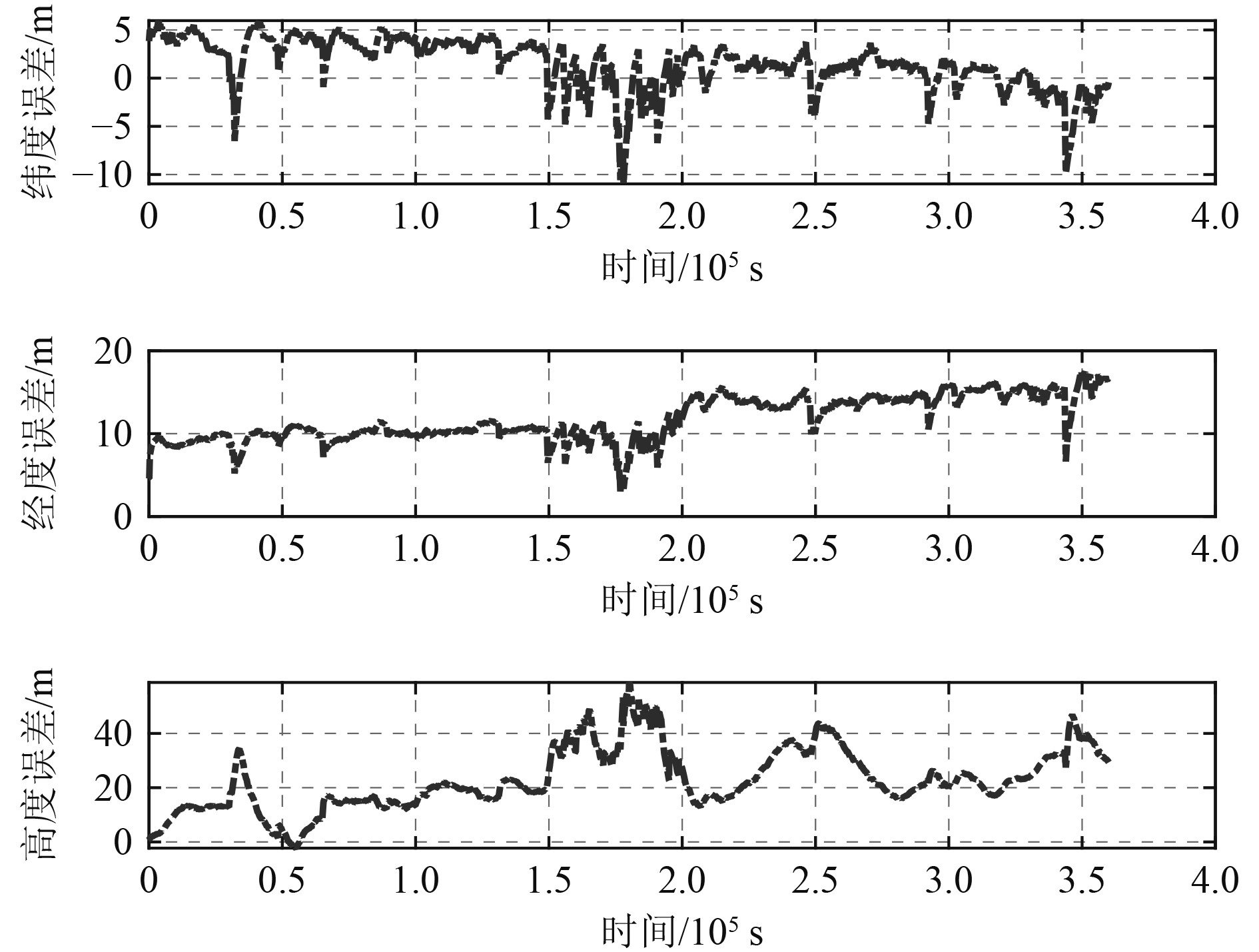
为了考察卫导受限或者数据链弱联通时惯导/数据链/卫导紧组合的性能，数据链2个主节点可联通，同时3颗卫星可见情况下，惯导/数据链/卫导紧组合的定位误差如图7所示。

理论上，数据链只有2个可用测距信息或卫导只有3颗可见星，这2种情况下都较难获得稳定的定位结果。通过惯导/数据链/卫导紧组合，充分利用二者的可用信息，可获得稳定的定位结果。经统计，纬度方向均方根误差为3.02 m，标准差为2.63 m；经度方向均方根误差为12.05 m，标准差为2.6 m；高度方向均方根误差为25.71 m，标准差为11.38 m。可见，通过采用惯导/数据链/卫导紧组合，可在卫导受限且数据链弱联通情况下，仍可获得较好的导航信息品质。

5 结　语

本文针对卫导受限或者数据链弱联通场景中，惯导/数据链/卫导组合导航系统难以保持输出高精度导航信息的问题，提出了卫导受限下惯导/数据链/卫导紧组合算法，该算法无需数据链或者卫导进行独立载体位置解算，充分利用场景中有限的卫导观测信息和数据链测距信息对惯导误差进行修正，从而使观测量不足的情况下，导航系统仍能维持较高精度。