水声换能器是声呐设备最基础的部件之一,其可靠性对声呐系统至关重要。而压电陶瓷材料作为换能器的核心材料,其居里温度一般在300℃左右[1],当换能器的工作温度超过压电陶瓷的居里温度时,压电陶瓷出现不可逆转的破坏,失去或降低压电性能,导致换能器功能失效[2]。不仅如此,试验证明如果换能器辐射面的温度过高,将导致换能器导流罩的透声橡胶软化为液体,橡胶特性发生严重变化,换能器电声参数出现异常,声波无法辐射至水介质。
为了避免水声换能器出现热失效,John等 [3]采用等效电路法计算了复合棒换能器的机械损耗和介电损耗,在此基础上采用有限元软件获得了连续波激励条件下不同激励电压时换能器的稳态温度,并对温升进行了测试,试验结果与理论计算具有较好的一致性。Stephon等[4]对压电陶瓷圆环换能器在大功率、连续波激励下的温度时间变化规律进行了仿真研究,在空气中进行了对比试验。但上述文献中的换能器为窄带换能器,仿真与试验在空气中进行,并且缺少实际工况下换能器各部位更为真实的瞬态温度随时间的变化情况。设计人员为了避免换能器系统热失效,需要了解温度分布及温升情况,以便进行针对性改进换能器散热环境。
为了进一步了解纵振换能器在水介质中大功率工作时换能器各部位温度分布情况,本文建立一种宽带复合棒水声换能器[6 − 8]的有限元瞬态热分析模型。开展了发射信号为连续正弦波和脉冲正弦波工况时换能器的温度场仿真,仿真计算了加载不同占空比脉冲发射信号时换能器的温度场分布,获得压电陶瓷内部温度最高部位以及换能器辐射面温度随工作时间的变化曲线,从曲线得到换能器最长可连续工作时间,对于指导换能器设计和试验具有重要意义。
1 换能器传热学基本理论换能器的热分析涉及到换能器各部分之间热传导问题和换能器与外界流体(空气或水)之间的热对流问题,因此应分别建立热传导和热对流方程 [5]。
| $ \frac{\partial T}{\partial t}=\alpha {\nabla }^{2}T+\frac{Q}{\rho C} ,$ | (1) |
式中:
热量扩散率
| $ \alpha = \frac{K}{{\rho C}} 。$ | (2) |
式中:
固体之间发生热传导时传递的热流量为:
| $ q = - KA\nabla T 。$ | (3) |
式中:
在换能器固体边界处与流体之间产生热对流,固体向流体对流的热流量可表示为:
| $ q = Ah(T - {T_\infty })。$ | (4) |
式中:
换能器单位体积能量变化率表达式为:
| $ \frac{{\partial U}}{{\partial t}} = \rho C\frac{{\partial T}}{{\partial t}} 。$ | (5) |
对于压电换能器,因介电损耗和机械损耗而产生的单位体积热功率为:
| $ Q = \omega {E^2}\varepsilon \tan {\delta _e} + \omega {E^2}\varepsilon {k_{eff}}\tan {\delta _m} 。$ | (6) |
式中:
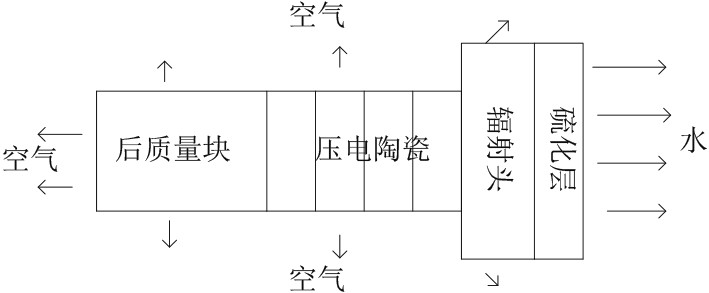
纵振水声换能器工作环境如图1所示,除了辐射头辐射面通过导流罩硫化层向水中散热外,换能器其余表面向空气中散热。
|
图 1 换能器工作环境示意图 Fig. 1 Sketch of transducer working surroundings |
根据图1建立水声换能器的有限元物理场模型,换能器主要由后质量块、压电陶瓷、预应力螺杆、辐射头等组成。其中后质量块和预应力螺杆为45#钢,压电陶瓷为PZT-4,辐射头为铝合金,硫化层为聚氨酯橡胶。
由于换能器结构和边界条件都是轴对称,因此为了提高计算速度和精度,采用二维模型进行分析。对换能器物理模型做简化处理,忽略电极引片、胶粘层和导线的影响,物理模型如图2所示。

|
图 2 换能器物理模型 Fig. 2 Physical model of transducer |
分析时设定换能器与外界空气的热对流系数为5 W/m2℃,与水介质的热对流系数为
假定外界环境温度为25℃,换能器在水中工作时表现为高阻抗,介电损耗产生的功率为主要发热源,因此仅考虑对压电陶瓷施加单位体积介电损耗功率,模拟换能器实际工作环境条件下的压电陶瓷内部温度分布情况,避免压电陶瓷材料的最高温度不超过压电材料的居里温度,同时辐射面处的温度也应低于透声聚氨酯橡胶的软化温度。
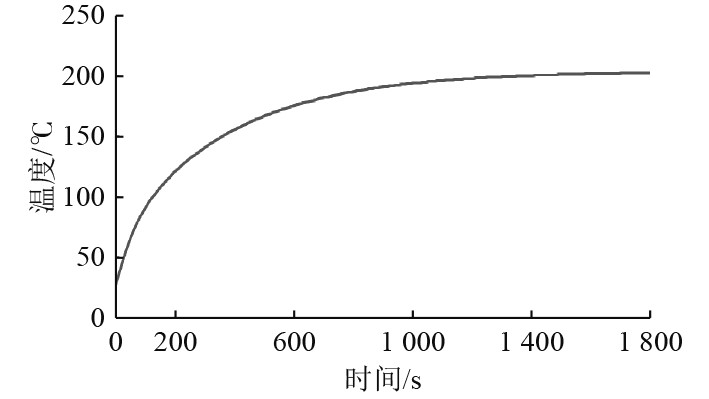
2.2 不同激励工况下的温度场仿真分析 2.2.1 激励信号为连续波时当换能器的激励信号为连续正弦波时,换能器持续工作。利用有限元软件对换能器进行瞬态热仿真计算,当工作
|
图 3 换能器压电陶瓷中间节点温度瞬态响应 Fig. 3 Transient temperature response of transducer taken from mid node of the piezoceramics |
可知,换能器
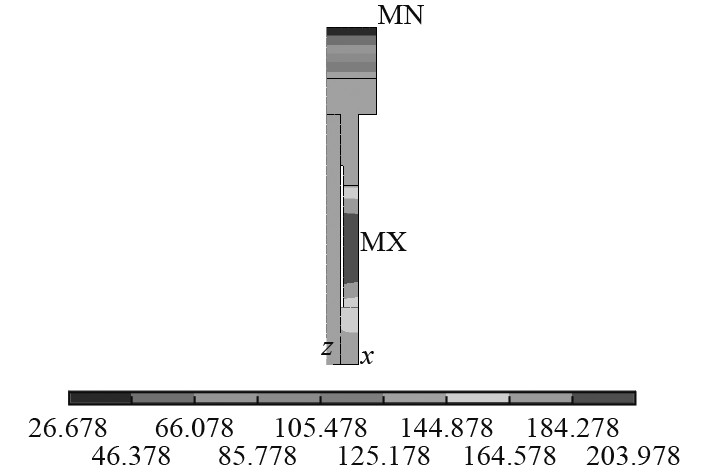
当换能器处于热稳态时,换能器温度分布见图4。对于压电陶瓷来说,它中间部分温度最高,而与上下金属接触面处温度最低,这是热量向外传导的结果。
|
图 4 换能器稳态温度分布 Fig. 4 Steady state temperature distribution of transducer |
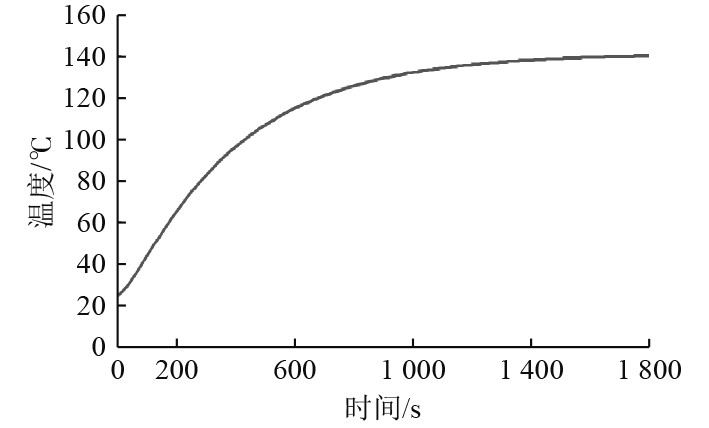
进一步可获得换能器辐射头辐射面处的温度瞬态响应曲线,如图5所示。
|
图 5 换能器辐射面中间节点温度瞬态响应 Fig. 5 Transient temperature response of transducer taken from mid node of the radiating surface |
当换能器达到热平衡后,辐射面温度超过100℃,将会使硫化层橡胶被加热软化,橡胶的透声性能和机械性能大幅降低。因此对这种没有散热处理的换能器系统,使用连续波激励应缩短其工作时间。
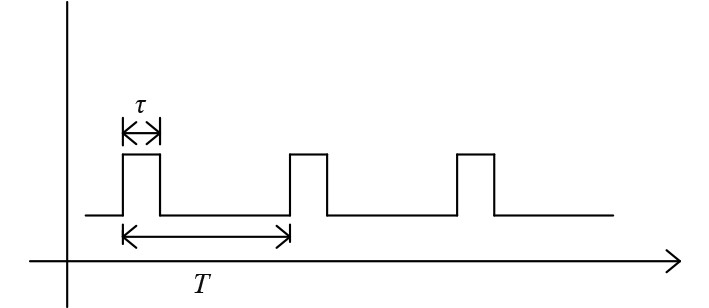
2.2.2 激励信号为脉冲波时当换能器的激励信号为脉冲正弦波时,其脉冲包络如图6所示,工作脉宽为τ,工作周期为T,换能器处于间歇工作状态。为了便于对比,此时的介电损耗功率与连续波时保持一致。
|
图 6 脉冲信号 Fig. 6 Pulse signal |
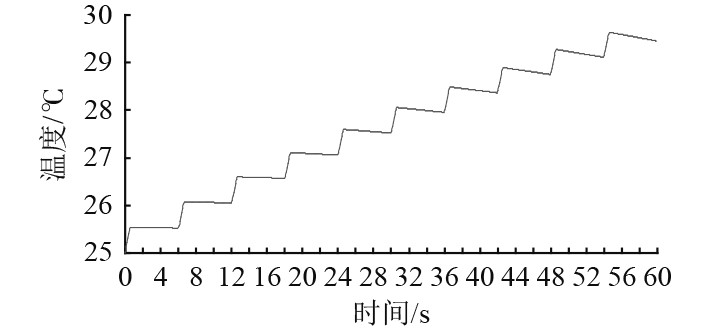
当
|
图 7 换能器压电陶瓷中间节点温度瞬态响应(时间=60 s) Fig. 7 Transient temperature response of transducer taken from mid node of the piezoceramics(time=60 s) |
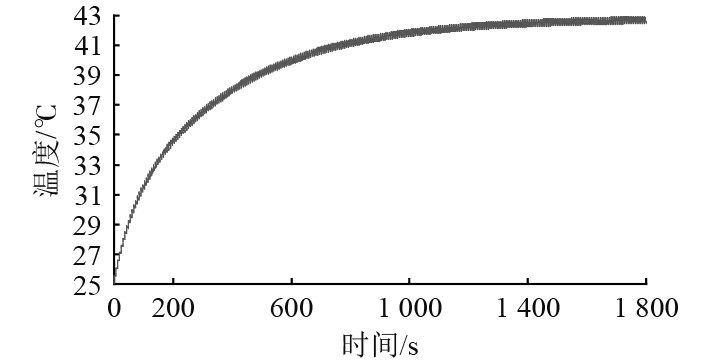
可知,对于脉冲激励,换能器的温度呈阶梯型增长趋势,由于散热条件差,非工作时间温度基本来不及降低。因此当发射脉冲时间足够长时,换能器达到热平衡状态,如图8所示,最高温度升高到42.9℃。
|
图 8
换能器压电陶瓷中间节点温度瞬态响应(时间= |
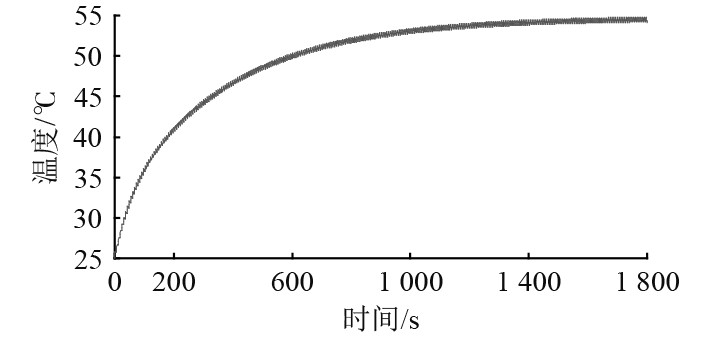
当
|
图 9 换能器压电陶瓷中间节点温度瞬态响应(τ/T=20%) Fig. 9 Transient temperature response of transducer taken from mid node of the piezoceramics(τ/T=20%) |
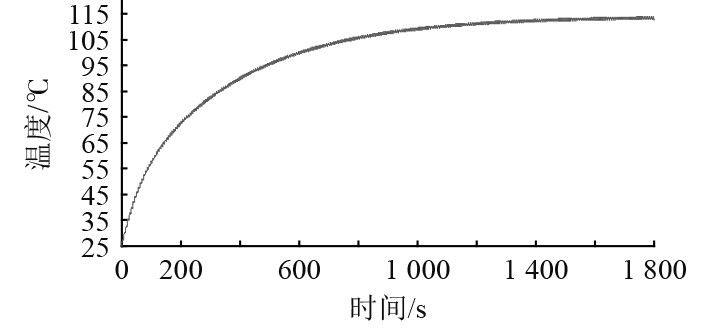
当
|
图 10 换能器压电陶瓷中间节点温度瞬态响应(τ/T=40%) Fig. 10 Transient temperature response of transducer taken from mid node of the piezoceramics(τ/T=40%) |

|
图 11 不同占空比下温度响应 Fig. 11 Temperature response for various ratio of pulse duration and pulse interval |
可知,相同的激励电压下,脉冲波的占空比越高,达到热平衡时换能器内部温度越高。当占空比达到80%时,其内部最高温度非常接近连续波激励工况下的温度情况。
3 结 语本文结合传热学基本理论和有限元仿真手段,仿真计算了一种复合棒结构水声换能器的瞬态温度场,针对不同工况,获得了换能器压电陶瓷处温度和辐射处面温度时间变化曲线。从仿真结果可知,当施加连续波时间超过
| [1] |
王荣津. 水声材料手册[M]. 北京: 科学出版社, 1983
|
| [2] |
张明宇, 王艳, 张睿, 等. 换能器大功率下温升规律初探[J]. 声学与电子工程, 2021(3): 30−32+48.
|
| [3] |
JOHN L. BUTLER J B, BLOTTMAN R E. Montgomery thermal model for piezoelectric transducers[J]. Journal Acoustical Society America, 2012, 132(4): 2161-2164. |
| [4] |
STEPHEN C, BUTLER A L, BUTLER A. Thermal analysis of high-drive ring transducer elements[R], 2005 NUWC-NPT Technical Report.
|
| [5] |
陈飞, 傅波. 压电换能器的热仿真分析[J]. 中国测试, 2009, 35(4): 104−106. CHEN Fei,FU Bo. Thermal simulation analysis of piezoelectric transducer[J]. China Measurement and Test, 2009, 35(4): 104−106. |
| [6] |
胡负稷, 张文波, 王明洲. 多激励宽度复合棒换能器设计[J]. 鱼雷技术, 2016, 24(6): 422-425. HU Fuji, ZHANG Wenbo, WANG Mingzhou. Design on multi-excitation broadband tonpilz transducer[J]. Torpedo Technology, 2016, 24(6): 422-425. |
| [7] |
胡负稷, 张喜顺, 张文波, 等. 两种多谐振宽带纵振换能器设计[J] 水下无人系统学报, 2017, 25(4): 377−380. HU Fuji, ZHANG Xishun, ZHANG Wenbo, et al. Design of two kinds of multi-rosonant broadband longitudinal vibration transducer[J]. Journal of Unmanned Undersea Systems, 2017, 25(4): 377−380. |
| [8] |
张文波, 王明洲, 郝保安. 双激励宽带水声换能器理论研究[J]. 鱼雷技术, 2007, 15(2): 34-37. ZHANG Wenbo, WANG Mingzhou, HAO Baoan. Theoretical study on broadband underwater transducer with double resonant mode[J]. Torpedo Technology, 2007, 15(2): 34-37. |
 2024, Vol. 46
2024, Vol. 46
