2. 中国船舶集团有限公司系统工程研究院,北京 100094;
3. 青岛国实科技集团有限公司,山东 青岛 266237
2. System Engineering Research Institute, China State Shipbuilding Corporation Limited, Beijing 100094, China;
3. Qingdao Gosci Technology Group, Qingdao 266237, China
无人水面艇(Unmanned Surface Vessel,USV)布放回收技术是将其快速、安全地部署到水面并高效、可靠地回收到母船的技术。主要包括吊放式、尾滑道式和坞舱式快速收放技术[1]。在吊放式的收放方式下,USV与母船吊钩的对接一直是行业的难题。业内通常采用人员驾驶小艇进行人工对接的方式,操作复杂、风险高、耗时长。因此,自动化、智能化将是未来USV布放回收技术的重要研究方向。
然而,USV始终在海洋环境中处于六自由度摇晃中。这使智能化布放回收时的自动瞄准变得困难,为辅助回收、确保回收时的安全性,需要对USV的运动姿态进行短期预测。
早期船舶运动姿态的预测主要以线性水动力学方程建模为基础,如Kaplan[2]提出使用Wiener滤波器来实现船舶运动的极短期预测,Triantafyllou等[3 − 4]提出一种以卡尔曼滤波技术为基础的预报方法对船舶6个自由度的运动进行预测。此类预测方法需要在频域内求解船舶水动力学方程,而频域内的水动力系数难以满足反映实际海况时变特点的要求,计算复杂、效率低,因此基于频域方法建立的运动方程难以符合实际应用的要求。
近些年神经网络模型得到不断发展,也被应用于大型船舶的运动姿态预测领域。刘煜城[5]对数值模拟生成的船舶运动时历数据进行经验模态分解(Empirical Mode Decomposition, EMD)后输入长短期记忆(Long-Short Term Memory, LSTM)网络模型进行预测,对于高海况下的船舶运动预测精度有所提高,然而对于较平稳的低海况下船舶运动,EMD反而会放大原始运动信号的非平稳性,导致预报结果变差。詹可等[6]提出一种融合运动频谱信息的滑动窗口方法,将卷积神经网络(Convolutional Neural Networks, CNN)与LSTM模型组合,构建CNN-LSTM网络模型进行船舶运动极值的预测,实验表明该模型对未来1~2个周期内的运动极值信息预报效果良好。
然而,上述研究的对象均为大型船舶,USV因为船体较小、重量较轻,六自由度的摇荡运动相较大型船舶要更加高频,对多步预测的要求更高。
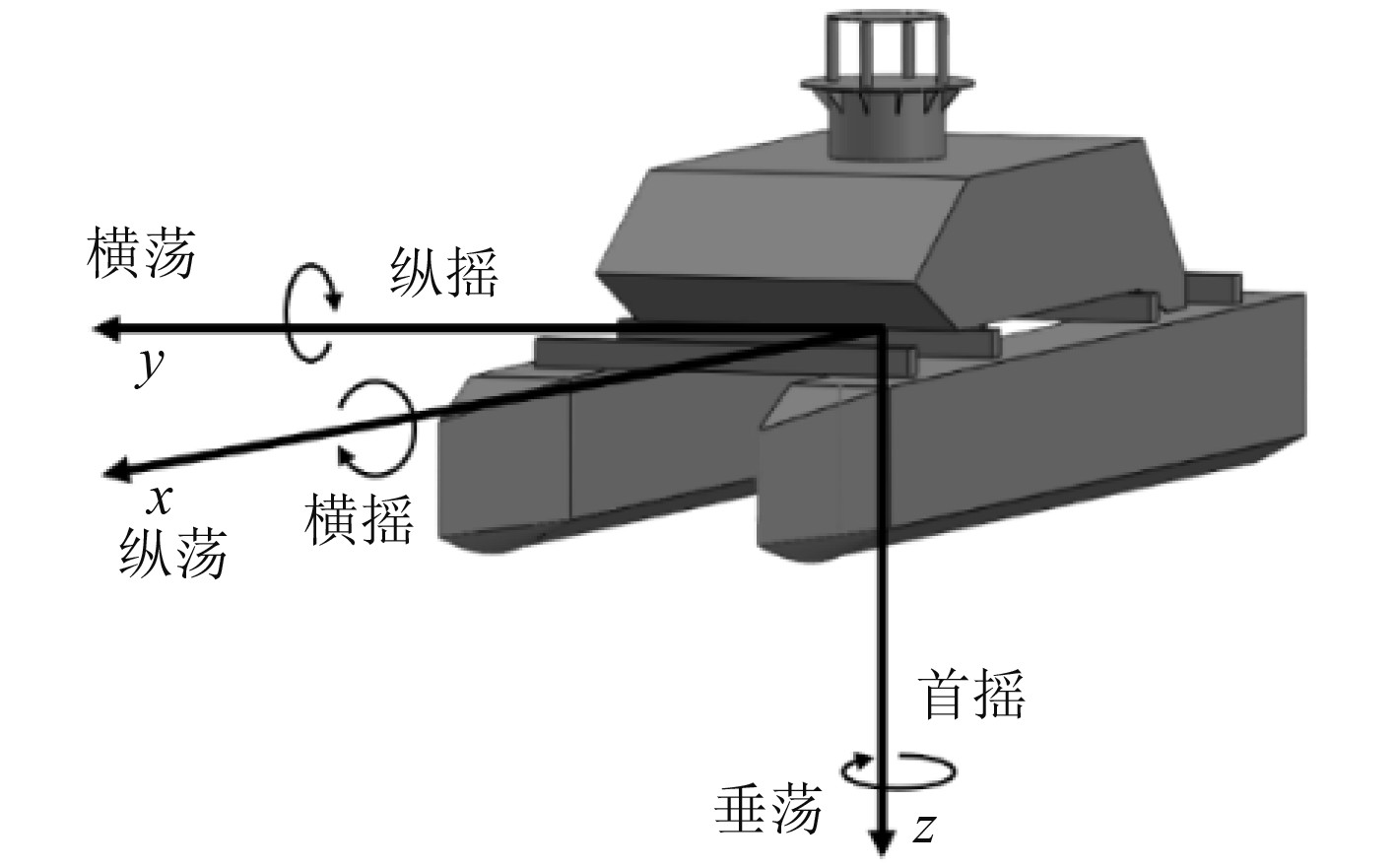
1 USV运动姿态实测数据集获取 1.1 USV六自由度运动姿态USV在水面上具有6个自由度的运动姿态,分别为垂荡、横荡、纵荡、横摇、纵摇、首摇,如图1所示。
|
图 1 USV运动姿态图 Fig. 1 USV motion diagram |
其中垂荡、横荡、纵荡运动难以测量,而首摇主要受自动导航操控,因而对USV运动姿态进行预测时主要关注横摇与纵摇[7]。
1.2 数据来源本文采用2023年5月15日对某型号USV在青岛附近海域采集到的实测运动姿态数据作为实验数据集。数据采样频率20 Hz,采样间隔0.05 s。
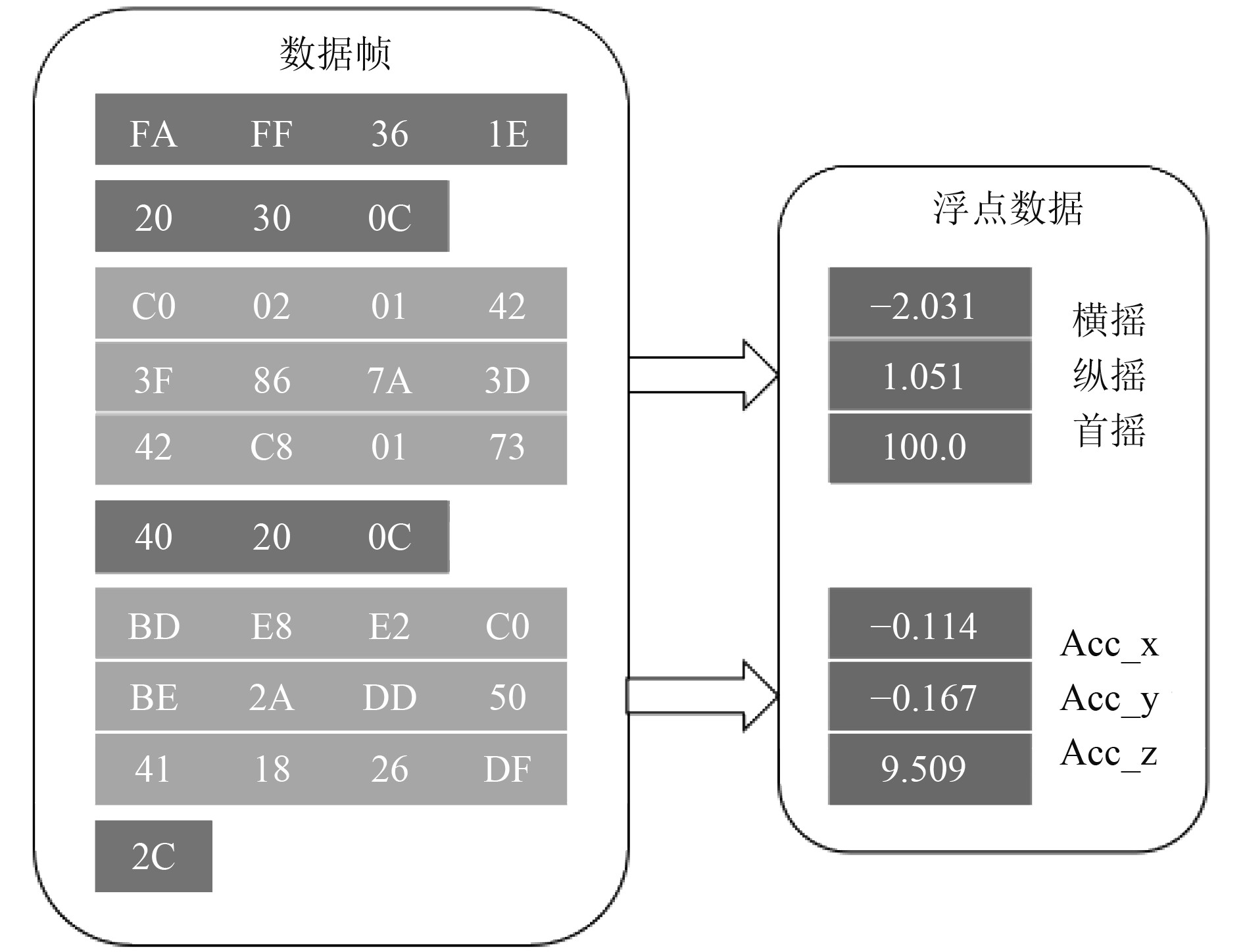
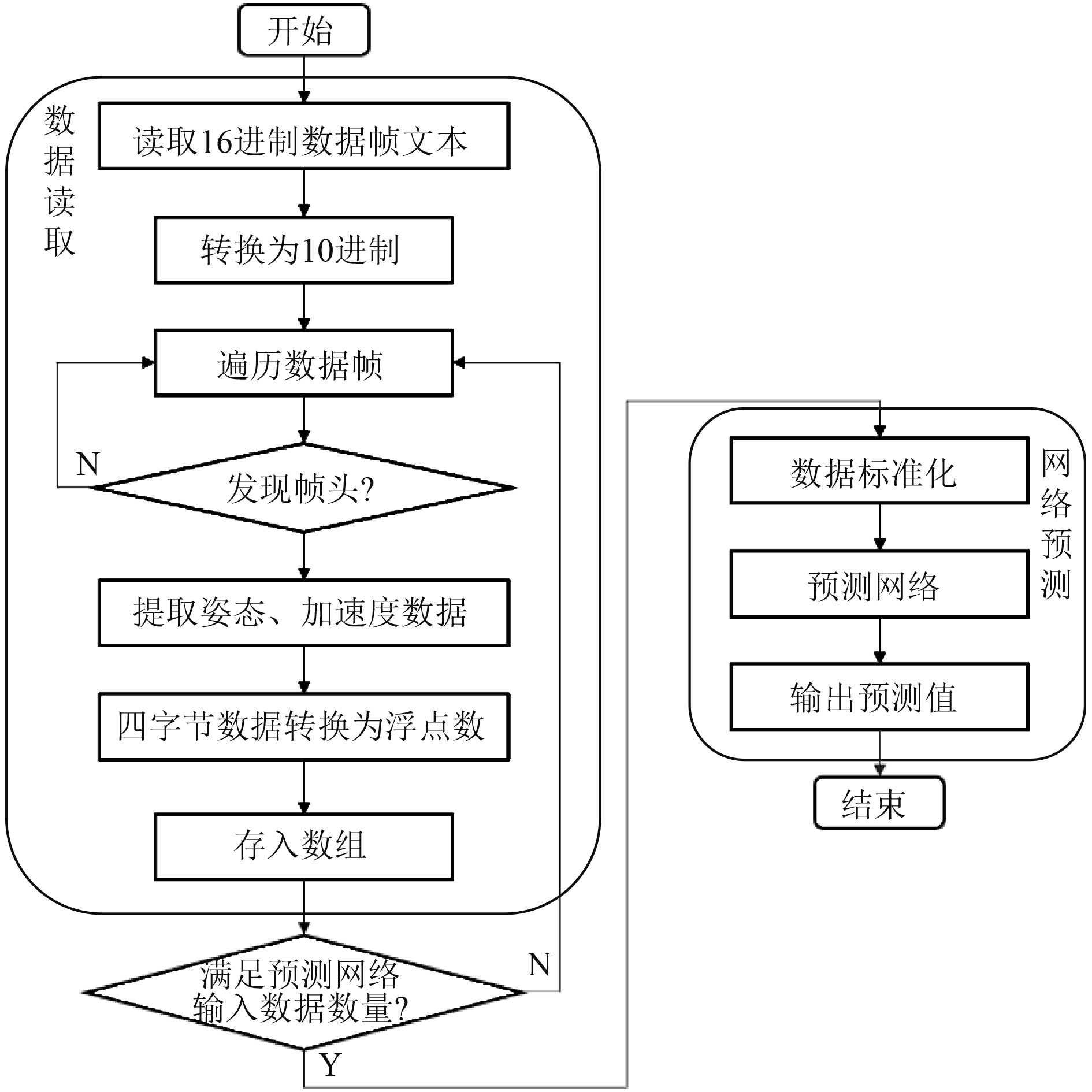
1.3 数据帧解析用MTI传感器采集的数据以数据帧形式储存,需要解析为浮点数的形式才能送入网络模型进行处理。一帧包含35个六进制字节,其中帧头3字节、数据长度1字节、姿态角数据ID和长度3字节、横摇、纵摇、首摇共12字节、加速度数据ID和长度3字节、三轴加速度各4字节共12字节、校验位1字节。数据帧与浮点数据之间的对应如图2所示。数据帧解析流程如图3所示。
|
图 2 数据帧与浮点数据的对应关系 Fig. 2 Correspondence between data frame and floating point data |
|
图 3 数据帧解析流程图 Fig. 3 Data frame parsing flowchart |
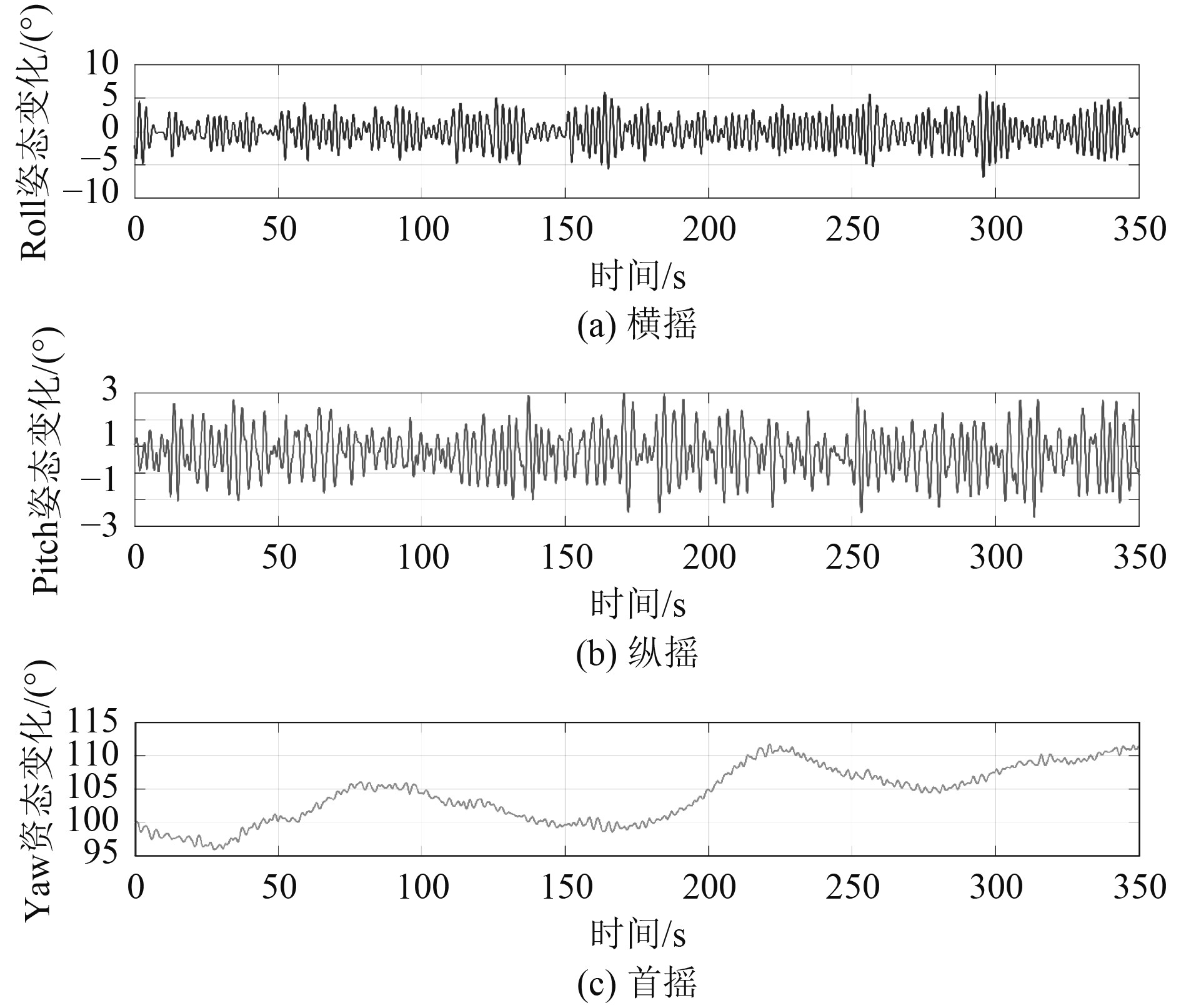
由实测数据解析出的USV横摇、纵摇、首摇姿态角变化情况如图4所示。
|
图 4 实测USV姿态角变化情况 Fig. 4 Change of measured USV attitude angle |
USV的运动姿态在时间上呈现出一种连续性,下一时刻姿态会受到上一时刻姿态的影响。因此,对USV运动姿态的预测问题属于典型的时间序列预测问题。
2.1 卷积神经网络模型CNN模型通过局部连接和共享权值的方式,交替使用卷积层和池化层对数据的局部特征进行提取。各应用领域将不同CNN作为特征提取的主干网络并添加不同的功能单元结构形成了新的应用模型,CNN目前已成为目标检测、语义分割、自然语言处理等领域的研究热点[8]。CNN的基本结构如图5所示。
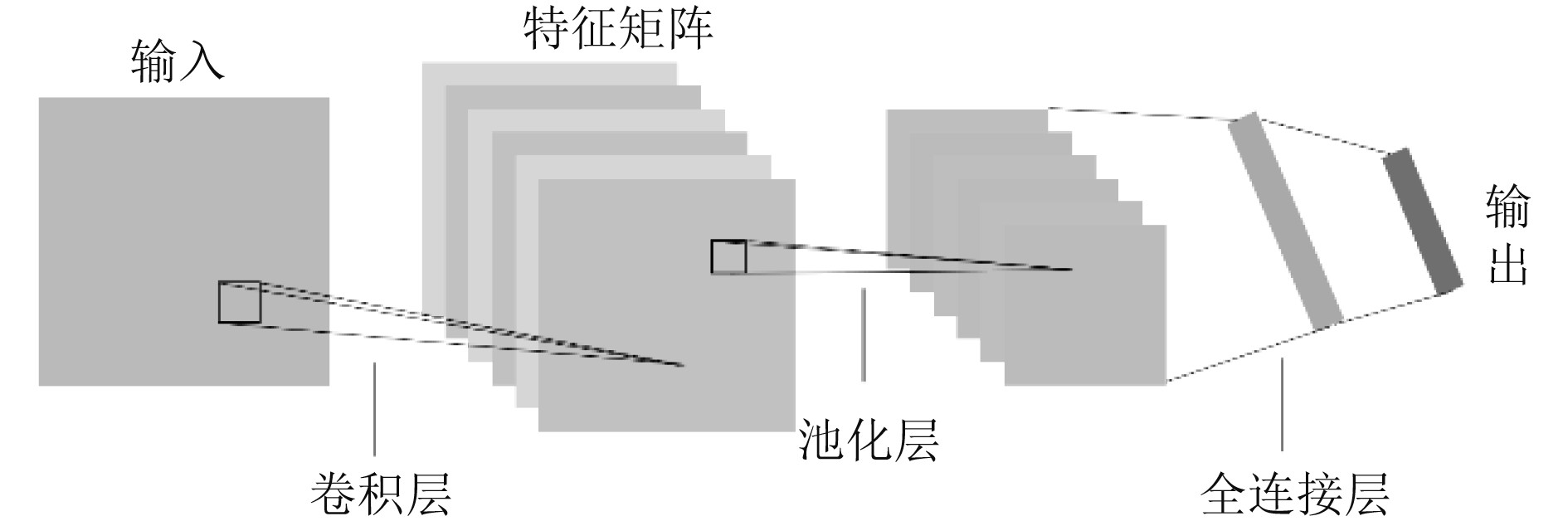
|
图 5 CNN结构 Fig. 5 Structure of CNN |
循环神经网络(Recurrent Neural Networks,RNN)最初是为处理序列数据提出,然而,标准RNN存在梯度消失和梯度爆炸的问题[9]。为缓解上述问题,Hochreiter等[10]提出了RNN的改进模型LSTM网络模型,模型单元结构如图6所示。Cho等[11]提出的门控循环单元(Gate Recurrent Unit,GRU)是LSTM的一种广泛流行的变体,模型单元结构如图7所示。
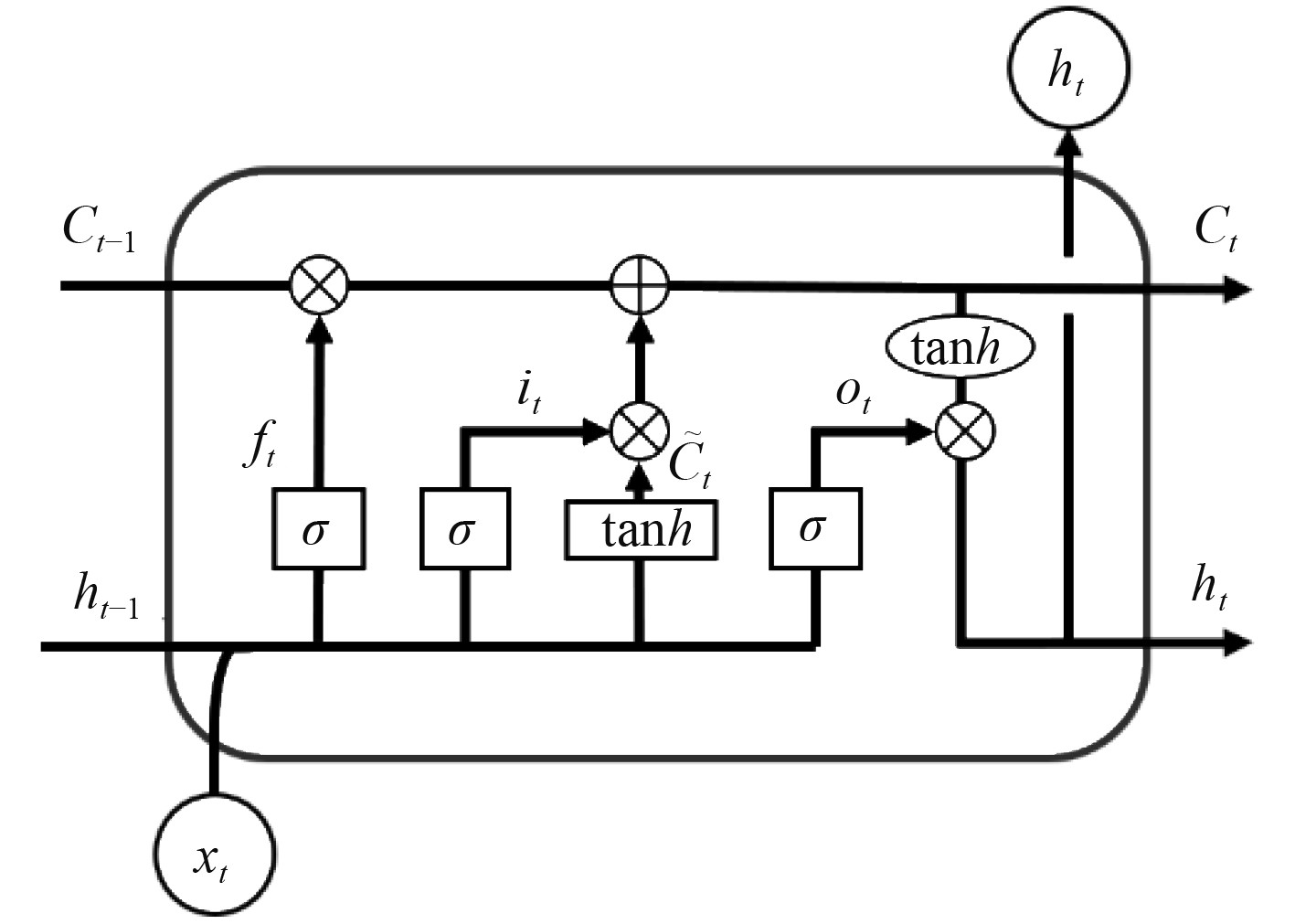
|
图 6 LSTM单元结构 Fig. 6 Unit structure of LSTM |
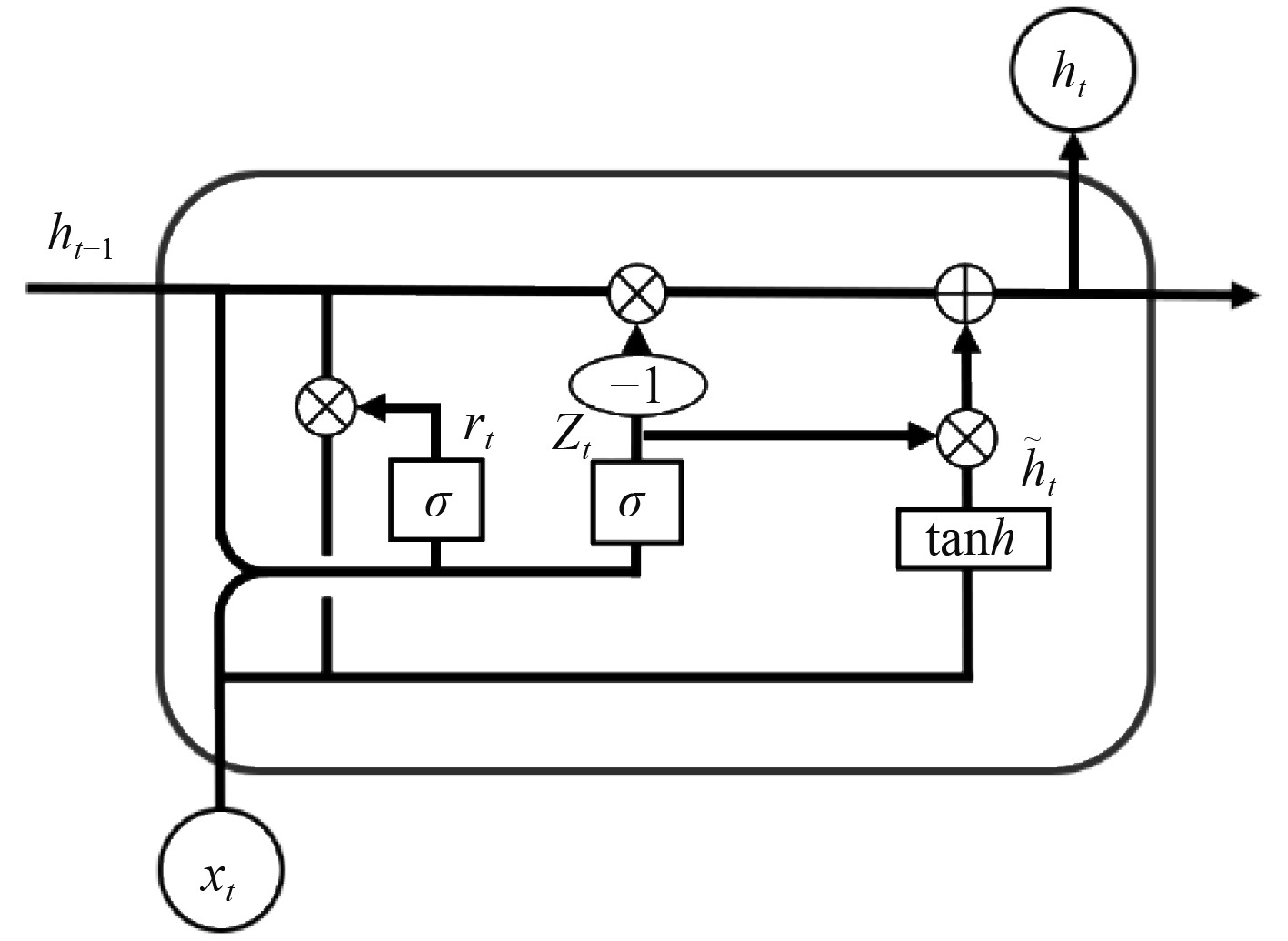
|
图 7 GRU单元结构 Fig. 7 Unit structure of GRU |
Chung等[12]分别使用GRU和LSTM网络模型在复调音乐建模、语音信号建模任务上进行评估。结果表明GRU和LSTM表现相当,但GRU将LSTM单元中的输入门和遗忘门合成为一个更新门,参数量更小,模型结构更简单。
GRU前向传播计算如下[13]:
| $ \begin{gathered}{c} \left\{\begin{gathered}{c} {\mathit{r}}_{t}=\sigma \left({\mathit{W}}_{r}\cdot\left[{\mathit{h}}_{t-1},{\mathit{x}}_{t}\right]\right),\\ {\mathit{z}}_{t}=\sigma \left({\mathit{W}}_{z}\cdot\left[{\mathit{h}}_{t-1},{\mathit{x}}_{t}\right]\right),\\ {\tilde{\mathit{h}}}_{t}={\text{tanh}}\left({\mathit{W}}_{\tilde{h}}\cdot\left[{\mathit{r}}_{t}\times {\mathit{h}}_{t-1},{\mathit{x}}_{t}\right]\right),\\ {\mathit{h}}_{t}=\left(\mathit{I}-{\mathit{z}}_{t}\right)\times {\mathit{h}}_{t-1}+{\mathit{z}}_{t}\times {\tilde{\mathit{h}}}_{t},\\ {\mathit{y}}_{t}=\sigma \left({\mathit{W}}_{o}\cdot{\mathit{h}}_{t}\right)。\qquad\qquad\qquad\end{gathered}\right. \end{gathered} $ | (1) |
式中:
本文首先通过CNN模块挖掘USV运动姿态时序数据的局部特征,再使用GRU模型进行多步预测,搭建了CNN-GRU混合网络模型,其基本结构如图8所示。

|
图 8 CNN-GRU混合网络模型 Fig. 8 CNN-GRU hybrid network model |
模型的CNN网络部分包含3个通道数分别为16、16、32,卷积核大小均为3×3的1维卷积层和3个最大值池化层。
GRU网络部分包含2个隐藏层,每个隐藏层包含32个隐藏单元。激活函数选用ReLU。最后的全连接(Dense)层可以指定输出的步长,当指定输出步长为n时,输入序列为
本文的姿态预测实验以横摇角为例,纵摇角预测过程与之类似。实验平台CPU为AMD Ryzen 5
为确保模型训练的效率,需要对数据进行预处理。
1) 训练集、测试集的划分
将2023年5月15日10:00到11:40的
2)数据标准化
数据的量纲会影响训练时模型参数优化的速度,因此需要对数据进行标准化。本文采用min-max标准化方法,为防止数据泄漏影响训练结果,选取训练集中数据的最大值、最小值,按式(2)将整个数据集数值归一化至[0,1]。
| $ {x}^{*}=\frac{x-{x}_{\text{min}}}{{x}_{\text{max}}-{x}_{\text{min}}}。$ | (2) |
式中:
神经网络训练所用的超参数如表1所示。训练时开启了学习率调度器(learning rate scheduler)以便模型更好地收敛。
|
|
表 1 超参数表 Tab.1 Hyperparameter value table |
本文选取平均绝对误差(Mean Absolute Error, MAE)为各模型预测性能的主要评价指标,均方根误差(Root Mean Square Error,RMSE)和相关指数(
| $ MAE=\frac{1}{n}\sum_{t=1}^{n}\left|{y}_{t}-\widehat{{y}_{t}}\right| ,$ | (3) |
| $ RMSE=\sqrt{\frac{1}{n}{\sum _{t=1}^{n}}{\left({y}_{t}-\widehat{{y}_{t}}\right)}^{2}} ,$ | (4) |
| $ {R}^{2}=1-\frac{\displaystyle \sum _{t=1}^{n}{\left({y}_{t}-\widehat{{y}_{t}}\right)}^{2}}{\displaystyle \sum _{t=1}^{n}{\left({y}_{t}-\stackrel-{{y}_{t}}\right)}^{2}} 。$ | (5) |
式中:
在上述指标中,MAE、RMSE数值越小,代表模型预测误差越小,而
实验选用XGBoost[14]模型、LSTM 模型和GRU模型作为CNN-GRU模型的对比模型。使用滑动窗口法构造输入序列,在输入步长为160步(8 s),预测提前量为10步(0.5 s)时,对测试集最后100个采样点各模型的横摇角预测结果如图9所示。可以看出本文CNN-GRU模型的预测曲线与真实曲线最为接近。
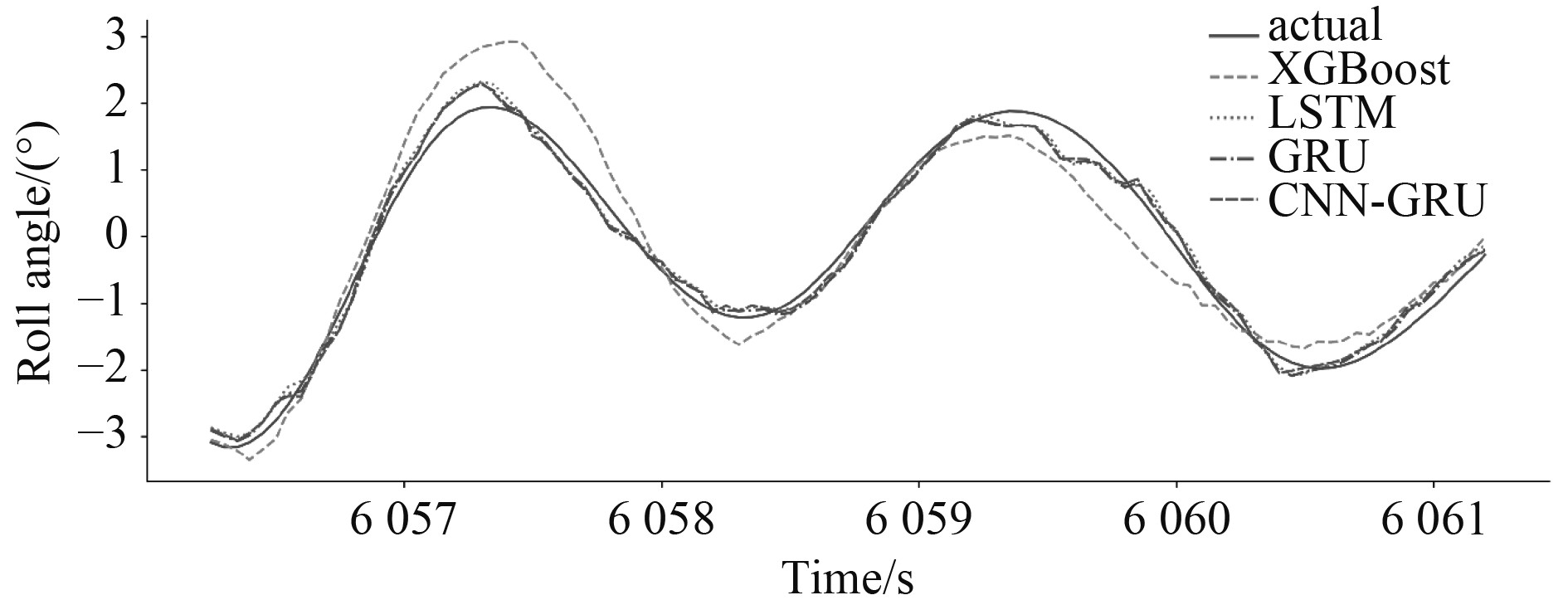
|
图 9 各模型预测结果(提前10步,10:00) Fig. 9 Prediction results of each model (10 steps in advance, 10:00 ) |
各模型在预测提前量分别为10步、20步、30步情况下的预测误差结果对比如表2所示。
|
|
表 2 不同预测步长下各模型预测误差(提前10步,10:00) Tab.2 Prediction errors of various models under different prediction steps (10 steps in advance, 10:00 ) |
可知,随着提前预测步长的增加,各模型预测精度均出现下降,这是由于RNN模型的结构并不能完全解决长期依赖的问题。而在各预测时间步长下,各项指标均是CNN-GRU模型表现更佳,说明CNN模块通过提取数据局部特征提升了GRU模型的预测性能。
为测试本文CNN-GRU模型的泛化能力,另选取了当天14:00~16:30的
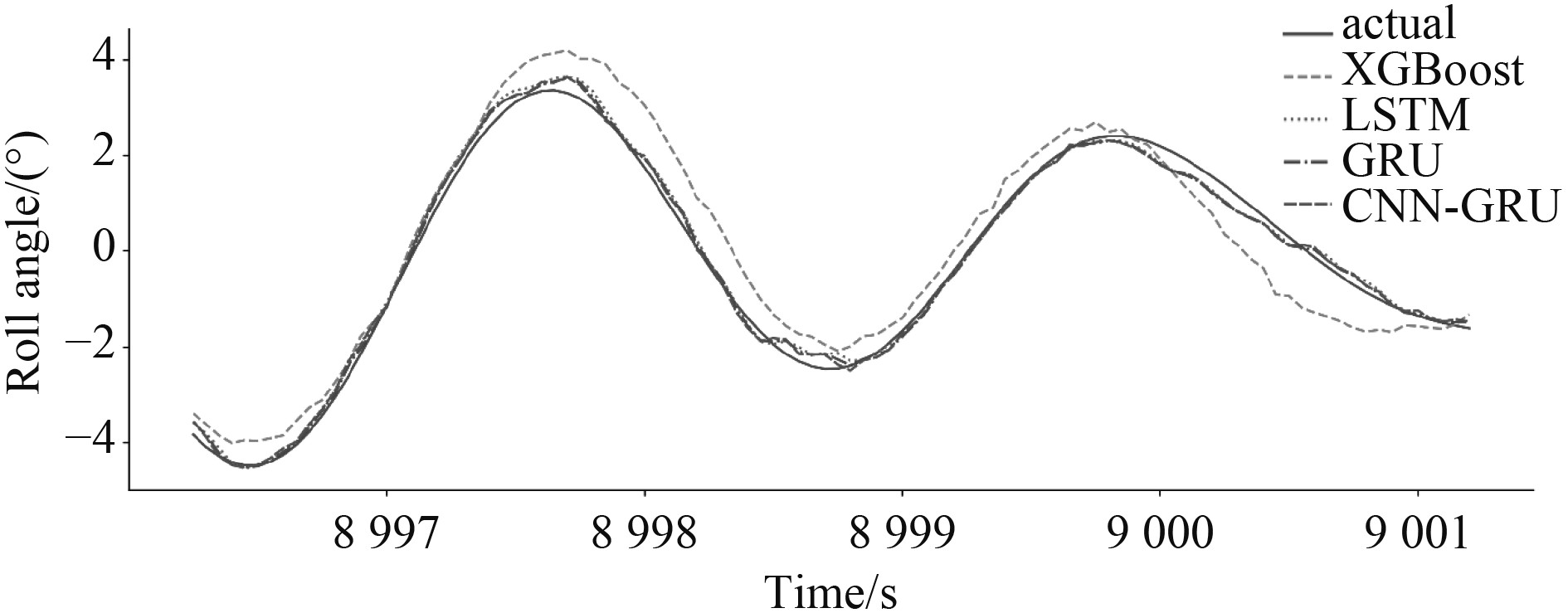
对数据最后100个采样点,各模型的横摇角预测结果如图10所示。预测误差结果对比如表3所示。
|
图 10 各模型预测结果(提前10步,14:00) Fig. 10 Prediction results of each model (10 steps in advance, 14:00) |
|
|
表 3 各模型预测误差(提前10步,14:00) Tab.3 Prediction error of each model (10 steps in advance, 14:00 ) |
通过对以上实验结果进行分析可以得出结论:本文模型对于同一天不同时段相似海况下USV的运动姿态预测有良好的泛化能力,且预测性能优于对比模型。
4 结 语本文为解决USV智能布放回收中难以瞄准的问题,提出一种USV运动姿态预测算法作为瞄准时的辅助算法。以运动姿态时序数据作为输入,构造了一种CNN-GRU多步预测网络模型。该模型通过CNN模块提取时序数据的局部特征,有效提高了GRU模型预测的精度。通过分析实验结果可以证明:在提前预测步长分别为10步、20步、30步的情况下,与XGBoost、LSTM、GRU等3种对照模型相比,CNN-GRU模型的预测结果与实际数据拟合程度最高,各评价指标下的预测误差最低,能做到对USV运动姿态的有效预测。后续研究工作可以着眼于提高进一步延长提前预测步长时模型的预测性能,以及研究构建更加轻量化的预测模型以保证预测的实时性。
| [1] |
张晓东, 刘世亮, 刘宇, 等. 无人水面艇收放技术发展趋势探讨[J]. 中国舰船研究, 2018(6): 50−57. ZHANG Xiaodong, LIU Shiliang, LIU Yu, et al. Review on development tendency of launch and recovery technology for USV[J]. Chinese Journal of Ship Research, 2018(6): 50−57. |
| [2] |
KAPLAN P. A study of prediction techniques for aircraft carrier motions at sea[J]. Journal of Hydronautics. 1969, 3(3): 121−131.
|
| [3] |
TRIANTAFYLLOU M, ATHANS M. Real time estimation of the heaving and pitching motions of a ship using a Kalman filter[C]// IEEE, Boston MA, 1981, 1090−1095.
|
| [4] |
TRIANTAFYLLOU M, BODSON M. Real time prediction of marine vessel motion using Kalman filtering techniques[C]// IEEE, Houston, Texas, 1982,159−165.
|
| [5] |
刘煜城. 基于深度学习的船舶运动极短期预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [6] |
詹可, 朱仁传. 一种CNN-LSTM船舶运动极值预报模型[J/OL]. 上海交通大学学报: 1−9[2023−07−17].
|
| [7] |
谷达京, 施哲源, 陈根良, 等. 基于神经网络的船体运动位姿预测方法[J]. 舰船科学技术, 2022(15): 55-59. GU Dajing, SHI Zheyuan, CHEN Genliang, et al. Deep learning for predicting ship motion from images, pitches and rolls[J]. Ship Science and Technology, 2022(15): 55-59. DOI:10.3404/j.issn.1672-7649.2022.15.012 |
| [8] |
严春满, 王铖. 卷积神经网络模型发展及应用[J]. 计算机科学与探索, 2021(1): 27-46. DOI:10.3778/j.issn.1673-9418.2008016 |
| [9] |
杨丽, 吴雨茜, 王俊丽, 等. 循环神经网络研究综述[J]. 计算机应用, 2018, (S2): 1−6.
|
| [10] |
HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [11] |
CHO K, VAN MERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN Encoder-Decoder for statistical machine translation[J]. arXiv Preprint, 2014, 2014(1406): 1078. |
| [12] |
CHUNG J, GULCEHRE C, CHO K, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J]. arXiv Preprint, 2014, 2014(1412): 3555. |
| [13] |
姚程文, 杨苹, 刘泽健. 基于CNN-GRU混合神经网络的负荷预测方法[J]. 电网技术. 2020, (9): 3416−3424.
|
| [14] |
CHEN T, GUESTRIN C. XGBoost: a scalable tree boosting system[C]// ACM SIGKDD International Conference on Knowledge & Data Mining, New York, 2016.
|
 2024, Vol. 46
2024, Vol. 46
