2. 张家港江苏科技大学产业技术研究院,江苏 张家港 215600;
3. 中科探海(苏州)海洋科技有限责任公司,江苏 张家港 215600
2. T-SEA Marine Technology Co., Ltd., Zhangjiagang 215600, China;
3. Zhangjiagang Industrial Technology Research Institute, Jiangsu University of Science and Technology, Zhangjiagang 215600, China
近年来,随着海洋资源的不断开发和利用,自主水下机器人(Autonomous Underwater Vehicle,AUV)因其巡航速度快、机动灵活等优势被广泛应用[1]。但如何解决复杂海洋环境下AUV的三维轨迹跟踪一直是水下机器人领域的研究难点。为此,叶辉等[2]通过设计基于干扰观测器的非线性运动控制器,解决了海流扰动及模型参数不确定性条件下的AUV跟踪控制,但是该控制器主要适用于对若干路径点的跟踪而非整条期望路径;Yuan等[3]提出基于滑模观测器的AUV控制方案,针对海洋中发生的时变和未知扰动,利用滑模观测器对控制力矩进行补偿,以抵抗水动力系数的扰动,仿真结果验证了所提控制器的有效性,然而滑模控制中不可避免的抖振问题还存在;杜佳璐等[4]构造了新超螺旋扩张状态器,通过在有限时间内对由不确定动态和海流扰动引起的AUV总干扰估计,实现了滑模控制中抖振问题的消弱,但仍未得到完全消除;Shojaei等[5]采用神经网络和自适应技术补偿海浪和洋流引起的时变扰动,并利用李雅普诺夫定理证明了系统的稳定性;2017年,Shojae等[6]又利用输入-输出反馈线性化方法设计了AUV的轨迹跟踪控制器,并基于双曲正切函数降低了AUV跟踪误差,但控制器参数需要人为调节,且参数固定的控制律很难适应复杂水下环境中AUV的轨迹跟踪;Liu等[7]设计了基于虚拟闭环系统的控制器,以缓解初始跟踪误差引起的抖振现象,但跟踪过程中的扰动等并未完全考虑;Campos等[8]设计了基于变参数的非线性控制器来代替参数固定的传统饱和函数,将传统的一阶二级分解算法与变换参数相结合,用于控制器的输出信号,然而该控制器主要适用于定点调节,是否适用复杂海洋环境需要进一步验证;Yao等[9]在MPC(Model Predictive Control)算法基础上构造了AUV轨迹跟踪控制器,并引入误差变化系数来调整权重矩阵,以减少轨迹跟踪误差,但所设计控制器主要适用于二维轨迹跟踪;陈巍等[10]提出基于非线性干扰观测器的自适应反演控制,并利用李雅普诺夫原理证明了控制系统的稳定性,但控制实验同样是基于二维轨迹跟踪。复杂海洋环境中AUV的三维轨迹跟踪已经引起国内外重点关注且近年来成果不断涌现,但也存在或未能充分考虑AUV作业中的海流、海浪等外界扰动,或基于参数固定的控制器不能实现扰动中的自适应轨迹跟踪;或未考虑海洋环境中AUV作业实际工况,仅开展了二维平面的轨迹跟踪研究等不足。为此,在建立AUV运动学模型基础上,设计了AUV轨迹跟踪控制器,并借鉴生物免疫系统的信息处理机制进一步构建了基于递归免疫网络在线辨识的AUV自整定控制器,最后针对有海流、海浪、水下噪声等扰动的4种三维路径进行了轨迹跟踪测试和对比,并验证了文中方法的有效性和优越性。
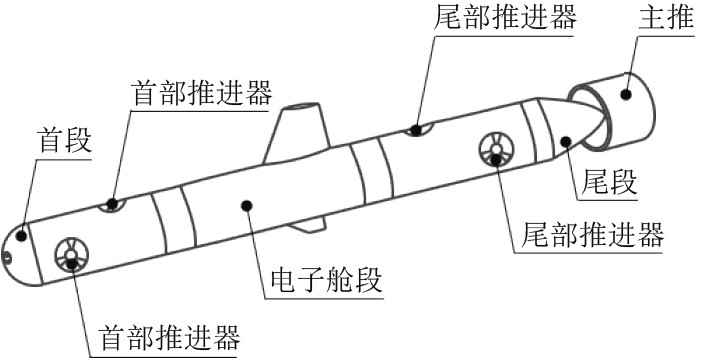
1 AUV运动学模型的建立文中三维轨迹跟踪控制的自主水下机器人结构如图1所示,主要由首段、电子舱段和尾段等部分组成。机器人的侧方和上方各安装2个旋向相反的电机,其中2个侧方推进器主要实现水下机器人在水平面方向的转动,而上方2个推进器则主要实现深度方向的控制。
|
图 1 水下机器人结构图 Fig. 1 Structure diagram of AUV |
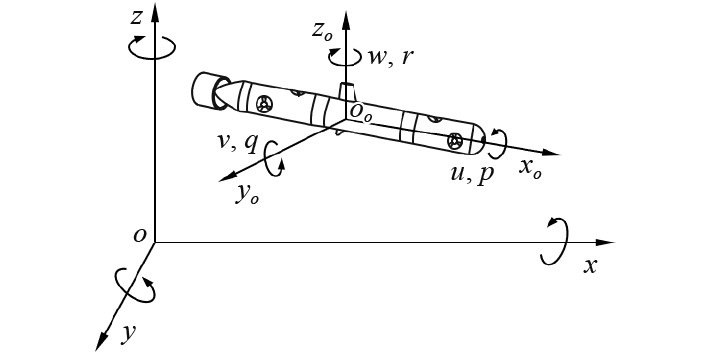
为了更好描述机器人的水下位置和速度等运动信息,建立如图2所示的大地坐标系(o-xyz)和运动坐标系(oo-xoyozo)。
|
图 2 AUV运动坐标系与大地坐标系 Fig. 2 AUV motion coordinate system and geodetic coordinate system |
图中u、v、w和p、q、r分别为各自由度上的线速度和角速度。为了便于设计控制器,在建立AUV运动学模型时作如下假设[11]:1) AUV整体结构关于主对称轴对称;2) AUV的横摇、俯仰及升沉运动对水平面影响完全忽略;3) AUV完全浸没水中,且为全粘湿状态。建立运动学方程:
| $ \left\{ \begin{gathered} \dot x = u\cos \psi \cos \theta - v\sin \psi + w\sin \theta \sin \psi,\\ \dot y = u\sin \psi \cos \theta + v\cos \psi + w\sin \theta \sin \psi ,\\ \dot z = - u\sin \theta + w\cos \theta,\\ \dot \theta = q,\\ \dot \psi = r/\cos \theta 。\\ \end{gathered} \right. $ | (1) |
式中:θ和ψ分别为水下机器人的俯仰角和首向角。
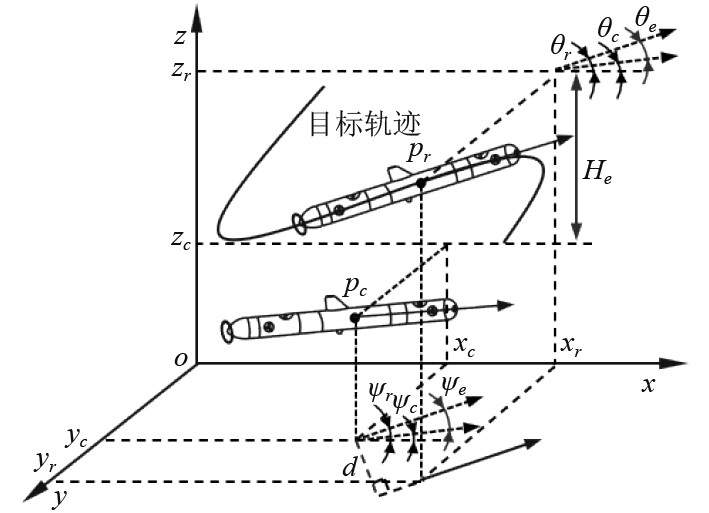
2 AUV轨迹跟踪控制器设计图3为自主水下机器人的位姿误差,图中pc(xc, yc, zc, ψc, θc)和pr(xr, yr, zr, ψr, θr)分别为机器人的当前和期望坐标和姿态。由于AUV横滚角较小且为了简化控制器的设计,将横滚角忽略不计[12]。AUV的轨迹跟踪目的是使机器人能够快速地跟踪上目标轨迹,而AUV为典型的非完整约束系统,且海流等外界扰动进一步增加了轨迹跟踪的控制难度,为此文中首先引入了具有鲁棒性强和可靠性高的PID控制器[13];其次考虑到机器人的有效跟踪是实现深度偏差He、首向角偏差ψe和俯仰角偏差θe的校正,因此进一步将三者作为控制变量。
|
图 3 水下机器人位姿误差示意图 Fig. 3 Pose errors of AUV |
PID控制器采用增量式,即:
| $ \begin{split}u\left(k\right)= & u\left(k-1\right)+\Delta u_H\left(k\right)+\Delta u_{\psi}\left(k\right)+\Delta u_{\theta}\left(k\right) = \\ & u\left(k - 1\right) + K_{p\_{ }H}\left(H_e\left(k\right) - H_e\left(k - 1\right)\right) + K_{i\_{ }H}H_e\left(k\right) + \\ & K_{d\_{ }H}\left(H_e\left(k\right)-2H_e\left(k-1\right)+H_e\left(k-2\right)\right)+ \\ & K_{p\_{ }\psi}\left(\psi_e\left(k\right)-\psi_e\left(k-1\right)\right)+K_{i\_{ }\psi}\psi_e\left(k\right)+ \\ & K_{d\_{ }\psi}\left(\psi_e\left(k\right)-2\psi_e\left(k-1\right)+\psi_e\left(k-2\right)\right)+ \\ & K_{p\_{ }\theta}\left(\theta_e\left(k\right)-\theta_e\left(k-1\right)\right)+K_{i\_{ }\theta}\theta_e\left(k\right)+ \\ & K_{d\_{ }\theta}\left(\theta_e\left(k\right)-2\theta_e\left(k-1\right)+\theta_e\left(k-2\right)\right)。\end{split} $ | (2) |
式中:u(k)和u(k−1)分别为k和k−1时刻的控制量;ΔuH(k)、Δuψ(k)和Δuθ(k)分别为k时刻机器人深度、首向角和俯仰角控制增量;Kp_H、Ki_H和Kd_H分别为深度控制器的比例、积分和微分系数;Kp_ψ、Ki_ψ和Kd_ψ 分别为首向角控制器的比例、积分和微分系数;Kp_θ、Ki_θ和Kd_θ分别为俯仰角控制器的比例、积分和微分系数;He(k)、He(k−1)和He(k−2)分别为k、k−1和k−2时刻的机器人深度偏差;ψe(k)、ψe(k−1)和ψe(k−2)分别为k、k−1和k−2时刻的机器人首向角偏差;θe(k)、θe(k−1)和θe(k−2)分别为k、k−1和k−2时刻的机器人俯仰角偏差。
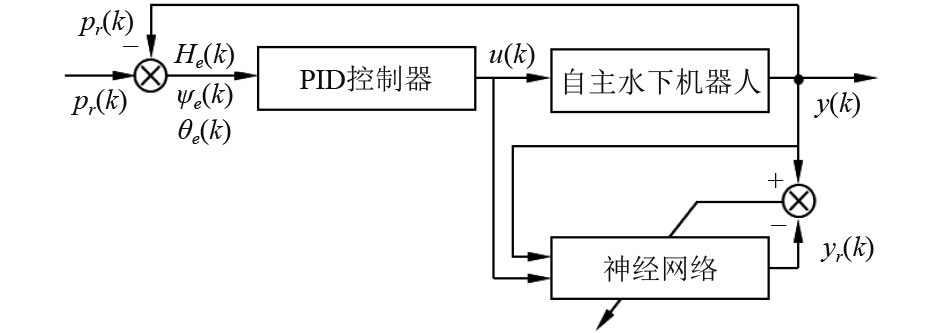
由于基本PID控制器参数固定,而水下机器人经常需要改变方向或克服海流等干扰影响,因此文中引入具有非线性映射和自学习等特点的神经网络来对被控AUV建立辨识模型,通过求取Jacobian灵敏度信息实现PID控制器的在线自整定,进而提高AUV的轨迹跟踪效果。基于神经网络在线辨识的AUV自整定PID控制器结构如图4所示。图中,y(k)为控制系统实际输出,yr(k)为神经网络辨识输出。
|
图 4 基于神经网络辨识的PID自整定控制器 Fig. 4 PID self-tuning controller based on neural network identification |
PID自整定控制器中,用于构建辨识模型的神经网络是关键。与前馈神经网络相比,递归神经网络更重视网络反馈,将其作为AUV轨迹跟踪控制的辨识网络,能够充分发挥其对非线性动态行为捕捉的性能[14]。此外,生物免疫系统的自组织、免疫记忆等优秀信息处理机制在工程问题解决中得到了广泛借鉴和应用,为此文中将其引入并提出了递归免疫网络。该网络主要包括输入层、隐层和输出层,而隐层由突触隐层和细胞隐层组成,细胞隐层将输出信息反馈到突触隐层实现辨识网络免疫层之间的信息调节,进而提高水下机器人在线轨迹跟踪能力。
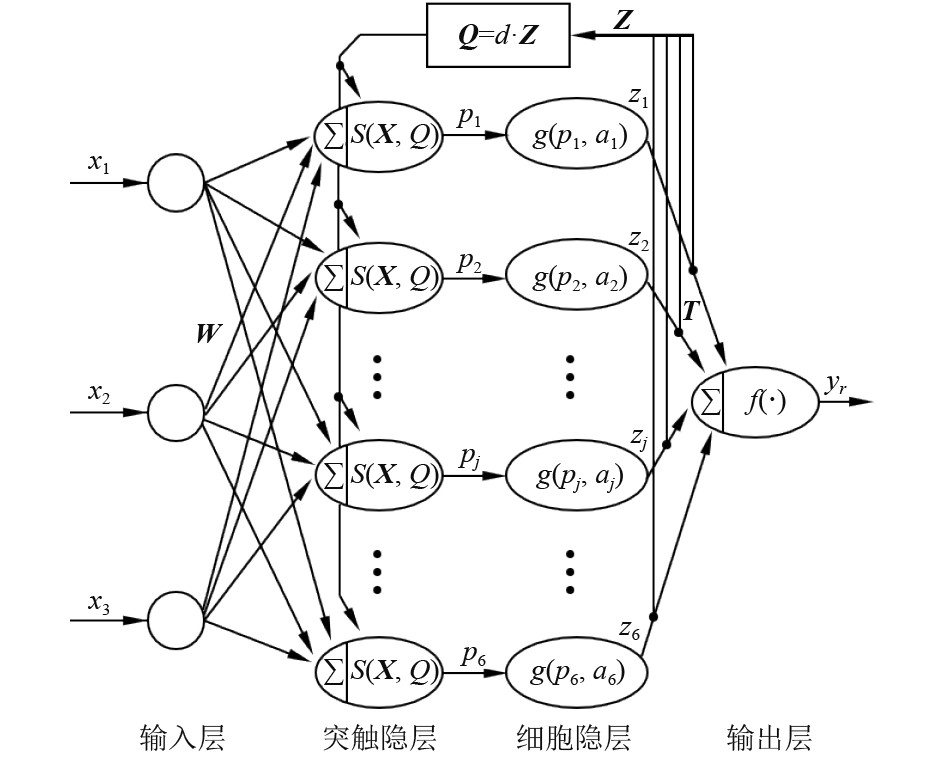
由式(2)可知,AUV的轨迹跟踪控制率主要取决于机器人的深度和姿态,由图3可知,机器人当前位姿距期望位姿在水平面上的侧向距离d反映了机器人航向和姿态的调整大小,对目标轨迹跟踪起到了预判作用,直接影响机器人的跟踪效率。为此,将侧向距离d作为疫苗进行提取并联合细胞隐层输出实现突触隐层接种。递归免疫网络拓扑结构如图5所示。
|
图 5 递归免疫网络拓扑模型 Fig. 5 Topological model of recursive immune network |
网络的输入层涉及到控制偏差量、控制输出,共3个节点,且X(k)=[x1(k), x2(k), x3(k)]T=[ΔuH(k)+ Δuψ(k)+ Δuθ(k), y(k), y(k-1) ]T。鉴于网络复杂度以及AUV在线实时规划要求,网络突触隐层和细胞隐层的节点数经数值测试后选为6,输出层节点数为1。图中,W为输入层与突触隐层的权值;T=[t1, t2, …, t6]T为细胞隐层与输出层之间的权值;S(·)、g(·)和f(·)分别为突触隐层、细胞隐层和输出层的激励函数;aj (j=1, 2, ···, 6)为网络的参变矢量;Z=[z1, z2, …, z6]T为细胞隐层输出,yr为网络输出。
3.2 递归免疫网络整定PID由所构建的递归免疫网络拓扑模型可知,突触隐层主要是将输入信号进行映射,增强网络对轨迹跟踪问题的处理能力。突触隐层的第j个节点输出值为:
| $ {S_j}(k) = {p_j}(k) = \sum\limits_{i = 1}^3 {{x_i}{w_{ij}}} + md{z_j} \text{,}j=1,2,…,6。$ | (3) |
式中:wij∈W;m为可调系数。
细胞隐层内部采用高斯函数形式,将带有疫苗d的内激活信号进行非线性变换。细胞隐层的第j个节点输出为:
| $ {g_j}(k) = {z_j}(k) = {a_j} \cdot \exp [ - \frac{{\left\| {{p_j} - {c_j}} \right\|}}{{2\sigma _j^2}}] \text{,}j=1,2,…,6。$ | (4) |
式中:cj和σj分别为细胞隐层第j个节点的中心和宽度;aj为可调节参数。
输出层得到最终辨识输出,即
| $ {y_r}(k) = {z_1}(k){t_1} + {z_2}(k){t_2} + \cdots + {z_6}(k){t_6} = \sum\limits_{j = 1}^6 {{z_j}(k){t_j}} 。$ | (5) |
建立递归免疫网络辨识器的性能指标函数:
| $ E(k)=\frac{1}{2}(y(k)-y_r(k))^2 。$ | (6) |
按照梯度下降法对网络权值tj和wij、基函数中心cj、基宽变量σj进行修正。为了提高网络学习速度并增加算法可靠性,修正过程中增加学习率λ和动量因子α,参数修正结果如下:
| $ \Delta {w_{ij}}(k) = - \frac{{\partial E(k)}}{{\partial {w_{ij}}}} = {a_j}(y(k) - {y_r}(k)){z_j},$ | (7) |
| $ {w_{ij}}(k) = {w_{ij}}(k - 1) + \eta \Delta {w_{ij}}(k) + \alpha ({w_{ij}}(k - 1) - {w_{ij}}(k - 2)),$ | (8) |
| $ \Delta {t_j}(k) = - \frac{{\partial E(k)}}{{\partial {t_j}}} = {a_j}(y(k) - {y_r}(k)){z_j},$ | (9) |
| $ {t_j}(k) = {t_j}(k - 1) + \eta \Delta {t_j}(k) + \alpha ({t_j}(k - 1) - {t_j}(k - 2))。$ | (10) |
同理:
| $ \Delta {\sigma _j}(k) = (y(k) - {y_r}(k)){t_j}{z_j}\frac{{{{\left\| {{p_j} - {c_j}} \right\|}^2}}}{{\sigma _j^3}} \cdot {a_j} ,$ | (11) |
| $ {\sigma _j}(k) = {\sigma _j}(k - 1) + \eta \Delta {\sigma _j}(k) + \alpha ({\sigma _j}(k - 1) - {\sigma _j}(k - 2)),$ | (12) |
| $ \Delta {c_j}(k) = (y(k) - {y_r}(k)){t_j}{z_j}\frac{{{p_j} - {c_j}}}{{b{j^2}}} \cdot {a_j},$ | (13) |
| $ {c_j}(k) = c{}_j(k - 1) + \eta \Delta {c_j}(k) + \alpha ({c_j}(k - 1) - {c_j}(k - 2)),$ | (14) |
| $ \Delta {a_i}(k) = (y(k) - {y_r}(k)){t_j},$ | (15) |
| $ {a_j}(k) = {a_j}(k - 1) + \eta \Delta {a_j}(k) + \alpha ({a_j}(k - 1) - {a_j}(k - 2))。$ | (16) |
Jacobian阵算法为:
| $ \frac{\partial y(k)}{\partial\Delta u(k)}\approx\frac{\partial y_r(k)}{\partial\Delta u(k)}=\sum\limits_{j=1}^6t_jz_j\frac{c_j-\Delta u(k)}{\sigma_j^2}。$ | (17) |
以求取深度控制器的PID参数为例,按照梯度下降法来调整Kp_H、Ki_H、Kd_H值:
| $\begin{aligned}[b] \Delta {K _{p\_H}}( k ) = {\lambda _{kp\_H}}{a_j}{H_e}( k )\frac{{\partial y( k )}}{{\partial \Delta u( k )}}({H_e}( k ) - {H_e}(k - 1))),\end{aligned}$ | (18) |
| $\begin{aligned} \Delta {K_{i\_H}}(k) = {\lambda _{ki\_H}}{a _j}{H_e}(k)\frac{{\partial y(k)}}{{\partial \Delta u( k )}}( {H_e}( k ) - {H_e}( k - 1 ) ) ),\end{aligned} $ | (19) |
| $\begin{split} \Delta {K_{d\_H}}(k) =& {\lambda _{kd\_H}}{a_j}{H_e}(k)\frac{{\partial y(k)}}{{\partial \Delta u(k)}}\times\\ &({H_e}(k) - 2{H_e}(k - 1) + {H_e}(k - 2))。\end{split}$ | (20) |
式中:λkp_H、λkp_H和λkp_H分别为Kp_H、Ki_H、Kd_H的学习率。Kp_H、Ki_H、Kd_H参数的最终在线调整表达式如下式:
| $ {K_{p\_H}}(k) = {K_{p\_H}}(k - 1) + \Delta {K_{p\_H}}(k),$ | (21) |
| $ {K_{i\_H}}(k) = {K_{i\_H}}(k - 1) + \Delta {K_{i\_H}}(k),$ | (22) |
| $ {K_{d\_H}}(k) = {K_{d\_H}}(k - 1) + \Delta {K_{d\_H}}(k) 。$ | (23) |
首向角控制器的Kp_ψ、Ki_ψ、Kd_ψ系数,以及俯仰角的Kp_θ、Ki_θ、Kd_θ系数在线调整同上。
3.3 递归免疫网络辨识PID的控制流程步骤1 参数初始化:输入层-突触隐层权值矩阵W、细胞隐层-输出隐层间权值矩阵T、学习率λ、动量因子α、参变矢量aj、初始PID参数等;
步骤2 根据水下机器人的运动信息,将侧向距离d提取为疫苗;
步骤3 根据式(17)计算水下机器人深度、首向角和俯仰角偏差的灵敏度信息;
步骤4 根据式(21)~式(23)计算水下机器人深度、首向角和俯仰角偏差控制的PID在线调整参数;
步骤5 根据式(2)计算水下机器人深度、首向角和俯仰角的控制量;
步骤6 水下机器人根据计算的控制量移动并判断是否到达目标点?
步骤7 若是则退出轨迹跟踪,否则转步骤2。
4 仿真及分析 4.1 跟踪路径设置为了验证PID-RINN方法在自主水下机器人三维轨迹跟踪中的有效性和优越性,在CPU2.50 GHZ、内存为8 GB的计算机上针对直线、三角形、正弦函数和螺旋线4种路径进行测试,并将测试结果与PID控制方法[15]、基于遗传优化的PID控制方法[16](PID Controller Optimized by Genetic Algorithm,PID_GA)和RBF网络辨识PID控制方法[17](PID Controller Identified by Radial Basis Function Network,PID_RBFN)进行了比较。为了使得仿真系统更接近实际系统,在仿真过程中增加了如式(24)所示的海流干扰。此外在整个跟踪历程中平均增加了4次幅值为0.5的暗流、海浪等干扰。考虑到干扰的随机性,每种控制方法在每种路径中共测试了50次。
| $ {d_u} = - 0.4 + 0.4\sin (1.2t + {\text π} /6) 。$ | (24) |
1)直线路径
| $ \left\{ \begin{gathered} x = 0.2t + 3 ,\\ y = 0.2t + 1 ,\\ z = 0.1t + 2 。\\ \end{gathered} \right.{\text{ }}t \in [0,600],$ | (25) |
水下机器人初始位姿为[0 0 0 45° 0°]。
2)三角形路径
| $ \left\{ \begin{gathered} z = x,{\text{ }}x \in [1,40),\\ z = - x + 80,{\text{ }}x \in [40,80]。\\ \end{gathered} \right. $ | (26) |
水下机器人初始位姿为[0 0 0 135° 0°]。
3)正弦路径
| $ \left\{ \begin{gathered} x = t ,\\ y = 100\sin (0.01t) ,\\ z = 0.05t。\\ \end{gathered} \right.{\text{ }}t \in [0,600] ,$ | (27) |
水下机器人初始位姿为[0 2 0 0° 0°]。
4)螺旋线路径
| $ \left\{ \begin{gathered} x = 100\sin (0.02t),\\ y = 100\cos (0.02t),\\ z = 0.1t。\\ \end{gathered} \right.{\text{ }}t \in [0,600],$ | (28) |
水下机器人初始位姿为[5 90 0 0° 0°]。
4.2 仿真结果及分析表1为4种路径的AUV跟踪比较结果。可知,基本 PID控制不仅受PID参数选取影响较大,且参数固定使得其很难适应不同路径的跟踪,因此跟踪性能是4种算法中最差的。经分布式优化的遗传PID由于提高了PID参数的选取效果,使得其跟踪效果优于基本PID,但由于仍然是参数固定型使得其总体跟踪效果不佳。基于RBF网络辨识的PID由于具有在线自适应调整功能,使得其能适应不同路径的跟踪,因此其跟踪效果明显优于前2种参数固定PID控制。基于递归免疫网络辨识的PID控制不仅实现了PID参数的实时调整,而且将机器人运动信息与跟踪结果通过疫苗接种实现了辨识网络层间信息传递时的反馈,相比起前3种轨迹跟踪方法,其平均和最大位置误差分别平均减少31.91%和25.81%,平均和最大首向角误差分别平均减少32.54%和25.27%,以及平均和最大俯仰角误差分别平均减少61.93%和61.26%,从而验证了所构建递归免疫网络及其对PID轨迹跟踪在线调整的有效性和优越性。
|
|
表 1 4种路径的跟踪对比结果 Tab.1 Comparisons of trajectory tracking results among four control strategies |
图6为4种方法针对4种三维轨迹路径的最优跟踪结果对比。可知,4种方法都能实现有效跟踪,但通过对有暗流等强扰动处的局部放大可知,2种参数固定的PID跟踪效果相对要弱于具有在线调整功能的2种网络辨识PID,尤其通过试凑法获得参数的基本PID跟踪效果最差,基于递归免疫网络整定PID由于具有对强扰动的抑制功能使得其跟踪效果最好,从而也进一步验证了其优异的三维轨迹跟踪性能。

|
图 6 4种方法的三维轨迹跟踪效果 Fig. 6 Three dimensional trajectory tracking effects of four methods |
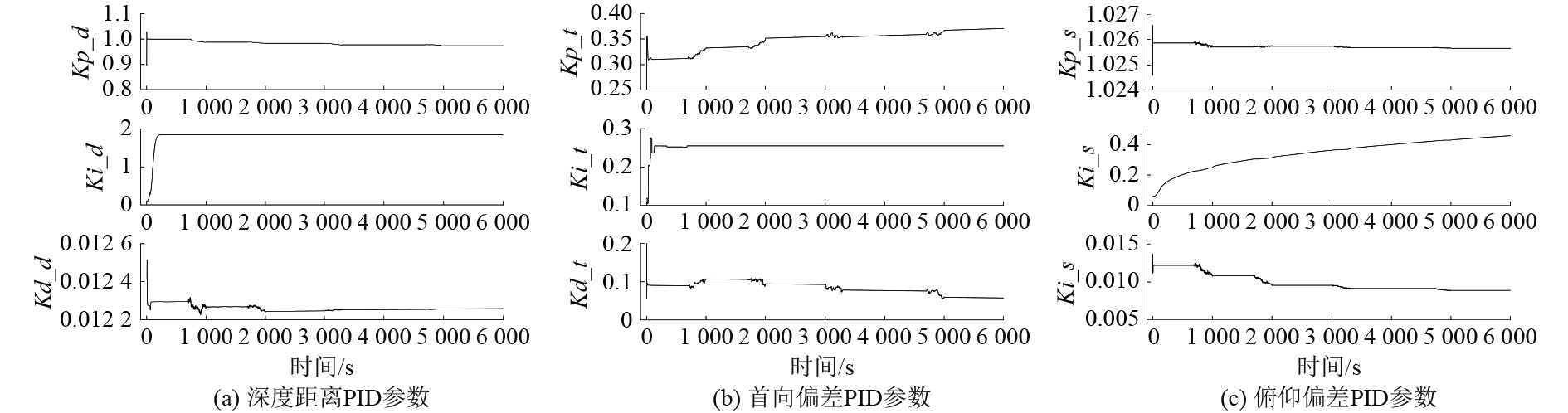
图7为AUV在螺旋轨迹最优跟踪过程中PID参数的自适应调整过程。可以看出,在起始位置,由于水下机器人离螺旋路径较远,因此深度距离、首向角和俯仰角偏差的PID参数变化较大,目的是使水下机器人能够快速跟上期望轨迹。当水下机器人跟踪上目标轨迹后,PID参数变化较小。为了抑制路径误差的累计,因此侧向距离和航向偏差的积分参数持续增加。由于在跟踪仿真过程中增加了4次暗流等干扰,因此比例和微分系数在相应位置有所调整。
|
图 7 螺旋轨迹跟踪中PID_RINN的PID参数 Fig. 7 PID parameters of PID_RINN during the spiral trajectory tracking |
图8为最优螺旋轨迹跟踪过程,4种方法的位置、首向角和俯仰角误差比。可以看出,相比起2种参数固定PID控制方法,2种网络辨识PID控制方法的3种误差都偏小,尤其在有强扰动干扰地方抑制更明显,从而验证了PID参数在线调整对外界干扰抑制以及快速精确跟踪的优越性。而文中PID_RINN方法将跟踪结果与侧向距离进行递归免疫网络的接种和反馈传递,进一步提高了跟踪精度使得其跟踪效果最优。

|
图 8 螺旋轨迹最优跟踪中误差比较 Fig. 8 Comparison of errors in optimal tracking of spiral trajectories |
1)在建立自主水下机器人的运动学模型,以及将其深度距离、首向角和俯仰角作为控制偏差的基础上,设计了基于神经网络辨识的水下机器人PID控制器,不仅提高了AUV三维轨迹跟踪时的鲁棒性,而且在线调整的PID参数有助于AUV实现不同路径的三维轨迹跟踪;
2) 借鉴递归神经网络的反馈机制,以及生物免疫系统的自组织和免疫记忆等优秀信息处理机制,设计了包括输入层、突触隐层、细胞隐层和输出层在内的递归免疫网络,并用于AUV轨迹跟踪控制过程中对其状态辨识,实现了机器人跟踪状态信息的实时反馈传递,提高了机器人的轨迹跟踪精度;
3)将机器人当前位姿距期望位姿在水平面上的侧向距离d提取为疫苗,并联合网络输出通过信息反馈接种到突触隐层,有助于水下机器人对目标路径的预判,进而提高AUV轨迹跟踪过程中位姿调整效率,对类似暗流等强干扰具有更好的抑制作用。
大量仿真实验表明,递归免疫网络的三维轨迹跟踪性能要优于参数固定PID和RBF网络辨识PID的跟踪性能。AUV可以根据跟踪路径的变化,尤其是跟踪过程中强扰动及时进行参数调整从而更好地抑制干扰和跟踪路径。
| [1] |
钟宏伟. 国外无人水下航行器装备与技术现状及展望[J]. 水下无人系统学报, 2017, 25(4): 215-225. |
| [2] |
叶辉, 王丽琦, 智鹏飞, 等. 基于干扰观测器的AUV三维路径自适应跟踪控制[J]. 江苏科技大学学报(自然科学版), 2019, 33(5): 52-59. |
| [3] |
YUAN C, SHUAI C, MA J, et al. An efficient control allocation algorithm for over-actuated AUVs trajectory tracking with fault-tolerant control[J]. Ocean Engineering, 2023, 273(5): 113-976. |
| [4] |
杜佳璐, 李健. 欠驱动水下机器人三维轨迹跟踪有限时间预设性能控制[J]. 控制理论与应用, 2022, 39(2): 383-392. |
| [5] |
SHOJAEI K, AREFI, MOHAMMAD M. On the neuro-adaptive feedback linearising control of underactuated autonomous underwater vehicles in three-dimensional space[J]. IET Control Theory and Applications, 2015, 9(8): 1264-1273. DOI:10.1049/iet-cta.2014.0472 |
| [6] |
SHOJAEI K, DOLATSHAHI M. Line-of-sight target tracking control of underactuated autonomous underwater vehicles[J]. Ocean Engineering, 2017, 133(15): 244-252. |
| [7] |
LIU X, ZHANG M J, CHEN Z Y. Trajectory tracking control based on a virtual closed-loop system for autonomous underwater vehicles[J]. International Journal of Control, 2020, 93(12): 2789-2803. DOI:10.1080/00207179.2019.1566637 |
| [8] |
CAMPOS E, MONROY J, ABUNDIS H, et al. A nonlinear controller based on saturation functions with variable parameters to stabilize an AUV[J]. International Journal of Naval Architecture and Ocean Engineering, 2019, 11(1): 211-224. DOI:10.1016/j.ijnaoe.2018.04.002 |
| [9] |
YAO F, YANG C, LIU X, et al. Experimental evaluation on depth control using improved model predictive control for autonomous underwater vehicle (AUVs)[J]. Sensors, 2018, 18(7): 20-22. |
| [10] |
陈巍, 魏延辉, 曾建辉, 等. 基于干扰观测器的欠驱动AUV自适应反演控制[J]. 中南大学学报(自然科学版), 2017, 48(1): 69-76. |
| [11] |
丁文俊, 张国宗, 刘海旻, 等. 面向海流扰动和通信时延的欠驱动AUV编队跟踪控制[J]. 兵工学报, 2023, 8(28): 1-13. DOI:10.12382/bgxb.2023.0417 |
| [12] |
周则兴. 基于DRNN-S控制的AUV三维轨迹跟踪方法[J]. 舰船科学技术, 2021, 43(21): 96-99. ZHOU Zexing. 3D trajectory tracking based on DRNN-S control for autonomous underwater vehicles[J]. Ship Science and Technology, 2021, 43(21): 96-99. |
| [13] |
吴子明, 杨柯, 唐杨周, 等. 基于反步滑模控制的欠驱动AUV定深运动研究[J]. 舰船科学技术, 2023, 45(1): 114-119. WU Ziming, YANG Ke, TANG Yangzhou, et al. Research on underactuated AUV depth motion based on backstepping sliding mode control[J]. Ship Science and Technology, 2023, 45(1): 114-119. |
| [14] |
YANG C, YAO F, ZHANG M J. Adaptive backstepping terminal sliding mode control method based on recurrent neural networks for autonomous underwater vehicle[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 31-36. DOI:10.1186/s10033-018-0237-2 |
| [15] |
王明阳. 基于模型预测的水下机器人养殖网箱巡检轨迹跟踪研究[D]. 大连: 大连海洋大学, 2022.
|
| [16] |
王通, 齐向东. 遗传算法PID控制在AUV姿态调节中的应用[J]. 自动化技术与应用, 2020, 39(4): 8-14. |
| [17] |
MUSTAFA W, NIZAR A. An adaptive neural network with nonlinear FOPID design of underwater robotic vehicle in the presence of disturbances, uncertainty and obstacles[J]. Ocean Engineering, 2023, 279(15): 29-36. |
 2024, Vol. 46
2024, Vol. 46

