水下航行器作为重要的水下载体,在军用和民用领域有着广泛的应用[1]。随着其功能多样性以及应用广泛性,产生了各式各样的附体结构,直接影响到其自身的水动力性能和噪声性能。特别是低速航行状态下,航行器会产生更为明显的阻力[2]。因此,附体结构对于航行器的影响分析以及附体结构的减阻优化设计极为重要。
由于附体结构的多样性以及复杂性,理论计算方法已很难对其阻力进行预报,试验测试方法预报流体动力需耗费大量的时间和经费,不太适合方案阶段设计,数值计算方法能够快速预报航行器阻力并对其流场特性进行可视化分析,成为较多科研工作者重要的研究手段。Wang等[3]以自主水下航行器为研究对象,采用数值研究方法分析了单个附体和多个附体对AUV水动力性能影响,研究表明附体会改变流场结构、影响湍流发展,进而在其运动方向产生额外的阻力。在此基础上,为降低附体阻力,作者对固定形状的附体结构进行了最佳位置的布局设计。柏铁朝等[4]采用数值研究手段开展了潜艇附体结构影响研究,研究结果表明附体产生了阻力增额与伴流场的不均匀性。倪守隆等[5]对船舶声呐导流罩的阻力特性进行分析,通过数值计算方法分析了导流罩关键结构参数对阻力的影响,最终给出了导流罩参数设计的建议范围。Liu等[6]比较分析了带附体结构的潜艇流场特性,研究结果表明附体结构导致流动减缓,并在附体后缘形成涡流,研究指出合理的附体结构设计可显著改善潜艇附近流场。
附体是在不改变已有航行器线型的基础上,改善其周围流场最简便可行的方法之一[7],合理地设计附体结构可有效改善水下航行器的阻力特性。目前对于附体结构研究的文献并不多,对于附体结构的设计和流动分析还不够具体。本文以某水下航行器为基本构型,以加装附体结构的需求为出发点,开展了几种不同附体结构设计和流场计算,旨在为水下航行器附体结构设计优化以及流场特性研究提供有益参考。
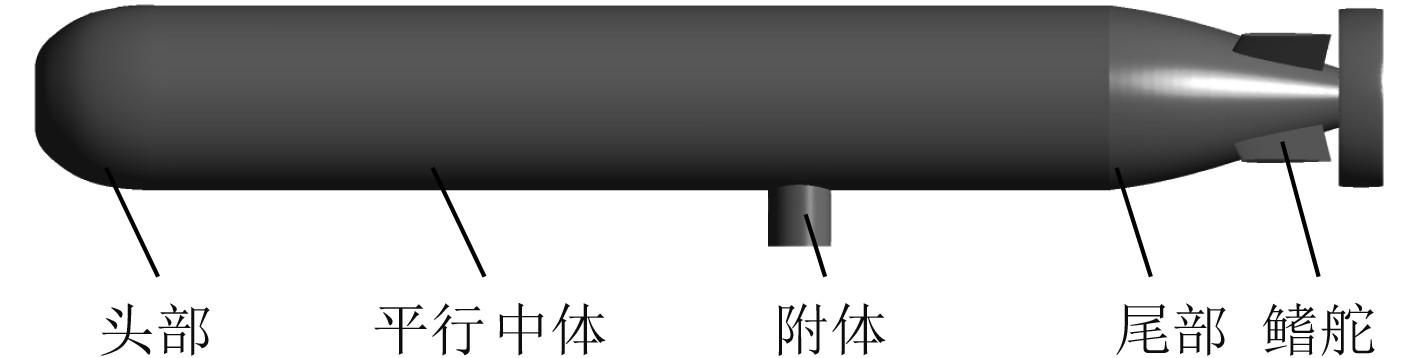
1 计算模型及网格条件 1.1 计算模型计算模型为某水下航行器,主要包括头段、平行中体和尾段。由于水声通信需要,需在航行器圆柱段外布置水声通信装置,基础模型为圆柱型,在此基础上设计了3种导流型附体结构。研究对象主体结构如图1所示。
|
图 1 计算模型示意图 Fig. 1 Schematic diagram of computational model |
计算采用水下航行器外流场计算常用圆柱形流域,流域尺寸和边界条件设置如下:
1)进口。进口面距离航行器头部端面为1L(L为航行器长度),设置为速度进口,速度为6 kn;圆柱体外径为10D(D为航行器直径),同样为速度进口边界条件。
2)出口。出口面距离航行器尾部端面为2L,设置为压力出口,根据航行深度设置环境压力值。
3)壁面。航行器表面为无滑移壁面条件。
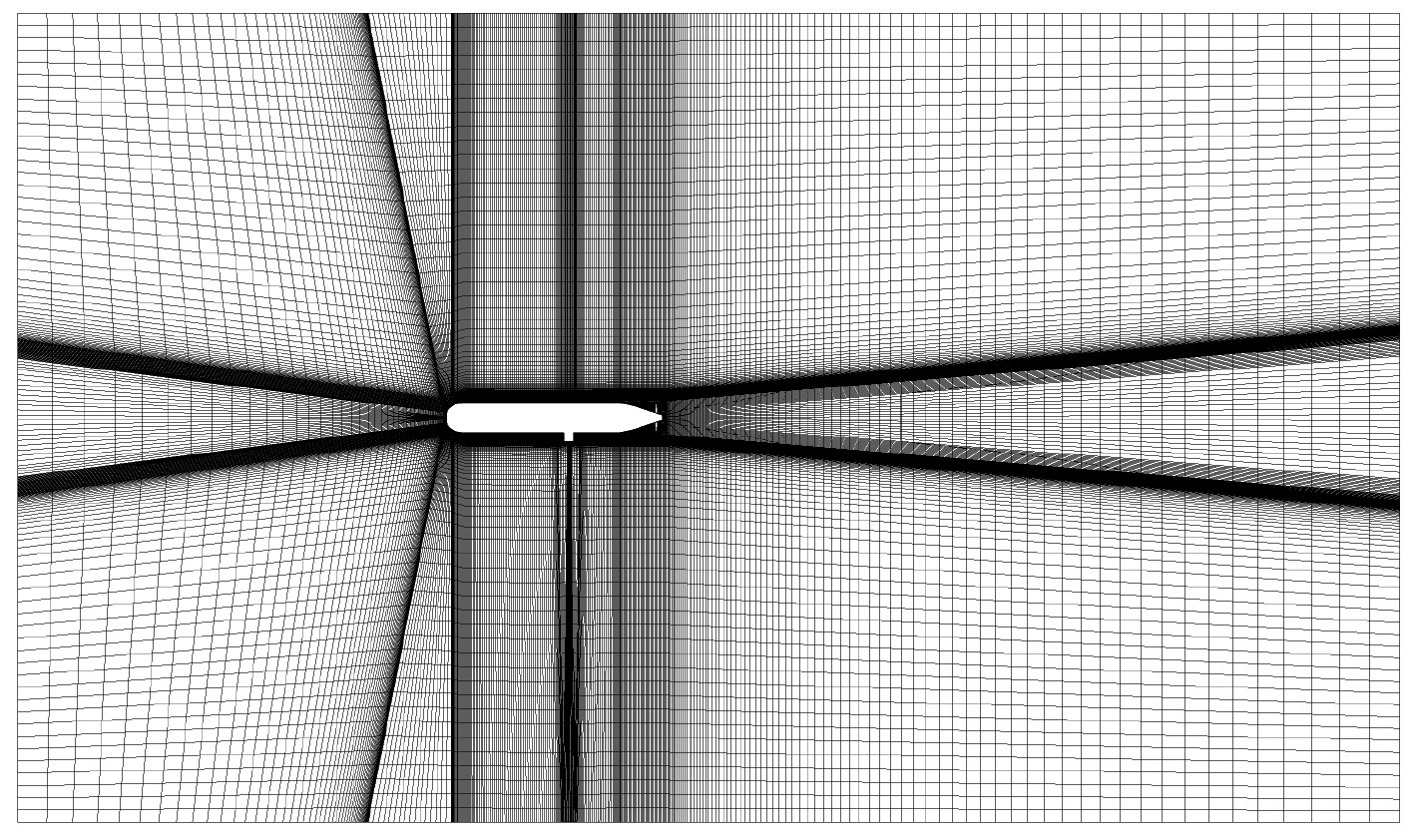
对计算流域进行网格离散,在航行器表面进行网格加密以及边界层处理,以精细化捕捉流场细节,最终选取的网格数量约为463万,网格示意如图2所示。
|
图 2 网格示意图 Fig. 2 Schematic diagram of grids |
数值计算基于有限体积方法,对雷诺时均Navier-Stokes(RANS)方程进行离散处理,求解过程涉及到的控制方程为连续性方程和RANS时均方程,其形式如下:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0,$ | (1) |
| $ \begin{aligned}[b] \rho \frac{{\partial {u_i}}}{{\partial t}} + & \rho \frac{{\partial {u_i}{u_j}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \\ & \frac{\partial }{{\partial {x_j}}}\left[ {\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}} - \frac{2}{3}{\delta _{ij}}\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right] + \frac{\partial }{{\partial {x_j}}}( - \overline {{{u'}_i}{{u'}_j}} )。\end{aligned} $ | (2) |
式中: 湍流模型,方程如下所示:
湍流模型,方程如下所示:
| $ \begin{aligned}[b] \frac{\partial }{{\partial t}}\left( {\rho k} \right) + &\nabla \cdot \left( {\rho \bar Uk} \right) = \\ & \nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\nabla k} \right] + {P_k} - \beta '\rho k\omega,\end{aligned} $ | (3) |
| $ \begin{aligned}[b] \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + &\nabla \cdot \left( {\rho \bar U\omega } \right) = \\ &\nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}} \right)\nabla \omega } \right] + \alpha \frac{\omega }{k}{P_k} - \beta \rho {\omega ^2},\end{aligned} $ | (4) |
式中,
| $ \begin{aligned}[b] {P_k} = &2{\mu _t}\left[ {{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial y}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial z}}} \right)}^2}} \right] + \\ &{\mu _t}{\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)^2} + {\mu _t}{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)^2} + \\ & {\mu _t}{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)^2} 。\end{aligned} $ | (5) |
式中,湍流粘度
| $ {\mu _t} = \rho \frac{k}{\omega }。$ | (6) |
各系数的推荐取值为
数值计算中压力速度耦合迭代采用SIMPLE算法,压力项采用二阶离散格式,动量项、湍动能项以及湍流耗散率项采用二阶迎风格式离散,以达到求解的稳定性和准确性。
2.2 数值计算准确性验证考虑到数值研究的准确性,本文以Suboff标准模型[10]为验证对象,对上述网格划分方式和数值计算方法进行计算验证,计算策略准确性验证结果如表1所示。可知,计算值与试验值吻合较好,且所受摩擦阻力与桑海公式计算值相近,计算精度均在5%以内,表明本文所采用的网格形式和数值方法计算精度较高,可用于水下航行器流体动力数值研究工作。
|
|
表 1 计算策略准确性验证结果 Tab.1 Verification results of calculation strategy |
水下航行器由于水声通信需要,需在航行器外布置圆柱型水声通信装置。对此,首先进行水下航行器带圆柱型附体结构的阻力计算,表2为航行器原型和圆柱型附体结构航行器计算结果,所用到的无因次表达式如下:
|
|
表 2 阻力系数计算结果 Tab.2 Calculation results of drag coefficientet |
| $ {C_x} = \frac{X}{{0.5\rho {v^2}s}} ,$ | (7) |
| $ \varepsilon = \frac{{X - {X_m}}}{X}。$ | (8) |
式中:
由表2可知,在低速航行状态下,水下航行器对水流的阻滞作用所形成的压差阻力并不明显,其所受阻力基本为粘性阻力,约占总阻力的72.6%。附体结构的存在会大幅增加其航行阻力,阻力系数增加值高达39.3%,其中主要是压差阻力成分,在航行器所提供动力和航速不变的情况下,其航程会大幅降低,进而会影响到航行器的总体性能指标,因而有必要在原始附体结构基础上,合理设计圆柱型附体导流方案,在提供水声通信装置安装空间的同时,降低附体结构航行阻力。
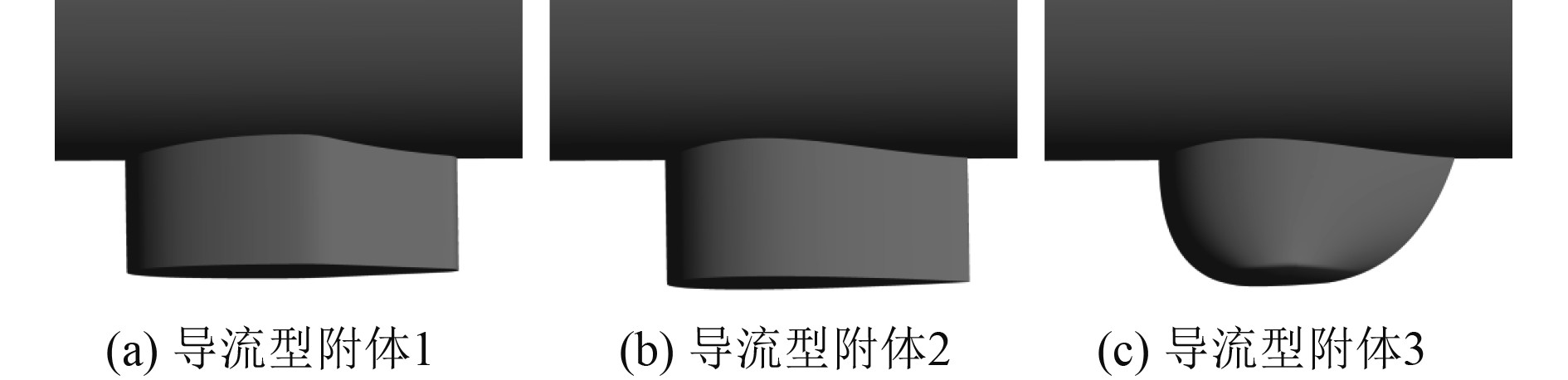
3.2 导流型附体结构的设计优化附体结构安装位置确定的基础上,附体结构的设计优化主要是自身流体外形设计,为尽可能降低附体对于航行器阻力的影响,附体结构的设计应满足以下要求:1)具有良好的流线型,曲线光滑过渡;2)尽可能避免流动分离,以降低流动前后的压差阻力;3)在满足安装要求基础上,可尽量减小附体表面沾湿面积。根据以上要求,本文给出了3种导流型附体结构,如下:
1)导流型附体1,附体前部分为曲线段,选用NACA0015翼型,后部分采用直线与曲线段衔接,形成的附体模型如图3(a)所示。
|
图 3 3种导流型附体结构示意图 Fig. 3 Schematic diagram of three kinds of diversion appendage structures |
2)导流型附体2,附体剖面采用整体翼型,在NACA0015翼型的基础上通过比例因子缩放,最终确定附体翼型型线,形成的附体模型如图3(b)所示。
3)导流型附体3,附体采用和模型2同样的翼型,并在垂直于流线方向采用曲线过渡,形成三元曲面附体模型,如图3(c)所示。
3.3 附体结构对航行器流场特征的影响4种带附体结构航行器阻力系数计算结果如表3所示。可以发现,带有附体结构的航行器,其航行阻力明显增大,这部分阻力增额主要是由附体结构引起,原因在于附体结构的存在很大程度影响流场细节分布,宏观上也使得带有附体结构的航行器阻力增加。计算结果表明,附体结构主要带来压差阻力的增加,不同附体结构所引起的阻力变化量不同,这也说明了附体结构优化设计的重要性。3种附体方案中,方案3减阻效果最为明显,相比无附体模型的航行器阻力仅增加11.9%,相比圆柱型附体模型减阻率为19.7%,表现出较好的减阻效果,因而有必要对其流场细节进行分析,以提供合理性解释。
|
|
表 3 阻力系数计算结果 Tab.3 Parameters of flexible intercepting net |
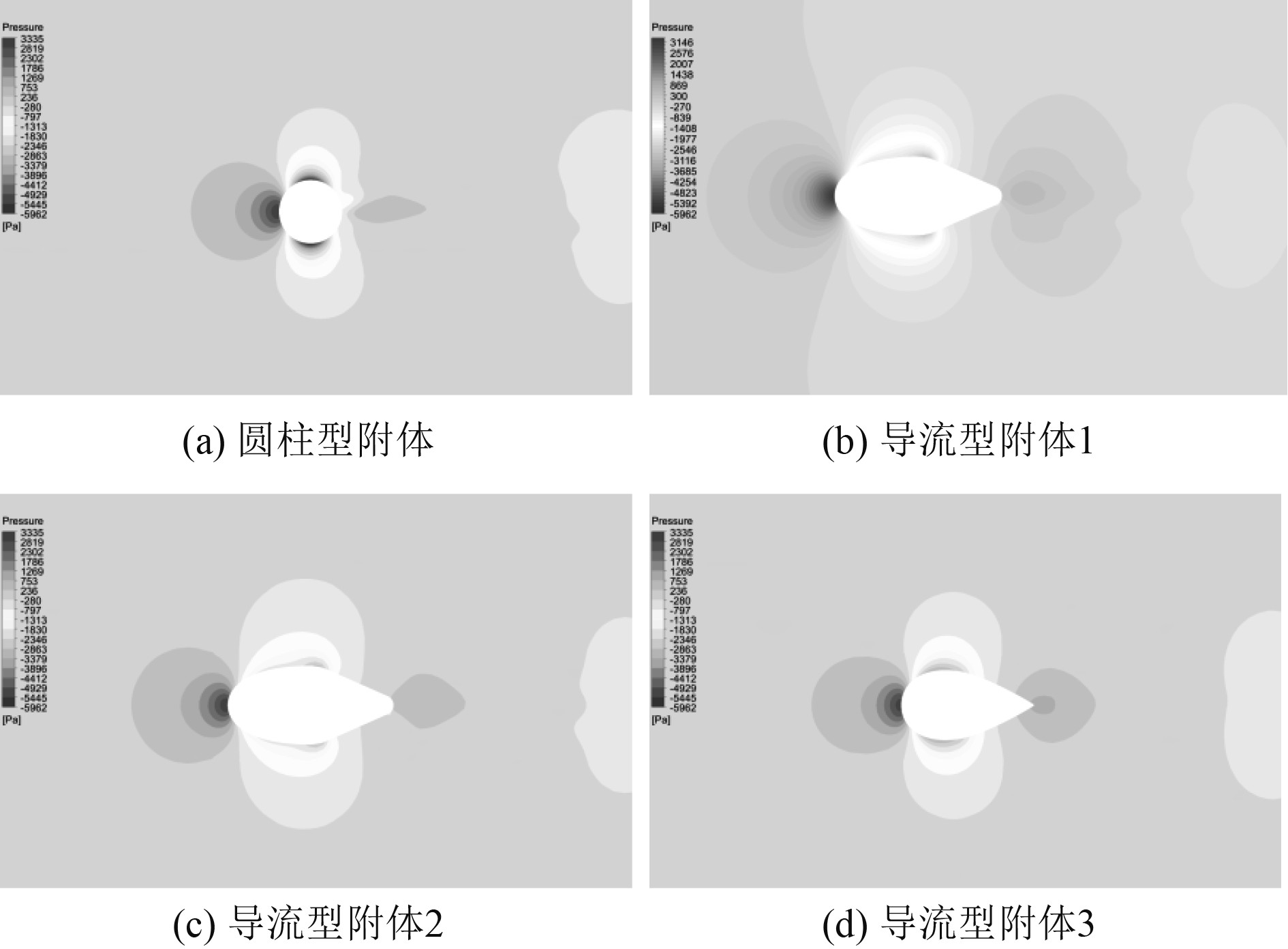
附体结构伴随航行器运动,对原有流场形成较大的扰动。图4为流向方向上附体结构中间截面的压力分布云图。可知,附体结构对水流的阻滞作用使其迎流面压力迅速增加,进而发生附面流动,速度逐渐增大,压力也随之减小。几种附体结构前缘压力分布相似,圆柱型附体结构在最大迎流面压力降至最低。压力分布主要不同之处在于附体尾缘位置,线型的不同很大程度影响了来流在附体尾缘的发展,形成不同的压力分布。可以明显看到,方案3中附体尾缘压力明显高于其他方案压力值,使其前后压差作用减小,而附体沾湿面积对于航行器沾湿面积而言是小量,因而航行器粘性阻力增加并不明显,压差阻力成为附体阻力的主要成分,方案3中附体前后压差值明显低于其他方案,这也与前文中阻力计算结果一致。
|
图 4 附体结构横向剖面压力分布云图 Fig. 4 Pressure distribution in transverse section of appendage structures |
除航行器流向方向流场信息外,图5为垂直于航行器来流方向的速度分布图。受水流粘性作用影响,在航行器和附体结构壁面流体流速下降,形成低速边界层区域,航行器周围低速区域分布大都一致,附体结构差异引起其周围速度变化较为明显。附体周围来流速度迅速增至最大,而后与主流作用向下游流动。不同的是,方案3附体底部与侧壁速度分布基本一致,并未在端面诱导产生明显的流动分离,这与附体下部导流结构有关。前几种方案在流向方向为翼型,垂直于来流方向均为二维翼型拉伸结构,在底部未采用过渡形式,因此在附体下部端面出现低速漩涡流动区;方案3在垂直于来流方向为渐缩型翼型,在其他几个方向也均为圆滑曲线过渡,其整体流动状态比较稳定。从能量的角度而言,抑制了端面绕流产生的漩涡,进而减少了附体周围流体能量消耗,所带来的阻力增额也相对减小。因此,附体外形设计时在考虑流向方向翼型选取、设计之外,也应综合考虑垂直于来流方向的流体外形设计。

|
图 5 附体结构纵向剖面速度分布云图 Fig. 5 Velocity distribution in longitudinal section of appendage structures |
为进一步揭示附体结构流场细节,在定常流场基础上,进行非定常流场特性计算研究。图6为Swirling Strength=26的涡量等值面分布图,其中Swirling Strength表示的旋涡强度提供了一种从流场识别中小尺度涡的方法,相比其他旋涡强度表达形式,可以更为有效地捕捉涡结构。可以看到,涡量主要集中于航行器结构突变处,主要分布于附体结构处。附体附近流动复杂,汇集着层状的涡结构,在附体结构与航行器主体接触部位产生典型的马蹄涡,附体结构下方因流动分离作用诱导产生涡对并在流向方向延展,该涡对会周期性地产生和脱落,最终受主流作用影响,发生能量耗散而消失。对比几种附体结构,主要区别在于附体结构尾缘处涡形态明显存在差异,方案4附体结构下方产生的涡管直径和流向长度明显减小,流动状态明显改善,其对下游流场的干扰也相对降低,可改善航行器尾部流动和螺旋桨进流条件,对于航行器噪声和推进效率也都有益。
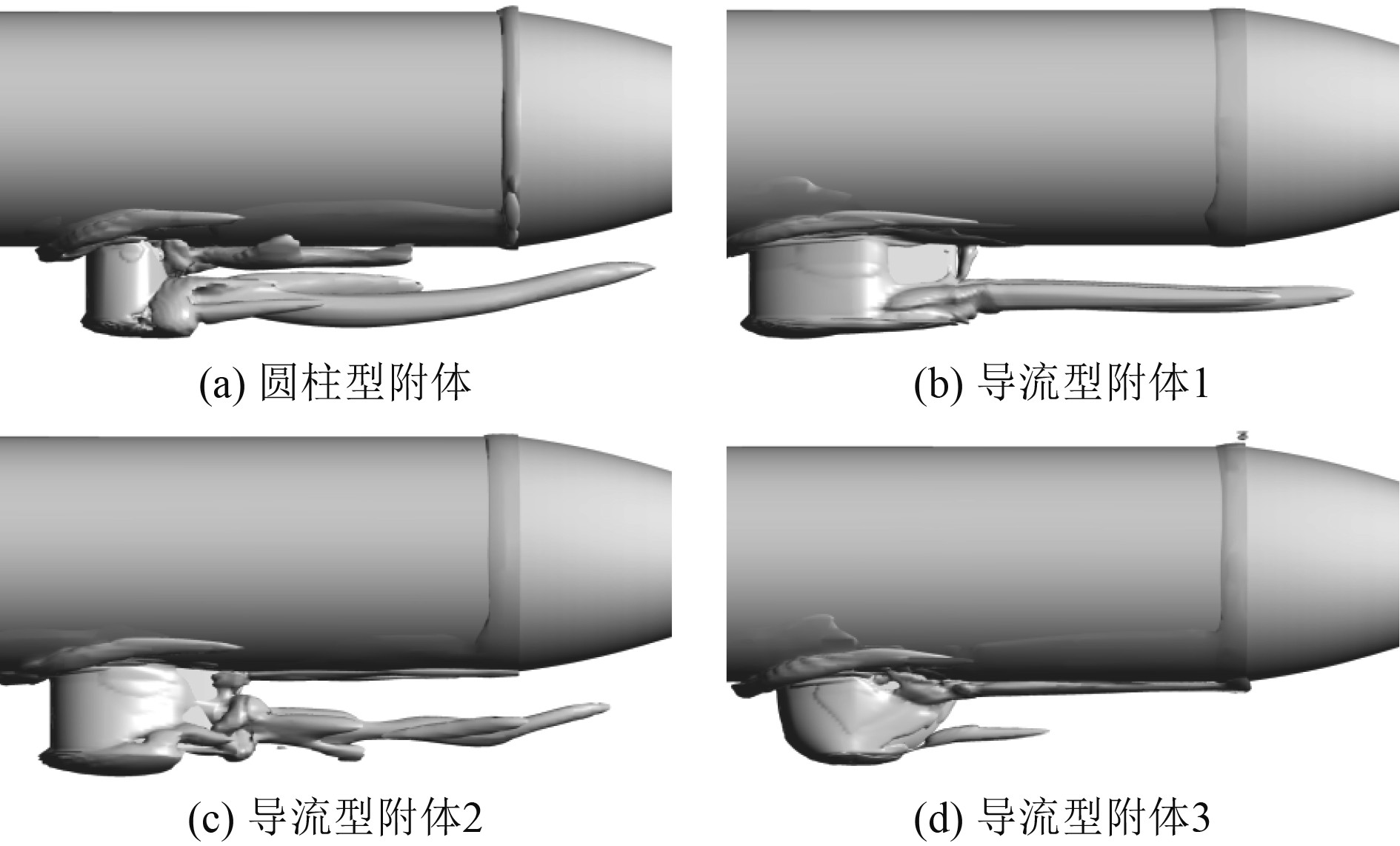
|
图 6 附体结构涡量等值面分布图 Fig. 6 Vorticity isosurface distribution of appendage structures |
通过对水下航行器几种不同附体结构流场特性的仿真分析,可以得到以下结论:
1)水下航行器低速航行状态下,附体阻力影响较为明显,且主要为压差阻力;
2)附体模型中,方案3导流型附体结构阻力增加值较小,相比无附体模型的航行器阻力仅增加11.9%,相比圆柱型附体模型减阻率为19.7%;
3)方案3导流型附体结构其前后压差作用减弱,附体结构下方产生的涡管直径和长度明显减小,底部低速不稳定区域得到抑制,减少了附体周围流体能量消耗,所带来的阻力增额也相对减小。
| [1] |
姚蓝, 陈燕. 发展UUV装备的几个问题[J]. 声学技术, 2011, 30(1): 1-8. YAO Lan, CHEN Yan. Discussions on development of UUV Equipment[J]. Technical Acoustics, 2011, 30(1): 1-8. DOI:10.3969/j.issn1000-3630.2011.01.001 |
| [2] |
ALLEN B, VORUS W S, PRESTERO T. Propulsion system performance enhancements on REMUS AUVs[C]// IEEE Oceans, 2000: 1869−1873.
|
| [3] |
WANG Yaxing, GAO Ting, PANG Yongjie, et al. Investiga-tion and optimization of appendage influence on the hy-drodynamic performance of AUVs[J]. Journal of Marine Science and Technology, 2019, 24(1): 297-305. DOI:10.1007/s00773-018-0558-y |
| [4] |
柏铁朝, 卢锦国. 附体对潜艇阻力及尾部伴流场的影响[J]. 舰船科学技术, 2013, 35(3): 47-51. BAI Tiechao, LU Jinguo. Analysis of the impact of ap-pendages on submarine resistance and wake flow field[J]. Ship Science and Technology, 2013, 35(3): 47-51. DOI:10.3404/j.issn.1672-7649.2013.03.010 |
| [5] |
倪守隆, 杜礼明, 于德壮. 声呐导流罩关键结构参数对航行阻力的影响[J]. 舰船科学技术, 2015, 37(1): 50-55. NI Shoulong, DU Liming, YU De-zhuang. Effect of key structure parameters for sonar dome on sailing re-sistance[J]. Ship Science and Technology, 2015, 37(1): 50-55. DOI:10.3404/j.issn.1672-7649.2015.01.010 |
| [6] |
LIU Qiumei, GAO Xin. Research on the virtual reality of impact of appendages on the flow characteristics of submarines based on neural networks and CFD[J]. Neural Computing & Applications, 2018, 29: 1293-1301. |
| [7] |
李创兰. 基于动网格的船舶及其附体阻力预报研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [8] |
BULL P. The validation of CFD predictions of nominal wake for the suboff fully appended submarine geometry[C]// Proceeding of 21st Symposium on Naval Hydrodynamics. Trondheim, Norway: Defence Research Agency, 1996.
|
| [9] |
杨琼方, 王永生, 张志宏. 全附体潜艇粘性流场的RANS模拟及场量和涡量的校验分析[J]. 计算力学学报, 2012, 29(4): 567-573. YANG Qiongfang, WANG Yongsheng, ZHANG Zhihong. RANS simulation of viscous flow over full appended submarine and field variables validation and vorticity analysis[J]. Chinese Journal of Computational Mechanics, 2012, 29(4): 567-573. |
| [10] |
LIU Han-Lieh, HUANG Thomas T. Summary of DARPA suboff experimental program data[R] Naval Surface Warfare Center, Carderock Division (NSWCCD), 1999.
|
 2024, Vol. 46
2024, Vol. 46
