2. 哈尔滨工业大学 电气工程及自动化学院,黑龙江 哈尔滨 150000
2. Department of Electrical Engineering, Harbin Institute of Technology, Harbin 150000, China
分布式汽轮发电机组在可再生能源发电、船舶动力、小型孤岛核电站等领域具有广泛应用[1 − 3],是构建微电网的关键设备,其可靠性和安全性直接影响微电网的持续供电能力。
大比例脉冲功率负荷普遍存在于分布式发电系统中[4 − 6],当有较大的负荷突加和突卸时,由于汽轮发电机组的动态响应性相对较慢,输出功率变化缓慢,瞬态调节过程中难与负载功率相平衡[7-8]。输出电压和频率会产生较大波动,超出电能质量规定的限值,会引起其他敏感设备故障、停机[9-10]。这些问题对微电网的安全稳定运行造成影响,降低了微电网的持续供电能力。
超级电容储能系统由于具有功率密度高、充放电效率高、循环寿命长、高低温性能好、维护方便等优点,应用于微电网可解决电网电压和频率的大幅波动问题[11-12]。超级电容储能可进行发电源输出功率补偿、快速负荷功率变化平滑、再生能量制动回收,并可在发电中断时作为备用电源,以提高供电的稳定性和可靠性[13-14]。采用功率协调控制方法,如改进PI控制[15]、滑模控制[16]、神经网络[17]和模糊逻辑控制[18]等方法,可实现超级电容储能系统与其他电源功率的有效分配,实现系统功率补偿。
本文将超级电容储能应用于汽轮发电机组,针对传统汽轮发电机组输出功率调节响应慢的问题,提出频差功率协调控制方法。通过超级电容储能电源的高功率动态响应弥补汽轮机输出功率动态响应低的问题,使系统实时处于瞬时功率平衡状态,保证系统频率的平稳,增强汽轮发电机组对大比例脉冲功率负荷的适应能力。
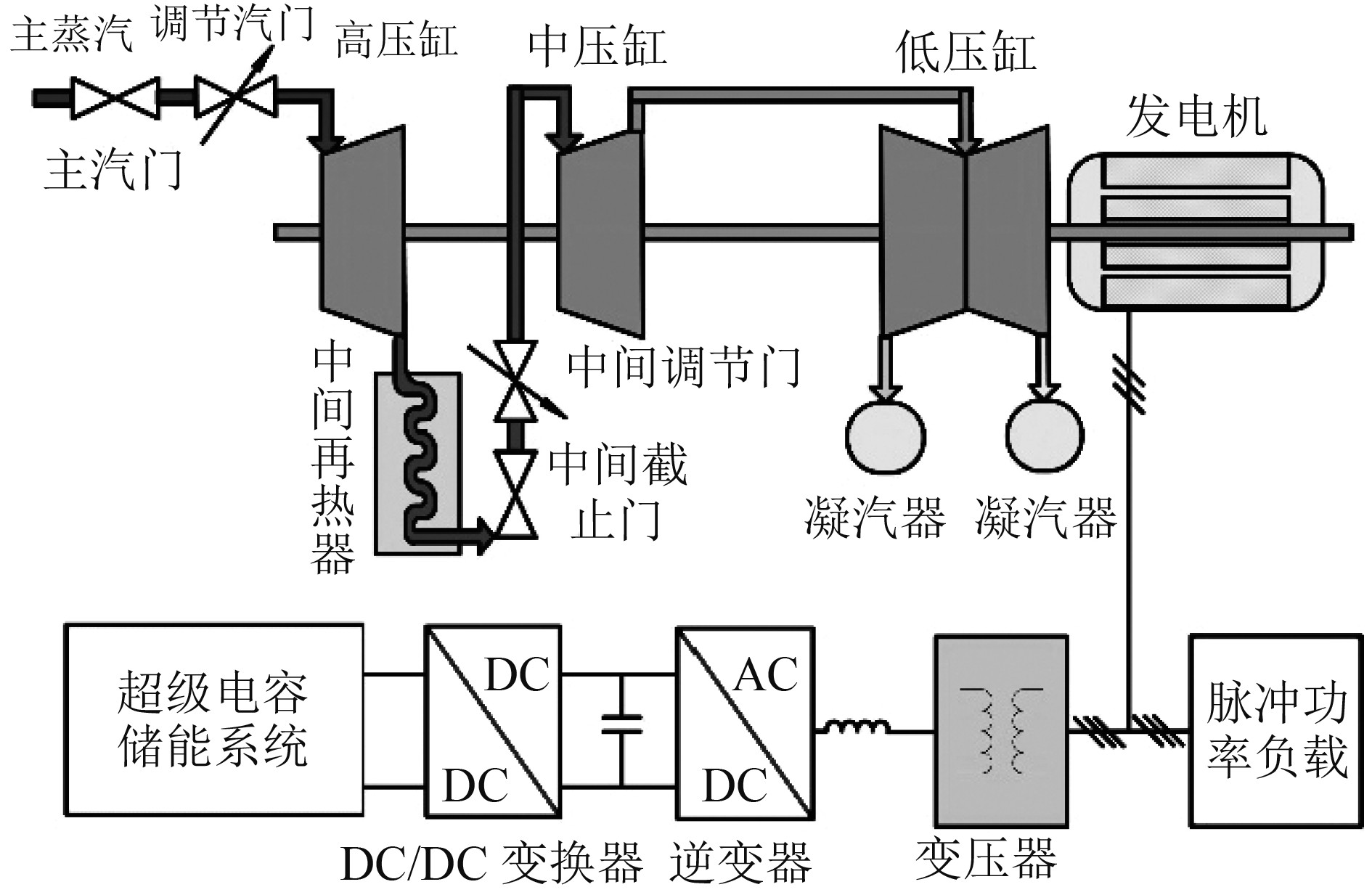
1 系统结构图1为汽轮机-超级电容混合发电系统主电路结构图。
|
图 1 汽轮机-超级电容混合发电系统主电路结构图 Fig. 1 Main circuit structure diagram of steam turbine-supercapacitor hybrid power generation system |
汽轮机输出功率响应缓慢,当系统突加脉冲功率负载时,脉冲功率负载会造成汽轮机转速的剧烈变化,高压缸和中压缸温度也会发生大范围变化,使得输出电能频率和电压的较大波动,降低了输出电能质量。当系统存在冲击减载时,负载功率的突然消失易导致系统转速的较大泵升,触发超速保护机制报警停机,严重情况下可能会造成飞车事故。
超级电容储能系统可抑制脉冲功率负载对整个系统稳定性和发电质量的不利影响。当系统突加冲击负载时,超级电容输出功率,迅速与负载功率相平衡,使系统保持稳定。当系统存在冲击减载时,超级电容储能电源迅速开始吸收能量,随着汽轮机输出功率的调整,所吸收能量逐渐减小,最后达到新平衡,保证了交流系统输出电压和频率的稳定。
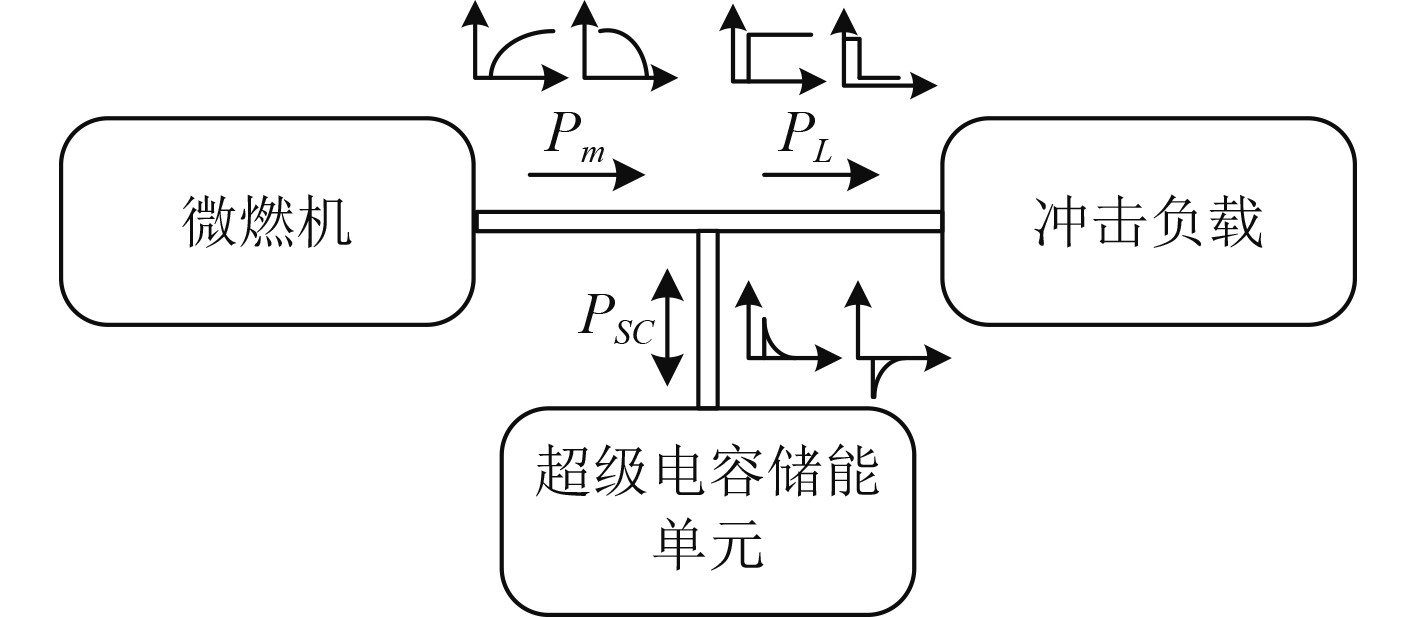
汽轮机-超级电容混合发电系统功率分配如图2所示。
|
图 2 汽轮机-超级电容混合发电系统功率分配图 Fig. 2 Power distribution map of MTGS |
Pm为汽轮机发电源输出功率,PL为负载功率,PSC为超级电容储能电源的功率,三者功率近似的有如下关系:
| $ {P_{{L}}} = {P_{{m}}} + {P_{{{SC}}}}。$ | (1) |
系统稳态运行时,存在如下关系:
| $ \left\{ \begin{gathered} {P_{{L}}} = {P_{{m}}},\\ {P_{{{SC}}}} = 0 。\\ \end{gathered} \right. $ | (2) |
存在冲击负载的瞬态过程中,汽轮机输出功率变化率与负载功率变化率的关系为:
| $ \frac{{{\text{d}}{P_{{m}}}}}{{{\text{d}}t}} < \frac{{{\text{d}}{P_{{L}}}}}{{{\text{d}}t}}。$ | (3) |
可知,汽轮机输出功率与冲击负载不匹配。此时,超级电容储能电源输出瞬态功率,与汽轮机发电源输出功率的和,在瞬态实现与负载功率匹配。
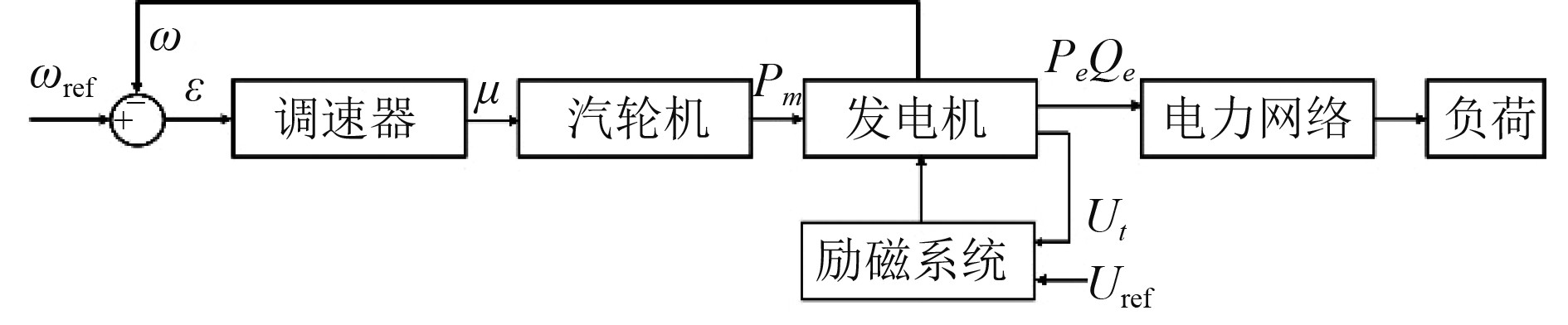
2 汽轮机模型及输出特性汽轮发电机组控制框图,如图3所示。
|
图 3 汽轮发电系统控制框图 Fig. 3 Control block diagram of steam turbine power generation system |
汽轮机系统传递函数为:
| $ \begin{split} {G_{\text{T}}}(s) = &\frac{1}{{{T_{\text{1}}}s + 1}} \cdot \frac{1}{{{T_{\text{2}}}s + 1}} \cdot \frac{1}{{{T_{\text{3}}}s + 1}} \cdot \left( {{C_{\text{H}}} + \frac{{1 - {C_{\text{H}}}}}{{{T_{\text{4}}}s + 1}}} \right)= \\ &\frac{{{C_{\text{H}}}{T_{\text{4}}}s + 1}}{{({T_{\text{1}}}s + 1)({T_{\text{2}}}s + 1)({T_{\text{3}}}s + 1)({T_{\text{4}}}s + 1)}}。\end{split} $ | (4) |
式中:T1为电液控制器时间常数;T2为油动机时间常数;T3为高压缸容积效应时间常数;T4为再热器容积效应时间常数;CH为高压缸功率占比。
VSR是转速控制器,为了保证系统稳定,稳态时没有静态误差,采用如下形式:
| $ {G_{{\text{VSR}}}}(s) = {k_{{p}}}{\text{ + }}\frac{{{k_{{i}}}}}{{{T_{{i}}}s + 1}} + {k_{{d}}}s 。$ | (5) |
同步发电机转子的运动方程为:
| $ {T_{{j}}}\omega \frac{{{\text{d}}\omega }}{{{\text{d}}t}} = {P_{{m}}} - {P_{{e}}}。$ | (6) |
式中:Tj为机组惯性时间常数。在稳态情况下,角速度变化相对较小,可近似认为其不变。
| $ \omega \approx 1 。$ | (7) |
将式(6)化简得:
| $ {T_{{j}}}\frac{{{\text{d}}\omega }}{{{\text{d}}t}} = {P_{{m}}} - {P_{{e}}}。$ | (8) |
由式(5)和式(8)可得汽轮发电机的控制框图如图4所示。

|
图 4 汽轮发电机的控制框图 Fig. 4 Control block diagram of steam turbine generator |
没有转速闭环控制时的汽轮发电机组开环传递函数为:
| $ {G_{{\text{noctrop}}}}(s) = \frac{{{C_{{H}}}{T_{\text{4}}}s + 1}}{{{T_{{j}}}s({T_{\text{1}}}s + 1)({T_{\text{2}}}s + 1)({T_{\text{3}}}s + 1)({T_{\text{4}}}s + 1)}}。$ | (9) |
由式(5)和图4可得,加入转速闭环控制后的系统闭环传递函数为:
| $ {G_{{{cl}}}}(s) = \frac{{({C_{{H}}}{T_{\text{4}}}s + 1)({T_{{i}}}{k_{{d}}}{s^2} + ({k_{{p}}}{T_{{i}}} + {k_{{d}}})s + {k_{{p}}} + {k_{{i}}})}}{{{T_{{j}}}sC(s) + ({C_{{H}}}{T_{\text{4}}}s + 1){C_1}\left( s \right)}} 。$ | (10) |
其中,
| $ C(s) = ({T_{\text{1}}}s + 1)({T_{\text{2}}}s + 1)({T_{\text{3}}}s + 1)({T_{\text{4}}}s + 1)({T_{\text{i}}}s + 1),$ |
| $ {C_1}\left( s \right) = {T_{{i}}}{k_{{d}}}{s^2} + ({k_{\text{p}}}{T_{{i}}} + {k_{{d}}})s + {k_{{p}}} + {k_{{i}}}。$ |
进而可得,负载功率扰动与转速偏差的传递函数为:
| $ {G_{{{PL}}}}(s) = \frac{{C(s)}}{{{T_{{j}}}sC(s) + ({C_{{H}}}{T_{\text{4}}}s + 1){C_1}\left( s \right)}}。$ | (11) |
在大比例冲击负载暂态过程中,由于汽轮机调节特性决定了交流母线频率会出现较大波动。超级电容储能电源的主要控制目标是限制交流母线频率的波动范围。
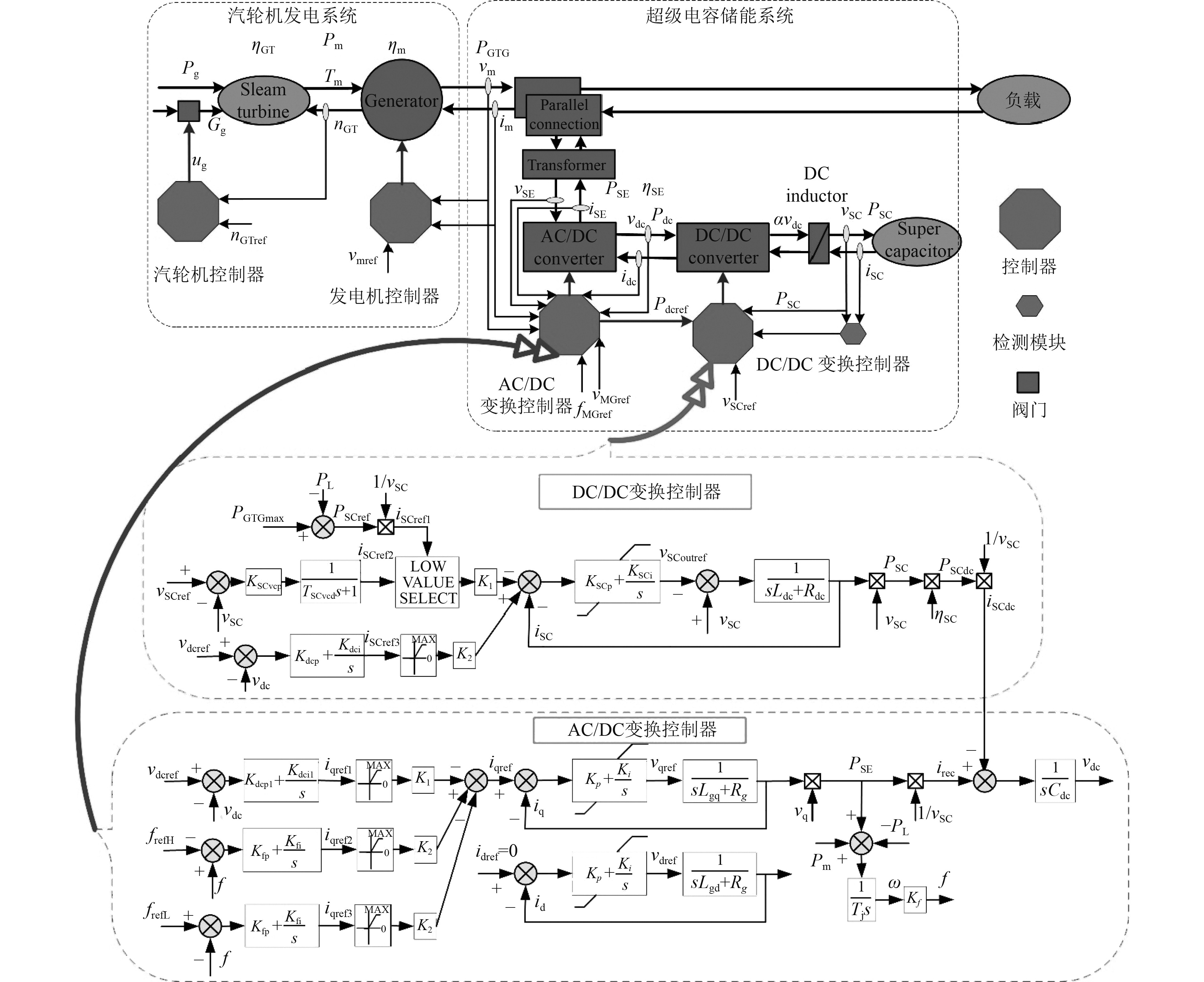
频差功率协调控制系统结构如图5所示。AC/DC变换器的控制目标是限制交流母线频率在
|
图 5 控制系统结构 Fig. 5 Configuration of control system |
| $ {i_{{\text{qref}}}} = {K_1}{i_{{\text{qref1}}}}{\text{ + }}{K_2}{i_{{\text{qref2}}}}{\text{ + }}{K_2}{i_{{\text{qref3}}}}。$ | (12) |
式中,
| $ {i_{{\text{qref1}}}} = \left( {{K_{{\text{dcp1}}}}{\text{ + }}\frac{{{K_{{\text{dci1}}}}}}{s}} \right)\left( {{v_{{\text{dcref}}}} - {v_{{\text{dc}}}}} \right),$ | (13) |
| $ {i_{{\text{qref2}}}} = \left( {{K_{{\text{fp}}}}{\text{ + }}\frac{{{K_{{\text{fi}}}}}}{s}} \right)\left( {f - {f_{{\text{refH}}}}} \right),$ | (14) |
| $ {i_{{\text{qref3}}}} = \left( {{K_{{\text{fp}}}}{\text{ + }}\frac{{{K_{{\text{fi}}}}}}{s}} \right)\left( {{f_{{\text{refL}}}} - f} \right),$ | (15) |
| $ \left\{ \begin{gathered} {K_{\text{1}}} = 1,\begin{array}{*{20}{c}} {} \end{array}{K_{\text{2}}} = 0,\begin{array}{*{20}{c}} {} \end{array}{f_{{\text{refL}}}} \leqslant f \leqslant {f_{{\text{refH}}}},\\ {K_{\text{1}}} = 0,\begin{array}{*{20}{c}} {} \end{array}{K_{\text{2}}} = 1,\begin{array}{*{20}{c}} {} \end{array}f < {f_{{\text{refL}}}}{\text{ or }}f > {f_{{\text{refH}}}}。\\ \end{gathered} \right. $ | (16) |
DC/DC变换器控制采用电压、电流双闭环结构。电压环包含超级电容电压控制器和直流母线电压控制器。超级电容电压控制器主要作用是控制超级电容电压
| $ {i_{{\text{SCref}}}} = - {K_1} \times {\text{MIN}}\left\{ {{i_{{\text{SCref1}}}},{i_{{\text{SCref2}}}}} \right\} + {K_2}{i_{{\text{SCref3}}}}。$ | (17) |
其中,
| $ {i_{{\text{SCref1}}}} = \frac{{{P_{{\text{SCref}}}}}}{{{v_{{\text{SC}}}}}} = \frac{{{P_{{\text{GTGmax}}}} - {P_{\text{L}}}}}{{{v_{{\text{SC}}}}}},$ | (18) |
| $ {i_{{\text{SCref2}}}} = \frac{{{K_{{\text{SCvcp}}}}}}{{{T_{{\text{SCvcd}}}}s{\text{ + }}1}}\left( {{v_{{\text{SCref}}}} - {v_{{\text{SC}}}}} \right),$ | (19) |
| $ {i_{{\text{SCref3}}}} = \left( {{K_{{\text{dcp}}}}{\text{ + }}\frac{{{K_{{\text{dci}}}}}}{s}} \right)\left( {{v_{{\text{dcref}}}} - {v_{{\text{dc}}}}} \right) 。$ | (20) |
超级电容储能系统中DC/AC变换器电流内环的闭环传函可表示为:
| $ {G_{\text{i}}}(s) = \frac{{{K_{{\text{ip}}}}s + {K_{{\text{ii}}}}}}{{{L_{{\text{AC}}}}{s^2} + ({R_{{\text{AC}}}} + {K_{{\text{ip}}}})s + {K_{{\text{ii}}}}}}。$ | (21) |
式中:Kip为电流环比例增益;Kii为电流环积分增益。LAC为DC/AC变换器输出滤波电感;
| $ {G_{{\text{fop}}}}(s) = \frac{{{V_{{m}}}{K_{{f}}}({K_{{\text{fp}}}}s + {K_{{\text{fi}}}})({K_{{\text{ip}}}}s + {K_{{\text{ii}}}})}}{{{T_{{j}}}{s^2}\left[ {{L_{{\text{AC}}}}{s^2} + ({R_{{\text{AC}}}} + {K_{{\text{ip}}}})s + {K_{{\text{ii}}}}} \right]}} 。$ | (22) |
式中:
| $ {G_{{\text{fcl}}}}(s) = \frac{{{T_j}{s^2}\left[ {{L_{{\text{AC}}}}{s^2} + ({R_{{\text{AC}}}} + {K_{{\text{ip}}}})s + {K_{{\text{ii}}}}} \right]}}{{{T_j}{s^2}{C_1}\left( s \right) + {V_{\text{m}}}{K_{\text{f}}}({K_{{\text{fp}}}}s + {K_{{\text{fi}}}})({K_{{\text{ip}}}}s + {K_{{\text{ii}}}})}}。$ | (23) |
其中,
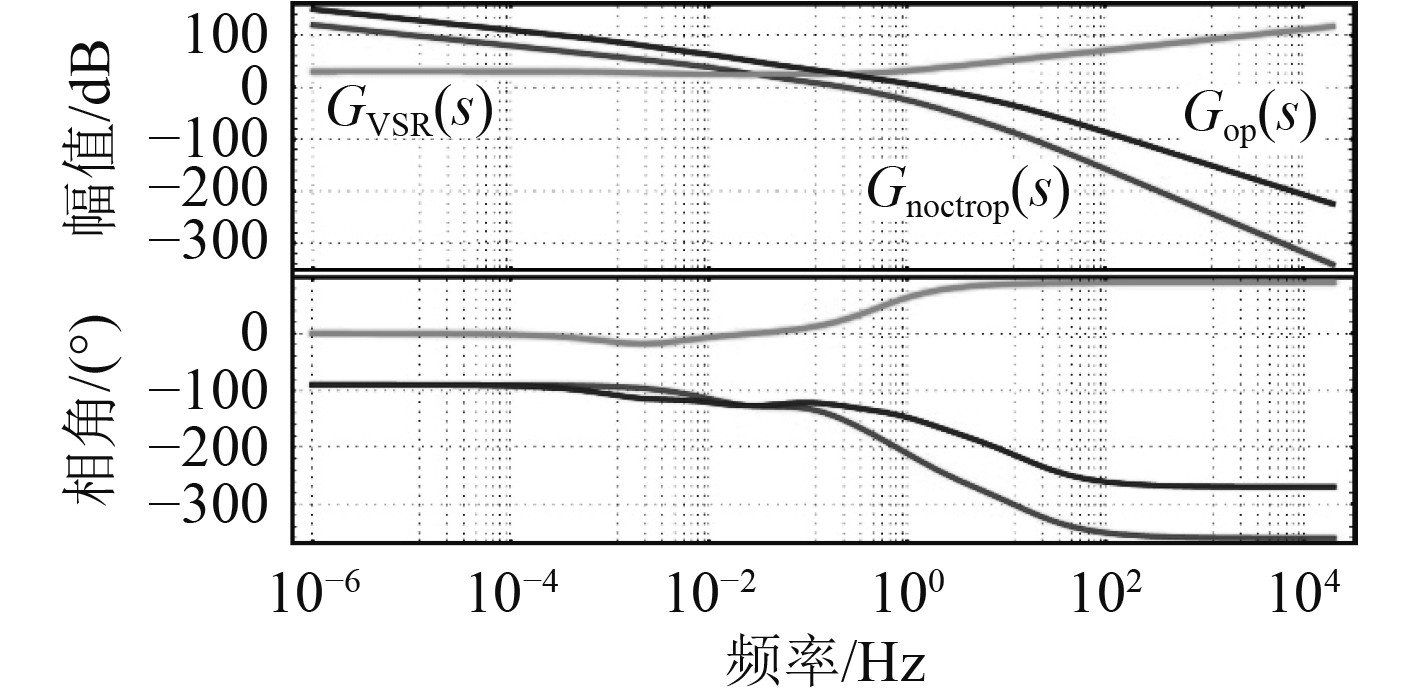
汽轮发电机组被控对象、控制器和系统开环传递函数伯德图,如图6所示。汽轮发电机组被控对象截止频率较低,为0.2 Hz,说明被控对象动态响应非常慢。参数优化后系统截止频率为1.5 Hz,相角裕度为27°。控制系统参数为
|
图 6 汽轮发电机组开环传函伯德图 Fig. 6 Bode diagram of open loop transfer function for steam turbine generator set |
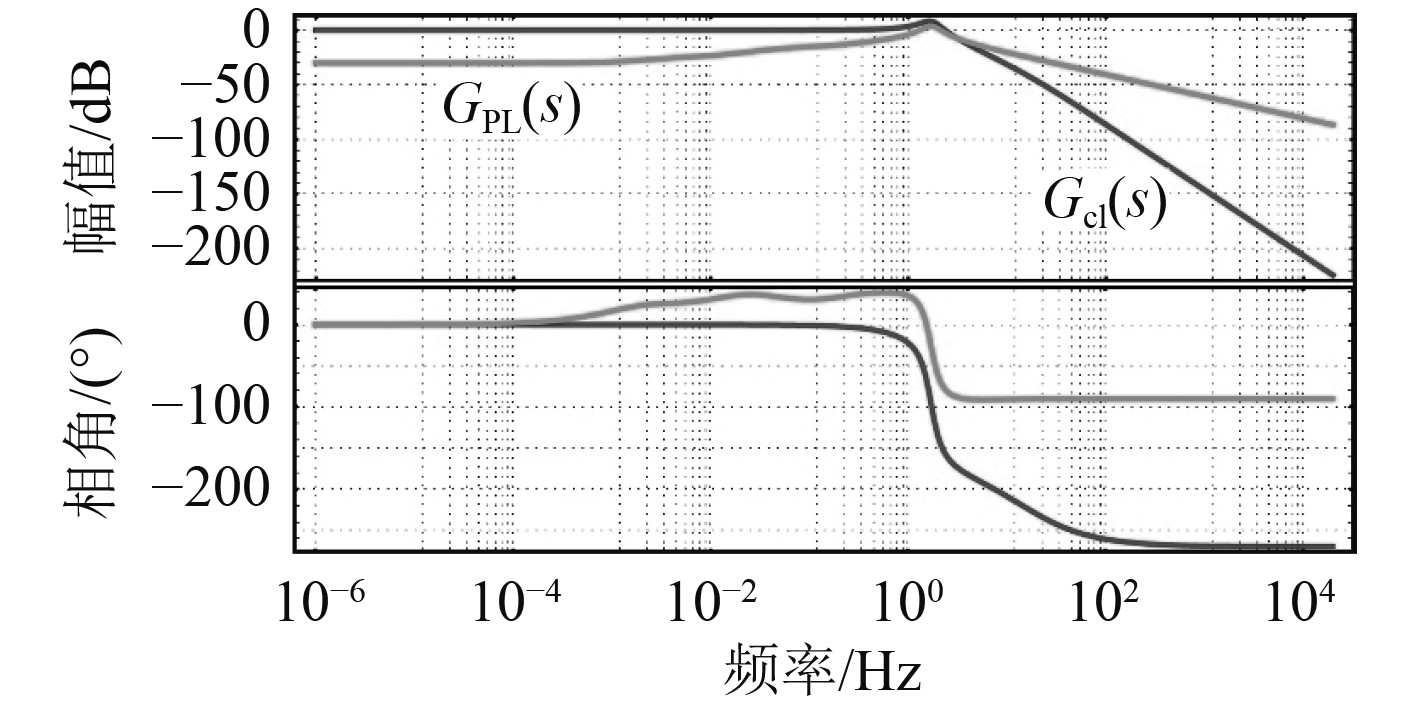
汽轮发电机组系统闭环传函和负载功率扰动传递函数的伯德图,如图7所示。可知,系统闭环截止频率为1.5 Hz,汽轮发电机组动态响应较慢,在截止频率附近抑制能力较差。
|
图 7 汽轮发电机组闭环传函伯德图 Fig. 7 Bode diagram of closed loop transfer function for steam turbine generator set |
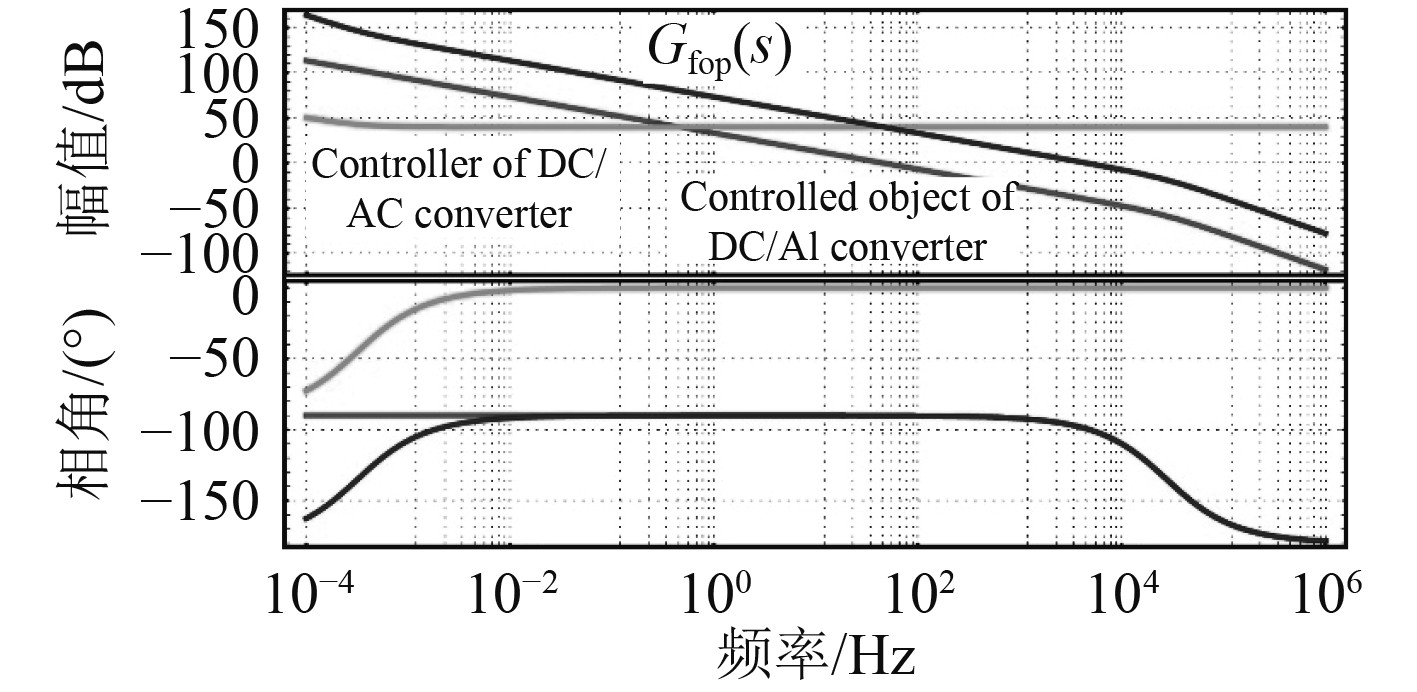
DC/AC变换器系统开环传递函数的伯德图,如图8所示。被控对象的截止频率为44 Hz,加入控制器在比例增益的作用下,系统动态响应大幅提高。参数优化后,系统截止频率为4.4 kHz、相角裕度为81°,加入控制器后系统动态响应性较快。控制系统参数确定为
|
图 8 DC/AC变换器开环传函伯德图 Fig. 8 Bode diagram of open loop transfer function for DC/AC converter |
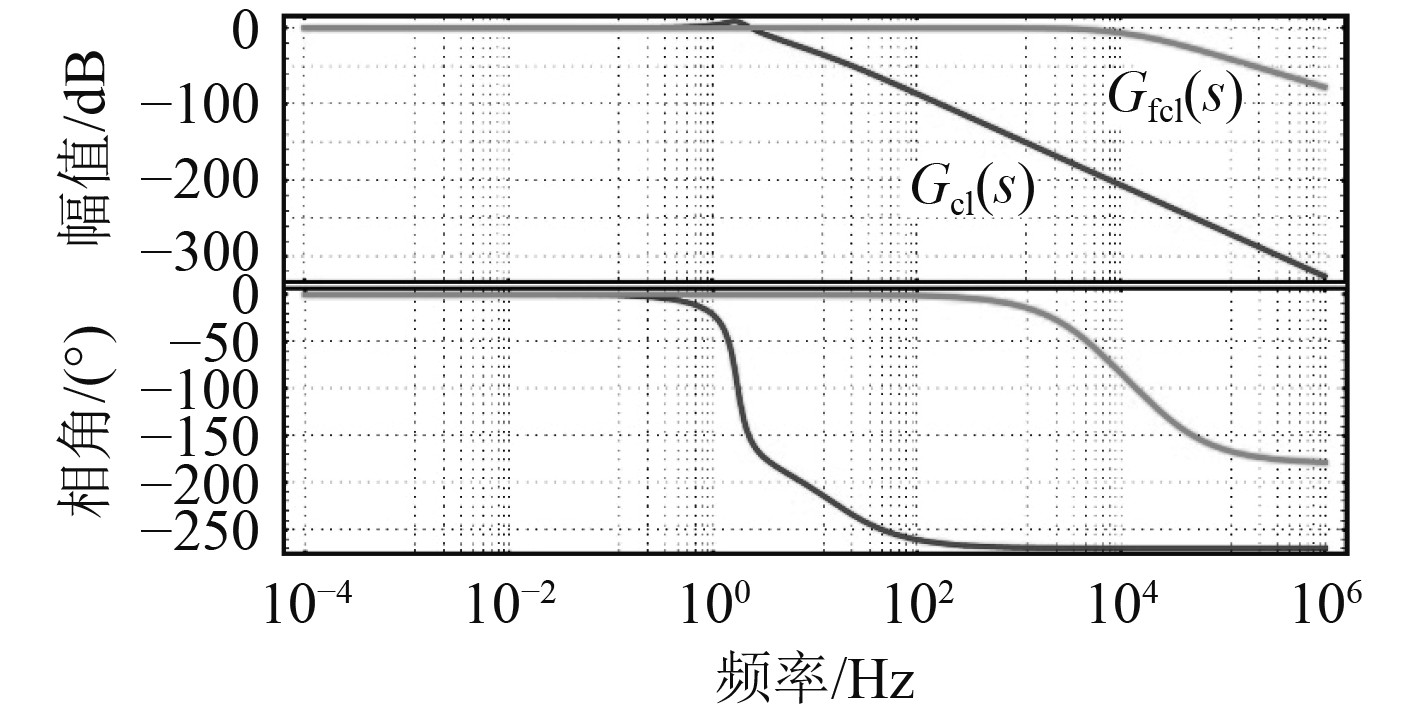
超级电容储能电源DC/AC变换器的闭环传函伯德图,如图9所示。可知,汽轮发电机组动态响应速度非常慢,不能满足大比例脉冲功率负载的需求,而超级电容储能系统DC/AC变换器的动态响应非常快,能响应快速变化的负载功率。
|
图 9 汽轮发电机组和DC/AC变换器闭环传函伯德图 Fig. 9 Bode diagram of closed loop transfer function for steam turbine generator set and DC/AC cinverter |
在Matlab/Simulink仿真环境中建立了汽轮发电机组和超级电容储能电源大比例脉冲功率负载扰动的仿真模型。汽轮发电机组、超级电容储能电源的参数,如表1所示,汽轮发电机组额定功率为25 MW,输出电压为10.5 kV,转速为
|
|
表 1 汽轮发电机组和超级电容储能电源参数 Tab.1 Parameters of steam turbine generator set and supercapacitor energy storage power supply |
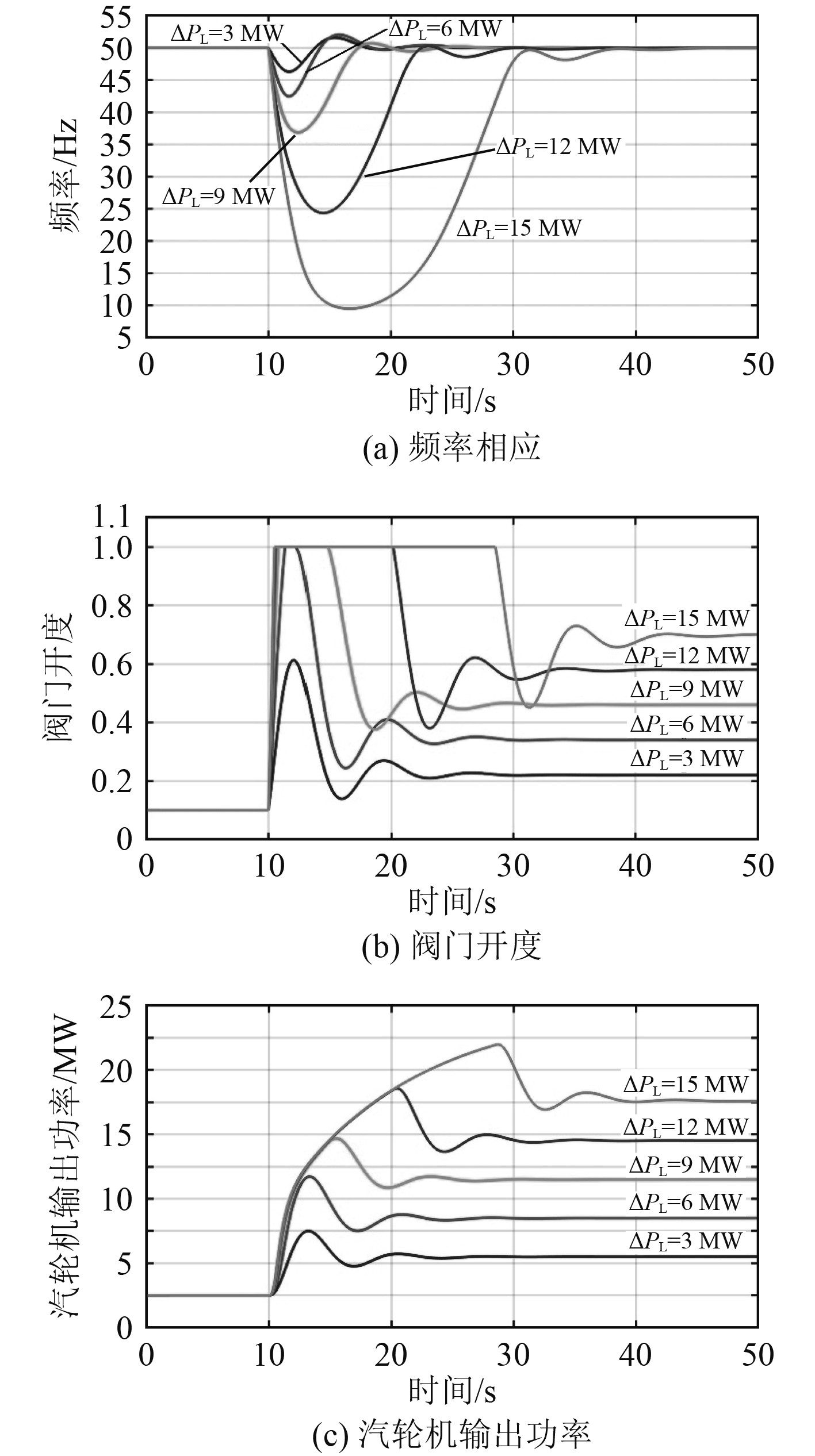
在没有超级电容参与工作的情况下,对汽轮发电机组的脉冲功率负载特性进行了仿真研究。图10为脉冲功率负载阶跃上升阶段的仿真结果,开始时负载为2.5 MW,频率为50 Hz。在10 s时负载分别阶跃增加3、6、9、12、15 MW。图10(a)为频率响应结果,脉冲功率负载阶跃量越大,频率下降越严重,负载阶跃为3、6、9、12、15 MW,时最低频率为46、42、37、24和9.5 Hz。在较大脉冲功率负载下,汽轮发电机组输出电能质量严重超标。图10(b)为汽轮机阀门开度的响应曲线,突增负载越大,阀门开度处于饱和的时间就越长,汽轮机发电频率和输出功率的调节时间也越长。图10(c)为汽轮机输出功率的响应曲线,负载阶跃量越大,汽轮机输出功率上升时间越长,经过较长时间的调节逐渐收敛到稳态值。
|
图 10 汽轮发电机组脉冲功率负载阶跃上升仿真结果 Fig. 10 Simulation results of pulsed power load step rise of steam turbine generator unit |
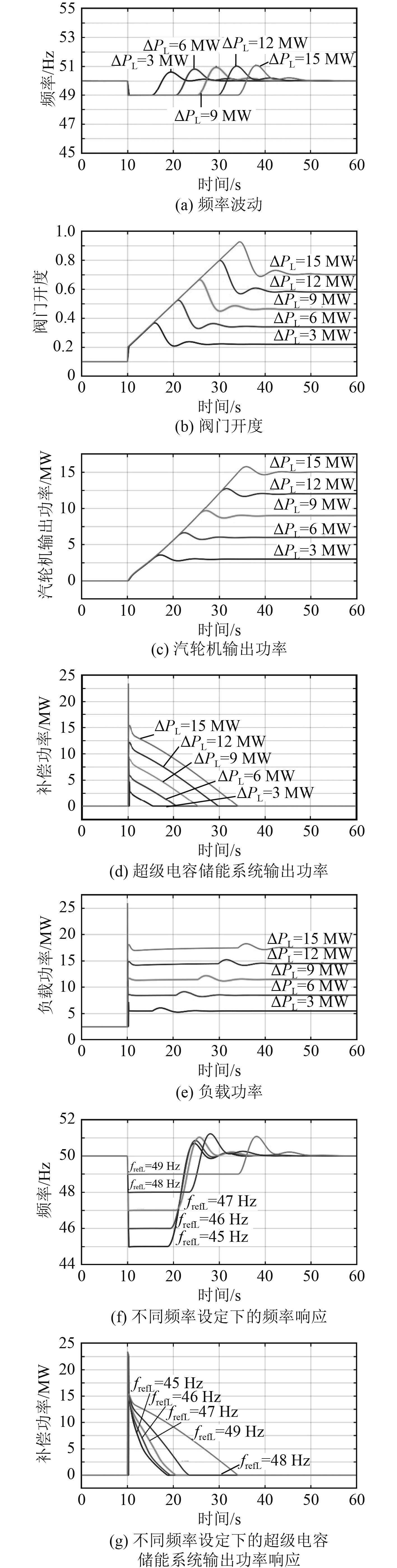
图11为双电源频差功率协调控制脉冲功率负载阶跃上升阶段的仿真结果。开始时负载为2.5 MW,频率为50 Hz,在10 s时负载分别阶跃增加3、6、9、12、15 MW。图11(a)为频率响应曲线,超级电容储能系统输出功率的频率下限给定为49 Hz,系统频率被箝位到了49 Hz,脉冲功率负载越大,系统频率被箝位的时间越长。不同的脉冲功率负载扰动下,频率的波动范围为49~51 Hz。与图10(a)对比可知,在超级电容储能电源的作用下,系统频率的波动范围大大缩小。由图11(b)可知,由于系统频率被箝位,阀门开度线性上升,不会达到饱和值,最后稳定到新的稳态值。图11(c)中汽轮机输出功率的上升趋势和阀门开度曲线类似。图11(d)为超级电容储能电源的输出功率的响应曲线,图11(e)为负载功率的响应曲线,超级电容储能电源输出功率开始时刻最大,为负载功率的阶跃量,而后随汽轮发电机组输出功率的增加而减小,直至为0,系统频率退出箝位状态,然后达到新的稳态。负载阶跃增加至15 MW的情况下,图11(f)为不同频率设定下的频率响应曲线,图11(g)为不同频率设定下的超级电容储能系统输出功率。储能电源动作的频率下限设定越小,储能电源输出的能量越少,但开始时刻输出功率不变,只和突变的负载增量有关。
|
图 11 双电源频差功率协调控制脉冲功率负载阶跃上升仿真结果 Fig. 11 Simulation results of power banlance control of dual power supply under pulse power load rise condition |
针对传统汽轮发电机组输出功率调节响应慢的问题,提出基于超级电容储能的汽轮发电系统频差功率协调控制。通过理论分析及仿真验证,得出以下结论:
1)频域分析证明,超级电容储能电源输出和吸收功率传输的响应频段较宽,汽轮发电机组的功率传递呈现超低频特点,二者组成的混合供电系统具有较宽的频率响应特性。
2)混合供电系统具有较强的抗大比例脉冲功率负载扰动的能力,能保证发电源与负载间的实时功率平衡,系统频率被箝位在很小的范围内。
3)在大比例脉冲功率负载扰动下,汽轮机发电机组不会处于饱和状态,能柔和过渡到新的稳态,避免了转速大范围波动对机组造成的严重危害,系统能可靠稳定工作。
| [1] |
何怡冲, 李永毅, 林育超, 等. 考虑透平背压影响的燃气轮机动态特性研究[J]. 中国电机工程学报, 2024, 44(8): 3155−3165.
|
| [2] |
于洋, 牛夕莹, 米泓博, 等. 船用燃气轮机低压盘腔系统流动特性研究[J]. 热能动力工程, 2023, 38(1): 1-8. YU Yang, NIU Xiying, MI Hongbo, et al. Study on flow characteristics of low pressure disk cavity system of marine gas turbine[J]. Journal of Engineering for Tnermal Energy and Power, 2023, 38(1): 1-8. |
| [3] |
WANG Congyu, SONG Ji, YOU Daning, et al. Combined heat and power plants integrated with steam turbine renovations: Optimal dispatch for maximizing the consumption of renewable energy[J]. Energy Conversion and Management, 2022, 258: 115-128. |
| [4] |
LASHWAY C R, ELSAYED A T, MOHAMMED O A. Hybrid energy storage management in ship power systems with multiple pulsed loads[J]. Electric Power System Research, 2016, 141: 50-62. DOI:10.1016/j.jpgr.2016.06.031 |
| [5] |
DUAN Jiandong, LIU Junjie, XIAO Qian, et al. Cooperative controls of micro gas turbine and super capacitor hybrid power generation system for pulsed power load[J]. Energy, 2019, 169(2): 1242-58. DOI:10.1016/j.energy.2018.12.004 |
| [6] |
张亚东, 姜里运, 宋少华, 等. 三轴燃气轮机发电机组突变负载控制策略研究[J]. 热能动力工程, 2016, 31(11): 26-31+118. ZHANG Yadong, JIANG Liyun, SONG Shaohua, et al. Research on control strategy for sudden load of three axis gas turbine generator set[J]. Journal of Engineering for Tnermal Energy and Power, 2016, 31(11): 26-31+118. |
| [7] |
刘家兴, 翟世杰, 赵晨旭. 针对脉冲发电机突变负载的微型燃气轮机工作性能研究[J]. 机械制造与自动化, 2022, 51(1): 203-206. |
| [8] |
张亚东, 姜里运, 韩晓光, 等. 燃气轮机发电机组突变负荷对性能的影响[J]. 航空动力学报, 2016, 31(12): 2824-2832. |
| [9] |
邵梦麟, 梁前超, 闫东, 等. 船用燃气轮机发电机组动态性能仿真[J]. 舰船科学技术, 2016, 38(7): 71-76. SHAO Menglin, LIANG Qianchao, YAN Dong, et al. Dynamic performance simulation of marine gas turbine generator set[J]. Ship Science and Technology, 2016, 38(7): 71-76. DOI:10.3404/j.issn.1672-7619.2016.07.016 |
| [10] |
栾永军, 孙鹏, 李东明. 发电用燃气轮机动态性能仿真[J]. 舰船科学技术, 2012, 34(4): 51-56. LUAN Yongjun, SUN Peng, LI Dongming. Dynamic performance simulation of gas turbines for power generation[J]. Ship Science and Technology, 2012, 34(4): 51-56. DOI:10.3404/j.issn.1672-7649.2012.04.011 |
| [11] |
YANG Bin, WANG Jun, SANG Yan, et al. Applications of supercapacitor energy storage systems in microgrid with distributed generators via passive fractional-order sliding-mode control[J]. Energy, 2019, 187: 115905.1−115905.13. DOI:10.1016/j.energy.2019.115905 |
| [12] |
张勤进, 孙小童, 刘彦呈, 等. 蓄电池/超级电容混合储能系统协调控制策略[J]. 电源技术, 2020, 44(9): 1345-1347+1365. DOI:10.3969/j.issn.1002-087X.2020.09.027 |
| [13] |
李学斌, 刘建伟. 采用二阶滤波的混合储能系统实时功率分配方法[J]. 电网技术, 2019, 43(5): 1650-1657. |
| [14] |
杨彦杰, 孙若愚, 张朝川. 一种基于模糊控制的混合储能系统能量管理策略研究[J]. 可再生能源, 2017, 35(12): 1881-1887. DOI:10.3969/j.issn.1671-5292.2017.12.023 |
| [15] |
刘勇, 刘大鹏, 穆勇. 基于GWO优化ICEEMDAN分解的混合储能系统功率分配策略[J]. 电气工程学报, 2022, 17(4): 257-267. |
| [16] |
赵源筱. 含高比例可再生能源电力系统自动发电控制策略研究[D]. 杭州: 浙江大学, 2021.
|
| [17] |
ARUNKUMAR C R, MANTHATI U B, PUNNA S, et al. Supercapacitor voltage based power sharing and energy management strategy for hybrid energy storage system[J]. Journal of Energy Storage, 2022, 50(6): 220−232.
|
| [18] |
ARUNKUMAR C R, MANTHATI U B, SRINIVAS P, Accurate modelling and analysis of battery–supercapacitor hybrid energy storage system in DC microgrid systems[J]. Energy System, 2021, 13(4): 1055−1073.
|
 2024, Vol. 46
2024, Vol. 46
