工况的剧烈变化可能导致一回路系统中法兰连接部位、泵的密封面等处发生泄漏。当泄漏率较小时,虽对堆芯安全影响有限,但对任务的完成度及系统的运行方案将产生较大影响。若操纵员在泄漏发生时能够对泄漏率进行准确预测,继而制定相应的运行方案则具有较大的现实意义。目前,对高温、高压及变温工况下法兰连接部位的泄漏率进行预测的研究不多。陆晓峰等[1]在考虑垫片和螺栓高温蠕变的基础上,建立了法兰接头的变形协调方程,并利用Monte Carlo方法对高温螺栓法兰接头的可靠度进行计算。喻健良等[2]对高温下螺栓-法兰-垫片系统密封性能进行研究,采用有限元技术分析了预紧、加压和升温后的螺栓及垫片的应力变化。孔慈宇等[3]以柔性石墨金属齿形复合垫片为研究对象,对不同尺寸的石墨金属齿形复合垫片进行泄漏率测试,在不考虑温变的情况下得到了垫片泄漏率与预紧应力、介质压力和垫片尺寸的关系。上述文献重点关注的是泄漏发生前温度和内压对结构性能的影响,虽然通过热-构耦合分析,得出法兰径向的温度梯度和内压是影响泄漏率的关键因素,但没有对泄漏发生后的流-热-构动态耦合过程进行分析,也没有就如何对该过程的泄漏率进行预测作进一步地研究。原因是要建立起准确的流体、传热和材料力学相互耦合的动态机理模型十分困难。
在这种实际的物理模型很难获取的情况下,高斯过程回归模型作为一种非参数替代模型受到了越来越多的关注[4]。郭后[5]提出基于高斯过程的备件预测算法,并利用该算法对空调备件的使用进行了预测。刘健[6]提出基于多高斯过程回归模型的锂离子电池剩余寿命预测方法,预测了锂离子电池的剩余使用寿命。曾聿赟[7]利用高斯过程回归模型对流动加速腐蚀的物理模型进行非参数修正,利用修正后的模型对管道的流动加速腐蚀速率进行研究。上述文献都涉及到对系统或者部件的未来状态进行预测的问题,但很少就建模过程中所产生的不确定性,以及在所建立模型中具有不可测参数的情况下,如何进行系统状态预测等问题进行研究。为此,本文利用具有较好不确定性表达能力的高斯过程回归模型作为替代模型进行了不确定性的定量评估,同时利用正态随机游走方法实现不可测温度参数的更新,并在此基础上利用所建模型对一回路泄漏率进行预测。
1 高斯过程回归模型替代物理模型 1.1 不确定性分析对复杂物理过程进行建模,得到物理模型方程[7]:
| $ y = f\left( {x,\nu } \right)。$ | (1) |
式中:
| $ y = f\left( x \right) + \nu ,\nu {\sim}N\left( {0,\sigma _\nu ^2\left( x \right)} \right)。$ | (2) |
当由于物理过程复杂导致该模型无法建立时,在获取一系列样本点
| $ \hat y = \varphi (x;D)。$ | (3) |
原物理模型与数据驱动模型输出之间的差异为:
| $ y - \hat y = \left( {f\left( x \right) - \varphi \left( {x;D} \right)} \right) + \nu 。$ | (4) |
可知,两模型输出的差异由2部分组成:等号右侧第1项为物理模型与数据驱动模型中确定的误差,为模型不确定性;第2项为物理模型的随机误差
当不考虑数据驱动模型的预测误差时,其输出近似服从正态分布[8]。由于模型不确定性与固有不确定性相互独立,故有分布方差:
| $ \begin{aligned}[b] \sigma_y^2=&\mathrm{var}\left[\left(f\left(x\right)-\varphi\left(x;D\right)\right)+\nu\right]= \\ &\mathrm{var}\left(f\left(x\right)-\varphi\left(x;D\right)\right)+\mathrm{var}\left(\nu\right)=\sigma_m^2\left(x\right)+\sigma_{\nu}^2\left(x\right)。\end{aligned} $ | (5) |
式中模型不确定性的估计值
| $ \hat \sigma _{\nu ,i}^2 = \max \left\{ {{{\left( {{y_i} - \varphi \left( {{x_i};D} \right)} \right)}^2} - \hat \sigma _m^2\left( {{x_i}} \right),0} \right\}。$ | (6) |
式中:
| $ MSE = \frac{1}{{{N_{test}}}}{\sum\limits_{i = 1}^{{N_{test}}} {\left( {\varphi \left( {{x_{t,i}}} \right) - {y_{t,i}}} \right)} ^2},$ | (7) |
| $ PIC = \frac{{{N_{PI}}}}{{{N_{\text{test}}}}} 。$ | (8) |
式中:
| $ \begin{aligned}[b] \varphi \left( {{x_{t,i}}} \right) - &\sqrt {\hat \sigma _m^2\left( {{x_{t,i}}} \right) + \hat \sigma _\nu ^2\left( {{x_{t,i}}} \right)} \leqslant {y_i} \leqslant\\ \varphi \left( {{x_{t,i}}} \right) + &\sqrt {\hat \sigma _m^2\left( {{x_{t,i}}} \right) + \hat \sigma _\nu ^2\left( {{x_{t,i}}} \right)}。\end{aligned}$ | (9) |
|
图 1 标准正态分布的概率密度函数图 Fig. 1 The pdf of normal distribution |
作为一种非参数模型,高斯过程回归模型在利用先验知识的基础上,通过贝叶斯方法实现状态预测并能够输出预测均值、方差和置信区间[4]。作为随机变量的集合,在高斯过程模型中,任意个随机变量的组合均服从由均值函数和协方差函数确定的联合高斯分布,如下式:
| $ f{\sim}GP\left( {m\left( x \right),k\left( {x,x} \right)} \right)。$ | (10) |
式中,
| $ Y\sim N\left( {0,k\left( {x,x} \right) + \sigma _n^2I} \right) 。$ | (11) |
观测值
| $ \left[ \begin{array}{l} Y \\ f' \\ \end{array} \right]\sim N\left( 0,\left[ \begin{array}{*{20}{c}} { \boldsymbol{k}\left( {x,x} \right) + \sigma _n^2{\boldsymbol I}}&{\boldsymbol{k}\left( {x,x'} \right) }\\ {\boldsymbol{k}\left( {x',x} \right)}&{\boldsymbol{k}\left( {x',x'} \right) } \end{array} \right] \right)。$ | (12) |
式中:
| $ f'|x,Y,x'\sim N\left(\overline{f}',\mathrm{cov}\left(f'\right)\right)。$ | (13) |
式(13)即为预测值
| $ \bar f' = k\left( {x',x} \right){\left[ {k\left( {x,x} \right) + \sigma _n^2I} \right]^{ - 1}}Y ,$ | (14) |
| $ \mathrm{cov}\left(f'\right) = k\left(x',x'\right) - k\left(x',x\right)\left[k\left(x,x\right) + \sigma_n^2I\right]^{-1}k\left(x,x'\right)。$ | (15) |
通过上述可知,确定均值核函数与协方差核函数是高斯过程回归模型求解的关键。平方差指数核函数和零均值核函数通常被用作高斯过程回归模型的核函数。然后,通过对核函数中的超参数进行优化即可得到所需的高斯过程回归模型[9]。超参数的优化一般通过极大似然估计法和共轭梯度法实现,其负对数似然函数为:
| $\begin{split} L\left( \theta \right) =& \frac{1}{2}{Y^{\mathrm{T}}}{\left[ {K\left( {x,x} \right) +\sigma _n^2I} \right]^{ - 1}} Y +\\ & \frac{1}{2}\log \left| {K\left( {x,x} \right) + \sigma _n^2I} \right| + \frac{n}{2}\log 2{\text π}。\end{split} $ | (16) |
式中:
由文献[1 - 2]可知,法兰连接处泄漏率的机理模型可表示为:
| $ L = f\left( {\Delta t,\Delta p,\eta ,{ P},\varepsilon } \right)。$ | (17) |
式中:单位时间压降
| $ \Delta {t_{k + 1}} = \Delta {t_k} + {\gamma _k}。$ | (18) |
式中:扰动项
为解决正态随机游走在模型参数中引入额外方差的问题,文献[10]利用核平滑的方法进行参数的转化,该方法主要分为2个步骤:
步骤1 收缩。将模型参数的分布向其均值进行收缩:
| $ \Delta {\tilde t_k} = \Delta {t_k}\sqrt {1 - {h^2}} + \Delta {\hat t_k}\left( {1 - \sqrt {1 - {h^2}} } \right)。$ | (19) |
式中:
步骤2 扰动。将收缩后的样本进行正态随机游走,扰动项方差取为:
| $ \sigma_r^2=h^2\mathrm{var}(\Delta t_k)。$ | (20) |
通过上述2步的变换,参数的转化过程不再引入额外方差。
2.2 基于高斯过程回归模型对泄漏率进行预测采用图2所示框架对一回路系统泄漏率进行预测。
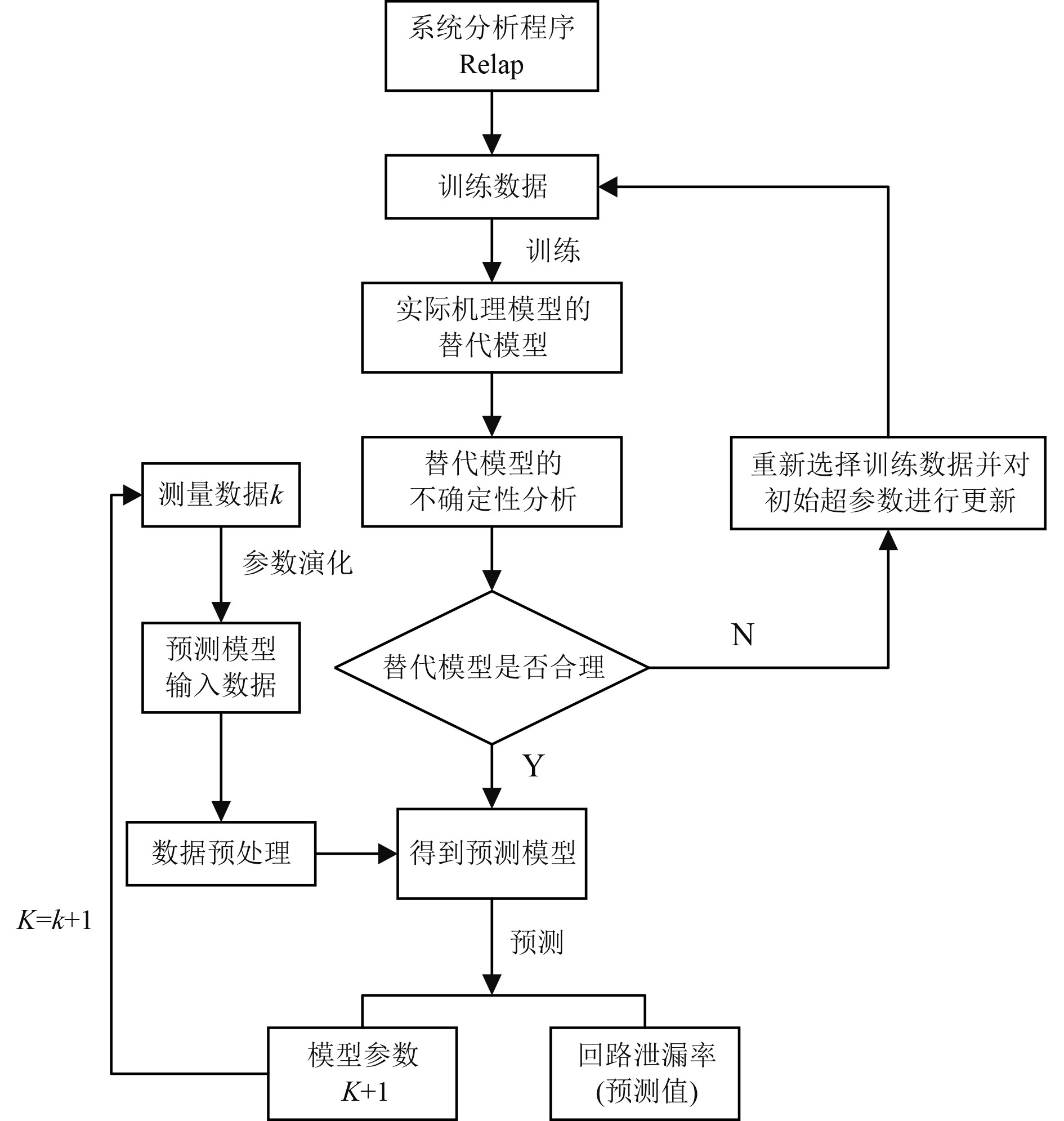
|
图 2 回路泄漏率计算流程图 Fig. 2 Flow chart of loop leakage calculation |
可知,通过某一体化反应堆系统的简化RELAP模型生成替代模型的训练数据,该模型的详细描述参见文献[11]。不考虑泄漏过程的实际物理机理,从观察到的现象来看,在泄漏率一定的情况下有相应的系统单位时间压降以及法兰径向的温度梯度与其相对应[2-3]。因此,通过给定的泄漏率,由RELAP模型就可以得到相应的系统单位时间压降以及法兰径向温度梯度。本文通过RELAP模型得到的216组归一化的训练数据如图3所示。

|
图 3 归一化的仿真训练数据 Fig. 3 Normalized simulation training data |
在进行替代模型训练时,高斯过程回归模型的协方差函数取为平方差指数核函数。根据图2流程图,首先从训练数据中选取样本容量分别为50、100、150的训练数据进行替代模型的训练,并根据式(6)计算出各样本点的固有不确定性方差,然后根据式(7)~式(9)分别计算出各不同样本容量所对应的均方误差(
|
|
表 1 不同样本容量的不确定性定量评估 Tab.1 Quantitative evaluation of uncertainty in different sample sizes |
可以看出,当对相邻近的50个测试样本点进行预测时,3种不同训练样本所得的替代模型均有不错的预测性能,具体表现为
为进一步对上述问题进行说明,分别采用样本容量为50和100的训练数据对高斯过程回归模型进行训练,并对一回路系统的泄漏率进行预测,结果如图4所示。
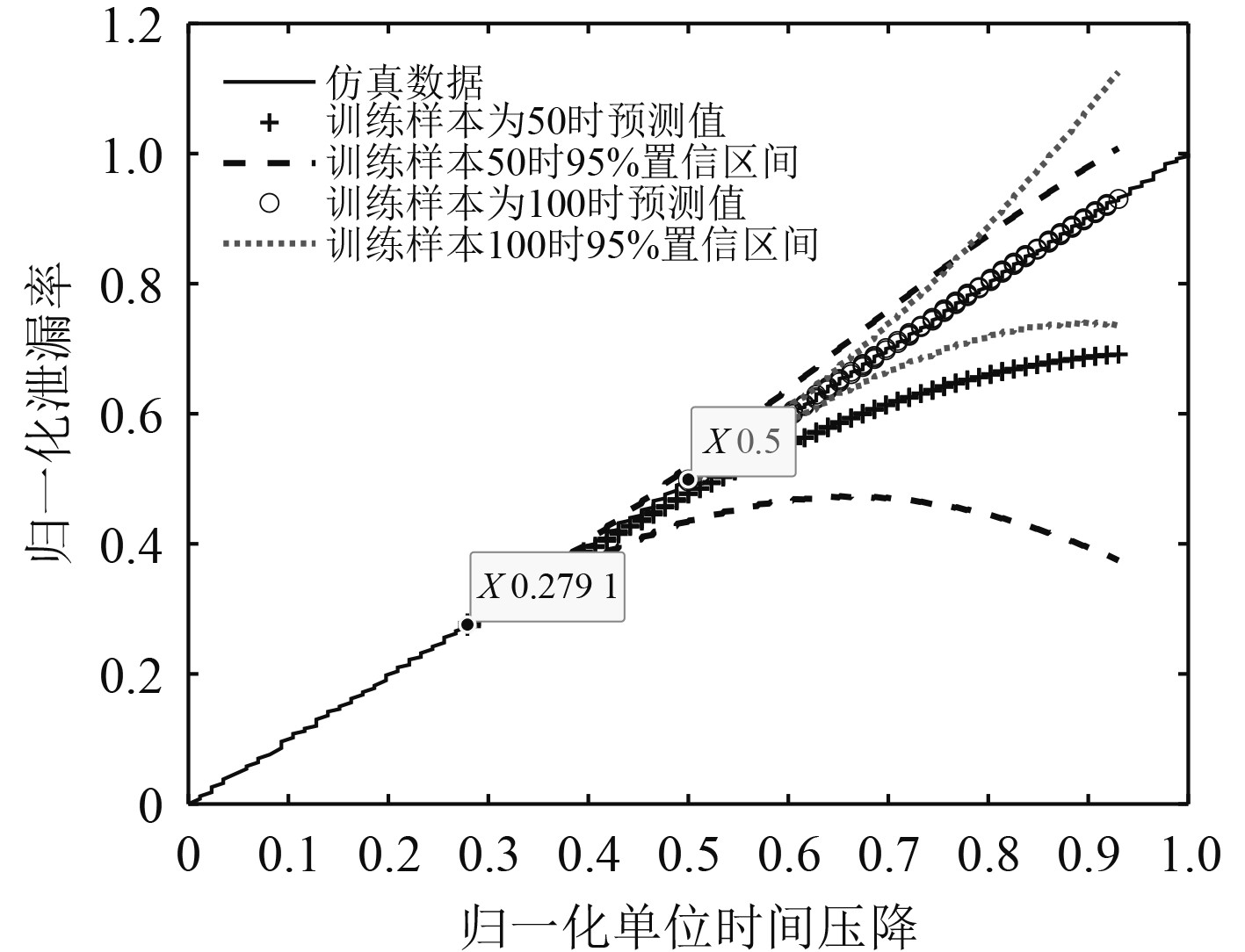
|
图 4 不同样本容量预测结果对比图 Fig. 4 Comparison of prediction results in different sample sizes |
可以看出,当样本容量为50时,即高斯过程回归模型在
在使用高斯过程回归模型进行回路泄漏率的预测时,遇到的另一个问题是:法兰径向的温度梯度无法直接进行测量。本文采用参数的正态随机游走与核平滑相结合的方法对该参数的演化过程进行模拟[10],在对回路的泄漏率做出预测的同时也可对法兰径向的温度梯度做出估计。
假设在运行过程中,一回路系统某法兰连接处发生泄漏,泄漏发生时的法兰径向温度梯度未知,需经过预测模型进行估计,一回路系统的单位时间压降为可测量,假设发生泄漏时观测到的归一化单位时间压降为
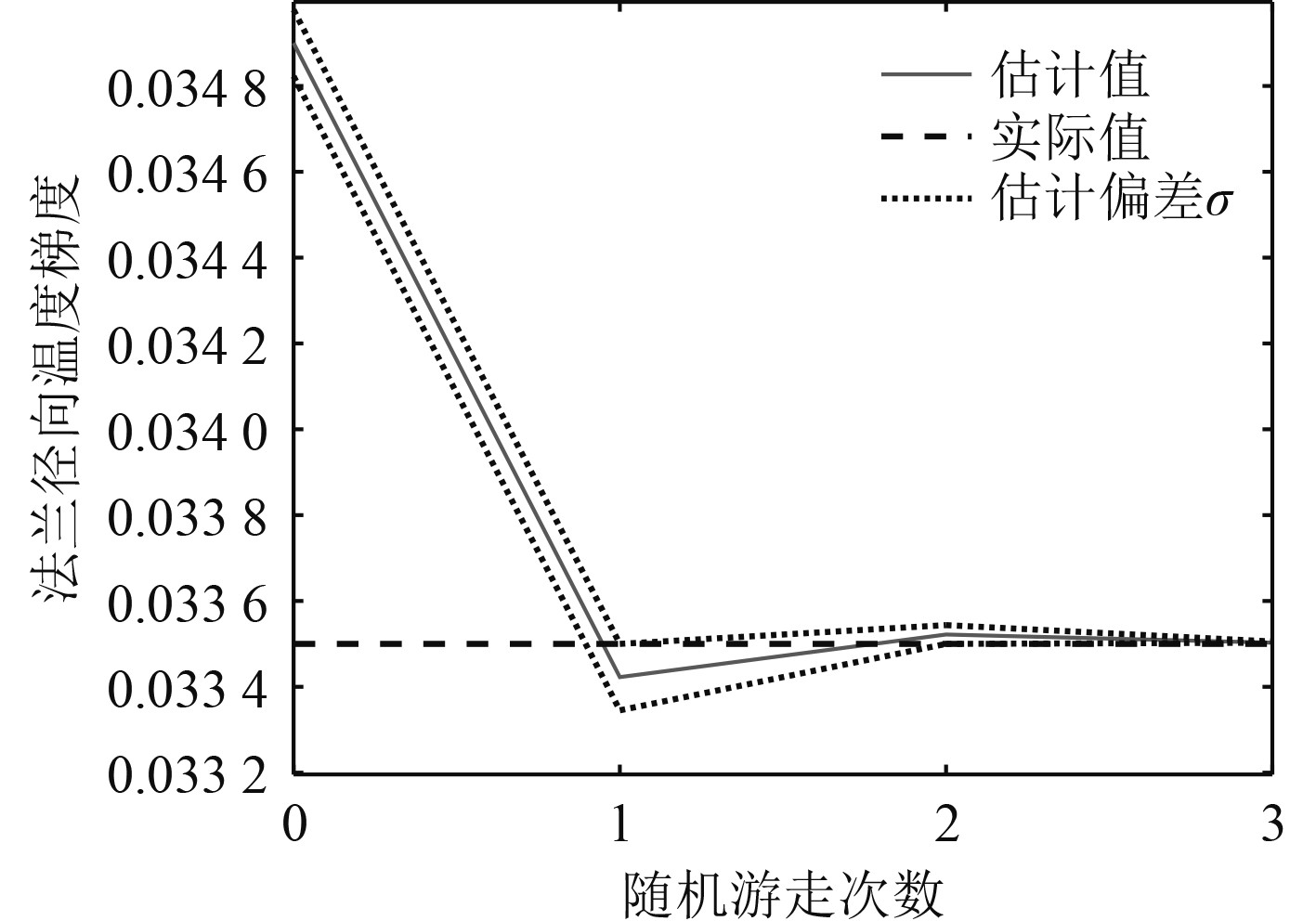
|
图 5 法兰径向温度梯度的演化结果 Fig. 5 Evolution of radial temperature gradient of flange |
法兰径向温度梯度的估计值及其置信区间
根据图2及所采用的参数同步更新的预测模型框架,在当前的模型参数分布的基础上,当观测到系统单位时间压降后,基于高斯过程回归模型进行外推即可得到泄漏率的预测值。图6为在训练数据样本容量为150时,泄漏率预测结果的局部放大图。
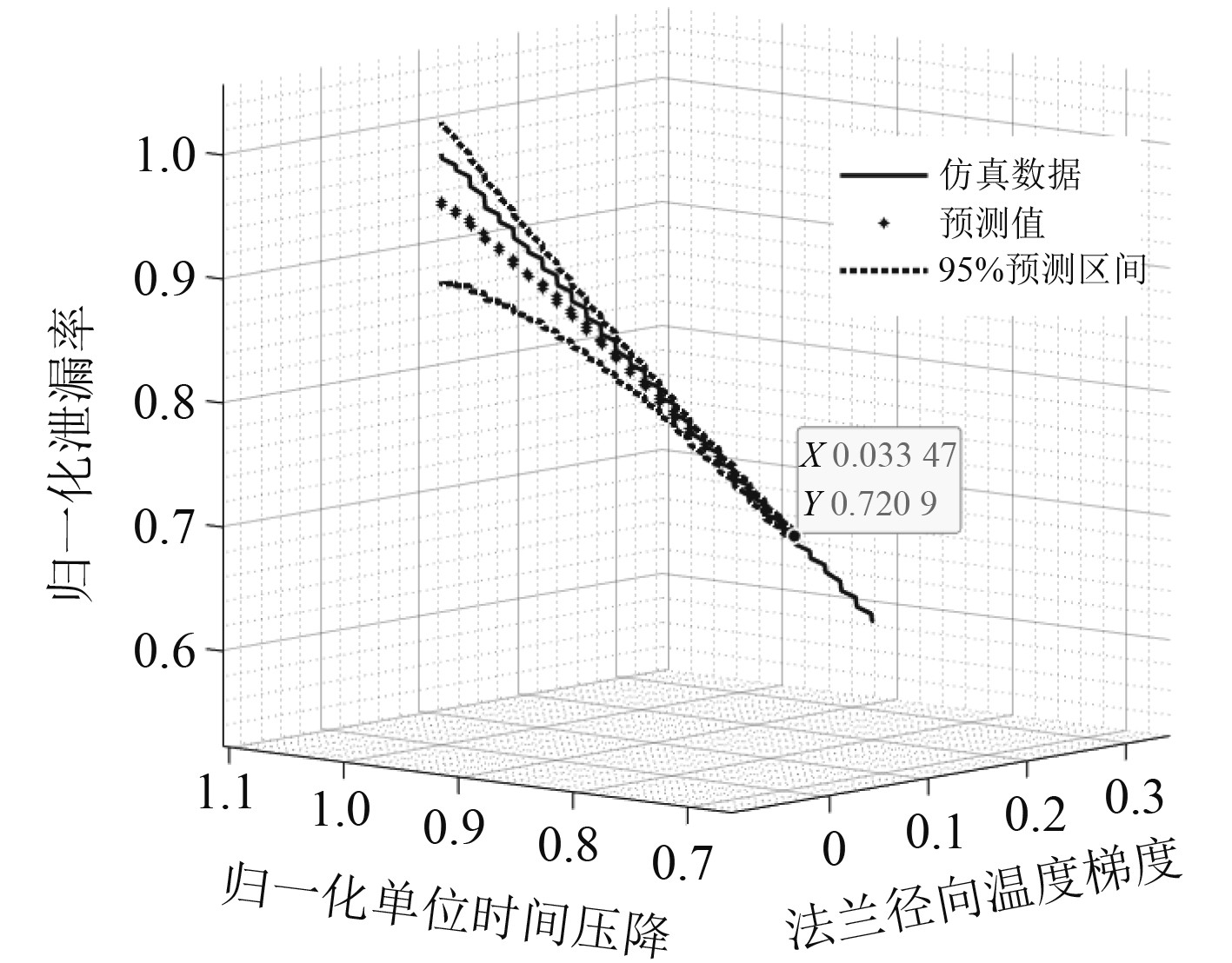
|
图 6 样本容量为150时泄漏率预测结果 Fig. 6 Prediction results of leakage rate when sample size is 150 |
由表1可知,当样本容量为150时,
本文利用高斯过程回归模型作为替代模型,并对替代模型的不确定性进行了定量分析。在对不可测参数进行正态随机游走的基础上,对温度应力条件下的一回路泄漏率进行了预测研究。主要得出如下结论:
1)利用观测数据对高斯过程回归模型进行训练时,训练样本容量越大,对模型的不确定性评估越准确,相应地用该模型进行预测时预测结果精度越高,稳定性越好;
2)将核平滑方法与正态随机游走相结合可迅速、准确地实现不可测参数的更新;
3)高斯过程回归模型能够在小样本容量的情况下得到较好的
| [1] |
陆晓峰, 沈轶. 高温法兰密封接头的可靠性分析[J]. 压力容器, 2007, 24(9): 20-24. DOI:10.3969/j.issn.1001-4837.2007.09.005 |
| [2] |
喻健良, 张忠华, 闫兴清, 等. 高温下螺栓-法兰-垫片系统密封性能研究[J]. 压力容器, 2012, 29(5): 5-9. |
| [3] |
孔慈宇, 陈春辉, 张斌, 等. 管法兰用柔性石墨金属齿形垫泄漏率及其预测模型[J]. 压力容器, 2019, 36(12): 12−15.
|
| [4] |
赵梦恩. 改进高斯过程回归算法及其应用研究[D]. 杭州: 浙江理工大学, 2019.
|
| [5] |
郭后. 基于高斯过程的备件消耗预测研究[D]. 武汉: 华中科技大学, 2016.
|
| [6] |
刘健. 基于高斯过程回归的锂离子电池剩余寿命预测研究[D]. 上海: 上海交通大学, 2019.
|
| [7] |
曾聿赟. 基于状态监测数据的核电厂设备寿命预测算法研究[D]. 北京: 清华大学, 2017.
|
| [8] |
BARALDI P, COMPARE M, SAUCO S, et al. Ensemble neural network-based particle filtering for prognostics[J]. Mechanical Systems and Signal Processing, 2013, 41(1): 288-300. |
| [9] |
王洪桥. 高斯过程回归在不确定性量化中的应用[D]. 上海: 上海交通大学, 2019.
|
| [10] |
HU Y, BARALDI P, DI M F, et al. A particle filtering and kernel smoothing-based approach for new design component prognostics[J]. Reliability Engineering and System Safety, 2015, 13(4): 19-31. |
| [11] |
刘守相, 于雷, 鄢炳火. 一体化压水堆强迫循环转自然循环过渡过程特性分析[J]. 原子能科学技术, 2012, 46(增刊): 220-224. |
 2024, Vol. 46
2024, Vol. 46
