目前,交流电机主要有3种调速方式:直接转矩控制(Direct Torque Control,DTC)、磁场定向控制(Field Oriented Control,FOC)以及模型预测控制(Predictive Control,MPC,简称“预测控制”)。前2种控制是船舶推进电机中应用最多的2种调速方式[1]。与前2种控制方式相比,预测控制作为交流电机一种新颖的控制方式[2],具有实时对系统滚动优化、减少逆变器开关量损耗、控制目标多样化且可实施约束以及处理非线性约束等优点[3 − 5]。根据控制目标不同,电机预测控制可分为模型预测转矩控制(Model Predictive Torque Control,MPTC,简称“预测转矩控制”)和模型预测电流控制(简称“预测电流控制”)。虽然预测控制运算量繁重,但由于微电子技术快速进步,其在以电机控制为代表电力电子行业已经得到广泛应用[5 − 6]。
MPC控制在船舶电机方面的研究及应用相对较少,郭燚等[7]将预测控制引入模块化多电平逆变器,对万吨级船舶电机进行仿真实验,有效降低电机转矩脉动,转矩和磁链几乎无超调;李英帅[8]和刘乐[9]将优化后的预测电流控制分别对船舶五相异步电机和三相永磁同步电机进行仿真实验,体现了优良的控制效果,前者指出需要通过选取合适的权重系数来达到较好的控制效果;胡云飞等[4, 10]使用卡尔曼滤波技术及新型滑模控制对预测转矩控制进行优化,对中铁渤海铁路轮渡“烟大轮”号的推进电机进行仿真实验,有效抑制船舶永磁同步电机磁链和转矩脉动,其采用的均为额定权重系数,在这种情况下MPTC本身控制效果并不为最优。
事实上,预测电流控制和预测转矩控制均涉及代价函数中权重系数的设定和优化问题,它的选取基本通过经验和大量的仿真实验得来,其缺乏科学的设计理论,而预测控制性能很大程度上又取决于合适的权重系数[11 − 13]。为解决权重系数的问题,国内外学者做了大量研究,例如权重系数消除法[14]:但其未考虑电机不同运行状态的情况,或者实质上还是对权重系数进行调节;神经网络设计法[15]:需要大量的数据集进行训练,进一步增大了预测控制的计算量;权重系数在线修正法[16 − 17]:无法保证预测模型最优解,或者对电机参数要求高。同时,船舶在海面上航行会受风、浪和流的影响,螺旋桨也会出现频繁进出海面的情况,造成船舶推进电机运行情况复杂多变,权重系数在这种工作条件下更加难以整定。电机MPC控制同样涉及速度反馈问题,而船舶上的电子器件工作环境湿度大,尤其是机舱内,环境温度高且粉尘多,不利于速度传感器工作,而且速度传感器的安装需要考虑成本及其故障处理问题。
本文首先通过仿真实验分析了MPTC控制的额定权重系数并不适用于船舶推进电机,然后在MPTC的基础上提出模型预测磁链控制(Adaptive Control−Predictive Flux Control, MARS-MPFC,简称“预测磁链控制”)作为船舶推进电机的控制方式,这种控制方式把MPTC中的以控制磁链和转矩为目的转化为对等效定子磁链的控制,以消除对权重系数的整定工作及其影响,提高预测控制在船舶电力推进电机控制中的性能。同时,本文对MPFC进行优化,提出模型参考自适应模型预测磁链控制(Model Reference Adaptive Control−Model Predictive Flux Control,MARS-MPFC,简称“自适应预测磁链控制”),通过使用自适应控制算法对电机的转速进行观测,从而避免船舶电机对速度传感器的使用。最后为了验证MARS - MPFC控制系统的可行性及控制效果,本文以船舶异步电机为对象,对DTC、MPTC以及MARS - MPFC等3种控制方式在相同条件下进行仿真对比研究。
1 船舶推进电机数学模型本文选取船舶电力推进中常用的三相异步电机进行举例,其相关数学方程如下。
电压方程:
| $ \left\{ \begin{gathered} {\boldsymbol{u}_s} = {{R}_{ s}}{\boldsymbol{i}_s} + \frac{{\text{d}{\boldsymbol{\psi} _s}}}{{\text{d}{\boldsymbol t}}},\\ {\boldsymbol u}_r = {{R}_{ r}}{\boldsymbol{i}_r} + \frac{{\text{d}{\boldsymbol{\psi} _r}}}{{\text{d}{\boldsymbol t}}}。\\ \end{gathered} \right. $ | (1) |
磁链方程:
| $ {\boldsymbol{\psi} _s} = {{L}_{ s}}{\boldsymbol{i}_s} + {{L}_{ m}}{\boldsymbol{i}_r} ,$ | (2) |
| $ {\boldsymbol{\psi} _r} = {{L}_{ r}}{{\boldsymbol i}_r} + {{L}_{ m}}{\boldsymbol{i}_s} 。$ | (3) |
机械运动方程:
| $ {\boldsymbol{T}_e} = {\boldsymbol{T}_m} + \frac{{{J}}}{{{{{n}}_{{P}}}}}\frac{{{\text d}{\boldsymbol{\omega} _r}}}{{\text d}{\boldsymbol t}}。$ | (4) |
电磁转矩方程:
| $ {\boldsymbol{T}_e} = \frac{3}{2}{{{n}}_{{p}}}{\boldsymbol{\psi} _s} \otimes {\boldsymbol{i}_s} 。$ | (5) |
式中:us和ur分别为定、转子电压;is为定子电流;Rs、Rr分别为定、转子电阻;Ψs、Ψr分别为定、转子磁链;Ls、Lr分别为定、转子电感;Lm为定转子间互感;Te、Tm分别为电磁转矩和负载转矩;np为极对数;J为转动惯量;
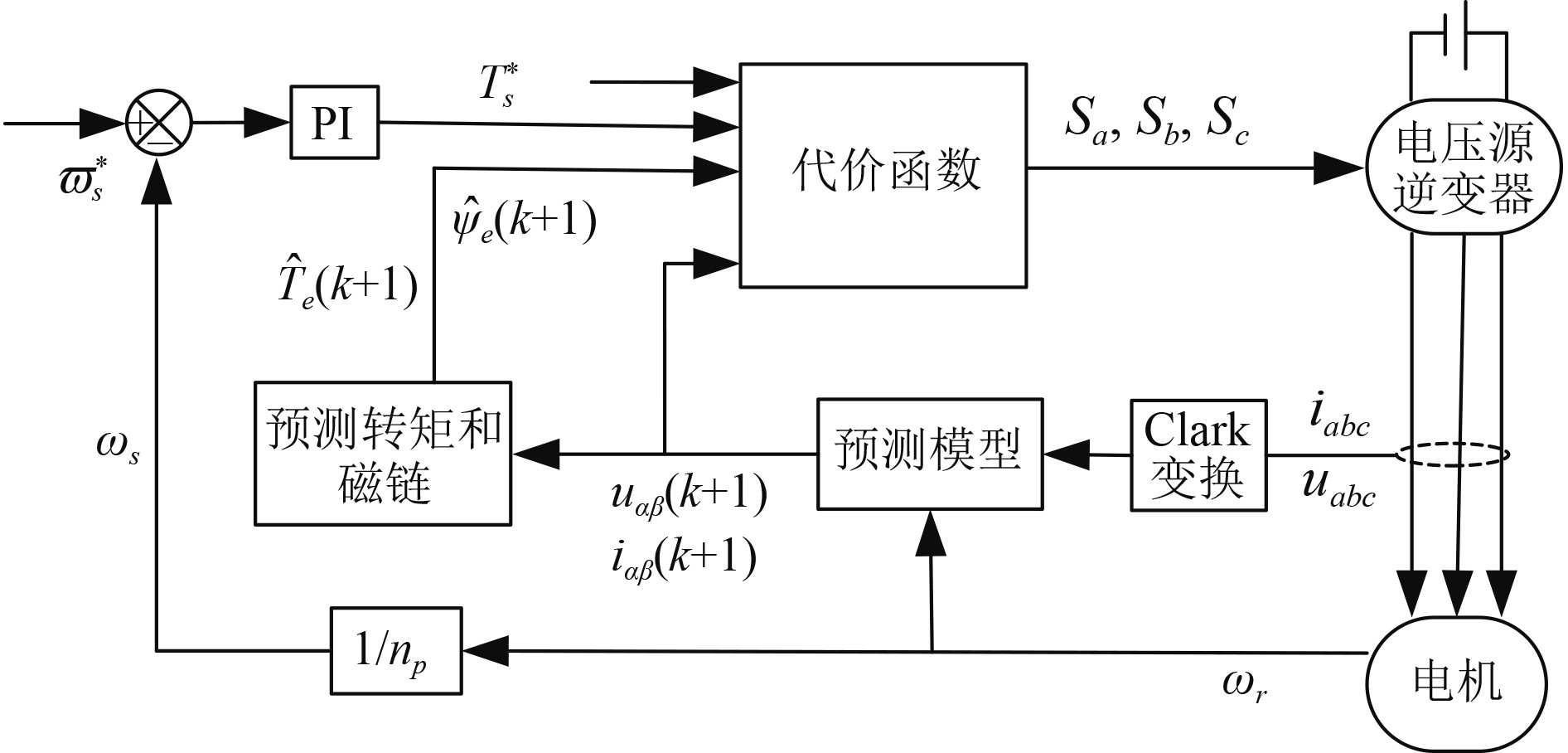
DTC控制技术发展成熟,本文不对其进行赘述,可参考文献[1,8]。MPTC控制和DTC控制一样,以控制磁链和转矩为目标,原理如图1所示。首先测量出在αβ坐标系下电机当前k时刻的电压
|
图 1 MPTC控制框图 Fig. 1 Control diagram of MPTC |
将式(1)的定子电压方程在αβ坐标轴上分解变换得到:
| $ \left\{ \begin{gathered} \frac{{\text{d}{\boldsymbol{\psi} _{s\alpha }}}}{{\text{d}{\boldsymbol t}}}{\text{ = }}{{\boldsymbol u}_{sa}} - {{ R}_s}{{\boldsymbol i}_{s\alpha }} ,\\ \frac{{\text{d}{\boldsymbol{\psi} _{s\beta }}}}{{\text{d}{\boldsymbol t}}}{\text{ = }}{{\boldsymbol u}_{s\beta }} - {{ R}_s}{{\boldsymbol i}_{s\beta }}。\\ \end{gathered} \right. $ | (6) |
设Ts为系统采样周期,将式(6)代入式(7),进行离散化得到式(8):
| $ \frac{{{\text d}{\boldsymbol x}}}{{{\text d}{\boldsymbol t}}} = \frac{{{\boldsymbol x}({\boldsymbol k} + 1) - {\boldsymbol x}({\boldsymbol k})}}{{{{{T}}_{{s}}}}} ,$ | (7) |
| $ \left\{ \begin{gathered} {\boldsymbol{\psi} _{s\alpha }}(\boldsymbol{k} + 1) = {\boldsymbol{\psi} _{s\alpha }}(\boldsymbol{k}) + {{ T}_{ s}}({\boldsymbol{u}_{s\alpha }}(\boldsymbol{k}) - {{ R}_{ s}}{\boldsymbol{i}_{s\alpha }}(\boldsymbol{k})) ,\\ {\boldsymbol{\psi} _{s\beta }}(\boldsymbol{k} + 1) = {\boldsymbol{\psi} _{s\beta }}(\boldsymbol{k}) + {{ T}_{ s}}({\boldsymbol{u}_{s\beta }}(\boldsymbol{k}) - {{ R}_{ s}}{\boldsymbol{i}_{s\beta }}(\boldsymbol{k}))。\\ \end{gathered} \right. $ | (8) |
再联合式(2)和式(3),重新选取电流和磁链作为控制系统状态变量,得到如下方程:
| $ \left\{ \begin{split} \frac{{{\text d}{{\boldsymbol i}_{s\alpha }}}}{{{\text d}t}} =& - \lambda({{R}_{\text s}}{L_r}{\text{ + }}{{R}_r}{L_s}){\boldsymbol{i}_{s\alpha }} - {\boldsymbol{\varpi} _r}{{\boldsymbol i}_{s\beta }} + \\ &\lambda{{R}_r}{\psi _{s\alpha }} + \lambda{L_r}{\boldsymbol{\varpi} _r}{\psi _{s\beta }} + \lambda{L_r}{\boldsymbol{u}_{s\alpha }} ,\\ \frac{{{\text d}{\boldsymbol{i}_{s\beta }}}}{{{\text d}t}} =& {\boldsymbol{\varpi} _r}{\boldsymbol{i}_{s\alpha }} - {\text{λ (}}{{R}_s}{L_r}{\text{ + }}{{{R}}_r}{L_s}{\text{)}}{\boldsymbol{i}_{s\beta }} - \\ & \lambda{L_r}{\boldsymbol{\varpi} _r}{\boldsymbol{\psi} _{s\alpha }} + \lambda{{R}_r}{\boldsymbol{\psi} _{s\beta }} + \lambda{L_r}{\boldsymbol{u}_{s\beta }} 。\\ \end{split} \right. $ | (9) |
式中:
假设系统机械时间远大于电磁时间,则将式(9)离散化得到:
| $ \left\{ \begin{split} {\widehat {\boldsymbol i}_{s\alpha }}({{\boldsymbol k}} + 1) =& {{\boldsymbol i}_{s\alpha }}({\boldsymbol k}) - \lambda{{ {T}}_{ {s}}}{ {(}}{{ {R}}_{ {s}}}{{ {L}}_{ {r}}}{ { + }}{{ {R}}_{ {r}}}{{ {L}}_{ {s}}}{ {)}}{{\boldsymbol i}_{s\alpha }}({\boldsymbol k}) -\\ & {{\boldsymbol \varpi} _r}{{ {T}}_{ {s}}}{{\boldsymbol i}_{s\beta }}({\boldsymbol k}) + \lambda{{ {R}}_{ {r}}}{{ {T}}_{ {s}}}{{\boldsymbol \psi} _{s\alpha }}({\boldsymbol k}) + \\ & \lambda{L_s}{{\boldsymbol \varpi} _r}{{ {T}}_{ {s}}}{{\boldsymbol \psi} _{s\beta }}({\boldsymbol k}) + \lambda{{ {L}}_{ {r}}}{{ {T}}_{ {s}}}{u_{s\alpha }}({\boldsymbol k}) ,\\ {\widehat {\boldsymbol i}_{s\beta }}({\boldsymbol k} + 1) =& {{\boldsymbol i}_{s\beta }}({\boldsymbol k}) + {{\boldsymbol \varpi} _r}{{ {T}}_{ {s}}}{{\boldsymbol i}_{s\alpha }}({\boldsymbol k}) - \lambda {{ {T}}_{ {s}}}{ {(}}{{ {R}}_{ {s}}}{{ {L}}_{ {r}}} + \\ & {{ {R}}_{ {r}}}{{ {L}}_{ {s}}}{ {)}}{{\boldsymbol i}_{s\beta }}({\boldsymbol k}) - \lambda{{ {L}}_{ {r}}}{{\boldsymbol \varpi} _r}{{ {T}}_s}{{\boldsymbol \psi} _{s\alpha }}({\boldsymbol k}) + \\ &\lambda{{ {R}}_{ {r}}}{{ {T}}_{ {s}}}{{\boldsymbol \psi} _{s\beta }}({\boldsymbol k}) + \lambda{{ {L}}_{ {r}}}{{ {T}}_{ {s}}}{u_{s\beta }}({\boldsymbol k}) 。\\ \end{split} \right. $ | (10) |
再将式(8)和式(10)代入电磁转矩方程式(5)可得到
| $ \begin{gathered} { {\boldsymbol T}_e}({\boldsymbol k} + 1) = 1.5{{{n}}_{{p}}}({{\boldsymbol \psi} _{s\alpha }}({\boldsymbol k} + 1) \times {\widehat {\boldsymbol i}_{s\beta }}({\boldsymbol k} + 1) - \\ {{\boldsymbol \psi} _{s\beta }}({\boldsymbol k} + 1) \times {\widehat {\boldsymbol i}_{s\alpha }}({\boldsymbol k} + 1)) 。\\ \end{gathered} $ | (11) |
最后,逆变器根据代价函数的最小值对应的开关变化动作最小的规则来选取最优电压矢量。设计代价函数如式(12),kψ为磁链幅值权重系数。
| $ {\boldsymbol{G}_n} = \left| {{\boldsymbol T}_e^* - {{\boldsymbol T}_e}({\boldsymbol k} + 1)} \right| + {{k}_{\psi }}\left| {\left| {\boldsymbol \psi _s^*} \right| - \left| {{{\boldsymbol \psi }_s}({\boldsymbol k} + 1)} \right|} \right| 。$ | (12) |
对于两电平逆变器,设ux为8个电压矢量,其中有2个零电压矢量和6个非零电压矢量,最优电压矢量选取表达式为式(13),从而实现了实时对电机控制系统优化的过程:
| $ \left\{ \begin{gathered} {{\boldsymbol u}_f} = \left| {{{\boldsymbol u}_x} - {{\boldsymbol u}_s}} \right|,{{\boldsymbol u}_x} \in \left\{ {{{{u}}_{\text{0}}}{\text{,}}{{{u}}_{\text{1}}}, \ldots ,{{{u}}_{\text{7}}}} \right\},\\ {{\boldsymbol u}_g} = \min \left\{ {{{\boldsymbol u}_f}} \right\}。\\ \end{gathered} \right. $ | (13) |
由2.1节可知,代价函数的选取决定着逆变器电压矢量的输出,从而直接影响电机的运行性能。通常,kψ的取值为额定转矩和给定磁链的比值,但上文指出该额定值不能直接使用。本文也从如下仿真实验进行论证说明,本实验在Matlab/Simulink上进行。电机参数如表1所示,给定磁链为0.4 Wb,kψ取额定值62.5。
|
|
表 1 电机参数表 Tab.1 Parameter table of the motor |
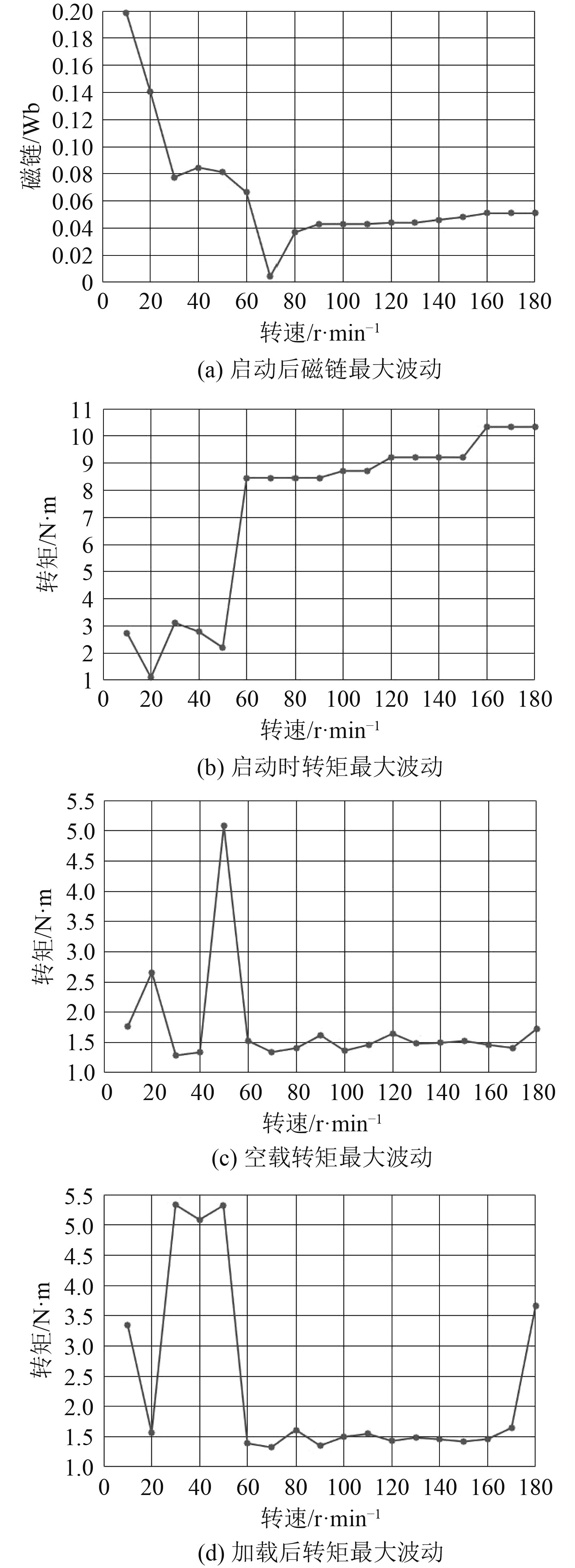
设仿真时间1 s,每次实验在0.1 s后设定不同给定转速共18组,0.5 s时负载由0变为20 N·m,该负载下最大可调转速为180 r/min。仿真结果表明,MPTC控制对各个转速都有很好的跟踪。下面对磁链、转矩以及电流进行分析,如图2 MPTC在额定系数下各转速性能分析图。
|
图 2 MPTC在额定权重系数下各转速性能分析 Fig. 2 Analysis of the performance of the MPTC at various speeds at the weighting factor |
由图2(a)可知,在转速低于50 r/min时,启动完成后的磁链幅值最大波动超过0.08 Wb,约为给定值的20%,波动较大。
实验中得到的启动转矩约为30 N·m,再由图2(b)可知,启动时的转矩最大波动总体上随着启动转速的增大而增大,转速超过50 r/min时波动最大幅值会发生突变,急剧上升,最大波动幅值约为启动转矩的33%。
由图2(c)和图2(d)可知,电机总体上在中高速时转矩脉动在1.5 N·m上下波动,运行平稳,而在低速段相对较差。在该负载下,转速接近可调最大转速时,加载后转矩最大波动幅值有上升趋势。
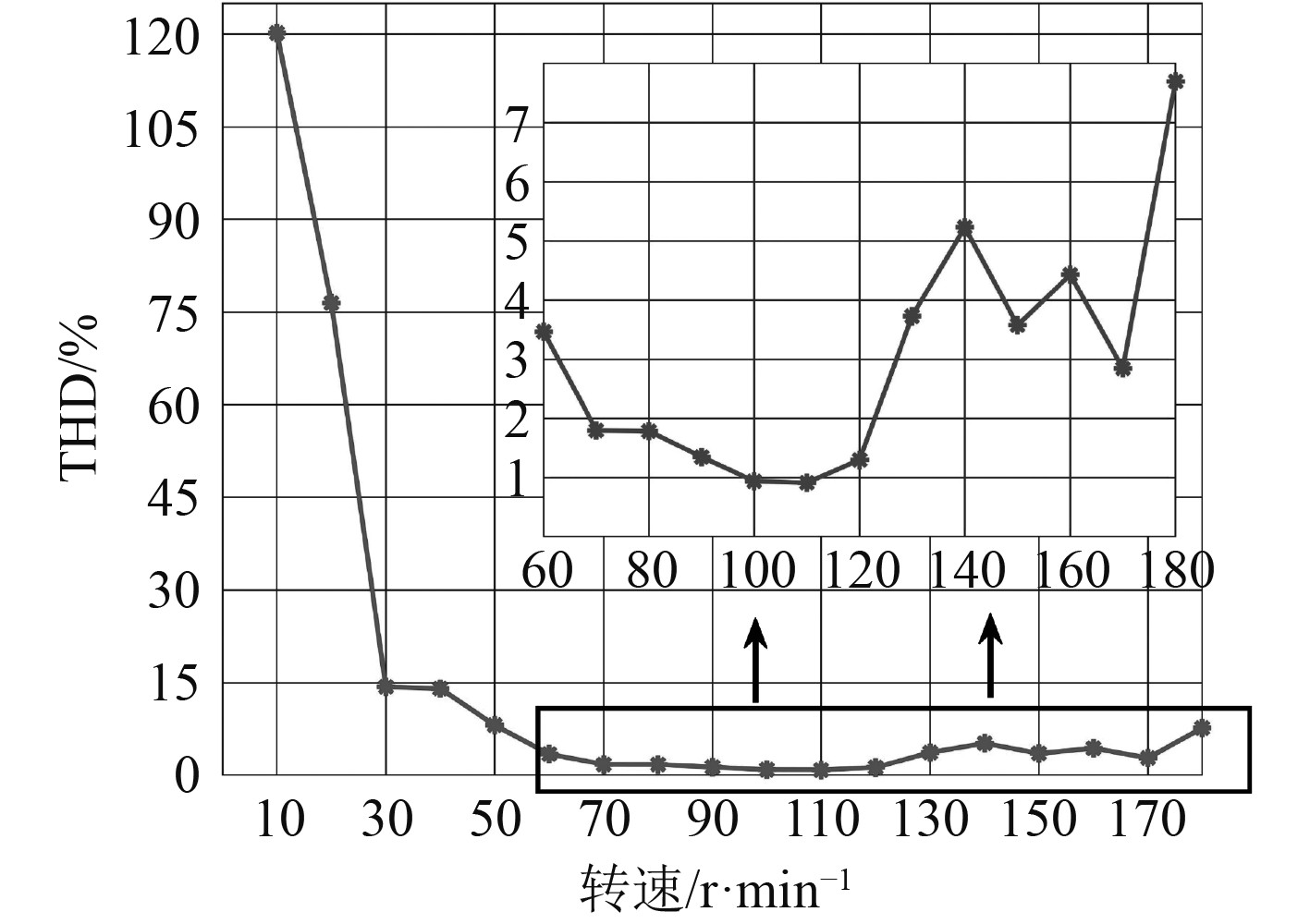
图3为各转速下整个过程的电流谐波失真(THD)图,转速为 50 r/min时电流THD为8.123%,因此低速段电流谐波失真过大;转速在60~120 r/min范围的THD平均为1.649%;转速在130~180 r/min范围THD平均为4.751%。因此,额定权重系数对中速段的电流谐波抑制相对较好。
|
图 3 各转速电流谐波失真 Fig. 3 Current harmonic distortion at various speeds |
综上,MPTC控制的额定权重系数并不是船舶推进的最优权重系数,不能使电机在各个工况下的运行性能达到最好,因此,需要根据不同的工况设计不同的权重系数使电机有良好的控制性能。但上文已说明合适系数的选取需通过大量的仿真实验得到且过程复杂,同时,船舶电力推进电机工作工况本身也极其复杂,这种情况下,权重系数也变得更加难以整定。因此,本文提出预测磁链控制以消除对权重系数的整定工作。
3 自适应预测磁链控制 3.1 等效磁链观测预测磁链控制方式将式(13)中2个控制目标
联合式(2)和式(3)求得is,代入电磁转矩方程(5)得:
| $ \begin{split} {{\boldsymbol T}_e} =\frac{3}{2}{{{n}}_{{p}}}{\text{λ }}{{{L}}_{{m}}}\left| {{{\boldsymbol \psi} _r}} \right|\left| {{{\boldsymbol \psi} _s}} \right|\sin \left( {\angle {{\boldsymbol \psi} _s} - \angle {{\boldsymbol \psi} _r}} \right)。\end{split} $ | (14) |
由式(14)变换可得:
| $ \angle {{\boldsymbol \psi} _s} = \angle {{\boldsymbol \psi} _r} + \arcsin \left( {\frac{{{{\boldsymbol T}_e}}}{{\displaystyle\frac{3}{2}{{p}\lambda}{{{L}}_{{m}}}\left| {{{\boldsymbol \psi} _r}} \right|\left| {{{\boldsymbol \psi} _s}} \right|}}} \right)。$ | (15) |
上式与电机外界因素无关,因此与
| $ \angle {\boldsymbol \psi} _e^{ref} = \angle {{\boldsymbol \psi} _r} + \arcsin \left( {\frac{{{\boldsymbol T}_e^*}}{{\displaystyle\frac{3}{2}{{p}\lambda}{{{L}}_{{m}}}\left| {{{\boldsymbol \psi} _r}} \right|{\boldsymbol \psi} _{{s}}^{\text{*}}}}} \right)。$ | (16) |
由此可得等效定子磁链:
| $ {{\boldsymbol \psi} }_{e}^{ref}={{\boldsymbol \psi} }_{{s}}^{\text{*}}\mathrm{exp}\left({j}·\angle {{\boldsymbol \psi} }_{e}^{ref}\right) 。$ | (17) |
相应代价函数变为式(18),从而消除了权重系数,同时也降低预测控制算法的复杂程度,提高了预测控制在船舶电力推进电机的控制性能。
| $ {{\boldsymbol G}_f} = \left| {{\boldsymbol \psi} _e^{ref} - {{{\boldsymbol \psi} }_s}({\boldsymbol k} + 1)} \right|。$ | (18) |
值得注意的是,可以根据控制系统的实际运行状态,对数字控制器延时情况进行补偿,实现无差拍控制,对一拍延时补偿措施进行举例说明,如表2所示。
|
|
表 2 一拍延时补偿 Tab.2 One beat delay compensation |
理想状态下应该在时刻k时施加的电压u(k),即逆变器开关动作,由于系统延时在k+1时刻执行。消除延时方法为:先预测k+1时刻的电流值和电压值,进而预测k+1时刻和k+2时刻的磁链和转矩,然后逆变器按k+2时刻的代价函数来确定k+1时刻的电压矢量,于是重新构造代价函数:
| $ {{\boldsymbol G}_{f2}} = \left| {{\boldsymbol \psi} _e^{ref} - {{ {\boldsymbol \psi} }_s}(k + 2)} \right| 。$ | (19) |
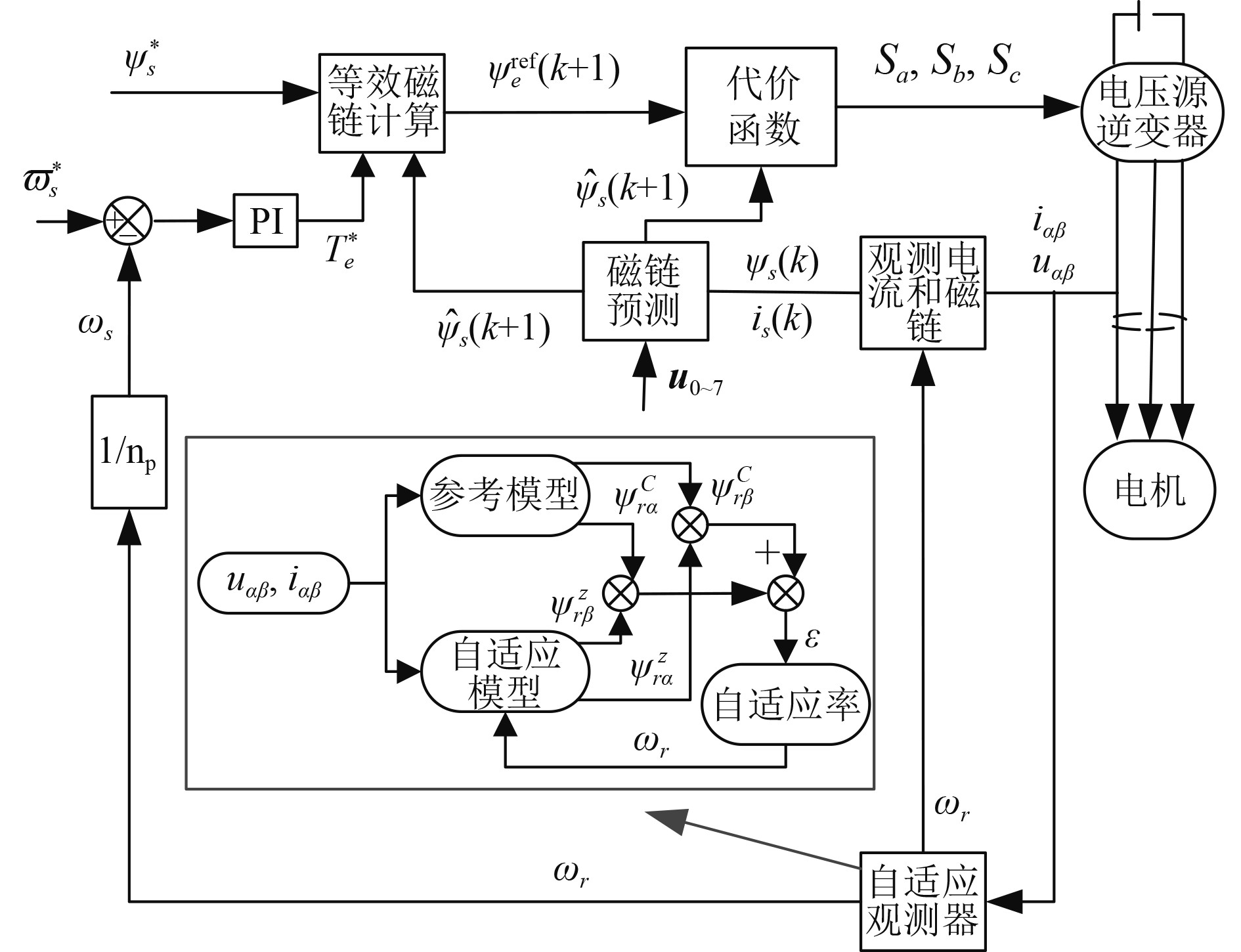
基于自适应算法的预测磁链控制原理图如图4所示,自适应观测器的输入为可测的电流值和电压值,其主要包含参考模型和自适应模型,其中自适应模型包含转速信息。通过2个模型的差值构建自适应率,对电机转速进行估算,可以在线调节自适应模型使其输出无限接近于参考模型,以实现自动调节的目的[18]。
|
图 4 MARS-MPFC控制原理图 Fig. 4 Control diagram of MARS-MPFC |
图4中参考模型状态方程如式(20),u为输入,xc为状态变量,Ac和Bc为系数矩阵。
| $ \left\{ \begin{gathered} \frac{{{\text d}{{\boldsymbol x}_c}}}{{{\text d}{\boldsymbol t}}} = {{\boldsymbol{A}}_{{c}}}{{\boldsymbol x}_c} + {{\boldsymbol{B}}_{{c}}}{\boldsymbol u},\\ {{\boldsymbol x}_c}\left( 0 \right) = {{\boldsymbol x}_{c0}}。\\ \end{gathered} \right. $ | (20) |
自适应模型状态方程为式(21),xz为模型状态变量,
| $ \left\{ \begin{gathered} \frac{{{\rm d}{{\boldsymbol x}_z}}}{{{\rm d}t}} = {{\boldsymbol A}_z}\left( {{\boldsymbol e},{\boldsymbol t}} \right){{\boldsymbol x}_z} + {{\boldsymbol B}_z}\left( {{\boldsymbol e},{\boldsymbol t}} \right)u ,\\ {{\boldsymbol x}_z}\left( 0 \right) = {{\boldsymbol x}_{z0}},{\boldsymbol A}\left( 0 \right) = {{\boldsymbol A}_{z0}},{\boldsymbol B}\left( 0 \right) = {{\boldsymbol B}_{z0}}。\\ \end{gathered} \right. $ | (21) |
式中:广义误差
本文基于转子磁链模型对转速进行观测,得到转子磁链电压参考模型如下:
| $ \left\{ \begin{gathered} {\boldsymbol \psi} _{_{r\alpha }}^c = \frac{{{{{L}}_{{r}}}}}{{{{{L}}_{{m}}}}}\left[ {\int {\left( {{{\boldsymbol u}_{s\alpha }} - {{{R}}_{{s}}}{{\boldsymbol i}_{s\alpha }} - {{\delta }}{{{L}}_{{s}}}\frac{{{\text{d}}{{\boldsymbol i}_{s\alpha }}}}{{{\text{d}}{\boldsymbol t}}}} \right){\text{d}}{\boldsymbol t}} } \right] ,\\ {\boldsymbol \psi} _{_{r\beta }}^c = \frac{{{{{L}}_{{r}}}}}{{{{{L}}_{{m}}}}}\left[ {\int {\left( {{{\boldsymbol u}_{s\beta }} - {{{R}}_{{s}}}{{\boldsymbol i}_{s\beta }} - {\text{δ }}{{{L}}_{{s}}}\frac{{{\text{d}}{{\boldsymbol i}_{s\beta }}}}{{{\text{d}}{\boldsymbol t}}}} \right){\text{d}}{\boldsymbol t}} } \right] 。\\ \end{gathered} \right. $ | (22) |
式中:
转子磁链电流自适应模型如式(23),其包含转速信息,可以对系统性能进行跟踪,
| $ \left\{ \begin{gathered} {\boldsymbol \psi} _{_{r\alpha }}^z = \frac{1}{{{{{T}}_{{r}}}}}\left[ {\int {\left( {{{{L}}_{{m}}}{{\boldsymbol i}_{s\alpha }} - {\boldsymbol \psi} _{_{r\alpha }}^z - {{\boldsymbol \varpi} _r}{{{T}}_{{r}}}{\boldsymbol \psi} _{_{r\beta }}^z} \right){\text d}{\boldsymbol t}} } \right],\\ {\boldsymbol \psi} _{_{r\beta }}^z = \frac{1}{{{{{T}}_{{r}}}}}\left[ {\int {\left( {{{{L}}_{{m}}}{{\boldsymbol i}_{s\beta }} - {\boldsymbol \psi} _{_{r\beta }}^z + {{\boldsymbol \varpi} _r}{{{T}}_{{r}}}{\boldsymbol \psi} _{_{r\alpha }}^z} \right){\text d}{\boldsymbol t}} } \right]。\\ \end{gathered} \right. $ | (23) |
式中:
本文根据Popov超稳定性理论设计自适应率[19],得到电机电角速度观测值:
| $ {{\boldsymbol \varpi} _r} = \left( {{{{k}}_{{p}}} + \frac{{{{{k}}_{{i}}}}}{{s} }} \right)\left( {{\boldsymbol \psi} _{_{r\alpha }}^z{\boldsymbol \psi} _{_{r\beta }}^c - {\boldsymbol \psi} _{_{r\alpha }}^c{\boldsymbol \psi} _{_{r\beta }}^z} \right) 。$ | (24) |
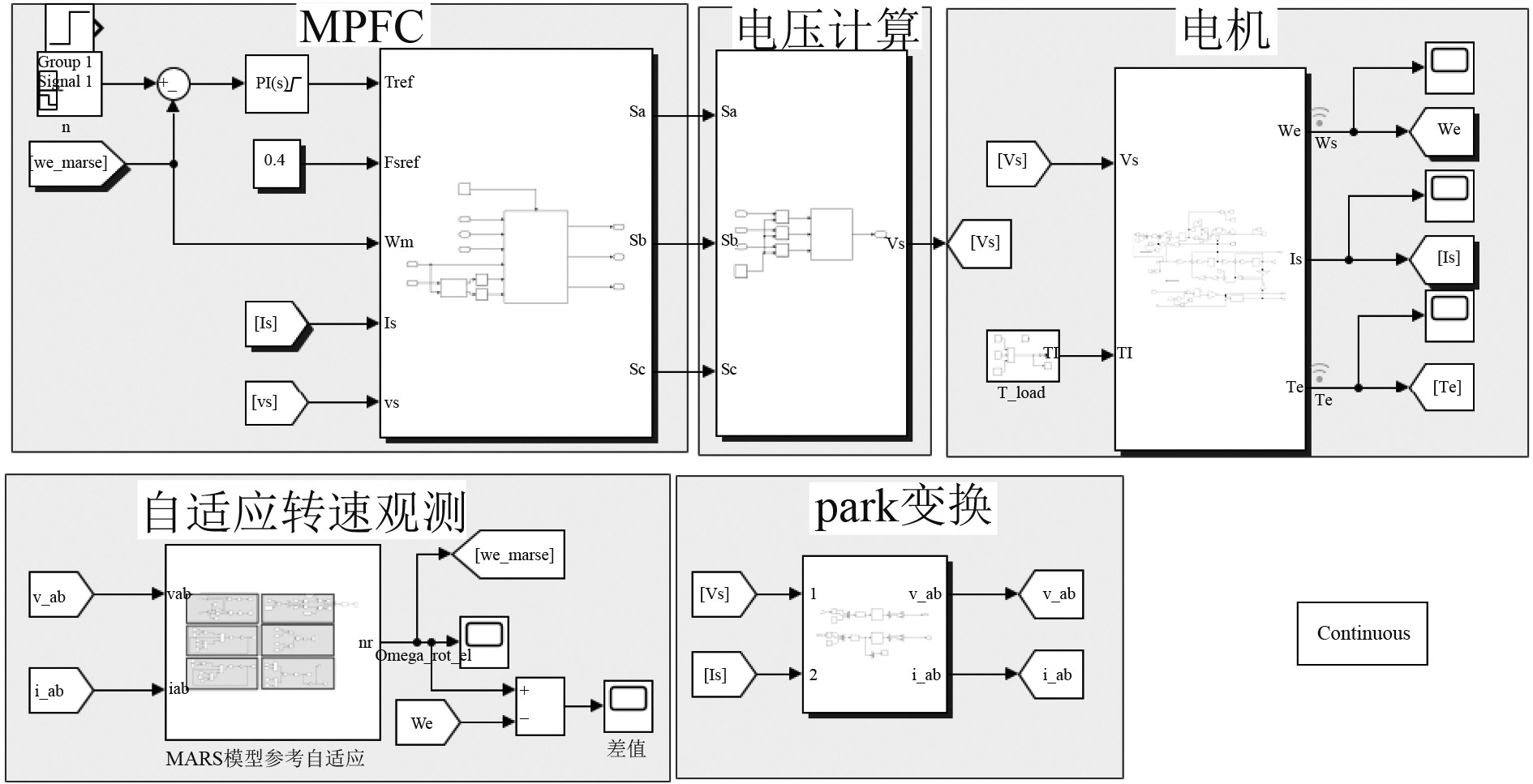
为验证MARS-MPFC控制的可行性和控制效果,对DTC、MPTC以及MARS-MPFC等3种控制方式进行仿真对比研究, MARS-MPFC控制的仿真模型如图5所示。以上3种控制方式均在相同条件及参数下进行,电机相关参数见表1。
|
图 5 MARS-MPFC仿真图 Fig. 5 Simulation diagram of MARS-MPFC |
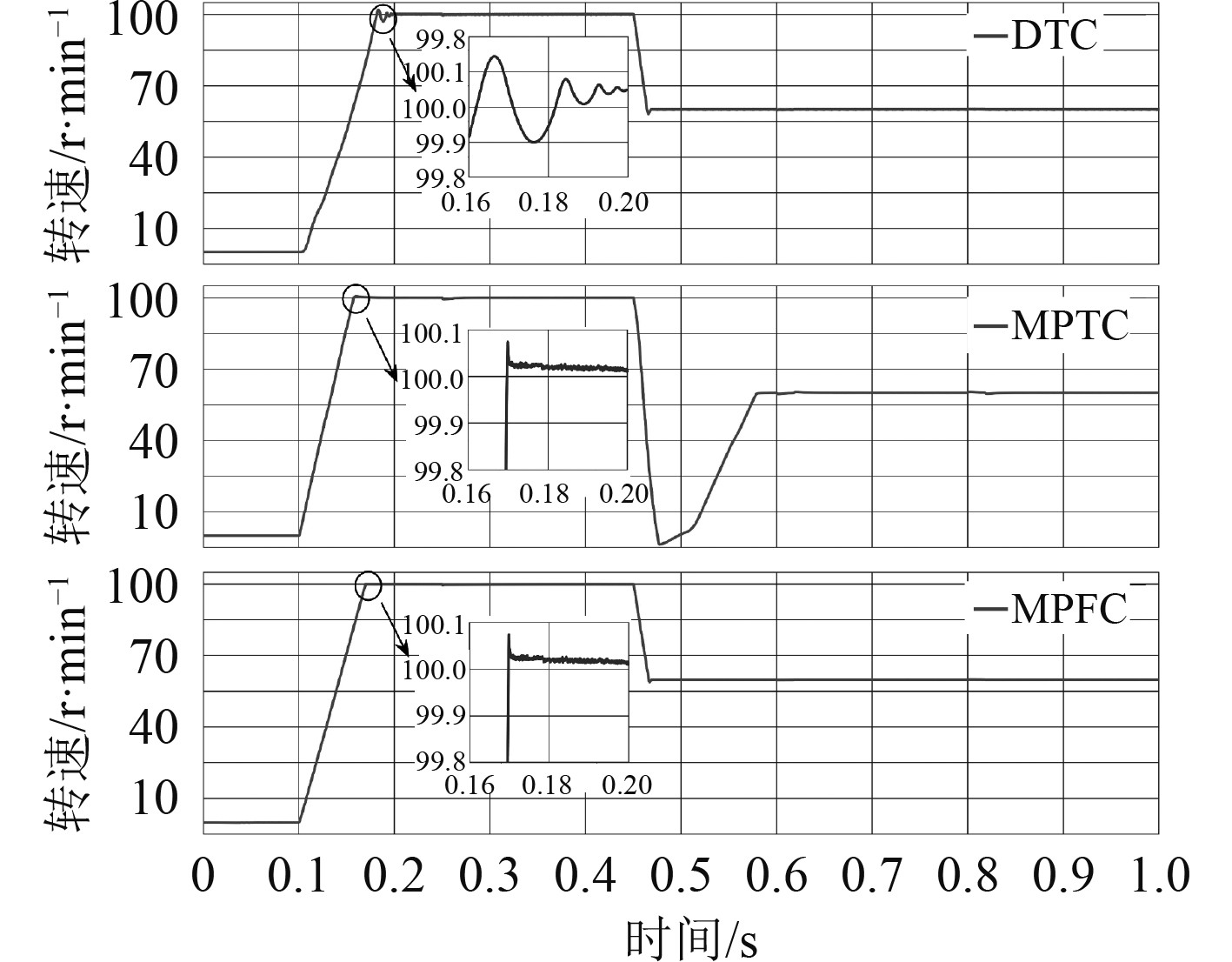
设定仿真时间1 s,定子磁链参考值0.4 Wb。电机空载启动,0.1 s和0.45 s分别设定转速为100 r/min和60 r/min以模拟船舶加减速过程,在0.6 s和0.8 s时设置短时间内负载的突增和突减,大小均为8 N·m,以模拟船舶螺旋桨短时间内进出海面的情况。仿真得到3种控制方式的转速对比(见图6)、转矩对比(见图7)、A相电流对比(见图8)以及MARS-MPFC控制实际转速与自适应算法估算的转速差值(见图9)。
|
图 6 3种控制转速对比图 Fig. 6 Speed comparison diagram of the three controls |
|
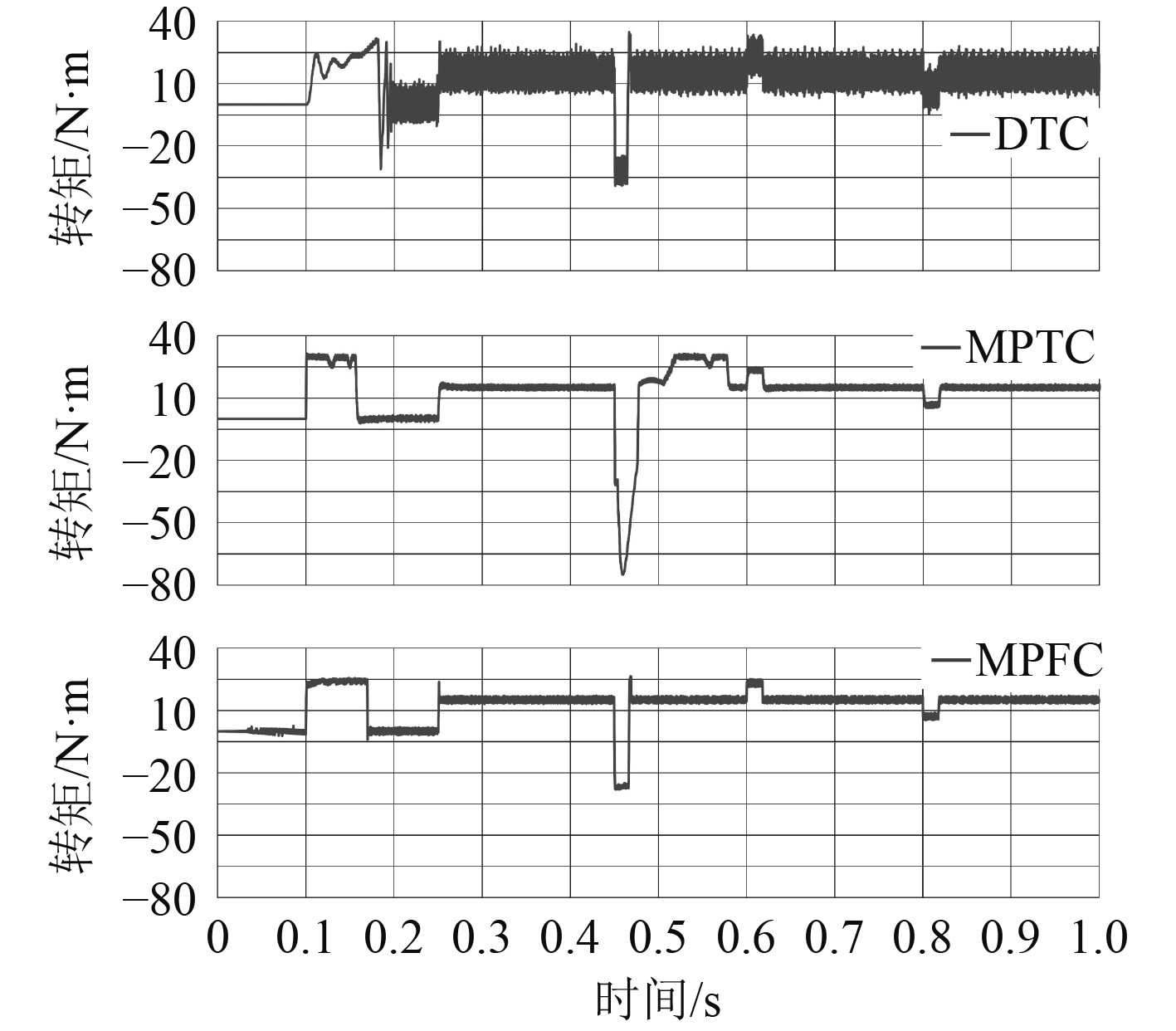
图 7 3种控制转矩对比图 Fig. 7 Torque comparison diagram of the three controls |
|
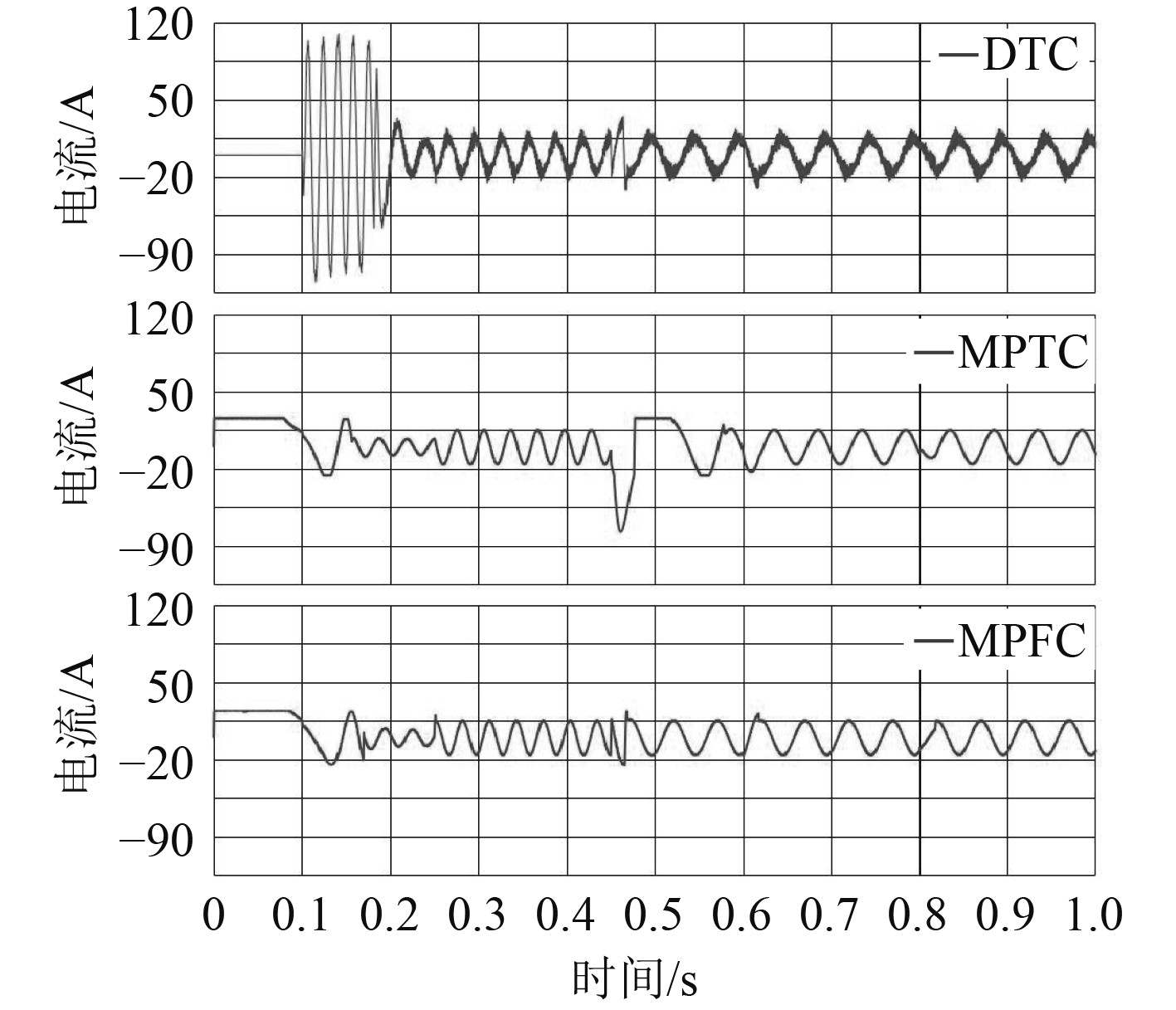
图 8 3种控制A相电流对比图 Fig. 8 Comparison diagram of phase A currents of the three controls |
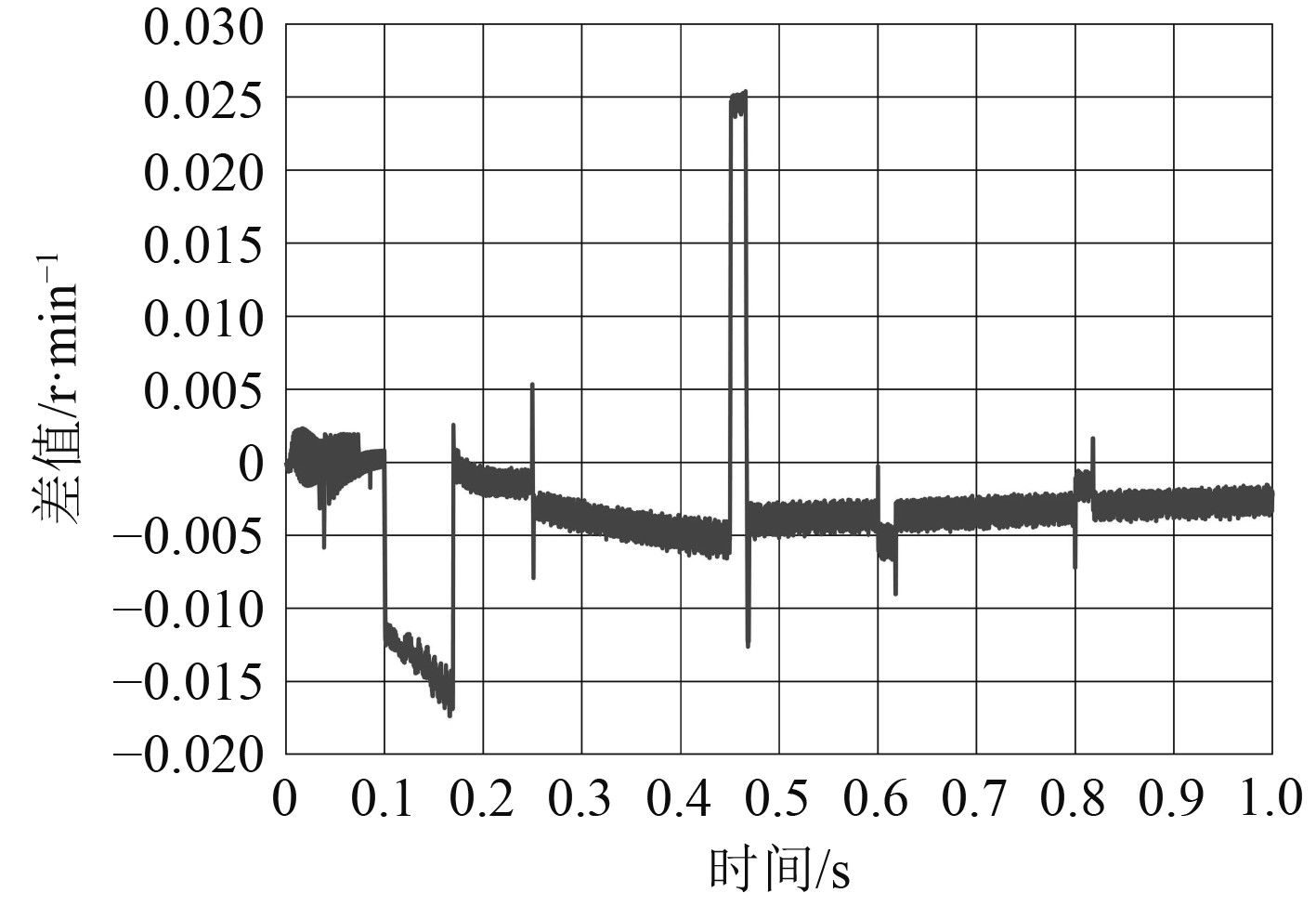
|
图 9 MARS观测转速与实际转速差 Fig. 9 The difference between the speed observed by MARS and the actual speed |
在相同条件下,根据图6可知,DTC控制和MPFC控制对转速的响应及调节精度都很好,但是从0.18 s时的放大图看,DTC控制在加速到达设定转速时有2%较小的超调量;虽然MPTC控制虽然仍能到达设定转速,但在0.45 s减速时有个明显过大的超调量,对减速过程的调节性能较弱;而MPFC控制具有相对较快的动态性能,且几乎无超调,并且由图9实际转速和观测器估算的转速差值可以看出,自适应算法在整个过程对转速都有十分精准的观测值,差值最大不超过0.025 r/min,具有较强的鲁棒性。
根据图7,2种预测控制在空载和加载后平稳运行状态下,转矩脉动幅值明显小于DTC。在0.1 s之后启动过程,MPFC控制电磁转矩总体稳定,DTC控制则明显可以看到有个振荡过程;而MPTC控制在0.1 s启动加速和0.5 s减速之后的稳定过程中在存在略微波动,因此MPC控制启动性能相对较好。
从图8可知,DTC控制启动电流大,最大值约为110 A,且波动频率大,而2种MPC控制启动电流最大幅值约为25 A,比DTC控制降低了77.3%。MPTC控制在0.5 s减速时,电流大幅度突变,这也是转速下降幅度大的原因,但MPFC控制则相对稳定。由于负载的突增和突减持续时间只有0.018 s,不足电流的1/4个周期,因此总体上变化不太明显。但仔细观察可以发现,相比于前后电流值,MPTC控制0.6 s后的短时间内有个较急剧的下降;并且MPFC控制和MPTC控制在0.6 s后的第一个幅值比前后的峰值都大。MPTC控制0.8 s负载突减后的短时减内,其电流变化较缓慢,且幅值比前后电流峰值都要小。MPFC控制也是在负载突减结束后,其电流值才突然增大到峰值15 A左右。
另外,对船舶电机A相电流进行总谐波失真对比分析,在转速100 r/min的条件下,DTC谐波失真
综上,MPFC控制对转速有着很好的控制效果,几乎无超调,没有MPTC控制减速时的转速过大超调量;和DTC以及MPTC控制相比,MPFC控制有着更小磁链和转矩脉动;MPC控制比DTC控制有着更小的启动电流,且有着更好的抑制谐波的能力;MARS算法对MPFC控制的电机转速有着非常精准的观测,可以有效解决船舶电机的速度传感器问题。
5 结 语本文提出预测磁链控制,解决了船舶推进电机传统预测控制中权重系数难以整定和优化的问题;同时,使用自适应算法对MPFC控制进行改进,解决了预测控制中涉及的速度传感器问题。通过相关的仿真实验得到如下结论:1)MPTC控制常用的额定权重系数并不能满足船舶电机所有调速范围,而MPFC控制可以成功消除对权重系数的整定工作及其影响。2)MARS-MPFC控制对转速有着优良的控制效果,启动性能好,并具有很好的稳态特性和鲁棒性,可以提高船舶推进电机的控制性能;3)虽然MPTC控制在减速时刻超调量较大,但是在其他过程也有很好的调速效果,值得进一步研究优化。4)本文未对不同权重系数对船舶电机性能的具体影响进行研究,后续可随着权重系数设计理论的完善,进一步对2种预测控制进行对比研究。
| [1] |
刘恩东, 高岚, 罗永吉, 等. 船舶电力推进系统VC与DTC调速控制策略建模与仿真研究[J]. 舰船科学技术, 2017, 39(6): 88-93. LIU Endong, GAO Lan, LUO Yongji, et al. Research on modeling & simulation analysis of marine electric propulsion system of VC/DTC speed control strategy[J]. Ship Science and Technology, 2017, 39(6): 88-93. |
| [2] |
TOBIAS G, GEORGIOS P. Direct torque control for lnduction motor drives: a model predictive control approach based on feasibility[J]. Hybrid Systems: Computation and Control. 2005, 3414: 274−290.
|
| [3] |
薛亚茹. 感应电机模型预测电流控制研究[D]. 北京: 北京交通大学, 2021.
|
| [4] |
胡云飞, 高岚, 徐合力, 等. 船舶永磁同步电机模型预测转矩控制[J]. 中国航海, 2019, 42(2): 27-31. |
| [5] |
VAZQUEZ S, RODRIGUEZ J, RIVERA M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics. 2017. Vol. 64(2): 935−947.
|
| [6] |
王利辉, 基于参数辨识的永磁同步电机预测控制研究[D]. 徐州: 中国矿业大学, 2020.
|
| [7] |
郭燚, 王超, 解文祥. 用于船舶永磁推进电机驱动控制的MMC模型预测方法[J]. 中国舰船研究, 2021, 6 (4): 179−189+198.
|
| [8] |
李英帅, 基于多相异步电动机的船舶电力推进系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [9] |
刘乐. 船舶电力推进系统性能仿真研究与软件实现[D]. 武汉: 武汉理工大学, 2018.
|
| [10] |
高岚, 朱师伦, 胡云飞. 基于MPTC的船舶推进电机新型SMO[J]. 船舶工程, 2019, 41(8): 73-78,83. |
| [11] |
HABIBULLAH M, DYLAN D, DAN X, et al. Low complexity predictive torque control strategies for a three-level inverter driven induction motor[J]. IET Electric Power Applications, 2017, 11(5): 776-783. DOI:10.1049/iet-epa.2016.0572 |
| [12] |
谢昊天, 汪凤翔, 柯栋梁, 等. 基于集成优化的感应电机无权重系数预测转矩控制[J]. 电工技术学报2022, 37 (12): 2992−3003.
|
| [13] |
ZHANG Yongchang, YANG Haitao. Model predictive control of lnduction motor drives: flux control versus torque control[J]. ICPE(ISPE), 2015: 86−91.
|
| [14] |
GEYER T. Algebraic tuning guidelines for model predictive torque and flux control[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4464-4475. DOI:10.1109/TIA.2018.2835375 |
| [15] |
DRAGIDEVIC T, NOVAK M. Weighting factor design in model predictive control of power electronic converters: n artificial neural network approach[J]. IEEE Transactions on industrial Electronics, 2019, 66(11): 8870-8880. DOI:10.1109/TIE.2018.2875660 |
| [16] |
魏玉春, 夏长亮, 刘涛. 两电机转矩同步系统有限集模型预测控制[J]. 电工技术学报2016, 31(19): 115−122.
|
| [17] |
ROJAS C, RODRIGUEZ J, VILLARROEL F, et al. Predictive torque and flux control without weighting factors[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 681-690.. DOI:10.1109/TIE.2012.2206344 |
| [18] |
HA Jung-lk, SUL Seung-Ki. Sensorless field-orientation control of an induction machine by high-frequency signal injection[J]. IEEE Transactions on Industry Applications, 1999, 35(1): 45-51. DOI:10.1109/28.740844 |
| [19] |
陈晓霖. 异步电机无速度传感器低速运行高性能控制技术研究[D]. 青岛: 山东科技大学, 2018.
|
 2024, Vol. 46
2024, Vol. 46
