0 引　言

船舶为海上运输的主要力量，在复杂多变的海洋环境下，风浪、潮汐等将给船舶航行带来诸多挑战^[1]。欠驱动船舶是指系统控制输入量个数少于船舶自由度维数的水面船舶。在海上航行的船舶中，大多数都属于欠驱动船舶，因其通常仅装备有螺旋桨主推进器和舵装置，用于推进和操纵船舶，但其配备的推进装置数量低于其自由度，导致其在某些方向上缺乏直接的推力控制，具有典型的强非线性运动特点^{[2 − 3]}。航向保持控制目标是使欠驱动船舶能在期望航向下持续稳定航行，以避免碰撞事故的发生，因此，对于船舶航向保持控制方法研究具有重要意义。

辛博鹏等^[4]通过构建的非线性反馈积分滑模控制器优势在于不仅响应效率高，而且在复杂海洋下具有较高的适应性。但该控制器容易产生控制抖振问题，导致航向保持控制误差较高。王化明等^[5]通过对船舶运动状态变量进行粒子滤波，去除噪声干扰，经过状态估计得到真实状态参数后，设计PID控制器实现船舶航向保持控制，但该方法存在依赖初始状态估计、粒子退化等问题。Li等^[6]采用三阶闭环增益整形算法设计航向保持控制器，并通过非线性开关反馈技术获得最终控制律，但该方法未考虑系统抖振问题，导致航向控制精度无法达到理想水平。Islam等^[7]基于滑模控制理论，设计超扭曲和终端滑模控制器，通过粒子群算法确定最佳控制参数，但由于粒子群算法可能过早收敛到局部最优解，将降低航向保持控制精度。

为解决上述问题，提出混合遗传算法下欠驱动船舶航向保持控制方法。构建欠驱动船舶数学模型，设计二阶跟踪微分器和数阶滑模控制器，使得航向保持控制状态在滑模面上滑动，结合禁忌搜索算法完成混合遗传算法的构建，提高航向跟踪效果，以应对复杂海洋环境的不确定性和扰动性，实现期望航向的高精度跟踪。

1 欠驱动船舶航向保持控制 1.1 构建欠驱动船舶数学模型

欠驱动船舶运动过程具有极高不确定性，风、浪、流等外界因素以及自身内部因素的存在，会使船舶运动状态与控制输入之间的关系变得非常复杂和非线性^[9]。Nomoto线性模型为一种常用的船舶运动模型，其在欠驱动船舶高度非线性运动特性描述上存在极大局限性。故需构建Nomoto非线性数学模型，将非线性项、外界扰动项引入到模型中，实现欠驱动船舶运动特性的精准刻画，描述公式为：

$ T\ddot \psi = Q\delta + \Delta - QH\left( {\dot \psi } \right)。$

(1)

其中：$ \psi $为欠驱动船舶航向角，$ \dot \psi $、$ \ddot \psi $分别为其一阶、二阶导数；其运动状态的非线性项通过$ H\left( {\dot \psi } \right) = {\alpha _1}\dot \psi + {\alpha _2}{\dot \psi ^3} $描述，$ {\alpha _1} $、$ {\alpha _2} $为转首速率的比例系数，通常用其描述船舶在受到舵角作用时，其首向（即船头方向）改变的速率，该参数与船舶的操纵性、舵效以及水流条件等因素有关；$ \Delta $表示外界扰动项，$ \delta $、$ T $与$ Q $分别为舵角、操纵指数。

将式（1）映射到状态空间，为欠驱动船舶航向保持控制提供便利，计算公式描述为：

$ \left\{ \begin{gathered} \dot \psi = r，\\ \dot r = b\delta + {d_{wr}} - f\left( r \right)。\\ \end{gathered} \right. $

(2)

其中：$ b =\displaystyle \frac{Q}{T} $为未知增益；$ f\left( r \right) = bH\left( {\dot \psi } \right) $为非线性阻尼项通过$ f\left( r \right) $；$ {d_{wr}} =\displaystyle \frac{\Delta }{T} $为外界扰动。

1.2 欠驱动船舶航向保持控制器设计

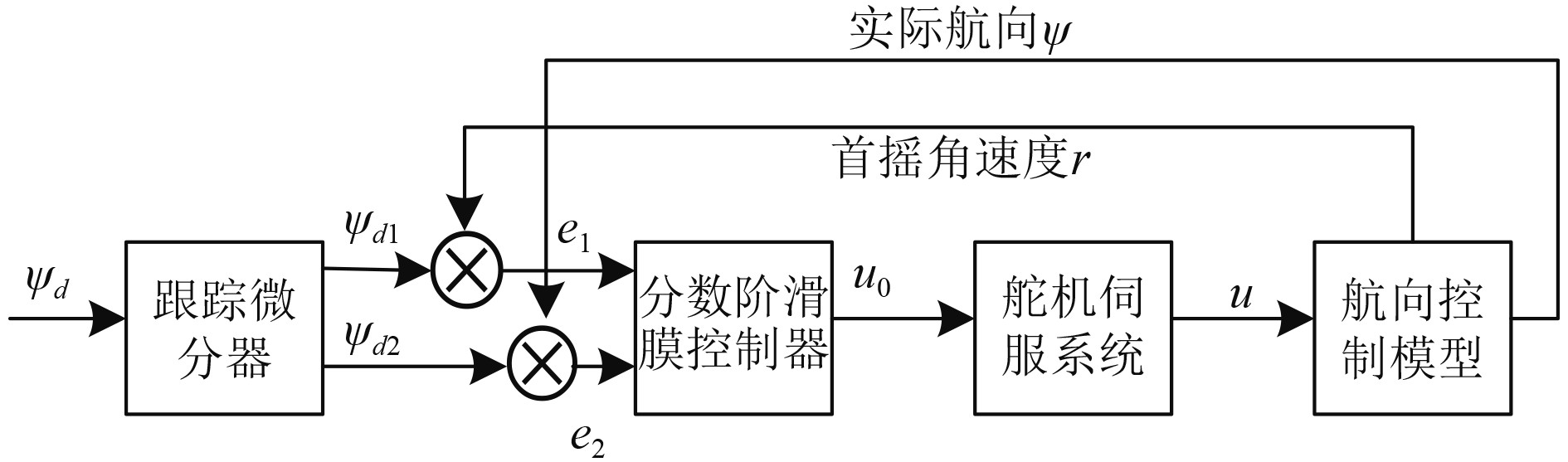
本文构建的欠驱动船舶航向保持控制器建立在分数阶滑模控制理论基础之上，跟踪微分器和分数阶滑模控制器为其重要组成部分，前者的作用是生成一个平滑过渡过程，使欠驱动船舶能逐渐稳定地过渡到期望航向，同时提供所需航向角速度信号供控制器使用。后者是一种基于滑模控制原理的控制器，基于分数阶微积分理论，通过设计适当的滑模面和控制律，使得航向保持控制状态在滑模面上滑动，达到快速、准确地跟踪期望航向的目的。欠驱动船舶航向保持控制器设计结构，如图1所示。

图中，欠驱动船舶航向保持控制的期望航向为$ {\psi _d} $，对其作降噪处理后，可得信号$ {\psi _{d1}} $；对其作微分处理，可得信号$ {\psi _{d2}} $；航向误差为$ {e_1} $，其一阶导数为$ {e_2} $；舵机响应延迟等因素会对欠驱动船舶航向保持控制造成极大影响，这些因素不予考虑的情况下，舵机伺服系统的虚拟输入为$ {u_0} $。

1.2.1 二阶跟踪微分器设计

本文构建二阶跟踪微分器，利用其生成期望航向的平滑过渡过程，并提供期望航向角速度和角加速度信号，从而为控制器提供更丰富的信息，使其能更准确地调整船舶的航向，具体公式描述为：

$ \left\{ \begin{gathered} {\psi _{d1}}\left( {k + 1} \right) = {\psi _{d1}}\left( k \right) + \zeta {\psi _{d2}}\left( k \right)，\\ {\psi _{d2}}\left( {k + 1} \right) = {\psi _{d2}}\left( k \right) + \\\;\;\; \zeta {f_{han}}\left( {{\psi _{d1}}\left( k \right) - {\psi _d}\left( k \right),{\psi _{d2}}\left( k \right),v,\zeta } \right)。\\ \end{gathered} \right. $

(3)

式中：$ v $为速度因子，其控制着TD内部动态过程的收敛速度，其值越大，TD跟踪期望信号的速度越快；$\zeta $为滤波因子，其扮演着增强滤波效果的角色，它的引入主要是抑制噪声和干扰对微分信号提取的影响，从而使输出信号更加平滑和可靠；$ {f_{han}} $为最速控制综合函数用于生成跟踪期望航向的控制量，其设计原则是在保证期望航向快速跟踪的同时，尽可能减小超调量。对参数$ \zeta $、$ v $进行优化，可提高TD对期望航向的追踪精度，即$ {\psi _{d1}} \to {\psi _d} $，$ {\psi _{d2}} \to {\psi _d} $。

1.2.2 欠驱动船舶航向保持控制器控制率确定

以欠驱动船舶航向误差作为分数阶滑模控制器的输入控制量，联立式（2）能得到通过下式描述的二阶航向保持控制系统：

$ \left\{ \begin{gathered} {e_1} = \psi - {\psi _d}，\\ {{\dot e}_1} = {e_2} ，\\ {{\dot e}_2} = f\left( r \right) + w - {{\dot \psi }_d} + bu。\\ \end{gathered} \right. $

(4)

为实现欠驱动船舶航向误差控制，本文采用的分数阶滑模切换函数可描述为：

$ s = B{e_1} + {}_0D_t^\lambda {e_2} 。$

(5)

其中：$ B $为滑模面增益；$ {}_0D_t^\lambda $为位于[0,t]上的整数阶微积分算子，阶次$ \lambda $具有可调性，当其达到最优时，航行保持控制系统可达到最优控制效果。

对于应用滑模变结构理论进行控制的系统，当系统状态在滑模面上快速切换时，控制输入的不连续性会导致系统产生高频抖动。本文通过式（6）描述的指数趋近律实现欠驱动船舶航向保持控制系统的抖动抑制：

$ {}_0D_t^\beta s = - ks - \varepsilon \mathrm{sgn} \left( s \right)。$

(6)

基于分数阶微积分理论，可将式（6）转变为：

$ \dot s = {}_0D_t^{1 - \lambda }\left[ { - ks - \varepsilon \mathrm{sgn} \left( s \right)} \right]。$

(7)

其中：$ - ks $、$ -\varepsilon \mathrm{sgn}\left(s\right) $分别为指数趋近项、等速趋近项；增益系数$ k $用于调整航行保持控制系统状态向滑模面收敛的速度，该值较大时，滑模控制的作用力会增强，航向控制系统状态能更快速地收敛到滑模面上；$ \varepsilon $通常为取值较小的正数，用于定义滑模面的边界层，以避免航向控制系统状态在滑模面上产生不连续的切换，减小抖振。

计算式（5）的一阶导数，可得：

$ \dot s = B{\dot e_1} + {}_0D_t^\lambda {\dot e_2}。$

(8)

联立式（7）与式（8），可确定$ {\dot e_2} $：

$ \dot{e}_2=_0D_t^{1-\lambda-\beta}\left[-ks-\varepsilon\mathrm{sgn}\left(s\right)\right]-_0D_t^{-\lambda}C\dot{e}_1。$

(9)

联立式（9）与式（4），可确定基于分数阶滑模控制的欠驱动船舶航向保持控制律，计算公式为：

$ u = \frac{_0D_t^{1-\lambda-\beta} \left[-ks - \varepsilon\mathrm{sgn}\left(s\right)\right] - _0D_t^{-\lambda}B\dot{x}_1 - f\left(r\right) - w + \ddot{\psi}_d}{b}。$

(10)

对于式（4）描述的欠驱动船舶航向保持控制系统，将式（5）作为其分数阶滑模面，根据式（10）所述的控制律，可使航向保持控制状态变量快速到达滑模面的同时，实现期望航向的快速且准确跟踪。

2 基于混合遗传算法的航向保持控制参数优化

遗传算法是模拟大自然生物体进化规律的智能算法，该算法在求解较为复杂的优化问题时，通常能更快获得较好的优化结果，但易出现“早熟”缺陷^[9-10]。本文结合禁忌搜索算法完成混合遗传算法的构建，利用其对欠驱动船舶航向保持控制器参数$ \zeta $、$ v $、$ k $、$ \varepsilon $、$ \lambda $进行优化调整，通过遗传算法产生航向保持控制器参数优化的初始解后，利用禁忌搜索算法对其进行持续优化，在提升遗传算法全局寻优性能的同时，最大程度改善其局部搜索性能。遗传算法步骤如下：

步骤1　编码。本文通过实数编码方式产生航向保持控制参数的最优解，即染色体，控制参数编号通过实数进行描述。对染色体长度$ N $进行初始设定，然后根据控制参数数量$ M $对其作分段处理，各个控制参数与染色体片段具有一一对应关系。

步骤2　对种群进行初始设定。包括训练次数、交叉率、变异率参数的配置。

步骤3　确定适应度值。将航向控制误差的倒数视作适应度值，适应度函数描述为：

$ Fitness = 1/q 。$

(11)

式中：$ q $为航向控制误差。

步骤4　选择处理。采用轮盘赌规则完成种群个体的选取，再按照精英策略确定具有较高适应度的个体。

步骤5　交叉处理。通过式（12）实现个体$ {X_i} $、$ {X_j} $的交叉处理，以获得其子代：

$ \left\{ \begin{gathered} {X_i} = \theta {X_i} + \left( {1 - \theta } \right){X_j}，\\ {X_j} = \theta {X_j} + \left( {1 - \theta } \right){X_i}。\\ \end{gathered} \right. $

(12)

步骤6　变异处理。从染色体中任意选择2个基因，对其基因位置顺序进行置换，生成新个体。

在遗传算法变异处理过程后引入禁忌搜索算法，禁忌表的使用，可防止最优控制参数的不断重复搜索，提高全局寻优性能。

3 实验分析

以航行于某海域的货船为实验对象，该货船的前进动力通过螺旋桨提供，转向动力则依赖于船体的水动力特性和可能存在的舵或其他辅助转向设备提供。该货船的长、宽分别为120 m、20.2 m，满载吃水深度可达8.2 m。利用Matlab仿真工具搭建欠驱动船舶航向保持控制实验环境，设定控制参数优化的初始种群中包含50个个体，交叉、变异概率分别设定为0.90、0.04，循环次数上限为400，邻域大小为35。将研究方法应用到欠驱动船舶航向保持控制中，分析其控制效果。

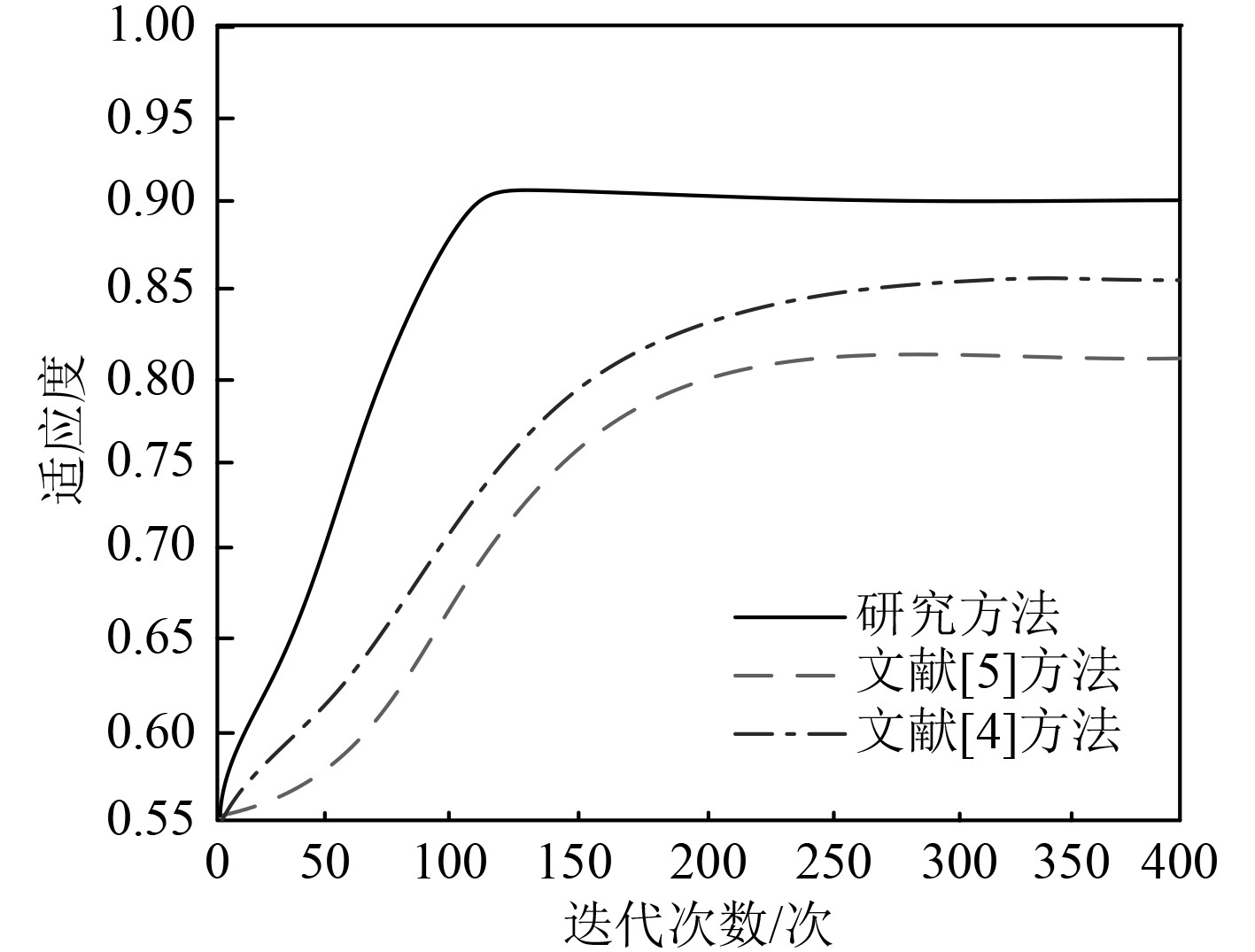
应用研究方法对航向保持控制器参数进行寻优，将文献[4]与文献[5]方法作为对比方法，通过对3种方法下的适应度函数曲线进行差异分析，验证研究方法的参数优化效果，实验结果如图2所示。

可知，随着循环次数的不断增加，适应度曲线呈持续增长趋势变化，文献[4]方法在300次迭代后方开始趋近稳定，最终适应度值为0.85；文献[5]方法在200次迭代后即可达到收敛状态，最大适应度值达到0.81；研究方法仅需100次迭代即可使适应度值上升至最大，其值达到0.91。

本文以期望航向误差的倒数设计适应度函数，当适应度值越大，期望航向误差越小，欠驱动船舶的航向保持控制效果越突出。实验结果表明，研究方法可实现控制参数寻优，且优化效果优于对比方法。

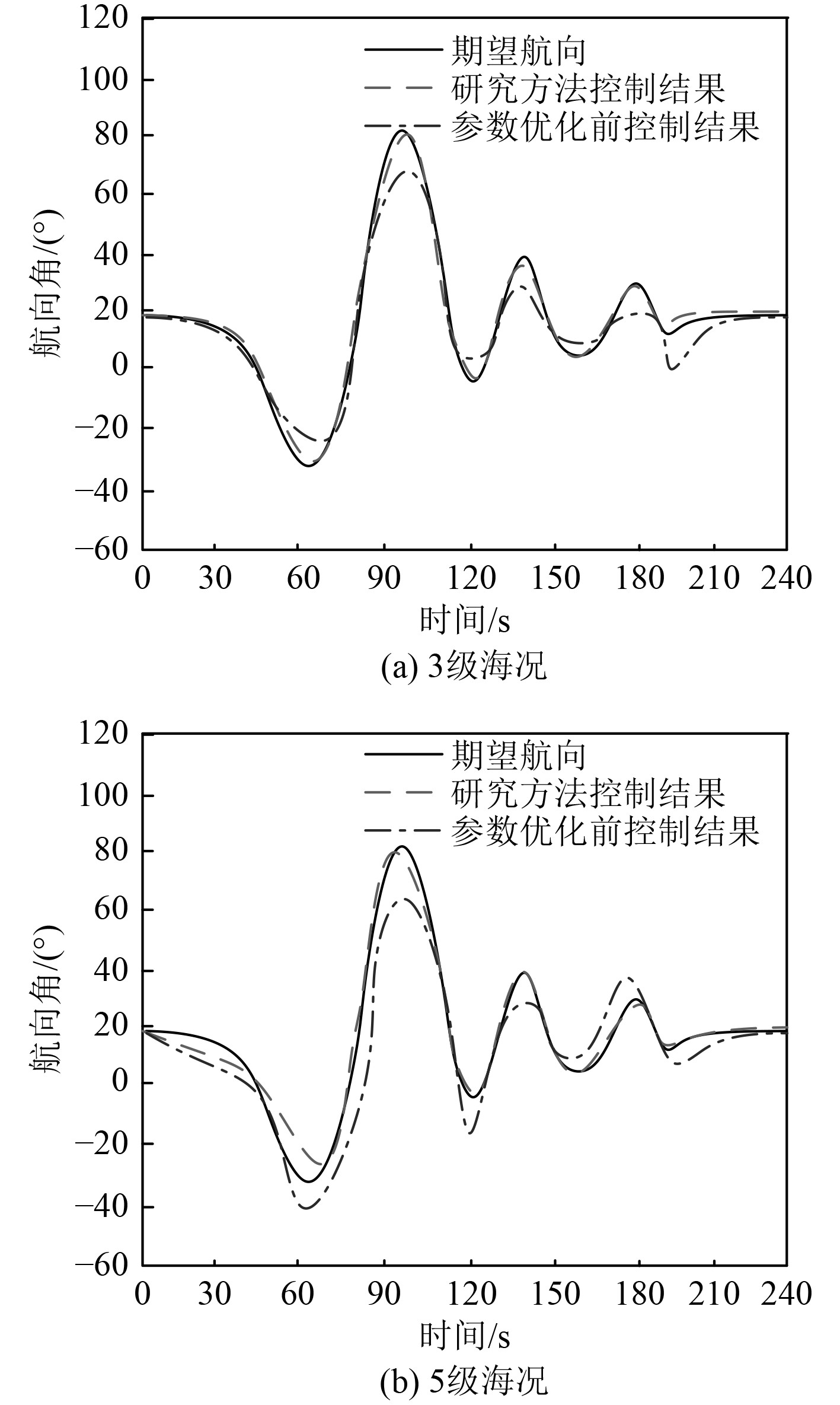
设定实验货船分别在3级、5级这2种海况下航行，对应波浪高度分别为0.6～2 m和2.5～4 m，采用研究方法分别对不同航行条件下的船舶进行航向保持控制，对比分析参数优化前后的航向角控制结果与期望航向角之间的差异，验证研究方法的实际应用性能，实验结果如图3所示。

由图3(a)可知，实验货船航行在3级海况条件下，船体会有摇晃，应用研究方法对其进行航向保持控制，可实现期望航向的准确跟踪，控制后的航向曲线与期望航向曲线具有很高的贴合度，二者近似重合；由图3(b)可知，5级海况下，受浪高等因素影响，船舶自身摇晃感增强，控制参数优化前的航向与期望航向存在极大偏离，导致此时航向保持控制效果大受影响，而研究方法通过参数优化，极大提高了航向保持控制精度，控制后航向与期望航向误差相对较小。实验结果表明，研究方法可实现欠驱动船舶航向保持控制，并取得较好的控制效果。

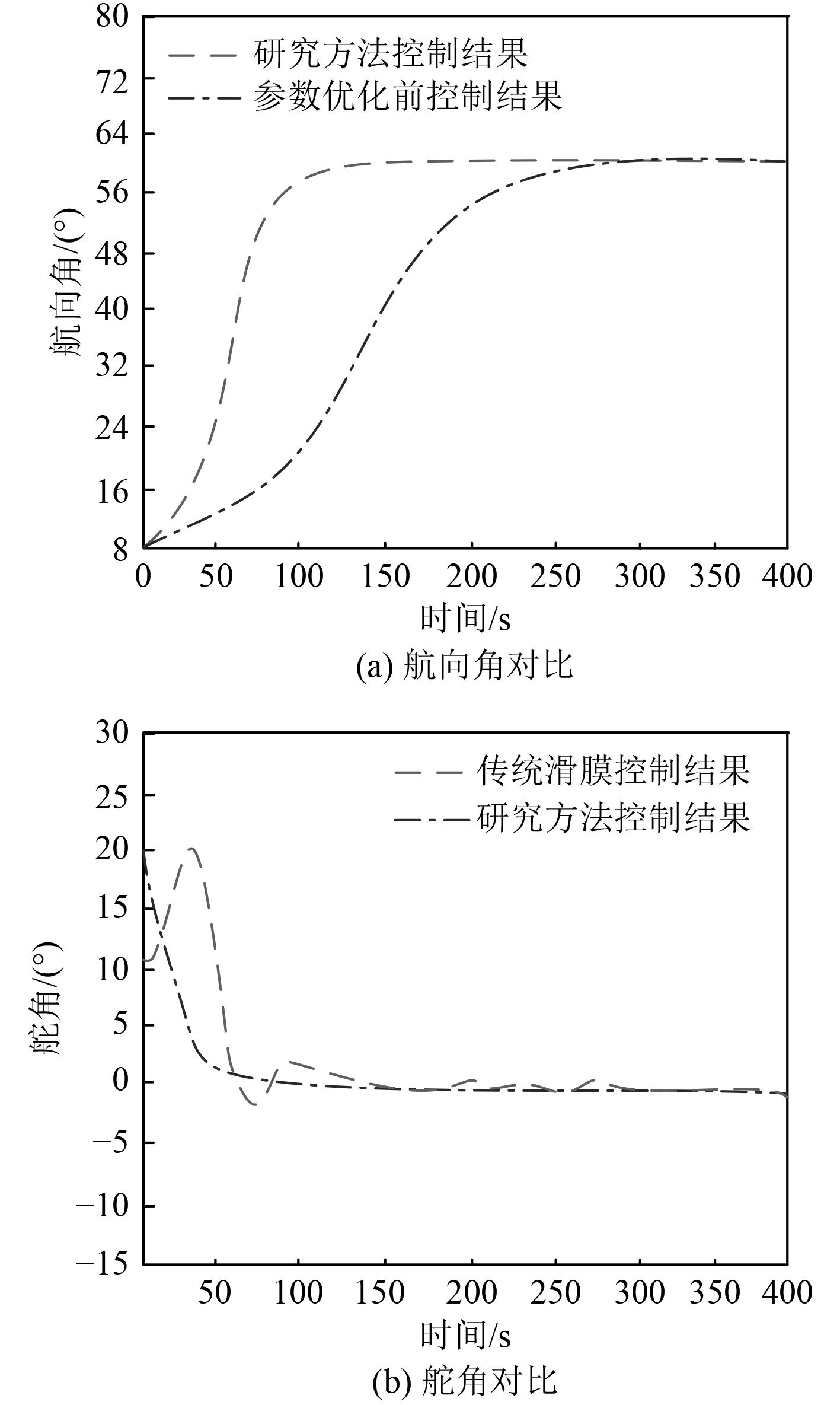
设定实验船舶在风平浪静的海面上，沿45°期望航向航行，分别对研究方法与传统滑膜控制下的航向角与舵角进行差异分析，验证研究方法的航向控制性能，实验结果如图4所示。

可知，研究方法在经过120 s控制后，完成期望航向的准确跟踪，控制后的航向不存在超调问题。舵角控制在[−2°,20°]区间，且曲线平滑；传统滑膜控制下，需经过多次转向才可大致跟踪到期望航向，且航向曲线存在微小超调量，控制时间也远超研究方法。实验结果表明，研究方法的航向保持控制性能更卓越，具有实际应用价值。

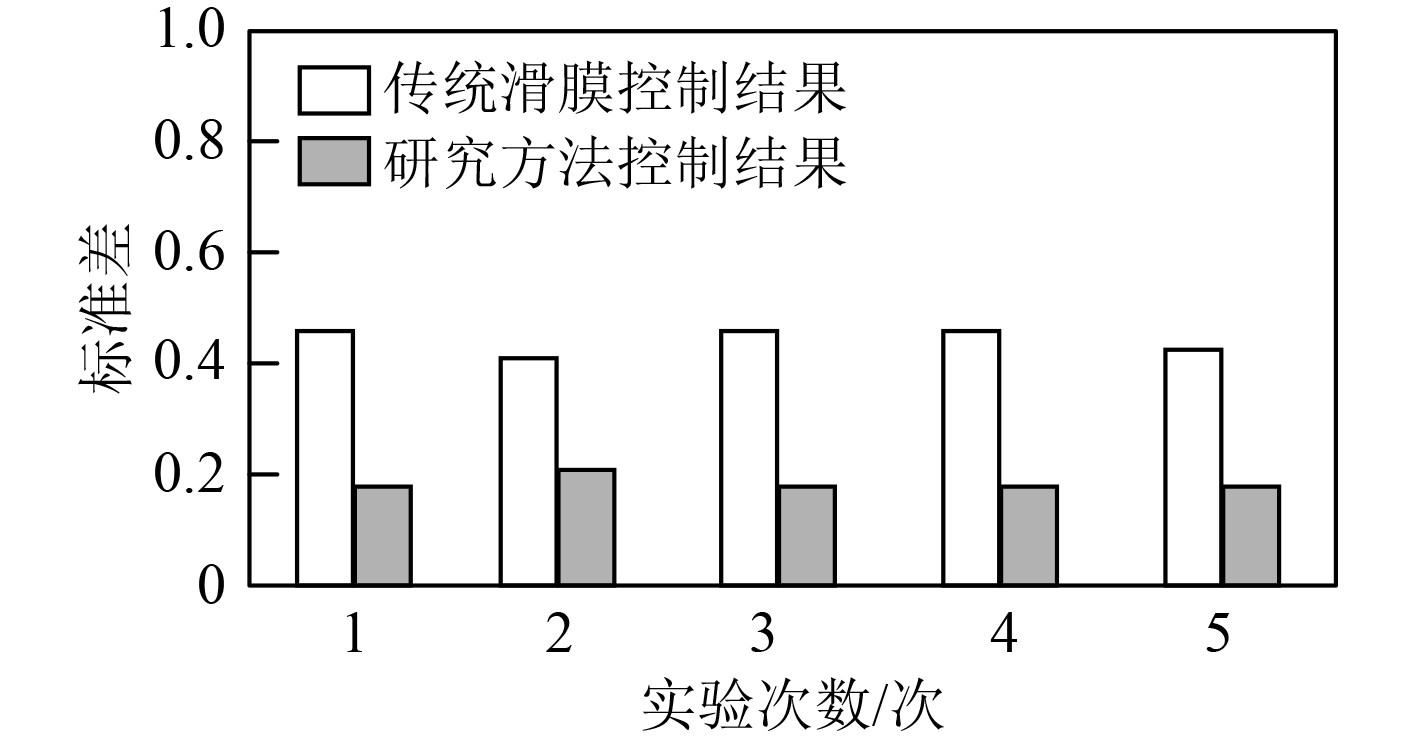
在欠驱动情况下，船舶可能会受到外部环境变化的影响，导致控制效果差。为此，以控制标准差为测试指标，该指标越低，表明控制稳定性越高，控制结果如图5所示。

可知，研究方法在5次实验中，控制标准差始终在0.2以下。反观未采用研究方法的控制标准差在0.4左右，虽采用该方法控制具有一定的稳定性，但仍然低于研究方法，进一步验证了研究方法的稳定性更高。

4 结　语

为提高欠驱动船舶航向保持控制精度，提出混合遗传算法下欠驱动船舶航向保持控制方法。结合TD、FOSMC设计航向保持控制器，将禁忌搜索算法引入到遗传算法中，提高欠驱动船舶航向保持控制精度，增强对不同海况的适应能力，分数阶滑膜控制理论的引入，使控制器能在船舶动态特性发生改变时，更灵活地调整控制策略，提高航向保持控制的鲁棒性。实验结果表明，研究方法具有突出的参数寻优能力，在降低迭代次数的同时，实现适应度值的有效提升。并且可实现在不同海况条件下期望航向的准确跟踪，控制效率更高、超调量更小。