2. 大连理工大学 海岸及近海工程国家重点实验室,辽宁 大连 116024
2. State Key Laboratory of Coast and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
海洋浮式平台正朝着大型化、多模块化方向发展。在模块化多浮体结构的研究进程中,由海上风、浪、流相互作用而形成的复杂载荷作用在结构物上,连接器作为关键部件承受着巨大载荷,其关系到模块化浮体的运营安全,故对连接器载荷的研究具有重要的意义[1 − 2]。
模块化多浮体结构涉及复杂的多体水动力耦合及连接器的机械耦合效应,构建高效、准确的时域分析模型对多浮体结构系统设计至关重要。Zou等[3] 提出一个将阻尼盖方法和状态空间模型相结合的时域模型(CPTDM),得出较大的阻尼盖因子有利于脉冲响应函数的衰减和低阶状态空间模型的发展,并且比Aqwa的时域模拟具有更好的精度和更高的效率。Chen等[4]采用带粘性修正的频域-时域数值模型研究了流体动力学-结构耦合响应,验证了该数值模型的可靠性。
模块化多浮体结构的模块选型和数量是连接器设置的基础。Michailides等[5]针对模块化多浮体结构的连接器受力特性展开研究,得出模块数量以及模块布局对连接器内部荷载具有较大影响。李洪仙等[6]使用Aqwa对6模块组成的模块化浮体结构进行了有限元分析,得出浮体响应幅值随连接件刚度变化会出现较大振荡区间现象。王永恒等[7]针对3模块的模块化浮体结构,分析连接器刚度对连接器载荷的影响特征,初步确定了连接器刚度最佳匹配原则。Ren等[8]提出一种近岸式7模块的模块化多浮体结构,研究不同联接器布设方案对其水动力响应的影响机理,得出柔性铰接联接器可以显著降低连接器负载。Jiang等[9]研究了模块布置对模块化多浮体结构水动力灵敏度的影响,结果表明,链式和并联式的水动力响应相似,且第一迎浪模块的运动响应最大。
目前,国内外关于模块化多浮体结构连接器的研究主要集中在连接器载荷和连接器设计上。祁恩荣等[10]设计了一种由球铰弹簧装置组成的柔性连接器模型,研究了组合载荷对连接器刚度的影响,得出组合荷载会导致2个球铰弹簧装置的受力和变形的不均匀性,连接器结构设计时应适当提高安全系数。Xia等[11]提出一种特殊的带有空气弹簧的主动控制连接器系统,通过改变空气弹簧内部的气压而减小浮动结构的振动。张波等[12]对7模块浮体进行3D水动力分析,计算了规则波和不规则波下连接器的荷载值,得出波浪入射角、波频和连接器刚度对连接器载荷响应具有显著影响。滕蓓等[13]提出了空心变截面的柔性铰接连接器,并对一个5模块8连接器的模块化浮体结构展开了研究,分析了连接器的荷载响应,验证了该连接器的强度可靠性。Shi等[14]针对串联VLFS提出了一种新型的面接触连接器,通过将连接器载荷传递到整个面端,进而减小连接器局部应力。
国内外的研究多是关于材料类型及结构形式对连接器载荷的影响,少有关于模块尺度效应对连接器载荷的研究。本文结合模块化多浮体结构系统尺度选择和连接器安全稳定的需求,考虑模块间多体水动力耦合及连接器机械耦合效应,基于RMFC(Rigid Module-Flexible Connection)方法,使用Ansys-Aqwa程序研究了典型海况下模块尺度效应对多浮体结构系统连接器载荷的影响特征。
1 理论基础及数值模型 1.1 模块化浮体结构概念设计提出基于张力腿平台的代表性三模块浮体结构,研究模块尺度效应对多浮体结构系统连接器载荷的影响特征。三模块浮体结构系统的主要设计参数如表1所示。
|
|
表 1 三模块浮体结构主要设计参数 Tab.1 The main design parameters of the three-module floating structure |
如图1所示,该浮体结构主要包括:
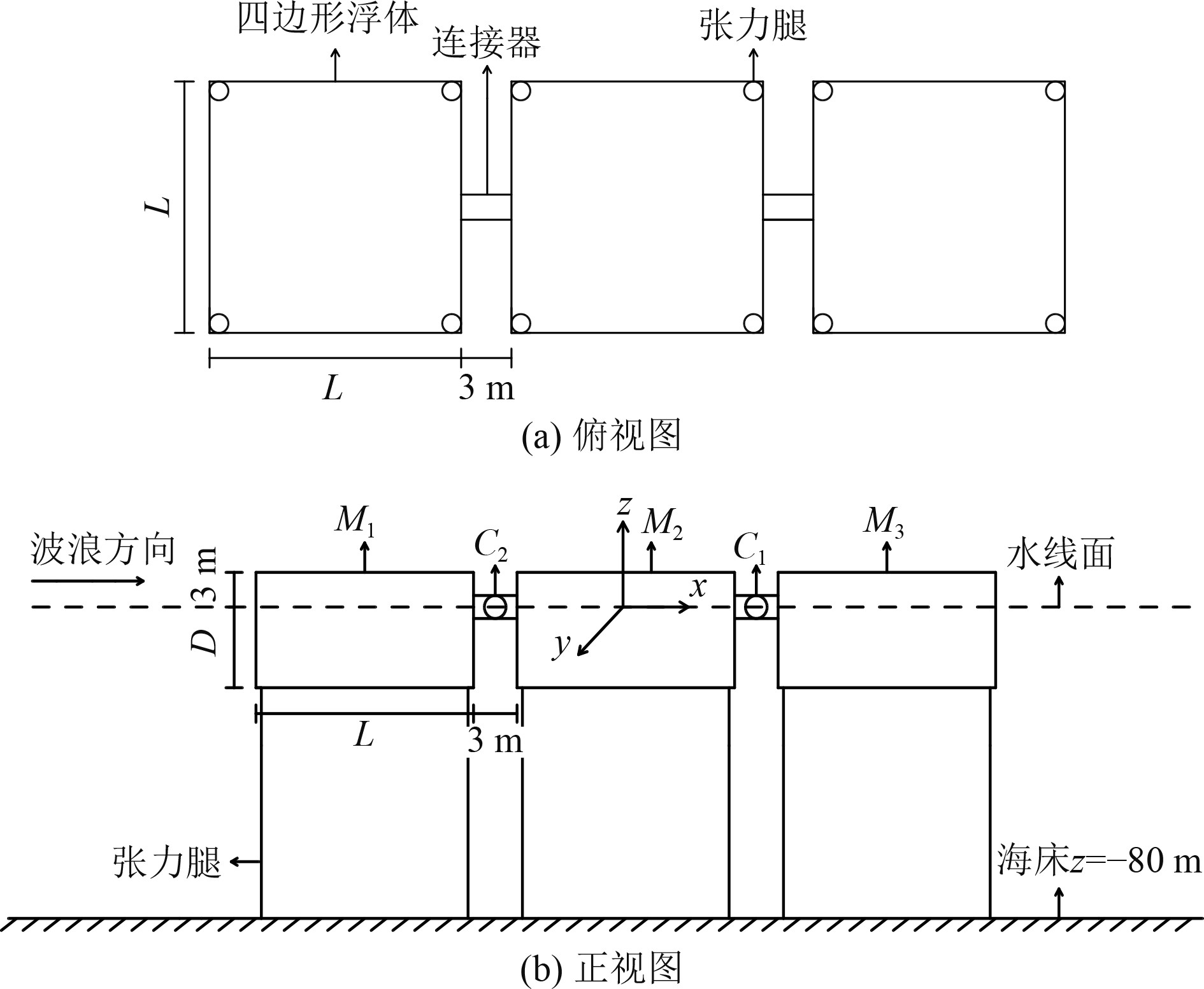
|
图 1 三模块浮体结构示意图 Fig. 1 Schematic diagram of the three-module floating structure |
1)基于张力腿平台的四边形浮体模块,张力腿均对称分布于浮体的边缘四角;
2)各模块之间采用铰接连接,其只允许模块之间发生相对纵摇,限制其他方向的运动。
1.2 多体动力学基本理论综合考虑多体水动力耦合和连接器机械耦合的影响,并使用RMFC模型下,其三模块浮体结构的运动学方程可表达为如下式,更多的相关理论基础可参考相关文献[5,15]。
综合考虑多体水动力耦合和连接器机械耦合的影响,并使用RMFC模型下,其三模块浮体结构的运动学方程表达式为:
| $ {\boldsymbol{M}} _{\boldsymbol{k}} {\ddot{\boldsymbol{U}}} _{\boldsymbol{k}} + \sum _{k = 1}^{3} ( {\boldsymbol{A}}_{\boldsymbol{k}}{\ddot{\boldsymbol{U}}}_{\boldsymbol{k}} + {\boldsymbol{B}}_{\boldsymbol{k}}{\dot{\boldsymbol{U}}}_{\boldsymbol{k}} ) + {\boldsymbol{S}}_{\boldsymbol{k}} {\boldsymbol{U}}_{\boldsymbol{k}} = {F}_{k,wave} + {F}_{k,con}{ + F}_{k,m} 。$ | (1) |
式中:Mk为浮体质量矩阵;Ak为附加质量矩阵;Bk为附加阻尼矩阵;Sk为恢复力系数矩阵;Fk,wave为波浪力;Fk,con为连接器作用在模块上的载荷;Fk,m为张力腿力。
Fk,wave和Fk,con可写成以下形式:
| $ {F}_{k,wave}={F}_{i,w}-\sum _{i=1}^{3}\sum _{j=1}^{6}\left({\boldsymbol{A}}_{\boldsymbol{k}}{\ddot{\boldsymbol{U}}}_{\boldsymbol{k}}+{\boldsymbol{B}}_{\boldsymbol{k}}{\dot{\boldsymbol{U}}}_{\boldsymbol{k}}\right){\boldsymbol{U}}_{\boldsymbol{k}} ,$ | (2) |
| $ {F}_{k,con}=\sum _{k=1}^{3}\left({\boldsymbol{\varphi }}_{\boldsymbol{i}\boldsymbol{j}}{\boldsymbol{K}}_{\boldsymbol{c}\mathit{i}\boldsymbol{j}}\boldsymbol{\delta }\left({\boldsymbol{X}}_{\boldsymbol{i}},{\boldsymbol{X}}_{\boldsymbol{j}}\right)\right) 。$ | (3) |
式中:Fi,w为波浪激动力;φij为一个拓扑矩阵,取值规律如下:若模块 i和模块 j 之间有连接器连接,该矩阵的对应位置为1,否则为0;Kcij为模块i和模块j之间的连接刚度矩阵;δ(Xi,Xj)为模块i和模块j之间的相对运动矩阵。
1.3 水动力数值模型基于三维非线性势流理论,利用Ansys-Aqwa程序构建三模块浮体结构水动力模型(见图2)。Aqwa[16]可有效考虑多体间水动力耦合效应、连接器机械耦合效应、二阶波浪力荷载及非线性系泊等因素,故十分契合该三模块结构系统的耦合动力响应分析[17]。

|
图 2 三模块浮体结构水动力模型 Fig. 2 Hydrodynamic model of three-module floating structure |
参考拟选址海域的波浪统计特征信息,选取典型规则波浪(H=2 m,T=7 s)海况,结合目前主要船坞尺度信息,对比研究3种代表性尺度模块(工况1、工况3、工况5)的三模块浮体结构的动力响应特征,结果如表2和表3所示。
|
|
表 2 典型规则波下三模块浮体结构系统各模块运动响应对比 Tab.2 Comparison of the motion response of each module of the three-module floating structure under typical regular waves |
|
|
表 3 典型规则波下三模块浮体结构各连接器荷载特征信息 Tab.3 Load characteristics of each connector of the three-module floating structure system under typical regular waves |
由表2可知,模块M1、M2和M3 的纵荡幅值基本一致,表明各浮体模块的纵荡运动具有协调相似性。而模块M1、M2和M3 的垂荡幅值微小,约为纵荡幅值0.04%,表明张力腿平台对于模块的垂向运动具有很好的约束。由表3可知,相比于连接器C1,连接器C2(见图1)的受力相对较大,表明迎浪侧模块连接器所受纵向荷载更大。由图3(b)可知,与纵向荷载值相比,连接器C1和C2的垂向荷载值相对较小,这是由于张力腿平台较小的相对垂荡运动所导致。鉴于波浪荷载对张力腿平台纵荡运动响应影响最为显著,因此,本文主要针对三模块浮体结构系统的纵荡运动和连接器的纵向荷载值进行分析。
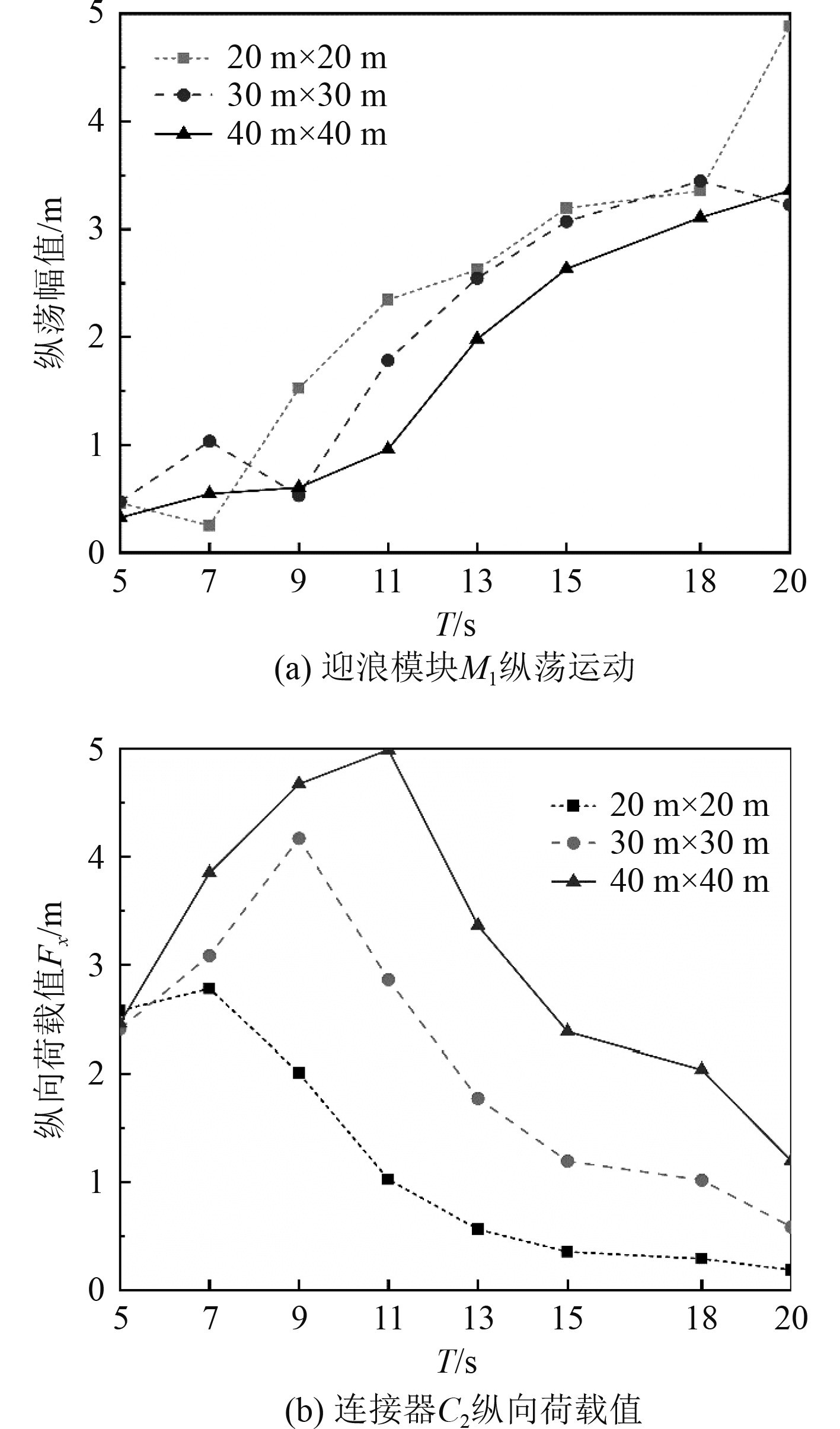
|
图 3 不同波浪周期下模块尺度效应对多浮体结构主要动力响应特征的影响 Fig. 3 Module scale effect on main dynamic responses of multi-floating structure under different wave periods |
进一步对迎浪侧模块M1及迎浪侧连接器C2在不同波浪周期下(H=2 m,T=5~20 s)的动力响应特征展开研究,结果如图3所示。
由图3(a)可知,3种代表性尺度模块M1的纵荡运动随波浪周期的增大而增大,在波浪周期T的区间为9~15 s内增长速度最快,且40 m×40 m模块的纵荡运动在整体波浪周期下最小,而20 m×20 m模块在波浪周期T为20 s时的纵荡幅值较大,说明模块尺度的增大能有效减小浮体的纵荡运动幅值。由图3(b)可知, 不同尺度模块迎浪侧连接器C2的纵向荷载值随着波浪周期的增大先增大后减小,表明各浮体模块间的相对纵荡也是先增大后减小。在典型规则波浪(H=2 m)海况下,波浪周期T为7、9、11 s时波长λ为76、126、162 m。20 m×20 m、30 m×30 m、40 m×40 m模块的连接器纵向荷载峰值分别出现在波浪周期T为7、9、11 s,这主要是由于模块结构尺寸与特征周期波长的对应比例关系所导致(结构尺寸约为对应波浪周期波长的1/4)。
鉴于不同尺度模块的排水量各不相同,进一步对比单位排水量下的主要动力响应特征,以便于模块尺度的初步优化选型,结果如表4及图4所示。
|
|
表 4 单位排水量下模块尺度效应对多浮体结构主要动力响应特征信息 Tab.4 The main dynamic response characteristics of multi floating structure under the scale effect of modules under unit displacement |
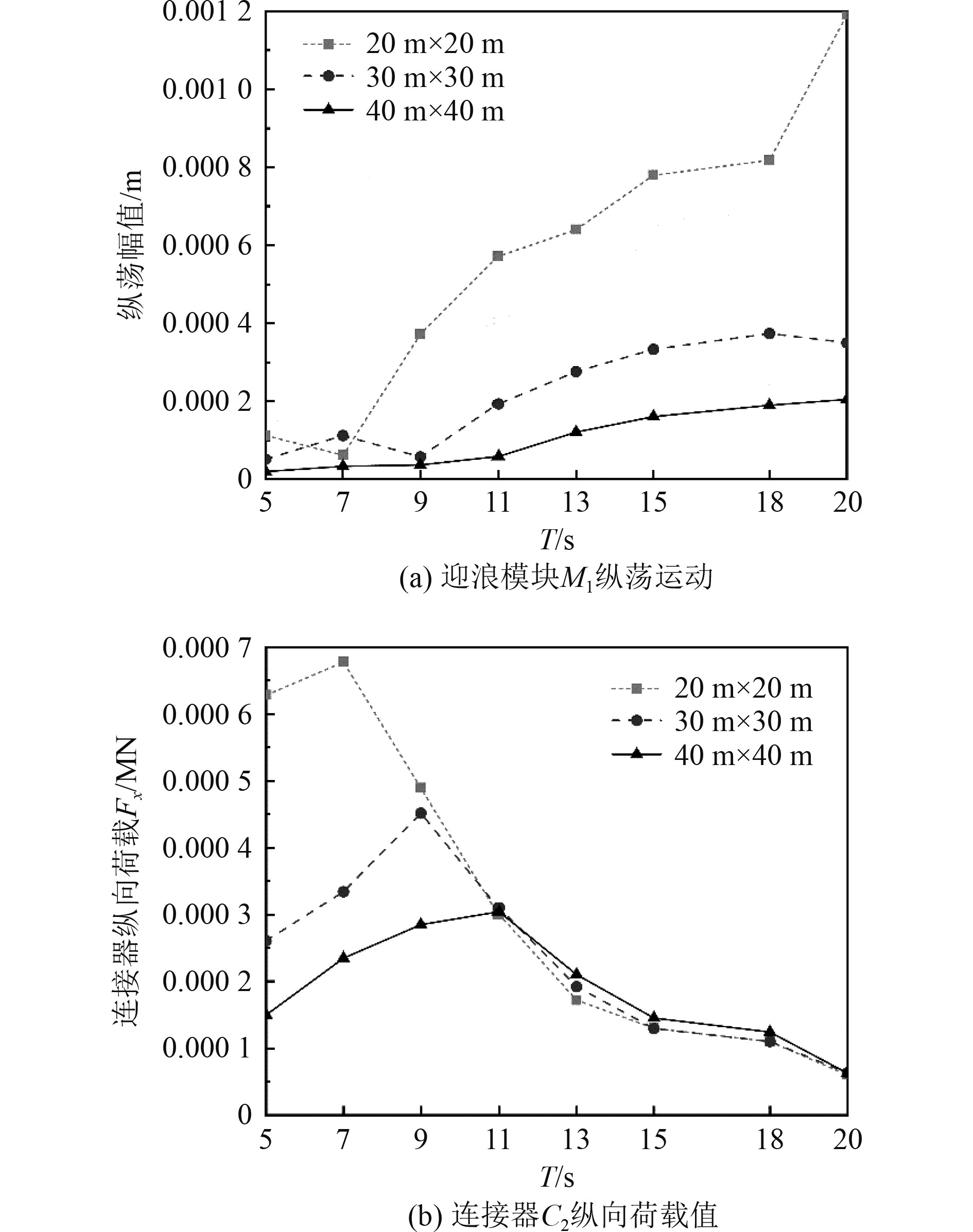
|
图 4 单位排水量下模块尺度效应对多浮体结构主要动力响应特征的影响 Fig. 4 Module scale effect on main dynamic responses of multi-floating structure under unit displacement |
可知,单位排水量下,模块尺度的增大能有效减小浮体的纵荡运动幅值。与40 m×40 m模块的纵荡运动响应幅值相比,20 m×20 m模块约为其6倍,30 m×30 m模块约为其3倍。由表4和图4(b)可知,单位排水量下,当波浪周期T>11 s时,三者连接器受力的纵向荷载值的曲线较为接近,表中三者连接器受力的纵向荷载值均从
可知,相同吃水深度下,模块尺度的增大能有效减弱浮体的纵荡运动幅值。大周期波浪的海况下,模块尺度与连接器荷载增大的比例近似线性关系,为对应尺度模块的排水量之比。
2.2 模块吃水效应影响分析进一步研究模块吃水对结构间连接器载荷的影响特征,基于同一排水量
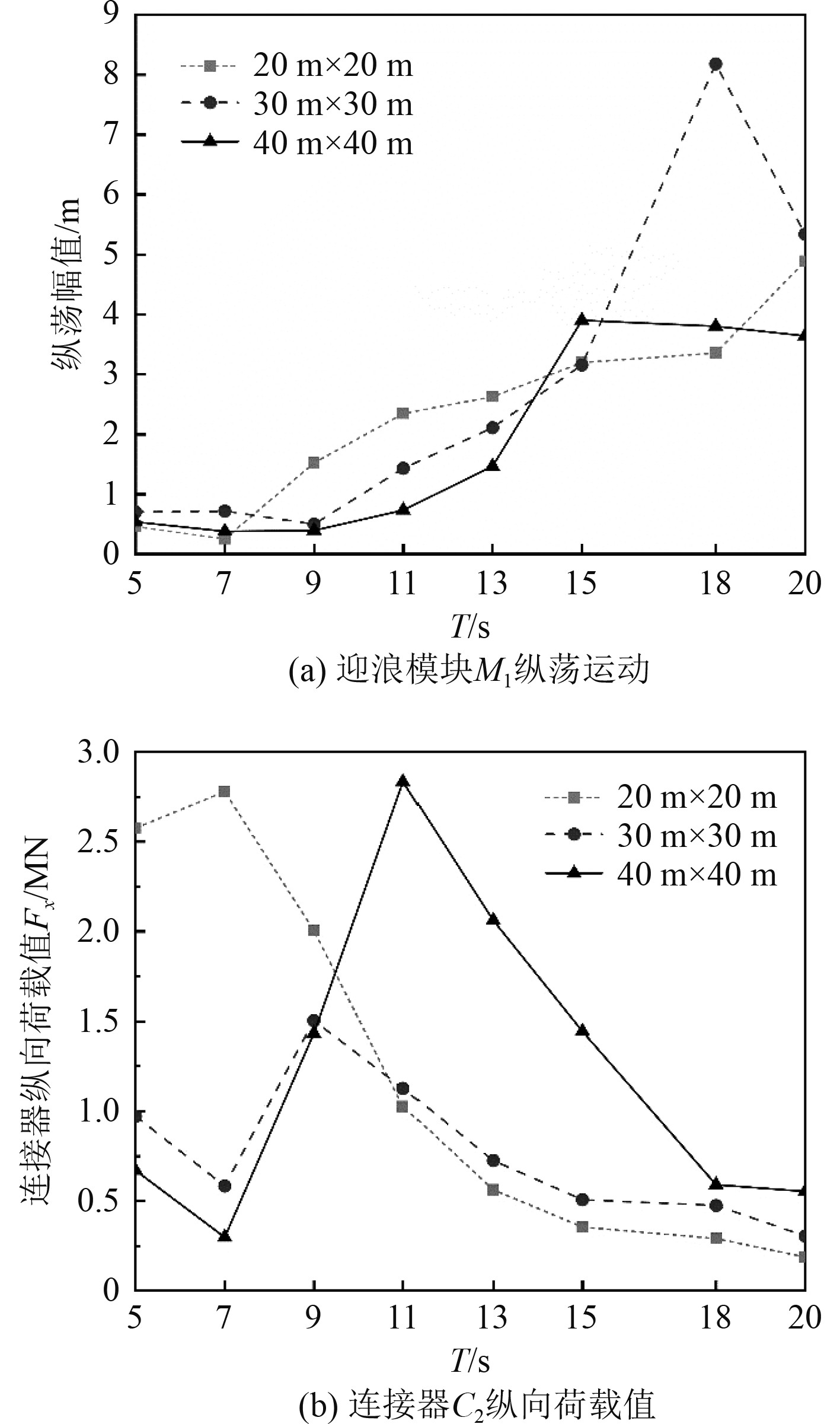
|
图 5 不同波浪周期下模块吃水效应对浮体结构系统主要动力响应特征的影响 Fig. 5 Module draft effect on main dynamic responses of multi-floating structure under different wave periods |
由图5(a)可知,当T<13 s时,40 m×40 m模块的纵荡运动幅值最小;当T>15 s时,20 m×20 m模块的纵荡运动幅值最优。说明同排水量浮体模块,小波浪周期的海况下(T<10 s),减小模块吃水可以有效减小浮体的纵荡运动幅值;大波浪周期的海况下(T>10 s),深吃水模块更加稳定。由图5(b)可知,当T<10 s时,40 m×40 m模块连接器的纵向荷载值最小;T>10 s时,20 m×20 m模块连接器的受力最优。说明小波浪周期的海况下,减小模块吃水可以有效减小连接器受力,大波浪周期的海况下,深吃水模块的连接器受力更优。
由以上分析可知,相同排水量下,在小波浪周期(T<10 s)的海况,减小模块吃水可有效减小浮体的纵荡运动幅值和连接器纵向荷载。
2.3 极端海况下安全校核进一步研究该三模块浮体结构在代表性极端海况下(HS=4 m,Tp=10 s,λ=3.3)的极值响应特征,对5种代表性模块尺度进行了对比分析,主要极值响应特征信息如表5所示。
|
|
表 5 极端海况下各浮体结构系统的主要动力响应特征值信息 Tab.5 Information of main dynamic responses of each floating structure system under extreme sea conditions |
可知,同一吃水(10 m)的三模块浮体结构,其模块尺度的增大可有效减小浮体纵荡运动极值。与20 m×20 m模块相比,30 m×30 m模块的纵荡运动极值减少了约18%;40 m×40 m模块的纵荡运动极值减少了约28%。并且由纵荡标准差对比信息也可推断40 m×40 m模块的纵荡稳定性最好。同等模块吃水下,模块连接器的总纵向载荷虽然随模块尺度的增大而增大,但相对于单位排水量的连接器载荷值(纵向载荷/排水量)却随模块尺度的增大而显著减小。此外,同等模块吃水下,张力腿受力极值与模块的排水量基本成线性比例,因此需要重点考虑大尺度模块张力腿系泊系统的极限承载能力。
同一排水量(
由以上分析可知,极端海况下,大尺度深吃水模块能有效减小单位排水量下模块的纵荡极值和连接器纵向荷载极值,有利于增强结构的安全性和舒适性。
3 结 语考虑多体水动力耦合效应及连接器机械耦合效应,研究了典型海况下模块化浮体结构尺度效应对连接器载荷的影响特征,并校核其安全性能。主要结论汇总如下:
1)相同吃水深度下,模块尺度的增大能有效减小浮体的纵荡运动幅值。大周期波浪的海况下,模块尺度与连接器荷载增大的比例近似线性关系,即其增长率近似为对应尺度模块的排水量之比。实际工程中,考虑目前船坞建造能力,建议选择大尺度的模块。
2)相同排水量下,在小波浪周期(T<10 s)的海况,减小模块吃水可有效减小浮体的纵荡运动幅值和连接器受力。拖航运输一般都是小周期海况,故在拖航运输中可选用大尺度小吃水的模块。遇到大波浪周期的海况时,通过注水来改变模块的吃水深度,使模块更加稳定。
3)极端海况下,大尺度深吃水模块能有效减小单位排水量下模块的纵荡极值和连接器纵向荷载极值。为了增强结构的安全性和舒适性,建议选择大尺度深吃水的模块。
综上所述,考虑目前船坞建造能力和各尺度模块水动力响应特征,建议尽量选用尺度较大的模块(如40 m×40 m)。本研究主要成果可为模块化多浮体结构的优化设计提供借鉴,并计划后续进一步开展此三模块浮体结构的物理模型试验验证研究。
| [1] |
崔维成, 吴有生, 李润培. 超大型海洋浮式结构物开发过程中需要解决的关键技术问题[J]. 海洋工程, 2000, 18(3): 1-8. DOI:10.3969/j.issn.1005-9865.2000.03.001 |
| [2] |
吕海宁, 杨建民, 张承懿. 半潜式超大型浮体的多刚体试验研究[J]. 船舶工程, 2004, 26(5): 33-37. DOI:10.3969/j.issn.1000-6982.2004.05.006 |
| [3] |
ZOU M Y, CHEN S Y, ZHU L, et al. A constant parameter time domain model for dynamic modelling of multi-body system with strong hydrodynamic interaction[J]. Ocean Engineering, 2023, 268: 113376. DOI:10.1016/j.oceaneng.2022.113376 |
| [4] |
CHEN S M, OUYANG M J, WANG Y, et al. A coupled hydrodynamic–structural model for flexible interconnected multiple floating bodies[J]. Journal of Marine Science and Engineering, 2023, 11: 813. DOI:10.3390/jmse11040813 |
| [5] |
CONSTANTINE M, EVA L, DEMOS C. Response analysis and optimum configuration of a modular floating structure with flexible connectors[J]. Applied Ocean Research, 2013, 43: 112-130. DOI:10.1016/j.apor.2013.07.007 |
| [6] |
李洪仙, 陈衍茂, 刘奇贤. 多浮体海上平台水动力响应分析[J]. 舰船科学技术, 2017, 39(19): 75-78. LI Hongxian, CHENG Yanmao, LIU Qixian. Hydrodynamic response analysis for modules-offshore platform[J]. Ship Sencine and Tenchlogy, 2017, 39(19): 75-78. DOI:10.3404/j.issn.1672-7649.2017.10.014 |
| [7] |
王永恒, 汪学锋, 徐胜文, 等. 多模块超大型浮体中连接器刚度对其运动响应的影响[J]. 海洋工程, 2018, 36(4): 11-18. |
| [8] |
REN N X, ZHANG C, Øyvind Hellan, et al. Hydrodynamic analysis of a modular multi-purpose floating structure system with different outermost connector types[J]. Ocean Engineering, 2019, 176: 158-168. DOI:10.1016/j.oceaneng.2019.02.052 |
| [9] |
JING C Q, MOCTAR O, SCHELLIN T E. Hydrodynamic sensitivity of moored and articulated multibody offshore structures in waves[J]. Journal of Marine Science and Engineering, 2021, 9: 1028. DOI:10.3390/jmse9091028 |
| [10] |
祁恩荣, 刘超, 夏劲松, 等. 超大型浮体模块柔性连接功能仿真模型试验研究[J]. 船舶力学, 2015, 19(10): 1245-1254. DOI:10.3969/j.issn.1007-7294.2015.10.009 |
| [11] |
XIA S Y, XU D L, ZHANG H C, et al. On retaining a multi-module floating structure in an amplitude death state[J]. Ocean Engineering, 2016, 121: 134-142. DOI:10.1016/j.oceaneng.2016.05.024 |
| [12] |
张波, 陈倩清, 赵春慧. 多模块MOB连接器动力特性研究[J]. 舰船科学技术, 2017, 39(9): 77-81+87. ZHAN Bo, CHENG Qianqing, ZHAO Chunhui. Research on the connector’s dynamic response of MOB[J]. Ship Sencine and Tenchlogy, 2017, 39(9): 77-81+87. DOI:10.3404/j.issn.1672-7619.2017.05.015 |
| [13] |
TENG B, LU Y, GUAN Y F, et al. Strength of hinge connector with hollow variable-section for very large floating structures[J]. Journal of Ship Mechanics, 2019, 23(3): 332-341. |
| [14] |
SHI Q X, XU D L, ZHANG H C, et al. A face-contact connector for modularized floating structure[J]. Marine Structures, 2022, 82: 103149. DOI:10.1016/j.marstruc.2021.103149 |
| [15] |
XU D L, ZHANG H C, XIA S Y, et al. Nonlinear dynamic characteristics of a multi-module floating airport with rigid-flexible connections[J]. Journal of Hydrodynamics, 2018, 30(5): 815-827. DOI:10.1007/s42241-018-0089-3 |
| [16] |
Ansys, Inc. Ansys AQWA Uer’s Manual[R]. (Release 13.0), 2010.
|
| [17] |
李延巍, 莫文渊, 任年鑫, 等. 人工鱼礁-波浪能模块化浮体耦合动力响应分析[J]. 太阳能学报, 2022, 43(12): 489-494. |
 2024, Vol. 46
2024, Vol. 46
