2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
船舶拖航是一个非线性和多重耦合的复杂系统,一般由拖船、拖缆和被拖船组成。随着航运业和海洋经济的不断发展,海上突发事件发生的可能性也在增大,船舶拖航作为事件发生后的应急手段与救助措施,进行系统研究对海上航行安全有着重要意义 [1-2]。
国内外学者对船舶拖航系统的研究主要集中在船舶的运动响应和拖缆张力2个方面。Inoue等 [3]对油轮拖航系统进行了动力学仿真研究, 得到拖船在不同海况下产生的最大张力。Meng等 [4]设计了拖缆张力补偿装置,对张力的变化进行仿真分析,验证了装置的可靠性。Kijima等 [5]研究了风速、风向对航道稳定性的影响。Li等[6]研究船尾鳍作为改善FPSO在拖曳操作中的不良航向稳定性的解决方案,研究了单鳍、双鳍以及双尾鳍的构型对拖曳稳定性的影响,特别分析了双鳍水动力相互作用的影响,基于线性化后的拖曳系统进行特征值分析。戚心源等 [7]以1∶30缩尺比模型对拖航系统在不规则波中进行了试验模拟,研究发现拖缆长度对系统的纵摇、横摇这2个自由度性能影响较小,对被拖船首摇影响较大,且拖缆张力具有长周期性,波频对张力影响很小,对系统运动影响较大。朱军等 [8]建立了拖船-拖缆-被拖船动力学方程,排除环境载荷作用,通过数值计算方法对拖航系统进行时域模拟,发现拖缆张力的高频振荡主要受拖缆长度和弹性的影响,航向角的高频振荡主要受拖缆长度和拖点位置的影响,在一定范围内可通过调整对应参数有效控制振荡。石丽娜 [9]在时域内对拖航系统进行运动仿真,研究拖航速度、拖缆长度、被拖船姿态,风、浪、流、水深等环境条件对拖航系统的运动状态和拖缆张力的影响,并对拖航最优方案选择提出建议。
1 环境载荷 1.1 波浪载荷对波浪载荷进行Volterra级数二阶展开[10]:
| $\begin{aligned}[b] & 19{F}^{\left(1\right)}\left(t\right)+{F}^{\left(2\right)}\left(t\right)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{h}_{1}\left(\tau \right)\eta (t-\tau ){\mathrm{d}}\tau + \\ & {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{h}_{2}\left({\tau }_{1},{\tau }_{2}\right)\eta \left(t-{\tau }_{1}\right)\eta \left(t-{\tau }_{2}\right){\mathrm{d}}{\tau }_{1}{\mathrm{d}}{\tau }_{2} 。\end{aligned}$ | (1) |
式中:
| $ 21{F}_{I}^{\left(1\right)}\left(t\right)=\mathit{Re}\left[{\sum }_{j=1}^{N}{A}_{j}{q}_{L}\left({\omega }_{j}\right){e}^{i\omega t}\right],$ | (2) |
| $\begin{aligned}[b] 22{F}_{I}^{\left(2\right)}\left(t\right)=\mathit{Re}&\Bigg[{\sum }_{j=1}^{N}{\sum }_{k=1}^{N}{A}_{j}{A}_{k}^{\mathrm{*}}{q}_{D}({\omega }_{j},-{\omega }_{k}){e}^{i{\omega }^-t}+ \Bigg. \\ &\Bigg.{\sum }_{j=1}^{N}{\sum }_{k=1}^{N}{A}_{j}{A}_{k}{q}_{S}({\omega }_{j},{\omega }_{k}){e}^{i{\omega }^+t}\Bigg] ,\end{aligned}$ | (3) |
| $ 23{F}_{I}={F}_{I}^{\left(1\right)}+{F}_{I}^{\left(2\right)}。$ | (4) |
式中:
| $ 25{S}_{F}^{\left(1\right)}\left(\omega \right)={S}_\eta\left(\omega \right){\left|{q}_{L}\left(\omega \right)\right|}^{2},$ | (5) |
| $ 26{S}_{F}^-\left(\omega \right) = 8 {{\int }_{0}^{\mathrm{\infty }} \left|{q}_{D}(\mu ,\omega -\mu )\right|}^{2} {S}_\eta\left(\mu \right){S}_\eta(\omega -\mu ){\mathrm{d}}{S}_\eta \left(\mu \right),$ | (6) |
| $\begin{aligned}[b] 27{S}_{F}^+\left(\omega \right)=&8{\int }_{0}^{\omega /2}{\left|{q}_{s}\left(\frac{\omega }{2}+\mu ,\frac{\omega }{2}-\mu \right)\right|}^{2}\\ &{S}_{n}\left(\frac{\omega }{2}+\mu \right){S}_{n}\left(\frac{\omega }{2}-\mu \right){\mathrm{d}}{S}_{\text{η} }\left(\mu \right)。\end{aligned}$ | (7) |
式中:
通过式(8)可计算出,一阶辐射势与二阶辐射势产生的力:
| $\begin{aligned}[b] 30{F}_{R}\left(t\right)=&\left({M}^{a}\left(\omega \right)-{\int }_{0}^{\mathrm{\infty }}R\left(t\right){\mathrm{cos}}\omega t{\mathrm{d}}t\right)\ddot{\varsigma }\left(t\right)-\\ & {\int }_{-\mathrm{\infty }}^{t}R(t-\tau )\dot{\varsigma }\left(\tau \right){\mathrm{d}}\tau。\end{aligned}$ | (8) |
式中:
总的波浪力可通过将式(2)、式(3)及式(8)相加得到:
| $ 33{F}_{T}={F}_{I}+{F}_{C}+{\stackrel{~}{F}}_{R}。$ | (9) |
AQWA在时域内进行仿真时,使用波浪谱模拟不规则波,本文选用JONSWAP波浪谱,形式如下[11]:
| $ 35S\left({\omega }_{i}\right)=\frac{\alpha {g}^{2}}{{\omega }^{2}}\mathrm{e}\mathrm{x}\mathrm{p}(-\beta {\left(\frac{{\omega }_{p}}{\omega }\right)}^{4}){\left(3.3\right)}^{\gamma }。$ | (10) |
根据OCIMF规范的相关规定[12],船舶受到的纵荡方向风力Fxw为:
| $ {F}_{xw}=\frac{1}{2}{C}_{xw}{\rho }_{w}{V}_{w}^{2}{A}_{T}。$ | (11) |
横荡方向风力Fyw为:
| $ 40{F}_{yw}=\frac{1}{2}{C}_{yw}{\rho }_{w}{V}_{w}^{2}{A}_{L}。$ | (12) |
首摇风力矩Mxyw为:
| $ 43{M}_{xyw}=\frac{1}{2}{C}_{xyw}{\rho }_{w}{V}_{w}^{2}{A}_{L}{L}_{BP}。$ | (13) |
式中:ρw、Vw、AT、AL、LBP分别为空气密度、风速、船舶的横向受风面积、船舶纵向受风面积和船舶的垂线间长;可根据船型、主尺度、方向角选取参数Cxw、Cyw和Cxyw。
1.3 流载荷根据OCIMF规范的有关规定[12],定常流作用下的船舶会有沿着流速方向的平面力及绕Z轴方向的首摇力矩。船舶受到的纵荡方向流力为Fxc:
| $ 47{F}_{xc}=\frac{1}{2}{C}_{xc}{\rho }_{c}{V}_{c}^{2}{L}_{BP}T。$ | (14) |
横荡方向流力为Fyc:
| $ 50{F}_{yc}=\frac{1}{2}{C}_{yc}{\rho }_{c}{V}_{c}^{2}{L}_{BP}T 。$ | (15) |
首摇流力矩为Mxyc:
| $ 53{M}_{xyc}=\frac{1}{2}{C}_{xyc}{\rho }_{c}{V}_{c}^{2}{L}_{BP}^{2}T。$ | (16) |
式中:ρc、Vc、T分别为海水密度、流速、吃水;可根据水深、船型、主尺度、方向角选取参数Cxc、Cyc和Cxyc。
2 研究对象本文研究的被拖船舶属于浅吃水、高干舷、边岛式上层建筑、全封闭、舷台外飘复合型船型。由于其特殊的船型特点,使得本舰干舷近20 m,需要采用数值模拟方式支撑船舶拖带设计,提高安全性与可靠性,本船主尺度如表1所示。
|
|
表 1 主尺度 Tab.1 Principal dimension |
本文选用的拖缆单根是直径为52 mm的钢丝绳,长为300 m,破断载荷为
在本文中,对被拖船舶坐标系和环境坐标系定义如图1所示。坐标系原点为船舶重心;X轴由船尾沿船体中心线指向船首;Y轴由船右舷指向左舷。首摇以X正轴向Y正轴转动的右手坐标系为正。风、浪、流载荷方向与X轴夹角以逆时针方向为正,即环境载荷沿船尾指向船首时,方向角为0°。
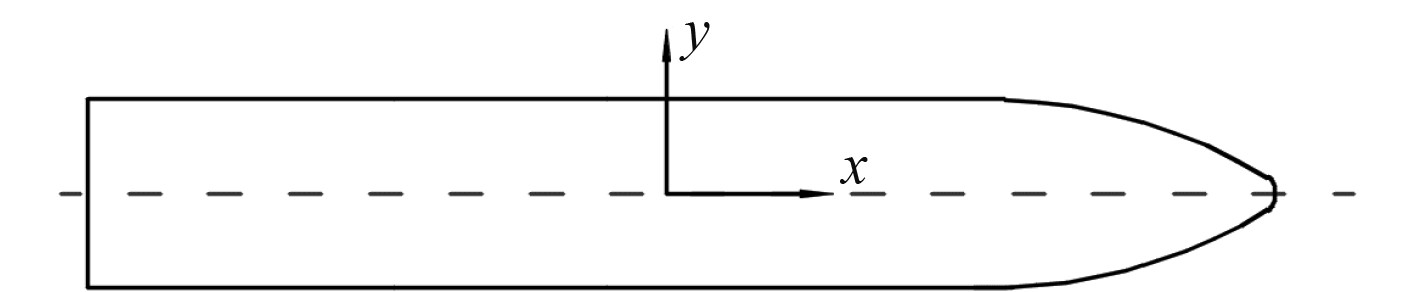
|
图 1 坐标系定义 Fig. 1 Coordinate system definition |
选取典型工况进行1根拖缆和2根拖缆对比分析,计算工况如表2所示。
|
|
表 2 不同拖缆数目拖航工况 Tab.2 Towing conditions with different number of streamers |
图2为不同拖缆数目船舶重心5个自由度运动幅值的对比。可知,在相同环境条件下,相比采用1根拖缆,采用2根拖缆拖航船舶运动响应较小。2根拖缆的船舶横荡幅值为0.065 m,比1根拖缆时减少2.25%;2根拖缆的船舶垂荡幅值为0.495 m,比1根拖缆时减少0.50%;2根拖缆的船舶横摇幅值为
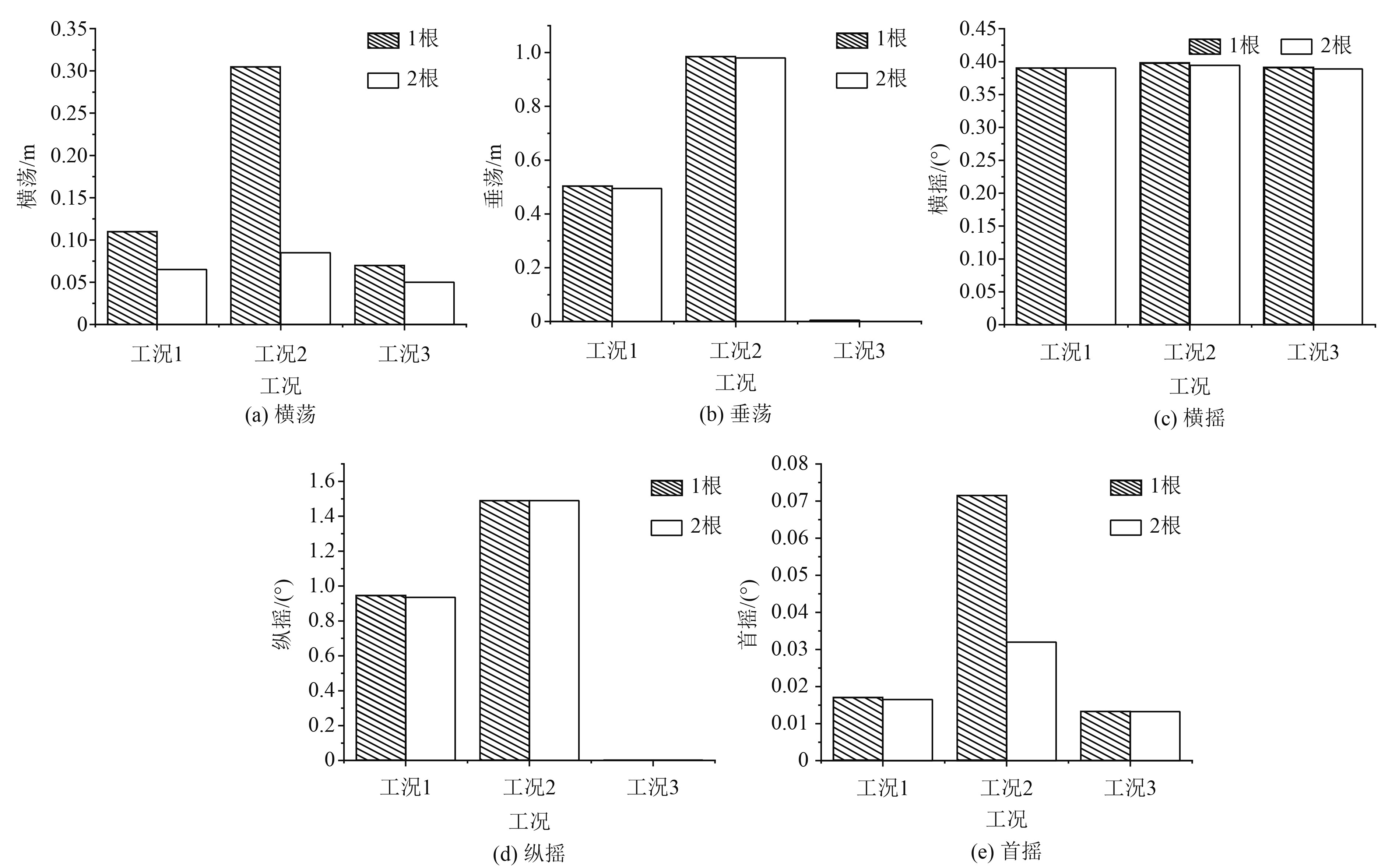
|
图 2 不同拖缆数目船舶运动幅值对比 Fig. 2 Comparison of ship motion amplitudes with different number of towing cables |
工况1~工况3的拖缆最大张力对比如图3所示。
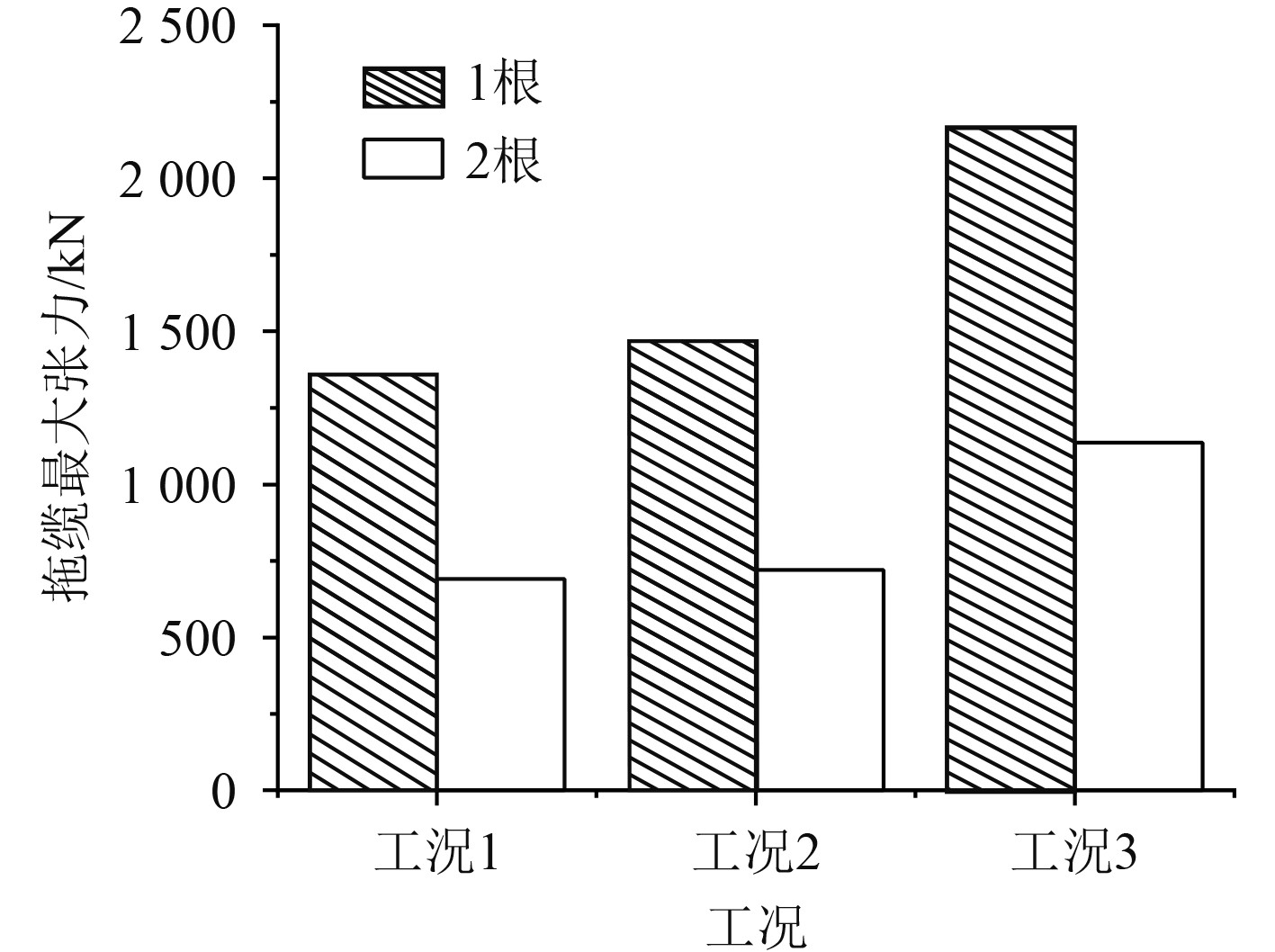
|
图 3 不同拖缆数目拖缆最大张力对比 Fig. 3 Comparison of maximum tension of streamers with different number of streamers |
可知,在相同环境条件下,相比采用1根拖缆,采用2根拖缆拖航时拖缆所受最大张力较小,工况1采用1根拖缆时最大张力为
选取典型工况进行拖速为4 kn、6 kn、8 kn的拖航对比分析,计算工况如表3所示。
|
|
表 3 不同拖速拖航工况 Tab.3 Towing conditions with different towing speeds |
图4为船舶不同航速下,船舶重心处除纵荡外2个自由度上重心幅值的对比。
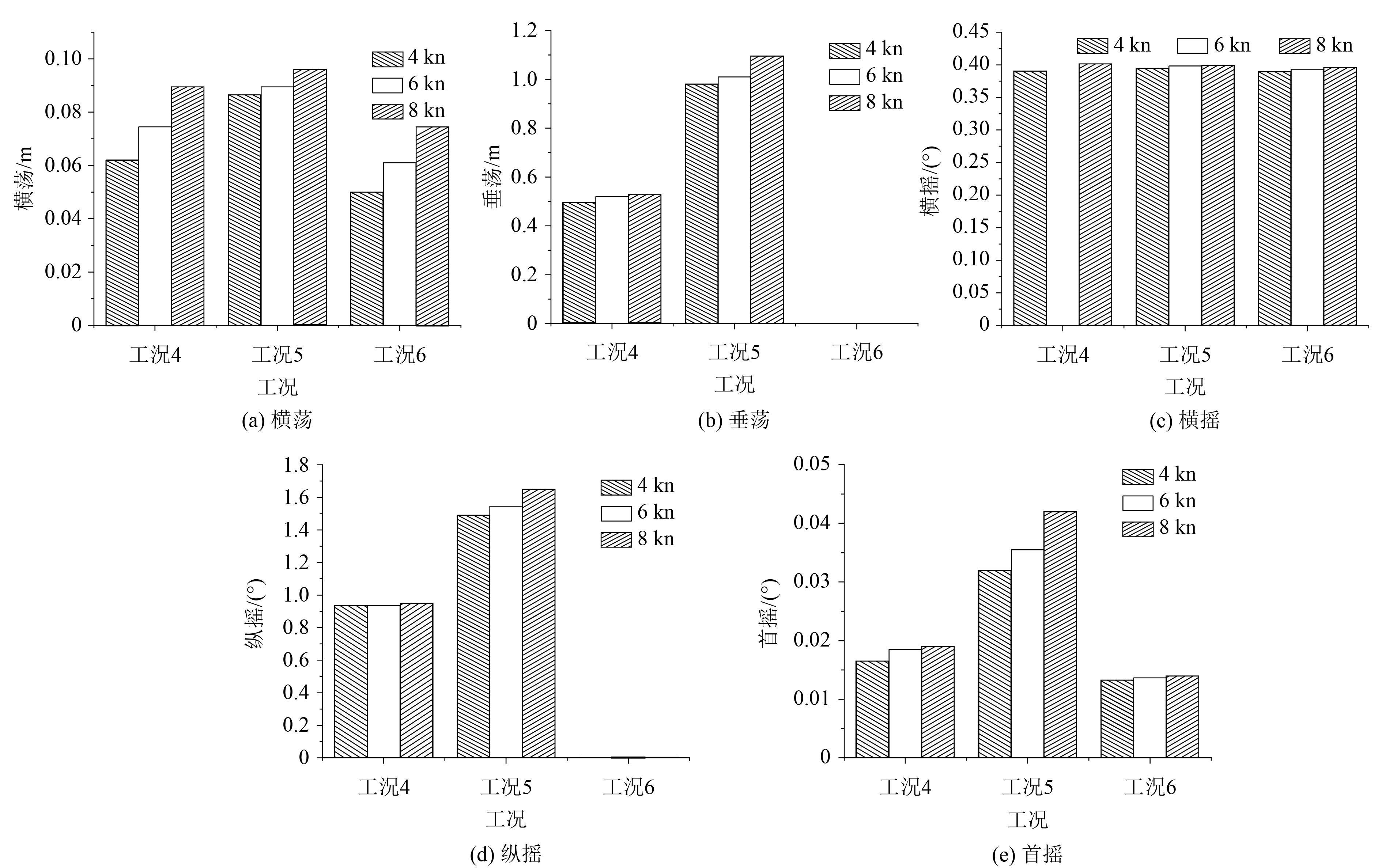
|
图 4 不同拖速船舶运动幅值对比 Fig. 4 Comparison of motion amplitudes of ships with different towing speeds |
可知,在相同环境条件下,相比船舶拖速为6 kn和8 kn,拖速4 kn时船舶运动响应较小。以工况4为例,拖速4 kn的船舶横荡幅值为0.062 m,比拖速6 kn时减少10.08%,比拖速8kn时减少22.18%;拖速4 kn的船舶垂荡幅值为0.495 m,比拖速6 kn时减少2.53%,比拖速8 kn时减少3.54%;拖速4 kn的船舶横摇幅值为
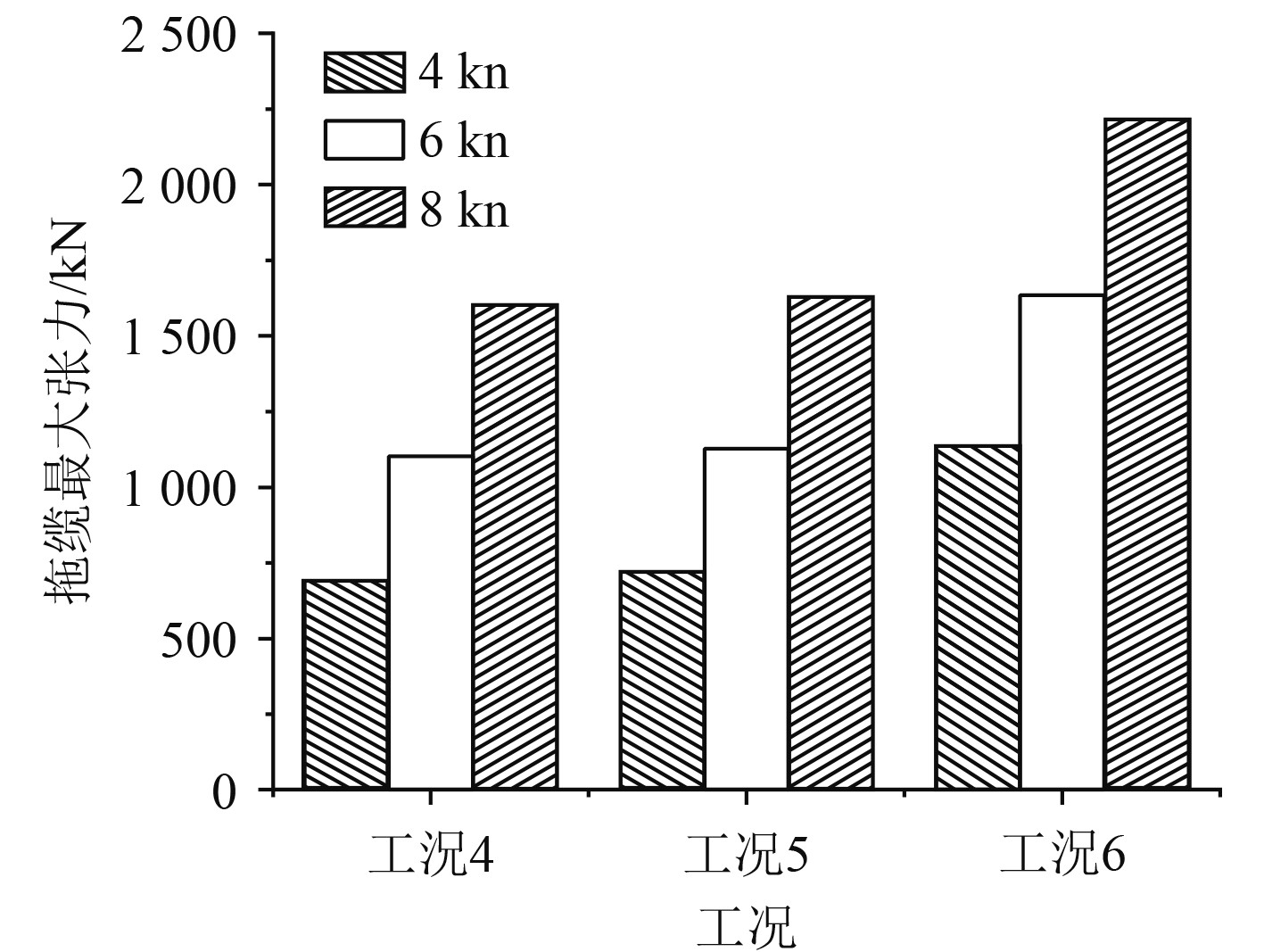
工况4~工况6的拖缆最大张力对比如图5所示。
|
图 5 不同拖速拖缆最大张力对比 Fig. 5 Comparison of maximum tension of streamers at different towing speeds |
可知,工况4、工况6拖速4 kn比拖速8 kn时拖缆最大张力平均减少53.78%,拖速6 kn比拖速8 kn时拖缆最大张力平均减少29.39%。在相同环境条件下,相比船舶拖速6 kn和 8 kn,拖速4 kn时拖缆所受最大张力较小。工况4拖速8 kn时拖缆最大张力为
本文采用数值仿真方法,对在风浪流载荷作用下的特殊船型船舶拖航进行时域耦合动力响应分析,研究了拖揽数目和拖速对船舶拖航的影响,支撑船舶拖带设计。可以得出以下结论:
1)在相同环境条件下,选取1根拖缆和2根拖缆进行船舶拖航时域耦合对比分析。结果表明,2根拖缆相较1根拖缆,横荡运动明显降低,拖索最大张力显著减小,平均减少49.18%。因此,设计时应优先选择2根托揽的拖带方式。
2)在相同环境条件下,选取不同拖速工况进行船舶拖航时域耦合对比分析。结果表明,拖速4 kn比拖速8 kn时,拖缆最大张力平均减少53.78%,拖速6 kn比拖速8 kn时,拖缆最大张力平均减少29.39%,拖速降低时拖航更安全。因此,设计中应参照较高拖速工况仿真结果考虑设计裕度,工程中尽量在较低拖速下进行拖航作业。
| [1] |
王祥. 海上应急拖带适应性研究[D]. 大连: 大连海事大学, 2022.
|
| [2] |
亓国才. 恶劣海况下双船的拖带性能研究[D] . 大连: 大连海事大学, 2022.
|
| [3] |
INOUE Y, SURENDRAN S, SHIMIZU T. Dynamic tension analysis of surface towing system [J]. The Japan Society of Naval Architects and Ocean Engineers, 2009, 1994(175): 241−250 .
|
| [4] |
MENG J, CHEN Z, JIANG T, et al. Controllable of underwater towing tension passive compensation device design research [C]//International Conference on Vehicle, Mechanical and Electrical Engineering, 2015 .
|
| [5] |
KIJIMA K, VARYANI K. Wind effect on course stability of two towed vessels[J]. Journal of the Society of Naval Architects of Japan, 1985(158): 137-148. DOI:10.2534/jjasnaoe1968.1985.158_137 |
| [6] |
LI B, HUANG W, LIANG H. An efficient method to assess effect of fin on the course stability of towing system [J]. Ocean Engineering, 2020, 217(2): 108005.1−108005.15.
|
| [7] |
戚心源, 朱祖祺, 严似松, 等. 不规则波中拖航系统的模型试验[J] . 水动力学研究与进展(A辑), 1995(1): 1−8. QI Xinyuan, ZHU Zuqi, YAN Sisong, et al. Model test of towing system in irregular waves [J]. Chinese Journal of Hydrodynamics(A), 1995(1): 1−8 . |
| [8] |
朱军, 张旭, 陈强. 缆船非线性拖带系统及数值仿真[J]. 中国造船, 2006(2): 1-9. ZHU Jun, ZHANG Xu, CHEN Qiang. Nonlinear towing system and numerical simulation of cable boats[J]. Shipbuilding of China, 2006(2): 1-9. DOI:10.3969/j.issn.1000-4882.2006.02.001 |
| [9] |
石丽娜. 基于AQWA的大型浮体拖航性能研究[D]. 大连: 大连理工大学, 2011.
|
| [10] |
郭建廷. 船舶码头系泊形式及水动力性能分析[D]. 镇江: 江苏科技大学, 2016.
|
| [11] |
FALTINSEN O. Sea loads on ships and offshore structures[M]. Cambridge University Press, 1993.
|
| [12] |
BEKIASHEV K A, SEREBRIAKOV V V. Oil companies international marine forum (OCIMF) [J]. Springer Netherlands, 1981, 94(9): 8263−8268.
|
 2024, Vol. 46
2024, Vol. 46
