0 引　言

喷水推进器因推进效率高，抗空泡性能好，噪声低等优点，目前被广泛应用于高速船和军事舰艇^[1]，其水动力学性能的研究也已取得了一定成果。仝博等^[2-4]已经对计及自由液面，带真实泵的喷水推进船的自航性能进行了数值模拟。有时为了方便考察，缩短计算周期，孙存楼^[5-6]指出水流进入推进喷泵之前需要经过流道的引流，而喷泵产生的影响也主要体现在流道的出口处，认为泵的旋转对流道进口处几乎没有影响，并且船模自航试验主要研究的是喷水推进装置与船体的相互作用，因此计算中可忽略泵的旋转效应对船体的影响，仅关注其在推力方面的作用，可采用2种方法来代替泵的作用：一是通过激盘模型代替泵作用；二是在采用流量边界条件代替泵作用，在泵前通过流量出口的边界条件来模拟泵的抽吸作用，在泵后通过流量入口的边界条件代替泵的喷射作用，进口和出口的流量保持一致，这样仅进行阻力数值计算即可。

T型喷口是一种附加在喷水推进装置后方，改变水流纵向喷射方向为横向的模型试验装置。它有2个特殊的作用，一是解决常规推进船模自航试验中，自航工况流量测试的问题，即改变水流方向的同时测T型喷口装置的纵向受力，再结合常规喷口横截面积，根据动量关系换算出流量，该方法在国外多个水池获得应用。Arash等^[7]指出，T型喷口和常规喷口在相同的自航点工况下，姿态保持一致时，叶轮的转矩仅有很微小的差异，可以保证两者流道内的流量一致。

另一方面，喷水推进船舶的阻力性能与常规船舶有着很大的不同，流道的安装会增大船舶阻力^[8]，在喷水推进船模自航性能换算中，直接采用流道封闭时的船模阻力并不合适。喷水推进船模自航时的阻力变化受2个因素影响：一是喷水推进器工作时，引起船体姿态发生变化，而纵倾角是引起阻力增加的重要因素；另外，流道的安装使得船底的几何面积减小，影响了船体的静压阻力和摩擦阻力，并且推进器的抽吸作用破坏了船尾的边界层，船底流场发生变化，影响动压阻力和摩擦阻力^[9]。而设计优良的T型喷口，喷口处流道的设计应尽量保证水流横向喷出，这样在对应常规喷口推进船模自航点工况下，喷水推进装置只在船体内部的流道上产生力的作用，既能反映常规喷口推进船模自航状态下，推进装置的抽吸作用对船尾边界层的影响，又对船的浮态影响很小，采用船模阻力试验和获流区的PIV流场测试，结合动量通量法，可将常规喷口推进船模自航工况下，推进装置对船体阻力的影响分离出来，这是T型喷泵在常规推进船模自航试验中的另一个作用，也是本文阐述的重点。

为了说明T型喷口的作用，减小由于流量不同对计算和试验结果分析的影响，采用流量边界条件法对常规喷口推进船模的自航性能和T型喷口推进船模的阻力性能进行数值模拟，流量采用试验提供的数据。T型喷口推进船模虽然用流量边界法模拟了叶轮的抽吸作用，但试验中采用的是与阻力试验一样的拖模试验，旨在获取船身阻力，因此本文仍称之为阻力计算，并将计算结果与试验结果进行比较。

同时对无流道裸船体的阻力性能进行了模拟，分析推进装置工作时，船身阻力与无流道裸船体阻力之间的差异，对T型喷口推进装置的工作原理进行说明。

文中以工况1表示无流道裸船体阻力性能计算，工况2表示常规喷口推进船模自航性能计算，工况3表示T型喷口推进船模阻力性能计算。

计算基于Numeca专业船舶流体力学计算软件，考虑自由面影响及船身姿态的变化。

1 控制方程

流场的控制方程包括连续方程和动量方程，直角坐标系下，不可压缩均质流体的连续方程可表达为：

$ \frac{{\partial {u_x}}}{{\partial x}} + \frac{{\partial {u_y}}}{{\partial y}} + \frac{{\partial {u_z}}}{{\partial z}} = 0 。$

(1)

式中：$ {u_x} $、$ {u_y} $、$ {u_z} $分别为X、Y、Z三个方向上的速度分量。

常密度和黏性系数流体的动量守恒方程：

$ \rho \frac{{{\rm d}\vec u}}{{{\rm d}t}} = \rho \vec f - {\rm{gradp}} + \mu {\nabla ^2}\vec u。$

(2)

式中：$ p $为压强；$ \vec f $为单位质量力；$ \vec u $为速度矢量；$ t $为时间；$ \mu $为流体动力黏度。

自由面波动是采用VOF方法追踪的，笛卡尔坐标系下，方程如下：

$ \frac{{\partial {a_q}}}{{\partial t}} + \frac{{\partial \left( {\mu {a_q}} \right)}}{{\partial x}} + \frac{{\partial \left( {\nu {a_q}} \right)}}{{\partial y}} = 0 \text{，}{{q}}=1,2 ，$

(3)

$ \sum\limits_{q = 1}^2 {{a_q}} = 1 。$

式中：$ {a_q} $为体积分数，表示单元内第$ q $相流体占的体积分数，$ q = 1 $表示空气相，$ q = 2 $表示水相，$ {a_q} = 0.5 $处为自由面。

2 数值计算方法

以配备4台喷水推进装置的船模为计算对象，计算所需部分参数如表1所示。

图1为采用流量边界条件法模拟喷泵抽吸作用的数值模型，工况2和工况3中，为了形成封闭实体，需要将流道在叶轮的上、下游进行分割。在本算例中，分别在叶轮上、下游做一等X 面对流道进行切割，保留定子和部分轴系，然后封闭切面，作为流量出口面和流量入口面。叶轮上游的封闭面作为流量出口面，给定流量边界条件模拟泵的抽吸作用，叶轮下游的封闭面作为流量入口面，通过给定流量边界条件模拟流体经过泵后的流动。

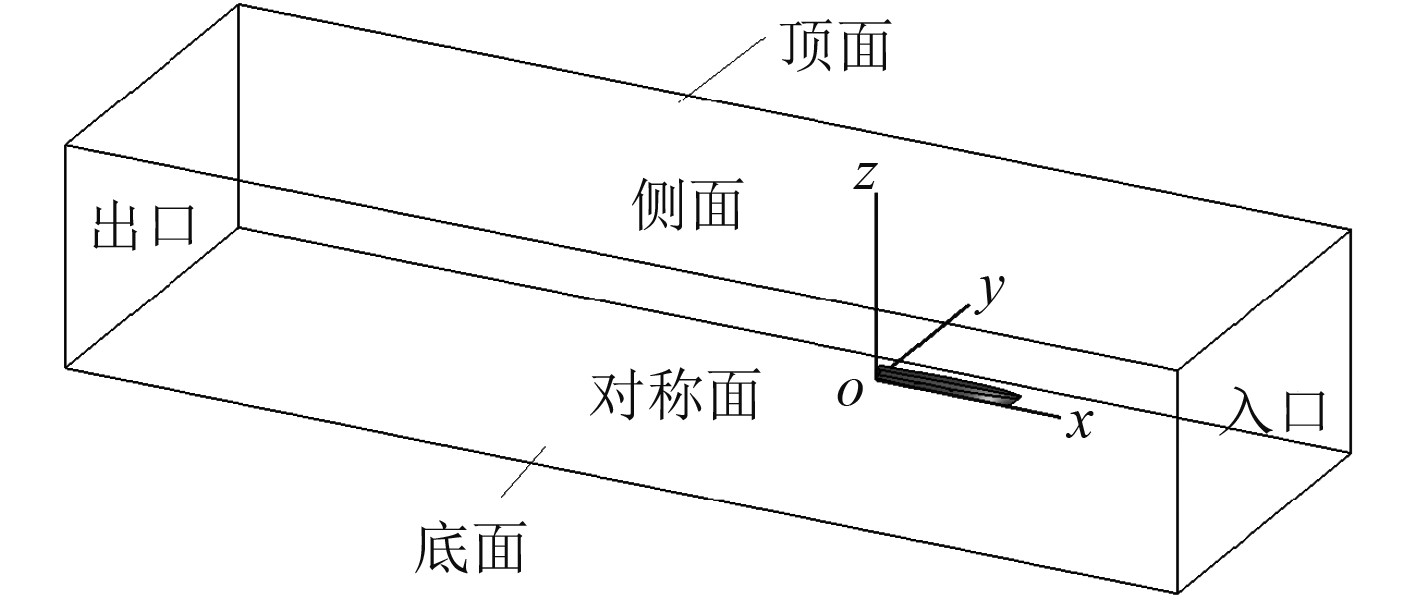
由于船的对称性，取半船进行计算，图2为计算域示意图。笛卡尔坐标系下，坐标原点在船的基点处，X轴沿船长方向，正向指向船首；Y轴沿船宽方向，正向指向船的左舷；Z轴垂直向上，满足右手法则。

考虑到计算傅式数达到0.534，兴波明显，且T型喷口有横向水流喷出，因此计算域下游和侧面尺寸较大。流场入口距船首1L_pp（L_pp为船的垂线间长），出口距船尾6L_pp，侧面距船中纵剖面2L_pp，顶面距船底0.5L_pp，底面距船底1L_pp。

计算网格在Numeca的前处理软件Hexpress中生成，网格形式为非结构化的六面体网格。工况1的体网格数约为270万，工况2的体网格数约为500万，工况3的体网格数约为580万。自由液面网格高度约为0.001L_pp，长宽方向与高度的长细比为128。船身表面铺设边界层网格，第一层网格离壁距离由Y⁺=30决定。

图3为获流区（通常取流道进口上游1.0倍泵特征直径处）处局部加密网格，图4为T型喷口出口所在区域的加密网格，用以精细捕捉流场信息，提高计算精度。

计算采用绝对坐标系，将船置于静水中，在给定时间内，速度由0加速到指定船速，采用k-ω（SST-Menter）湍流模式，定常计算。

表2为计算采用的边界条件设置。工况2和工况3中，用数值模型代替了泵的抽吸作用，流量入口面和流量出口面给定速度边界条件，由流量值和切面面积的比值决定，因为船本身有速度，出、入口的速度为相对于船的速度。

3 计算结果分析方法

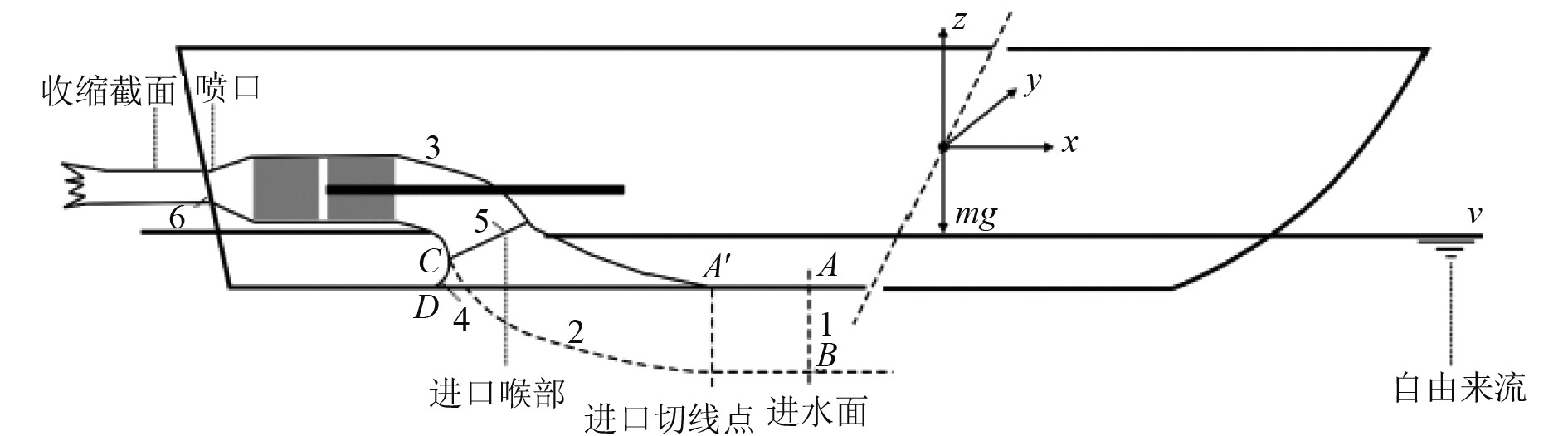
通常采用对喷水推进控制体的研究，来考察喷泵的作用。图5为喷水推进控制体示意图^[5]，分别获取喷水推进装置获流区（面1）和喷口（面6）的动量通量，二者之差为作用在船体上的推力。

$ \Delta {\overline M _x} = {T } ，$

(4)

$ \Delta {\overline M _x} = {\overline M _{x6}} - {\overline M _{x1}} 。$

(5)

下标x代表船行方向，对于常规喷口推进船模，控制体的动量通量差计算式为：

$ \Delta {\overline M _x} = \frac{{\rho Q_J^2}}{{{A_6}}}\cos {\theta _6} - \rho {Q_J}{c_{m1}}{V_0} 。$

(6)

式中：$ {Q_J} $为推进器的体积流量；$ {\theta _6} $为纵倾角；A₆为6站的出口面积；$ {V_0} $为未被干扰的来流速度；${c_{m1}}$为由于粘性边界层速度分布引起的在截面1（获流区）处的动量速度系数，通过物理测量或仿真测试得到速度分布，具体如下：

$ {C_{m1}} = \frac{1}{{\sqrt {(1 - C_p^2)} {Q_J}{V_0}}}\int\limits_{{A_1}} {u_x^2} {\rm d}A ，$

(7)

$ {C_p} $为静压系数：

$ C_p^{} = \frac{{{p_s} - {p_0}}}{\displaystyle{\frac{1}{2}\rho V_0^2}} 。$

(8)

式中：$ {p_0} $为大气压；${u_x}$为进口前获流区的速度在推力方向上分量的分布；A₁为垂直于推力方向的有效获流区面积。

对于T型喷口推进船模，喷口处水流是横向喷出，即$ {\overline M _{x6}} = 0 $，因此：

$ \Delta {\overline M _x} = - {\overline M _{x1}} = - \rho {Q_J}{c_{m1}}{V_0}。$

(9)

喷水推进器工作时，获流区的形状近似为半椭圆形^[10]，如图6所示。在进行后处理时，在获流区所在纵向位置作一个等X的获流面，从流量出口面往船的上游拖出流线，找到获流面上距船中纵剖面最近和最远的点，这2个点通常在获流面与船体的交线上。通过两点的Y值和Z值，可确定椭圆的长轴，椭圆中心以及长轴与水平面的夹角。

椭圆方程中，长轴和椭圆中心确定后，根据流线穿过获流面的范围，基本可以确定短轴的大小，再通过微幅调整短轴的长度，使得获流区内的流量等于给定流量，从而确定椭圆方程。

椭圆方程确定以后，获流区的形状也就固定了，再对获流区内的流体动量进行积分，结合上述公式，可以得到获流区的动量通量，进一步得到T型喷口推进船模推进控制体的动量通量差。

4 计算与试验结果的比较

表3为无流道裸船体工况1计算与试验阻力结果的比较，其中纵倾角θ以尾倾为正，重心升沉量T_Z以下沉为正。

计算与试验的阻力值偏差为−2.1%。与试验波形照对比发现，船首出现一定翻浪及飞溅，在目前的CFD网格尺度下，还不足以精确捕捉到该现象，因此计算值比试验值偏小。姿态的差异可能是由于计算的重心和试验拖车的作用点不完全重合导致。

常规喷口推进船模自航试验中，采用系泊状态，压差标定的方法来确定喷口流量，自航点工况下，流道内流量Q=0.01331 m³/s。

在T型喷口阻力试验中，采用对应常规喷口推进船模自航点的船速和叶轮转速，测得的总阻力包含常规阻力（流道进出口封闭状态）、喷水推进系统的阻力、喷水推进装置工作对船体影响产生的阻力3部分。因此用总阻力减去由动量通量法求出的喷水推进系统产生的阻力和封闭状态下的裸船体阻力，即为由喷水推进系统对船体的影响引起的阻力。

CFD的计算结果中，采用流量边界条件法代替了真实叶轮的抽吸作用，采用推进控制体来代替整个喷泵系统，即总阻力同样包括用动量通量法求出的喷水推进系统产生的阻力和封闭状态下的裸船体阻力以及由喷水推进系统对船体的影响引起的阻力。

表4为T型喷口推进船模阻力计算与试验结果的比较，由式（8）知，控制体的动量通量差$ \Delta {\overline M _x} $即为喷水推进系统的阻力，船体阻力R_h为总阻力R_t与$ \Delta {\overline M _x} $的差值，阻力增量△R为R_h与裸船体阻力R_m的差值，即喷水推进系统对船体的影响引起的阻力。

通过对计算结果的分析，流道封闭的裸船体阻力为226.9 N，开流道后且推进器工作时，船身阻力增加至234.5 N，增加了3.3%；由于喷泵的抽吸作用，使得部分水体进入流道，尾部船底压力减小，船身尾倾和重心下沉量增加，这些均与裸船体阻力有所差别。

T型喷口阻力试验中，推进系统的抽吸作用使得船身阻力较流道封闭的裸船体阻力由231.8 N增至240.6 N，增加了约3.8%，船身姿态也有明显差异。

表5为计算的和PIV试验获得的控制体动量通量比较，靠近船中纵剖面的内侧控制体动量通量差计算与试验的偏差为−4.4%，离船中纵剖面较远的外侧控制体动量通量差计算与试验的偏差为−1.0%，可能内侧控制体获流区处的船体边界层较厚，该处物理量受边界层的影响较为明显。

5 T型喷口推进装置的工作原理

为说明T型喷口推进装置工作原理，需保证常规喷口推进船模与T型喷口推进船模的运动速度和叶轮的转速相同，即流道内的流量保持一致，流量值取试验数据Q=0.01331 m³/s。

表6为工况1、工况2、工况3船体上阻力以及运动姿态的计算结果。工况2和工况3的阻力值比工况1分别大3.0%和3.3%，说明推进系统工作时，船体阻力较流道封闭裸船体的阻力有所增加，船体运动姿态也有所不同，尾倾角和重心下沉量均稍有增加，主要原因是喷水推进器的抽吸作用改变了船底，尤其是尾部的压力分布^[11]。

工况2和工况3的阻力值相差较小，小于1%，说明T型喷口对阻力的影响与常规喷口差不多。

表7和表8为工况2、工况3的内、外侧获流区水动力性能比较，用边界层对进流动量的影响系数$ \alpha $以及边界层对进流动能的影响系数$ \beta $^[12]，以及获流区的动量通量$ {\overline M _x} $来考察。

$ \alpha = \frac{1}{{{V_0}}} \frac{\displaystyle{\int_{{A_1}} {u_x^2{\rm d}A} }}{\displaystyle{\int_{{A_1}} {u_x^{}{\rm d}A} }} \text{，} \beta = \frac{1}{{V_0^2}} \frac{\displaystyle{\int_{{A_1}} {u_x^3{\rm d}A} }}{\displaystyle{\int_{{A_1}} {u_x^{}{\rm d}A} }}。$

(10)

式中：$ {A_1} $为控制体获流区的面积；$ {u_x} $为获流区处的轴向速度；$ {V_0} $为船速。$ \displaystyle \int_{{A_1}} {{u_x}} {\rm d}A $为获流区处的流量；$ \displaystyle \rho \int_{{A_1}} {u_x^2} {\rm d}A $为获流区处的动量（$ \rho $为流体密度）；$ \displaystyle \frac{\rho }{2}\int_{{A_1}} {u_x^3} {\rm d}A $为获流区处的动能。

T型喷口推进船模和常规喷口推进船模，在相同计算工况下，内、外侧的获流区上的各物理量几乎一样，进一步说二者对获流区流动影响一致。

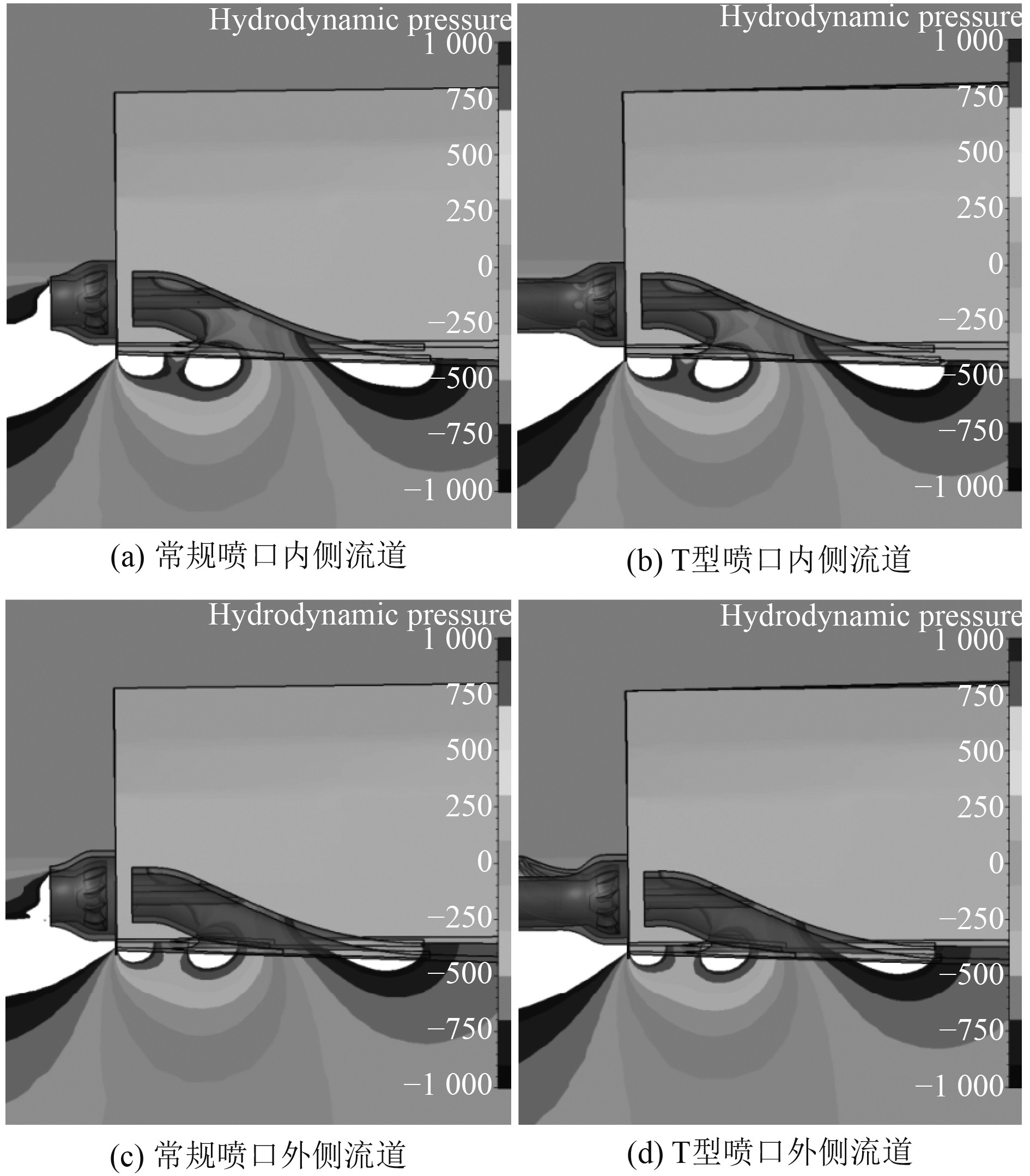
图7为2种喷口推进船模获流面上的边界层分布比较，图8为内、外侧流道中纵剖面上的压力分布比较，二者的分布特点相差无几。

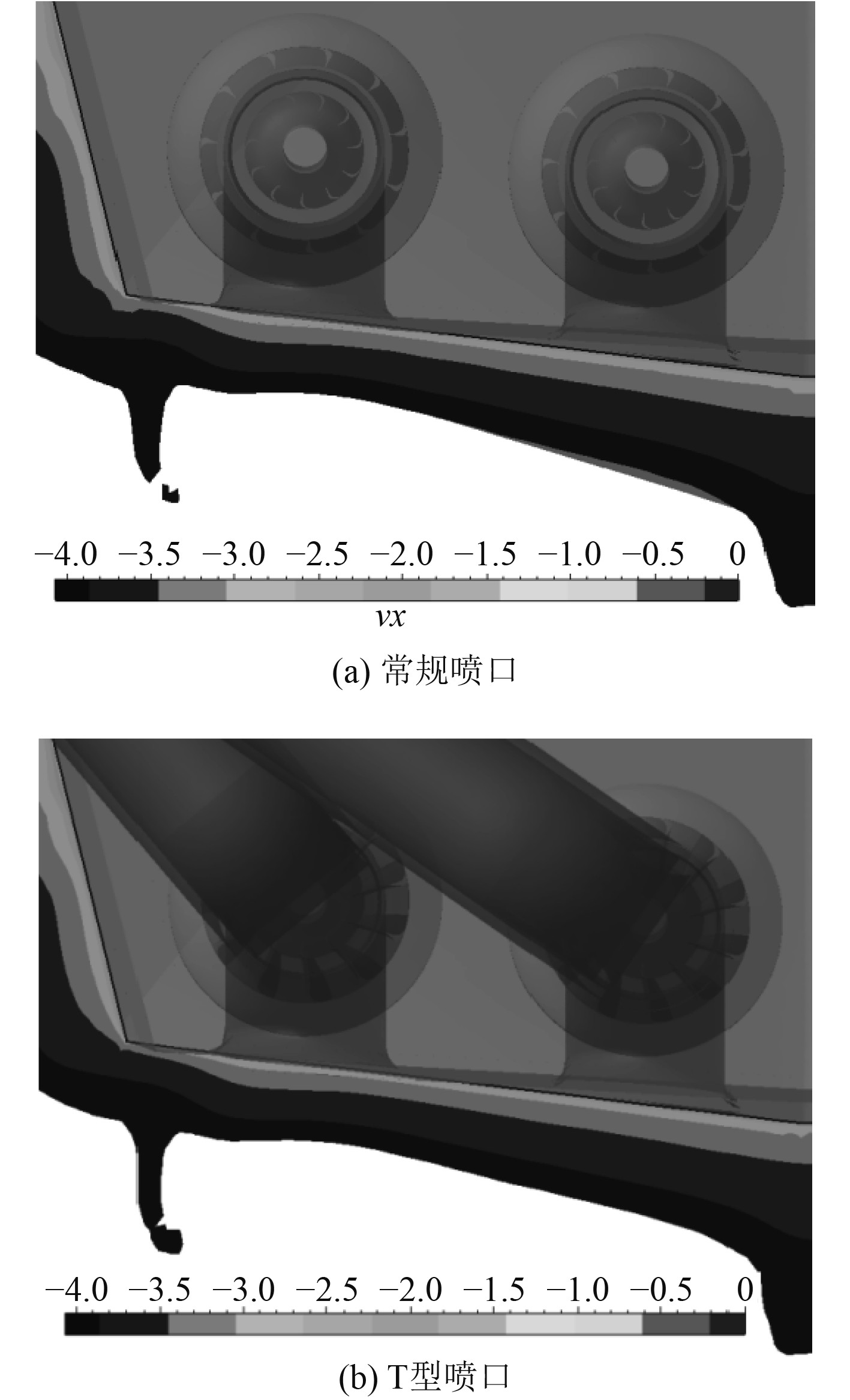
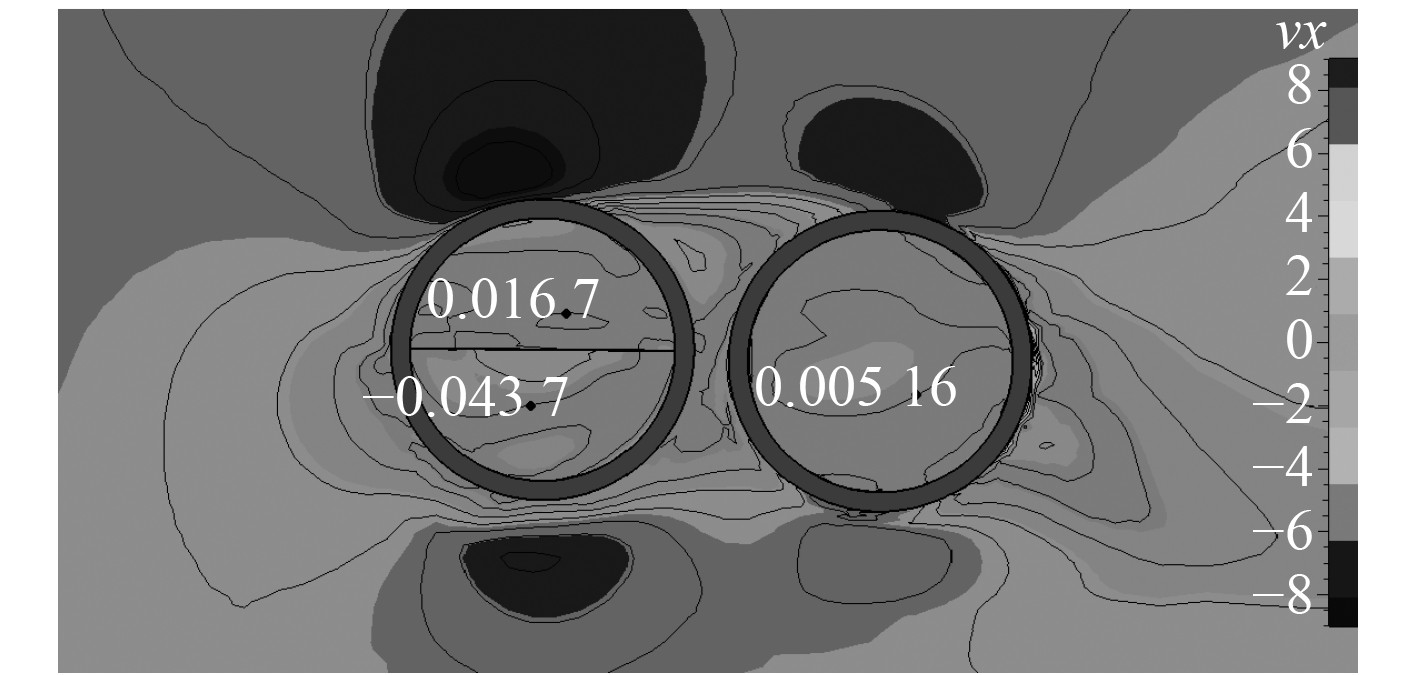
图9为T型喷口推进船模，喷口端面上的轴向速度的分布。喷口端面的轴向速度都几乎为0，说明目前设计的T型喷口保证了水流横向喷出，对船模纵向方向上的运动影响很小。

6 结　语

本文通过对T型喷口推进船模的阻力计算，分析了T型喷口模型试验装置的作用之一，并进一步说明其工作原理，得到以下结论：

1）通过对T型喷口推进船模的阻力数值模拟以及对获流区的动量通量提取，可以将常规喷口推进船模自航点上，推进装置工作时对船体阻力的影响分离出来。

2）T型喷口端面处轴向速度接近0，说明T型喷口改变了流道内的水流方向，使其横向喷出，既能反映自航状态下喷泵抽吸作用对船尾边界层的影响，对船的纵倾和升沉影响也很小，获流区处的物理量与常规喷口推进船模几乎一致。