0 引　言

水下航行体在做大舵角回转/潜浮机动，或者事故状态应急挽回操控等极限大机动过程中，由于来流攻角较大，背流面将会产生明显流动分离，诱发较强的涡旋结构，使得作用在水下航行体上的水动力非线性特征十分明显，表现为随着攻角的增大，水下航行体垂向水动力递增明显，而俯仰力矩先增大后减小，再反向增大，水动力作用中心位置则呈现出前后移动的变化特征，这显然给水下航行体深度方向和姿态角的稳定控制带来了难度^[1,2]。另一方面，水下航行体尾部流动分离及涡旋发放不仅使得舵前方来流品质较差，影响舵效，还会因为较大的舵前方来流攻角，导致舵面出现失速现象，使得舵效大幅下降，大大影响水下航行体的水动力性能。并且，高航速下的水下航行体运动姿态剧烈变化也将会使得水下航行体失事的风险大为增加^[3,4]。

鉴于此，本文以Suboff标模为研究对象，采用大涡模拟数值计算方法开展水下航行体大机动工况下的流体动力性能，完成水下航行体尾部及舵面流动分离涡旋结构的精细捕捉。本文研究成果可为后续极限机动工况下水下航行体流动控制提供技术支撑。

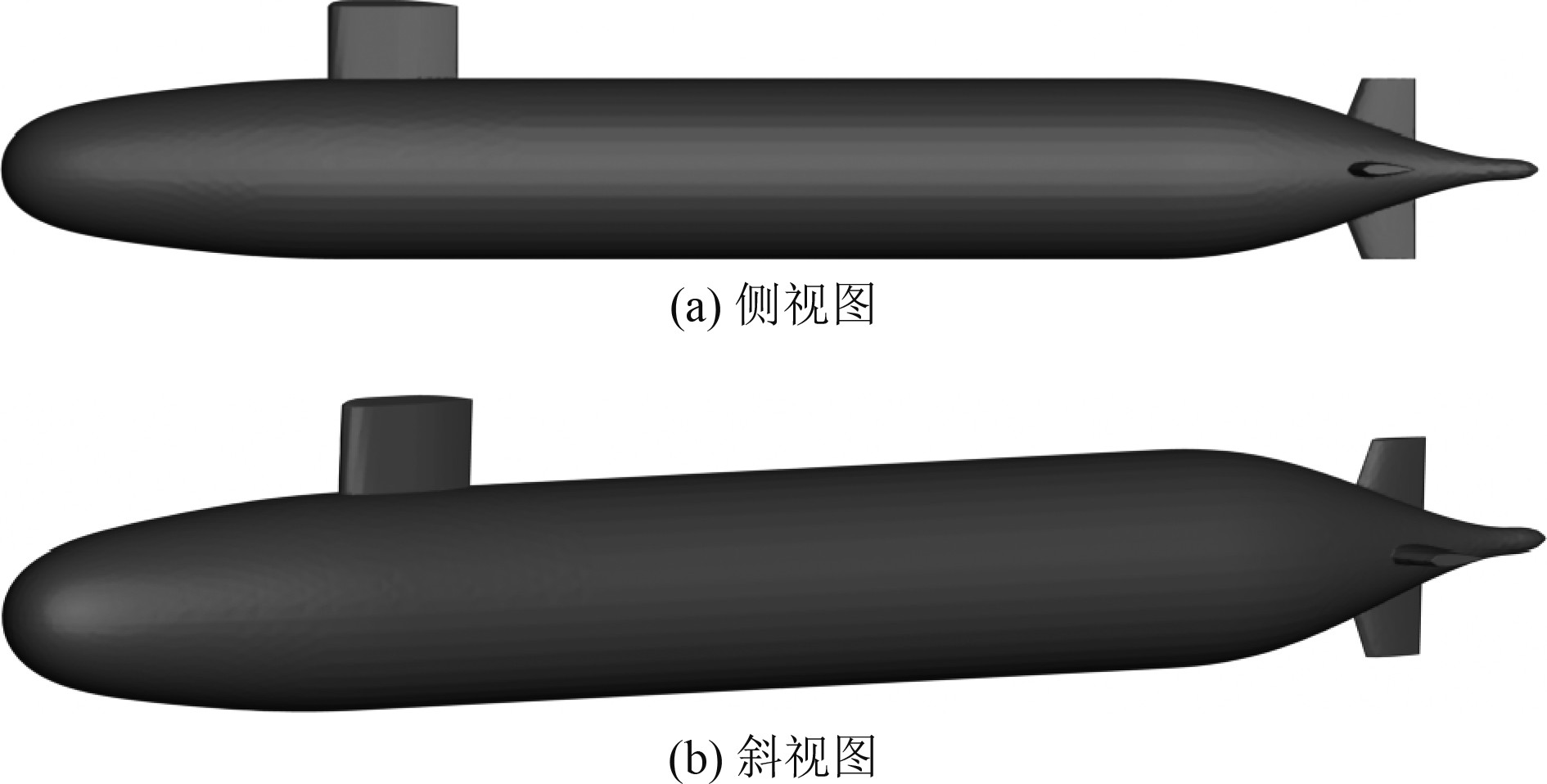
1 计算模型

图1为本文计算模型Suboff标模，由主体、围壳和操纵面组成。具体主尺度参数见表1。

2 数值方法 2.1 控制方程

本文采用大涡模拟方法（Large Eddy Simulation，LES）求解大机动工况下水下航行体的流体动力性能。大涡模拟方法模拟湍流的思路是：负责质量、动量和能量输运的大涡被直接求解，小涡对大涡运动的影响则通过一定的模型来模拟^[5]。

不可压缩粘性流体的运动控制方程为：

$ \begin{gathered} \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ，\\ \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} = \upsilon \frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}}。\\ \end{gathered} $

(1)

任意一个瞬时变量可写成如下形式：

$ \phi = \overline \phi + {\phi ^{'}}。$

(2)

式中：$ \overline \phi $为空间过滤后的变量，可由大涡模拟直接解出，称为可解尺度脉动；$ {\phi ^{'}} $为剩余脉动量，该部分为不可解的亚格子变量，需通过亚格子应力模型体现。物理空间的滤波过程表示为：

$ \overline \phi (x) = \int\limits_D {G(x,\xi )} \phi (\xi ){\rm d}\xi 。$

(3)

式中：$ \overline \phi (x) $为滤波后的函数；$ G(x,\xi ) $为滤波函数；D为滤波空间^[6]。

本文选用动态Smagorinsky亚格子模型进行求解剩余脉动量。

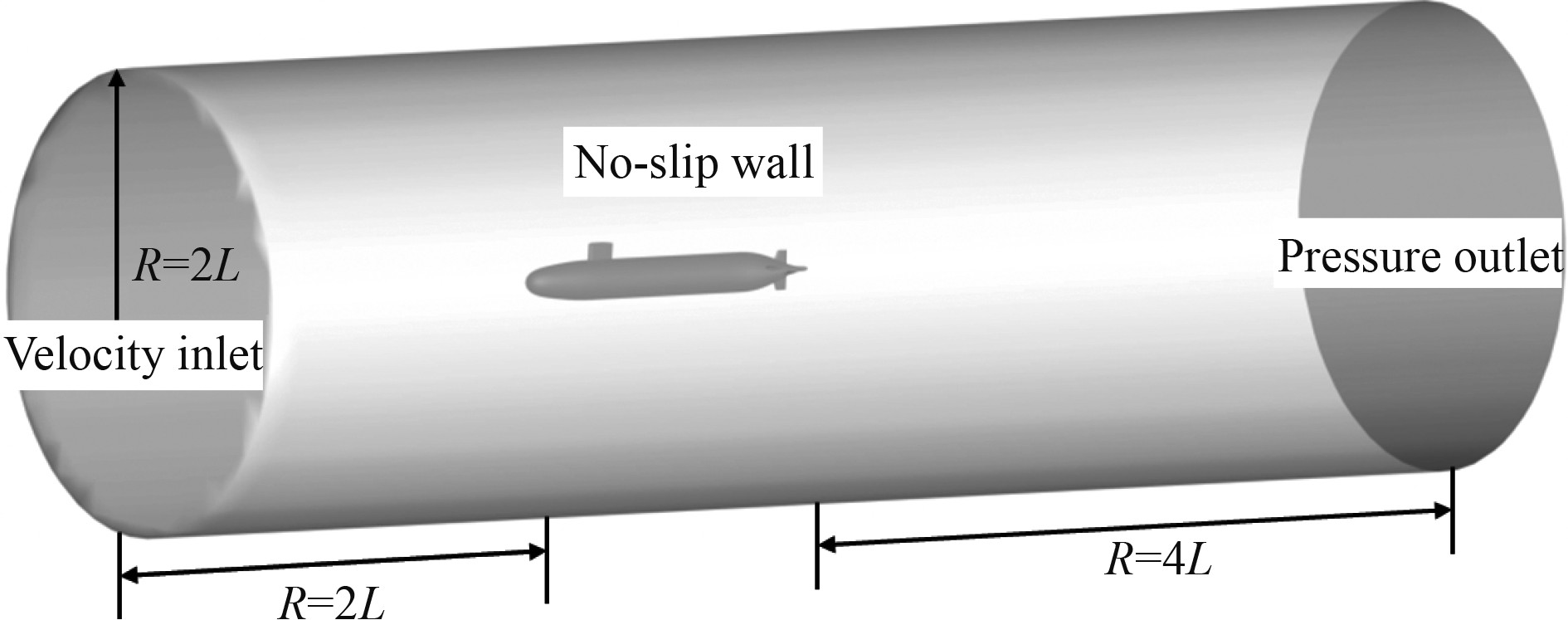
2.2 计算域及网格

如图2所示，本文选取圆柱体计算域。计算域的长度为Suboff艇长的7倍，其中计算域左侧距离Suboff首部2倍艇长距离，计算域右侧距离Suboff尾部4倍艇长距离，侧向圆周距离Suboff中心均2倍艇长距离。

对于边界条件的设定，根据相对运动的观点保证Suboff不动，通过对计算域前方的面与侧向面设置来流速度来模拟不同来流工况。因此除了计算域右侧的面设置为压力出口边界条件之外，计算域其他面均设置为速度进口条件；Suboff表面采用无滑移壁面边界条件。

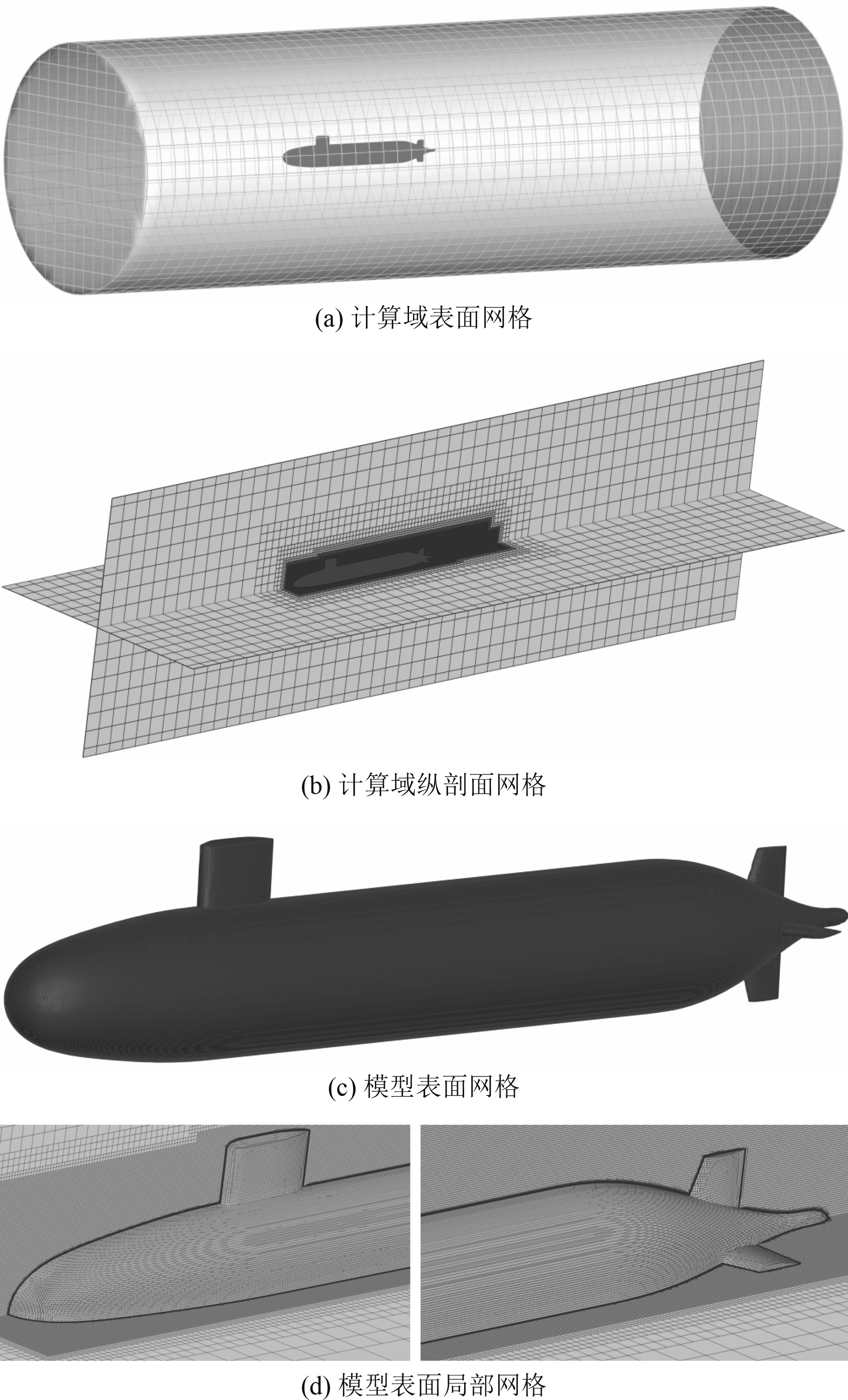
关于网格划分，对于整个计算域的网格划分采用切割体网格、棱柱层网格以及表面重构这三者相结合的方法进行网格的生成。由于本文采用LES方法求解，因此Suboff表面第一层网格高度满足y⁺ ≈ 1。其中y⁺的表达式为$ {y^ + } = y{u_\tau }/\nu $，$ {u_\tau } = \sqrt {({\tau _w}/\rho )} $。$ {\tau _w} $为壁面剪切应力, y表示第一层网格距离壁面的法向距离^[7]。图3为计算网格示意图，另外，由于本文网格数量巨大（10⁷量级），为避免图中漆黑一片的情况，能够清晰展示网格形式，计算网格图采用隔点稀疏显示。

3 计算结果及分析

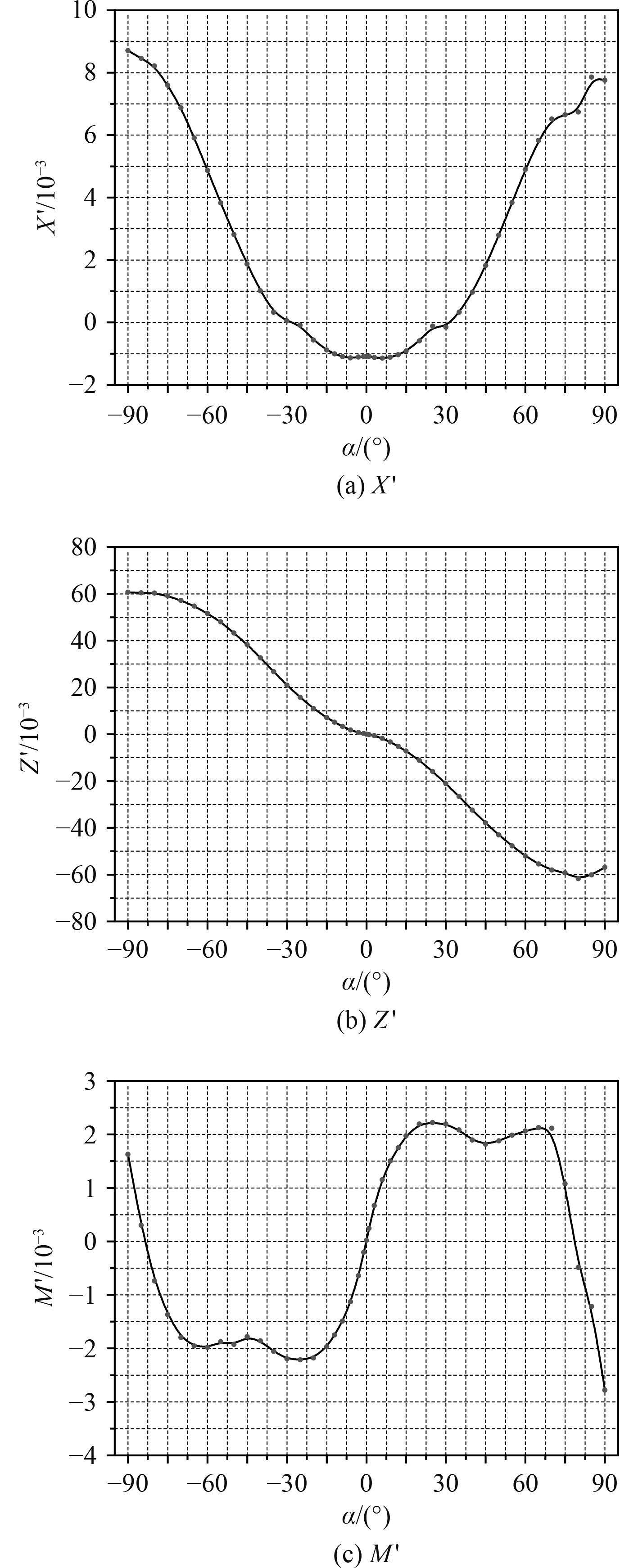
不同攻角下Suboff的水动力系数值如图4所示。计算结果表明，攻角−90°～90°范围内，随着攻角α的增大，X′绝对值呈现逐渐增大的趋势，且在小攻角范围内（−12°～12°）近似呈现线性分布。另外正负攻角下X′的值对称性不是很好，这主要是由于Suboff本身垂向的不对称性引起；对于Z′，随着攻角α的增大，Z′绝对值亦呈现逐渐增大的趋势，但是当攻角大于70°后，其增长幅度极小；而对应的力矩系数M′则先增大，在攻角60°时达到最大值，后迅速减小。在攻角 0°～90°范围内，Z′、M′正负攻角对称性较好。

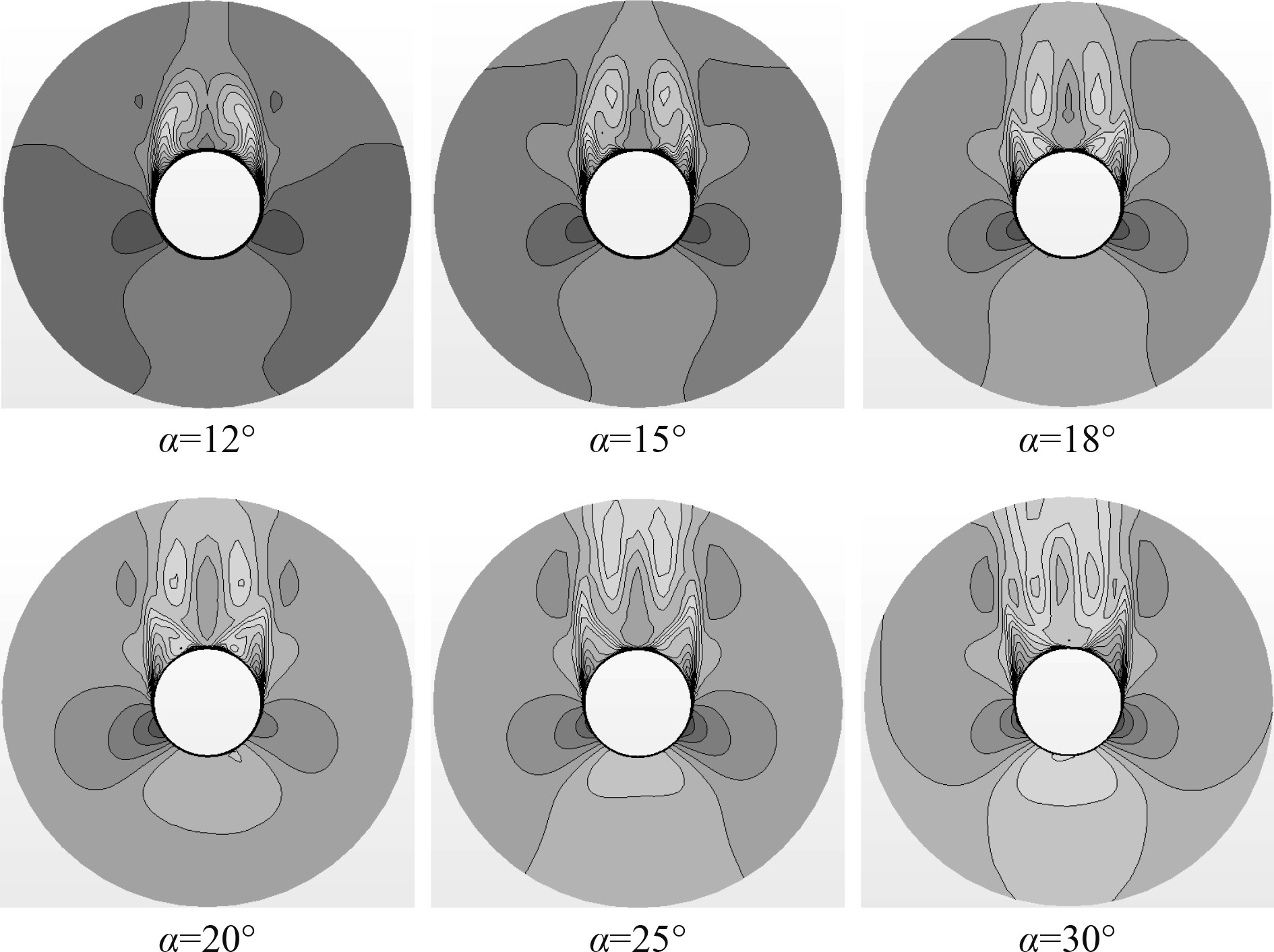
此外，图5为典型攻角下Suboff纵向截面处（x/L = 0.9）速度流线分布云图。可知，随着来流攻角的增加，Suboff横截面处二次分离点逐渐提前。具体地，当攻角为12°时，二次分离点近似为47°；当攻角为15°时，二次分离点近似为36°；随着攻角的进一步增大（α = 30°），二次分离点在周向角为19°时出现。

图6和图7为典型攻角下Suboff的涡流场结构。本文采用Q判据捕捉涡旋结构，其定义为：

$ Q = - \frac{1}{2}\frac{{\partial {u_i}}}{{\partial {x_j}}}\frac{{\partial {u_j}}}{{\partial {x_i}}},{\text{ }}i{\text{, }}j{\text{ = 1, 2 , 3}} 。$

(4)

式中：u_i、u_j均为速度；x_i、x_j均为坐标。此外，本文涡流场结构采用x方向的来流速度进行染色。

结合图6和图7可知，不同来流攻角下Suboff的尾部均出现了明显地脱落涡旋结构，且这些涡旋结构呈现出多尺度、高旋转、易破碎等特征。随着来流攻角的增大，围壳后方以及艇体表面的涡旋结构逐渐脱离，脱落后的涡旋结构方向与来流方向近似保持一致；随着攻角的进一步增大（α = 18°），艇体表面涡旋结构脱落在时间和空间上都呈现出不同的特征，具体地，在空间上，来流攻角的增加使得艇体表面涡脱落点呈现出向前移动的特征；在时间上，来流攻角越大，脱落的时间则越早提前。

4 结　语

本文采用LES大涡模拟方法，开展Suboff大机动工况下流动分离与水动力精细预报的CFD非定常数值模拟方法研究，完成艇体尾部及舵面流动分离涡旋结构的精细捕捉，尤其是涡旋结构随时间变化的发放特性。本文研究成果可为后续极限机动工况下潜艇流动控制提供技术支撑。