0 引　言

自20世纪50年代Irwin提出采用应力强度因子K描述裂尖应力场以来，线弹性断裂力学（Linear Elastic Fracture Mechanics, LEFM）得到了迅猛发展，为含裂纹缺陷材料和结构剩余强度及疲劳寿命分析提供了重要理论支撑，并在桥梁建筑、航空航天、船舶交通等工程领域得到广泛应用^[1]。

在线弹性理论框架下，裂尖完整应力场由奇异项、常数项以及若干高阶项组成^[2]。传统LEFM采用应力强度因子K单一参量表征裂尖应力场，并将K作为含裂纹材料和结构安全性评定和疲劳裂纹扩展分析的计算参量。工程实际结构中的裂纹可能为I型、II型和III型3种基本类型裂纹中的任意2种或3种组合而成的混合型裂纹。基于单一K参量建立的如最大环向应力准则^[3]（MTS）、最小密度因子准则^[4-5]（SED）和平均应变能密度准则^[6]（ASED）等断裂准则为混合型裂纹材料与构件断裂破坏提供了重要判据，解释了裂纹起裂偏折方向和起裂条件^[7]，并分别得到了印证和应用。

然而，研究表明当裂纹受到高约束时，裂尖应力场中与裂纹尖端距离无关、平行于裂纹面的常数项$T$应力对裂纹扩展（起裂扩展条件、扩展偏折角度）的影响不能简单忽略^[8-16]。Larsson等^[9]研究了T应力对紧凑拉伸试样、三点弯曲试样、中心裂纹拉伸试样和双边裂纹拉伸试样裂纹尖端塑性区形状和尺寸的影响，结果表明T应力的正负对裂纹塑性区形状和尺寸有强烈影响；Ayatollahi等^[10]对5种不同裂纹试样I型载荷作用下的PMMA材料裂纹偏折路径及断裂极限进行了试验研究，研究发现I型加载情况下裂纹会发生偏折，且偏折路径及断裂极限存在很大不同；美国材料与试验协会于2015年发布的“拉伸及弯曲载荷作用下平板表面裂纹初始断裂韧性标准测试方法”（ASTM E2899-15）指出，裂尖应力场常数项$T$应力对裂纹起裂扩展的影响不可忽略^[11]。

本文对考虑裂尖应力场常数项影响的修正MTS准则^[12-13]、修正SED准则^[14-15]和修正ASED准则^[16]进行介绍，给出计及裂尖应力场常数项影响的裂纹偏折角和断裂判据表达式；在此基础上，对比分析应力场常数项以及泊松比对工程中常见的I型裂纹起裂扩展行为的影响，研究应力场常数项对I型裂纹偏折、起裂扩展影响阀值及一般规律，为含裂纹材料及结构断裂力学评估提供一定参考。

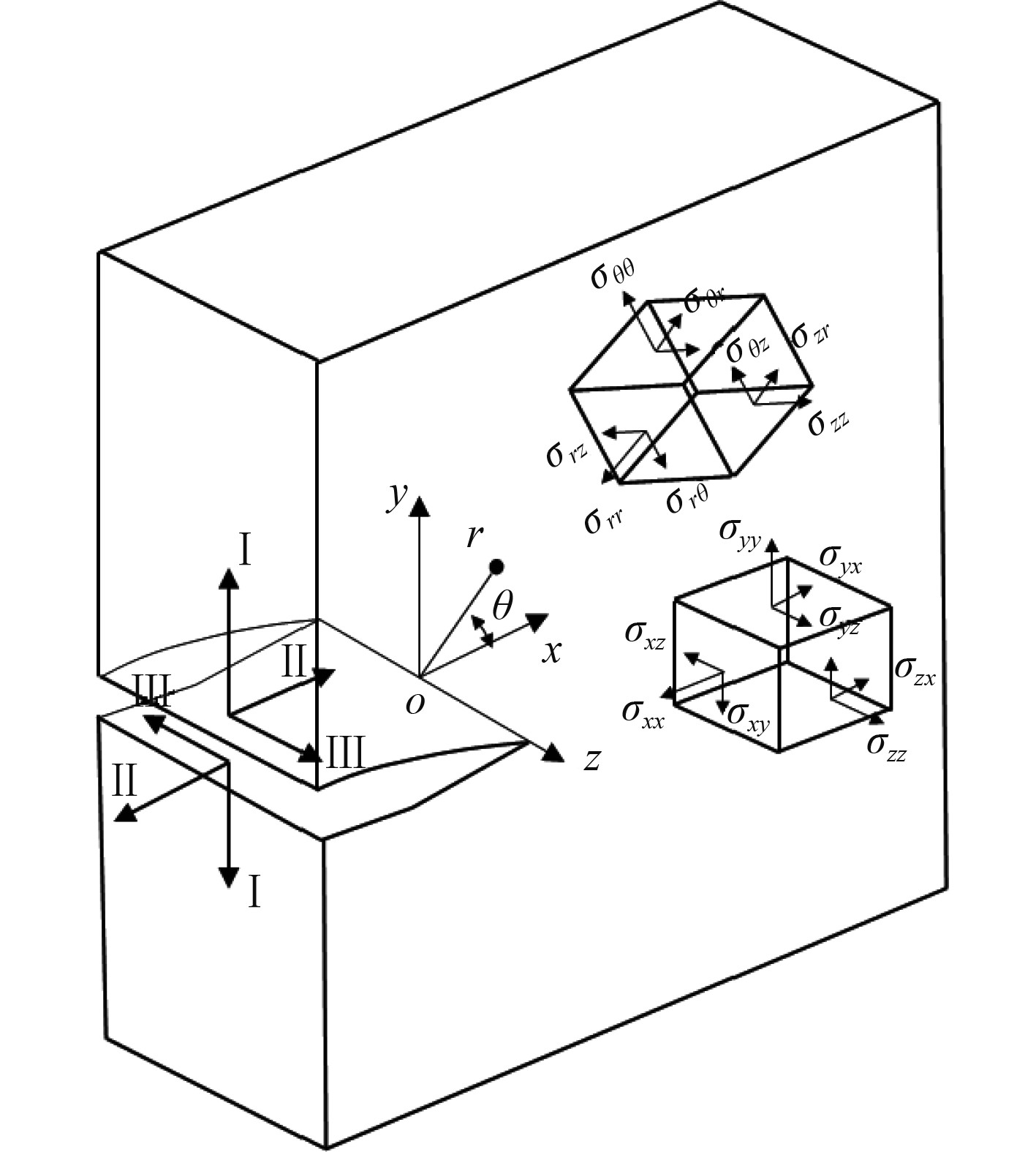
1 裂纹尖端应力场

裂纹尖端应力场示意如图1所示。任意线弹性裂纹体中裂纹尖端附近应力场特征级数展开包括奇异项（${r}^{1/2}$）、常数项以及高阶项（O$\left({r}^{1/2}\right)$）。Williams裂纹尖端应力场特征级数表达式为^[2]：

$\begin{aligned}[b] & {\sigma }_{ij}=\frac{{K}_{\mathrm{{\rm I}}}}{\sqrt{2{\text π} r}}{f}_{ij}^{\mathrm{I}}\left(\theta \right)+\frac{{K}_{\mathrm{{\rm I}}\mathrm{I}}}{\sqrt{2{\text π} r}}{f}_{ij}^{\mathrm{I}\mathrm{I}}\left(\theta \right)+\frac{{K}_{\mathrm{{\rm I}}\mathrm{I}\mathrm{I}}}{\sqrt{2{\text π} r}}{f}_{ij}^{\mathrm{I}\mathrm{I}\mathrm{I}}\left(\theta \right)+\\ & T{\delta }_{1i}{\delta }_{1j}+\left(\upsilon T+E{\varepsilon }_{33}\right){\delta }_{3i}{\delta }_{3j}+O\left({r}^{\frac{1}{2}}\right) 。\end{aligned}$

(1)

式中：$\theta$为距离裂纹尖端$r$处与裂纹面之间的夹角；$r$为裂纹尖端距离；$E$为材料杨氏模量；${f}_{ij}^{\mathrm{I}}\left(\theta \right)$、${f}_{ij}^{\mathrm{I}\mathrm{I}}\left(\theta \right)$和${f}_{ij}^{\mathrm{I}\mathrm{I}\mathrm{I}}\left(\theta \right)$分别为I型、II型和III型应力场主导项的无量纲空间角度分布；${K}_{\mathrm{{\rm I}}}$、${K}_{\mathrm{{\rm I}}\mathrm{I}}$和${K}_{\mathrm{{\rm I}}\mathrm{I}\mathrm{I}}$分别为I型、II型和III型应力强度因子；$T$应力为特征级数展开常数项；$\upsilon$为泊松比；${\delta }_{1i}$、${\delta }_{1j}$、${\delta }_{3i}$和${\delta }_{3j}$为克罗尼克尔记号（Kronecker symbol）；${\varepsilon}_{33}$为裂纹尖端正应变分量。

极坐标系下，考虑裂纹尖端应力场特征级数展开前2项（奇异项和常数项）的混合型裂纹尖端应力场表达式为^[2]：

$\left[ \begin{array}{l}{\sigma }_{rr}\\ {\sigma }_{\theta \theta }\\ {\sigma }_{r\theta }\\ {\sigma }_{zz}\end{array} \right] = {\left[ \begin{gathered}{c} \frac{1}{\sqrt{2{\text π} r}}\mathrm{cos}\frac{\theta }{2}\left[{K}_{\mathrm{I}}\left(1 + {\mathrm{sin}}^{2}\frac{\theta }{2}\right) + {K}_{\mathrm{{\rm I}}\mathrm{I}}\left(\frac{3}{2}\mathrm{sin}\theta - 2\mathrm{tan}\frac{\theta }{2}\right)\right] + T{\mathrm{cos}}^{2}\theta \\ \frac{1}{\sqrt{2{\text π} r}}\mathrm{cos}\frac{\theta }{2}\left[{K}_{\mathrm{I}}{\mathrm{cos}}^{2}\frac{\theta }{2}-\frac{3}{2}{K}_{\mathrm{I}\mathrm{I}}\mathrm{sin}\theta \right]+T{\mathrm{sin}}^{2}\theta \\ \frac{1}{2\sqrt{2{\text π} r}}\mathrm{cos}\frac{\theta }{2}\left[{K}_{\mathrm{I}}\mathrm{sin}\theta +{K}_{\mathrm{I}\mathrm{I}}\left(3\mathrm{cos}\theta -1\right)\right]-T\mathrm{sin}\theta \mathrm{cos}\theta \\ {\upsilon }^{'}\left({\sigma }_{rr}+{\sigma }_{\theta \theta }\right)\qquad\qquad\qquad \qquad\qquad\qquad\qquad\qquad\qquad \end{gathered}\right]。}$

(2)

式中：参数${\upsilon }^{'}=0$（平面应力问题）；${\upsilon }^{'}=\upsilon$（平面应变问题）。令式（2）中${K}_{\mathrm{{\rm I}}\mathrm{I}}=0$，便得到I型裂纹尖端应力场。

一般通过引入无量纲参数$B=T\sqrt{{\text π} a}/{K}_{{e}{f}{f}}$和参数$\alpha =\sqrt{2{r}_{{c}}/a}$来研究应力场常数项对混合型裂纹扩展行为的影响^[11]。其中，${K}_{{e}{f}{f}}$为有效应力强度因子，${K}_{{e}{f}{f}}= \sqrt{{K}_{\mathrm{I}}^{2}+{K}_{\mathrm{I}\mathrm{I}}^{2}}$；$a$为裂纹长度；${r}_{\mathrm{c}}$为断裂控制区域临界距离，可由$\displaystyle\frac{1}{2{\text π} }{\left(\frac{{K}_{{{I}}{c}}}{{\sigma }_{{t}}}\right)}^{2}$进行估算（${\sigma }_{{t}}$为材料拉伸极限）。

反映裂纹应力场常数项$T$应力的无量纲参数$B\alpha$的一般表达式为^[12]：

$B\alpha =\frac{T\sqrt{2{\text π} {r}_{\mathrm{c}}}}{{K}_{{e}{f}{f}}}=\frac{{K}_{{{I}}{c}}T}{{\sigma }_{\mathrm{t}}\sqrt{{K}_{\mathrm{I}}^{2}+{K}_{\mathrm{I}\mathrm{I}}^{2}+{K}_{\mathrm{I}\mathrm{I}\mathrm{I}}^{2}}} 。$

(3)

对于I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$），参数$B\alpha =T\sqrt{2{\text π} {r}_{\mathrm{c}}}/{K}_{\mathrm{I}}= {K}_{{{I}}{c}}T/\left({\sigma }_{{t}}{K}_{\mathrm{I}}\right)$。

2 断裂准则理论基础

断裂准则可为混合型裂纹材料与构件断裂破坏提供重要判据，能够解释裂纹起裂偏折方向和起裂条件^[7]。本章对工程中常用的最大环向应力准则（MTS）、最小应变能密度因子准则（SED）和平均应变能密度准则（ASED）考虑应力场常数项修正的断裂准则理论进行介绍，给出相应断裂准则裂纹偏折角度和起裂扩展判据计算式。

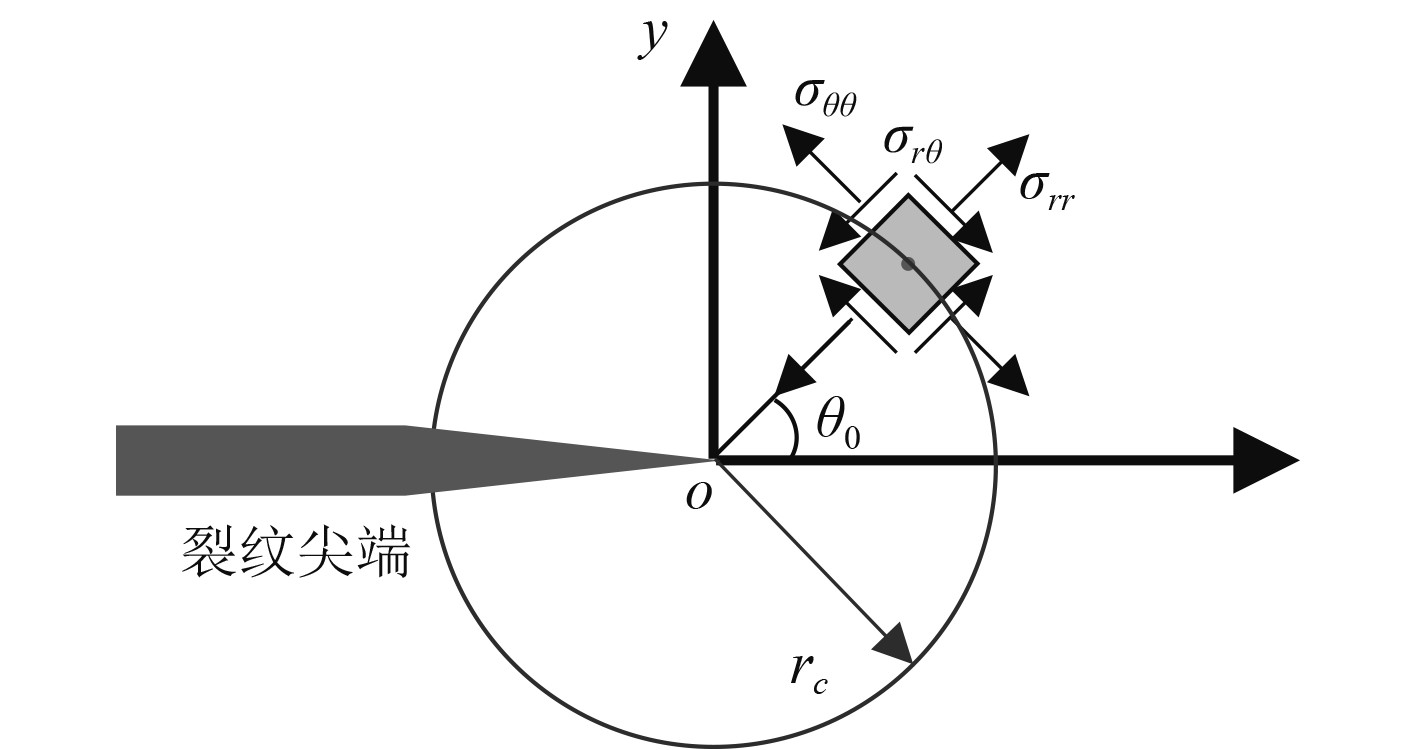
2.1 修正MTS准则

Erdogan等^[3]根据具有中心斜裂纹树脂玻璃板均匀拉伸试验结果提出了著名的最大环向应力准则（MTS准则），MTS准则认为裂纹沿临界距离${r}_{{c}}$上最大环向应力的${\theta }_{0}$方向扩展，如图2所示，当临界距离${r}_{{c}}$上${\theta }_{0}$方向的环向应力达到断裂应力${\sigma }_{\mathrm{c}}$时裂纹起裂扩展。MTS准则^[3]可表示为：

$\left\{\begin{array}{c} {\left.\displaystyle\frac{\partial {\sigma }_{\theta \theta }}{\partial \theta }\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}}=0，\\ {\left.\displaystyle\frac{{\partial }^{2}{\sigma }_{\theta \theta }}{\partial {\theta }^{2}}\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}} < 0，\end{array}\right.$

(4)

${\left({\sigma }_{\theta \theta }\right)}_{\mathrm{m}\mathrm{a}\mathrm{x}}={\left.{\sigma }_{\theta \theta }\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}}={\sigma }_{{c}}。$

(5)

式中，断裂应力${\sigma }_{c}$可通过纯I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$，$T=0$）起裂扩展条件确定^[3]：

${\left.{\sigma }_{\theta \theta }\right|}_{\begin{subarray}{c}\theta =0\\ r={r}_{{c}}\end{subarray}}=\frac{1}{\sqrt{2{\text π} {r}_{{c}}}}{K}_{{Ic}}={\sigma }_{{c}}。$

(6)

将式（2）中环向应力${\sigma }_{\theta \theta }$代入式（4），求解得到考虑裂尖应力场常数项的修正MTS准则裂纹偏折角${\theta }_{0}$，具体可由式（7）确定^[12-13]：

$\left[ {K}_{\mathrm{I}}\mathrm{sin}{\theta }_{0} + {K}_{\mathrm{I}\mathrm{I}}\left(3\mathrm{cos}{\theta }_{0} - 1\right) \right] - \frac{16}{3}T \sqrt{2{\text π} {r}_{{c}}}\mathrm{sin}\frac{{\theta }_{0}}{2}\mathrm{cos}{\theta }_{0} = 0 。$

(7)

然后，将求解得到裂纹偏折角${\theta }_{0}$代入式（2）中${\sigma }_{\theta \theta }$计算式，结合式（5）和式（6）得到修正MTS准则裂纹起裂判据^[12-13]

$\mathrm{cos}\frac{{\theta }_{0}}{2}\left({K}_{\mathrm{I}}{\mathrm{cos}}^{2}\frac{{\theta }_{0}}{2} - \frac{3}{2}{K}_{\mathrm{I}\mathrm{I}}\mathrm{sin}{\theta }_{0}\right) + T\sqrt{2{\text π} {r}_{{c}}}{\mathrm{sin}}^{2}{\theta }_{0} = {K}_{{Ic}}。$

(8)

引入参数$B\alpha$后，修正MTS准则裂纹偏折、断裂判据计算式（7）、式（8）将转换为式（9）、式（10）：

$\left[ {K}_{\mathrm{I}}\mathrm{sin}{\theta }_{0} + {K}_{\mathrm{I}\mathrm{I}} \left(3\mathrm{cos}{\theta }_{0} - 1\right) \right] - \frac{16}{3} \left( B\alpha \right) {K}_{{e}{f}{f}}\mathrm{sin}\frac{{\theta }_{0}}{2}\mathrm{cos}{\theta }_{0} = 0 ，$

(9)

$\mathrm{cos}\frac{{\theta }_{0}}{2}\left( {K}_{\mathrm{I}}{\mathrm{cos}}^{2}\frac{{\theta }_{0}}{2} - \frac{3}{2}{K}_{\mathrm{I}\mathrm{I}}\mathrm{sin}{\theta }_{0} \right) + \left( B\alpha \right){K}_{{e}{f}{f}}{\mathrm{sin}}^{2}{\theta }_{0} = {K}_{\mathrm{I}\mathrm{c}} 。$

(10)

修正MTS准则裂纹起裂偏折角及等效应力强度因子计算式包含临界半径${r}_{{c}}$一个材料参数（在$B\alpha$中），与材料常数泊松比无关，不能区分平面应力和平面应变状态。当$B\alpha =0$时（$T=0$），修正MTS准则将蜕化为MTS准则计算式。

根据修正MTS准则，考虑裂纹应力场常数项$T$应力影响的I型裂纹偏折角及断裂判据计算式为

$\mathrm{sin}{\theta }_{0}-\frac{16}{3}\left(B\alpha \right)\mathrm{sin}\frac{{\theta }_{0}}{2}\mathrm{cos}{\theta }_{0}=0 ，$

(11)

$\left[{\mathrm{cos}}^{3}\frac{{\theta }_{0}}{2}+\left(B\alpha \right){\mathrm{sin}}^{2}{\theta }_{0}\right]{K}_{\mathrm{I}}={K}_{{Ic}}。$

(12)

可知，考虑裂纹尖端应力场常数项$T$应力影响后的I型裂纹起裂判据不再是${K}_{\mathrm{I}\mathrm{f}}={K}_{\mathrm{I}\mathrm{c}}$，称等式（12）左端为修正MTS准则I型裂纹等效应力强度因子${K}_{\mathrm{I}\mathrm{e}\mathrm{q}}$。

2.2 修正SED准则

Sih^[4-5]基于裂纹尖端应力应变场能量理论提出了最小应变能密度因子准则（SED准则）。SED准则利用应变能密度因子$S$预测裂纹的偏折。Sih定义应变能密度因子$S$表达式^[3]

$S=wr=\frac{r}{2G}\left[\frac{1+\kappa }{8}{\left({\sigma }_{rr}+{\sigma }_{\theta \theta }\right)}^{2}-{\sigma }_{rr}{\sigma }_{\theta \theta }+{\sigma }_{r\theta }^{2}\right]。$

(13)

式中：$w$为线弹性体应变能密度；$r$为极坐标系下一点距裂尖的距离；$G$为剪切模量；$\kappa$为材料常数，$\kappa = (3- \upsilon )/\left(1+\upsilon \right)$（平面应力状态），$\kappa =3-4\upsilon$（平面应变状态）。

SED准则假设当裂纹尖端临界距离${r}_{{c}}$上的最小应变能密度因子${S}_{\mathrm{m}\mathrm{i}\mathrm{n}}$达到临界值${S}_{{c}}$时裂纹起裂扩展，裂纹起裂扩展方向为临界距离${r}_{{c}}$上应变能密度因子极小值方向。SED准则可表示为：

$\left\{ \begin{array}{c}{\left.\displaystyle\frac{\partial S}{\partial \theta }\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}}=0，\\ {\left.\displaystyle\frac{{\partial }^{2}S}{\partial {\theta }^{2}}\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}} > 0，\end{array}\right.$

(14)

${S}_{\mathrm{m}\mathrm{i}\mathrm{n}}={\left.S\right|}_{\begin{subarray}{c}\theta ={\theta }_{0}\\ r={r}_{{c}}\end{subarray}}={S}_{\mathrm{c}} 。$

(15)

将式（2）代入式（13）可得到考虑裂尖应力场奇异项和常数项的应变能密度因子$S$表达式^[14]：

$\begin{aligned}[b] S= & \frac{1}{16{\text π} G} [{a}_{1}{K}_{\mathrm{I}}^{2}+{a}_{2}{K}_{\mathrm{I}\mathrm{I}}^{2}+{a}_{3}{K}_{\mathrm{I}}{K}_{\mathrm{I}\mathrm{I}}+{a}_{4}\sqrt{2{\text π} {r}_{c}}{K}_{\mathrm{I}}T+ \\ & {a}_{5}\sqrt{2{\text π} {r}_{{c}}}{K}_{\mathrm{I}\mathrm{I}}T+{a}_{6}\left(2{\text π} {r}_{{c}}\right){T}^{2} ]。\end{aligned}$

(16)

式中，系数${a}_{1}$、${a}_{2}$、${a}_{3}$、${a}_{4}$、${a}_{5}$和${a}_{6}$分别为：

$\left\{\begin{gathered}{a}_{1}=\left(1+\mathrm{cos}\theta \right)\left({{k}} -\mathrm{cos}\theta \right) ，\\ {a}_{2}=\left[{{k}} \left(1-\mathrm{cos}\theta \right)+\mathrm{cos}\theta \left(3\mathrm{cos}\theta +1\right)\right]，\\ {a}_{3}=2\mathrm{sin}\theta \left(2\mathrm{cos}\theta -{{k}} +1\right)，\\ {a}_{4}=2\mathrm{cos}\frac{\theta }{2}\left(\mathrm{cos}2\theta -\mathrm{cos}\theta +{{k}} -1\right)，\\ {a}_{5}=-2\mathrm{sin}\frac{\theta }{2}\left(\mathrm{cos}2\theta +\mathrm{cos}\theta +{{k}} +1\right)，\\ {a}_{6}=\left({{k}} +1\right)/2。\qquad\qquad\qquad\qquad\quad \end{gathered}\right.$

(17)

式（15）中临界值${S}_{{c}}$可通过纯I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$，$T=0$）起裂扩展条件确定：

${S}_{\mathrm{m}\mathrm{i}\mathrm{n}}={\left.S\right|}_{\begin{subarray}{c}\theta =0\\ r={r}_{{c}}\end{subarray}}=\frac{{\text{κ}} -1}{8{\text π} \mu }{K}_{{Ic}}^{2}={S}_{{c}} ，$

(18)

将式（16）代入式（14），求解得到考虑裂尖应力场常数项的修正SED准则裂纹偏折角${\theta }_{0}$，具体可由式（19）确定^[14]

$\begin{aligned}[b] & {b}_{1}{K}_{\mathrm{I}}^{2}+{b}_{2}{K}_{\mathrm{I}\mathrm{I}}^{2}+{b}_{3}{K}_{\mathrm{{\rm I}}}{K}_{\mathrm{{\rm I}}\mathrm{{\rm I}}}+{b}_{4}\left(B\alpha \right){K}_{\mathrm{I}}{K}_{{e}{f}{f}}+\\ & {b}_{5}\left(B\alpha \right){K}_{\mathrm{I}\mathrm{I}}{K}_{{e}{f}{f}}+{b}_{6}{\left(B\alpha \right)}^{2}{K}_{{e}{f}{f}}^{2}=0。\end{aligned}$

(19)

式中，系数${b}_{1}$、${b}_{2}$、${b}_{3}$、${b}_{4}$、${b}_{5}$和${b}_{6}$分别为：

$\left\{\begin{gathered}{b}_{1}=\left(2\mathrm{cos}{\theta }_{0}-\kappa +1\right)\mathrm{sin}{\theta }_{0}，\\ {b}_{2}=\left(\kappa -1-6\mathrm{cos}{\theta }_{0}\right)\mathrm{sin}{\theta }_{0}，\\ {b}_{3}=2\left[2\mathrm{cos}2{\theta }_{0}-\left(\kappa -1\right)\mathrm{cos}{\theta }_{0}\right]，\\ {b}_{4}=-\mathrm{sin}\frac{{\theta }_{0}}{2}\left[5\left(\mathrm{cos}2{\theta }_{0}+\mathrm{cos}{\theta }_{0}\right)+\kappa +1\right]，\\ {b}_{5}=-\mathrm{cos}\frac{{\theta }_{0}}{2}\left[5\left(\mathrm{cos}2{\theta }_{0}-\mathrm{cos}{\theta }_{0}\right)+\kappa +3\right]，\\ {b}_{6}=0。\qquad\qquad\qquad\qquad\qquad\qquad\quad \end{gathered}\right.$

(20)

将式（19）求解得到的裂纹偏折角${\theta }_{0}$代入式（16），结合式（15）、式（18）便可得到修正SED准则混合型裂纹断裂判据^[14]：

${\sqrt{{c}_{1} {K}_{\mathrm{I}}^{2} + {c}_{2} {K}_{\mathrm{I}\mathrm{I}}^{2}+{c}_{3}{K}_{\mathrm{{\rm I}}}{K}_{\mathrm{{\rm I}}\mathrm{{\rm I}}} + {c}_{4}\left( B\alpha \right){K}_{\mathrm{I}}{K}_{e f f} + {c}_{5}\left( B\alpha \right){K}_{\mathrm{I}\mathrm{I}}{K}_{e f f} + {c}_{6}{\left( B\alpha \right)}^{2}{K}_{e f f}^{2}} = {K}_{Ic} }。$

(21)

式中，系数${c}_{1}$、${c}_{2}$、${c}_{3}$、${c}_{4}$、${c}_{5}$和${c}_{6}$分别为：

$\left\{\begin{gathered}{c}_{1}=\frac{1}{2\left({k} -1\right)}\left(1+\mathrm{cos}{\theta }_{0}\right)\left({k} -\mathrm{cos}{\theta }_{0}\right)，\\ {c}_{2}=\frac{1}{2\left({k} -1\right)}\left[{k} \left(1-\mathrm{cos}{\theta }_{0}\right)+\mathrm{cos}{\theta }_{0}\left(3\mathrm{cos}{\theta }_{0}+1\right)\right]，\\ {c}_{3}=\frac{1}{\left({k} -1\right)}\mathrm{sin}{\theta }_{0}\left(2\mathrm{cos}{\theta }_{0}-{k} +1\right)，\\ {c}_{4}=\frac{1}{\left({k} -1\right)}\mathrm{cos}\frac{{\theta }_{0}}{2}\left(\mathrm{cos}2{\theta }_{0}-\mathrm{cos}{\theta }_{0}+{k} -1\right)，\\ {c}_{5}=-\frac{1}{\left({k} -1\right)}\mathrm{sin}\frac{{\theta }_{0}}{2}\left(\mathrm{cos}2{\theta }_{0}+\mathrm{cos}{\theta }_{0}+{k} +1\right)，\\ {c}_{6}=\frac{\left({k} +1\right)}{4\left({k} -1\right)}。\qquad\qquad\qquad\qquad\qquad\qquad\qquad \end{gathered}\right.$

(22)

根据式（19）和式（20）可知，修正SED准则裂纹偏折角及裂纹起裂判据计算式中不仅包含临界半径${r}_{{c}}$，还能够区分平面应力及平面应变状态，能够反映材料泊松比ν对裂纹起裂扩展行为的影响。当$B\alpha =0$时（$T=0$），修正SED准则将蜕化为SED准则。

根据修正SED准则，I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$）偏折角计算式及断裂判据为：

${b}_{1}+{b}_{4}\left(B\alpha \right)=0 ，$

(23)

$\sqrt{{c}_{1}+{c}_{4}\left(B\alpha \right)+{c}_{6}{\left(B\alpha \right)}^{2}}{K}_{\mathrm{I}}={K}_{\mathrm{I}\mathrm{c}} 。$

(24)

称式（24）左端为修正SED准则I型裂纹等效应力强度因子${K}_{\mathrm{I}\mathrm{e}\mathrm{q}}$。

2.3 修正ASED准则

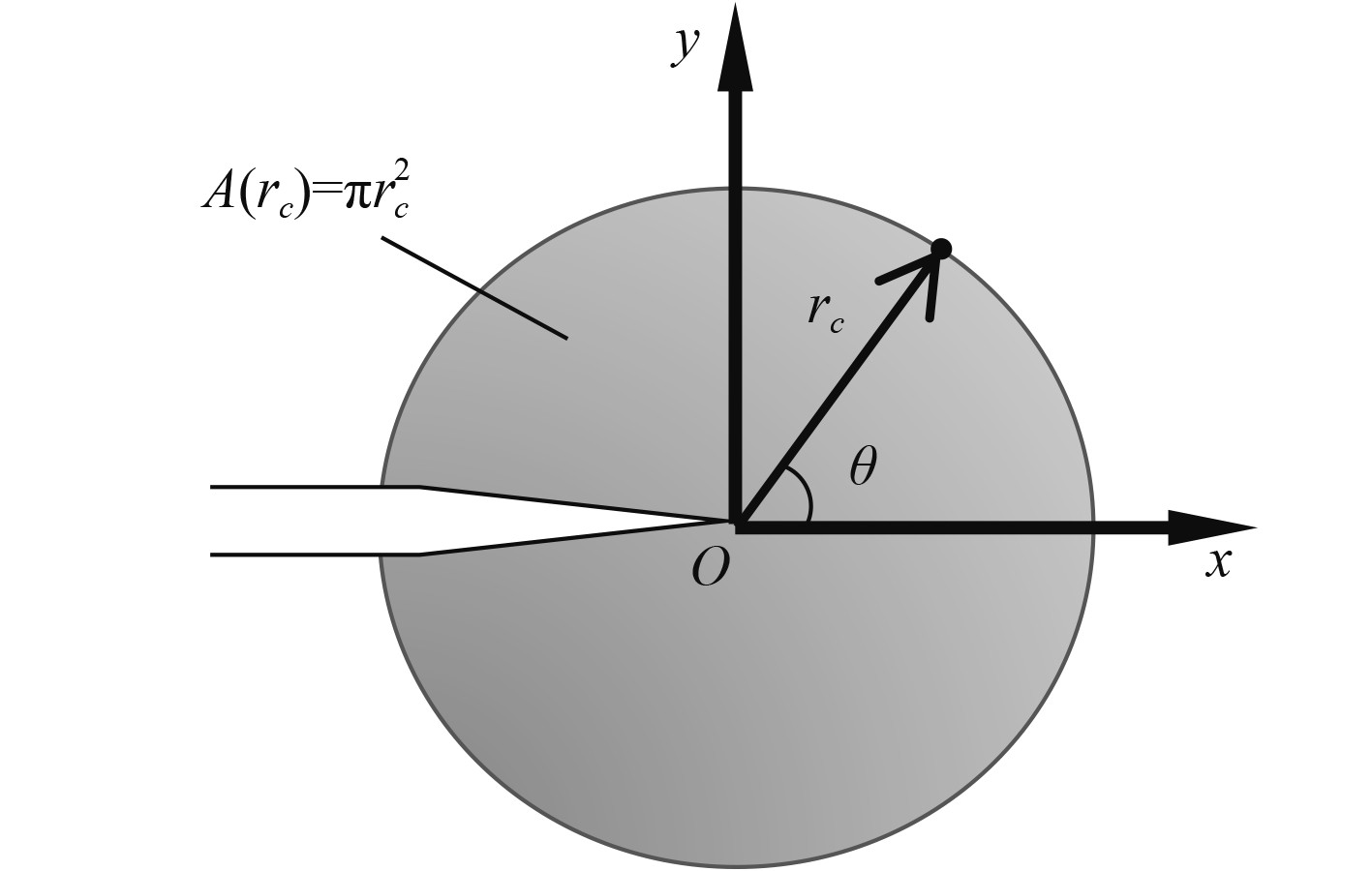
Lazarrin等^[6]提出基于能量观点的平均应变能密度准则（ASED准则），该准则认为裂纹尖端临界距离${r}_{{c}}$为半径的圆形区域内的平均应变能$\bar{E}\left({r}_{{c}}\right)$达到其临界值${\bar{E}}_{{c}}$时，裂纹发生起裂扩展，如图3所示。平均应变能密度准则为能量参数准则，考虑了裂纹尖端临界距离${r}_{c}$为半径的圆形区域内所有应力分量，物理意义明确。

ASED准则可表示为：

$\bar {E}\left({r}_{{c}}\right)=\frac{{\displaystyle\int }_{0}^{{r}_{\mathrm{c}}}{\displaystyle\int }_{-{\text π} }^{{\text π} }S\mathrm{d}\theta \mathrm{d}r}{{\text π} {r}_{{c}}^{2}}={\bar {E}}_{{c}}，$

(25)

将应变能密度因子表达式（16）代入式（25），可得到考虑裂尖应力场奇异项和常数项的平均应变能$\bar{E}\left({r}_{{c}}\right)$表达式：

$\bar{E}\left( {r}_{{c}} \right) = \frac{\left( -1 + 2{k} \right)}{16\mu {\text π} {r}_{\mathrm{c}}} {k}_{\mathrm{I}}^{2} + \frac{\left(3 + 2{k} \right)}{16\mu {\text π} {r}_{\mathrm{c}}} {k}_{\mathrm{I}\mathrm{I}}^{2} + \frac{\sqrt{2}\left(-7 + 5{k} \right)}{15\sqrt{{\text π} }\mu {\text π} \sqrt{{r}_{\mathrm{c}}}} {k}_{\mathrm{I}}T + \frac{\left( 1 + {k} \right)}{16\mu }{T}^{2}。$

(26)

式（25）中临界值${\bar{E}}_{{c}}$可由纯I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$，$T=0$）起裂扩展条件求得：

${\bar{E}}_{{c}}=\frac{\left(2{k} -1\right)}{16{\text π} G{r}_{{c}}}{K}_{{I}{c}}^{2}。$

(27)

结合式（25）～式（27）便可得到修正ASED准则混合型裂纹断裂判据表达式为^[16]：

${{ \sqrt{{K}_{\mathrm{I}}^{2} + \displaystyle\frac{3 + 2{k} }{-1 + 2{k} }{K}_{\mathrm{I}\mathrm{I}}^{2} + \displaystyle\frac{16\left( -7 + 5{k} \right)}{15{\text π} \left( -1 + 2{k} \right)}\left(B\alpha \right){K}_{\mathrm{I}}{K}_{e f f} + \displaystyle\frac{\left(1+{k} \right)}{2\left( -1 + 2{k} \right)}{\left(B\alpha \right)}^{2}{K}_{e f f}^{2}} = {K}_{Ic} }}。$

(28)

根据式（28）可知，修正ASED准则同样能够考虑泊松比的影响，可区分平面应力及平面应变状态。当$B\alpha =0$时（$T=0$），修正ASED准则将蜕化为ASED准则。

根据修正ASED准则，I型裂纹（${K}_{\mathrm{I}\mathrm{I}}=0$）断裂判据为：

$\sqrt{1+\frac{16\left(-7+5{k} \right)}{15{\text π} \left(-1+2{k} \right)}\left(B\alpha \right)+\frac{\left(1+{k} \right)}{2\left(-1+2{k} \right)}{\left(B\alpha \right)}^{2}}{K}_{\mathrm{I}}={K}_{Ic} 。$

(29)

称式（29）左端为修正ASED准则I型裂纹等效应力强度因子${K}_{{I}{e}{q}}$。

3 应力场常数项对I型裂纹起裂扩展行为的影响

工程结构中最常见的裂纹形式为I型裂纹，对于不考虑裂尖应力场常数项$T$应力影响的I型裂纹，根据传统断裂准则可知，裂纹在扩展过程中不会发生偏折（偏折角为0°），裂纹起裂扩展条件（断裂判据）为裂纹尖端I型应力强度因子${K}_{\mathrm{I}}$达到I型断裂极限${K}_{{If}}$，并认为${K}_{If}$不受几何构型及加载方式影响，其数值上为材料平面应变断裂韧性${K}_{Ic}$。

3.1 基于修正MTS准则分析

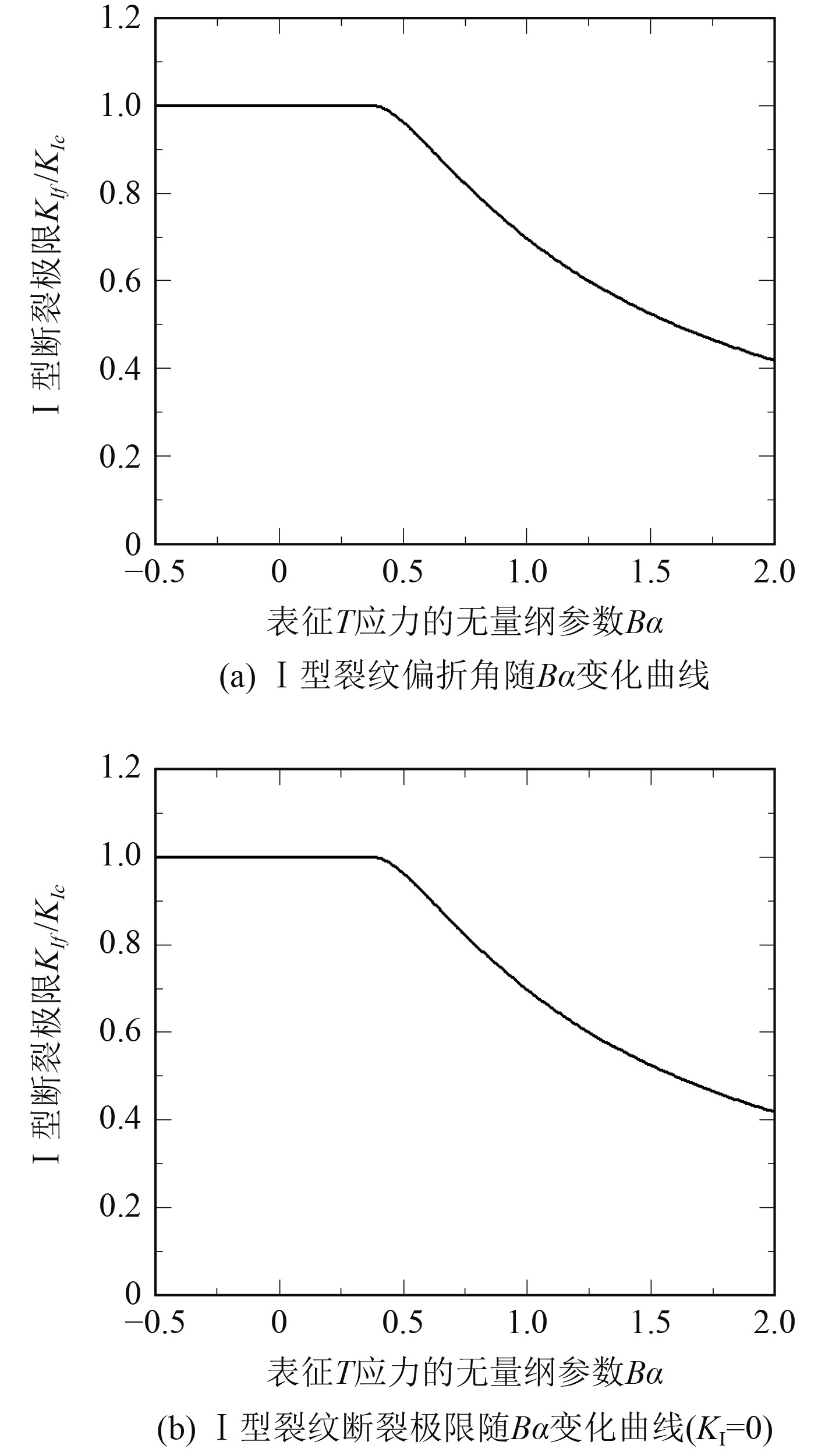
图4为基于修正MTS准则得到的I型裂纹初始偏折角度${\theta }_{0}$、断裂极限值${K}_{f}$随参数$B\alpha$的变化曲线。

由图4（a）可知，当$B\alpha \leqslant 0.38$时，$T$应力对I型裂纹初始偏折角没有影响，I型裂纹偏折角度为0°；当$B\alpha > 0.38$时，I型裂纹不再沿裂纹面扩展，初始偏折角${\theta }_{0}$将取决于$B\alpha$值并随$B\alpha$值的增大而迅速增大，如当$B\alpha =1.0$时，${\theta }_{0}=\pm 72.4\text{°}$。

由图4（b）可知：当$B\alpha \leqslant 0.38$时，$T$应力对I型裂纹断裂极限值${K}_{{I}{f}}$没有影响，此时I型裂纹断裂极限值${K}_{If}={K}_{Ic}$；当$B\alpha > 0.38$时，I型裂纹断裂极限值${K}_{If}$将不再是材料断裂韧性${K}_{Ic}$，而取决于$B\alpha$值并随$B\alpha$值的增大而降低，如当$B\alpha =1.0$时，$K_{If}=0.70\ K_{Ic}$，即考虑$T$应力时的I型裂纹断裂韧性降低了30.0%。

3.2 基于修正SED准则分析

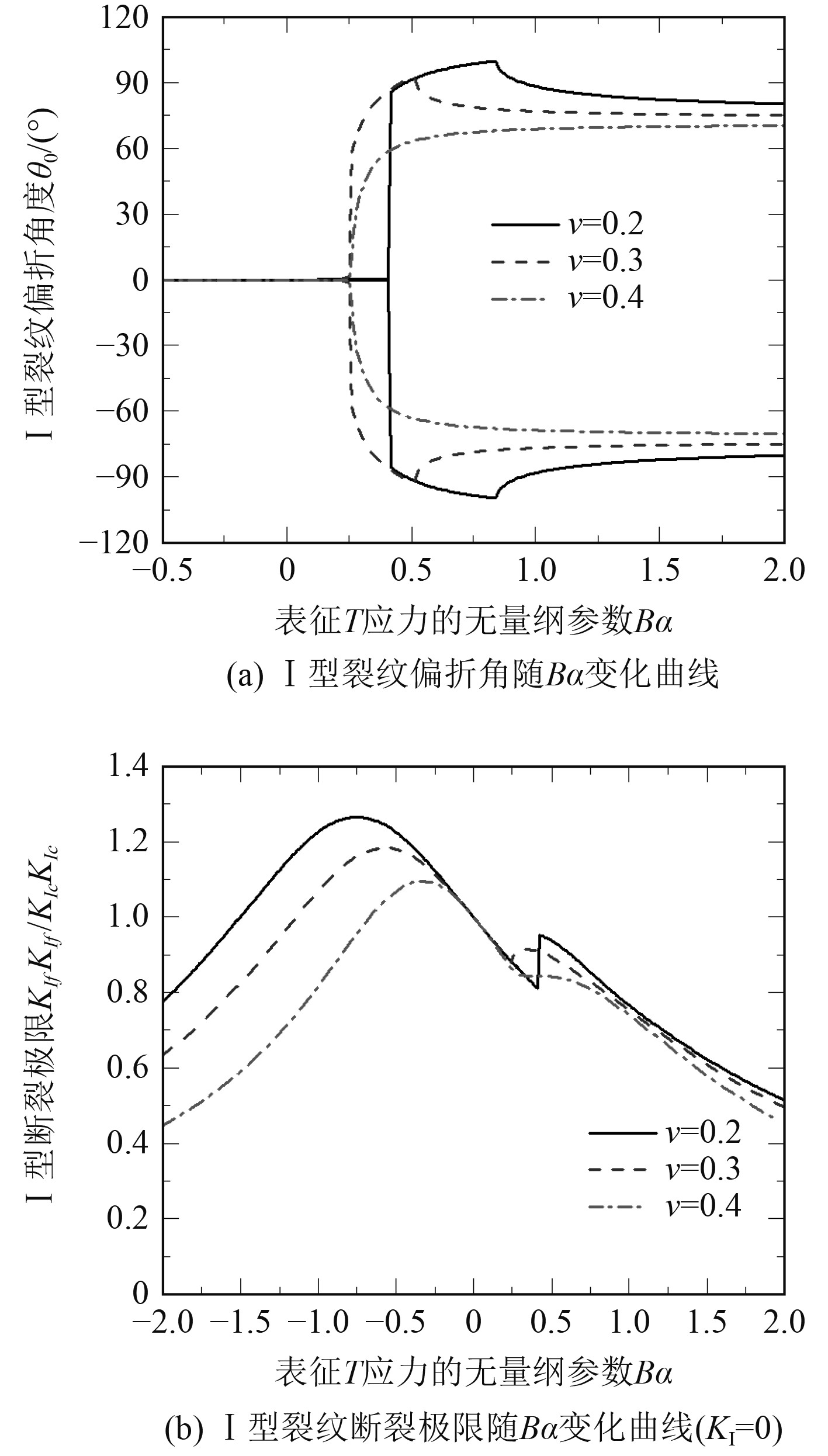
图5为基于修正SED准则得到的平面应变状态、不同泊松比$\upsilon$情况下I型裂纹初始偏折角度${\theta }_{0}$、断裂极限值${K}_{{f}}$随参数$B\alpha$的变化曲线。

由图5（a）可知，泊松比$\upsilon =0.3\mathrm{、}0.4$情况下：当$B\alpha \leqslant 0.25$时，$T$应力对I型裂纹初始偏折角没有影响，I型裂纹偏折角度为0°，$B\alpha > 0.25$，I型裂纹不再沿裂纹面扩展，初始偏折角${\theta }_{0}$将取决于$B\alpha$值，如当$B\alpha = 1.0$时，${\theta }_{0}$分别为±76.8°（$\upsilon =0.3$）和±68.7°（$\upsilon =0.4$）。泊松比$\upsilon =0.2$情况下：当$B\alpha \leqslant 0.41$时，$T$应力对I型裂纹初始偏折角没有影响，I型裂纹偏折角度为0°；当$B\alpha > 0.41$，I型裂纹不再沿裂纹面扩展，初始偏折角${\theta }_{0}$将取决于$B\alpha$值，如当$B\alpha =1.0$时，${\theta }_{0}$=±88.2°。一般情况，当$B\alpha$值为超过I型裂纹偏折阀值的某一给定值时（如$B\alpha =1.0$），裂纹偏折角${\theta }_{0}$随泊松比$\upsilon$的增大而减小。

由图5（b）可知，对于某一给定泊松比情况下（如泊松比$\upsilon =0.3$），裂尖应力场常数项$T$应力对I型裂纹断裂时刻应力强度因子极限值${K}_{ {{ I}} {f}}$有较大的影响，当$B\alpha < 0$时（裂尖应力场常数项$T$应力为负值），${K}_{ {{ I}} {f}}$随$B\alpha$减小而增大直到达到最大值${K}_{ {{ I}} {f} {\rm{max}}}$，随后随$B\alpha$的继续增大而下降；$B\alpha$在某一区间内I型裂纹断裂极限值${K}_{ {I} {f}}$高于${K}_{ {I} {c}}$，可认为此区间内裂尖应力场常数项$T$应力增大了I型裂纹断裂韧性（${K}_{ {{ I}} {f}}$数值超过1.0${K}_{ {{ I}} {c}}$），即增加了材料裂纹起裂阻力；正的$T$应力将降低I型裂纹断裂极限值${K}_{ {{ I}} {f}}$，如当$B\alpha =1.0$时，$K_{ {I} {f}}=0.75K_{ {I} {c}}$，即考虑$T$应力时的I型裂纹断裂韧性降低了25.0%，即正的$T$应力降低了材料裂纹起裂阻力。

由图5（b）可知基于修正SED准则理论的泊松比$\upsilon$对I型裂纹断裂极限${K}_{ {I} {f}}$的影响规律：材料泊松比越高，材料抵抗裂纹起裂扩展能力越差，如$B\alpha =1.0$、泊松比分别取0.2、0.3和0.4时的I型裂纹断裂极限分别为$0.77K_{ {I} {c}}$、$0.75{K}_{ {I} {c}}$、$0.73{K}_{ {I} {c}}$，$B\alpha =-1.0$、泊松比分别取0.2、0.3和0.4时的I型裂纹断裂极限分别为$1.22{K}_{ {I} {c}}$、$1.07{K}_{ {I} {c}}$、$0.82{K}_{ {I} {c}}$；材料泊松比$\upsilon$越高，${K}_{ {{ I}} {f} {\rm{max}}}$越小，泊松比$\upsilon$分别取0.2、0.3和0.4时，${K}_{ {{ I}} {f} {\rm{max}}}$分别为$1.26{K}_{ {{ I}} {c}}$、$1.18{K}_{ {{ I}} {c}}$和$1.10{K}_{ {{ I}} {c}}$；材料泊松比$\upsilon$越高，I型裂纹断裂韧性增大区间（${K}_{ {{ I}} {f}}$数值超过1.0${K}_{ {{ I}} {c}}$的区间）逐渐变小，$\upsilon$分别取0.2、0.3和0.4时，$B\alpha$区间范围分别为$-1.50 < B\alpha < 0$、$-1.14 < B\alpha < 0$和$-0.66 < B\alpha < 0$；裂纹尖端应力场常数项为负值时（$B\alpha < 0$），材料常数泊松比$\upsilon$对I型裂纹断裂极限${K}_{ {I} {f}}$的影响更为显著。

3.3 基于修正ASED准则分析

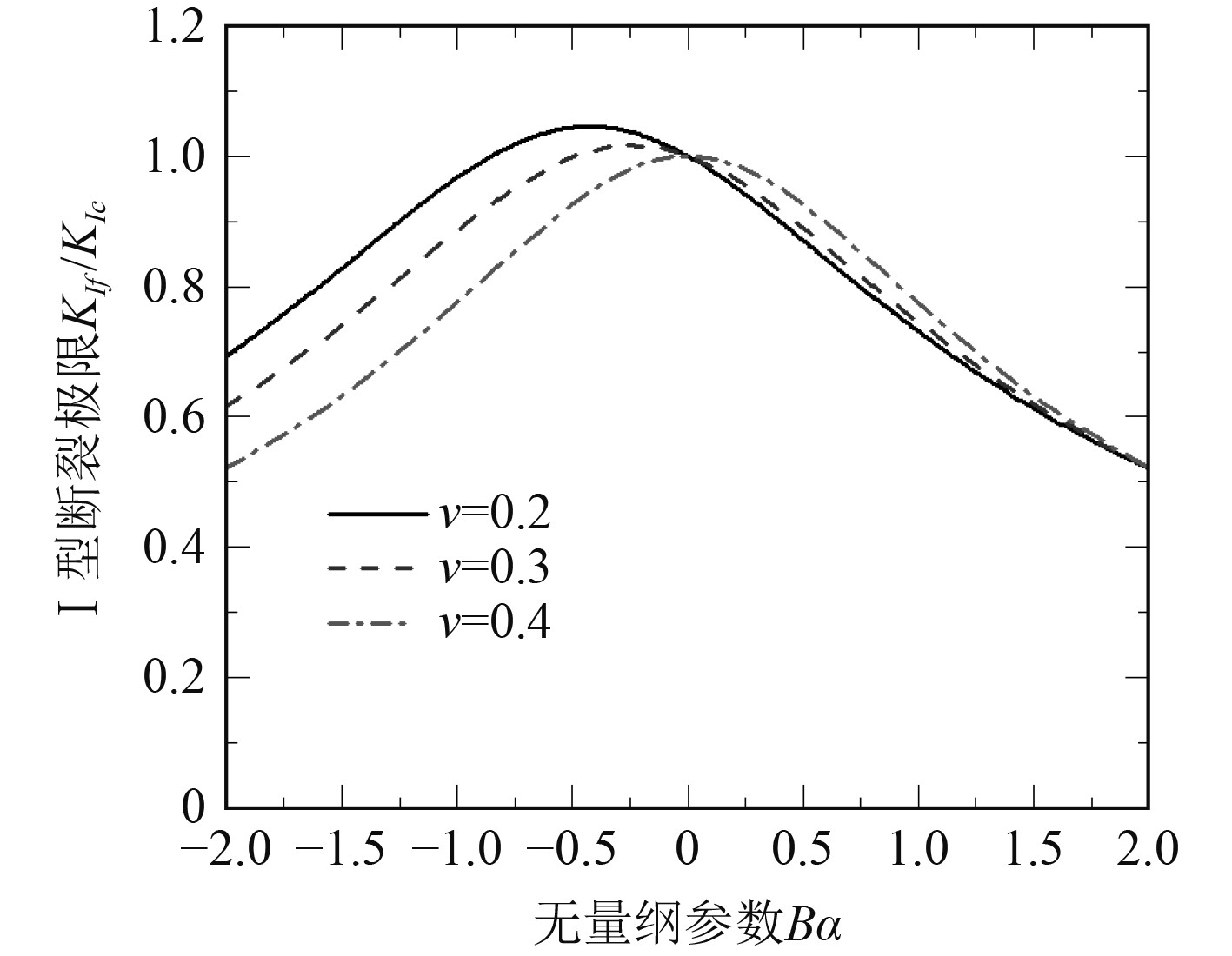
图6为基于修正ASED准则得到的平面应变状态、不同泊松比$\upsilon$情况下的I型裂纹断裂极限值${K}_{{{ I}}{f}}$随$B\alpha$的变化曲线。

可知，对于某一给定泊松比情况下（如以泊松比$\upsilon =0.3$为例）：裂尖应力场常数项$T$应力对I型裂纹断裂极限值${K}_{ {{ I}} {f}}$有较大的影响，当$B\alpha < 0$时（$T$应力为负值），${K}_{ {{ I}} {f}}$随$B\alpha$减小而增大直到达到最大值${K}_{ {{ I}} {f} {\rm{max}}}$，随后随$B\alpha$的继续增大而下降；$B\alpha$在某一区间内I型裂纹断裂极限值${K}_{ {I} {f}}$高于${K}_{ {I} {c}}$，可认为此区间内裂尖应力场常数项$T$应力增大了I型裂纹断裂韧性（${K}_{ {{ I}} {f}}$数值超过1.0${K}_{ {{ I}} {c}}$），即增加了材料裂纹起裂阻力；正值$T$应力将降低I型裂纹断裂极限值${K}_{ {{ I}} {f}}$；无量纲参数$\left|B\alpha \right|$相同时，正值$T$应力对应的I型裂纹断裂极限${K}_{ {{ I}} {f}}$低于负值$T$应力对应的I型裂纹断裂极限${K}_{ {{ I}} {f}}$，如当$B\alpha =1.0$时，I型裂纹断裂极限${K}_{ {{ I}} {f}}=0.75{K}_{ {I} {c}}$（考虑$T$应力时的I型裂纹断裂韧性降低了25.0%），当$B\alpha =-1.0$时，I型裂纹断裂极限${K}_{ {{ I}} {f}}=0.88{K}_{ {I} {c}}$，即考虑$T$应力时的I型裂纹断裂韧性降低了12.0%。

由图6可知，基于修正ASED准则理论的泊松比$\upsilon$对I型裂纹断裂极限${K}_{ {I} {f}}$的影响规律：裂纹尖端应力场常数项$T$应力为负值时（$B\alpha < 0$），材料常数泊松比$\upsilon$对I型裂纹断裂极限${K}_{ {{ I}} {f}}$的影响更为显著；常数项$T$应力为负值的某一给定值时，材料泊松比越高，材料抵抗裂纹起裂扩展能力越差，如$B\alpha =-1.0$，泊松比分别取0.2、0.3和0.4时的I型裂纹断裂极限分别为$0.97{K}_{ {I} {c}}$、$0.88{K}_{ {I} {c}}$、$0.77{K}_{ {I} {c}}$；裂尖应力场常数项$T$应力为正值的某一给定值时，材料泊松比越高，材料抵抗裂纹起裂扩展能力越强，如$B\alpha =1.0$，泊松比分别取0.2、0.3和0.4时的I型裂纹断裂极限分别为$0.73{K}_{ {I} {c}}$、$0.75{K}_{ {I} {c}}$、$0.77{K}_{ {I} {c}}$。

4 结果分析

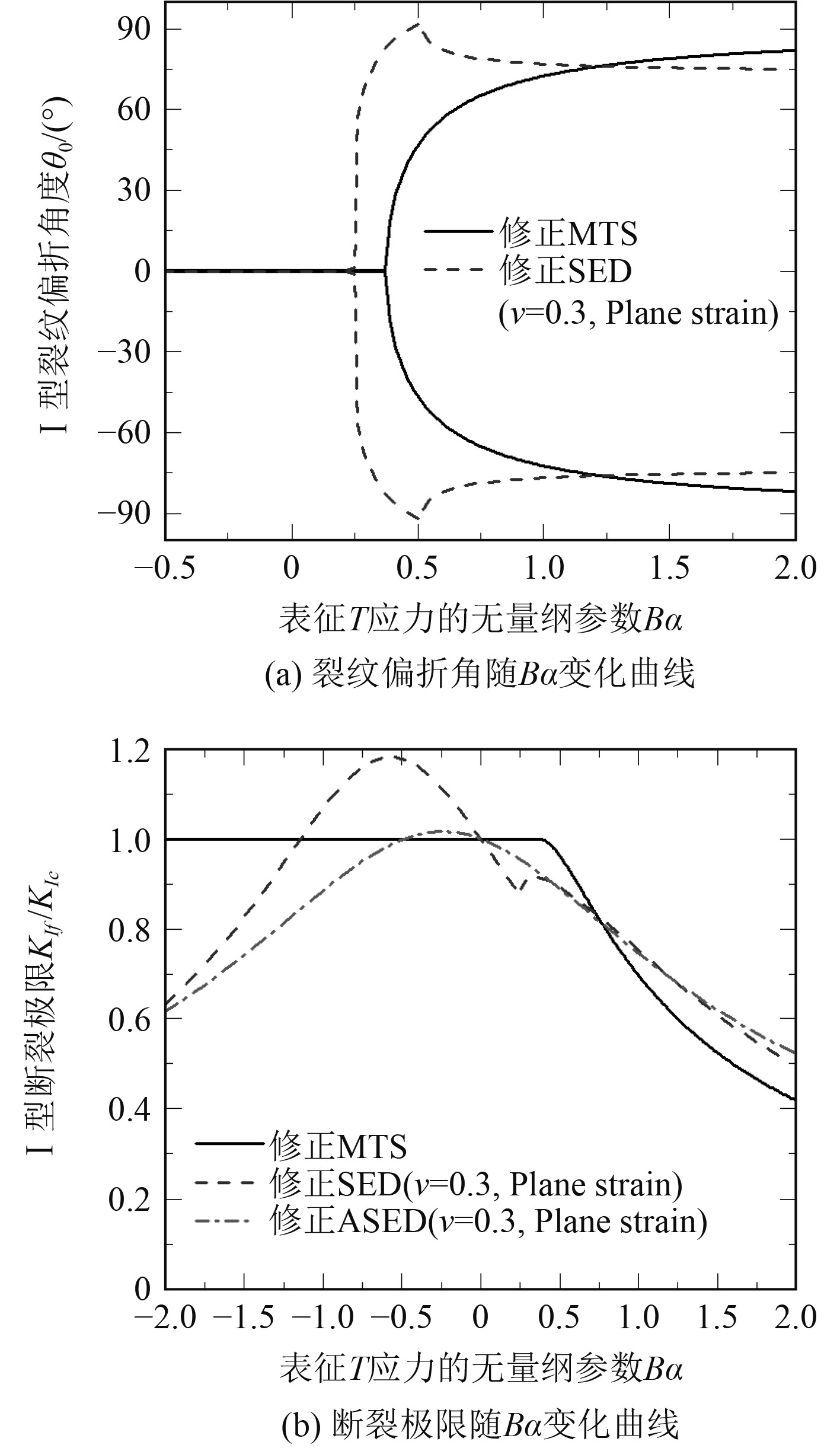
将基于修正MTS准则、修正SED准则以及修正ASED准则获得的I型裂纹断裂极限与断裂韧性的比值${K}_{{I}thrm{f}}/{K}_{{I}{c}}$随$B\alpha$的变化曲线绘制于图7中（平面应变状态、泊松比0.3）。

由图7（a）可知，1）根据修正MTS准则，当$B\alpha \leqslant 0.38$时，$T$应力对I型裂纹偏折角无影响；2）根据修正SED准则，当$B\alpha \leqslant 0.25$时，$T$应力对I型裂纹偏折角无影响。

由图7（b）可知，1）当裂尖应力场常数项$T$应力为负值时，修正ASED准则为最保守的准则（如当$B\alpha =-1$时，根据修正MTS准则${K}_{ {I} {f}}={K}_{ {{ I}} {c}}$；根据修正SED准则${K}_{ {I} {f}}=1.07\ {K}_{ {{ I}} {c}}$；根据修正ASED准则${K}_{ {I} {f}}= 0.88\ {K}_{ {{ I}} {c}}$）；2）当$T$应力为正值时，修正SED准则和修正ASED准则${K}_{ {I} {f}}/{K}_{ {I} {c}}$曲线基本一致，而修正MTS准则只有当$B\alpha > 0.38$时，裂尖应力场常数项$T$应力才对I裂纹断裂时刻${K}_{ {I} {f}}$产生影响；3）当$B\alpha > 0.77$时，修正MTS准则为最保守的准则（如当$B\alpha =1.0$时，根据修正MTS准则${K}_{ {I} {f}}=0.70\ {K}_{ {I} {c}}$；根据修正SED准则${K}_{ {I} {f}}=0.75\ {K}_{ {I} {c}}$；根据修正ASED准则${K}_{ {I} {f}}=0.75\ {K}_{ {I} {c}}$。

5 结　语

分别基于修正MTS准则、修正SED准则和修正ASED准则，对比分析了裂尖应力场常数项及泊松比对I型裂纹偏折、起裂扩展影响，得到以下结论：

1）根据修正MTS准则，当参数$B\alpha \leqslant 0.38$时，裂尖应力场常数项$T$应力不会引起I型裂纹偏折，也并不影响I型裂纹断裂极限，$B\alpha ＞0.38$时，I型裂纹断裂极限${K}_{\mathrm{I}\mathrm{f}}$随$B\alpha$的变大而减小。

2）根据修正SED准则，当$B\alpha \leqslant 0.25$（泊松比$\upsilon =0.3\mathrm{、}0.4$）、$B\alpha \leqslant 0.41$（泊松比$\upsilon =0.2$）时裂尖应力场常数项$T$应力不会引起I型裂纹偏折；当$B\alpha$值为超过I型裂纹偏折阀值时，裂纹偏折角${\theta }_{0}$随材料泊松比的增大而减小；材料泊松比越高，材料抵抗裂纹起裂扩展能力越差，断裂韧性增大区间逐渐变小；材料常数泊松比对I型裂纹断裂极限${K}_{\mathrm{I}\mathrm{f}}$的影响在常数项为负值时更为显著。

3）根据修正ASED准则，裂尖应力场常数项$T$应力为负值时，材料泊松比越高，材料抵抗裂纹起裂扩展能力越差，$T$应力为正值时，材料泊松比越高，材料抵抗裂纹起裂扩展能力越高；材料常数泊松比对I型裂纹断裂极限${K}_{{I}{f}}$的影响在常数项为负值时更为显著。

4）当裂纹尖端应力场常数项为负值时，修正ASED准则断裂判据为最保守；当裂纹尖端应力场常数项为正值时，修正SED准则和修正ASED准则断裂判据基本一致；当$B\alpha ＞0.77$时，修正MTS准则断裂判据为最保守，但与其他2个准则的断裂判据差别不大。

在进行材料与结构I型裂纹断裂力学评估时，应具体结合材料断裂特性实验结果最终确定相应的断裂准则。