2. 天津瀚海蓝帆海洋科技有限公司,天津 300457
2. Tianjin Hanhai Lanfan Marine Technology Co., Ltd., Tianjin 300457, China
泵喷推进器作为一种水下推进装置,具有高效率、低噪声、结构紧凑、可实现扭矩自平衡功能等优点,已逐渐成为各种水下航行器推进装置中的首选。但常规泵喷推进器的螺旋桨与导管之间存在一定的间隙,间隙中的涡流会导致推进器的流噪声和结构振动噪声增加,并且常规泵喷推进器的驱动方式为轴系驱动,轴向贯穿泵喷推进器的轮毂占据了较大的内部空间,同时电机通过轴系传动引起的结构振动也对低噪性能不利[1]。针对这两点不足,在船用推进装置中为人关注的轮缘推进器可以有效解决,然而常规轮缘推进器普遍由导管和螺旋桨组成,由于没有前置定子和后置定子的存在,其不具备扭矩自平衡的能力,并且难以作为单独主推安装于水下航行器尾段。因此在泵喷推进器的基础上将驱动方式改进为轮缘驱动对提高水下航行器的推进性能、噪音性能有着重要的意义。
轮缘驱动泵喷推进器由导管、前置定子、后置定子、螺旋桨和驱动电机组成。电机定子嵌入导管内部,电机转子为环状转子,与定子具有很小的间隙,水流会在螺旋桨工作时于间隙中流动,可有效解决电机散热问题[2]。螺旋桨叶片与环状转子集成在一起以获取电机的扭矩输入实现旋转。前置定子位于导管入口位置,一方面起到均匀螺旋桨来流的作用,另一方面在推进器与航行器安装过程中起到固定支撑的作用。后置定子位于导管出口位置,能够梳理螺旋桨的旋转尾流,回收能量提升效率,同时后置定子剖面型线采用非对称翼型,能够产生与螺旋桨扭矩方向相反的反滚扭矩,实现推进器的扭矩自平衡功能。
对于传统泵喷推进器,王涛等[3]发现叶顶间隙会显著影响螺旋桨叶片通道,后置定子流场及导管周围的流体速度。胡斌[4]的研究显示间隙流会明显提高叶梢附近流体的径向速度。Li[5]研究发现前置定子对螺旋桨来流起到预旋作用,能够降低桨叶表面的波动强度。武建国[6]的研究显示后置定子的安装角度对平衡泵喷推进器的扭矩,提升推进器的效率具有重要作用。对于轮缘推进器,克雷洛夫造船研究所的Yakovlev等[7]研究结果表明无桨毂式轮缘推进器的水动力性能要高于有桨毂式。杨蕾等[8]将导管桨改造为轮缘推进器,并结合数值模拟方法给出了此推进器的优化方法。Liu等[9]采用CFD方法对比了导管桨和轮缘推进器的水动力性能,结果表明轮缘推进器的整体效率明显低于导管桨。Shen等[10]提出了一种海水冷却的高功率密度磁力无槽永磁无刷电机,并与泵喷桨叶集成,设计出一款无轴泵喷推进器。
本文将采用天津瀚海蓝帆海洋科技有限公司自主研发的一款250 kW泵喷推进器作为基础模型,将其轴系驱动方式优化为轮缘驱动,暂不考虑导管和前后定子对推进器的影响,只改变螺旋桨的孔径比和桨叶厚度分布方式,从而得到多款轮缘泵喷推进器模型,对其进行流体力学仿真并对比分析,完成轮缘驱动泵喷推进器的螺旋桨性能优化研究。
1 数值计算及模型建立 1.1 数值模型采用Reynolds-Averaged Navier-Stokes(RANS)方程对推进器及周围流场进行求解。对于不可压缩牛顿流体,连续性方程和动量方程分别如下式:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $\begin{aligned}[b] \rho \left( {\frac{{\partial ui}}{{\partial t}} + uj\frac{{\partial ui}}{{\partial {x_j}}}} \right) = - &\frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right] + \\ &\frac{\partial }{{\partial xj}}\left( { - \overline {\rho u_i^{'}u_j^{'}} } \right)。\end{aligned} $ | (2) |
式中:t为流动时间;ρ为流体密度;μ为动力粘度;p为压力;ui和uj为平均速度分量;
雷诺应力的直接建模基于Boussinesq假设,该假设假定雷诺应力是平均速度梯度的线性函数。对于不可压缩的牛顿流体,雷诺应力的计算公式为:
| $ - \rho \overline {u_i^\prime u_j^\prime } = {\mu _t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho k\delta_{ij} 。$ | (3) |
式中:μt为湍流涡流粘度;δij为Kronecker符号。
采用由Menter发展而来的SST k-ω湍流模型来建立方程,因为SST k-ω湍流模型集合了k-ω模型和k-ε模型的优点,在解决逆压力梯度流动问题中展现出很大的优势,并且对于远壁面问题和近壁面问题都具有很好的处理能力。以上方程式结合使用STAR CCM+商用软件进行求解。
1.2 网格无关性验证及模型验证在开展网格划分和仿真计算工作之前,确定网格数量对计算结果的影响情况以及确保仿真计算方法足够可靠,因此本文选用来自于荷兰的标准模型Ka4-70-19A导管桨进行网格无关性验证及模型仿真验证。该导管桨的结构主参数如表1所示,三维模型如图1所示。
|
|
表 1 Ka4-70-19A导管桨结构主参数 Tab.1 Ka4-70-19A duct propeller structure main parameters |

|
图 1 Ka4-70-19A导管桨三维示意图 Fig. 1 3D schematic diagram of Ka4-70-19A duct propeller |
本文采用长度为10D,直径为5D的圆柱形计算域,其中D为螺旋桨的直径,速度进口处距推进器中心距离为3D,压力出口处距推进器中心距离为7D,计算域分为两部分,一部分为包裹螺旋桨的旋转区域,另一部分为旋转区域以外的静止区域,计算域整体分布如图2所示。网格采用STAR-CCM+中的切割体网格生成器进行划分,并在螺旋桨表面附加边界层,边界层第一层高度为0.05 mm,以保证壁面Y+值在5以下,满足SST k-ω湍流模型的计算。

|
图 2 计算域整体分布 Fig. 2 Calculate the overall distribution of domains |
本文用到的水动力相关参数,定义如下:
| $ J = \frac{{{V_a}}}{{nD}},$ | (4) |
| $ 10{K_Q} = \frac{{10Q}}{{\rho {n^2}{D^5}}} ,$ | (5) |
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}} ,$ | (6) |
| $ \eta = \frac{J}{{2{\text π} }}\frac{{{K_T}}}{{{K_Q}}} 。$ | (7) |
式中:
由于螺旋桨具有一定的转速,其周围流场相对来说更为复杂,故通过改变桨的面网格参数、旋转区域体网格尺寸以及推进器周围加密区域的体网格尺寸来获得粗、中、细3套不同密度的网格,并在J=0.5的工况下对3套网格进行仿真计算,计算结果如表2所示。
|
|
表 2 3种网格数量下的推力系数、扭矩系数计算结果 Tab.2 Calculation results of thrust coefficient and torque coefficient under three grid quantities |
通过对比每2套网格之间推力系数和10倍扭矩系数的变化率发现,3套网格的计算结果变化幅度都不大,而中密度网格与细密度网格相比,推力系数变化率为1.03%,与粗密度网格计算结果相比变化更为微弱,变化率在3%以下,同时考虑节约计算成本,故最终选择中密度网格继续进行另外2个工况的计算,并与已经公开的Ka4-70-19A导管桨的实验数据进行对比。仿真数据与实验数据[11]对比结果如表3所示,对比图如图3所示。
|
|
表 3 数据对比结果 Tab.3 Data comparison results |

|
图 3 仿真数据与实验数据对比图 Fig. 3 Comparison of simulation data and experimental data |
通过仿真数据与实验数据的对比结果可以发现,仿真计算结果的误差均在3%以内,说明本文采用的仿真计算方法和得到的计算结果具有较高的可靠性和准确性。
1.3 轮缘驱动泵喷推进器模型建立基础模型三维示意图如图4所示,螺旋桨直径Dr=320 mm,桨叶数为7叶,导管为33号减速型导管,前置定子为5叶,剖面型线为NACA0012对称翼型,后置定子为5叶,剖面型线为NACA6412非对称翼型。

|
图 4 基础模型三维示意图 Fig. 4 3D schematic diagram of the base model |
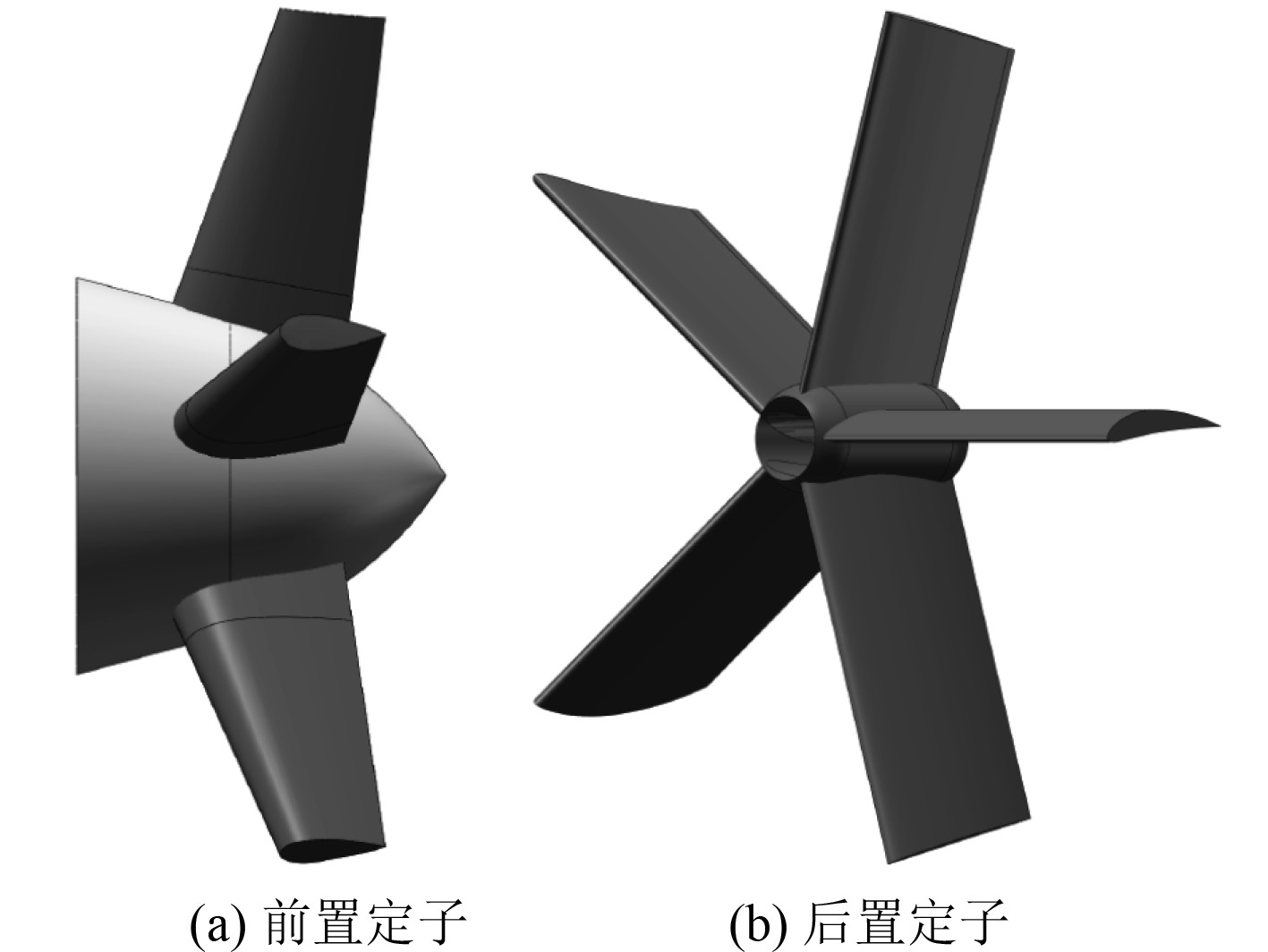
将驱动方式优化为轮缘驱动后,去除了基础模型中的轮毂,为推进器内部节省出了很大的空间。但为了得到一款适和作为水下航行器主推的轮缘驱动泵喷推进器,应保留前置定子叶根处的轮毂,用来衔接水下航行器尾部段,固定安装推进器,如图5(a)所示。后置定子处加设中空圆柱式轮毂,用以加强后置定子的安装强度,避免后置定子出现悬臂梁结构,中空结构可尽量避免后轮毂阻挡前方来流而产生阻力,如图5(b)所示。
|
图 5 前、后定子三维示意图 Fig. 5 3D schematic diagram of front and rear stator |
如图6所示,轮缘驱动泵喷推进器的螺旋桨与电机转子集成在一起,消除了传统螺旋桨叶稍间隙和桨毂的存在,原桨毂位置处变成了通孔,通孔直径用Dk表示,并定义Dk/Dr为螺旋桨的孔径比,其中Dr为螺旋桨的直径。

|
图 6 轮缘驱动螺旋桨三维示意图 Fig. 6 3D schematic diagram of a rim driven propeller |
为降低前置定子轮毂前端面在推进器水动力计算时产生的阻力,对其进行圆滑过渡处理,将前置定子、后置定子、导管和轮缘驱动螺旋桨装配在一起,得到整体的轮缘驱动泵喷推进器模型,如图7所示。

|
图 7 轮缘驱动泵喷推进器整体示意图 Fig. 7 Overall schematic diagram of the rim-driven pump jet propulsor |
为研究螺旋桨中心通孔的大小对推进器敞水性能的影响,分别建立孔径比为0.1、0.2、0.3的3个轮缘驱动螺旋桨的模型,并分别将3个模型命名为0.1Dr,0.2Dr,0.3Dr,3个孔径比的轮缘驱动螺旋桨模型如图8所示。

|
图 8 3种孔径比螺旋桨示意图 Fig. 8 Schematic diagram of a propeller with three aperture ratios |
对装配有3种孔径比螺旋桨的轮缘驱动泵喷推进器分别进行相同工况下的水动力仿真计算,其计算结果对比如图9所示。3款推进器在各工况下的推力系数相差甚微,扭矩系数具有一定差距,导致其敞水效率也出现了不同。10倍扭矩系数对比结果显示,随着孔径比的减小,螺旋桨产生的扭矩普遍呈降低趋势,在10种工况下,0.1孔径比螺旋桨产生的扭矩比0.3孔径比螺旋桨产生的扭矩最大降低了3.78%。敞水效率对比结果显示,3款推进器的敞水效率随着进速系数的增加,均呈现出先升高后降低的趋势,其中,0.1孔径比推进器的敞水效率高于另外2款推进器,比0.3孔径比推进器的敞水效率最大提升了3.25%。基于此对比结果,后续研究将采用0.1孔径比螺旋桨继续进行。

|
图 9 3种孔径比推进器敞水性能曲线对比图 Fig. 9 Comparison chart of open water performance curves of three aperture ratio thrusters |
传统轴系驱动泵喷推进器的螺旋桨叶根处与轴集成在一起,故桨叶叶根处厚度最大,叶稍处厚度最小,而将驱动方式优化为轮缘驱动后,螺旋桨叶稍处与电机转子集成在一起,考虑到原螺旋桨叶稍处的厚度难以满足工作时所需的结构强度,因此需要对螺旋桨不同半径处的厚度重新进行分配。最直接的厚度分布方式是将原桨叶不同半径处的最大厚度直接反置,即由原来的叶根处最厚和叶稍处最薄变为叶根处最薄和叶稍处最厚,考虑到叶稍处弦向距离要远大于叶根处,故可以对直接反置后的厚度进行适当减薄处理。
本文给出了3种桨叶厚度分布方案,各方案不同半径处桨叶截面的最大厚度值如表4所示,r为桨叶各截面处的半径,mm,R为螺旋桨半径,mm。方案A为在螺旋桨厚度直接反置的基础上,对各半径处的厚度统一减薄50%;方案B为在厚度直接反置的基础上,对各半径处的厚度统一减薄60%;方案C为在厚度直接反置的基础上,对各半径处的厚度统一减薄70%。各方案不同半径处桨叶截面厚度示意图如图10所示。
|
|
表 4 各方案不同半径处桨叶截面的最大厚度值 Tab.4 The maximum thickness value of the blade section at different radii for each scheme |

|
图 10 各方案不同半径处桨叶截面厚度分布示意图 Fig. 10 Schematic diagram of the thickness distribution of blade section at different radii of each scheme |
对3种方案下的轮缘驱动泵喷推进器和采用原桨的轴系驱动泵喷推进器分别进行相同工况下的水动力仿真计算,首先对比原桨和方案A桨的计算数据,敞水性能曲线对比图如图11所示。对比结果显示,随着进速系数的增加,方案A推进器产生的推力要高于采用原桨的泵喷推进器所产生的推力,这说明将驱动方式优化为轮缘驱动后,推进器的推力性能得到了提升,然而推力提升的同时,螺旋桨产生的扭矩也大幅度提升,且提升幅度要远大于推力的提升幅度,根据式(7)中的定义,导致的结果为方案A的敞水效率较原桨大幅度降低,10种工况下最大降低了23.3%。

|
图 11 原桨与方案A桨敞水性能对比图 Fig. 11 Comparison chart of open water performance of original propeller and scheme A paddle |
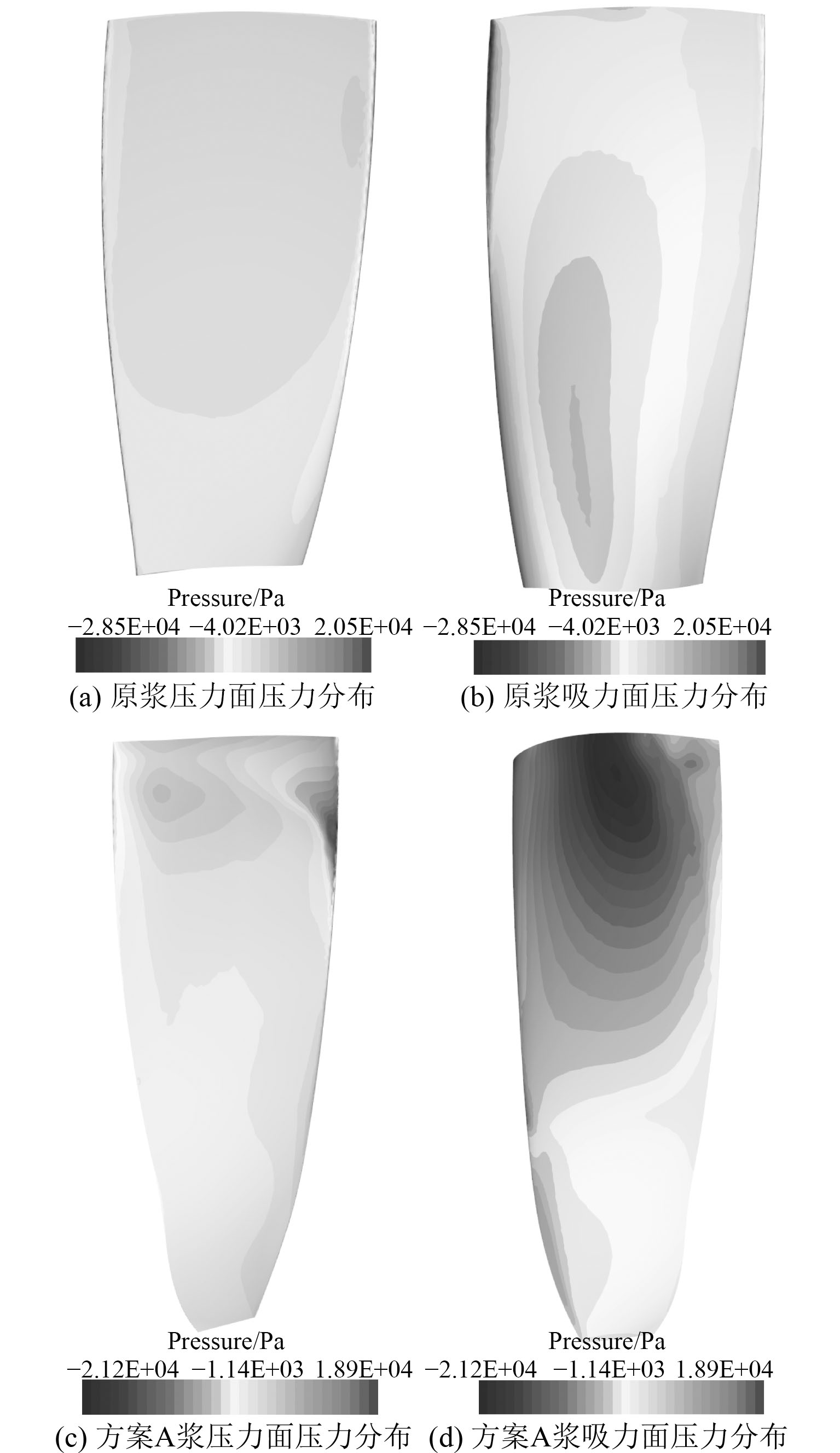
为探究原桨与方案A桨性能对比过程中导致扭矩大幅度提升的机理,给出了2种方案螺旋桨压力面与吸力面的压力分布对比图,如图12所示。对比结果显示,原桨的压力面与吸力面上的压力分布相对更加均匀,主要做功区域集中在螺旋桨的中上部,而方案A桨的压力分布则更加混乱,整体的主要做功区域也集中在桨的中上部,但是其压力面上的高压区域和吸力面上的低压区域更加集中,均集中在桨的高半径处,并且吸力面上的负压值明显低于原桨吸力面的负压值,且负压区域面积远大于原桨,这就导致了压力面与吸力面间的压差值相差悬殊,从而2个螺旋桨产生的扭矩值也大为不同,这是由于其厚度过大且分布不均匀导致的。
|
图 12 原桨与方案A桨压力面与吸力面压力分布对比图 Fig. 12 Comparison of pressure distribution between original propeller and scheme A propeller pressure surface and suction surface |
为了更加直观地了解方案A桨厚度分布对螺旋桨压力差的影响,本文对比了原桨与方案A桨不同半径处截面上的压力分布,如图13所示,图中纵坐标Cp为压力系数,横坐标做无量纲化处理,其中z为压力监测点到螺旋桨截面中心沿弦线方向上的距离,c为螺旋桨截面的弦长,以z与c的比值表示压力监测点的位置,比值为0代表截面中心处,比值为负代表靠近螺旋桨导边处。对比结果显示,原桨整体的截面压力分布更加均匀,在低半径处具有较大的压力差,而方案A桨在高半径处的截面压力分布并不均匀,并且在高半径处具有较大的压力差,且压力差要高于原桨的压力差,同时考虑到高半径处叶片弦向距离要大于低半径处,因此方案A桨的厚度分布方式导致其产生了更大的压力差,从而产生了更大的扭矩值。

|
图 13 原桨与方案A桨截面压力分布对比图 Fig. 13 Comparison of cross-sectional pressure distribution between the original propeller and the scheme A propeller |
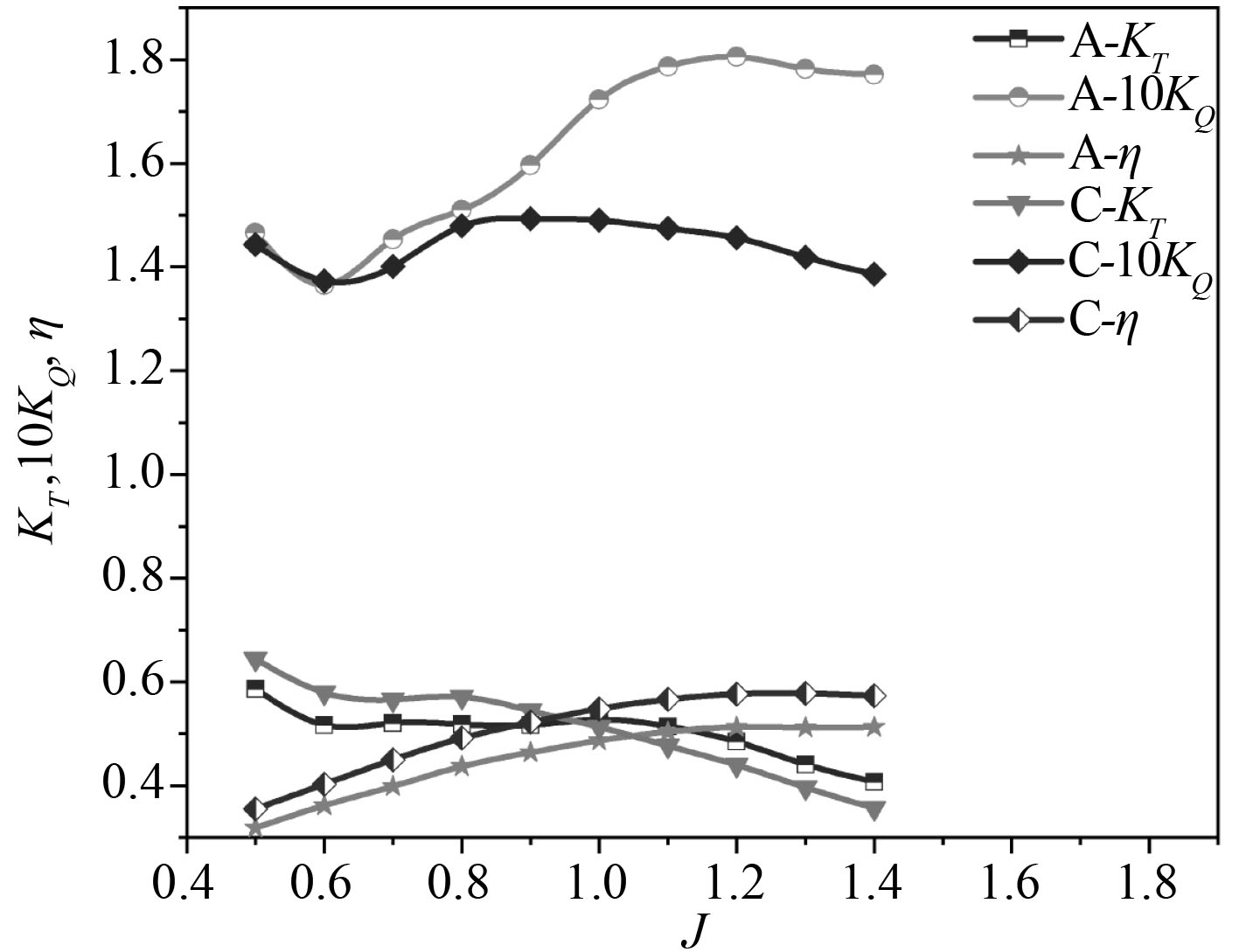
由于方案A的厚度分布方式导致螺旋桨扭矩大幅度提升,从而导致了敞水效率大幅度降低,为进一步优化螺旋桨的敞水性能,分别对比了厚度进一步减薄的方案B桨和方案C桨与方案A桨的敞水性能曲线,如图14和图15所示。对比结果显示,轮缘驱动螺旋桨的厚度越薄,其产生的扭矩越低,推力变化幅度不大,敞水效率越高,其中方案B桨的扭矩比方案A最大降低了10.25%,敞水效率最大提升了7.32%,方案C桨的扭矩比方案A最大降低了21.74%,敞水效率最大提升了12.9%。

|
图 14 方案B桨与方案A桨敞水性能对比图 Fig. 14 Comparison chart of open water performance of scheme B propeller and scheme A propeller |
|
图 15 方案C桨与方案A桨敞水性能对比图 Fig. 15 Comparison chart of open water performance of scheme C propeller and scheme A propeller |
1)轮缘驱动螺旋桨的孔径比越小,推进器的敞水效率越高。其中0.1孔径比推进器比0.3孔径比推进器的敞水效率最大提升了3.25%。
2)方案A桨的厚度分布方式导致叶片压差在高半径处产生突变,致使扭矩较原桨大幅提升,敞水效率最大降低了23.3%。
3)轮缘驱动螺旋桨的厚度大小高度影响其敞水性能,厚度越小,桨扭矩越低,敞水效率越高。其中方案B桨的扭矩比方案A最大降低了10.25%,敞水效率最大提升了7.32%,方案C桨的扭矩比方案A最大降低了21.74%,敞水效率最大提升了12.9%。
| [1] |
曹奇宏, 张冠军. 泵喷推进器的流激声振特性研究[J]. 武汉理工大学学报(交通科学与工程版), 2023, 47(3): 460−464.
|
| [2] |
王雨楠. 桨叶参数对轮缘推进器水动力性能影响分析[D]. 大连: 大连理工大学, 2022.
|
| [3] |
王涛, 周连第. 泵喷推进器内间隙流与主流相互作用的数值模和机理研究[C]//2004 年船舶水动力学学术会议论文集, 武汉, 2004: 215−226.
|
| [4] |
胡斌. 集成电机推进器总体设计技术研究[D]. 西安: 西北工业大学, 2013.
|
| [5] |
LI Han, HUANG Qiaogao, PAN Guang, et al. The transient prediction of a pre−swirl stator pump−jet propulsor and a comparative study of hybrid RANS/LES simulations on the wake vortices[J]. Ocean Engineering, 2020, 203: 107224
|
| [6] |
武建国, 武天龙. 泵喷推进器扭矩自平衡优化分析[J]. 舰船科学技术, 2022, 44(12): 10−15. WU Jianguo, WU Tianlong, Torque self−balancing optimization analysis of pump − jet propeller [J]. Ship Science and Technology, 2022, 44(12): 10−15. |
| [7] |
YAKOVLEV A Y, SOKOLOV M A, MARINICH N V. Numerical design and experimental verification of a rim−driven thruster[C]//Proceedings of second international symposium on marine propulsors, 2011: 396−403.
|
| [8] |
杨蕾, 周军伟, 闫文辉, 等. 轮缘推进器反厚度规律桨叶的翼型对比分析[J]. 中国造船, 2022, 63(1): 113-125. DOI:10.3969/j.issn.1000-4882.2022.01.010 |
| [9] |
LIU B, VANIERSCHOT M. Numerical study of the hydrodynamic characteristics comparison between a ducted propeller and a rim−driven thruster[J]. Applied Sciences, 2021, 11(11): 4919. DOI:10.3390/app11114919 |
| [10] |
SHEN Y, HU P, JIN S, et al. Design of novel shaftless pump−jet propulsor for multi−purpose long−range and high−speed autonomous underwater vehicle[J]. IEEE Transactions on Magnetics, 2016, 52(7): 1-4. |
| [11] |
OOSTERVELD M W C. Wake adapted ducted propellers[R]. Tech. Rep. Delft University of Technology, Delft, 1970.
|
 2024, Vol. 46
2024, Vol. 46
